2021年中考数学复习难题训练：黄金分割专题训练

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学复习难题训练：黄金分割专题训练一、选择题1.若P是线段AB的黄金分割点(PA>PB)，设AB=1，则PA的长约为()A. 0.191B. 0.382C. 0.5D.0.6182.上海东方明珠电视塔高468m.其上球体位于塔身的黄金分割点，那么它到塔底部的距离大约是()A. 289.2mB. 178.8mC. 110.4mD. 468m3.如果把一条线段分为两部分，使其中较长的一段与整条线段的长度比是黄金比，那么较短一段与较长一段的长度比也是黄金比．由此，假设整条线段长为1，较长的一段为x，可以列出的方程为()A. 1−xx =x1B. 1−x1=1xC. x1−x=1−x1D. 1−xx=x√54.已知点C是线段AB的黄金分割点(AC>BC)，AB=4，则线段AC的长是()A. 2√5−2B. 6−2√5C. √5−1D. 3−√55.一条线段的黄金分割点有()个A. 1B. 2C. 3D. 无数个6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法．如图所示，以线段AB为边作正方形ABCD，取AD的中点E，连结BE，延长DA至点F，使得EF=BE，以AF为边作正方形AFGH，则H即是线段AB的黄金分割点．若记正方形AFGH的面积为S1，矩形BCIH的面积为S2，则S1与S2的大小关系是()A. S1>S2B. S1<S2C. S1=S2D. 不能确定7.已知点C把线段AB分成两条线段AC、BC，且AC>BC，下列说法错误的是()A. 如果ACAB =BCAC，那么线段AB被点C黄金分割B. 如果AC2=AB⋅BC，那么线段AB被点C黄金分割C. 如果线段AB被点C黄金分割，那么BC与AB的比叫做黄金比D. 0.618是黄金比的近似值8.如图，在△ABC中，AB=AC，∠BAC=108°，AD、AE将∠BAC三等分交边BC于点D，点E，则下列结论中错误的是()A. 点D是线段BC的黄金分割点B. 点E是线段BC的黄金分割点C. 点E是线段CD的黄金分割点D. EDBE =√5−12二、填空题9.据有关测定，当气温处于人体正常体温(37℃)的黄金比值时，人体感到最舒适，则这个气温约为_________℃(结果保留整数)．10.如果线段AB=10cm，P是线段AB的黄金分割点，那么线段BP=________cm．11.如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割(BC<AC).已知AB=4cm，则BC的长约为________cm.(结果精确到0.1)12.在自然界中，蝴蝶的身长与双翅展开后的长度的比接近于0.618.若双翅展开后的长度约为5.62cm，则其身长约为_______cm(保留两位小数)13.美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．某女模特身高165cm，下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果，她应穿的高跟鞋的高度大约为____．14.在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm，则宽约为________(精确到1cm)．15.已知点C为线段AB的黄金分割点，且AC>BC，若P点为线段AB上的任意一点，则P点出现在线段AC上的概率为________．三、解答题16.拥有一个完美的身材是很多人的梦想，世界著名的雕像“维纳斯”就被认为是最美的身材。

黄金分割专项练习30题（有答案）1．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC 中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．2．如图，用长为40cm的细铁丝围成一个矩形ABCD（AB＞AD）．（1）若这个矩形的面积等于99cm2，求AB的长度；（2）这个矩形的面积可能等于101cm2吗？若能，求出AB的长度，若不能，说明理由；（3）若这个矩形为黄金矩形（AD与AB之比等于黄金比），求该矩形的面积．（结果保留根号）3．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=2，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．4．作一个等腰三角形，使得腰与底之比为黄金比．（1）尺规作图并保留作图痕迹；（2）写出你的作法；（3）证明：腰与底之比为黄金比．5．（1）已知线段AB的长为2，P是AB的黄金分割点，求AP的长；（2）求作线段AB的黄金分割点P，要求尺规作图，且使AP＞PB．6．如图，线段AB的长度为1．（1）线段AB上的点C满足系式AC2=BC?AB，求线段AC的长度；（选做）（2）线段AC上的点D满足关系式AD2=CD?AC，求线段AD的长度；（选做）（3）线段AD上的点E满足关系式AE2=DE?AD，求线段AE的长度；上面各题的结果反映了什么规律？（提示：在每一小题中设x和l）7．如图，在△ABC中，AB=AC，∠A=36°，∠1=∠2，请问点D是不是线段AC的黄金分割点．请说明理由．8．在△ABC中，AB=AC=2，BC=﹣1，∠A=36°，BD平分∠ABC，交于AC于D．试说明点D是线段AC的黄金分割点．9．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．11．如图，已知△ABC中，D是AC边上一点，∠A=36°，∠C=72°，∠ADB=108°．求证：（1）AD=BD=BC；（2）点D是线段AC的黄金分割点．12．已知AB=2，点C是AB的黄金分割线，点D在AB上，且AD2=BD?AB，求的值．13．如果一个矩形ABCD（AB＜BC）中，≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．14．五角星是我们常见的图形，如图所示，其中，点C，D分别是线段AB的黄金分割点，AB=20cm，求EC+CD的长．15．人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？16．如图所示，以长为2的定线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上．（1）求AM，DM的长；（2）点M是AD的黄金分割点吗？为什么？17．如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S1，以PB为宽和以AB为长的矩形面积为S2，试比较S1与S2的大小．18．如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，求CF的长．19．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．20．（如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果，那么称点P为线段AB的黄金分割点，设=k，则k就是黄金比，并且k≈0.618．（1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：；（2）如图1，设AB=1，请你说明为什么k约为0.618；（3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；（4）图3中的△ABC的黄金分割线有几条？21．在人体躯干（脚底到肚脐的长度）与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人以美感．张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该选择多高的高跟鞋穿上看起来更美？（精确到十分位）22．已知线段AB，按照如下的方法作图：以AB为边作正方形ABCD，取AD的中点E，连接EB，延长DA到F，使EF=EB，以线段AF为边，作正方形AFGH，那么点H是线段AB的黄金分割点吗？请说明理由．23．如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．24．如图，用纸折出黄金分割点：裁一张边长为2的正方形纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落在线段EA上，折出点B的新位置F，因而EF=EB．类似的，在AB上折出点M使AM=AF．则M是AB的黄金分割点吗？若是请你证明，若不是请说明理由．25．如图，在△ABC中，点D在边AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长；③在直线AB或BC上是否存在点P（点A、B除外），使△PDC是黄金三角形？若存在，在备用图中画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．26．宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：第一步：作一个正方形ABCD；第二步：分别取AD，BC的中点M，N，连接MN；第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；第四步：过E作EF⊥AD，交AD的延长线于F．请你根据以上作法，证明矩形DCEF为黄金矩形．27．在△ABC中，AB=AC，∠A=36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM 与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．28．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）29．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB=AC，且∠A=36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1=A1C1，∠A1=108°，且A1B1=AB，请直接写出的值．30．如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．（4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．黄金分割专项练习30题参考答案: 1．（1）证明：∵AB=AC=1，∴∠ABC=∠C=（180°﹣∠A）=（180°﹣36°）=72°，∵BD平分∠ABC交AC于点D，∴∠ABD=∠CBD=∠ABC=36°，∴∠BDC=180°﹣36°﹣72°=72°，∴DA=DB，BD=BC，∴AD=BD=BC，易得△BDC∽△ABC，∴BC：AC=CD：BC，即BC2=CD?AC，∴AD2=CD?AC，∴点D是线段AC的黄金分割点；（2）设AD=x，则CD=AC﹣AD=1﹣x，∵AD2=CD?AC，∴x2=1﹣x，解得x1=，x2=，即AD的长为2．解：（1）设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=99，整理得x2﹣20x+99=0，解得x1=9，x2=11，当x=9时，20﹣x=11；当x=11时，20﹣11=9，而AB＞AD，所以x=11，即AB的长为11cm；（2）不能．理由如下：设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=101，整理得x2﹣20x+101=0，因为△=202﹣4×101=﹣4＜0，所以方程没有实数解，所以这个矩形的面积可能等于101cm2；（3）设AB=xcm，则AD=（20﹣x）cm，根据题意得20﹣x=x，解得x=10（﹣1），则20﹣x=10（3﹣），所以矩形的面积=10（﹣1）?10（3﹣）=（400﹣800）cm2．3．解：（1）∵∠A=36°，AB=AC，∴∠ABC=∠ACB=72°，∵BD平分∠ABC，∴∠CBD=∠ABD=36°，∠BDC=72°，∴AD=BD，BC=BD，∴△ABC∽△BDC，∴=，即=， ∴AD 2=AC?CD ．∴点D 是线段AC 的黄金分割点．（2）∵点D 是线段AC 的黄金分割点，∴AD=AC ，∵AC=2，∴AD=﹣14．解：（1）腰与底之比为黄金比为黄金比如图，（2）作法：①画线段AB 作为三角形底边；②取AB 的一半作AB 的垂线AC ，连接BC ，在BC 上取CD=CA ．③分别以A 点和B 点为圆心、以BD 为半径划弧，交点为E ；④分别连接EA 、EB ，则△ABE 即是所求的三角形．（3）证明：设AB=2，则AC=1，BC=，AE=BE=BD=BC ﹣CD=﹣1，=． 5．解：（1）由于P 为线段AB=2的黄金分割点，则AP=2×=﹣1，或AP=2﹣（﹣1）=3﹣； （2）如图，点P 是线段AB 的一个黄金分割点．6．解：（1）设AC=x ，则BC=AB ﹣AC=1﹣x ，∵AC 2=BC?AB ，∴x 2=1×（1﹣x ），整理得x 2+x ﹣1=0，解得x 1=，x 2=（舍去），所以线段AC 的长度为； （2）设线段AD 的长度为x ，AC=l ，∵AD 2=CD?AC ，∴x 2=l×（l ﹣x ），∴x 1=，x 2=（舍去），∴线段AD 的长度AC ；（3）同理得到线段AE 的长度AD ； 上面各题的结果反映：若线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），则C 点为AB 的黄金分割点7．解：D 是AC 的黄金分割点．理由如下：∵在△ABC 中，AB=AC ，∠A=36°，∴∠ABC=∠ACB==72°．∵∠1=∠2，∴∠1=∠2=∠ABC=36°．∴在△BDC中，∠BDC=180°﹣∠2﹣∠C=72°，∴∠C=∠BDC，∴BC=BD．∵∠A=∠1，∴AD=BC．∵△ABC和△BDC中，∠2=∠A，∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，AD=BC=BD，∴，∴AD2=AC?CD，即D是AC的黄金分割点8．证明：∵AB=AC，∠A=36°，∴∠ABC=（180°﹣36°）=72°，∵BD平分∠ABC，交于AC于D，∴∠DBC=×∠ABC=×72°=36°，∴∠A=∠DBC，又∵∠C=∠C，∴△BCD∽△ABC，∴∵AB=AC，∴=，∵AB=AC=2，BC=﹣1，∴（﹣1）2=2×（2﹣AD），解得AD=，AD：AC=（）：2．∴点D是线段AC的黄金分割点．9．证明：在AB上截取AE=BC，DF=BC，连接EF．∵AE=BC，DF=BC，∴AE=DF=BC=AD，又∵∠ADF=90°，∴四边形AEFD是正方形．BE=，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．解：设正方形ABCD的边长为2，在Rt△AEB中，依题意，得AE=1，AB=2，由勾股定理知EB===，∴AH=AF=EF﹣AE=EB﹣AE=﹣1，HB=AB﹣AH=3﹣；∴AH2=（）2=6﹣2，AB?HB=2×（3﹣）=6﹣2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．11．证明：（1）∵∠A=36°，∠C=72°，∴∠ABC=180°﹣36°﹣72°=72°，∵∠ADB=108°，∴∠ABD=180°﹣36°﹣108°=36°，∴△ADB是等腰三角形，∵∠BDC=180°﹣∠ADC=180°﹣108°=72°，∴△BDC是等腰三角形，∴AD=BD=BC．（2）∵∠DBC=∠A=36°，∠C=∠C，∴△ABC∽△BDC，∴BC：AC=CD：BC，∴BC2=AC?DC，∵BC=AD，∴AD2=AC?DC，∴点D是线段AC的黄金分割点．12．解：∵D在AB上，且AD2=BD?AB，∴点D是AB的黄金分割点而点C是AB的黄金分割点，∴AC=AB=﹣1，AD=AB﹣AB=AB=3﹣或AD=﹣1，AC=3﹣，∴CD=﹣1﹣（3﹣）=2﹣4，∴==或==．13．解：矩形ABFE是黄金矩形．∵AD=BC，DE=AB，∴==﹣1==．∴矩形ABFE是黄金矩形．14．解：∵D为AB的黄金分割点（AD＞BD），∴AD=AB=10﹣10，∵EC+CD=AC+CD=AD，∴EC+CD=（10﹣10）cm．15．解：设他的肚脐到脚底的长度为xm时才是黄金身段，根据题意得x：1.70=0.618，即x=1.70×0.618≈1.1（m）．答：他的肚脐到脚底的长度为1.1m时才是黄金身段．16．解：（1）在Rt△APD中，AP=1，AD=2，由勾股定理知PD===，∴AM=AF=PF﹣AP=PD﹣AP=﹣1，DM=AD﹣AM=3﹣．故AM的长为﹣1，DM的长为3﹣；（2）点M是AD的黄金分割点．由于=，∴点M是AD的黄金分割点．17．解：∵点P是线段AB的黄金分割点，且AP＞BP，∴AP2=BP×AB，又∵S1=AP2，S2=PB×AB，∴S1=S2．18．解：∵四边形ABCD为平行四边形，∴∠CBF=∠AEB，∠BCF=∠BAE，∴△BCF∽△EAB，∴，即，把AD=，AB=+1代入得，=，解得：CF=2．故答案为：2．19．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB=DC=AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．20．解：（1）满足≈0.618的矩形是黄金矩形；（2）由=k得，BP=1×k=k，从而AP=1﹣k，由得，BP2=AP×AB，即k2=（1﹣k）×1，解得k=，∵k＞0，∴k=≈0.618；（3）因为点P是线段AB的黄金分割点，所以，设△ABC的AB上的高为h，则，∴∴直线CP是△ABC的黄金分割线．（4）由（2）知，在BC边上也存在这样的黄金分割点Q，则AQ也是黄金分割线，设AQ与CP交于点W，则过点W的直线均是△ABC的黄金分割线，故黄金分割线有无数条．21．解：根据已知条件得下半身长是160×0.6=96cm，设选择的高跟鞋的高度是xcm，则根据黄金分割的定义得：=0.618，解得：x≈7.5cm．故她应该选择7.5cm左右的高跟鞋穿上看起来更美．22．解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB==a，∴AH=AF=EF﹣AE=EB﹣AE=（﹣1）a，HB=AB﹣AH=（3﹣）a；∴AH2=（6﹣2）a2，AB?HB=2a×（3﹣）a=（6﹣2）a2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．23．证明：设正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，又∵B′E=BE=1，∴AB′=AE﹣B′E=﹣1，∴AB″∴点B″是线段AB的黄金分割点．24．证明：∵正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，∵EF=BE=1，∴AF=AE﹣EF=﹣1，∴AM=AF=﹣1，∴AM：AB=（﹣1）：2，∴点M是线段AB的黄金分割点．25．解：（1）∵BD=DC=AC．则∠B=∠DCB，∠CDA=∠A．设∠B=x，则∠DCB=x，∠CDA=∠A=2x．又∠BOC=108°，∴∠B+∠A=108°．∴x+2x=108，x=36°．∴∠B=36°；（2）①有三个：△BDC，△ADC，△BAC．∵DB=DC，∠B=36°，∴△DBC是黄金三角形，（或∵CD=CA，∠ACD=180°﹣∠CDA﹣∠A=36°．∴△CDA是黄金三角形．或∵∠ACE=108°，∴∠ACB=72°．又∠A=2x=72°，∴∠A=∠ACB．∴BA=BC．∴△BAC是黄金三角形．②△BAC是黄金三角形，∴，∵BC=2，∴AC=﹣1．∵BA=BC=2，BD=AC=﹣1，∴AD=BA﹣BD=2﹣（﹣1）=3﹣，③存在，有三个符合条件的点P1、P2、P3．ⅰ）以CD为底边的黄金三角形：作CD的垂直平分线分别交直线AB、BC得到点P1、P2．ⅱ）以CD为腰的黄金三角形：以点C为圆心，CD为半径作弧与BC的交点为点P3．26．证明：在正方形ABCD中，取AB=2a，∵N为BC的中点，∴NC=BC=a．在Rt△DNC中，．又∵NE=ND，∴CE=NE﹣NC=（﹣1）a．∴．故矩形DCEF为黄金矩形．27．解：（1）（2）CM=AB（4分）28．证明：如图，连接GF，设正方形ABCD的边长为1，则DF=．在Rt△BCF中，BF==，则A′F=BF﹣BA′=﹣1．设AG=A′G=x，则GD=1﹣x，在Rt△A′GF和Rt△DGF中，有A'F2+A'G2=DF2+DG2，即，解得x=，即点G是AD的黄金分割点（AG＞GD）．29．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD=BD，∴∠ABD=∠A．∵∠A=36°，AB=AC，∴∠ABC=∠C=72°，∴∠ABD=∠DBC=36°．又∵∠BDC=∠A+∠ABD=72°，∴∠BDC=∠C，∴BD=BC，∴△BCD是黄金三角形．（3）设BC=x，AC=y，由（2）知，AD=BD=BC=x．∵∠DBC=∠A，∠C=∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2=0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE=AC，连接AE．∵∠A=36°，AB=AC，∴∠ACB=∠B=72°，∴∠ACE=180°﹣72°=108°，∴∠ACE=∠B1A1C1．∵A1B1=AB，∴AC=CE=A1B1=A1C1，∴△ACE≌△B1A1C1，∴AE=B1C1．由（3）知，∴，，∴．30．解：（1）直线CD是△ABC的黄金分割线．理由如下：设△ABC的边AB上的高为h．则，，，∴，．又∵点D为边AB的黄金分割点，∴，∴．故直线CD是△ABC的黄金分割线．（2）∵三角形的中线将三角形分成面积相等的两部分，∴，即，故三角形的中线不可能是该三角形的黄金分割线．（3）∵DF∥CE，∴△DFC和△DFE的公共边DF上的高也相等，∴S△DFC=S△DFE，∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF，S△BDC=S四边形BEFC．又∵，∴．因此，直线EF也是△ABC的黄金分割线．（7分）（4）画法不惟一，现提供两种画法；画法一：如答图1，取EF的中点G，再过点G作一条直线分别交AB，DC于M，N点，则直线MN就是平行四边形ABCD的黄金分割线．画法二：如答图2，在DF上取一点N，连接EN，再过点F作FM∥NE交AB于点M，连接MN，则直线MN 就是平行四边形ABCD的黄金分割线．（9分）。

专题27.13 黄金分割（基础篇）（专项练习）一、单选题1．大自然巧夺天工，一片树叶也蕴含着“黄金分割”．如图，P为AB的黄金分割点（AP>PB），如果AB的长度为8cm，那么BP的长度是（）A．12-B．9-C．4D．42．已知点C是线段AB的黄金分割点，且2<，则AC长是（）AB=，AC BCA B1C．3D3523．把2米的线段进行黄金分割，则分成的较短的线段长为（）A．3B1C．1D．34．已知2AB=，点P是线段AB上的黄金分割点，且AP BP>，则AP的长为（）A1B C35D．325．下列说法正确的是（）A．每条线段有且仅有一个黄金分割点B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC2＝AB•BCD．以上说法都不对6．下列说法正确的是（）A．每一条线段有且只有一个黄金分割点B．黄金分割点分一条线段为两段，其中较短的一段是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC是AB和BC的比例中项D．黄金分割点分一条线段为两段，其中较短的一段与较长的一段的比值约为0.6187．下列命题正确的是（）A．任意两个等腰三角形一定相似B．任意两个正方形一定相似C ．如果C 点是线段AB 的黄金分割点，那么AC AB =D ．相似图形就是位似图形8．如图，线段1AB =，点1P 是线段AB 的黄金分割点(且11AP BP <)，点2P 是线段1AP 的黄金分割点（212AP PP <），点3P 是线段3AP 的黄金分割点()323,,AP P P <依此类推，则线段2020AP 的长度是（ ）A ．2020⎝⎭B ．2021⎝⎭C ．2020⎝⎭D ．2021⎝⎭9．已知点C 把线段AB 分成两条线段AC 、BC ，且AC BC >，下列说法错误的是（ ） A ．如果AC BCAB AC=，那么线段AB 被点C 黄金分割 B ．如果2AC AB BC =⋅，那么线段AB 被点C 黄金分割C ．如果线段AB 被点C 黄金分割，那么BC 与AB 的比叫做黄金比D ．0.618是黄金比的近似值10．等腰△ABC 中，AB=AC ，△A=36°，D 是AC 上的一点，AD=BD ，则以下结论中正确的有（ ）△△BCD 是等腰三角形；△点D 是线段AC 的黄金分割点；△△BCD△△ABC ；△BD 平分△ABC ． A ．1个B ．2个C ．3个D ．4个11．在△ABC 中，△A=36°，AB=AC ，BD 是△ABC 的角平分线，下列结论： △△ABD ，△BCD 都是等腰三角形； △AD=BD=BC ； △BC 2=CD•CA ； △D 是AC 的黄金分割点 其中正确的是（ ）A ．1个B ．2个C ．3个D ．4个二、填空题12．在线段AB 上，点C 把线AB 分成两条线段AC 和BC ，若AC BCAB AC=，则点C 叫做线段AB 的黄金分割点．若点P 是线段MN 的黄金分割点（PM PN >），当1MN =时，PM 的长是__________．13．勾股定理与黄金分割是几何中的双宝，前者好比黄金，后者堪称珠玉，生活中到处可见黄金分割的美．如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割，已知AB=10 cm，AC＞BC，那么AC的长约为____________cm（结果精确到0.1 cm）．14．把2米长的线段进行黄金分割，则分成的较长的线段长为__________.15．古希腊时期，（称为黄金分割比例），著名的“断臂维纳斯” 2.236≈，则黄金分割比例约为______________．（精确到0.01）16．已知AB=2,点C是线段AB的黄金分割点（AC>BC），则AC= .17．把长度为4cm的线段进行黄金分割，则较长线段的长是__________cm．18．已知线段4AB=，点P是线段AB的黄金分割点（AP BP>），那么线段AP=______.（结果保留根号）19．已知线段AB长为2cm，P是AB的黄金分割点，则较长线段PA＝___；PB＝______．200.61803398=…，将这个分割比保留4个有效数字的近似数是．21．若点C为线段AB的黄金分割点，且AC＜BC，若AB＝10，则BC＝_____．22．若点P是线段AB的黄金分割点，AB=10cm，则较长线段AP的长是_____cm．三、解答题23．已知C、D是线段AB上的点，CD＝(√5﹣2)AB，AC＝BD，则C、D是黄金分割点吗？为什么？24．已知线段MN = 1，在MN 上有一点A ，如果AN =，求证：点A 是MN 的黄金分割点.25．（1）对于实数a 、b ，定义运算“⊕”如下：2a b a b ⊕=-．若(1)(2)8x x +⊕-=，求: 2(2)(23)x x x -⊕-的值；（2）已知点C 是线段AB 的黄金分割点（AC ＜BC ），若AB ＝4，求AC 的长．26．（1）我们知道，将一条线段AB 分割成大小两条线段AP 、PB ，使AP ＞PB ，点P 把线段AB 分成两条线段AP 和BP ，且=AP BP AB AP ，点P 就是线段AB 的黄金分割点，此时PAAB的值为 （填一个实数）：（2）如图，Rt△ABC 中，△B=90°，AB=2BC ，现以C 为圆心、CB 长为半径画弧交边AC 于D ，再以A 为圆心、AD 长为半径画弧交边AB 于E ． 求证：点E 是线段AB 的黄金分割点．27．某校要设计一座2m 高的雕像(如图)，使雕像的点C (肚脐)为线段AB (全身)的黄金分割点，上部AC (肚脐以上)与下部BC (肚脐以下)的高度比为黄金比．则雕像下部设计的高度应该为______(结果精确到0.001)米． 2. 236=，结果精确到0.001)．28．在等边三角形ABC中，点D，E分别在BC，AC上，且DC=AE，AD与BE交于点P，连接PC．(1)证明：ΔABE△ΔCAD．(2)若CE=CP，求证△CPD=△PBD．(3)在(2)的条件下，证明：点D是BC的黄金分割点.参考答案1．A【分析】根据黄金分割的定义得到AP AB，然后把AP的长度代入可求出AB的长．【详解】解：△P为AB的黄金分割点（AP＞PB），△AP AB，△AB的长度为8cm，△AP×8=4（cm），△BP=AB-AP=8-（4）=12-故选：A．【点拨】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC 是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC AB．2．C【分析】利用黄金分割比的定义即可求解.【详解】由黄金分割比的定义可知BC AB===21△21)3=-=-=AC AB BC故选C【点拨】本题主要考查黄金分割比，掌握黄金分割比是解题的关键.3．A【分析】根据黄金分割的定义列式进行计算即可得解.【详解】解: 较短的线段长=2⨯(1=2故选A.【点拨】本题考查了黄金分割的概念, 熟记黄金分割的比值是解题的关键.4．A【分析】根据黄金分割点的定义和AP BP=，代入数据即可得出AP的长度．>得出AP AB【详解】解：由于P为线段AB＝2的黄金分割点，且AP BP>，则21==．ABAP=故选：A．35，2．5．B【分析】根据黄金分割的定义分别进行解答即可．【详解】A．每条线段有两个黄金分割点，故本选项错误；B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍，正确；C．若点C把线段AB黄金分割，则AC2＝AB•BC，不正确，有可能BC2＝AB•AC．故选B．【点拨】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．6．D【分析】根据比例中项和黄金分割的概念分析各个说法.【详解】解：A、每一条线段有两个黄金分割点，错误；B、黄金分割点分一条线段为两段，其中较长的一段是这条线段的0.618倍，错误；C、若点C把线段AB黄金分割，则AC是AB和BC的比例中项，错误；D、黄金分割点分一条线段为两段，其中较长的一段与这条线段的比值约为0.618，正确；故选D．【点拨】此题考查黄金分割问题，理解比例中项、黄金分割的概念，是解题的关键． 7．B 【分析】根据相似多边形的概念、黄金分割点及位似可直接进行排除选项． 【详解】解：A 、任意两个等腰三角形的底角或顶角相等，则这两个等腰三角形相似，故原命题错误； B 、任意两个正方形一定相似，故原命题正确；C 、如果C 点是线段AB 的黄金分割点（AC ＞BC ），那么AC AB =D 、相似图形不一定是位似图形，故原命题错误； 故选B ．【点拨】本题主要考查相似多边形的概念、黄金分割点及位似，熟练掌握相似多边形的概念、黄金分割点及位似是解题的关键． 8．C 【分析】根据把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线叫做黄金比进行解答即可． 【详解】解：根据黄金比的比值，1BP =则11AP ==2323,,AP AP ==⎝⎭⎝⎭…依此类推，则线段20202020AP =⎝⎭，故选C ．【点拨】本题考查的是黄金分割的知识，理解黄金分割的概念，找出黄金分割中成比例的对应线段是解决问题的关键． 9．C 【解析】【分析】根据黄金分割的定义判断即可.【详解】根据黄金分割的定义可知A、B、D正确;C.如果线段AB被点C黄金分割（AC>BC）,那么AC与AB的比叫做黄金比,所以C错误.所以C选项是正确的.【点拨】本题考查了黄金分割的概念:把线段AB分成两条线段AC和BC（AC>BC）,且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB 的黄金分割点.注意线段AB的黄金分割点有两个.10．D【详解】△AB=AC，△△ABC=△C=12（180°-△A）=12（180°-36°）=72°，△AD=BD，△△DBA=△A=36°，△△BDC=2△A=72°，△△BDC=△C，△△BCD为等腰三角形，所以△正确；△△DBC=△ABC-△ABD=36°，△△ABD=△DBC，△BD平分△ABC，所以△正确；△△DBC=△A，△BCD=△ACB，△△BCD△△ABC，所以△正确；△BD：AC=CD：BD，而AD=BD，△AD：AC=CD：AD，△点D是线段AC的黄金分割点，所以△正确．故选D.11．D【解析】试题分析：在△ABC，AB=AC，△A=36°，BD平分△ABC交AC于点D，可推出△BCD，△ABD 为等腰三角形，可得AD=BD=BC，利用三角形相似解题．解：如图，△AB=AC，△A=36°，△△ABC=△C=72°，△BD平分△ABC交AC于点D，△△ABD=△CBD=△ABC=36°=△A，△AD=BD，△BDC=△ABD+△A=72°=△C ， △BC=BD ，△△ABD ，△BCD 都是等腰三角形，故△正确； △BC=BD=AD ，故△正确； △△A=△CBD ，△C=△C ， △△BCD△△ACB ， △，即BC 2=CD•AC ，故△正确； △AD=BD=BC ，△AD 2=AC•CD=（AD+CD ）•CD ， △AD=CD ，△D 是AC 的黄金分割点．故△正确， 故选D ．考点：相似三角形的判定与性质；黄金分割．12 【分析】根据若点P 是线段MN 的黄金分割点（PM PN >），则PM MN 计算即可． 【详解】当PM ＞PN 时，，．是解题的关键． 13．6.2 【分析】黄金分割又称黄金率，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为1：0.618或1.618：1，即长段为全段的0.618，0.618被公认为最具有审美意义的比例数字．上述比例是最能引起人的美感的比例，因此被称为黄金分割．【详解】由题意知AC:AB=BC:AC，△AC:AB≈0.618，△AC=0.618×10cm≈6.2(结果精确到0.1cm)故答案为6.2.【点拨】本题考查黄金分割，解题关键是掌握黄金分割定理.14．米【解析】【分析】把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分叫做黄金比．【详解】解：△将长度为2米的线段进行黄金分割，△较长的线段=2⨯米.是解的关键．15．0.62【分析】把黄金分割比例按要求进行计算即可．【详解】解： 2.236≈，≈2.23612-≈0.62，故答案为：0.62．【点拨】本题考查了求一个数的近似值，有理数的除法，正确计算是解题的关键．161【解析】21AC==17．()2cm．【解析】根据黄金分割的定义得到较长线段的长=×4，然后进行二次根式的运算即可．解：较长线段的长=×4=（2）cm．故答案为（2）cm．18．2【分析】计算即可.【详解】解：△点P是线段AB的黄金分割点（AP>BP）△AP2AB==故答案为：2.【点拨】本题考查的知识点是黄金分割，熟记黄金分割点的比值是解题的关键.19．)1cm (3cm【分析】根据黄金分割的概念得到较长线段AB，则PB=AB-352AB，然后把AB=2cm代入计算即可．【详解】解：△P是AB的黄金分割点，△较长线段AB，△PB=AB-352AB，而AB=2cm，△PA=)1cm，PB=(3cm．故答案为：)1cm；(3cm．【点拨】本题考查了黄金分割的概念：一个点把一条线段分成两段，其中较长线段是较短线段与整个线段的比例中项，那么就说这条线段被这点黄金分割，这个点叫这条线段的黄金分倍．20．0.6180【解析】根据有效数字的定义，运用四舍五入法保留4个有效数字，需观察第五位有效数字，由于第五位有效数字是，不需往前面进一位．所以0.61803398…≈0.618021．5【分析】根据黄金分割点的定义，知BC为较长线段；则BC AB，代入数据即可得出AC的值．【详解】解：由于C为线段AB＝10的黄金分割点，且AC＜BC，BC为较长线段；则BC＝＝5．故答案为：5．【点拨】本题考查黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AB≈0.618AB，并且线段AB的黄金分割点有两个．22．5【解析】△P是线段AB的黄金分割点，AP＞BP，AB，△AB=10cm，△AP=105=.故答案为5．点睛：若点P 是线段AB 的黄金分割点，且AP>BP ，则AP 2=BP·AB ，即AB. 23．C 、D 是黄金分割点.【解析】【分析】 根据题意求出AC 与AB 的关系，计算出AD 与AB 的关系，根据黄金比值进行判断即可．【详解】解：C 、D 是黄金分割点，△AC+CD+BD ＝AB ，CD ＝(√5﹣2)AB ，AC ＝BD ，△AC ＝3−√52AB ， AD ＝AC+CD ＝3−√52AB+(√5﹣2)AB ＝√5−12AB ， △D 是AB 的黄金分割点，同理C 也是AB 的黄金分割点．【点拨】本题考查黄金分割，关键是掌握黄金分割的概念和黄金比.24．见解析【解析】试题分析：先求得AM=√5−12，即可得到AM MN =AN AM =√5−12，结论得证。

黄金分割专项练习30题(有答案)1，点C 在线段AB 上，若满足AC 2=BC?AB ，则称点C 为线段AB 的黄金分割点.如图 2, △ ABC ,/ A=36 ° BD 平分 / ABC 交 AC 于点 D .D 是线段AC 的黄金分割点；AD 的长.3. 定义：如图1，点C 在线段 如图 2, △ ABC 中，AB=AC=2 (1) 求证：点D 是线段AC 的黄金分割点;C t3--- >40cw2.如图，用长为40cm 的细铁丝围成一个矩形 ABCD (AB > AD ). 1 .定义：如图 中，AB=AC=1 (1) 求证：点 (2) 求出线段 (1) 若这个矩形的面积等于(2) 这个矩形的面积可能等于(3)若这个矩形为黄金矩形( 99cm 2,求AB 的长度； 101cm 2吗？若能，求出 AB 的长度，若不能，说明理由; AD 与AB 之比等于黄金比 伍 ~ ' 2 ),求该矩形的面积.(结果保留根号)AB 上，若满足AC 2=BC?AB ，则称点C 为线段AB 的黄金分割点. ,/A=36 ° BD 平分 / ABC 交 AC 于点 D .e(2)求出线段AD的长.4.作一个等腰三角形，使得腰与底之比为黄金比.(1)尺规作图并保留作图痕迹；(2)写出你的作法；(3)证明：腰与底之比为黄金比.5.(1)已知线段AB的长为2, P是AB的黄金分割点，求AP的长;(2)求作线段AB的黄金分割点P,要求尺规作图，且使AP >PB .』 --------------------- E6.如图，线段AB的长度为1 .(1)线段AB上的点C满足系式AC2=BC?AB，求线段AC的长度；(选做)(2)线段AC上的点D满足关系式AD2=CD?AC，求线段AD的长度;(选做)(3)线段AD上的点E满足关系式AE2=DE?AD，求线段AE的长度；上面各题的结果反映了什么规律？(提示：在每一小题中设x和I)7.如图，在△ ABC中，AB=AC , / A=36 ° / 1 = / 2,请问点D是不是线段AC的黄金分割点.请说明理由.&在^ ABC 中，AB=AC=2 , BC=｛亏-1 , / A=36 ° BD 平分/ ABC ，交于AC 于D .试说明点 D 是线段AC 的黄 金分割点.为黄金矩形ABCD •请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成. D Q10.如图，设 AB 是已知线段，在 AB 上作正方形 ABCD ;取AD 的中点E ，连接EB ;延长DA 至F ,使EF=EB ; 以线段AF 为边作正方形 AFGH •则点H 是AB 的黄金分割点.为什么说上述的方法作出的点 H 是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说.E ______ JG£'11.如图，已知△ ABC 中，D 是 AC 边上一点，/ A=36 ° / C=72 ° / ADB=108 ° 求证:(1) AD=BD=BC ;(2) 点D 是线段AC 的黄金分割点.9.在数学上称长与宽之比为黄金分割比的矩形为黄金矩形, 如在矩形ABCD 中，当扭」+产£C 时，称矩形ABCD15•人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段.一个身高1.70m 的人，他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)？ 16. 如图所示，以长为 2的定线段AB 为边作正方形 ABCD ，取AB 的中点P ,连接PD ,在BA 的延长线上取点 F ， 使PF=PD ，以AF 为边作正方形 AMEF ，点M 在AD 上.(1) 求AM , DM 的长；(2) 点M 是AD 的黄金分割点吗？为什么？ F— r— D•/a匚12 .已知 AB=2 , 点C 是AB 的黄金分割线，点 D 在AB 上，且AD 2=BD?AB ，求器的值. 13.如果一个矩形AR A 斥-1 ABCD (AB < BC )中，竺 —— BC 2 -0.618,那么这个矩形称为黄金矩形， 黄金矩形给人以美感. 在 ABFE (如图)，请问矩形ABFE 是否是黄金矩形？请说明你14•五角星是我们常见的图形，如图所示，其中，点的长.C ,D 分别是线段 AB 的黄金分割点，AB=20cm ，求EC+CD C黄金矩形ABCD的结论的正确性. A E3 F17. 如图，点P 是线段AB 的黄金分割点，且 AP >BP ,设以AP 为边长的正方形面积为 S 1,以PB 为宽和以AB 为 长的矩形面积为S 2，试比较S 1与S 2的大小.Sr3斥一 1 18•如图，在平行四边形 ABCD 中，E 为边AD 延长线上的一点，且 D 为AE 的黄金分割点，即ADJBE 交DC 于点F ,已知AB=V5 + 1,求CF 的长.2折叠方法进行折叠，折叠后再展开，可以得到一个正方形 ABEF 和一个矩形 EFDC ，那么EFDC 这个矩形还是黄金矩形吗？若是，请根据图 2证明你的结论；若不是，请说明理由./A / / '團3AE ，19•图1是一张宽与长之比为徨丄：1的矩形纸片，我们称这样的矩形为黄金矩形•同学们都知道按图 2所示的(ffl 2)20.(如图 1), 点P 将线段AB 分成一条较小线段 AP 和一条较大线段BP ,如果善兰?，那么称点P 为线段AB 的 br Ai? 黄金分割点，设 柱影k ，则k 就是黄金比，并且k 战618 .BPJ(ffll ) E CS '團2尸(1) 以图1中的AP 为底，BP 为腰得到等腰△ APB (如图2),等腰△APB 即为黄金三角形，黄金三角形的定义为: 满足簷諾备-0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：; (2) 如图1,设AB=1，请你说明为什么(3) 由线段的黄金分割点联想到图形的3),点P 是线段AB 的黄金分割点，那么直线 CP 是△ ABC 的黄金分割线吗？请说明理由;(4) 图3中的△ ABC 的黄金分割线有几条？21.在人体躯干(脚底到肚脐的长度)与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人 以美感.张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m ，她应该选择多高的高跟鞋穿上看起来更美？(精确到十分位) 22. 已知线段AB ，按照如下的方法作图：以 AB 为边作正方形 ABCD ，取AD 的中点E ,连接EB ，延长DA 到F , AF 为边，作正方形 AFGH ，那么点H 是线段AB 的黄金分割点吗？请说明理由.23•如图，用纸折出黄金分割点：裁一张正方的纸片ABCD ，先折出BC 的中点E ,再折出线段AE ，然后通过折叠 使EB 落到线段EA 上，折出点B 的新位置B',因而EB'=EB .类似地，在 AB 上折出点B 〃使AB ''=AB 这时B " 就是AB 的黄金分割点.请你证明这个结论. k 约为 0.618; 黄金分割线”，类似地给出 黄金分割线”的定义：直线I 将一个面积为S 的 图形分成面积为S i 和面积为S 2的两部分（设S 1< S 2）,如果 ，那么称直线I 为该图形的黄金分割线.(如图24.如图，用纸折出黄金分割点：裁一张边长为 2的正方形纸片 ABCD ，先折出BC 的中点E ,再折出线段 AE , 后通过折叠使 EB 落在线段EA 上，折出点B 的新位置F ，因而EF=EB .类似的，在AB 上折出点M 使AM=AF . M 是AB 的黄金分割点吗？若是请你证明，若不是请说明理由.25.如图，在 △ ABC 中，点 D 在边 AB 上，且 DB=DC=AC ，已知 / ACE=108 ° BC=2 .（1） 求/ B 的度数；（2） 我们把有一个内角等于 36°勺等腰三角形称为黄金三角形.它的腰长与底边长的比（或者底边长与腰长的比） 等于黄金比逅二i .2① 写出图中所有的黄金三角形，选一个说明理由；② 求AD 的长；③ 在直线AB 或BC 上是否存在点P （点A 、B 除外），使△PDC 是黄金三角形？若存在，在备用图中画出点P,要说明画出点P 的方法（不要求证明）；若不存在，说明理由.- 126•宽与长的比是违一的矩形叫黄金矩形•心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美 感•现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）： 第一步：作一个正方形 ABCD ;第二步：分别取 AD , BC 的中点M , N ，连接MN ; 第三步：以N 为圆心，ND 长为半径画弧，交 第四步：过E 作EF 丄AD ，交AD 的延长线于请你根据以上作法，证明矩形 DCEF 为黄金矩形. BC 的延长线于E ; F .27.在△ ABC 中，AB=AC , / A=36 °把像这样的三角形叫做黄金三角形.(1)请你设计三种不同的分法，将黄金三角形 ABC 分割成三个等腰三角形，使得分割成的三角形中含有两个黄金 三角形(画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法， 求证明.分别画在图 1，图2，图3中) 注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法.28 •折纸与证明 —— 用纸折出黄金分割点：第一步：如图(1),先将一张正方形纸片 ABCD 对折，得到折痕 EF ;再折出矩形 BCFE 的对角线第二步：如图(2),将AB 边折到BF 上，得到折痕 BG ,试说明点G 为线段AD 的黄金分割点(AG > GD )(2)29•三角形中，顶角等于 36 °勺等腰三角形称为黄金三角形，如图 1，在△ ABC 中，已知：AB=AC ，且/ A=36 ° (1) 在图1中，用尺规作 AB 的垂直平分线交 AC 于D ，并连接BD (保留作图痕迹，不写作法);(2) △ BCD 是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；(3) 设匹二k ，试求k 的值； F E ------- 7^ ---/ ' / '■ / \ J 1■ ■ ■ ■ ■ E ■■r*t *E 不要 (2)如图4中， 与AB 之间的数量关系？只需说明结果，不用证明.答：CM 与AB 之间的数量关系是BF 平分/ ABC 交AC 于F ,取AB 的中点E ,连接EF 并延长交 BC 的延长线于M .试判断CM cA lB l =A lC l , / A l =108°且 A 1B 1=AB ,请直接写出 亠 的值.30 .如图1,点C 将线段AB 分成两部分，如果警丿習，那么称点C 为线段AB 的黄金分割点.某研究小组在进行 A D AC 黄金分割线”类似地给出 黄金分割线”的定义：直线I 将一个面积为S 的图形 课题学习时，由黄金分割点联想到 分成两部分，这两部分的面积分别为 S 1, S 2,如果—=-^,那么称直线I 为该图形的黄金分割线. S S1(1) 研究小组猜想：在 △ ABC 中, 线.你认为对吗？为什么？ (2) (3) 连接 (4) 若点D 为AB 边上的黄金分割点(如图 2)，则直线CD 是^ ABC 的黄金分割 请你说明：三角形的中线是否也是该三角形的黄金分割线？研究小组在进一步探究中发现： 过点C 任作一条直线交 AB 于点E ,再过点D 作直线DF // CE ，交AC 于点F , EF (如图3),则直线EF 也是△ ABC 的黄金分割线.请你说明理由. 如图4,点E 是平行四边形 ABCD 的边AB 的黄金分割点，过点 是平行四边形ABCD 的黄金分割线.请你画一条平行四边形 各边黄金分割点. E 作EF // AD ，交DC 于点F ，显然直线 EF ABCD 的黄金分割线，使它不经过平行四边形 ABCD S3黄金分割专项练习30题参考答案:1. (1)证明：•/ AB=AC=1 ,••• / ABC= / C=2 (180°- / A )=丄(180。

最最中考复习--黄金分割专题训练（一）一、选择题1.若P是线段AB的黄金分割点(PA>PB)，设AB=1，则PA的长约为()A. 0.191B. 0.382C. 0.5D. 0.6182.上海东方明珠电视塔高468m.其上球体位于塔身的黄金分割点，那么它到塔底部的距离大约是()A. 289.2mB. 178.8mC. 110.4mD. 468m3.如果把一条线段分为两部分，使其中较长的一段与整条线段的长度比是黄金比，那么较短一段与较长一段的长度比也是黄金比．由此，假设整条线段长为1，较长的一段为x，可以列出的方程为()A. 1−xx =x1B. 1−x1=1xC. x1−x=1−x1D. 1−xx=x√54.已知点C是线段AB的黄金分割点(AC>BC)，AB=4，则线段AC的长是()A. 2√5−2B. 6−2√5C. √5−1D. 3−√55.一条线段的黄金分割点有()个A. 1B. 2C. 3D. 无数个6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法．如图所示，以线段AB为边作正方形ABCD，取AD的中点E，连结BE，延长DA至点F，使得EF=BE，以AF为边作正方形AFGH，则H即是线段AB的黄金分割点．若记正方形AFGH的面积为S1，矩形BCIH的面积为S2，则S1与S2的大小关系是()A. S1>S2B. S1<S2C. S1=S2D. 不能确定7.已知点C把线段AB分成两条线段AC、BC，且AC>BC，下列说法错误的是()A. 如果ACAB =BCAC，那么线段AB被点C黄金分割B. 如果AC2=AB⋅BC，那么线段AB被点C黄金分割第 2 页 共 15 页C. 如果线段AB 被点C 黄金分割，那么BC 与AB 的比叫做黄金比D. 0.618是黄金比的近似值8. 如图，在△ABC 中，AB =AC ，∠BAC =108°，AD 、AE 将∠BAC 三等分交边BC 于点D ，点E ，则下列结论中错误的是( )A. 点D 是线段BC 的黄金分割点B. 点E 是线段BC 的黄金分割点C. 点E 是线段CD 的黄金分割点D. EDBE =√5−12二、填空题9. 据有关测定，当气温处于人体正常体温(37℃)的黄金比值时，人体感到最舒适，则这个气温约为_________℃(结果保留整数)．10. 如果线段AB =10cm ，P 是线段AB 的黄金分割点，那么线段BP =________cm ． 11. 如图是一种贝壳的俯视图，点C 分线段AB 近似于黄金分割(BC <AC).已知AB =4 cm ，则BC 的长约为________cm.(结果精确到0.1)12. 在自然界中，蝴蝶的身长与双翅展开后的长度的比接近于0.618.若双翅展开后的长度约为5.62 cm ，则其身长约为_______cm(保留两位小数)13. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．某女模特身高165cm ，下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果，她应穿的高跟鞋的高度大约为____．14. 在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm ，则宽约为 ________ (精确到1 cm)．15. 已知点C 为线段AB 的黄金分割点，且AC >BC ，若P 点为线段AB 上的任意一点，则P 点出现在线段AC 上的概率为________．三、解答题16.拥有一个完美的身材是很多人的梦想，世界著名的雕像“维纳斯”就被认为是最美的身材。

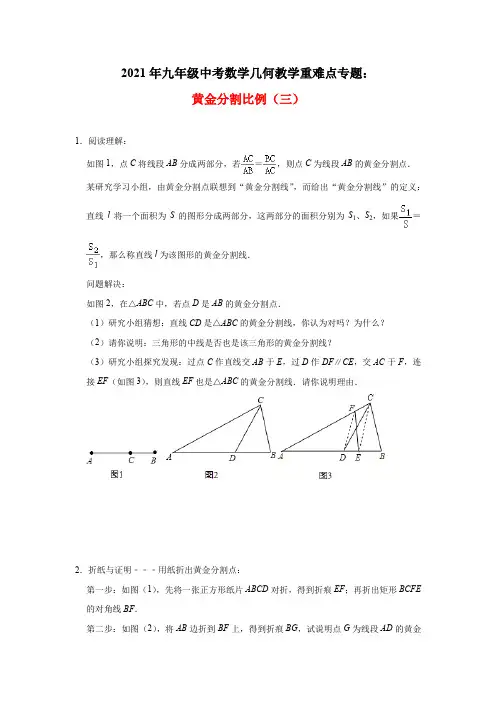
2021年九年级中考数学几何教学重难点专题：黄金分割比例（三）1．阅读理解：如图1，点C将线段AB分成两部分，若＝，则点C为线段AB的黄金分割点．某研究学习小组，由黄金分割点联想到“黄金分割线”，而给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果＝，那么称直线l为该图形的黄金分割线．问题解决：如图2，在△ABC中，若点D是AB的黄金分割点．（1）研究小组猜想：直线CD是△ABC的黄金分割线，你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组探究发现：过点C作直线交AB于E，过D作DF∥CE，交AC于F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．2．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE 的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）3．若一个矩形的短边与长边的比值为（黄金分割数），我们把这样的矩形叫做黄金矩形．（1）操作：请你在如图所示的黄金矩形ABCD（AB＞AD）中，以短边AD为一边作正方形AEFD；（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由．4．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB＝AC，且∠A＝36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1＝A1C1，∠A1＝108°，且A1B1＝AB，请直接写出的值．5．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．6．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF 和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．7．如图1所示，点C将线段AB分成两部分，如果，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；（2）请你说明：三角形的中线是否是该三角形的黄金分割线．8．在△ABC中，AB＝AC，∠A＝36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．9．“黄金分割”在人类历史上有着重要的作用和影响，世界上许多著名的建筑和艺术品中都蕴涵着“黄金分割”．下面我们就用黄金分割来设计一把富有美感的纸扇：假设纸扇张开到最大时，扇形的面积与扇形所在圆的剩余部分的比值等于黄金比，请你来求一求纸扇张开的角度．（黄金比取0.6）10．如图，在△ABC中，点D在边AB上，且BD＝DC＝AC，已知∠ACE＝108°，BC＝2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长．参考答案1．解：（1）直线CD 是△ABC 的黄金分割线．理由如下： ∵点D 是AB 的黄金分割点，∴＝，∵＝，＝，∴＝，∴直线CD 是△ABC 的黄金分割线；（2）∵三角形的中线把AB 分成相等的两条线段，即AD ＝BD ， ∴＝，＝＝1，∴三角形的中线不是该三角形的黄金分割线；（3）∵DF ∥CE ，∴S △FDE ＝S △FDC ，S △DEC ＝S △FEC ，∴S △AEF ＝S △ADC ，S 四边形BEFC ＝S △BDC ，∵＝，∴＝，∴直线EF 是△ABC 的黄金分割线．2．证明：如图，连接GF ，设正方形ABCD 的边长为1，则DF ＝． 在Rt △BCF 中，BF ＝＝，则A ′F ＝BF ﹣BA ′＝﹣1． 设AG ＝A ′G ＝x ，则GD ＝1﹣x ，在Rt △A ′GF 和Rt △DGF 中，有A 'F 2+A 'G 2＝DF 2+DG 2， 即，解得x＝，即点G是AD的黄金分割点（AG＞GD）．3．解：（1）如图：以A为圆心，在AB上截取AE＝AD，以D为圆心，在DC上截取DF＝DA，连接EF，所以四边形AEFD为所求作的正方形；（2）答：四边形EBCF是黄金矩形．证明：∵四边形AEFD是正方形，∴∠AEF＝90°，∴∠BEF＝90°，∵四边形ABCD是矩形，∴∠B＝∠C＝90°∴∠BEF＝∠B＝∠C＝90°，∴四边形EBCF是矩形．设CD＝a，AD＝b，则有，∴，∴矩形EBCF是黄金矩形．4．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD＝BD，∴∠ABD＝∠A．∵∠A＝36°，AB＝AC，∴∠ABC＝∠C＝72°，∴∠ABD＝∠DBC＝36°．又∵∠BDC＝∠A+∠ABD＝72°，∴∠BDC＝∠C，∴BD＝BC，∴△BCD是黄金三角形．（3）设BC＝x，AC＝y，由（2）知，AD＝BD＝BC＝x．∵∠DBC＝∠A，∠C＝∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2＝0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE＝AC，连接AE．∵∠A＝36°，AB＝AC，∴∠ACB＝∠B＝72°，∴∠ACE＝180°﹣72°＝108°，∴∠ACE＝∠B1A1C1．∵A1B1＝AB，∴AC＝CE＝A1B1＝A1C1，∴△ACE≌△B1A1C1，∴AE＝B1C1．由（3）知，∴，，∴．5．证明：在AB上截取AE＝BC，DF＝BC，连接EF．∵AE＝BC，DF＝BC，∴AE＝DF＝BC＝AD，又∵∠ADF＝90°，∴四边形AEFD是正方形．BE＝，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．6．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB＝DC＝AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．7．解：∵，，又∵D是AB的黄金分割点，∴，，∴CD是△ABC的黄金分割线；（2）不是．∵CD是△ABC的中线，∴AD＝DB，∴＝，而＝1，∴≠，∴中线不是黄金分割线．8．解：（1）（3分）（2）CM＝AB（4分）9．解：设扇形的半径为R，圆心角为n，则剩余扇形的圆心角为（360°﹣n），由题意得，：＝0.6，即n：（360°﹣n）＝0.6，解得：n＝135，答：纸扇张开的角度为135°．10．解：（1）设∠B＝x，∵BD＝DC，∴∠DCB＝∠B＝x，∴∠ADC＝∠B+∠DCB＝2x，∵AC＝DC，∴∠A＝∠ADC＝2x，∵∠ACE＝∠B+∠A，∴x+2x＝108°，解得x＝36°，即∠B的度数为36°；（2）①△ABC、△DBC、△CAD都是黄金三角形．理由如下：∵DB＝DC，∠B＝36°，∴△DBC为黄金三角形；∵∠BCA＝180°﹣∠ACE＝72°，而∠A＝2×36°＝72°，∴∠A＝∠ACB，而∠B＝36°，∴△ABC为黄金三角形；∵∠ACD＝∠ACB﹣∠DCB＝72°﹣36°＝36°，而CA＝CD，∴△CAD为黄金三角形；②∵△BAC为黄金三角形，∴＝，而BC＝2，∴AC＝﹣1，∴CD＝CA＝﹣1，∴BD＝CD＝﹣1，∴AD＝AB﹣BD＝2﹣（﹣1）＝3﹣．。

4.4.4 黄金分割一、目标导航1．黄金分割定义:点C 把线段AB 分成两条线段AC 和BC ，如果AC :AB =BC :AC ，那么称线段AB 被点C 黄金分割．点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比．2．618.0215≈-=AB AC ． 二、基础过关 1．若点P 是AB 的黄金分割点，则线段AP 、PB 、AB 满足关系式 ．2．黄金矩形的宽与长的比大约为________（精确到0.001）．3．电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台AB 长为20m ，试计算主持人应走到离A 点至少 m 处？，如果他向B 点再走 m ，也处在比较得体的位置．（结果精确到0.1m ）三、能力提升4．有以下命题：①如果线段d 是线段a ， b ，c 的第四比例项，则有dc b a =；②如果点C 是线段AB 的中点，那么AC 是AB 、BC 的比例中项；③如果点C 是线段AB 的黄金分割点，且AC >BC ，那么AC 是AB 与BC 的比例中项；④如果点C 是线段AB 的黄金分割点，AC >BC ，且AB =2，则AC =5－1．其中正确的判断有( )A ． 1个B ．2个C ．3个D ．4个 5．已知点M 将线段AB 黄金分割(AM ＞BM )，则下列各式中不正确的是( )A ．AM ∶BM =AB ∶AM B ．AM =215-AB C ．BM =215-AB D ．AM ≈0．618AB 6．已知C 是线段AB 的黄金分割点(AC ＞BC ）， 则AC ∶BC = ( )A ．(5－1)∶2B ．（5 +1）∶2C ．（3－5）∶2D ．（3+5）∶27．在长度为1的线段上找到两个黄金分割点P ，Q ．则PQ ＝( )A ．215-B ．53-C ．25-D ．253- 8．已知线段MN = 1，在MN 上有一点A ，如果AN =253-． 求证：点A 是MN 的黄金分割点．四、聚沙成塔9．如图，以长为2的线段AB 为边作正方形ABCD ，取AB 的中点P ，连结PD ，在BA 的延长线上取点F ，使PF =PD ，以AF 为边作正方形AMEF ，点M 在AD 上．（1）求AM 、DM 的长．（2）求证：AM 2=AD ·DM ．（3）根据（2）的结论你能找出图中的黄金分割点吗？10．如果一个矩形ABCD (AB ＜BC )中，215-=BC AB ≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD 内作正方形CDEF ，得到一个小矩形ABFE (如图)，请问矩形ABFE 是否是黄金矩形？请说明你的结论的正确性．参考答案1．AP 2=BP ·AB 或PB 2=AP ·AB ；2．0.618；3．7.6，4.8；4．C ；5．C ；6．B ；7．C ；8证得AM 2=AN ·MN 即可；9．⑴AM =5－1；DM =3－5；⑵略；⑶点M 是线段AD 的黄金分割点；10．通过计算可得215-=AB AE ，所以矩形ABFE 是黄金矩形．。

19.2 黄金分割基础能力训练★回归教材 注重基础 ◆黄金分割的定义1.已知AB=10 cm,P 、Q 是线段AB 的两个黄金分割点,则PQ=________.2.已知线段AB=1,点P 是线段AB 的黄金分割点,则AP=________.3.已知线段AB=b,C 为其黄金分割点,求下列各式的值(AC>BC)：(1)=BA AC _______;(2)=AC BC_______； (3)=BCAC _______;(4)AC －BC=________.4.正常人的体温一般是37℃左右,室温太高、太低,人都会感觉不舒服,多少摄氏度比较合适呢?有人研究认为该温度正好是人正常体温的黄金分割点,则这个温度约为________.5.(·南京模拟)顶角为36°的等腰三角形被称为黄金三角形,在∠A=36°的△ABC 中,AB=AC,BD 是∠ABC 的角平分线,交AC 于D,若AC=4 cm,则BC=___________.6.若S 是线段PQ 的黄金分割点,且PS>SQ,则( ) A.SQ 2=PS·PQ B.PS 2=SQ·PQ C.PQ PSPS •=22D.22PQ PS PS SQ +•= 7.已知M 是线段AB 的黄金分割点,且AM>BM.(1)写出线段AB 、AM 、BM 之间的比例式. (2)如果AB=12 cm,求AM 、BM 的长.8.如图19－2－4所示,线段AB 长10cm,点C 是线段AB 的黄金分割点,AC>BC,设以AC 为边的正方形ACDE 的面积为S 1,以BC 为一边，AB 长为另一边的矩形BCFG 的面积为S 2,试比较S 1和S 2的大小.◆黄金分割点的作图9.采用如下方法也可以得到黄金分割点：如图19－2－5所示,设AB 为已知线段,以AB 为边作正方形ABCD ；取AD 的中点E,联结EB ；延长DA 至F,使EF=EB ；以线段AF 为边作正方形AFGH,点H 就是AB 的黄金分割点.任意作一条线段,用上述方法作出这条线段的黄金分割点,你能说出这种作法的道理吗?10.求作已知线段AB 的黄金分割点.(不写作法) 综合创新训练★登高望远 课外拓展 ◆创新应用11.如图19－2－6所示,正五角星中,线段AD=2,试问图中阴影部分图形的周长是多少?12.举例说明黄金分割在日常生活中的一些应用. ◆开放探索13.若一个矩形的短边与长边的比值为215-(黄金分割数),我们把这样的矩形叫做黄金矩形.(1)操作：请你在如图19－2－7所示的黄金矩形ABCD(AB>AD)中,以短边AD 为一边作正方形AEFD.(2)探究：(1)中的四边形EBCF 是不是黄金矩形?若是,请说明理由;若不是,也给予说明. (3)归纳：通过上述操作及探究,请概括出具有一般性的结沦(不需要证明).参考答案1答案：)25(10-cm2答案：215-或253- 解析：本题应考虑到同一线段上的黄金分割点有两个.3答案：(1)215-(2)215-(3)215+(4)b )25(- 4答案：23℃5答案：)15(2-cm 解析：∵等腰△ABC 为黄金三角形,∴ACBC为黄金比. ∴AC BC 215-=,∴)15(2-=BC cm.6答案：B 7答案：(1)AMBMAB AM =(2))656(-=AM cm,)5618(-=BM cm 8答案：)53(5021-==S S cm 29答案：解析：设AB=2,那么在Rt △BAE 中,5122222=+=+=AE AB BE .于是EF=BE=5,AH=AF=BE －AE=15-,BH=AB －AH=53-.因此,AHBHAB AH =,点H 是线段AB 的黄金分割点. 10答案：略11答案：解析：由于点B 、C 都是线段AD 的黄金分割点,于是有：53)15(2,152152-=--=-=-=-=-⨯==AC AD BD AD AB AC BD , ∴452)53()15(-=---=-=AB AC BC . ∴阴影部分的周长为20510-.12答案：解析：例如：报幕员站在舞台宽度的黄金分割点处,显得最和谐；当矩形的宽与长的比约为0.618时显得美观；拍照时,常把主要景物放在画面的黄金分割点处,会显得更加协调、悦目；二胡中的“千金”分弦的比符合0.618：1时,奏出来的音调最悦耳；优选法中的“0.618法”足黄金分割的重要应用等等. 13答案：解析：(1)如图所示.(2)四边形EBCF 是黄金矩形,因为EF=AE=AB 215-,AB BE 253-=,则EF BE 215-=,所以四边形EBCF 是黄金矩形.(3)在黄金矩形中以短边为边长作一个正方形,另一部分仍为黄金矩形.英语不规则动词归类记忆表原形过去式过去分词 汉语意思read read read 读 cut cut cut 切，割 let let let 让 put put put 放 cost cost cost 花费，值 hit hit hit 撞，击 set set set 安排，安置 hurt hurt hurt 使…伤痛 二、ABA 型（原形→过去式→原形）三、ABC 型原形 过去式 过去分词 汉语意思 blow blew blown 吹 draw drew drawn 画原形 过去式 过去分词 汉语意思 become became become 成为 come came come 来 runranrun跑四、ABB型不规则单词测试卷（1）微信添加“小魔方站”或“fifteen1617”免费获得更多中考资料与模拟试题不规则单词测试卷（2）不规则单词测试卷（3）不规则单词测试卷（4）。

.中考中的黄金分割问题一、黄金分割点例1（湖北十堰）如图1，已知线段AB，点C在AB 上，且有AC BCAB AC，则ACAB的数值为______；若AB的长度与中央电视台演播厅舞台的宽度一样长，那么节目主持人应站在_____位置最好．2.（2005?太原）如图，乐器上的一根弦AB=80cm，两个端点A、B固定在乐器板面上，支撑点C是靠近点B的黄金分割点（即AC是AB与BC的比例中项），支撑点D是靠近点A的黄金分割点，则AC= cm，DC= cm．3.（2009?浙江）在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20cm，则它的宽约为（）A ．12.36cm B．13.6cm C．32.36cm D．7.64cm4．（2009?孝感）美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．如图，某女士身高165cm，下半身长x与身高l的比值是0.60，为尽可能达到好的效果，她应穿的高跟鞋的高度大约为（）A．4cm B．6cm C．8cm D．10cm二、黄金三角形例1.（2010?本溪）如图，△ABC顶角是36°的等腰三角形（底与腰的比为的三角形是黄金三角形），若△ABC、△BDC、△DEC都是黄金三角形，已知AB=4，则DE= _________ ．2．（2010四川内江）如图，在△ABC中，AB＝AC，点E、F 分别在AB和AC上，CE与BF相交于点D，若AE＝CF，D为BF的中点，则AE∶AF的值为 .3.顶角为36°的等腰三角形被称为黄金三角形，在∠A=36°的△ABC中，AB=AC，BD是∠ABC的角平分线，交AC于D，若AC=4cm，则BC= cm．4．（2007·太原）数学课上，同学们探究下面命题的正确性：顶角为36°的等腰三角形具有一种特性，即经过它某一顶点的一条直线可把它分成两个小等腰三角形.为此，请你解答问题(1).已知：如图(1)，在△ABC中，AB=AC，∠A=36°，直线BD平分∠ABC交AC 于点D.求证：△ABD与△DBC都是等腰三角形图(1)归纳提升：本题综合考查等腰三角形的性质与判别，还可这样反思：条件改为“在△ABC中，AB=AC，AD=BD=BC”，求△ABC中各内角的度数.(2)在证明了该命题后，小颖发现：下列两个等腰三角形如图(2)、(3)也具有这种特性请你在图(2)、图(3)中分别画出一条直线，把它们分成两个小等腰三角形，并在图中标出所画等腰三角形两个底角的度数；(3)接着，小颖又发现：直角三角形和一些非等腰三角形也具有这样的特性，如：直角三角形斜边上的中线可把它分成两个小等腰三角形.请你画出两个具有这种特性的三角形的示意图，并在图中标出三角形各内角的度数.说明：要求画出的两个三角形不相似，而且既不是等腰三角形也不是直角三角形.三、黄金矩形例 1 （扬州市）若一个矩形的短边与长边的比值为51-（黄金分割数），我们把这样的矩形叫做黄金矩形．（1）操作：请你在如图2所示的黄金矩形()ABCD AB AD>中，以短边AD为一边作正方形AEFD；（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由；（3）归纳：通过上述操作及探究，请概括出具有一般性的结论（不需要证明）．1．宽与长的比是512-的矩形叫黄金矩形，心理学测试表明，黄金矩形令人赏心悦目，它给我们以协调，匀称的美感，现将同学们在教学活动中，折叠黄金矩形的方法归纳出以下作图步骤（如图所示）： 第一步：作一个任意正方形ABCD ；第二步：分别取AD BC ，的中点M N ，，连接MN ；第三步：以N 为圆心，ND 长为半径画弧，交BC 的延长线于E ；第四步：过B 作EF AD ⊥交AD 的延长线于F ，请你根据以上作法，证明矩形DCEF 为黄金矩形，（可取2AB =）2.（2010 嵊州市）如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F 、C ，CD ，垂足为D ，若CD ＝CF ，过点C 作AM 的垂线则=ADAE .3. 已知线段AB ，点P 是它的黄金分割点，AP ＞BP ，设以AP 为边的正方形的面积为S 1，以PB ，AB 为边的矩形面积为S 2，则S 1与S 2的关系是（ ）A 、S 1＞S 2B 、S 1＜S 2C 、S 1=S 2D 、S 1≥S 2一、选择题1、若3a=4b ，则（a ﹣b ）：（a+b ）的值是（ ）A 、B 、7C 、﹣D 、﹣72、（2002?太原）已知，P 是线段AB 上一点，且，则等于（ ）A 、B 、C 、D 、3、已知点P 是线段MN 的黄金分割点，MP ＞NP ，且MP=（﹣1）cm ，则MN 等于（ ）A 、2cmB 、4cmC 、6cmD 、无法计算4、如图所示，以长为2的线段AB 为边作正方形ABCD ，取AB 的中点P ，连接PD ，在BA 的延长线上取点F ，使PF=PD ，以AF 为边作正方形AMEF ，点M 在AD 上，则AM 的长为（ ）A 、﹣1B 、C 、3﹣D 、6﹣2二、填空题5、若点C是线段AB的黄金分割点且AC＞BC，则，= ．6、在线段AB上取一点P，使AP：PB=1：3，则AP：AB= ，AB：PB= ．7、若点C是线段AB的黄金分割点，则等于．8.（2008?枣庄）将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为．。