海淀区高三年级第一学期期中练习 数学(文科)

海淀区高三年级第一学期期中练习
数学（文科）2018.11
本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要
求的一项。

1.
A. B. C. D.
2.
A. B.Ｃ.
3.
A. 0 C. D. 1
4.
C. D.
5.
B. C. D.
6.
A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
7.
A. B. C. D.
8.a b b c c a
值是
a b B. b c C. c a D. 不能确定的
二、填空题共6小题，每小题5分，共30分。

9. 。

10. 中为整数的项的个数为。

AE
11.
12. 上的最大值为。

13.
是。

14.
（1；
（2的取值范围是
三、解答题共6小题，共80分。

解答应写出文字说明、演算步骤或证明过程。

15. （本小题满分13分）
.
16.（本小题满分13分）
.
17. （本小题满分13分）
.
18. （本小题满分14分）
（只需直接写出数值）
19. （本小题满分13分）
（Ⅱ）求证:
20. （本小题满分14分）。

2018-2019学年北京市海淀区高三（上）期中数学试卷（文科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目温馨提示：多少汗水曾洒下，多少期待曾播种，终是在高考交卷的一刹尘埃落地，多少记忆梦中惦记，多少青春付与流水，人生，总有一次这样的成败，才算长大。

高考保持心平气和，不要紧张，像对待平时考试一样去做题，做完检查一下题目，不要直接交卷，检查下有没有错的地方，然后耐心等待考试结束。

最新试卷十年寒窗苦，踏上高考路，心态放平和，信心要十足，面对考试卷，下笔如有神，短信送祝福，愿你能高中，马到功自成，金榜定题名。

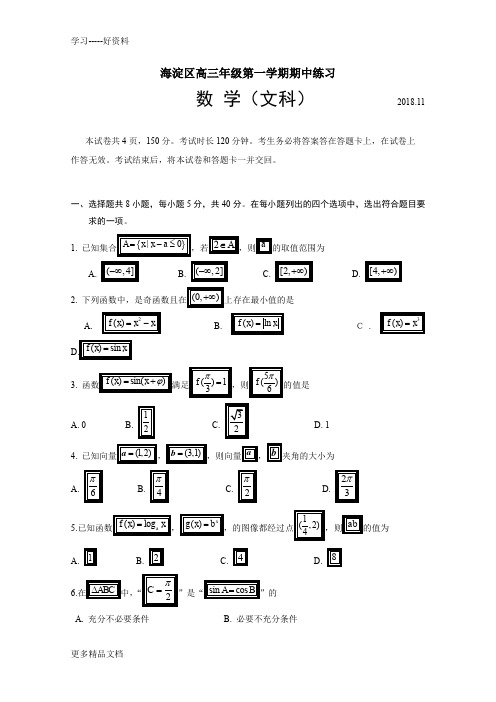
要求的一项．1．已知集合A={x|x＞2}，B={x|（x﹣1）（x﹣3）＜0}，则A∩B=（）A．{x|x＞1} B．{x|2＜x＜3}C．{x|1＜x＜3}D．{x|x＞2或x＜1}2．已知向量=（﹣1，x），=（﹣2，4）．若∥，则x的值为（）A．﹣2 B． C．D．23．已知命题p：?x＞0，x+≥2命题q：若a＞b，则ac＞bc．下列命题为真命题的是（）A．q B．￢p C．p∨q D．p∧q4．若角θ的终边过点P（3，﹣4），则tan（θ+π）=（）A．B． C．D．5．已知函数y=x a，y=log b x的图象如图所示，则（）A．b＞1＞a B．b＞a＞1 C．a＞1＞b D．a＞b＞16．设，是两个向量，则“|+|＞|﹣|”是“?＞0”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件7．给定条件：①?x0∈R，f（﹣x0）=﹣f（x0）；②?x∈R，f（1﹣x）=f（1+x）的函数个数是下列三个函数：y=x 3，y=|x﹣1|，y=cosπx中，同时满足条件①②的函数个数是（）A．0 B．1 C．2 D．38．已知定义在R上的函数f（x）=，若方程f（x）=有两个不相等的实数根，则a的取值范围是（）A．﹣≤a＜B．C．0≤a＜1 D．二、填空题共6小题，每小题5分，共30分．9．计算lg2﹣lg+3lg5=．10．已知sinα=，则cos2α=．11．已知函数y=f（x）的导函数有且仅有两个零点，其图象如图所示，则函数y=f（x）在x=处取得极值．12．在正方形ABCD中，E是线段CD的中点，若=λ+μ，则λ﹣μ=．13．在△ABC中，cosA=，7a=3b，则B=．14．去年某地的月平均气温y（℃）与月份x（月）近似地满足函数y=a+bsin（x+φ）（a，b为常数，0＜φ＜）．其中三个月份的月平均气温如表所示：x 5 8 11y 13 31 13则该地2月份的月平均气温约为℃，φ=．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．已知函数f（x）=cos（2x﹣）﹣cos2x．（Ⅰ）求f（0）的值；（Ⅱ）求函数f（x）的最小正周期和单调递增区间．16．已知数列{a n}是等差数列，且a2=﹣1，数列{b n}满足b n﹣b n﹣1=a n（n=2，3，4，…），且b1=b3=1．（Ⅰ）求a1的值；（Ⅱ）求数列{b n}的通项公式．17．如图，△ABC是等边三角形，点D在边BC的延长线上，且BC=2CD，AD=．（Ⅰ）求的值；（Ⅱ）求CD的长．18．已知函数f（x）=．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当a＜0时，求函数f（x）在区间[0，1]上的最小值．19．已知{a n}是等比数列，a2=2且公比q＞0，﹣2，a1，a3成等差数列．（Ⅰ）求q的值；（Ⅱ）已知b n=a n a n+2﹣λna n+1（n=1，2，3，…），设S n是数列{b n}的前n项和．若S1＞S2，且S k＜S k+1（k=2，3，4，…），求实数λ的取值范围．20．已知函数f（x）=x 3﹣9x，g（x）=3x2+a．（Ⅰ）若曲线y=f（x）与曲线y=g（x）在它们的交点处具有公共切线，求a的值；（Ⅱ）若存在实数b使不等式f（x）＜g（x）的解集为（﹣∞，b），求实数a的取值范围；（Ⅲ）若方程f（x）=g（x）有三个不同的解x1，x2，x3，且它们可以构成等差数列，写出实数a的值．（只需写出结果）2016-2017学年北京市海淀区高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合A={x|x＞2}，B={x|（x﹣1）（x﹣3）＜0}，则A∩B=（）A．{x|x＞1} B．{x|2＜x＜3}C．{x|1＜x＜3}D．{x|x＞2或x＜1}【考点】交集及其运算．【分析】求出B中不等式的解集确定出B，找出A与B的交集即可．【解答】解：由B中不等式解得：1＜x＜3，即B={x|1＜x＜3}，∵A={x|x＞2}，∴A∩B={x|2＜x＜3}，故选：B．2．已知向量=（﹣1，x），=（﹣2，4）．若∥，则x的值为（）A．﹣2 B． C．D．2【考点】平行向量与共线向量．【分析】利用向量共线的充要条件，列出方程求解即可．【解答】解：向量=（﹣1，x），=（﹣2，4）．若∥，可得﹣2x=﹣4，解得x=2．故选：D．3．已知命题p：?x＞0，x+≥2命题q：若a＞b，则ac＞bc．下列命题为真命题的是（）A．q B．￢p C．p∨q D．p∧q【考点】命题的真假判断与应用．【分析】判断四个选项的真假，首先判断命题p和q的真假，对于p，根据基本不等式即可得出命题p为真命题，对于q，若a＞b＞0，c＜0，显然ac＞bc不成立，从而得出命题q为假命题，这样即可找出正确选项．【解答】解：∵x＞0时，，当且仅当x=1时取“=”；∴命题p为真命题，则￢p假；若a＞b＞0，c＜0，则ac＞bc不成立；∴命题q为假命题；∴p∨q为真命题．故选C．4．若角θ的终边过点P（3，﹣4），则tan（θ+π）=（）A．B． C．D．【考点】任意角的三角函数的定义．【分析】利用任意角的三角函数的定义，诱导公式，求得要求式子的值．【解答】解：∵角θ的终边过点P（3，﹣4），则tan（θ+π）=﹣tanθ=﹣=﹣=，故选：C．5．已知函数y=x a，y=log b x的图象如图所示，则（）A．b＞1＞a B．b＞a＞1 C．a＞1＞b D．a＞b＞1【考点】函数的图象．【分析】由图象得到0＜a＜1，b＞1，【解答】解：由图象可知，0＜a＜1，b＞1，故选：A．6．设，是两个向量，则“|+|＞|﹣|”是“?＞0”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据向量数量积的定义和性质结合充分条件和必要条件的定义进行判断即可．【解答】解：若|+|＞|﹣|，则等价为|+|2＞|﹣|2，即||2+||2+2?＞||2+||2﹣2?，即4?＞0，则?＞0成立，反之，也成立，即“|+|＞|﹣|”是“?＞0”的充要条件，故选：C．。

海淀区高三年级第一学期期中练习数 学 （文科） 2012.11本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上 作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集=R U ，集合{|10}A x x =-≤，则U A =ð( )A. (,1)-∞B.(1,)+∞C. (,1]-∞D.[1,)+∞2. 下列函数中，在定义域内是减函数的是( )A. ()f x x =B.()f x =C. 1()2xf x =D.()ln f x x =3. 在平面直角坐标系中，已知点(0,0),(0,1),O A B ，则OA AB ⋅的值为( )A. 1114.函数21()x f x x+=（122x ≤≤）的值域为（ ）A. [2,)+∞B.5[,)2+∞C. 5[2,]2D.(0,2]5. 设0.53π, log 2, cos2a b c ===，则（ ）A. c a b <<B. a c b <<C. b c a <<D. c b a <<6. 已知函数()f x 是定义在实数集R 上的偶函数，则下列结论一定成立的是( )A. R x ∀∈,()()f x f x >-B.0R x ∃∈,00()()f x f x >-C. R x ∀∈,()()0f x f x -≥D. 0R x ∃∈,00()()0f x f x -<7. 已知函数1, 0,() 1, 0,x f x x -<⎧=⎨≥⎩则不等式(1)1xf x -≤的解集为( )A. [1,1]-B. [1,2]C. (,1]-∞D.[1,)-+∞8. 已知集合{(,)|()}M x y y f x ==，若对于任意11(,)x y M ∈，存在22(,)x y M ∈，使得12120x x y y +=成立 ，则称集合M 是“好集合 ”. 给出下列3个集合：①1{(,)|}M x y y x==②{(,)|cos }M x y y x ==③{(,)|e 2}xM x y y ==-其中所有“好集合”的序号是（ ） A. ①②B. ②③C.③D.①②③二、填空题:本大题共6小题,每小题5分,共30分.9. 已知数列{}n a 中，11a =，12n n a a +=，则5a =________.10.2(sin15cos15)______.+=11.已知函数1()f x x=，则曲线()y f x =在点(1,(1))f 处的切线方程为_________. 12.在OAB ∆中，点M 为边AB 中点，若//OP OM ，且(0)OP xOA yOB x =+≠，则____.yx= 13.已知函数()y g x =的图象可以由()sin2f x x =的图象向右平移(0π)ϕϕ<<个单位得到，这两个函数的部分图 象如图所示，则ϕ=________.14.数列{}n a 中，如果存在k a ,使得“1k k a a ->且1k k a a +>”成立(其中2,N k k *≥∈) ,则称k a 为{}n a 的一个峰值.(Ⅰ) 若|7|n a n =--,则{}n a 的峰值为___________________。

海淀区高三年级第一学期期中练习(答案)数学（文科） 2013.11一、选择题：本大题共8小题，每小题5分，共40分。

BDCA B A AB二、填空题:本大题共6小题，每小题5分，共30分。

9. (,1][0,)-∞-+∞ 10.111. 312.2π3,π613. 314.3；6(31)n - （说明：第12和14题的两空，第一空3分，第二空2分）三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程. 15.（本小题满分14分）解：（I ）π()cos(2)2f x x x =+- ---------------------------------------2分sin 2x x + -------------------------------------------------4分π2sin(2)3x =+ -------------------------------------------------6分 ()f x 最小正周期为T π=， -------------------------------------------------8分（II ）因为ππ32x -≤≤，所以ππ4π2333x -≤+≤ --------------------------------------10分所以πsin(2)13x ≤+≤ ---------------------------------------12分所以π2sin(2)23x ≤+≤，所以()f x 取值范围为[.---------------14分 16.（本小题满分13分）解：（Ⅰ）由60A = 和ABC S ∆=1sin602bc = 分 所以6bc =，--------------------------------------3分又32,b c =所以2,3b c ==. ------------------------------------5分（Ⅱ）因为2,3b c ==,60A = ,由余弦定理2222cos a b c bc A =+-可得 ------------------------------------7分2222367a =+-=，即a =. ------------------------------------9分由正弦定理sin sin a b A B =2sin B=，---------------------------------12分所以sin 7B =.------------------------------------13分 17.（本小题满分13分）解：（I ）设等比数列{}n a 的公比为q ，由313a a -=得21(1)3a q -=① ----------------------------------2分由123a a +=得1(1)3a q +=②----------------------------------4分两式作比可得11q -=，所以2q =， ----------------------------------5分把2q =代入②解得11a =，----------------------------------6分所以12n n a -=. ----------------------------------7分（II ）由（I ）可得21141n n n b a -=+=+ ----------------------------------8分易得数列1{4}n -是公比为4的等比数列，由等比数列求和公式可得141(41)143n n n S n n -=+=-+-.------------------------------13分 （说明：未舍1q =-扣1分，若以下正确，给一半分；两个求和公式各2分，化简结果1分）18.（本小题满分13分）解：（I t ，所以点P 的横坐标为21t -,----------------------------2分因为点H 在点A 的左侧，所以2111t -<，即t -<由已知0t >，所以0t << -------------------------------------4分所以2211(1)12,AH t t =--=-所以APH ∆的面积为21()(12),02f t t t t =-<<.---------------------------6分 （II ）233'()6(2)(2)22f t t t t =-=-+- --------------------------7分 由'()0f t =，得2t =-（舍）,或2t =. --------------------------8分 函数()f t 与'()f t 在定义域上的情况如下：------------------------------------12分 所以当2t =时，函数()f t 取得最大值8. ------------------------------------13分19.（本小题满分14分）解：（I ）当1a =时，()ln f x x x =+，1'()1(0)f x x x=+>------------------------------1分 (1)1f =，'(1)2f = -------------------------------3分 所以切线方程为210x y --= --------------------------------5分 （II ）'()(0)x a f x x x+=> -----------------------------6分 当0a ≥时，在(0,)x ∈+∞时'()0f x >，所以()f x 的单调增区间是(0,)+∞；-8分 当0a <时，函数()f x 与'()f x 在定义域上的情况如下：------------------------------------10分 （III ）由（II ）可知①当0a ≥时，(0,)+∞是函数()f x 的单调增区间，且有11()1110a a f e e --=-<-=，(1)10f =>， ---------------11分所以，此时函数有零点，不符合题意；---------------12分②当0a <时，()f a -是函数()f x 的极小值，也是函数()f x 的最小值，所以，当()(ln()1)0f a a a -=-->，即e a >-时，函数()f x 没有零点，-------13分 综上所述，当e 0a -<<时，()f x 没有零点.-----------------14分20.（本小题满分13分）解：（I ）集合A 的所有元素为：4,5,6,2,3,1. ----------------------3分（说明：学生若写成{4,5,6,2,3,1}A =，不扣分，写不全的两个元素给1分） （II ）不妨设成等比数列的这连续7项的第一项为k a ，如果k a 是3的倍数，则113k k a a +=；如果k a 是被3除余1，则由递推关系可得22k k a a +=+，所以2k a +是3的倍数，所以3213k k a a ++=；如果k a 被3除余2，则由递推关系可得11k k a a +=+，所以1k a +是3的倍数，所以2113k k a a ++=. 所以，该7项的等比数列的公比为13.又因为*n a ∈N ，所以这7项中前6项一定都是3的倍数，而第7项一定不是3的倍数（否则构成等比数列的连续项数会多于7项），设第7项为p ，则p 是被3除余1或余2的正整数，则可推得63k a p =⨯ 因为67320143<<，所以63k a =或623k a =⨯.由递推关系式可知，在该数列的前1k -项中，满足小于2014的各项只有： 1k a -=631,-或6231⨯-,2k a -=632,-或6232⨯-,所以首项a 的所有可能取值的集合为{663,23⨯,6631,231,-⨯-6632,232-⨯-}. -----------------------8分（III ）若k a 被3除余1，则由已知可得11k k a a +=+,2312,(2)3k k k k a a a a ++=+=+； 若k a 被3除余2,则由已知可得11k k a a +=+,21(1)3k k a a +=+,31(1)13k k a a +≤++； 若k a 被3除余0，则由已知可得113k k a a +=,3123k k a a +≤+； 所以3123k k a a +≤+， 所以312(2)(3)33k k k k k a a a a a +-≥-+=- 所以，对于数列{}n a 中的任意一项k a ，“若3k a >，则3k k a a +>”.因为*k a ∈N ，所以31k k a a +-≥.所以数列{}n a 中必存在某一项3m a ≤（否则会与上述结论矛盾！）若1m a =,结论得证.若3m a =,则11m a +=；若2m a =,则123,1m m a a ++==,所以1A ∈. -----------------------------------------13分说明：对于以上解答题的其它解法，可对照答案评分标准相应给分。

海淀区高三第一学期期中数学文科试题正式版-+评分标准海淀区高三年级第一学期期中练习数学（文科）级第一学期期中练习参考答案.11数学（文科）阅卷须知:1.评分参考中所注分数，表示考生正确做到此步应得的累加分数.2.其它正确解法可以参照评分标准按相应步骤给分.一、选择题：本大题共8小题，每小题5分，共40分.题号12345678选项CDCDACBD二、填空题:本大题共6小题，每小题5分，共30分.(有两空的小题第一空3分)9.10.11.12.；13.14.或（答对一个给3分）三、解答题:本大题共6小题，共80分.15.（本题13分）解：（I） (1)分……3分（、值各1分）…………4分（II）…………8分（一个公式2分）.…………10分令…………12分得所以函数的单调递增区间为.…………13分说明：①如果没有代入的过程或没有和的函数值，但最后结果正确扣1分；如果第（I）问先化简的，按照第（II）问相应的评分标准给分。

②（II）问中解析式化简可以写成，参照上面步骤给分。

③求单调区间时，正确，但没有写成区间形式、无，只要居其一扣一分，不累扣。

16．（本题13分）解：（Ⅰ）设等比数列的公比为.因为，且所以，得，…………2分又因为，所以，得，.…………4分所以（N+），…………5分所以…………6分…………7分（Ⅱ）因为，所以，…………9分所以.…………11分所以数列的前项和…………12分.…………13分17．（本题13分）解：（Ⅰ）因为△为正三角形，，所以在△中，，所以.所以............1分=............3分（一个公式2分）因为在△中，，............4分所以.............5分所以.............6分（Ⅱ）方法1：在△中，，由正弦定理得：，......8分所以............9分又在正△中，，，所以在△中，，............10分由余弦定理得：............12分所以的长为.............13分方法2：在△中，由正弦定理得：， (8)分所以,............9分............10分所以.............11分在△中，由余弦定理得............12分.所以的长为.............13分18.（本题13分）解：（Ⅰ）由，得,............1分所以，又............3分所以曲线在点处的切线方程为：，即：.............4分（Ⅱ）令，得.............5分与在区间的情况如下：-0+极小值............7分因为............8分所以函数在区间上的最大值为 6.............9分（Ⅲ）证明：设=，则，............10分令，得.与随x的变化情况如下：(-∞,-1)-1(-1,1)1(1,+∞)h(x)+0-0+hx↗极大值↘极小值↗则的增区间为，，减区间为.............11分又，，所以函数在没有零点，......12分又，所以函数在上有唯一零点.............13分综上，在上存在唯一的，使得.19.（本题14分）解：（Ⅰ）； (2)分（Ⅱ）设，则，…………4分所以是以1为首项，2为公差的等差数列，…………5分所以.…………6分（Ⅲ）解法1：，，所以是以1为首项，为公差的等差数列，…………7分所以数列的前n个奇数项之和为…………8分由（Ⅱ）可知，，所以数列的前n个偶数项之和为…………10分所以，…………11分所以.因为，且所以数列是以为首项，为公差的等差数列.............12分由可得，............13分所以当或时，数列的前项和的最小值为.............14分解法二：由得①，............7分②， (8)分把①②两个等式相加可得，，所以.............10分所以数列的前项和，............11分（或：由得............7分 (10)分............11分）所以.因为，且所以数列是以为首项，为公差的等差数列.............12分由可得，............13分所以当或时，数列的前项和的最小值为.............14分20．（本题14分）（Ⅰ）证明：证法1：的定义域为...............1分由得， (2)分...................3分当时，，，故在上单调递增； (4)分当时，，，故在上单调递减；...............5分(此处为推理说明，若用列表说明则扣1分)所以1是函数的极值点. (6)分证法2：（根据极值的定义直接证明）的定义域为 (1)分，……………3分当时，，即；………………4分当时，，即；……………5分根据极值的定义，1是的极值点.………………6分（Ⅱ）由题意可知，证法1：，令，，故在上单调递增.………………7分又，又在上连续，使得，即，………………8分.（*）………………9分随x的变化情况如下：↘极小值↗………………10分.………………11分由（*）式得，代入上式得.………………12分令，，故在上单调递减.………………13分，又，.即.………………14分证法2：，令，………………7分，令得.………………8分随x的变化情况如下：↘极小值↗，即，当且仅当时取到等号 (10)分，令得...................11分随x的变化情况如下：↘极小值↗..................12分，即，当且仅当时取到等号. (13)分.即.………………14分。

海淀区高三年级第一学期期中练习数 学(文科) 2010.11一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1．已知集合{}1,2,3,4,5,6,7U =，{}1,3,5,7A =，{}1,3,5,6,7B =，则集合()U A B ⋂ð是（ ）A ． {2,4,6}B ． {1,3,5,7}C ． {2,4}D ．{2,5,6} 2. 下列函数中，是奇函数且在区间(0,1)内单调递减的函数是（ ） A ．12log y x = B ．1y x=C ．3y x =D ．x y tan =3．已知命题:0p x ∃≥，使23x =，则A ．:0p x ⌝∀<，使23x ≠B ．:0p x ⌝∀≥，使23x ≠C ．:0p x ⌝∃≥，使23x ≠D ．:0p x ⌝∃<，使23x ≠ 4．函数()sin()(0)f x x ωϕω=+>的一段图象如图所示，则ω ＝（ ）A. 41 B.21 C.4πD.2π5.已知160sin ,3log ,222===c b a ，则c b a ,,的大小关系为（ ）A ．c b a <<B ．b c a <<C ． b a c <<D ． a b c <<6．已知向量=a （1，0），=b （0，1），b a c λ+=（∈λR ），向量d 如图所示.则（ ） A ．存在0>λ，使得向量c 与向量d 垂直 B ．存在0λ>，使得向量c 与向量d 夹角为︒60C ．存在0λ<，使得向量c 与向量d 夹角为30︒D ．存在0>λ，使得向量c 与向量d 共线7. 已知321,,a a a 为一等差数列，321,,b b b 为一等比数列，且这6个数都为实数，则下面四个结论中正确的是（ ）①21a a <与32a a >可能同时成立； ②21b b <与32b b >可能同时成立； ③若021<+a a ，则032<+a a ； ④若021<⋅b b ，则032<⋅b bA ．①③B ．②④C ．①④D ．②③ 8．若存在负实数使得方程 112-=-x a x成立，则实数a 的取值范围是（ ）A ．),2(+∞ B. ),0(+∞ C. )2,0( D. )1,0(二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9．已知角α的终边经过点)1,1(-, 则αsin 的值是____________.10. 在锐角ABC ∆中，角C B A ,,的对边分别为c b a ,,，已知,47sin ,6,5===A c b 则==a A ______,cos __________.11．已知直线ex y =与函数xe xf =)(的图象相切，则切点坐标为 .12．在矩形A B C D 中，,12== 且点F E ,分别是边CD BC ,的中点，则=⋅+AC AF AE )(_________.13．如图（１）是反映某条公共汽车线路收支差额（即营运所得票价收入与付出成本的差）y 与乘客量x 之间关系的图象．由于目前该条公交线路亏损，公司有关人员提出了两种调整的建议，如图（２）（３）所示.(1)(2)(3)给出下说法：①图（2）的建议是：提高成本，并提高票价；②图（2）的建议是：降低成本，并保持票价不变； ③图（3）的建议是：提高票价，并保持成本不变； ④图（3）的建议是：提高票价，并降低成本．其中所有说法正确的序号是 ．14．设数列{}n a 的通项公式为*23,(),n a n n N =-∈ 数列}{m b 定义如下：对于正整数m ，m b 是使得不等式n a m ≤成立的所有n 中的最大值，则2b =____________，数列}{m b 的通项公式m b =________．三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15．（本小题共13分）已知在等比数列}{n a 中，11=a ，且2a 是1a 和13-a 的等差中项. （I ）求数列}{n a 的通项公式；（II ）若数列}{n b 满足)(12*N n a n b n n ∈+-=，求}{n b 的前n 项和n S .16. （本小题共13分）已知函数x x x f 2cos )62sin()(+-=π.（I ）若1)(=θf ，求θθcos sin ⋅的值； （II ）求函数)(x f 的单调增区间.17．（本小题共14分）已知函数)(x f 是定义在R 上的偶函数，且0≥x 时，xx f )21()(=.（I ）求)1(-f 的值； （II ）求函数)(x f 的值域A ； （III ）设函数a x a x x g +-+-=)1()(2的定义域为集合B ，若B A ⊆，求实数a 的取值范围.18．（本小题共13分）已知定义在区间]6,0[上的二次函数c bx ax x f ++=2)(满足0)6()0(==f f ，且最大值为9.过动点))(,(t f t P 作x 轴的垂线，垂足为A ，连接O P （其中O 为坐标原点）. （I ）求()f x 的解析式；（Ⅱ）记OAP ∆的面积为S ，求S 的最大值. 19．（本小题共14分）在数列}{n a 中，123...n n a a a a n a ++++=-（1,2,3...n =）． （I ）求123,,a a a 的值；（II ）设1-=n n a b ，求证：数列}{n b 是等比数列；（III ）设)(2n n b c n n -⋅= （1,2,3...n =），如果对任意*n N ∈，都有5t c n <，求正整数t 的最小值.20．（本小题共13分）对x R ∈，定义1, 0sgn()0, 01, 0x x x x >⎧⎪==⎨⎪-<⎩．（I ）求方程)sgn(132x x x =+-的根；（II ）求函数)ln ()2sgn()(x x x x f -⋅-=的单调区间； （III ）记点集()()(){}sgn 1sgn 1,10,0,0x y S x y xyx y --=⋅=>>，点集()(){}lg ,lg ,T x y x y S =∈，求点集T 围成的区域的面积．海淀区高三第一学期期中练习数 学 (文科)参考答案及评分标准一、选择题（本大题共8小题,每小题5分,共40分）分） （9）22 （10）3, 44（11） ),1(e （12）215 （13） ②③（14）2， ⎪⎪⎩⎪⎪⎨⎧++=是偶数是奇数m m m m b m,22,23也可以写成：⎪⎩⎪⎨⎧∈=+∈-=+=)(2,1)(12,1**N k k m k N k k m k b m 三、解答题(本大题共6小题,共80分) （15）（本小题共13分）解：（I ）设等比数列}{n a 的公比为 q 2a 是1a 和13-a 的等差中项3312)1(2a a a a =-+=∴ ……………………………………….2分 223==∴a a q ………………………………………4分)(2*111N n qa a n n n ∈==∴--………………………………………6分 （II ）n n a nb +-=12)212()25()23()11(12-+-+++++++=∴n n n S . ……….8分)2221()]12(531[12-+++++-+++=n n ………..9分21212)12(1--+⋅-+=nn n ……….11分122-+=n n ....……13分 16．（本小题共13分） 解：（I ）22cos 16sin2cos 6cos2sin )(xx x x f ++-=ππ...3分（只写对一个公式给2分）212sin 23+=x ..........5分由1)(=θf ，可得332sin =θ ............7分所以θθθ2sin 21cos sin =⋅ ............8分63= ............9分（II ）当Z k k x k ∈+≤≤+-,22222ππππ， ...........11分即Z k k k x ∈++-∈],4,4[ππππ时，)(x f 单调递增.所以，函数)(x f 的单调增区间是Z k k k ∈++-],4,4[ππππ........... 13分17．（本小题共14分）解：（I ） 函数)(x f 是定义在R 上的偶函数)1()1(f f =-∴ ...........1分又 0≥x 时，xx f )21()(=21)1(=∴f ...........2分 21)1(=-f ...........3分（II ）由函数)(x f 是定义在R 上的偶函数，可得函数)(x f 的值域A 即为0≥x 时，)(x f 的取值范围. ..........5分当0≥x 时，1)21(0≤<x...........7分故函数)(x f 的值域A =]1,0( ...........8分 （III ）a x a x x g +-+-=)1()(2∴定义域}0)1({2≥+-+-=a x a x x B ...........9分 方法一 ：由0)1(2≥+-+-a x a x 得0)1(2≤---a x a x ，即 0)1)((≤+-x a x ...........11分 B A ⊆],,1[a B -=∴且1≥a ...........13分 ∴实数a 的取值范围是}1{≥a a ...........14分 方法二：设a x a x x h ---=)1()(2B A ⊆当且仅当⎩⎨⎧≤≤0)1(0)0(h h ...........11分 即⎩⎨⎧≤---≤-0)1(10a a a ...........13分∴实数a 的取值范围是}1{≥a a ...........14分18．（本小题共13分）解：（I ）由已知可得函数()f x 的对称轴为3=x ，顶点为)9,3( ..........2分 方法一：由⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=944320)0(2a b ac a bf 得0,6,1==-=c b a ...........5分 得2()6,[0,6]f x x x x =-∈ ...........6分方法二：设9)3()(2+-=x a x f ...........4分由0)0(=f ，得1-=a ...........5分2()6,[0,6]f x x x x =-∈ ...........6分（II ）)6,0(),6(2121)(2∈-=⋅=t t t t AP OA t S ...........8分)4(23236)('2t t tt t S -=-= ...........9分列表 ...........11分由上表可得4t =时，三角形面积取得最大值. 即2m ax 1()(4)4(644)162S t S ==⨯⨯-=. ...........13分19．（本小题共14分） 解：（I ）由已知可得 111a a -=，得211=a ...........1分2212a a a -=+，得432=a ...........2分33213a a a a -=++，得873=a ...........3分（II ）由已知可得：n n a n S -= 2≥∴n 时，11)1(----=n n a n S2≥∴n 时，111--+-=-=n n n n n a a S S a ……….4分得21211+=-n n a a ..........5分2≥∴n 时，)1(212121111-=-=---n n n a a a ……….6分即2≥n 时，121-=n n b b ，021111≠-=-=a b ...........7分 ∴数列}{n b 是等比数列，且首项为21-，公比为21 ............8分（III ）由（II ）可得，nn b 21-= ...........9分∴nn n n n n n b c 2)(22-=-⋅= ...........10分∴121212)3(22)1()1(+++-=--+-+=-n nn n n n n n n n n c c ...........11分∴ >>=<<54321c c c c c∴n c 有最大值4343==c c ...........12分对任意*n N ∈，都有5t c n <，当且仅当543t <， ...........13分即415>t ，故正整数t 的最小值是4. ...........14分20． （本小题共13分）解：（I ）当0>x 时，1)sgn(=x ，解方程1132=+-x x ，得0=x （舍）或3=x当0=x 时，0)sgn(=x ，0不是方程0132=+-x x 的解 当0<x 时，1)sgn(-=x ，解方程1132-=+-x x ，得1=x （舍）或2=x （舍） 综上所述，3=x 是方程)sgn(132x x x =+-的根. ...........3分 （每一种情况答对即得1分）（II ）函数)(x f 的定义域是}0{>x x ...........4分 当2>x 时，x x x f ln )(-=，011)('>-=xx f 恒成立 ...........5分 当20<<x 时，)ln ()(x x x f --=，11)('-=xx f解0)('>x f 得10<<x ...........6分 解0)('<x f 得21<<x ...........7分 综上所述，函数)ln ()2sgn()(x x x x f -⋅-=的单调增区间是),2(),1,0(+∞，单调减区间是)2,1(. ...........8分（III ）设点(),P x y T ∈，则()10,10x yS ∈．于是有10)10()10()110sgn()110sgn(=⋅--yxy x ，得()()sgn 101sgn 1011xyx y ⋅-+⋅-=当0>x 时，x x xx x =-=->-)110sgn(,1)110sgn(,0110当0<x 时，x x xx x -=--=-<-)110sgn(,1)110sgn(,0110∴x x x=-)110sgn(同理，y y y=-)110sgn(∴}1),{(=+=y x y x T ...........11分点集T 2． ...........13分 说明：其它正确解法按相应步骤给分.。

海淀区高三年级第一学期期中练习数学（文科） 2007.11学校： 班级： 姓名：一、选择题：本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.（1）设集合{1,2,3,4}A =，集合{1,3,5,7}B =，则AB = （ ）（A ）{1,3} （B ） {1,2,3,4} （C ）{1,3,5,7} （D ）{1,2,3,4,5,7} ﹙2﹚函数)13lg(13)(2++-=x xx x f 的定义域是 （ ）（A ）),31(+∞- （B ）)1,31(- （C ） )31,31(- （D ）)31,(--∞ （3） “1a >”是“11a<”成立的 （ ） （A ）充分不必要条件 （B ）必要不充分条件（C ）充分必要条件 （D ）既非充分也非必要条件（4）在等差数列{}n a 中，已知1233,15,a a a =+=则456a a a ++等于 （ ） （A ）45 （B ）43 （C ）42 （D ）40 （5）下列函数中，在其定义域内是增函数的是 （ ） （A ）2log y x =-（0x >） （B ）3x y -=（x ∈R ） （C ）3y x x =+（x ∈R ） （D ）1y x=（x ∈R ，0≠x ） （6）在1，2，3，4，5这五个数字组成的无重复数字的三位数中，奇数共有（ ） （A ）9个 （B ）18个 （C ） 36个 （D ）40个 （7）给出下列命题：①如果函数()f x 对任意的x ∈R ，满足(2)()f x f x +=，那么函数()f x 是周期函数；②如果函数()f x 对任意12,,x x ∈R 且12x x ≠，都有1212)[()()]0x x f x f x -->(，那么函数()f x 在R 上是增函数；③如果函数()f x 对任意的x ∈R ，都有()()f a x f a x +=- (a 是常数)，那么函数()f x 必为偶函数. 其中真命题有 （ ） （A ）3个 （B ）2个 （C ）1个 （D ）0个（8）如果数列{}n a 满足：首项 11a =，且12,2,n n a n a a n +⎧=⎨+⎩为奇数,为偶数,那么下列说法中正确的是 （ ）（A ）该数列的奇数项135,,,a a a 成等比数列，偶数项246,,,a a a 成等差数列 （B ）该数列的奇数项135,,,a a a 成等差数列，偶数项246,,,a a a 成等比数列（C ）该数列的奇数项135,,,a a a 分别加4后构成一个公比为2的等比数列 （D ）该数列的偶数项246,,,a a a 分别加4后构成一个公比为2的等比数列二、填空题：本大题共6小题，每小题5分，共30分.请把答案填在题中横线上. （9）函数[)()52,0,f x x x =-∈+∞的反函数()1f x -= ，其定义域为 .（10）函数()30y x x x=+>的最小值为 . （11）2621()x x +展开式中的常数项是 .（用数字作答） （12）数列{a n }是公差不为0的等差数列，且a 1, a 3, a 7为等比数列{b n }的连续三项，则等比数列{b n }的公比q = .（13）若不等式22a x x <-对于一切[]2,3x ∈-恒成立，则实数a 的取值范围为_ __ . （14）近年来，在欧美等国家流行一种“数独”推理游戏，游戏规则如下：① 在9×9的九宫格子中,分成9个3×3的小九宫格,用1到9这9个数字填满整个格子; ② 每一行与每一列都有1到9的数字，每个小九宫格里也有1到9的数字，并且一个数字在每行、每列及每个小九 宫格里只能出现一次，既不能重复也不能少.图中A 处应填入的数字为_______；若每行每列填满数字后，所 有数字之和为________.三、解答题：本大题共6小题，共80分.解答应写出文字说明、演算步骤或证明过程. （15）（本小题共13分）已知全集U =R ，集合{}|21,A x x =-<集合3|02x B x x -⎧⎫=>⎨⎬+⎩⎭. （I ）求A ，B ； (II) 求()U A B ð.已知函数()f x ＝3a x 3＋bx 2＋4cx ()x ∈R 是奇函数，函数()f x 在点()()1,1f 处的切线的斜率为－6, 且当x ＝2时，函数()f x 有极值. （I ）求b 的值；（II ）求函数()f x 的解析式； （Ⅲ）求函数()f x 的单调区间.某区有4家不同的达美乐比萨连锁分店，有3名同学前去就餐（假设每位同学选择某店就餐失等可能的）.﹙Ⅰ﹚求这3位同学选择在同一连锁分店就餐的概率；﹙Ⅱ﹚求这3位同学选择在三家连锁分店就餐的概率；﹙Ⅲ﹚求这3位同学中恰有两位同学选择在同一连锁分店就餐的概率.已知等差数列}{n a 的前n 项和为n S ，且35a =，15225S =. 数列}{n b 是等比数列，32325,128b a a b b =+=(其中1,2,3,n =…).（I ）求数列}{n a 和{}n b 的通项公式；（II ）记,{}n n n n n c a b c n T =求数列前项和.今有一长2米宽1米的矩形铁皮，如图，在四个角上分别截去一个边长为x 米的正方形后，沿虚线折起,做成一个无盖的长方体形水箱（接口连接问题不考虑）.（I ）求水箱容积的表达式()f x ，并指出函数()f x 的 定义域；（II ）若要使水箱容积不大于43x 立方米的同时，又使得底面积最大，求x 的值？设函数()f x 的定义域为R ，若()f x x ≤对一切实数x 均成立，则称函数()f x 为Ω函数． （I ）求证：若函数()f x 为Ω函数，则(0)0f =；（II ）试判断函数1()sin f x x x =、()2e e 1x x f x -=+和()322e e 1x x x f x =+中哪些是Ω函数，并说明理由；（III ）若()f x 是奇函数且是定义在R 上的可导函数，函数()f x 的导数()f x '满足|()|1f x '<，试判断函数()f x 是否为Ω函数，并说明理由.海淀区高三年级第一学期期中练习数学（文科）参考答案及评分标准 2007.11一. 选择题（本大题共8小题，每小题5分，共40分）二. 填空题（本大题共6小题，每小题5分.有两空的小题，第一空3分，第二空2分，共30分）(9)(]1(5),,52x --∞ (10)(13) (),8-∞- (14) 4，405三.解答题 （本大题共6小题,共80分） (15) （共13分）解：﹙Ⅰ﹚由已知得：121,x -<-< 解得，13x << ………………. 3分∴集合{|13}A x x =<<. ……………….4分 由已知得：(2)(3)0,x x +-< 解得23x -<<. ……………….8分 ∴集合{|23}B x x =-<<. ………………. 9分 ﹙Ⅱ﹚由（I ）可得：{|1U A x x =…ð或3}x ≥， ……………….11分 故(){|21}U A B x x =-<≤ð. .……………….13分﹙16﹚（共14分）解：（I ）由函数()f x 是奇函数，∴()()f x f x -=-，0b ∴=. 2分 （II ）由()f x =3a x 3＋4cx , 有=')(x f ax 2＋4c 且 0)2(,6)1(='-='f f .∴46,44 0,a c a c +=-⎧⎨+=⎩解得 2,2.a c =⎧⎨=-⎩ 6分 故32()83f x x x =-. ……………………………………………… 8分 ﹙Ⅲ﹚ f （x ）＝32x 3－8x ，∴()f x '=2x 2－8＝2（x ＋2）（x －2）. 10分令)(x f '>0得x <－2或x >2 , 令)(x f '<0得－2<x <2. 12分 ∴函数()f x 的单调增区间为（]2,-∞-，[2,＋∞);单调减区间为[－2,2]. 14分 （或增区间为(,2)-∞，（2,＋∞)；减区间为（－2,2）） （17）（共12分）解：﹙Ⅰ﹚ “这3位同学选择在同一连锁分店就餐”的事件记为A ，由题意16144)(3==A p . ……………….4分 答：这3位同学选择在同一连锁分店就餐的概率为116.﹙Ⅱ﹚“这3位同学选择在三家连锁分店就餐”的事件记为B ，由题意1664234)(3=⨯⨯=B p 38=. ……………….8分 答：这3位同学选择在三家连锁分店就餐的概率为38.﹙Ⅲ﹚“这3位同学中恰有两位同学选择同一连锁分店就餐”的事件记为C ，由题意169434)(323=⨯⨯=C C p . ……………….12分 答：这3位同学中恰有两位同学选择同一连锁分店就餐的概率为916. (18)（ 共14分）解（I ）设等差数列}{n a 的公差为d ，则⎩⎨⎧=⨯+=+,22571515,5211d a d a 2分12,2,11-=⎩⎨⎧==∴n a d a n 故(1,2,3,n =)….4分设等比数列}{n b 的公比为q ，⎪⎩⎪⎨⎧=⋅=,128,82333q b q b b 则 .2,83==∴q b 6分n n n q b b 233=⋅=∴-(1,2,3,n =)….8分（II ）,2)12(n n n c ⋅-= 2323252(21)2,n n T n ∴=+⋅+⋅++-⋅ 10分.2)12(2)32(2523221432+⋅-+⋅-++⋅+⋅+=n n n n n T作差：115432)12(22222++⋅--+++++=-n n n n T3112(12)2(21)212n n n -+-=+--⋅-31122122(21)(21)222822n n n n n n n -++++=+---⋅=+--+1(23)26n n T n +∴=-⋅+(1,2,3,n =)…. 14分 . （19）（共14分） 解：（I ）由已知该长方体形水箱高为x 米，底面矩形长为（22x -）米，宽（12x -）米. 2分∴该水箱容积为()(22)(12)f x x x x =--32462x x x =-+. 4分其中正数x 满足22010.1202x x x ->⎧∴<<⎨->⎩，，∴所求函数()f x 定义域为102x x ⎧⎫<<⎨⎬⎩⎭. 7分 （II ）由3()4f x x ≤，得0x ≤或13x ≥.函数()f x 定义域为102x x ⎧⎫<<⎨⎬⎩⎭,1132x <≤∴. 9分此时底面积为2()(22)(12)462S x x x x x =--=-+ 11[,)32x ∈. 11分 由231()4()44S x x =--，可知()S x 在11[,)32上是减函数， 13分 ∴1.3x =14分 答：满足条件的x 为13米. （20）（共13分）解：（I ）∵函数()f x 的定义域为R ，且()f x x ≤，∴()00f ≤，又()00f ≥，∴(0)0f =. 2分（II ）∵|||sin |||x x x ≤，∴1()sin f x x x =是Ω函数； 4分∵21(0)02f =≠∴2e ()e 1x x f x -=+不是Ω函数； 6分∵22e 2|||||e 1e e x x x x x x x x -==++≤，∴322e ()e 1x xx f x =+是Ω函数. 8分 （III ）∵函数()f x 是定义在R 上的奇函数，∴(0)0f =.∵|()|1f x <’， ∴1()1f x -<<’. 当0x ≥时，设函数()()F x f x x =-和()()G x f x x =+.∴()()10F x f x ''=-<，()()10G x f x ''=+>.∴()()F x f x x =-在[0,)+∞上是减函数，()()G x f x x =+在[0,)+∞上是增函数. ∴()()(0)0F x f x x F =-=≤，()()(0)0G x f x x G =+=≥. ∴()x f x x -≤≤. ∴当0x ≥时，|()|||f x x ≤成立. 当0x <时，则0x ->，∴|()|||f x x -<-，∵()f x 为奇函数，∴|()|||f x x -<-即|()|||f x x ≤成立. ∴当R x ∈时， |()|||f x x ≤对一切实数x 均成立.故函数()f x 是Ω函数. 13分说明：其他正确解法按相应步骤给分.。

北京市海淀区2022-2023学年第一学期期中练习高三数学本试卷分为第一部分（选择题）和第二部分（非选择题），满分150分，考试时长120分钟。

考生务必将答案写在答题纸上，在试卷上作答无效。

考试结束后，将本试卷和答题纸一并交回。

第一部分（选择题 共40分）一、选择题：共10小题，每小题4分，共40分。

在每小题列出的四个选项中，选出符合 题目要求的一项。

1. 已知全集{}0U x x =>，集合{}23A x x =≤≤，则U C A = A.(0,2][3,)+∞U B.(0,2)(3,)+∞U C.(,2][3,)-∞+∞UD.(,2)(3,)-∞+∞U2. 在同一个坐标系中，函数log a y x =与x y a =(01)a a >≠且的图像可能是A BC D3. 已知向量,a b 在正方形网格中的位置如图所示. 若网格中每个小正方形的边长均为1，则 ⋅=a bA.4B. C.4-D.-4. 若等差数列{}n a 和等比数列{}n b 满足11a b =，222a b ==，48a =，则{}n b 的公比为 A.2 B.2- C.4 D.4-5. 已知实数,a b 满足a b >，则下列不等式中正确的是 A.||a b > B.||a b >C.2a ab >D.2ab b >6. 在平面直角坐标系xOy 中，角α与角β均已Ox 为始边，它们的终边关于直线y x =对称. 若3sin 5α=，则cos β= A.45-B.45 C.35-D.357. 已知函数()f x . 甲同学将()f x 的图像向上平移1个单位长度，得到图像1C ；乙同学将 ()f x 的图像上所有点的横坐标变为原来的12（纵坐标不变），得到图像2C . 若1C 与2C 恰好重合，则下列给出的()f x 中符合题意的是A.12()log f x x =B.2()log f x x =C.()2x f x =D.1()()2x f x =8. 已知函数()e e x x f x a b -=+(0)ab ≠，则“0a b +=”是“()f x 为奇函数”的 A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件9. 若P 是ABC △内部或边上的一个动点，且AP xAB yAC =+u u u r u u u r u u u r，则xy 的最大值是 A.14B.12C.1D.210. 我们可以用下面的方法在线段上构造出一个特殊的点集：如图，取一条长度为1的线段，第1次操作，将该线段三等分，去掉中间一段，留下两段；第2次操作，将留下的两段分别三等分，各去掉中间一段，留下四段；按照这种规律一直操作下去. 若经过n 次这样的操作后，去掉的所有线段的长度总和大于99100，则n 的最小值为（参考数据：lg 20.301≈，lg30.477≈） A.9 B.10C.11D.12第二部分（非选择题 共110分）二、填空题共5小题，每小题5分，共25分。

1 / 1
北京市海淀区2019届高三上学期期中考试数学（文科）试题一学期期中练习
数 学(文科) 2009.11
本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1至2页,第II 卷3至9页,共150分.考试时间120分钟.考试结束,将本试卷和答题卡一并交回.第I 卷(选择题共40分)注意事项 ：
1.答卷前将学校、班级、姓名填写清楚.
2.选择题的每小题选出答案后,用铅笔把答题卡上对应的题目的答案标号涂黑.其它小题用钢笔或圆珠笔将答案直接写在试卷上.一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,
选出符合题目要求的一项.
1.已知全集}6,5,4,3,2,1{=U 集合{
}6,4,3,1=A ,{}6,5,4,2=B ,则U A B I a ?等于( ) A.{
}3,1 B.{}5,2 C.{}4 D.∅ 2.函数2()23f x x x =-++的定义域是( )
A.[1,3)-
B. [1,3]-
C. (1,3)-
D. (,1][3,)
-∞-+∞U 3. 下列函数中,在),0(+∞上为减函数的是( )
A.x y 3=
B.x y 1-=
C.x y =
D.x y 2
1log =。