【新课标地区】2014届高三上学期数学月考二(B卷)

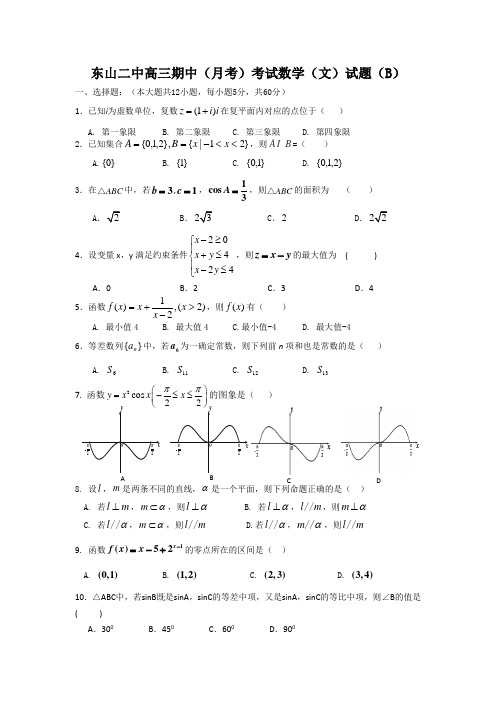
A C D 东山二中高三期中（月考）考试数学（文）试题（B ）一、选择题：（本大题共12小题，每小题5分，共60分）1．已知i 为虚数单位，复数(1)z i i =+在复平面内对应的点位于（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2．已知集合}21|{},2,1,0{<<-==x x B A ，则A B =（ ）A.}0{B. }1{C. }1,0{D. }2,1,0{3．在ABC △中，若3b =,1c =，1cos3A =，则ABC △的面积为 （）AB ．C ．2D ．4．设变量x ，y 满足约束条件20424x x y x y -≥⎧⎪+≤⎨⎪-≤⎩，则z x y =-的最大值为 ( )A ．0B ．2C ．3D ．45．函数)2(,21)(>-+=x x x x f ，则)(x f 有（ ） A. 最小值4B. 最大值4C.最小值-4D. 最大值-46．等差数列}{n a 中，若6a 为一确定常数，则下列前n 项和也是常数的是（ ）A. 6SB. 11SC. 12SD. 13S7. 函数2cos 22y x x x ππ⎛⎫=-≤≤ ⎪⎭的图象是（ ）8. 设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（ ）A. 若l m ⊥，m α⊂，则l α⊥B. 若l α⊥，l m //，则m α⊥C. 若l α//，m α⊂，则l m //D.若l α//，m α//，则l m // 9. 函数1()52x f x x -=-+的零点所在的区间是（ ）A. (0,1)B. (1,2)C. (2,3)D. (3,4)10．△ABC 中，若sinB 既是sinA ，sinC 的等差中项，又是sinA ，sinC 的等比中项，则∠B 的值是( )A ．300B ．450C ．600D ．90011.下列命题正确的是( )A.若Z k k x ∈≠,π,则224sin 41sin x x +≥+ B. 若,0<a 则44-≥+aaC.若0,0a b >>,则lg lg a b +≥D. 若0,0a b <<,则2b aa b+≥12．我们把函数()f x 连续进行n 次求导后得到的函数，称为函数()f x 的n 阶导函数，记为()()n f x （其中n N +∈）．比如：若3()f x x =，则(2)()6f x x =．现给出下列函数： ①()x f x e =；②()ln f x x =；③()sin f x x =；④()cos f x x =；⑤()2f x =． 其中“n N +∃∈，()()n f x =()f x ”的是( )Ａ．①②③ Ｂ．①③⑤ Ｃ．③④⑤ Ｄ．①③④ 二. 填空题：（本大题共4小题，每小题4分，共16分.把答案填在答题卷的相应位置上） 13.如图所示一个空间几何体的三视图(单位：cm )则该几何体的体积为 _______3cm14．已知m>0,n>0,向量()()111a m b n ==-，，，，且a //b ， 则12m n+的最小值是 15．已知函数()f x =2,0,21,0.x x x x ⎧<⎪⎨-≥⎪⎩若2(1)()1f f a -+=，则a = 。

河北省邯郸市2014届高三第二次模拟考试文科数学试卷（带解析）1．已知集合{}1,0,1A =-，{}11B x x =-≤<，则AB =（ ）A.{}0B.{}1,0-C.{}0,1D.{}1,0,1- 【答案】B 【解析】试题分析：由题意知{}1,0A B =-，故选B.考点：集合的交集运算2．复数z 满足()()25z i i --=，则z =（ ）A.22i --B.22i -+C.22i -D.22i + 【答案】D 【解析】试题分析：由题意知()()()()525252222225i i z i i z i i i i ++-====+⇒=+--+，故选D. 考点：复数的除法3．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验，根据收集到的数据（如下表），由最小二乘法求得回归直线方程0.6854.6y x =+，利用下表中数据推断的值为（ ）A.68.2B.68C.69D.67 【答案】B 【解析】 试题分析：1020304050305x ++++==，由于回归直线0.6854.6y x =+过样本中心点(),x y ，所以0.683054.675y =⨯+=，而()162758189755y a =++++=，解得68a =，故选B. 考点：回归直线4．已知双曲线的离心率为2，焦点是()4,0-，()4,0，则双曲线方程为（ ）A.221412x y -= B.221124x y -= C.221106x y -= D.221610x y -= 【答案】A 【解析】试题分析：不妨设双曲线的方程为()222210,0x y a b a b-=>>，焦距为()20c c >，则4c =，离心率为422c e a a a===⇒=，b ∴==为221412x y -=，故选A. 考点：双曲线的方程5．如图，正三棱柱111ABC A B C -的各棱长均为2，其正（主）视图如图1所示，则此三棱柱侧（左）视图的面积为（ ）A.4【答案】D 【解析】试题分析：由题意知，正三棱柱111ABC A B C -的底面是边长为2的正三角形，其边上的高为2sin 60=2=2的矩形，因此，三棱柱的侧2= D. 考点：三视图6．函数x x y cos 2=部分图象可以为（ ）A.B.C.D.【答案】A 【解析】试题分析：易知函数2cos y x x =为偶函数，排除C 、D 选项；当02x π<<，cos 0x >，则2cos 0x x >，排除B 选项，故选A.考点：1.函数的奇偶性；2.函数的图象7．如图是一个算法的程序框图，当输入的x 值为5时，输出y 的结果恰好是31，则①处的关系式是（ ）A.31x y = B.3-=x y C.x y 3= D.3x y = 【答案】C 【解析】试题分析：输入x 的值为5时，经过循环后x 的值变为1-，若①处的函数为13y x =，输出的值为y =()1311-=-，A 选项不正确；若①处的函数为3y x -=，则输出的值为()311y -=-=-，B选项错误；若①处的函数为3x y =，则输出的值为1133y -==，C 选项正确；若①处的函数为3y x =，输出的值为()31y =-1=-，D 选项错误.综上所述，选C.考点：算法与程序框图8．四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，这样交替进行下去，那么第202次互换座位后，小兔坐 在第 号座位上A.1B.2C.3D.4 【答案】B 【解析】试题分析：考虑小兔所坐的座位号，第一次坐在1号位上，第二次坐在2号位上，第三次坐在4号位上，第四次坐在3号位上，第五次坐在1号位上，因此小兔的座位数更换次数以4为周期，因为2025042=⨯+，因此第202次互换后，小兔所在的座位号与小兔第二次互换座位号所在的座位号，因此小兔坐在2号位上，故选B. 考点：1.推理；2.周期性9．已知等比数列前n 项和为n S ，若42=S ,164=S ，则=8S （ ） A.160 B.64 C.64- D.160- 【答案】A 【解析】试题分析：由等比数列的性质可知2S 、42S S -、64S S -、86S S -成等比数列，因此()242S S -=()()()2242264642164364S S S S S S S S ---⇒-===，同理可得()226486423610812S S S S S S --===-， 因此()()()8866442210836124160S S S S S S S S =-+-+-+=+++=，故选A. 考点：等比数列的性质10．若在区间[]0,2中随机地取两个数，则这两个数中较小的数大于32的概率是（ ） A.31 B.32 C.94 D.91 【答案】C 【解析】试题分析：设所选取的两个数分别为x 、y ，且x y <，事件“这两个数中较小的数大于32”所表示的集合为()2,02,02,,3x y x y x y x ⎧⎫≤≤≤≤<>⎨⎬⎩⎭，所表示的平面区域如下图中的阴影部分所表示，其面积等于一个腰长为2的等腰直角三角形减去一个腰长为23的等腰直角三角形的面积而得到，其中阴影部分的面积为221121622239S ⎛⎫=⨯-⨯= ⎪⎝⎭，因此事件“这两个数中较小的数大于32”的概率为 216142949S P ==⨯=，故选C.考点：几何概型11．已知四面体P ABC -的外接球的球心O 在AB 上，且PO ⊥平面ABC ，2AB AC =，若四面体P ABC -的体积为1639，则该球的表面积为（ ） A.π29 B.323π C.16π D.π9【答案】D【解析】试题分析：如下图所示，由于四面体P ABC -的外接球的球心O 在AB 上，则AB 为其外接球的一条直径，OCBAP因此90ACB ∠=，设球O 的半径为r ，在Rt ABC ∆中，22AB AC r AC r ∴==⇒=， 由勾股定理得BC ===，21122ABC S AC BC r ∆∴=⋅==，由于P 为球O 上一点，则PO r =，且PO ⊥平面ABC ，所以231133P ABC ABC V PO S r -∆=⋅===，3r ∴=27382r =⇒=，所以球O 的表面积为2234492r πππ⎛⎫=⨯= ⎪⎝⎭，故选D. 考点：1.勾股定理；2.三角形的面积；3.三棱锥的体积；4.球的表面积12．已知函数()()f x x a a R =+∈在[]1,1-上的最大值为()M a ，则函数()()21g x M x x =--的零点的个数为（ ）A.1个B.2个C.3个D.4个 【答案】C 【解析】试题分析：(),,x a x af x x a x a--≤-⎧=⎨+>-⎩，当1a -≤-时，即当1a ≥时，[]1,1x ∀∈-，()f x x a =+，此时函数()f x 在区间[]1,1-上单调递增，则()()11M a f a ==+；当1a -≥时，即当1a ≤-时，[]1,1x ∀∈-，()f x x a =--，此时函数()f x 在区间[]1,1-上单调递减，则()()11M a f a =-=-+； 当11a -<-<时，即当11a -<<时，(),1,1x a x af x x a a x ---≤≤-⎧=⎨+-<≤⎩，则函数()f x 在区间[]1,a --上单调递减，在[],1a -上单调递增，因此函数()f x 在1x =-处或1x =处取得最大值，且()11f a -=-+，()11f a =+， 显然，当10a -<≤时，()()11f f -≥，此时()()11M a f a =-=-+， 当01a <<时，()()11f f -<，此时()()11M a f a ==+， 综上所述，()1,01,0a a M a a a -+≤⎧=⎨+>⎩，在同一直角坐标系中作出函数()y M x =与函数21y x =-的图象如下图所示，由图象可知，函数()y M x =与函数21y x =-的图象有且仅有三个公共点，故选C.考点：1.函数的最值；2.分类讨论；3.函数的零点；4.函数图象13．若x 、y 满足约束条件⎪⎩⎪⎨⎧≤≤≥+-≥+30030x y x y x ，则y x z -=2的最小值为_______________.【答案】3-. 【解析】试题分析：作出不等式组⎪⎩⎪⎨⎧≤≤≥+-≥+30030x y x y x 所表示的平面区域如下图中的阴影部分所表示，x-y直线30x y -+=交y 轴于点()0,3A ，作直线:2l z x y =-，则z 可视为直线l 轴上截距的2倍，当直线l 经过可行域上的点()0,3A 时，此时直线l 上的截距最大值，此时z 取最大值，即max 2033z =⨯-=-.考点：线性规划14．已知1a =，()1,3b =，()b a a -⊥，则向量a 与向量b的夹角为_______________.【答案】3π. 【解析】试题分析：由题意知(212b =+，()()20b a a b a a a b a -⊥⇔-⋅=⋅-=，即2cos ,0a b a b a ⋅⋅-=，即2112cos ,10cos ,2a b a b ⨯⨯-=⇒=，0,a b π≤≤，,3a b π∴=，因此向量a 与向量b 的夹角为3π. 考点：1.平面向量垂直条件的转化；2.平面向量的数量积；3.平面向量的夹角 15．在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，1=a ，3π=B ，当ABC∆的tan C =_______________.【答案】-. 【解析】 试题分析：11sin 1sin 2234ABC S ac B c π∆==⨯⨯⨯==4c ∴=，由余弦定理得2b = 22222cos 14214cos133a c ac B π+-=+-⨯⨯⨯=，由正弦定理得sin sin cbC B=⇒sin sin 4sin 43c B C b π==⨯==，由余弦定理得222cos 2ab c C ab+-=22214+-==，所以sin tan cos C C C ⎛===- ⎝ 考点：1.三角形的面积；2.余弦定理；3.正弦定理；4.同角三角函数的基本关系16．如图所示点F 是抛物线x y 82=的焦点，点A 、B 分别在抛物线x y 82=及圆()22216x y -+=的实线部分上运动，且AB 总是平行于x 轴，，则FAB ∆的周长的取值范围是_______________.【答案】()8,12. 【解析】试题分析：易知圆()22216x y -+=的圆心坐标为()2,0，则圆心为抛物线28y x =的焦点，圆()22216x y -+=与抛物线28y x =在第一象限交于点()2,4C ，作抛物线28y x =的准线2x =-，过点A 作AD 垂直于直线2x =-，垂足为点D ，由抛物线的定义可知AF AD =，则AF AB AD AB BD +=+=，当点B 位于圆()22216x y -+=与x 轴的交点()6,0时，BD 取最大值8，由于点B 在实线上运动，因此当点B 与点C 重合时，BD 取最小值为4，此时A 与B 重合，由于F 、A 、B 构成三角形，因此48BD <<，所以812BF BD <+<，因此FAB ∆的周长的取值范围是()8,12.17．已知{}n a 为正项等比数列，23a =，6243a =，n S 为等差数列{}n b 的前n 项和，13b =，535S =. （1）求{}n a 和{}n b 的通项公式； （2）设1122n n n T a b a b a b =+++，求n T .【答案】（1）13n n a -=，21n b n =+；（2）3n n T n =⋅. 【解析】试题分析：（1）利用方程组求出等比数列{}n a 的首项与公比以及等差数列{}n b 的首项与公差，从而确定数列{}n a 与{}n b 的通项公式；（2）先确定数列{}n n a b 的通项公式，然后利用错位相减法求出n T .（1）1513243a q a q =⎧⎨=⎩，113a q =⎧∴⎨=⎩，13n n a -∴=，又11351035b b d =⎧⎨+=⎩，132b d =⎧∴⎨=⎩，21n b n ∴=+；（2）()21133537321n n T n -=⨯+⨯+⨯++⋅+，()()2313333537321321n n n T n n -=⨯+⨯+⨯++⋅-+⋅+，相减得 ()2123323232321n n n T n --=+⨯+⨯+⨯-⋅+()()2132333321n n n -=+⨯++-⋅+()3321n n n =-+23n n =-⋅，3n n T n ∴=⋅.考点：1.等差数列与等比数列的通项公式；2.错位相减法求和API（1）根据以上数据估计该城市这30天空气质量指数API 的平均值；（2）若该城市某企业因空气污染每天造成的经济损失S （单位：元）与空气质量指数API （记为w ）的 关系式为0,01004400,1003002000,300350w S w w w ≤≤⎧⎪=-<≤⎨⎪<≤⎩若在本月30天中随机抽取一天，试估计该天经济损失S 大于200元且不超过600元的概率.【答案】（1）175；（2）1330. 【解析】 试题分析：（1）将每组的中点值乘以相应的天数，求和后再除以总的天数即可求出API 的平均值；（2）利用200600S <≤结合分段函数的解析式求出w 的取值范围，从而确定相应的w 的天数，从而确定相应事件的概率.（1）该城市这30天空气质量指数API 的平均值为()2527541255175922542753325330175⨯+⨯+⨯+⨯+⨯+⨯+⨯÷=；（2）设“在本月30天中随机抽取一天，该天经济损失S 大于200元且不超过600元”为事件A ，由200600S <≤得150250w <≤， 根据表格数据得共有9413+=天， 所以()1330P A =. 考点：1.平均数；2.古典概型19．如图，在三棱锥ABC S -中，⊥SA 底面ABC ，90=∠ABC ，且AB SA =，点M 是SB 的中点，SC AN ⊥且交SC 于点N . （1）求证：⊥SC 平面AMN ；（2）当1AB BC ==时，求三棱锥SAN M -的体积.【答案】（1）详见解析；（2）136.【解析】试题分析：（1）由已知条件SA ⊥平面ABC 得到SA BC ⊥，再由已知条件得到BC AB ⊥，从而得到BC ⊥平面SAB ，进而得到B C A M ⊥，利用等腰三角形三线合一得到A M S B ⊥，结合直线与平面垂直的判定定理得到AN ⊥平面SBC ，于是得到AM SC ⊥，结合题中已知条件AN SC ⊥以及直线与平面垂直的判定定理得到SC ⊥平面AMN ；（2）利用（1）中的结论SC ⊥平面AMN ，然后以点S 为顶点，以SN 为高， 结合等体积法求出三棱锥M SAN -的体积.（1）证明：SA ⊥底面ABC ，BC SA ∴⊥，又易知BC AB ⊥， BC ∴⊥平面SAB ，BC AM ∴⊥，又SA AB =，M 是SB 的中点，AM SB ∴⊥， AM ∴⊥平面SBC ，AM SC ∴⊥， 又已知SC AN ⊥， ⊥∴SC 平面AMN ；（2）SC ⊥平面AMN ，SN ∴⊥平面AMN ， 而1SA AB BC ===，AC ∴=SC =又AN SC ⊥，AN ∴=， 又AM ⊥平面SBC ，AM AN ∴⊥，而2AM =，6MN ∴=，122AMB S ∆∴=⨯=， 11336S AMN AMN V S SN -∆∴=⋅=，361==∴--AMN S SAN M V V .考点：1.直线与平面垂直；2.等体积法求三棱锥的体积 20．已知函数()()22xf x eax b x x =+++，曲线()y f x =经过点()0,1P ，且在点P 处的切线为:41l y x =+. （1）求a 、b 的值；（2）若存在实数k ，使得[]1-2，-∈x 时，()()221f x x k x k ≥+++恒成立，求k 的取值范围.【答案】（1）1a =，1b =；（2）⎪⎪⎭⎫⎢⎣⎡+∞-,4123e .【解析】试题分析：（1）利用条件“曲线()y f x =经过点()0,1P ，且在点P 处的切线为:41l y x =+”得到()01f =以及()04f '=，从而列出方程组求解a 、b 的值；（2）利用参数分离法将问题等价转化为()121x e x k x +≥+在区间[]2,1--上恒成立，并构造新函数()()121x e x g x x +=+，转化为()max k g x ≥，利用导数求出函数()g x 在区间[]2,1--的最大值，从而可以求出实数k 的取值范围. （1）()()22xf x eax a b x '=++++，依题意，()()0401f f '=⎧⎪⎨=⎪⎩，即⎩⎨⎧==++142b b a ，解得⎩⎨⎧==11b a ；（2）由()()221f x x k x k ≥+++，得：()()121xex k x +≥+，[]2,1x ∈--时，012<+x()()221f x x k x k ∴≥+++即()()121xe x k x +≥+恒成立，当且仅当()121x e x k x +≥+， 设()()121x e x g x x +=+，[]2,1x ∈--，()()2223()21x e x x g x x +'=+， 由()0g x '=得0x =（舍去），32x =-， 当32,2x ⎛⎫∈--⎪⎝⎭，()0g x '>；当3,12x ⎛⎫∈-- ⎪⎝⎭，()0g x '<， ∴()()121x e x g x x +=+在区间[]2,1-- 上的最大值为323124g e -⎛⎫-= ⎪⎝⎭， 所以常数k 的取值范围为⎪⎪⎭⎫⎢⎣⎡+∞-,4123e .考点：1.导数的几何意义；2.不等式恒成立21．已知1F 、2F 为椭圆E 的左右焦点，点31,2P ⎛⎫⎪⎝⎭为其上一点，且有1PF24PF +=.（1）求椭圆C 的标准方程；（2）过1F 的直线1l 与椭圆E 交于A 、B 两点，过2F 与1l 平行的直线2l 与椭圆E 交于C 、D 两点，求四边形ABCD 的面积ABCD S 的最大值.【答案】（1）22143x y +=；（2）6. 【解析】试题分析：（1）设椭圆E 的标准方程为()222210x y a b a b+=>>，先利用椭圆定义得到2a 的值并求出a 的值，然后将点P 的坐标代入椭圆方程求出b 的值，最终求出椭圆E 的方程；（2）根据平行四边形的几何性质得到4ABCD OAB S S ∆=，即先求出OAB ∆的面积的最大值，先设直线AB 的方程为1x my =-，且()11,A x y 、()22,B x y ，将此直线的方程与椭圆E 的方程联立，结合韦达定理将OAB ∆的面积表示成只含m 的表达式，并利用换元法将代数式进行化简，最后利用基本不等式并结合双勾函数的单调性来求出OAB ∆面积的最大值，从而确定平行四边形ABCD 面积的最大值.（1）设椭圆E 的标准方程为()222210x y a b a b +=>>，由已知124PF PF +=得24a =，∴2a =， 又点31,2P ⎛⎫⎪⎝⎭在椭圆上，∴219144b+=∴b = 椭圆E 的标准方程为22143x y +=； （2）由题意可知，四边形ABCD 为平行四边形 ∴4ABCD OAB S S ∆=， 设直线AB 的方程为1x my =-，且()11,A x y 、()22,B x y ，由221143x my x y =-⎧⎪⎨+=⎪⎩得()2234690m y my +--=，122634m y y m ∴+=+，122934y y m =-+， 11112121122OABOF A OF B S S S OF y y y y ∆∆∆=+=⋅-=-，==令21m t+=，则1t≥，OABS∆==又()19g t tt∴=+在[)1,+∞上单调递增，∴()()110g t g∴≥=，∴OABS∆的最大值为32，所以ABCDS的最大值为6.考点：1.椭圆的定义与方程；2.直线与椭圆的位置关系；3.韦达定理；4.基本不等式22．已知，AB为圆O的直径，CD为垂直AB的一条弦，垂足为E，弦AG交CD于F.（1）求证：E、F、G、B四点共圆；（2）若24GF FA==，求线段AC的长.BA【答案】（1）详见解析；（2）【解析】试题分析：（1）证明90BEF BGF∠=∠=，利用四边形BEFG对角互补证明E、F、G、B四点共圆；（2）利用（1）中的结论结合割线定理得到AF AG AE AB⋅=⋅，然后在Rt ABC∆中利用射影定理得到2AC AE AB=⋅从而计算出AC的值.（1）如图，连结GB，由AB为圆O的直径可知90AGB∠=，BA又CD AB ⊥，所以90AGB BEF ∠=∠=，因此E 、F 、G 、B 四点共圆；（2）连结BC ，由E 、F 、G 、B 四点共圆得AF AG AE AB ⋅=⋅， 又2AF =，6AG =，所以12AE AB ⋅=，因为在Rt ABC ∆中，2AC AE AB =⋅所以AC =考点：1.四点共圆；2.割线定理；3.射影定理23．已知圆C 的极坐标方程为2cos ρθ=，直线l 的参数方程为121122x x t ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数），点A 的极坐标为24π⎛⎫⎪ ⎪⎝⎭，设直线l 与圆C 交于点P、Q . （1）写出圆C 的直角坐标方程； （2）求AP AQ ⋅的值.【答案】（1）()2211x y -+=；（2）12. 【解析】试题分析：（1）在极坐标方程2cos ρθ=的两边同时乘以ρ，然后由222x y ρ=+，cos x ρθ=即可得到圆C 的直角坐标方程；（2）将直线l 的标准参数方程代入圆的直角坐标方程，消去x 、y 得到有关t 的参数方程，然后利用韦达定理求出AP AQ ⋅的值. （1）由2cos ρθ=，得22cos ρρθ=222x y ρ=+，cos x ρθ=，222x y x ∴+=即()2211x y -+=，即圆C 的直角坐标方程为()2211x y -+=；（2）由点A的极坐标4π⎫⎪⎪⎝⎭得点A 直角坐标为11,22⎛⎫⎪⎝⎭，将1211y 22x t⎧=⎪⎪⎨⎪=+⎪⎩代入()2211x y -+=消去x 、y，整理得211022t t --=，设1t 、2t为方程2102t -=的两个根，则1212t t =-，所以1212AP AQ t t ⋅==. 考点：1.圆的极坐标方程与直角坐标方程之间的转化；2.韦达定理 24．已知函数()1f x x x a =-+-. （1）当2a =时，解不等式()4f x ≥；（2）若不等式()2f x a ≥恒成立，求实数a 的取值范围. 【答案】（1）1722x x x ⎧⎫≤-≥⎨⎬⎩⎭,或；（2）⎥⎦⎤ ⎝⎛∞-31,. 【解析】试题分析：（1）将2a =代入函数()f x 的解析式，利用零点分段法将区间分成三段，去绝对值符号，并求出相应的不等式；（2）将问题转化为()min 2f x a ≥，利用双绝对值函数12y x x x x =-+-的最小值为min y12x x -，于是得到()m i n 1f x a =-，问题转化为12a a -≥来求解，解出不等式12a a -≥即可.（1）由()4f x ≥得，⎩⎨⎧≥-≤4231x x ，或⎩⎨⎧≥<<4121x ，或⎩⎨⎧≥-≥4322x x ，解得：12x ≤-或72x ≥，原不等式的解集为1722x x x ⎧⎫≤-≥⎨⎬⎩⎭,或； （2）由不等式的性质得：()1f x a ≥-， 要使不等式()2f x a ≥恒成立，则a a 21≥-，解得：1-≤a 或31≤a 所以实数a 的取值范围为⎥⎦⎤ ⎝⎛∞-31,.考点：1.零点分段法求解不等式；2.不等式恒成立。

试卷类型：B2014届高三月考试题二数学适用地区：新课标地区考查范围：集合、逻辑、函数、导数、三角、向量、数列、不等式建议使用时间：2013年9月底本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.考生作答时，将答案答在答题卡上．在本试卷上答题无效．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上．2．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚．3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效． 4．保持卡面清洁，不折叠，不破损．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．【2013高考真题辽宁】 已知集合A ＝{}x|0<log 4x<1，B ＝{}x|x≤2，则A∩B＝( )A ．(0，1)B ．(0，2]C ．(1，2)D ．(1，2]【答案】D 【解析】∵A＝{x|1<x<4}，B ＝{x|x≤2}，∴A∩B＝{x|1<x≤2}，故选D.2．【2012高考真题辽宁理4】已知命题p ：∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≥0，则⌝p 是（ ） A.∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0 B.∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)≤0 C.∃x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<0 D.∀x 1，x 2∈R ，(f (x 2)-f (x 1))(x 2-x 1)<0 【答案】C【解析】命题p 为全称命题，所以其否定⌝p 应是特称命题，又“(f (x 2)－f (x 1))(x 2－x 1)≥0”的否定为“(f (x 2)－f (x 1))(x 2－x 1)<0”，故“∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≥0”的否定是“∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<0”.故而答案选C.3. (宁夏银川一中2012届高三年级第三次月考数学理)各项均为正数的等比数列{}n a 中，且21431,9a a a a =-=-，则54a a +等于（ ）A.16B.27C.36D.－27 【答案】B【解析】由21431,9a a a a =-=-,得12341,9a a a a +=+=，由等比数列的性质可得，1223344,,,a a a a a a a a ++++依次构成等比数列，又等比数列{}n a 中各项均为正数，所以可得23453,27a a a a +=+=.4. (宁夏银川一中2012届高三年级第三次月考数学理)已知ABC ∆的三边长成公差为2的等差数列，且最大角的正弦值为23，则这个三角形的周长是（ ） A.18 B.21 C.24 D.15 【答案】D【解析】不妨设三边长,,a b c 依次构成公差为2的等差数列，则角C 为最大角.所以由已知得sin C =.所以1c o s 2C=-（C 为最大角，不可能1cos 2C =，否则60C =︒，不符合题意）.由2221cos 22a b c C ab +-==-，及2,4b a c a =+=+，解得3,5,7a b c ===.所以周长为15a b c ++=.5. 【2012高考新课标文5】已知正三角形ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z=－x+y 的取值范围是（ ）A.(1－3，2)B.(0，2)C.(3－1，2)D.(0，1+3) 【答案】A【解析】作出三角形的区域如图，由图象可知当直线z x y +=经过点()1,3B 时，截距最大，此时231=+-=z ，当直线经过点C 时，截距最小.因为x AB ⊥轴，所以2231=+=C y .又ABC ∆的边长为2，设点)2,(x C ，则2)12()1(22=-+-=x AC ，解得31±=x .因为顶点C 在第一象限，所以31+=x .即点()12C +.将点()12C 代入直线y x z +-=，得312)31(-=++-=z ，所以z 的取值范围是()12.选A.6.（理）【湖北省黄冈市2013届高三年级3月份质量检测数学理】已知A ，B ，C ，D 是函数sin()(0,0)2y x πωω=+Φ><Φ<一个周期内的图象上的四个点，如图所示，(,0),6A π-B 为y 轴上的点，C 为图象上的最低点，E 为该函数图象的一个对称中心，B 与D 关于点E 对称，CD 在x 轴上的投影为12π，则,ωΦ的值为 A.2,3πω=Φ= B.2,6πω=Φ= C.1,23πω=Φ= D.1,26πω=Φ=【答案】A【解析】因为CD 在x 轴上的投影为12π，又点,06A π⎛⎫- ⎪⎝⎭，所以函数的四分之一个最小正周期为6124πππ+=，即函数的最小正周期为π.故22πωπ==.又点,06A π⎛⎫- ⎪⎝⎭是处于递增区间上的零点，所以226k πϕπ⎛⎫⨯-+= ⎪⎝⎭，则()23k k πϕπ=+∈Z .又因为02πϕ<<，所以3πϕ=.故选A.（文）【2012高考新课标文9】已知ω>0，πϕ<<0，直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴，则φ=（ ） A.π4 B.π3 C.π2 D.3π4【答案】A 【解析】因为4π=x 和45π=x 是函数图象中相邻的对称轴，所以2445T=-ππ，解得2T π=.又πωπ22==T ，所以1=ω.所以)s i n ()(ϕ+=x x f .因为4π=x 是函数的对称轴，所以()42k k ππφπ+=+∈Z ，所以()4k k πφπ=+∈Z .因为πϕ<<0，所以4πϕ=.检验知此时45π=x 也为对称轴，所以选A.7.（河南省郑州市2012届高三第一次质量预测数学理）已知曲线⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛+=x x y 4cos 4sin 2ππ与直线21=y 相交，若在y 轴右侧的交点自左向右依次记为P 1, P 2, P 3…，则|51P P |等于（ ） A.π B. 2π C. 3π D. 4π【答案】B【解析】因为22sin cos 2sin cos 2sin 1444244y x x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-=+-+=+=- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ cos 21sin 22x x π⎛⎫+=+ ⎪⎝⎭，令11sin 22x +=，得1sin 22x =-，所以226x k ππ=-或5226x k ππ=-、()k ∈Z ，则12x k ππ=-或()512x k k ππ=-∈Z .故点1571311,,,122122P P ππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,所以153171212PP ππ=- 2π=.8. [2013·湖南卷] 函数f(x)＝2ln x 的图像与函数g(x)＝x 2－4x ＋5的图像的交点个数为( )A ．3B ．2C ．1D ．0【答案】B 【解析】 法一：作出函数f(x)＝2ln x ，g(x)＝x 2－4x ＋5的图像如图：可知，其交点个数为2，选B. 法二：也可以采用数值法：可知它们有2个交点，选B.9.（河南省郑州市2012届高三第一次质量预测数学理）若0a b >>,则代数式)(12b a b a -+的最小值为（ ）A.2B.3C. 4D. 5【答案】C【解析】因为0a b >>，所以0a b ->.所以222222114()2a a a b a b a a b a b +≥+=+≥-+-⎛⎫⎪⎝⎭4=，当且仅当224a a =且b a b =-，即2a b ==时等号同时成立.故代数式)(12b a b a -+的最小值为4.10.（理）（山西省太原市2012届高三模拟试题（二）数学文）已知函数()()31log 13xf x x ⎛⎫=-- ⎪⎝⎭有两个零点12,x x ，则（ ）A.121x x <B.1212x x x x >+C.1212x x x x =+D.1212x x x x <+ 【答案】D【解析】3311()log (1)0log (1)33x xf x x x ⎛⎫⎛⎫=--=⇒-= ⎪ ⎪⎝⎭⎝⎭，在同一坐标系中作出函数3log (1)y x =-与13xy ⎛⎫= ⎪⎝⎭的图象，不妨设12x x <，则由函数对称性可知3132log (1)log (1)0x x -+-<，得31212log [()1]0x x x x -++<，即1212()11x x x x -++<.所以1212x x x x <+.（文）(宁夏银川一中2012届高三年级第三次月考数学理)已知函数2()1,()43x f x e g x x x =-=-+-,若有()()f a g b =,则b 的取值范围为（ ）A.2⎡⎣B.(2C.[]1,3D.()1,3【答案】B【解析】()11x f x e =->-,若有()()f a g b =,则2()431g b b b =-+->-，解得22b <+11.(宁夏银川一中2012届高三年级第三次月考数学文)对于非零向量,，定义运算“*”：θs i n ||||n m n m ⋅=*，其中θ为n m ,的夹角，有两两不共线的三个向量c b a 、、，下列结论正确的是( )A.若*=*a b a c ，则=b cB.()*=-*a b a bC.()()*=*a b c a b cD.()*=*+*a+b c a c b c 【答案】D【解析】对于A 项，由*=*a b a c ，得s i ns i n 'θθ=a b a c ，得s i n s i n 'θθ=b c ，不能得到=b c ，故A 项错误； B 项只有在夹角为0时才成立，故B 项错误；对于C 项，()*a b c 是一个与c 共线的向量，()*a b c 是一个与a 共线的向量，又它们两两不共线，显然不可能相等；故C 项错误；故选D 项.12.【2012高考新课标文12，理16】数列{a n }满足a n +1＋(－1)na n ＝2n －1，则{a n }的前60项和为（ ） A.3690 B.3660 C.1845 D.1830 【答案】D【解析】由12)1(1-=-++n a a n n n ,得12]12)1[()1(12)1(112++-+--=++-=-++n n a n a a n n n n n n 12)12()1(++--+-=n n a n n ，即1212)1(2++--=++n n a a n n n ）（，也有3212)1(13+++--=+++n n a a n n n ）（，两式相加得44)1(2321++--=++++++n a a a a n n n n n .设k 为整数，则10`164)14(4)1(21444342414+=+++--=++++++++k k a a a a k k k k k .于是1830)10`16()(14443424141460=+=+++=∑∑=++++=k a a a aS K k k k k K .第II 卷二、填空题（本大题共4小题，每小题5分，共20分。

试卷类型：A2014届高三月考试题二数学适用地区：新课标地区考查范围：集合、逻辑、函数、导数、三角、向量、数列、不等式建议使用时间：2013年9月底本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.考生作答时，将答案答在答题卡上.在本试卷上答题无效.考试结束后，将本试卷和答题卡一并交回.注意事项：1.答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上.2.选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚.3.请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效.4.保持卡面清洁，不折叠，不破损.第Ⅰ卷一、选择题：本大题共12小题，每小题5分，满分60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.[2013高考真题山东] 已知集合A＝{0，1，2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是( )A．1 B．3 C．5 D．9【答案】C0，1，2，∴x－y值只可能为－2，－1，0，1，2五种情况，∴集合B中【解析】∵x，y∈{}元素的个数是5.2. 【2013·新课标全国卷Ⅱ】设a＝log36，b＝log510，c＝log714，则( )A．c＞b＞a B．b＞c＞aC．a＞c＞b D．a＞b＞c【答案】D【解析】 a－b＝log36－log510＝(1＋log32)－(1＋log52)＝log32－log52>0，b －c ＝log 510－log 714＝(1＋log 52)－(1＋log 72)＝log 52－log 72>0， 所以a>b>c ，选D.3.（理）【2012高考真题辽宁理6】在等差数列{a n }中，已知a 4＋a 8＝16，则该数列前11项和S 11＝（ ）A.58B.88C.143D.176 【答案】B【解析】由等差数列性质可知，a 4＋a 8＝a 1＋a 11＝16，S 11＝a 1＋a 112＝88.（文）【2012高考真题辽宁文4】在等差数列{a n }中，已知a 4＋a 8＝16，则a 2＋a 10＝（ ）A.12B.16C.20D.24 【答案】B【解析】由等差数列的性质“m ＋n ＝i ＋j ，m ，n ，i ，j ∈N *，则a m ＋a n ＝a i ＋a j ”，得a 4＋a 8＝a 2＋a 10＝16.4. 【2012高考真题山东理7】若42ππθ⎡⎤∈⎢⎥⎣⎦，，sin 2θ，则sin θ=（ ）A.35 B.45 D.34【答案】D【解析】因为,42ππθ⎡⎤∈⎢⎥⎣⎦，所以2,2πθπ⎡⎤∈⎢⎥⎣⎦.所以02cos <θ.所以812sin 12cos 2-=--=θθ.又81sin 212cos 2-=-=θθ，所以169sin 2=θ.又由,42ππθ⎡⎤∈⎢⎥⎣⎦，得sin 0θ>，所以43sin =θ.选D.5. 【2012高考真题新课标理5】已知{}n a 为等比数列，472a a +=，568a a =-，则110a a +=（ ）A.7B.5C.-5D.-7【答案】D【解析】因为}{n a 为等比数列，所以87465-==a a a a .又274=+a a ，所以2474-==a a ，或4274=-=a a ，.若2474-==a a ，，解得18101=-=a a ，，此时7101-=+a a ；若4274=-=a a ，，解得18110=-=a a ，，仍有7101-=+a a .综上, 7101-=+a a .选D.6.【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为（ ）A.2B.0C.－1D.1-【答案】A【解析】因为90≤≤x ，所以6960ππ≤≤x .则67363ππππ≤-≤-x ，所以当336πππ-=-x 时，函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最小值为2sin 3π⎛⎫-= ⎪⎝⎭；当236πππ=-x 时，函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值为22sin 2=π，所以最大值与最小值之和为32-.选A.7.（理）（山西省太原市2012届高三模拟试题（二）数学理）下列判断错误的是（ ）A. “22am bm <”是”a b <”的充分不必要条件B.命题“2,10x x x ∀∈--≤R ”的否定是“ 2000,10x x x ∃∈-->R ” C.若,p q 均为假命题，则p q ∧为假命题 D.若()4,0.25B ξ，则1D ξ=【答案】D【解析】A 项中，22am bm a b <⇒<；但a b <不能推出22am bm <,例如：当0m =时，22am bm =，故A 正确；B 项显然正确；C 项中,,p q 均为假可以推出p q ∧为假，正确；D 项中，()40.2510.250.75D ξ=⨯⨯-=错误.（文）（山西省太原市2012届高三模拟试题（二）数学文）下列判断正确的是（ ）A. 若命题p 为真命题，命题q 为假命题，则命题“p q ∧”为真命题B.命题“若0xy =，则0x =”的否命题为“若0xy =，则0x ≠”C. “1sin 2α=”是” 6πα=”的充分不必要条件D. .命题“,20xx ∀∈>R ”的否定是“ 00,20x x ∃∈≤R ”【答案】D【解析】A 项中，因为p 真q 假，所以p q ∧为假命题.故A 项错误；B 项中，“若0xy =，则0x =”的否命题为“若0xy ≠，则0x ≠”， 故B 项错误；C 项中，1sin 2α=是6πα=的必要不充分条件，故C 项错误；D 选项正确.8.（东北三省四市教研协作体等值诊断联合考试（2012长春三模）数学文）函数21()3coslog 22f x x x π=--的零点个数为（ ） A.2 B.3 C.4 D.5【答案】B【解析】在同一坐标系内画出函数3cos 2y x π=和21log 2y x =+的图象，可得交点个数为3. 故选B.9. 【2013高考真题山东卷】 函数y ＝xcos x ＋sin x 的图像大致为( )【答案】D 【解析】∵f(－x)＝－xcos(－x)＋sin(－x)＝－(xcos x ＋sin x)＝－f(x)，∴y ＝xcos x ＋sin x 为奇函数，图像关于原点对称，排除选项B.当x ＝π2时，y ＝1>0，排除选项C ；x ＝π，y ＝－π<0，排除选项A ；故选D.10.（河南省郑州市2012届高三第一次质量预测文）在ABC ∆中，若2AB AB AC BA BC CA CB =++，则ABC ∆是( )A.等边三角形B.锐角三角形C.钝角三角形D.直角三角形 【答案】D【解析】由2AB AB AC BA BC CA CB =++，得()()AB AB AC BC BA CA -=-，得AB CB =BC BC ，得()0BC BC AB +=，得0BC AC =,故BC AC ⊥.故ABC ∆是直角三角形.11. (河北省石家庄市2012届高中毕业班第二次模拟考试数学文)已知函数()2,0,2,0.x f x x x ≥⎧=⎨-+<⎩则满足不等式()()232f x f x -<的x 的取值范围为( )A. B. (-3,1) C. [-3,0) D. (-3,0)【答案】D【解析】当22030x x ≥⎧⎨-<⎩时，满足2232x >-+,无解；当22030x x <⎧⎨-≥⎩时，满足222x <-+，解得0x ≤<；当22030x x <⎧⎨-<⎩时，满足23222x x -+<-+，解得3x -<<.综上可知，x 的范围为(3,0)-.12. (河北省石家庄市2012届高中毕业班第二次模拟考试数学理)设不等式组表示的平面区域为,n n D a 表示区域D n 中整点的个数(其中整点是指横、纵坐标都是整数的点），则=( )A. 1012B. 2012C. 3021D. 4001 【答案】C【解析】因为0y >，所以令4004nx n x -+>⇒<<,又x 为整数，所以1,2,3x =.当x=1时，43y n n n ≤-+=，有3n 个整数点；当x=2时，242y n n n ≤-+=，有2n 个整数点；当x=3时，34y n n n ≤-+=，有n 个整数点.综上，共有6n 个整数点，所以6,n a n n =∈N .则数列2{}n a 是以212a =为首项，公差为12的等差数列.故()220122462012()100611201220122a a a a a a +⨯++++=⨯ 3021=.第Ⅱ卷二、填空题（本大题共4小题，每小题5分，共20分。

乌鲁木齐地区2014年高三年级第二次诊断性测验理科数学（问卷）（卷面分值：150分考试时间：120分钟）注意事项：1.本卷分为问卷和答卷两部分，答案务必书写在答卷（或答题卡）的指定位置上.2.答卷前，先将答卷密封线内（或答题卡中的相关信息）的项目填写清楚.第Ⅰ卷（选择题共60分）一、选择题：共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合A={x|x2<1}, B=[0, 1)，则A∩B=A. (0, 1)B. (0, 1]C. [0, 1)D. [0, 1]2.已知复数z1=a+bi与z2=c+di (a, b, c, d∈R, z2≠0)，则z1z2∈R的充要条件是A. ad+bc=0B. ac+bd=0C. ac-bd=0D. ad-bc=03.已知数列{a n}是各项均为正数的等比数列，若a2=2, 2a3+a4=16，则a5=A. 4B. 8C. 16D. 324.某几何体的三视图如图所示，根据图中标出的尺寸（单位: cm）可得这个几何体的体积是A. 13cm3 B. 23cm3C. 43cm3 D. 83cm35.已知函数y=f(2x)+x是偶函数，且f(2)=1，则f(-2) =A. 2B. 3C. 4D. 56.阅读如右图所示的程序框图，若输入n的值为6，运行相应程序，则输出的n的值为A. 3B. 5C. 10D. 167.若平面向量,,a b c两两所成的角相等，且||1,||1,||3a b c===，则||a b c++等于A. 2B. 5C. 2或5D. 2或 58.已知⊙A1：(x+2)2 + y2=12和点A2(2, 0)，则过点A2且与⊙A1 相切的动圆圆心P的轨迹方程为A. x23- y2 = 1 B. x23+ y2 = 1C. x2 - y2 = 2D. x212+y28= 1正视图侧视图俯视图9.将函数f(x)=sin(2x+θ) (-π2 < θ < π2 )的图象向右平移φ（φ > 0）个单位长度后得到函数g(x)的图象，若f(x), g(x)的图象都经过点P(0, 32)，则φ的值可以是A. 5π3B. 5π6C. π2D. π6 10.设a = log 0.10.2，b = log 0.20.4，c = log 0.30.6，则A. a > b> cB. a > c > bC. b > c > aD. c > b > a 11.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数，这个数能被3整除的概率为A. 827B. 1927C. 1954D. 3554 12.若直线ax + by + c = 0与抛物线y 2=2x 交于P ，Q 两点，F 为抛物线的焦点，直线PF ，QF 分别交抛物线于点M ，N ，则直线MN 的方程为A. 4cx -2by + a=0B. ax -2by + 4c=0C. 4cx + 2by + a=0 C.ax + 2by + 4c=0 第Ⅱ卷（非选择题 共90分）本卷包括必考题和选考题两部分.第13题 ~ 第21题为必考题，每个试题考生都必须作答.第22题 ~ 第24题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分13.设等差数列{a n }的前n 项和为S n ，若S 9=11，S 11=9，则S 20= ； 14.如图，矩形OABC 内的阴影部分由曲线f(x)=sinx 及直线x=a(a ∈(0,2π) )与x 轴围成.向矩形OABC 内随机掷一点，该点落在阴影部分的概率为12，则a= ；15.直三棱柱ABC -A 1B 1C 1的各个顶点都在同一个球面上. 若AB=AC=AA 1=2，∠BAC=120°，则此球的表面积等于 . 16.已知直线x+y+1=0与曲线C ：y = x 3-3px 2相交于点A ，B ，且曲线C 在A ，B 处的切线平行，则实数p 的值为 .三、解答题第17~21题每题12分，解答应在答卷的相应各题中写出文字说明，证明过程或演算步骤.17.（本小题满分12分）如图，已知OPQ 是半径为3，圆心角为π3的扇形，C 是扇形弧上的动点，ABCD 是扇形的内接矩形，记∠COP 为x ，矩形ABCD 的面积为f(x)。

绝密*启用前最新2014年全国高考理科数学二模试题及答案（新课标）理科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。

第一卷一． 选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

（1）已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈；,则B 中所含元素的个数为（ ）()A 3 ()B 6 ()C 8 ()D 10【解析】选D5,1,2,3,4x y ==，4,1,2,3x y ==，3,1,2x y ==，2,1x y ==共10个 （2）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（ ）()A 12种 ()B 10种 ()C 9种 ()D 8种【解析】选A甲地由1名教师和2名学生：122412C C =种（3）下面是关于复数21z i=-+的四个命题：其中的真命题为（ ） 1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p ()C ,p p 24 ()D ,p p 34【解析】选C 22(1)11(1)(1)i z i i i i --===---+-+--1:p z =22:2p z i =，3:p z 的共轭复数为1i -+，4:p z 的虚部为1-（4）设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，P 为直线32ax =上一点，∆21F PF 是底角为30的等腰三角形，则E 的离心率为（ ）()A 12 ()B 23 ()C 34()D 45【解析】选C∆21F PF 是底角为30的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔== （5）已知{}n a 为等比数列，472a a +=，568a a =-，则110a a +=（ ）()A 7 ()B 5 ()C -5 ()D -7【解析】选D472a a +=，56474784,2a a a a a a ==-⇒==-或472,4a a =-= 471101104,28,17a a a a a a ==-⇒=-=⇔+=- 471011102,48,17a a a a a a =-=⇒=-=⇔+=-（6）如果执行右边的程序框图，输入正整数(2)N N ≥和实数12,,...,n a a a ，输出,A B ，则（ ）()A A B +为12,,...,n a a a 的和 ()B 2A B+为12,,...,n a a a 的算术平均数 ()C A 和B 分别是12,,...,n a a a 中最大的数和最小的数 ()D A 和B 分别是12,,...,n a a a 中最小的数和最大的数【解析】选C（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）()A 6 ()B 9 ()C 12 ()D 18【解析】选B该几何体是三棱锥，底面是俯视图，高为3 此几何体的体积为11633932V =⨯⨯⨯⨯=（8）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线x y 162=的准线交于,A B两点，AB =；则C 的实轴长为（ ）()A ()B ()C 4 ()D 8【解析】选C设222:(0)C x y a a -=>交x y 162=的准线:4l x =-于(A -(4,B --得：222(4)4224a a a =--=⇔=⇔=（9）已知0ω>，函数()sin()4f x x πω=+在(,)2ππ上单调递减。

邯郸市2014届高三第二次模拟考试理科数学答案一、选择题1—5 CDDAC 6--10 BCBAD 11--12 BA二、填空题 13、12, 14、 7, 15、 122n -+, 16、 3 三、解答题17.解：(Ⅰ)23()2cos 2f x x x =+-1cos 232222x x +=+- =sin(2)16x π+- ……………………2分 所以()f x 最小正周期22T ππ== ……………………4分 70,2,2666x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦ 1sin(2),162x π⎡⎤∴+∈-⎢⎥⎣⎦()f x ∴最大值为0. ……………………6分 (Ⅱ) 由1()2f A =-得1sin(2)62A π+= 又132666A πππ<+< 5266A ππ∴+= 3A π∴= ……………………8分解法一：由余弦定理得,222222cos a b c bc A b c bc =+-=+-22223()()()3()44b c b c b c bc b c ++=+-≥+-= ………………10分即4b c +≤=,6a b c ∴++≤ （当且仅当2b c ==时取等号）所以6L =………………12分 解法二：由正弦定理得2sin sin sin 3b c B Cπ==，即,b B c C ==，所以sin )b c B C +=+ ……………………8分2sin()]4sin()36B B B ππ=+-=+ ……………………10分 2503666B B ππππ<<∴<+< 1sin()126B π∴<+≤（当且仅当3B C π==时取最大值） 4b c ∴+≤，∴6a b c ++≤所以6L =……………12分18. 解:（Ⅰ）设A 表示事件“雨雪天”， B 表示事件“非雨雪天”， C 表示事件“打出租上班”， ()()()()()()B C P A C P A P BC P AC P C P +=+= …………………………2分18.01.08.05.020.0%10112836194121112836194=⨯+⨯≈⨯⎪⎭⎫ ⎝⎛+-+⨯+= ……4分 （Ⅱ）X 的可能取值为0，2，20，40 ………………6分()0=X P 72.09.08.0%901128361941=⨯≈⨯⎪⎭⎫ ⎝⎛+-= ()2=X P 10.05.020.021112836194=⨯≈⨯+= ()20=X P 08.01..08.0%101128361941=⨯≈⨯⎪⎭⎫ ⎝⎛+-= ()40=X P 10.05.020.021112836194=⨯≈⨯+= …………10分 ∴X 的分布列为x y ()80.510.04008.02010.0272.00=⨯+⨯+⨯+⨯=X E （元）…………12分19. 解:(Ⅰ)证明: SA ABC ⊥底面,BC SA ∴⊥,又易知BC AB ⊥BC SAB ∴⊥平面BC AM ∴⊥ ……………………2分又AD SA = ,M 是SD 的中点, AM SB ∴⊥,AM SBC ∴⊥平面AM SC ∴⊥， ……………………4分又已知SC AN ⊥,⊥∴SC 平面AMN . ………………6分(Ⅱ) 解法一:如图,以A 为坐标原点,AB 为x 轴，AS 为z 轴,建立空间直角坐标系xyz A -,由于AB SA =,可设1AB SA ==,则()()()()0,0,0,1,0,01,1,0,0,0,1A B C S 11(,0,M11(,0,(1,1,0)22AM AC ∴==………………8分设平面ACM 的一个法向量(,,)n x y z = 则⎪⎩⎪⎨⎧=∙=∙00n n 即011022x y x z +=⎧⎪⎨+=⎪⎩ 可得(1,1,1)n =- ………………10分由（1）可知CS AMN 为面的法向量，易求(1,1,1)CS =-- 1cos ,3||||CS n CS n CS n ⋅∴== ∴ 二面角N MA C --的余弦值是13 . …………12分 20. 解：（I ）设椭圆E 的标准方程为22221(0)x y a b a b+=>> 由已知12||||4PF PF +=得24a =，∴2a = ……………………2分又点3(1,2P 在椭圆上，∴219144b+= ∴b =椭圆E 的标准方程为22143x y += ……………………4分 （II ）由题意可知，四边形ABCD 为平行四边形 ∴A B C D S =4OAB S ∆设直线AB 的方程为1x my =-，且1122((A x y B x y ,)、,)由221143x my x y =-⎧⎪⎨+=⎪⎩得22(34)690m y my +--= ∴12122269,3434m y y y y m m +==-++ ……………………6分 OAB S ∆=1OF A S ∆+1OF B S ∆=12112||||OF y y ⋅-=1212||y y - =12…………………………8分 令21m t +=，则1t ≥ O A B S ∆== 10分 又1()9g t t t=+在[1,)+∞上单调递增 ∴()(1)10g t g ≥= ∴O A B S ∆的最大值为32所以ABCD S 的最大值为6. ………………………………12分21.解：（Ⅰ）当1a =-时，22()(2)ln 2f x x x x x =-⋅-+，定义域(0,)+∞()(22)ln (2)2f x x x x x '=-⋅+--.……………………1分(1)3f '∴=-，又(1)1f =，()f x 在(1,(1))f 处的切线方程340x y +-= …………………………2分（Ⅱ）（ⅰ）令()()2g x f x x =--=0 则22(2)ln 22x x x ax x -⋅++=+即1(2)ln x x a x--⋅= …………………………4分 令1(2)ln ()x x h x x--⋅=， 则2221122ln 12ln ()x x x h x x x x x ---'=--+= 令()12ln t x x x =--22()1x t x x x--'=--=， ()0t x '<，()t x 在(0,)+∞上是减函数…………………6分又(1)(1)0t h '==，所以当01x <<时，()0h x '>，当1x <时，()0h x '<，所以()h x 在(0,1)上单调递增，在(1,)+∞上单调递减，max ()(1)1h x h ∴==，所以当函数()g x 有且仅有一个零点时1a= …………………8分 （ⅱ）当1a =，22()(2)ln g x x x x x x =-⋅+-，若2e x e -<<，()g x m ≤，只需证明max ()g x m ≤，()(1)(32ln )g x x x '=-⋅+，令()0g x '= 得321xx e -==或 ………………10分 又2e x e -<<，∴函数()g x 在322(,)e e --上单调递增，在32(,1)e -上单调递减，在(1,)e 上单调递增 又333221()22g e e e ---=-+ ， 2()23g e e e =-333322213()2222()()22g e e e e e e e g e----=-+<<<-=即32()()g e g e-<2max()()23g x g e e e==-223m e e∴≥-………………12分22.解：（I）如图，连结GB，由AB为圆O的直径可知90AGB∠=又CD AB⊥，所以90AGB BEF∠=∠=因此E F G B、、、四点共圆………………4分（II）连结BC，由E F G B、、、四点共圆得AF AG AE AB⋅=⋅又2,6AF AG==，所以12AE AB⋅=因为在Rt ABC∆中，2A C A E A B=⋅所以AC=……………………10分23.解：（I）由2cosρθ=，得22cosρρθ=222x yρ=+，cos xρθ=……………………2分222x y x∴+=即22(1)1x y-+=即圆C的直角坐标方程为22(1)1x y-+=……………………4分（II）由点A的极坐标)4π得点A直角坐标为11(,)22……………6分将12211y22xt⎧=+⎪⎪⎨⎪=+⎪⎩代入22(1)1x y-+=消去,x y整理得212t-=，……………………8分BA设12t t 、为方程211022t t --=的两个根，则1212t t =- 所以||||AP AQ ⋅=121||2t t =. ……………………10分 24解：（Ⅰ）由4)(≥x f 得，⎩⎨⎧≥-≤4231x x ，或⎩⎨⎧≥<<4121x ，或⎩⎨⎧≥-≥4322x x …………2分 解得：27,21≥-≤x x 或原不等式的解集为⎭⎬⎫⎩⎨⎧≥-≤2721x x x ，或 …………4分 （Ⅱ）由不等式的性质得：1)(-≥a x f ， …………6分 要使不等式a x f 2)(≥恒成立，则a a 21≥- ……………………8分解得：1-≤a 或31≤a 所以实数a 的取值范围为⎥⎦⎤ ⎝⎛∞-31, ……………………10分。

1 / 42014年高考模拟考试试卷高三数学（理科）（考试时间120分钟，满分150分）考生注意：1． 每位考生应同时领到试卷与答题纸两份材料，所有解答必须写在答题纸上规定位置，写在试卷上或答题纸上非规定位置一律无效；2． 答卷前，考生务必将姓名、准考证号码等相关信息在答题纸上填写清楚； 3． 本试卷共23道试题，满分150分，考试时间120分钟。

一、填空题（本大题共14小题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分。

1、经过点 (1, 0)A 且法向量为(2, 1)n =-的直线l 的方程是 ．2、已知集合1|1, A x x R x ⎧⎫=<∈⎨⎬⎩⎭，集合B 是函数lg (1)y x =+的定义域，则A B = ．3、方程22124x y m +=+表示焦点在y 轴上的双曲线，则实数m 取值范围是 ．4、已知数列{}n a 是首项为1，公差为2的等差数列，()n S n N *∈表示数列{}n a 的前n 项和，则2lim1nn S n →∞=- ．5、在261)x x-（的展开式中，含3x 项的系数等于 ．（结果用数值作答） 6、方程sin cos 1x x +=-的解集是 ． 7、实系数一元二次方程20x ax b ++=的一根为131ix i+=+（其中i 为虚数单位），则 a b += ．8、某高中共有学生1000名，其中高一年级共有学生380人，高二年级男生有180人．如果在 全校学生中抽取1名学生，抽到高二年级女生的概率为0.19，现采用分层抽样（按年级分层） 在全校抽取100人，则应在高三年级中抽取的人数等于 ．9、已知()2x f x =的反函数为111(), ()(1)(1)y f x g x f x f x ---==--+，则不等式()0g x <的解集是．10、已知圆柱M 的底面圆的半径与球O 的半径相同，若圆柱M 与球O 的表面积相等，则它们的体积之比V V 圆柱球：= （结果用数值作答）． 11、在极坐标系中，圆4sin ρθ=的圆心到直线 ()6R πθρ=∈的距离等于 ．12、如果函数(]()210,1()311,ax x f x ax x ⎧-∈⎪=⎨-∈+∞⎪⎩，2()log g x x =，关于x 的不等式()()0f x g x ⋅≥ 对于任意(0, )x ∈+∞恒成立，则实数a 的取值范围是 ．2 / 413、已知二次函数2() ()f x x ax a x R =-+∈同时满足：①不等式()0f x ≤的解集有且只有一个元素；②在定义域内存在120x x <<，使得不等式12()()f x f x >成立．设数列{}n a 的前n 项 和为n S ，且()n S f n =．规定：各项均不为零的数列{}n b 中，所有满足10i i b b +⋅<的正整数i 的个数称为这个数列{}n b 的变号数．若令1n nab a =-（*n N ∈），则数列{}n b 的变号数等 于 ．14、已知圆22: (01)O x y c c +=<≤，点 (, )P a b 是该圆面（包括⊙O 圆周及内部）上一点，则a b c ++的最小值等于 ．二、选择题（本大题共4小题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分。

北京市东城区 2014 届高三（上）第二次月考数学试卷参照答案一、选择题（本大题共10 小题，每题 4 分，共40 分）1．已知圆的直角坐标方程为22x +y ﹣ 2y=0．在以原点为极点， x 轴正半轴为极轴的极坐标系中，该圆的方程为（）A ．ρ=2cosθB．ρ=2sin θC．ρ=﹣ 2cosθD．ρ=﹣ 2sinθ答案： B22．若会合， B={1 ， 2} ，则“m=1 ”是“A∪ B={0 ，1， 2} ”的（）A{0 ， m }A ．充要条件B．充足不用要条件C．必需不充足条件D．既不充足又不用要条件答案： B3．以下函数中，与函数 y=x 同样的函数是（）x logA ．B．D．C． y=lg10y=2 2x y=y=答案： C4．以下函数中，在区间（ 0，+∞）上是增函数的是（）A ． y=﹣ x 2B． y=x2﹣ 2C．y=D．y=log 2答案： B5．和直线 3x﹣ 4y+5=0 对于 x 轴对称的直线的方程为（）A ． 3x+4y ﹣ 5=0B． 3x+4y+5=0C．﹣ 3x+4y ﹣ 5=0D．﹣ 3x+4y+5=0解答：解：和直线 3x﹣ 4y+5=0 对于 x 轴对称的直线，其斜率与直线3x﹣ 4y+5=0 的斜率相反，设所求直线为3x+4y+b=0 ，两直线在 x 轴截距相等，因此所求直线是3x+4y+5=0 ．应选 B．6．实数﹣?+lg4+2lg5的值为（）A ． 2B． 5C． 10D． 20答案： D7．若函数 f（ x）=log a x（ 0＜ a＜1）在区间 [a，2a]上的最大值是最小值的 3 倍，则 a 等于（）A ．B．C．D．答案： A8．已知函数则“﹣2≤a≤0”是“f（x）在 R 上单一递加”的（）A ．充分而不用要条件B．必需而不充足条件C．充足必需条件D．既不充足也不用要条件解答： 解：函数 f （ x ） =x 2+ax+1 在 [1，+∞）上单一递加则a ≥﹣ 2函数 f （ x ）=ax 2+x+1 在（﹣ ∞， 1）上单一递加则≤a ≤0而函数在 R 上单一递加则≤a ≤0≤a ≤0? ﹣ 2≤a ≤0∴ “﹣2≤a ≤0”是 “f （ x ）在 R 上单一递加 ”的必需而不充足条件应选： B9．双曲线 ﹣ =1 的渐近线与圆2 2相切，则双曲线离心率为（）x +（ y ﹣ 2） =1 A ． B ．C ． 2D ． 3解答：解：∵双曲线 ﹣ =1（ a ＞ 0， b ＞ 0）的渐近线为 bx ±ay=0，依题意，直线 2 2bx ±ay=0 与圆 x +（ y ﹣2） =1 相切， 设圆心（ 0， 2）到直线 bx ±ay=0 的距离为 d ， 则 d== =1，∴双曲线离心率e= =2．应选 C ．10．已知函数，若方程f （ x ） =x+a 有且只有两个不相等的实数根，则实数a 的取值范围是（）A ．（ ﹣∞，1]B ． （ 0，1）C ． [0，+∞）D ． （﹣ ∞，1）解答：解：函数的图象如下图，当 a ＜ 1 时，函数 y=f （ x ）的图象与函数 y=x+a 的图象有两个交点， 即方程 f （x ） =x+a 有且只有两个不相等的实数根应选： D二、填空题（本大题共7 小题，每题 5 分，共 35 分）11．函数的定义域为（，1]．12．（ 5 分）若点在幂函数 y=f （ x）的图象上，则f（ x）=．13．（ 5 分）已知32是奇函数，则 a﹣ b=﹣ 1 ．f（ x）=2x +ax +b﹣1解答：解：∵ f（ x）是 R 上的奇函数，∴f（ 0）=0，得 b﹣ 1=0 ，解得 b=1 ．3 2∴f（ x） =2x +ax ．又∵ f（﹣ x）+f（ x）=0，∴﹣ 2x 3232，化为+ax +2x +ax =0立．∴ a=0．∴ a﹣ b= ﹣1．故答案为﹣ 1．2ax =0，对于随意实数R 都成14．已知，假如f（x0）=3，那么x0=．解答：解：∵ f（ x） =，∴若 x0＜0， f（ x0） ==3 ，∴x0=﹣；同理若 x0＞ 0， f（ x0）=x 0+1=3 ，∴x0=2．故答案为： 2，﹣．15．（ 5 分）（坐标系与参数方程选做题）参数方程（θ为参数）表示的图形上的点到直线y=x 的最短距离为．22x=2 或 4x﹣ 3y 16．经过点 M （ 2， 1），而且与圆 x +y ﹣ 6x﹣ 8y+24=0 相切的直线方程是﹣5=0 ．22﹣ 6x﹣8y+24=0 化为标准方程为（22解答：解：圆 x +y x﹣ 3）+（ y﹣4） =1 ，圆心（ 3， 4），半径 R=1当斜率不存在时，x=2 是圆的切线，知足题意；斜率存在时，设方程为y﹣ 1=k（ x﹣ 2），即 kx ﹣y+1﹣ 2k=0∴由圆心到直线距离d=R，可得=1∴k= ，∴直线方程为 4x﹣ 3y﹣ 5=0综上，所求切线方程为x=2 或 4x﹣ 3y﹣ 5=0故答案为： x=2 或 4x﹣ 3y﹣5=017．如图，已知椭圆的左极点为 A ，左焦点为F，上极点为B，若∠BAO+ ∠ BFO=90 °，则该椭圆的离心率是．解答：解：设椭圆的右焦点为 F′，由题意得 A （﹣ a， 0）、B（ 0，b）， F′（ c， 0），∵∠ BAO+ ∠ BFO=90 °，且∠ BFO= ∠ BF′O，∴∠ BAO+ ∠ BF′O=90 °，∴?=0，222∴（ a， b）?（ c，﹣ b） =ac﹣ b =ac﹣ a +c =0，∴ e﹣ 1+e 2=0 ，解得e=，故答案为：．三、解答题（本大题共 6 小题，共 75 分）2﹣ x ﹣ 118．（ 10 分）定义在 R 上的奇函数 f （x ），当 x ＞0 时， f （ x ）=x （Ⅰ）求 f （ x ）的分析式；（Ⅱ）写出函数 f （ x ）的单一区间． （不用证明）解答：解：（Ⅰ）设 x ＜ 0，则﹣ x ＞0，由题意可得 f （﹣ x ）=（﹣ x ）2﹣（﹣ x ）﹣ 1=﹣ f （ x ），∴ f （ x ） =﹣x 2﹣ x+1 ．再由 f （ 0）=0 ，可得 f （x ） =．（Ⅱ）联合函数f （ x ）的图象可得函数f （x ）的单一增区间为： （﹣ ∞，﹣）、（，+∞），减区间为（ ， 0）、（0，）．19．（ 13 分）已知函数 f （ x ） =lg （ 1+x ） +lg （ 1﹣ x ）． （Ⅰ）求函数 f （ x ）的定义域； （Ⅱ）判断函数 f （ x ）的奇偶性；（Ⅲ）判断 f （x ）在（ 0， 1）内的单一性并证明． 解答：解：（ 1）由函数的分析式可得，解得﹣ 1＜x ＜ 1，故函数的定义域为（﹣1， 1）．（ 2）因为函数的定义域对于原点对称，且 f （﹣ x ） =lg （ 1﹣ x ） +lg （ 1+x ） =f （x ），故函数为偶函数．（ 3）因为函数 f （ x ）=lg （ 1+x ） +lg （ 1﹣ x ） =lg （ 1﹣ x 2），可得函数 f （x ）在（ 0， 1）内的单一递减．证明：当 0＜ x ＜ 1 时，令 t=1 ﹣x 2，则 t ′=﹣ 2x ＜ 0，故函数 t 在（ 0， 1）内的单一递减，再联合复合函数的单一性可得f （x ）在（ 0， 1）内的单一递减．22内有最大值﹣ 5，求 a 的值及函数 20．（ 13 分）已知 f （ x ）=﹣ 4x +4ax ﹣ 4a ﹣ a 在区间 [0，1] 表达式 f （ x ）． 解答： ﹣ 4a ，此抛物线极点为．解∵ f （ x ）=﹣ 4222±1＜ 2（舍当≥1，即 a≥2 时， f （x）取最大值﹣ 4﹣a ．令﹣ 4﹣ a =﹣ 5，得 a =1，a=去）．当 0＜＜ 1，即 0＜ a＜ 2 时， x= 时， f（ x）取最大值为﹣4A 、令﹣ 4a=﹣ 5，得 a= ∈（ 0， 2）．当≤0，即 a≤0 时， f （ x）在 [0， 1] 内递减，∴ x=0 时， f （ x）取最大值为﹣4a﹣ a 2，22令﹣ 4a﹣ a =﹣ 5，得 a2+4a ﹣ 5=0，解得 a=﹣5，或 a=1，此中﹣ 5∈（﹣∞， 0]．综上所述， a=或 a=﹣ 5时， f（ x）在 [0， 1] 内有最大值﹣ 5．∴ f（ x） =﹣4x 22﹣20x﹣ 5．+5x ﹣或 f （ x） =﹣ 4x21．（ 13 分） m 为什么值时，直线222x﹣ y+m=0 与圆 x +y =5（Ⅰ）无公共点；（Ⅱ）截得的弦长为2；（Ⅲ）交点处两条半径相互垂直．解答：解：由圆方程得：圆心（0， 0），半径 r=，∴圆心到直线 2x﹣y+m=0 的距离 d=，（Ⅰ）若直线与圆无公共点，则有d＞r，即＞，解得： m＞ 5 或 m＜﹣ 5；（Ⅱ）依据题意得： 2=2，即5﹣ =1，解得： m=±2；（Ⅲ）依据题意得：弦长的平方等于2r 2，即（ 222，） =2r∴4（ 5﹣） =10，解得： m=±．22．（ 13 分）已知 f（ x）=2+log 3x， x∈[1， 9] ，求 y=[f （ x） ]2+f （ x 2）的最大值及y 取最大值时 x 的值．解答：解：∵ f（ x） =2+log3x，x∈[1，9]，2222）∴ y=[f （ x） ] +f （ x） =（2+log 3x）+（ 2+log3 x3233x=（ log x） +6log x+6，令 t=log由题意可得即 1≤x≤3，则 t∈[0， 1]∴ y=t 2+6t+6= （ t+3 ） 23 在 [0， 1]上 增当 t=1 即 x=3 ，函数有最大 ， y max =1323．（ 13 分）已知 的右焦点F （ 1，0）， M 的上 点，O 坐 原点，且△ OMF是等腰直角三角形．（Ⅰ）求 的方程；（Ⅱ）能否存在直l 交 于P ，Q 两点，且使点F △PQM 的垂心（垂心：三角形三高 的交点）？若存在，求出直 l 的方程；若不存在， 明原因．解答：解：（Ⅰ）由 △OMF 是等腰直角三角形，得 b=1 ，a=b= ，故 方程．⋯（5 分）（Ⅱ）假 存在直l 交 于 P ， Q 两点，且使点F △PQM 的垂心，P （ x 1， y 1），Q （ x 2 ，y 2），因 M （0， 1），F （ 1， 0），因此 k PQ =1．⋯（7 分）于是 直 l 的方程 y=x+m ，代入 方程，消元可得3x 2+4mx+2m 2 2=0．由 △ ＞0，得 m 2＜ 3，且 x 1+x 2=，x 1x 2=．⋯（9 分）由 意 有，因此 x 1（ x 2 1） +y 2（ y 1 1） =0，因此 2x 1x 2+（ x 1+x 2）（ m 1） +m 2m=0．整理得 2×（ m1）+m 2m=0 ．解得 m=或 m=1．⋯（ 12 分），当m=1 ， △ PQM 不存在，故舍去．当 m=，所求直l 存在，且直l 的方程y=x．⋯（ 13 分）。

孝感市２０１３—２０１４学年度高中三年级第二次统一考试数学（理科）(含答案)本试卷满分１５０分，考试时间１２０分钟．注意事项：１２照题号顺序在各题的答题区域内作答，超出答题区域书写的答案无效．３一、选择题：本大题共１０小题，每小题５分，共５０分．在每小题给出的四个选项中，只有一项是符合题目要求的．１的共轭复数是Ａ.Ｂ.Ｃ.Ｄ.２，，，则｜ａ＋ｂ＋ｃ｜＝Ａ.０Ｂ.３Ｃ.Ｄ.３集数据如下：经检验，这组样本数据具有线性相关关系，那么对于加工零件的个数ｘ与加工时间ｙ这两个变量，下列判断正确的是ＡＢ０，７６）ＣＤ４ξ服从正态分布，若，则Ｐ（ξ＜０）＝Ａ５，则输入的ｘ可能为Ａ.－１Ｂ.０Ｃ.１Ｄ.５６的最大值是Ａ.２Ｂ.Ｃ.７的最大值是Ａ.２Ｂ.１Ｃ.Ｄ.３８与ｘ轴交于Ａｎ、Ｂｎ两点，以ＡｎＢｎ表示这两点间的距离，则Ａ１Ｂ１＋Ａ２Ｂ２＋…＋Ａ２０１４Ｂ２０１４的值是Ａ. Ｂ. Ｃ.Ｄ.９{１，２，３}，Ｎ＝{１，２，３，４}．定义映射ｆ：Ｍ→Ｎ，则从中任取一个映射满足由点Ａ（１，ｆ（１）），Ｂ（２，ｆ（２）），Ｃ（３，ｆ（３））构成△ＡＢＣ且ＡＢ＝ＢＣ的概率为Ａ. Ｂ. Ｃ. Ｄ.１０(ａ＞０，ｂ＞０)的右焦点为Ｆ，过点Ｆ作与ｘ轴垂直的直线ｌ交两渐近线于Ａ、Ｂ两点，且与双曲线在第一象限的交点为Ｐ，设Ｏ为坐标原点，若(λ，μ∈Ｒ)，λμ＝，则该双曲线的离心率为Ａ. Ｂ. Ｃ. Ｄ二、填空题：本大题共６小题，考生共需作答５小题，每小题５分，共２５分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．（一）必考题（１１－１４题）１１簧伸长的长度成正比．如果２０Ｎ的力能使弹簧伸长３ｃｍ，则把弹簧从平衡位置拉长６ｃｍ（在弹性限度内）时所做的功为．（单位：焦耳）１２．若目标函数ｚ＝ａｂｘ＋ｙ（ａ＞０，ｂ＞０）的最大值为８，则ａ＋ｂ的最小值为．１３．１４续偶数２、４；第三次取３个连续奇数５、７、９；第四次取４个连续偶数１０、１２、１４、１６；第五次取５个连续奇数１７、１９、２１、２３、２５．按此规则一直取下去，得到一个子数列１，２，４，５，７，９，１０，１２，１４，１６，１７，…．则在这个子数列中，由１开始的第２９个数是，第２０１４个数是．（二）选考题（请考生在第１５、１６两题中任选一题作答，如果全选，则按第１５题作答结果计分）１５△ＡＢＣ的面积，则∠ＢＡＣ＝．１６取相同的长度单位．已知直线ｌ的极坐标方程为，圆Ｃ的参数方程为（θ为参数），则直线ｌ被圆Ｃ截得的弦长为．三、解答题：本大题共６小题，满分７５分，解答应写出文字说明，证明过程或演算步骤．１７．（本小题满分１２分）已知函数，ｘ∈Ｒ．（１）求函数ｆ（ｘ）的最小正周期及单调增区间；（２）在△ＡＢＣ中，角Ａ、Ｂ、Ｃ所对的边分别是ａ、ｂ、ｃ，又，ｂ＝２，△ＡＢＣ的面积等于３，求边长ａ的值．１８题满分１２分）已知{ａｎ}为等差数列，Ｓｎ为其前ｎ项和，且．（１）求ａｎ，Ｓｎ；（２）若ａｋ，ａ２ｋ－２，ａ２ｋ＋１（ｋ∈Ｎ{ｂｎ}的前三项，设Ｔｎ＝ａ１ｂ１＋ａ２ｂ２＋ａ３ｂ３＋…＋ａｎｂｎ，求Ｔｎ．１９交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，交通指数取值范围为０～１０，分为五个级别，０～２畅通；２～４基本畅通；４～６轻度拥堵；６～８中度拥堵；８～１０严重拥堵．早高峰时段，从某市交通指挥中心随机选取了四环以内的５０个交通路段，依据其交通指数数据绘制的直方图如右图．（１）这５０个路段为中度拥堵的有多少个？（２）据此估计，早高峰四环以内的三个路段至少有一个是严重拥堵的概率是多少？（３）某人上班路上所用时间若畅通时为２０分钟，基本畅通为３０分钟，轻度拥堵为３６分钟，中度拥堵为４２分钟，严重拥堵为６０分钟，求此人所用时间的数学期望．２０如图①，在平面内，ＡＢＣＤ是∠ＢＡＤ＝６０°且ＡＢ＝ａ的菱形，ＡＤＭＡ１和ＣＤＮＣ１都是正方形．将两个正方形分别沿ＡＤ，ＣＤ折起，使Ｍ与Ｎ重合于点Ｄ１．设直线ｌ过点Ｂ且垂直于菱形ＡＢＣＤ所在的平面，点Ｅ是直线ｌ上的一个动点，且与点Ｄ１位于平面ＡＢＣＤ同侧（图②）．（１）求证：不管点Ｅ如何运动都有ＣＥ∥面ＡＤＤ１；（２）当线段ＢＥ＝时，求二面角Ｅ—ＡＣ—Ｄ１的大小．２１已知曲线Ｃ１：和曲线Ｃ２：（０＜λ＜１）．曲线Ｃ２的左顶点恰为曲线Ｃ１的左焦点．（１）求λ的值；（２）设Ｐ（ｘ０，ｙ０）为曲线Ｃ２上一点，过点Ｐ作直线交曲线Ｃ１于Ａ，Ｃ两点，直线ＯＰ交曲线Ｃ１于Ｂ，Ｄ两点，若Ｐ为ＡＣ中点．①求证：直线ＡＣ的方程为ｘ０ｘ＋２ｙ０ｙ＝２；②四边形ＡＢＣＤ的面积是否为定值？若是，请求出该定值；若不是，请说明理由．２２已知函数ｆ（ｘ）＝ａｌｎｘ－ａｘ－３（ａ∈Ｒ）．（１）讨论函数ｆ（ｘ）的单调性；（２）若函数ｙ＝ｆ（ｘ）的图象在点（２，ｆ（２））处的切线的倾斜角为４５°，对于任意的ｔ∈［１，２］，函数在区间（ｔ，３）上总不是单调函数，求实数ｍ的取值范围；（３）求证：。