命题及其逆命题、否命题与逆否命题,

四种命题及其关系本节课主要讲解了命题的概念及其结构，命题是能够判断真假的陈述句，其中真命题为真实陈述，假命题为虚假陈述。

需要注意的是，不是任何语句都是命题，只有能够判断真假的陈述句才是命题。

命题通常可以改写成“若p，则q”的形式，其中p为命题的条件，q为命题的结论。

类型二：四种命题及其关系本节课还介绍了四种命题及其关系，包括原命题、逆命题、否命题和逆否命题。

其中，逆命题和否命题是互为逆命题的，逆否命题和原命题是互为逆否命题的。

需要注意的是，四种命题之间的真假关系并不总是有必然联系，只有互为逆否命题的两个命题同真同假。

因此，在判断命题真假时需要仔细分析其结构和关系。

本课程介绍了命题的概念和结构，以及四种命题及其关系。

命题是能够判断真假的陈述句，其中真命题为真实陈述，假命题为虚假陈述。

需要注意的是，只有能够判断真假的陈述句才是命题，而命题通常可以改写成“若p，则q”的形式，其中p 为命题的条件，q为命题的结论。

四种命题包括原命题、逆命题、否命题和逆否命题，其中逆命题和否命题是互为逆命题的，逆否命题和原命题是互为逆否命题的。

需要注意的是，四种命题之间的真假关系并不总是有必然联系，只有互为逆否命题的两个命题同真同假。

因此，在判断命题真假时需要仔细分析其结构和关系。

判断下列语句中哪些是命题，是命题的判断其是真命题还是假命题。

1) 末位是5的整数能被5整除。

2) 平行四边形的对角线相等且互相平分。

3) 两直线平行，则斜率相等。

4) 在三角形ABC中，若∠A=∠B，则sinA=sinB。

5) 余弦函数是周期函数吗？举一反三：变式1】判断下列语句是否为命题？若是，判断其真假。

1) x>1；2) 当x=1时，x>1；3) 你是男生吗？4) 求证：π是无理数。

变式2】下列语句中是命题的是（）A。

|x+a|B。

{0}∈NC。

元素与集合D。

真子集变式3】判断下列语句是否是命题。

1) 这是一棵大树。

2) sin30°=1/2.3) x+1>0；4) 梯形是平行四边形。

第1讲命题及其关系、充分条件与必要条件1.了解“p，则q”形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系.2.理解必要条件、充分条件与充要条件的意义.1.命题的概念在数学中用语言、符号或式子表达的，可以的陈述句叫做命题.其中的语句叫真命题，的语句叫假命题.2.四种命题及其关系(1)四种命题(2)四种命题间的关系(3)四种命题的真假关系①两个命题互为逆否命题，它们有的真假性；②两个命题互为逆命题或互为否命题，它们的真假性[思考探究]一个命题的“否命题”与“否定”是同一个命题吗？提示：不是.命题的否命题既否定命题的条件又否定命题的结论，而命题的否定仅是否定命题的结论.3.充分条件与必要条件(1)如果p⇒q，则p是q的，q是p的；(2)如果p⇒q，q⇒p，则p是q的.1.命题真假的判定对于命题真假的判定，关键是分清命题的条件与结论，只有将条件与结论分清，再结合所涉及的知识才能正确地判断命题的真假.2.四种命题的关系的应用掌握原命题和逆否命题，否命题和逆命题的等价性，当一个命题直接判断它的真假不易进行时，可以转而判断其逆否命题的真假.[特别警示]当一个命题有大前提而写出其他三种命题时，必须保留大前提，大前提不动.※ 分别写出下列命题的逆命题、否命题、逆否命题、命题的否定，并判断它们的真假： (1)若q ≤1，则方程x 2＋2x ＋q ＝0有实根；(2)若x 、y 都是奇数，则x ＋y 是偶数；(3)若xy ＝0，则x ＝0或y ＝0；(4)若x 2＋y 2＝0，则x 、y 全为0.1.利用定义判断(1)若p ⇒q ，则p 是q 的充分条件； (2)若q ⇒p ，则p 是q 的必要条件；(3)若p ⇒q 且q ⇒p ，则p 是q 的充要条件；(4)若p ⇒q 且q p ，则p 是q 的充分不必要条件； (5)若p q 且q ⇒p ，则p 是q 的必要不充分条件；(6)若p q 且q p ，则p 是q 的既不充分也不必要条件. 2.利用集合判断记条件p 、q 对应的集合分别为A 、B ，则： 若A ⊆B ，则p 是q 的充分条件； 若A B ，则p 是q 的充分不必要条件； 若A ⊇B ，则p 是q 的必要条件； 若A B ，则p 是q 的必要不充分条件； 若A ＝B ，则p 是q 的充要条件；若A ⊈ B ，且A ⊉ B ，则p 是q 的既不充分也不必要条件.[特别警示] 从集合的角度理解，小范围可以推出大范围，大范围不能推出小范围. ※ 指出下列各组命题中，p 是q 的什么条件？(1) p ：a ＋b ＝2，q ：直线x ＋y ＝0与圆(x －a )2＋(y －b )2＝2相切； (2) p ：|x |＝x ，q ：x 2＋x ≥0；(3) 设l ，m 均为直线，α为平面，其中l ⊄α，m ⊂α，p ：l ∥α，q ：l ∥m ； (4) 设α∈)2,2(ππ-，β∈)2,2(ππ-，p ：α＜β，q ：tan α＜tan β.1.条件已知证明结论成立是充分性.结论已知推出条件成立是必要性；2.证明分为两个环节，一是充分性；二是必要性.证明时，不要认为它是推理过程的“双向书写”，而应该进行由条件到结论，由结论到条件的两次证明；3.证明时易出现必要性与充分性混淆的情形，这就要分清哪是条件，哪是结论.※求证：关于x的方程x2 ＋mx ＋1＝0有两个负实根的充要条件是m≥2.若关于x的方程x2 ＋mx ＋1＝0有两个正实根，求m的取值范围？第2讲简单的逻辑联结词、全称量词与存在量词1.简单的逻辑联结词：了解逻辑联结词“或”、“且”、“非”的含义.2.全称量词与存在量词(1)理解全称量词与存在量词的意义(2)能正确地对含有一个量词的命题进行否定.1.命题p∧p2.全称量词3.1.判断含有逻辑联结词的命题真假的关键是对逻辑联结词“或”、“且”、“非”含义的理解. 数学中的逻辑联结词“或”与日常生活中的“或”意义不同，日常生活中的“或”带有不能同时具备之意.数学中的逻辑联结词“且”与日常生活中的“且”意义基本一致，表示而且的意思. 数学中的逻辑联结词“非”与日常生活中的“非”意义基本一致，表示否定的意思.2.解决该类问题基本步骤为：(1)弄清构成它的命题p 、q 的真假； (2)弄清它的结构形式；(3)根据真值表判断构成新命题的真假.※ 已知命题p ：∃x ∈R ，使tan x ＝1，命题q ：x 2－3x ＋2＜0的解集是{x |1＜x ＜2}，下列结论： ①命题“p ∧q ”是真命题； ②命题“p ∧q ”是假命题； ③命题“p ∨q ”是真命题； ④命题“p ∨q ”是假命题. 其中正确的是 ( )A. ②③B. ①②④C. ①③④D. ①②③④1.要判断一个全称命题是真命题，必须对限定的集合M 中的每一个元素x ，验证p (x )成立.2.要判断一个全称命题是假命题，只要能举出集合M 中的一个x ＝x 0，使p (x 0)不成立即可.3.要判断一个特称命题是真命题，只要在限定的集合M 中，至少能找到一个x ＝x 0，使p (x 0)成立即可，否则这一特称命题就是假命题.※ 判断下列命题是否是全称命题或特称命题，若是，用符号表示，并判断其真假. (1)有一个实数α，sin 2α＋cos 2α≠1；(2)任何一条直线都存在斜率；(3)所有的实数a ，b ，方程ax ＋b ＝0有唯一解； (4)存在实数x ，使得2112=+-x x 。

第一章常用逻辑用语单元复习教学目标：（1）了解命题及其逆命题，否命题与逆否命题．（2）理解必要条件、充分条件与充要条件的意义，会分析四种命题的相互关系．（3）简单的逻辑联结词：了解逻辑联结词“或”、“且”、“非”的含义．(4)全称量词与存在量词：①理解全称量词与存在量词的意义；②能正确地对含有一个量词的命题进行否定． 教学重点：必要条件、充分条件与充要条件的意义及四种命题的相互关系，逻辑联结词“或”、“且”、“非”的含义 全称量词与存在量词的意义以及对含有该量词的命题的否定.教学难点：一个命题的否命题及命题的否定，必要条件、充分条件与充要条件的判断.基本知识：（1）命题的定义： 。

由 条件 和结论构成（2）命题的四种形式及其真假关系 ，（3）逻辑联结词“或”、“且”、“非”的含义在集合中分别相当于 并 、 交 、补（4）充分条件、必要条件、充要条件的概念（5）全称量词与存在量词的定义及含有一个该量词的命题的否定 典型例题例1．分别指出下列复合命题的构成形式及构成它的简单命题：（1）x=2或x=3是方程x 2-5x+6=0的根（2）π既大于3又是无理数（3）直角的大小不等于90︒（4）垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧例2．分别写出由下列各种命题构成的“p 或q ”“p 且q ”“非p ”形式的复合命题,并判断它们的真假：（1）p ：末位数字是0的自然数能被5整除 q ：5∈{x|x 2+3x-10=0}（2）p ：四边都相等的四边形是正方形 q ：四个角都相等的四边形是正方形（3）p ：Φ∈0； q ： {}R x x x ⊆<--053|2（4）p ：不等式x 2+2x -8<0的解集是：{x|-4<x<2} q ：不等式x 2+2x -8<0的解集是：{x| x<-4或x> 2}例3．写出下列命题的逆命题、否命题、逆否命题，并分别判断真假：（1）面积相等的两个三角形是全等三角形。

高考数学复习考点知识与题型专题讲解命题及其关系、充分条件与必要条件考试要求1.理解命题的概念.2.了解“若p，则q”形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系.3.理解必要条件、充分条件与充要条件的含义．知识梳理1．命题用语言、符号或式子表达的，可以判断真假的陈述句叫做命题，其中判断为真的语句叫做真命题，判断为假的语句叫做假命题．2．四种命题及其相互关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题，它们具有相同的真假性．②两个命题为互逆命题或互否命题，它们的真假性没有关系．3．充分条件、必要条件与充要条件的概念若p⇒q，则p是q的充分条件，q是p的必要条件p是q的充分不必要条件p⇒q且q⇏pp是q的必要不充分条件p⇏q且q⇒pp是q的充要条件p⇔qp是q的既不充分也不必要条件p⇏q且q⇏p常用结论充分、必要条件与对应集合之间的关系设A＝{x|p(x)}，B＝{x|q(x)}．①若p是q的充分条件，则A⊆B；②若p是q的充分不必要条件，则A B；③若p是q的必要不充分条件，则B A；④若p是q的充要条件，则A＝B.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)“x2－2x－3>0”是命题．(×)(2)“x>1”是“x>0”的充分不必要条件．(√)(3)若原命题为真，则这个命题的否命题、逆命题、逆否命题中至少有一个为真．(√)(4)p是q的充分不必要条件等价于q是p的必要不充分条件．(√)教材改编题1．“a>b”是“ac2>bc2”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案B解析当a>b时，若c2＝0，则ac2＝bc2，所以a>b⇏ac2>bc2，当ac2>bc2时，c2≠0，则a>b，所以ac2>bc2⇒a>b，即“a>b”是“ac2>bc2”的必要不充分条件．2．命题“同位角相等，两直线平行”的逆否命题是____________________________．答案两直线不平行，同位角不相等3．方程x2－ax＋a－1＝0有一正一负根的充要条件是________．答案a∈(－∞，1)解析依题意得a－1<0，∴a<1.题型一命题及其关系例1(1)(2022·玉林质检)下列四个命题为真命题的个数是()①命题“若x>1，则x2>1”的否命题；②命题“梯形不是平行四边形”的逆否命题；③命题“全等三角形面积相等”的否命题；④命题“若两条直线没有公共点，则这两条直线是异面直线”的逆命题．A ．1B ．2C ．3D ．4答案B解析 ①命题“若x >1，则x 2>1”的否命题为“若x ≤1，则x 2≤1”，不正确，例如取x ＝－2.②命题“梯形不是平行四边形”是真命题，因此其逆否命题也是真命题．③命题“全等三角形面积相等”的否命题“不是全等三角形的面积不相等”是假命题． ④命题“若两条直线没有公共点，则这两条直线是异面直线”的逆命题“若两条直线是异面直线，则这两条直线没有公共点”是真命题．综上可得真命题的个数为2.(2)能说明“若f (x )>f (0)对任意的x ∈(0,2]都成立，则f (x )在[0,2]上是增函数”为假命题的一个函数是________________．答案f (x )＝sin x ，x ∈[0,2](答案不唯一)解析设f (x )＝sin x ，则f (x )在⎣⎢⎡⎦⎥⎤0，π2上是增函数，在⎣⎢⎡⎦⎥⎤π2，2上是减函数．由正弦函数图象的对称性知，当x ∈(0,2]时，f (x )>f (0)＝sin0＝0，故f (x )＝sin x 满足条件f (x )>f (0)对任意的x ∈(0,2]都成立，但f (x )在[0,2]上不一直都是增函数．教师备选(2022·合肥模拟)设x ，y ∈R ，命题“若x 2＋y 2>2，则x 2>1或y 2>1”的否命题是()A ．若x 2＋y 2≤2，则x 2≤1或y 2≤1B．若x2＋y2>2，则x2≤1或y2≤1C．若x2＋y2≤2，则x2≤1且y2≤1D．若x2＋y2>2，则x2≤1且y2≤1答案C解析根据否命题的定义可得命题“若x2＋y2>2，则x2>1或y2>1”的否命题是“若x2＋y2≤2，则x2≤1且y2≤1”．思维升华判断命题真假的策略(1)判断一个命题为真命题，需要推理证明；判断一个命题是假命题，只需举出反例即可．(2)根据“原命题与逆否命题同真同假，逆命题与否命题同真同假”这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假．跟踪训练1(1)(2022·安顺模拟)命题“若x，y都是奇数，则x＋y是偶数”的逆否命题是() A．若x，y都是偶数，则x＋y是奇数B．若x，y都不是奇数，则x＋y不是偶数C．若x＋y不是偶数，则x，y都不是奇数D．若x＋y不是偶数，则x，y不都是奇数答案D解析命题“若x，y都是奇数，则x＋y是偶数”的逆否命题是“若x＋y不是偶数，则x，y不都是奇数”．(2)命题p：若m≤a－2，则m<－1.若p的逆否命题为真命题，则a的取值范围是________．答案(－∞，1)解析依题意，命题p 的逆否命题为真命题，则命题p 为真命题，即“若m ≤a －2，则m <－1”为真命题，则a －2<－1，解得a <1.题型二 充分、必要条件的判定例2(1)已知p ：⎝ ⎛⎭⎪⎫12x <1，q ：log 2x <0，则p 是q 的() A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案B解析由⎝ ⎛⎭⎪⎫12x <1知x >0，所以p 对应的x 的范围为(0，＋∞)， 由log 2x <0知0<x <1，所以q 对应的x 的范围为(0,1)，显然(0,1)(0，＋∞)，所以p 是q 的必要不充分条件．(2)(2021·全国甲卷)等比数列{a n }的公比为q ，前n 项和为S n .设甲：q >0，乙：{S n }是递增数列，则()A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D．甲既不是乙的充分条件也不是乙的必要条件答案B解析当a1<0，q>1时，a n＝a1q n－1<0，此时数列{S n}单调递减，所以甲不是乙的充分条件．当数列{S n}单调递增时，有S n＋1－S n＝a n＋1＝a1q n>0，若a1>0，则q n>0(n∈N*)，即q>0；若a1<0，则q n<0(n∈N*)，不存在．所以甲是乙的必要条件．教师备选在△ABC中，“AB2＋BC2＝AC2”是“△ABC为直角三角形”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案A解析在△ABC中，若AB2＋BC2＝AC2，则∠B＝90°，即△ABC为直角三角形，若△ABC为直角三角形，推不出∠B＝90°，所以AB2＋BC2＝AC2不一定成立，综上，“AB2＋BC2＝AC2”是“△ABC为直角三角形”的充分不必要条件．思维升华充分条件、必要条件的两种判定方法(1)定义法：根据p⇒q，q⇒p进行判断，适用于定义、定理判断性问题．(2)集合法：根据p，q对应的集合之间的包含关系进行判断，多适用于条件中涉及参数范围的推断问题．跟踪训练2(1)“a>2，b>2”是“a＋b>4，ab>4”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案A解析若a>2，b>2，则a＋b>4，ab>4.当a＝1，b＝5时，满足a＋b>4，ab>4，但不满足a>2，b>2，所以a＋b>4，ab>4⇏a>2，b>2，故“a>2，b>2”是“a＋b>4，ab>4”的充分不必要条件．(2)(2022·成都模拟)若a，b为非零向量，则“a⊥b”是“(a＋b)2＝a2＋b2”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案C解析因为a⊥b，所以a ·b ＝0，则(a ＋b )2＝a 2＋2a ·b ＋b 2＝a 2＋b 2，所以“a ⊥b ”是“(a ＋b )2＝a 2＋b 2”的充分条件；反之，由(a ＋b )2＝a 2＋b 2得a ·b ＝0，所以非零向量a ，b 垂直，“a ⊥b ”是“(a ＋b )2＝a 2＋b 2”的必要条件．故“a ⊥b ”是“(a ＋b )2＝a 2＋b 2”的充要条件．题型三 充分、必要条件的应用例3已知集合A ＝{x |x 2－8x －20≤0}，非空集合B ＝{x |1－m ≤x ≤1＋m }．若x ∈A 是x ∈B 的必要条件，求m 的取值范围．解由x 2－8x －20≤0，得－2≤x ≤10，∴A ＝{x |－2≤x ≤10}．由x ∈A 是x ∈B 的必要条件，知B ⊆A .则⎩⎪⎨⎪⎧ 1－m ≤1＋m ，1－m ≥－2，∴0≤m ≤3.1＋m ≤10，∴当0≤m ≤3时，x ∈A 是x ∈B 的必要条件，即所求m 的取值范围是[0,3]．延伸探究本例中，若把“x ∈A 是x ∈B 的必要条件”改为“x ∈A 是x ∈B 的充分不必要条件”，求m 的取值范围．解∵x ∈A 是x ∈B 的充分不必要条件，∴A B ，则⎩⎪⎨⎪⎧ 1－m ≤－2，1＋m >10或⎩⎪⎨⎪⎧1－m <－2，1＋m ≥10，解得m ≥9，故m 的取值范围是[9，＋∞)． 教师备选(2022·泰安检测)已知p ：x ≥a ，q ：|x ＋2a |<3，且p 是q 的必要不充分条件，则实数a 的取值范围是()A ．(－∞，－1]B ．(－∞，－1)C ．[1，＋∞)D ．(1，＋∞)答案A解析因为q ：|x ＋2a |<3，所以q ：－2a －3<x <－2a ＋3，记A ＝{x |－2a －3<x <－2a ＋3}，p ：x ≥a ，记为B ＝{x |x ≥a }．因为p 是q 的必要不充分条件，所以A B ，所以a ≤－2a －3，解得a ≤－1.思维升华 求参数问题的解题策略(1)把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解．(2)要注意区间端点值的检验．跟踪训练3(1)使2x ≥1成立的一个充分不必要条件是()A ．1<x <3B ．0<x <2C ．x <2D ．0<x ≤2答案B解析由2x ≥1得0<x ≤2，依题意由选项组成的集合是(0,2]的真子集，故选B.(2)若不等式(x －a )2<1成立的充分不必要条件是1<x <2，则实数a 的取值范围是________． 答案[1,2]解析由(x －a )2<1得a －1<x <a ＋1，因为1<x <2是不等式(x －a )2<1成立的充分不必要条件，所以满足⎩⎪⎨⎪⎧a －1≤1，a ＋1≥2且等号不能同时取到，解得1≤a≤2.课时精练1．(2022·韩城模拟)设p：2<x<3，q：|x－2|<1，那么p是q的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案A解析解不等式|x－2|<1得－1<x－2<1，解得1<x<3，因为{x|2<x<3}{x|1<x<3}，因此p是q的充分不必要条件．2．(2022·马鞍山模拟)“若x，y∈R，x2＋y2＝0，则x，y全为0”的逆否命题是() A．若x，y∈R，x，y全不为0，则x2＋y2≠0B．若x，y∈R，x，y不全为0，则x2＋y2＝0C．若x，y∈R，x，y不全为0，则x2＋y2≠0D．若x，y∈R，x，y全为0，则x2＋y2≠0答案C解析根据命题“若p，则q”的逆否命题为“若綈q，则綈p”，可以写出“若x，y∈R，x2＋y2＝0，则x，y全为0”的逆否命题是“若x，y∈R，x，y 不全为0，则x2＋y2≠0”．3．(2021·浙江)已知非零向量a，b，c，则“a·c＝b·c”是“a＝b”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件答案B解析由a·c＝b·c，得到(a－b)·c＝0，所以(a－b)⊥c或a＝b，所以“a·c＝b·c”是“a＝b”的必要不充分条件．4．已知a，b，c，d是实数，则“ad＝bc”是“a，b，c，d成等比数列”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案B解析当a＝b＝c＝d＝0时，ad＝bc，但a，b，c，d不成等比数列，当a，b，c，d成等比数列时，ad＝bc，则“ad＝bc”是“a，b，c，d成等比数列”的必要不充分条件．5．(2022·太原模拟)下列四个命题：①“在△ABC中，若AB>AC，则∠C>∠B”的逆命题；②“若ab＝0，则a＝0”的逆否命题；③“若ac＝cb，则a＝b”的逆命题；④“若a＝b，则a2＝b2”的否命题．其中是真命题的为()A．①④B．②③C．①③D．②④答案C解析①“在△ABC中，若AB>AC，则∠C>∠B”的逆命题是“在△ABC中，若∠C>∠B，则AB>AC”，是真命题；②“若ab＝0，则a＝0”是假命题，所以其逆否命题也是假命题；③“若ac＝cb，则a＝b”的逆命题是“若a＝b，则ac＝cb”，是真命题；④“若a＝b，则a2＝b2”的否命题是“若a≠b，则a2≠b2”，是假命题．6．(2022·青岛模拟)“∀x>0，a≤x＋4x＋2”的充要条件是()A．a>2B．a≥2 C．a<2D．a≤2 答案D解析因为x>0，所以x＋4x＋2＝x＋2＋4x＋2－2≥2(x＋2)×4x＋2－2＝2，当且仅当x ＋2＝4x ＋2，即x ＝0时等号成立，因为x >0，所以x ＋4x ＋2>2， 所以“∀x >0，a ≤x ＋4x ＋2”的充要条件是a ≤2. 7．已知命题“若m －1<x <m ＋1，则1<x <2”的逆命题是真命题，则m 的取值范围是()A ．(1,2)B ．[1,2)C ．(1,2]D ．[1,2]答案D解析命题的逆命题“若1<x <2，则m －1<x <m ＋1”成立，则⎩⎪⎨⎪⎧ m ＋1≥2，m －1≤1，得⎩⎪⎨⎪⎧m ≥1，m ≤2，得1≤m ≤2， 即实数m 的取值范围是[1,2]．8．(2022·厦门模拟)已知命题p ：x <2m ＋1，q ：x 2－5x ＋6<0，且p 是q 的必要不充分条件，则实数m 的取值范围为()A ．m >12B ．m ≥12C ．m >1D ．m ≥1答案D解析∵命题p ：x <2m ＋1，q ：x 2－5x ＋6<0，即2<x <3，p 是q 的必要不充分条件，∴(2,3)(－∞，2m ＋1)，∴2m ＋1≥3，解得m ≥1.实数m 的取值范围为m ≥1.9．(2022·延边模拟)若“方程ax 2－3x ＋2＝0有两个不相等的实数根”是真命题，则a 的取值范围是________．答案a <98且a ≠0 解析由题意知⎩⎪⎨⎪⎧Δ＝(－3)2－8a >0，a ≠0， 解得a <98且a ≠0. 10．(2022·衡阳模拟)使得“2x >4x ”成立的一个充分条件是________．答案x <－1(答案不唯一)解析由于4x ＝22x ，故2x >22x 等价于x >2x ，解得x <0，使得“2x >4x ”成立的一个充分条件只需为集合{x |x <0}的子集即可．11．直线y ＝kx ＋1与圆x 2＋y 2＝a 2(a >0)有公共点的充要条件是________．答案a ∈[1，＋∞)解析直线y ＝kx ＋1过定点(0,1)，依题意知点(0,1)在圆x2＋y2＝a2内部(包含边界)，∴a2≥1.又a>0，∴a≥1.12．给出下列四个命题：①命题“在△ABC中，sin B>sin C是B>C的充要条件”；②“若数列{a n}是等比数列，则a22＝a1a3”的否命题；③已知a，b是非零向量，“若a·b>0，则a与b的夹角为锐角”的逆命题；④命题“直线l与平面α垂直的充要条件是l与平面α内的两条直线垂直．”其中真命题是________．(填序号)答案①③解析对于①，在△ABC中，由正弦定理得sin B>sin C⇔b>c⇔B>C，①是真命题；②“若数列{a n}是等比数列，则a22＝a1a3”的否命题是“若数列{a n}不是等比数列，则a22≠a1a3”，取a n＝0，可知②是假命题；③已知a，b是非零向量，“若a·b>0，则a与b的夹角为锐角”的逆命题“若a与b的夹角为锐角，则a·b>0”为真命题；④直线l与平面α内的两条直线垂直是直线l与平面α垂直的必要不充分条件，④是假命题．13．设集合A ＝{x |－2－a <x <a ，a >0}，命题p ：1∈A ，命题q ：2∈A .若p 和q 中有且只有一个为真命题，则实数a 的取值范围是()A ．0<a <1或a ≥2B ．0<a <1或a >2C ．1<a ≤2D ．1≤a ≤2答案C解析若p 和q 中有且只有一个为真命题，则有p 真q 假或p 假q 真，当p 真q 假时，则⎩⎪⎨⎪⎧ －2－a <1<a ≤2，a >0，解得1<a ≤2；当p 假q 真时，则⎩⎪⎨⎪⎧1≤－2－a <2<a ，a >0，无解， 综上，1<a ≤2.14．若“x 2－4x ＋3<0”是“x 2－mx ＋4<0”的充分条件，则实数m 的取值范围为________． 答案m ≥5解析依题意有x 2－4x ＋3<0⇒1<x <3，x 2－mx ＋4<0⇒mx >x 2＋4，∵1<x <3，∴m >x ＋4x ，设f (x )＝x ＋4x (1<x <3)，则函数f (x )在(1,2)上单调递减，在(2,3)上单调递增，∴f (1)＝5，f (2)＝4，f (3)＝133，因此函数f (x )＝x ＋4x (1<x <3)的值域为[4,5)，∵“x 2－4x ＋3<0”是“x 2－mx ＋4<0”的充分条件，∴m ≥5.15．若“x >1”是“不等式2x >a －x 成立”的必要不充分条件，则实数a 的取值范围是()A ．a >3B ．a <3C ．a >4D ．a <4答案A解析若2x >a －x ，即2x ＋x >a .设f (x )＝2x ＋x ，则函数f (x )为增函数．由题意知“2x ＋x >a 成立，即f (x )>a 成立”能得到“x >1”，反之不成立．∵当x >1时，f (x )>3，∴a >3.16．已知r >0，x ，y ∈R ，p ：|x |＋|y |2≤1，q ：x 2＋y 2≤r 2，若p 是q 的必要不充分条件，则实数r 的取值范围是________．答案⎝⎛⎦⎥⎤0，255 解析画出|x |＋|y |2≤1表示的平面区域(图略)，由图可得p 对应的平面区域是一个菱形及其内部，当x >0，y >0时，可得菱形的一边所在的直线的方程为x ＋y 2＝1，即2x ＋y －2＝0.由p 是q 的必要不充分条件，可得圆x 2＋y 2＝r 2的圆心(0,0)到直线2x ＋y －2＝0的距离d＝222＋1＝255≥r ，又r >0，所以实数r 的取值范围是⎝ ⎛⎦⎥⎤0，255.。

四种命题及其关系一、四种命题的概念1. 原命题- 定义：若用p表示条件，q表示结论，则原命题为“若p，则q”，例如“若x = 1，则x^2=1”。

2. 逆命题- 定义：将原命题的条件和结论互换得到的命题，即“若q，则p”。

对于上面的例子，其逆命题为“若x^2=1，则x = 1”。

3. 否命题- 定义：将原命题的条件和结论都进行否定得到的命题，即“若¬ p，则¬q”。

对于“若x = 1，则x^2=1”，其否命题为“若x≠1，则x^2≠1”。

4. 逆否命题- 定义：将逆命题的条件和结论都进行否定得到的命题，即“若¬ q，则¬p”。

对于“若x = 1，则x^2=1”，其逆否命题为“若x^2≠1，则x≠1”。

二、四种命题之间的关系1. 原命题与逆命题- 关系：原命题的条件和结论是逆命题的结论和条件，它们之间是互逆的关系。

原命题为真时，逆命题不一定为真。

例如原命题“若a = 0，则ab=0”是真命题，其逆命题“若ab = 0，则a = 0”是假命题（因为当b = 0时，a可以不为0）。

2. 原命题与否命题- 关系：原命题与否命题是互否的关系，原命题为真时，否命题不一定为真。

例如原命题“若x>2，则x>1”是真命题，其否命题“若x≤slant2，则x≤slant1”是假命题。

3. 原命题与逆否命题- 关系：原命题与逆否命题是同真同假的关系。

例如原命题“若a = b，则a^2=b^2”是真命题，其逆否命题“若a^2≠ b^2，则a≠ b”也是真命题；原命题“若x = 1且y = 2，则x + y=3”是真命题，其逆否命题“若x + y≠3，则x≠1或y≠2”也是真命题。

4. 逆命题与否命题- 关系：逆命题与否命题是互为逆否的关系，所以它们也是同真同假的关系。

例如对于原命题“若p，则q”，其逆命题“若q，则p”和否命题“若¬ p，则¬q”，若逆命题为真，则否命题也为真；若逆命题为假，则否命题也为假。

常用逻辑用语：命题及其关系要求层次重难点 “若p ，则q ”形式的命题及其逆命题、否命题与逆否命题A 理解四种命题的相互关系；掌握充要条件的判定四种命题的相互关系B 充要条件C（一） 知识内容1．对于“如果p ，则q ”形式的命题，p 称为命题的条件，q 称为命题的结论．定理：经过证明为真的命题．当命题“如果p ，则q ”经过推理证明断定是真命题时，我们就说则p 可以推出q ，记作p q ，读作“p 推出q ”．2．命题的四种形式：命题“如果p ，则q ”是由条件p 和结论q 组成的，对p q ，进行“换位”和“换质（否定）”后，可以构成四种不同形式的命题． ⑴原命题：如果p ，则q ； ⑵原命题的逆命题：如果q ，则p ； ⑶原命题的否命题：如果非p ，则非q ； ⑷原命题的逆否命题：如果非q ，则非p ．否逆为互逆为互否互否互逆互否互逆如果非q ,则非p如果非p ,则非q如果 q,则 p如果 p,则 q3．命题“如果p ，则q ”的四种形式之间有如下关系：⑴互为逆否命题的两个命题等价（同真或同假）．因此证明原命题，也可以改证它的逆否命题．例题精讲高考要求常用逻辑用语：命题及其关系板块一：命题的四种形式⑵互逆或互否的两个命题不等价．<教师备案>注意命题的否定与否命题之间的区别，前者是命题的反面，且与命题的真假恰好相反；后者是对条件与结论同时进行否定，它的真假与原命题的真假没有绝对的联系．（二）典例分析【例1】 判断下列语句是否是命题：⑴张三是四川人；⑵1010是个很大的数；⑶220x x +=；⑷260x +>；⑸112+>；【例2】 判断下列命题的真假．⑴空间中两条不平行的直线一定相交； ⑵垂直于同一个平面的两个平面互相垂直； ⑶每一个周期函数都有最小正周期； ⑷两个无理数的乘积一定是无理数； ⑸若A B ，则A B B ≠；⑹若1m >，则方程220x x m -+=无实数根． ⑺已知a b c d ∈R ，，，，若a c ≠或b d ≠，则a b c d +≠+； ⑻已知a b c d ∈R ，，，，a b c d +≠+，则a c ≠或b d ≠．【例3】 设语句()p x ：πcos()sin 2x x +=-，写出π()3p ，并判断它是不是真命题；【例4】 下面有四个命题：①若a -不属于N ，则a 属于N ；②若a b ∈∈N N ，，则a b +的最小值为2；③212x x +=的解可表示为{}11，．其中真命题的个数为（ ） A ．0个 B ．1个 C ．2个 D ．3个【例5】 如果两个三角形全等，那么它们的面积相等； ①如果两个三角形的面积相等，那么它们全等； ② 如果两个三角形不全等，那么它们的面积不相等； ③ 如果两个三角形的面积不相等，那么它们不全等； ④ 命题②、③、④与命题①有何关系？【例6】 写出下列命题的否命题，并判断否命题的真假．⑴命题p ：“若0,ac ≥则二次方程20ax bx c ++=没有实根”； ⑵命题q ：“若x a ≠且x b ≠，则2()0x a b x ab -++≠”； ⑶命题r ：“若(1)(2)0x x --=，则1x =或2x =”．⑷命题l ：“ABC ∆中，若90C ︒∠=，则A ∠、B ∠都是锐角”； ⑸命题s ：“若0abc =，则a b c ，，中至少有一个为零”．【例7】 下列命题中正确的是（ ）①“若220x y +≠，则x y ，不全为零”的否命题 ②“正多边形都相似”的逆命题③“若0m >，则20x x m +-=有实根”的逆否命题④“若x x 是无理数”的逆否命题A ．①②③④B ．①③④C ．②③④D ．①④【例8】 写出下列命题的逆命题，否命题，逆否命题，并判断它们的真假．⑴“负数的平方是正数”；⑵“若a 和b 都是偶数，则a b +是偶数”； ⑶“当0c >时，若a b >，则ac bc >”； ⑷“若5x y +=，则3x =且2y =”；【例9】 ⑴命题：“若220()，a b a b +=∈R ，则“0a b ==”的逆否命题是（ ） A ．若0()，a b a b ≠≠∈R ，则220a b +≠ B ．若0a ≠且0()，b a b ≠∈R ，则220a b +≠ C ．若0()，a b a b =≠∈R ，则220a b +≠ D ．若0a ≠或0()，b a b ≠∈R ，则220a b +≠ ⑵有下列四个命题：①命题“若1xy =，则x ，y 互为倒数”的逆命题；②命题“面积相等的三角形全等”的否命题；③命题“若1≤m ，则220x x m -+=有实根”的逆否命题；④命题“若A B B =，则A B ⊆”的逆否命题．其中是真命题的是 （填上你认为正确的命题的序号）．【例10】 ⑴ “在ABC ∆中，若90C ∠=︒，则A ∠、B ∠都是锐角”的否命题为；⑵（2007重庆）命题：“若21x <，则11x -<<”的逆否命题是（ ） A ．若21≥x ，则1≥x 或1≤x - B ．若11x -<<，则21x < C ．若1x >或1x <-，则21x > D ．若1≥x 或1≤x -，则21≥x【例11】 下列命题中_________为真命题．①“A B A =”成立的必要条件是“A B ”；②“若220x y +=，则x ，y 全为0”的否命题； ③“全等三角形是相似三角形”的逆命题；④“圆内接四边形对角互补”的逆否命题．【例12】 已知命题“如果1≤a ，那么关于x 的不等式22(4)(2)10≥a x a x -++-的解集为∅”．它的逆命题、否命题、逆否命题及原命题中是假命题的共有（ ）A ．0个B ．2个C ．3个D ．4个【例13】 已知等比数列{}n a 的前n 项和为n S ．⑴若m S ，2m S +，1m S +成等差数列，证明m a ，2m a +，1m a +成等差数列； ⑵写出⑴的逆命题，判断它的真伪，并给出证明．【例14】 ⑴命题p ：奇函数一定有(0)0f =；命题q ：函数1y x x=+的单调递减区间是[10)(01]，，-．则下列四个判断中正确的是（ ）A ．p 真q 真B ． p 真q 假C ． p 假q 真D ． p 假q 假 ⑵设α和β为不重合的两个平面，给出下列命题：①若α内的两条相交直线分别平行于β内的两条直线，则α平行于β； ②若α外一条直线l 与α内的一条直线平行，则l 和α平行；③设α和β相交于直线l ，若α内有一条直线垂直于l ，则α和β垂直； ④直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直． 上面命题中，真命题的序号是 ____ ．（写出所有真命题的序号）【例15】 设V 是已知平面M 上所有向量的集合，对于映射:，f V V a V →∈，记a 的象为()f a ．若映射:f V V →满足：对所有，a b V ∈及任意实数，λμ都有()()()f a b f a f b λμλμ+=+，则f 称为平面M 上的线性变换．现有下列命题： ①设f 是平面M 上的线性变换，则(0)0f =；②对a V ∈，设()2f a a =，则f 是平面M 上的线性变换； ③若e 是平面M 上的单位向量，对a V ∈设()f a a e =-，则f 是平面M 上的线性变换；④设f 是平面M 上的线性变换，，a b V ∈，若，a b 共线，则()()，f a f b 也共线． 其中真命题是 （写出所有真命题的序号）【例16】 对于四面体ABCD ，下列命题正确的是 （写出所有正确命题的编号）．①相对棱AB 与CD 所在的直线是异面直线；②由顶点A 作四面体的高，其垂足是BCD ∆的三条高线的交点；③若分别作ABC ∆和ABD ∆的边AB 上的高，则这两条高所在的直线异面； ④分别作三组相对棱中点的连线，所得的三条线段相交于一点；⑤最长棱必有某个端点，由它引出的另两条棱的长度之和大于最长棱．【例17】 设直线系:cos (2)sin 1(02π)M x y θθθ+-=≤≤，对于下列四个命题：A ．M 中所有直线均经过一个定点B ．存在定点P 不在M 中的任一条直线上C ．对于任意整数(3)n n ≥，存在正n 边形，其所有边均在M 中的直线上D ．M 中的直线所能围成的正三角形面积都相等其中真命题的代号是 （写出所有真命题的代号）．【例18】 关于x 的方程()222110x x k ---+=，给出下列四个命题：①存在实数k ，使得方程恰有2个不同的实根；②存在实数k ，使得方程恰有4个不同的实根； ③存在实数k ，使得方程恰有5个不同的实根； ④存在实数k ，使得方程恰有8个不同的实根； 其中假．命题的个数是（ ） A ．0 B ．1C ．2D ．3【例19】 命题“若x y =，则||||x y =”，写出它的逆命题、否命题、逆否命题，并判断它们的真假【例20】 有下列四个命题：①“若0x y +=，则,x y 互为相反数”的逆命题； ②“全等三角形的面积相等”的否命题；③“若1q ≤，则220x x q ++=有实根”的逆否命题； ④“等边三角形的三个内角相等”逆命题；其中真命题的个数为（ ） A ．1 B ．2 C ．3 D ．4【例21】 原命题：“设a b c ∈R ，，，若a b >，则22ac bc >”以及它的逆命题、否命题、逆否命题中，真命题共有（ ）个．A ．0B ．1C ．2D ．4【例22】 下面有五个命题：①函数44sin cos y x x =-的最小正周期是π． ②终边在y 轴上的角的集合是π|2k a a k ⎧⎫=∈⎨⎬⎩⎭Z ，． ③在同一坐标系中，函数sin y x =的图象和函数y x =的图象有三个公共点．④把函数π3sin 23y x ⎛⎫=+ ⎪⎝⎭的图象向右平移π6得到3sin 2y x =的图象．⑤函数πsin 2y x ⎛⎫=- ⎪⎝⎭在()0π，上是减函数． 其中真命题的序号是 ．【例23】 设a ，b 是两条直线，α，β是两个平面，则a b ⊥的一个充分条件是（ ）A ．a α⊥，b β∥，αβ⊥B ．a α⊥，b β⊥，αβ∥C ．a α⊂，b β⊥，αβ∥D ．a α⊂，b β∥，αβ⊥【例24】 命题“若ABC ∆不是等腰三角形，则它的任何两个内角不相等”的逆否命题是 ．【例25】 给出以下四个命题：①“若0x y +=，则x y ，互为相反数”的逆命题； ②“全等三角形的面积相等”的否命题；③“若1q -≤，则20x x q ++=有实根”的逆否命题；④“不等边三角形的三内角相等”的逆否命题．其中真命题是（ ）A ．①②B ．②③C ．①③D ．③④【例26】 对于直角坐标平面内的任意两点11()，A x y 、22()，B x y ，定义它们之间的一种“距离”： 1212AB x x y y =-+-．给出下列三个命题：①若点C 在线段AB 上，则AC CB AB +=； ②在ABC ∆中，若90C ∠=︒，则222AC CB AB +=； ③在ABC ∆中，AC CB AB +>． 其中真命题的个数为（ ）A ．1个B ．2个C ．3个D ．4个【例27】 有下列四个命题：①“若0x y +=，则，x y 互为相反数”的逆命题；②“全等三角形的面积相等”的否命题；③“若1≤q ，则220x x q ++=有实根”的逆否命题；④“不等边三角形的三个内角相等”逆命题．其中真命题为（ ）A ．①②B ．②③C ．①③D ．③④【例28】 已知三个不等式：000，，c dab bc ad a b>->->（其中，，，a b c d 均为实数）．用其中两个不等式作为条件，余下的一个不等式作为结论组成一个命题，可组成真命题的个数是（ ） A ．0 B ．1 C ．2 D ．3【例29】 命题：“若21x <，则11x -<<”的逆否命题是（ ）A ．若21x ≥，则1x ≥或1x -≤B ．若11x -<<，则21x <C ．若1x >或1x <-，则21x >D ．若1x ≥或1x -≤，则21x ≥【例30】 已知m n ，是两条不同直线，αβγ，，是三个不同平面，下列命题中正确的是（ ） A ．若m n αα∥，∥，则m n ∥ B ．若αγβγ⊥⊥，，则αβ∥ C ．若m m αβ∥，∥，则αβ∥D ．若m n αα⊥⊥，，则m n ∥【例31】 已知直线m 、n 与平面α、β，给出下列三个命题：①若m α∥，n α∥，则m n ∥；②若m α∥，n α⊥，则n m ⊥；③若m α⊥，m β∥，则αβ⊥． 其中真命题的个数是（ ）A ．0B ．1C ．2D ．3。

1.3.2命题的四种形式学习目标 1.了解四种命题的概念，会写出所给命题的逆命题、否命题和逆否命题.2.认识四种命题之间的关系以及真假性之间的联系.3.会利用命题的等价性解决问题．知识点一四种命题的概念命题“如果p，则(那么)q”是由条件p和结论q组成的，对p，q进行“换位”和“换质”，一共可以构成四种不同形式的命题．(1)原命题：如果p，则q；(2)条件和结论“换位”：如果q，则p，这称为原命题的逆命题；(3)条件和结论“换质”(分别否定)：如果綈p，则綈q，这称为原命题的否命题．(4)条件和结论“换位”又“换质”：如果綈q，则綈p，这称为原命题的逆否命题．知识点二四种命题间的相互关系(1)四种命题间的关系(2)四种命题间的真假关系由上表可知四种命题的真假性之间有如下关系：①两个命题互为逆否命题，它们有相同的真假性，即两命题等价；②两个命题为互逆命题或互否命题，它们的真假性没有关系，即两个命题不等价．1．有的命题没有逆命题．(×)2．两个互逆命题的真假性相同．(×)3．对于一个命题的四种命题，可以一个真命题也没有．(√)4．一个命题的四种命题中，真命题的个数一定为偶数．(√)题型一四种命题的结构形式例1把下列命题写成“若p，则q”的形式，并写出它们的逆命题、否命题与逆否命题．(1)正数的平方根不等于0；(2)当x＝2时，x2＋x－6＝0；(3)对顶角相等．解(1)原命题：若a是正数，则a的平方根不等于0.逆命题：若a的平方根不等于0，则a是正数．否命题：若a不是正数，则a的平方根等于0.逆否命题：若a的平方根等于0，则a不是正数．(2)原命题：若x＝2，则x2＋x－6＝0.逆命题：若x2＋x－6＝0，则x＝2.否命题：若x≠2，则x2＋x－6≠0.逆否命题：若x2＋x－6≠0，则x≠2.(3)原命题：若两个角是对顶角，则它们相等．逆命题：若两个角相等，则它们是对顶角．否命题：若两个角不是对顶角，则它们不相等．逆否命题：若两个角不相等，则它们不是对顶角．反思感悟由原命题写出其他三种命题的关键是找到原命题的条件和结论，根据其他三种命题的定义，确定所写命题的条件和结论．跟踪训练1写出下列命题的逆命题、否命题、逆否命题．(1)实数的平方是非负数；(2)等底等高的两个三角形是全等三角形．解(1)逆命题：若一个数的平方是非负数，则这个数是实数．否命题：若一个数不是实数，则它的平方不是非负数．逆否命题：若一个数的平方不是非负数，则这个数不是实数．(2)逆命题：若两个三角形全等，则这两个三角形等底等高．否命题：若两个三角形不等底或不等高，则这两个三角形不全等．逆否命题：若两个三角形不全等，则这两个三角形不等底或不等高．题型二四种命题的真假判断例2写出下列命题的逆命题、否命题、逆否命题，并判断其真假．(1)若a>b，则ac2>bc2；(2)若四边形的对角互补，则该四边形是圆的内接四边形．解(1)逆命题：若ac2>bc2，则a>b.真命题．否命题：若a≤b，则ac2≤bc2.真命题．逆否命题：若ac2≤bc2，则a≤b.假命题．(2)逆命题：若四边形是圆的内接四边形，则该四边形的对角互补．真命题．否命题：若四边形的对角不互补，则该四边形不是圆的内接四边形．真命题．逆否命题：若四边形不是圆的内接四边形，则该四边形的对角不互补．真命题．反思感悟若原命题为真命题，则它的逆命题、否命题可能为真命题，也可能为假命题．原命题与逆否命题互为逆否命题，否命题与逆命题互为逆否命题．互为逆否命题的两个命题的真假性相同．在原命题及其逆命题、否命题、逆否命题中，真命题的个数要么是0，要么是2，要么是4. 跟踪训练2下列命题中为真命题的是()①“若x2＋y2≠0，则x，y不全为零”的否命题；②“正三角形都相似”的逆命题；③“若m>0，则x2＋x－m＝0有实根”的逆否命题；④“若x－2是有理数，则x是无理数”的逆否命题．A．①②③④B．①③④C．②③④D．①④答案 B解析 ①原命题的否命题为“若x 2＋y 2＝0，则x ，y 全为零”．故为真命题．②原命题的逆命题为“若两个三角形相似，则这两个三角形是正三角形”．故为假命题． ③原命题的逆否命题为“若x 2＋x －m ＝0无实根，则m ≤0”． ∵方程无实根，∴判别式Δ＝1＋4m <0，∴m <－14<0.故为真命题．④原命题的逆否命题为“若x 不是无理数，则x －2不是有理数”． ∵x 不是无理数，∴x 是有理数．又2是无理数，∴x －2是无理数，不是有理数．故为真命题． 故正确的命题为①③④，故选B. 题型三 等价命题的应用例3 证明：已知函数f (x )是(－∞，＋∞)上的增函数，a ，b ∈R ，若f (a )＋f (b )≥f (－a )＋f (－b )，则a ＋b ≥0.证明 原命题的逆否命题为“已知函数f (x )是(－∞，＋∞)上的增函数，a ，b ∈R ，若a ＋b <0， 则f (a )＋f (b )<f (－a )＋f (－b )”． 若a ＋b <0，则a <－b ，b <－a . 又∵f (x )在(－∞，＋∞)上是增函数， ∴f (a )<f (－b )，f (b )<f (－a )， ∴f (a )＋f (b )<f (－a )＋f (－b )． 即原命题的逆否命题为真命题． ∴原命题为真命题．反思感悟 因为原命题与其逆否命题是等价的，可以证明一个命题的逆否命题成立，从而证明原命题也是成立的．正确写出原命题的逆否命题是证题的关键．跟踪训练3 判断命题“已知a ，x 为实数，若关于x 的不等式x 2＋(2a ＋1)x ＋a 2＋2≤0的解集不是空集，则a ≥1”的逆否命题的真假． 解 先判断原命题的真假．因为a ，x 为实数，且关于x 的不等式x 2＋(2a ＋1)x ＋a 2＋2≤0的解集不是空集， 所以Δ＝(2a ＋1)2－4(a 2＋2)≥0，即4a －7≥0，解得a ≥74，a ≥74⇒a ≥1，所以原命题为真，又因为原命题与其逆否命题等价，所以逆否命题为真．命题的等价性典例 主人邀请张三、李四、王五三个人吃饭，时间到了，只有张三、李四准时赴约，王五打电话说：“临时有急事，不能去了．”主人听了，随口说了句：“该来的没有来．”张三听了脸色一沉，起来一声不吭地走了，主人愣了片刻，又道了句：“不该走的又走了．”李四听了大怒，拂袖而去．请你用逻辑学原理解释二人离去的原因．解 张三走的原因是：“该来的没有来”的逆否命题是“来了不该来的”，张三觉得自己是不该来的．李四走的原因是：“不该走的又走了”的逆否命题是“没走的应该走”，李四觉得自己是应该走的．[素养评析] 逻辑推理是在数学活动中进行交流的基本思维品质，本例是利用原命题与其逆否命题的等价性的逻辑原理，得出相应的合理解释．1．命题“如果a ∉A ，则b ∈B ”的否命题是( ) A ．如果a ∉A ，则b ∉B B ．如果a ∈A ，则b ∉B C ．如果b ∈B ，则a ∉A D ．如果b ∉B ，则a ∉A答案 B解析 命题“如果p ，则q ”的否命题是“如果綈p ，则綈q ”，“∈”与“∉”互为否定形式．2．命题“若綈p ，则q ”的逆否命题为( ) A ．若p ，则綈q B ．若綈q ，则綈p C ．若綈q ，则p D ．若q ，则p 答案 C3．下列命题为真命题的是( ) A ．命题“若x >y ，则x >|y |”的逆命题 B ．命题“若x ＝1，则x 2>1”的否命题C．命题“若x＝1，则x2＋x－2＝0”的否命题D．命题“若x2>1，则x>1”的逆否命题答案 A解析对A，即判断：若x>|y|，则x>y的真假，显然是真命题．4．在原命题“若A∪B≠B，则A∩B≠A”与它的逆命题、否命题、逆否命题中，真命题的个数为________．答案 4解析逆命题为“若A∩B≠A，则A∪B≠B”；否命题为“若A∪B＝B，则A∩B＝A”；逆否命题为“若A∩B＝A，则A∪B＝B”，全为真命题．5．已知命题p：“若ac≥0，则二次不等式ax2＋bx＋c>0无解”．(1)写出命题p的否命题；(2)判断命题p的否命题的真假．解(1)命题p的否命题为：“若ac<0，则二次不等式ax2＋bx＋c>0有解”．(2)命题p的否命题是真命题．判断如下：因为ac<0，所以－ac>0⇒Δ＝b2－4ac>0⇒二次方程ax2＋bx＋c＝0有实根⇒ax2＋bx＋c>0有解，所以该命题是真命题．写一个命题的否命题时，要对命题的条件和结论都进行否定，避免出现不否定条件，而只否定结论的错误．若由p经逻辑推理得出q，则命题“若p，则q”为真；确定“若p，则q”为假时，则只需举一个反例说明即可．一、选择题1．“如果x>y，则x2>y2”的逆否命题是()A．如果x≤y，则x2≤y2B．如果x>y，则x2<y2C．如果x2≤y2，则x≤y D．如果x<y，则x2<y2答案 C解析由互为逆否命题的定义可知，把原命题的条件的否定作为结论，原命题的结论的否定作为条件即可得逆否命题．2．命题“如果a>－3，则a>－6”以及它的逆命题、否命题、逆否命题中，真命题的个数为() A．1 B．2 C．3 D．4答案 B解析原命题显然为真命题，故其逆否命题为真命题，而其逆命题为“如果a>－6，则a>－3”，这是假命题，从而否命题也是假命题，因此只有两个真命题．3．“△ABC中，若∠C＝90°，则∠A，∠B全是锐角”的否命题为()A．△ABC中，若∠C≠90°，则∠A，∠B全不是锐角B．△ABC中，若∠C≠90°，则∠A，∠B不全是锐角C．△ABC中，若∠C≠90°，则∠A，∠B中必有一钝角D．以上都不对答案 B解析若∠C≠90°，则∠A，∠B不全是锐角，此处“全”的否定是“不全”．4．若命题p的否命题为q，命题p的逆否命题为r，则q与r的关系是()A．互逆命题B．互否命题C．互为逆否命题D．以上都不正确答案 A解析设p为“如果A，则B”，那么q为“如果綈A，则綈B”，r为“如果綈B，则綈A”．故q与r为互逆命题．5．有下列四个命题：①“如果x＋y＝0，则x，y互为相反数”的逆命题；②“全等三角形的面积相等”的否命题；③“如果q≤1，则x2＋2x＋q＝0有实根”的逆命题；④“不等边三角形的三个内角相等”的逆否命题．其中真命题的序号为()A．①②B．②③C．①③D．③④答案 C解析 命题①：“如果x ，y 互为相反数，则x ＋y ＝0”是真命题；命题②：可考虑其逆命题“面积相等的三角形是全等三角形”是假命题，因此命题②是假命题；命题③：“如果x 2＋2x ＋q ＝0有实根，则q ≤1”是真命题；命题④是假命题．6．原命题为“若a n ＋a n ＋12<a n ，n ∈N ＋，则{a n }为递减数列”，关于其逆命题、否命题、逆否命题真假性的判断依次如下，正确的是( ) A ．真、真、真 B ．假、假、真 C ．真、真、假 D ．假、假、假答案 A解析 从原命题、逆命题的真假入手，a n ＋a n ＋12<a n ⇔a n ＋1<a n ⇔{a n }为递减数列，即原命题、逆命题都为真命题，则其逆否命题、否命题也为真命题．7．设原命题：若a ＋b ≥2，则a ，b 中至少有一个不小于1，则原命题与其逆命题的真假情况是( )A ．原命题为真命题，逆命题为假命题B ．原命题为假命题，逆命题为真命题C ．原命题与逆命题均为真命题D ．原命题与逆命题均为假命题 答案 A解析 逆否命题：若a ，b 都小于1，则a ＋b <2，是真命题，所以原命题是真命题．逆命题：若a ，b 中至少有一个不小于1，则a ＋b ≥2.例如，a ＝3，b ＝－3满足条件a ，b 中至少有一个不小于1，但a ＋b ＝0，故逆命题是假命题．故选A.8．关于命题“若拋物线y ＝ax 2＋bx ＋c 开口向下，则{x |ax 2＋bx ＋c <0}⇏∅”的逆命题、否命题、逆否命题的真假性，下列结论正确的是( ) A ．都是真命题 B ．都是假命题 C ．否命题是真命题 D ．逆否命题是真命题 答案 D解析 原命题为真命题，所以其逆否命题也为真命题．逆命题“若{x |ax 2＋bx ＋c <0}D ＝/∅，则拋物线y ＝ax 2＋bx ＋c 开口向下”是一个假命题，因为当不等式ax 2＋bx ＋c <0的解集非空时，可以有a >0，即拋物线的开口可以向上，因此否命题也是假命题，故选D. 二、填空题9．下列命题：①“如果xy ＝1，则x ，y 互为倒数”的逆命题； ②“四边相等的四边形是正方形”的否命题； ③“梯形不是平行四边形”的逆否命题； ④“如果ac 2>bc 2，则a >b ”的逆命题． 其中真命题是________．(填序号) 答案 ①②③解析 ①“如果xy ＝1，则x ，y 互为倒数”的逆命题是“如果x ，y 互为倒数，则xy ＝1”，是真命题；②“四边相等的四边形是正方形”的否命题是“四边不都相等的四边形不是正方形”，是真命题；③“梯形不是平行四边形”本身是真命题，所以其逆否命题也是真命题；④“如果ac 2>bc 2，则a >b ”的逆命题是“如果a >b ，则ac 2>bc 2”，是假命题．所以真命题是①②③.10．已知命题“若m －1<x <m ＋1，则1<x <2”的逆命题为真命题，则m 的取值范围是________． 答案 [1,2]解析 由已知得，若1<x <2成立，则m －1<x <m ＋1也成立．∴⎩⎪⎨⎪⎧m －1≤1，m ＋1≥2，∴1≤m ≤2. 11．下列命题中：①若一个四边形的四条边不相等，则它不是正方形； ②若一个四边形对角互补，则它内接于圆； ③正方形的四条边相等； ④圆内接四边形对角互补； ⑤对角不互补的四边形不内接于圆；⑥若一个四边形的四条边相等，则它是正方形．其中互为逆命题的有________；互为否命题的有______；互为逆否命题的有________． 答案 ②和④，③和⑥ ①和⑥，②和⑤ ①和③，④和⑤解析 命题③可改写为“若一个四边形是正方形，则它的四条边相等”；命题④可改写为“若一个四边形是圆内接四边形，则它的对角互补”；命题⑤可改写为“若一个四边形的对角不互补，则它不内接于圆”，再依据四种命题间的关系便不难判断． 三、解答题12．判断下列命题的真假．(1)对角线不相等的四边形不是等腰梯形；(2)若x∉A∩B，则x∉A且x∉B；(3)若x2＋y2≠0，则xy≠0.考点四种命题间的相互关系题点利用四种命题的关系判断真假解(1)该命题的逆否命题是“若一个四边形是等腰梯形，则它的对角线相等”，它为真命题，故原命题为真．(2)该命题的逆否命题是“若x∈A或x∈B，则x∈A∩B”，它为假命题，故原命题为假．(3)该命题的逆否命题是“若xy＝0，则x2＋y2＝0”，它为假命题，故原命题为假．13．判断命题：“若b≤－1，则关于x的方程x2－2bx＋b2＋b＝0有实根”的逆否命题的真假．解方法一(利用原命题)因为原命题与逆否命题真假性一致，所以只需判断原命题真假即可．方程判别式为Δ＝4b2－4(b2＋b)＝－4b，因为b≤－1，所以Δ≥4>0，故此方程有两个不相等的实根，即原命题为真，故它的逆否命题也为真．方法二(利用逆否命题)原命题的逆否命题为“若关于x的方程x2－2bx＋b2＋b＝0无实根，则b>－1”．方程判别式为Δ＝4b2－4(b2＋b)＝－4b，因为方程无实根，所以Δ<0，即－4b<0，所以b>0，所以b>－1成立，即原命题的逆否命题为真．14．已知命题“非空集合M中的元素都是集合P中的元素”是假命题，那么下列命题中真命题的个数为()①M中的元素都不是P的元素；②M中有不属于P的元素；③M中有属于P的元素；④M 中的元素不都是P的元素．A．1 B．2 C．3 D．4考点四种命题间的相互关系题点利用四种命题的关系判断真假命题的个数答案 B解析由于“M⊆P”为假命题，故M中至少有一个元素不属于P，∴②④正确．M中可能有属于P的元素，也可能都不是P的元素，故①③错误．故选B.15．已知条件p ：|5x －1|＞a ＞0，其中a 为实数，条件q ：12x 2－3x ＋1＞0，请选取一个适当的a 值，利用所给出的两个条件p ，q 分别作为集合A ，B ，构造命题“若A ，则B ”，并使得构造的原命题为真命题，而其逆命题为假命题，这样的一个原命题可以是什么？ 考点 四种命题间的相互关系题点 利用四种命题的关系判断真假解 由|5x －1|＞a ＞0，得5x －1＜－a 或5x －1＞a ，即x ＜1－a 5或x ＞1＋a 5. 由12x 2－3x ＋1＞0，得2x 2－3x ＋1＞0， 解得x ＜12或x ＞1. 为使“若A ，则B ”为真命题，而其逆命题为假命题，则需A B .令a ＝4，得p ：x ＜－35或x ＞1， 满足题意，故可以选取a ＝4，此时原命题是“若|5x －1|＞4，则12x 2－3x ＋1＞0”。

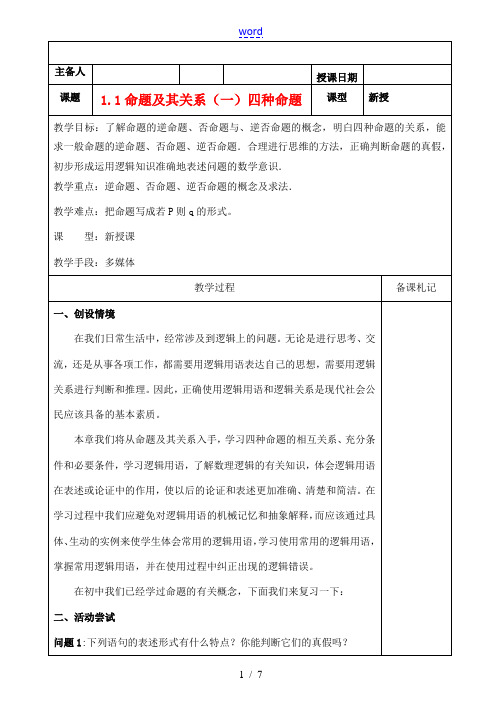
=，则
B B
不能被2整除；
结论：这些语句都是陈述句，且它们都能判断真假。

一般地，我们用语言、符号或式子表达的，可以判断真假的陈述句，叫做命题；其中判断为正确的命题，
例如，如果原命题是：⑴同位角相等，两直线平行；
它的逆命题就是：⑵两直线平行，同位角相等.
2.否命题与逆否命题的知识
即在两个命题中，一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定，这样的两个命题就叫做互否命题，若把其中一个命题叫做原命题，则另一个就叫做原命题的否命题.
例如⑶同位角不相等，两直线不平行；
⑷两直线不平行，同位角不相等.
3. 原命题与逆否命题的知识
即在两个命题中，一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定，这样的两个命题就叫做互为逆否命题，若把其中一个命题叫做原命题，则另一个就叫做原命题的否命题.
概括地说，设命题⑴为原命题，则命题⑵为逆命题；命题⑶为否命题；命题⑷为逆否命题.
关于逆命题、否命题与逆否命题，也可以这样表述：
⑴交换原命题的条件和结论，所得的命题是逆命题；
⑵同时否定原命题的条件和结论，所得的命题是否命题；
⑶交换原命题的条件和结论，并且同时否定，所得的命题是逆否命题.
4.四种命题的形式
一般到，我们用p和q分别表示原
命题的条件和结论，用┐p和┐q分别
表示p和q的否定，于是四种命题的形
式就是：
原命题：若p则q；。

逆命题,否命题,逆否命题表格
摘要：
1.逆命题、否命题、逆否命题的定义与区别
2.逆命题和否命题的关系
3.逆否命题的性质及其应用
正文：
在数学中，逆命题、否命题和逆否命题是命题逻辑中的基本概念，它们在逻辑推理和问题求解中具有重要作用。

下面我们详细了解一下这三种命题及其关系。

首先，我们来了解这三种命题的定义：
1.逆命题：如果一个命题P 可以表示为“如果A，则B”，那么它的逆命题就是“如果非B，则非A”。

简单来说，逆命题就是把原命题的前提和结论都取反得到的新命题。

2.否命题：如果一个命题P 可以表示为“如果A，则B”，那么它的否命题就是“如果A，则非B”。

也就是说，否命题是在原命题的前提和结论上都取反得到的新命题。

3.逆否命题：一个命题的逆否命题是指，对原命题的前提和结论都取反，并把“如果...则...”改为“如果非...则非...”得到的新命题。

接下来，我们来探讨逆命题和否命题之间的关系。

可以发现，逆命题和否命题实际上是等价的，它们具有相同的真假性。

也就是说，如果一个命题的逆命题为真，那么它的否命题也为真；反之，如果一个命题的否命题为真，那么
它的逆命题也为真。

最后，我们来看一下逆否命题的性质及其应用。

逆否命题有一个非常重要的性质，即原命题和逆否命题具有相同的真假性。

这意味着，如果我们要证明一个命题的真假，可以通过证明它的逆否命题的真假来实现。

逆否命题在数学证明和问题求解中具有广泛的应用，它是我们判断一个命题是否成立的重要工具。

综上所述，逆命题、否命题和逆否命题在命题逻辑中具有重要作用。

否命题、逆否命题、命题的否定与反证法熊明军读了秋屏在新华网撰写的文章《数学中的致命错误——反证法》，意识到不在数学体系框架内研究的数学都是伪数学。

也意识到有很多学生甚至教师对基本逻辑中的否命题、逆否命题、命题的否定与反证法的基本概念、形式及应用都存在极其模糊地认识。

下面，从概念、区别与联系、应用三个方面来简要叙述一下，以期达到清醒认识的目的。

一、概念讨论原命题的否命题、逆否命题、否定必须是在命题为“若p ，则q ”的形式（或可以改写为“若p ，则q ”的形式）的前提下进行的。

不具备“若p ，则q ”形式的命题，讨论其否命题、逆否命题、否定是毫无意义的。

原命题：若p ，则q ；命题的否定：若p ，则q ⌝； 否命题：若p ⌝，则q ⌝； 逆否命题：若q ⌝，则p ⌝；反证法：（Reductio ad absurdum ，又称归谬法、背理法）是一种论证方式，拉丁语的意思为“转化到不可能”，阿基米德经常使用它。

反证法是由证明q p ⇒，转向证明t q ⇒⌝，进而得t 与已知矛盾或与相关定理、结论矛盾，然后判定q ⌝为假，从而推出q 为真的证明方法。

它首先假设某命题不成立（即做出原命题的否定），然后把假设作为已知条件的一部分，和原来的已知条件合并在一起，推理出明显矛盾的结果，最后得出原结论正确。

二、区别与联系①区别：否命题是对原命题若p ，则q 既否定其条件，又否定其结论； 命题的否定是对原命题若p ，则q 不否定其条件，只否定其结论；逆否命题是对否命题若p ⌝，则q ⌝条件与结论地位的互换； 逆否命题是对原命题若p ，则q 条件与结论都否定后地位的互换。

②联系：逆否命题与原命题的真假性相同，与否命题的真假性没有关系； 命题的否定与原命题的真假性相反，命题的否定就是q ⌝，与反证法的假设是一个意思。

③辨析：逆否命题与原命题进行的是等价转化；而反证法与原命题不是等价转化，是先对原命题否定，再把否定后的结论作为条件的一部分，引出矛盾的新结论。

逻辑学中否命题和逆否命题的区别
否命题和逆否命题是逻辑学中的两个基本概念，其区别如下：
否命题：在逻辑学中，一个命题的否命题是通过否定命题的主语而得到的新命题。

例如，原命题为“所有人都可以学习逻辑”，则对其主语“所有人”进行否定得到否命题“不是所有人都可以
学习逻辑”。

否命题可以是真的，也可以是假的。

逆否命题：逆否命题是在否命题的基础上进一步进行推理得到的命题。

其方法是将否命题的主语和谓语分别取反并倒置。

例如，由于否命题“不是所有人都可以学习逻辑”是真的，因此逆否命题为“不会学习逻辑的人不是所有人”。

逆否命题也可以是真的，也可以是假的。

因此，否命题和逆否命题的区别在于推理方法不同。

在逻辑推理中，通过推导出命题的否命题和逆否命题，可以更全面地理解命题的含义，从而做出更准确的判断。

清泉州阳光实验学校常用逻辑知识“p且q〞形式复合命题的真假可以用下表表示：p q p且q真真真真假假假真假假假假“p且q〞形式复合命题的真假可以用下表表示：p q P或者者q真真真真假真假真真假假假注：1°像上面表示命题真假的表叫真值表；2°由真值表得：“非p〞形式复合命题的真假与p的真假相反；“p且q〞形式复合命题当p与q同为真时为真，其他情况为假；“p或者者q〞形式复合命题当p与q同为假时为假，其他情况为真；3°真值表是根据简单命题的真假，判断由这些简单命题构成的复合命题的真假，而不涉及简单命题的详细内容。

3．四种命题假设第一个命题的条件是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互为逆命题；假设一个命题的条件和结论分别是原命题的条件和结论的否认，那么这两个命题叫做互否命题，这个命题叫做原命题的否命题；假设一个命题的条件和结论分别是原命题的结论和条件的否认，那么这两个命题叫做互为逆否命题，这个命题叫做原命题的逆否命题。

两个互为逆否命题的真假是一样的，即两个互为逆否命题是等价命题.假设判断一个命题的真假较困难时，可转化为判断其逆否命题的真假。

4．条件一般地，假设p q，那么就说：p是q的充分条件；q是p的必要条件。

可分为四类：〔1〕充分不必要条件，即p q,而q⇒p；(2)必要不充分条件，即p⇒q,而q p；(3)既充分又必要条件，即p q，又有q p；(4)既不充分也不必要条件，即p⇒q，又有q⇒p。

一般地，假设既有p q，又有q p，就记作：p⇔q.“⇔〞叫做等价符号。

p⇔q表示p q 且q p。

这时p既是q的充分条件，又是q的必要条件，那么p是q的充分必要条件，简称充要条件。

5．全称命题与特称命题这里，短语“所有〞在陈述中表示所述事物的全体，逻辑中通常叫做全称量词，并用符号∀表示。

含有全体量词的命题，叫做全称命题。

短语“有一个〞或者者“有些〞或者者“至少有一个〞在陈述中表示所述事物的个体或者者部分，逻辑中通常叫做存在量词，并用符号∃表示，含有存在量词的命题，叫做存在性命题。