第五章 模糊逻辑与模糊推理

人工智能的模糊推理与模糊逻辑人工智能的模糊推理与模糊逻辑在当今信息时代发展中扮演着重要的角色。

随着人工智能技术的不断进步，越来越多的领域开始应用模糊推理与模糊逻辑，以解决现实世界中存在的复杂问题。

模糊推理是指基于模糊集合理论的推理方法，能够应对模糊、不确定和不完全信息的推理和决策问题。

而模糊逻辑则是一种扩展了传统逻辑的形式，用于处理模糊概念和模糊语言的推理问题。

模糊推理与模糊逻辑的基础是模糊集合理论。

模糊集合理论是20世纪60年代由日本学者山下丰提出的，用来描述现实世界中存在的模糊、不确定性和不完全性现象。

在模糊集合理论中，每个元素都有一个隶属度，表示其属于该模糊集合的程度。

通过模糊集合的交集、并集和补集等运算，可以对模糊信息进行处理和推理，从而实现对不确定性问题的分析和决策。

在人工智能领域，模糊推理与模糊逻辑的应用范围非常广泛。

其中一个重要的应用领域是模糊控制系统。

在传统的控制系统中，输入和输出之间的关系通常是通过清晰明确的数学模型来描述的，但是现实世界中很多系统存在着模糊性和不确定性，这时就需要使用模糊推理和模糊逻辑来构建模糊控制系统。

通过模糊控制系统，可以有效地处理复杂系统的控制问题，提高系统的性能和稳定性。

另一个重要的应用领域是模糊信息检索和决策支持系统。

在信息爆炸的时代，人们需要从海量的数据中获取有用的信息，模糊推理和模糊逻辑可以帮助人们快速、准确地找到他们需要的信息。

通过模糊信息检索和决策支持系统，可以有效地处理模糊查询和不完全信息的检索问题，提高信息检索的效率和准确性。

除了以上两个应用领域外，模糊推理与模糊逻辑还可以应用于模式识别、专家系统、人工智能语音识别等领域。

在模式识别领域，模糊推理和模糊逻辑可以帮助系统更准确地识别复杂模式和特征，提高模式识别的准确性和鲁棒性。

在专家系统领域，模糊推理和模糊逻辑可以帮助系统模拟人类专家的知识和推理过程，实现对复杂问题的自动化处理和分析。

在人工智能语音识别领域，模糊推理和模糊逻辑可以帮助系统更好地理解和处理人类语音，提高语音识别的准确性和鲁棒性。

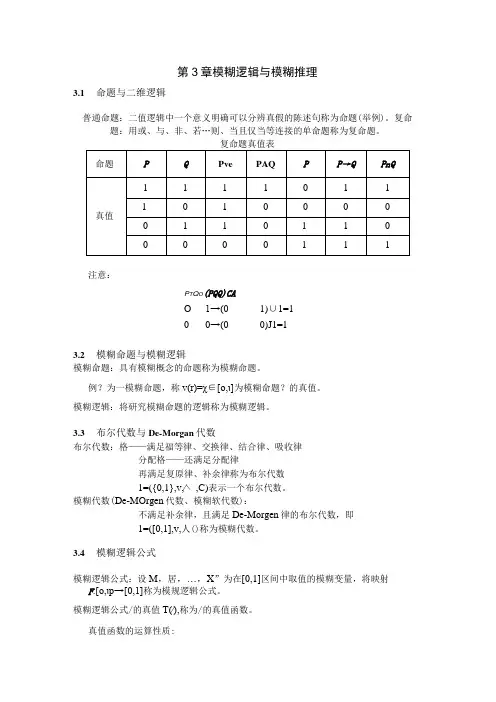
第3章模糊逻辑与模糊推理3.1命题与二维逻辑普通命题：二值逻辑中一个意义明确可以分辨真假的陈述句称为命题(举例)。

复命题：用或、与、非、若…则、当且仅当等连接的单命题称为复命题。

注意：P T Q O(PQQ)CAO 1→(01)∪1=10 0→(00)J1=13.2模糊命题与模糊逻辑模糊命题：具有模糊概念的命题称为模糊命题。

例？为一模糊命题，称v(r)=χ∈[o,ι]为模糊命题？的真值。

模糊逻辑：将研究模糊命题的逻辑称为模糊逻辑。

3.3布尔代数与De-Morgan代数布尔代数：格——满足福等律、交换律、结合律、吸收律分配格——还满足分配律再满足复原律、补余律称为布尔代数1=({0,1},v,∕∖,C)表示一个布尔代数。

模糊代数(De-MOrgen代数、模糊软代数)：不满足补余律，且满足De-Morgen律的布尔代数，即1=([0,1],v,人()称为模糊代数。

3.4模糊逻辑公式模糊逻辑公式：设M，居，…，X”为在[0,1]区间中取值的模糊变量，将映射F:[o,ιp→[0,1]称为模规逻辑公式。

模糊逻辑公式/的真值T(∕),称为/的真值函数。

真值函数的运算性质:T(F)=I-T(F)T(F vF)=max(T(F),T(F))T(F A F)=min(T(FXnF))T(F→F)=min(1,I-T(F)+T(F))了真——F 中一切赋值均为T(F)≥J2 /假——尸中一切赋值均为TX 产)<g1 .模糊逻辑函数的分解例：模糊逻辑函数/(x,y,z)=0V 取丫兀由，确定/(x,y,z)在〃=2处于第一级时变量的取值范围。

解：为满足了处于第一级，则Jf(X,y,z)≥6 于是，疝≥%或xyz ≥见或xyz≥a i 则有：x≥i -a↑x≥a↑y≥∖-a[或y≥a↑z≥a 1 [z≤∖-a↑2 .模糊逻辑函数范式——标准型析取形式：∕=∑n/∙»=17=1 合取形式：F=<=1j=1举例：f(x,y,z)=[(xVy)A V[(xvz)A y]=(xvy)v(xvz)v(yvz)3.5 语言变量及其集合描述自然语言：具有模糊性，灵活。

模糊逻辑中的模糊关系与模糊推理在人工智能中的应用与挑战第一节：引言人工智能（Artificial Intelligence，AI）作为一门新兴的学科，旨在开发智能机器，使其能够以人类类似的方式思考、学习和解决问题。

在人工智能的发展过程中，模糊逻辑作为一种重要的推理方法，被广泛应用于解决信息处理中的模糊问题。

本文将探讨模糊逻辑中的模糊关系与模糊推理在人工智能中的应用与挑战。

第二节：模糊关系的概念与表示模糊关系是模糊逻辑中的重要概念之一，用于描述对象之间模糊的关联关系。

与传统的二值逻辑不同，模糊关系可以包含连续的取值范围，不仅适用于具有明确二元属性的情况，还适用于具有模糊属性的情况。

模糊关系可以使用模糊矩阵、模糊图或模糊规则等形式进行表示。

第三节：模糊推理的基本原理与方法模糊推理是模糊逻辑的核心内容之一，用于基于模糊关系进行不确定信息的推理。

模糊推理可以通过模糊关系的传递、蕴涵、模糊规则的匹配等方式实现。

常用的模糊推理方法包括模糊综合评判、模糊关联分析和模糊神经网络等。

第四节：模糊关系与模糊推理在人工智能中的应用模糊关系与模糊推理在人工智能领域有着广泛的应用。

首先，模糊关系可以用于描述复杂的现实世界中的模糊问题，如模糊控制系统、模糊识别和模糊决策等。

其次，模糊推理可以应用于专家系统和认知系统中，实现对不确定性信息的推理和决策。

此外，模糊逻辑还可以用于自然语言处理、模式识别和数据挖掘等领域。

第五节：模糊关系与模糊推理在人工智能中面临的挑战虽然模糊关系与模糊推理在人工智能中具有广泛的应用前景，但也面临着一些挑战。

首先，模糊关系的建立需要消耗大量的时间和资源，因此如何高效地构建模糊关系是一个挑战。

其次，模糊推理存在一定的计算复杂性，需要进行有效的算法设计和优化。

此外，模糊关系与模糊推理的结果可解释性较差，如何提高其可解释性也是一个重要问题。

第六节：结论本文探讨了模糊逻辑中的模糊关系与模糊推理在人工智能中的应用与挑战。

模糊逻辑中的模糊集合与模糊推理模糊逻辑是一种基于模糊集合与模糊推理的推理方法，旨在处理现实世界中存在的不确定性与模糊性问题。

模糊集合是一种可以包含各种程度成员关系的集合，而模糊推理则是利用模糊集合进行推理和决策。

一、模糊集合的概念与特点在传统的集合论中，一个元素要么是集合的成员，要么不是成员，不存在中间的状态。

但是在现实世界中，很多概念不具有明确的边界，例如“高矮”、“富贵”等。

模糊集合的引入就是为了解决这个问题。

1.1 模糊集合的定义模糊集合是一种扩展了传统集合概念的数学工具，它允许元素具有属于集合的程度，这个程度用隶属度函数来表示。

隶属度函数取值范围在[0,1]之间，表示了元素与该集合的关联度。

1.2 模糊集合的特点（1）模糊集合可以同时属于多个集合，而传统集合只能属于一个集合。

（2）模糊集合的隶属度可以是连续的，而传统集合的隶属度只能是离散的。

（3）模糊集合的隶属度函数可以是非线性的，而传统集合的隶属度函数通常是线性的。

二、模糊推理的方法与应用模糊推理是一种基于模糊集合的推理方法，它通过对模糊集合进行运算和推导，得出模糊结论。

模糊推理可以用于各种领域，如控制系统、决策分析、模式识别等。

2.1 模糊推理的原理模糊推理的基本原理是利用模糊集合的隶属度函数进行运算，通过模糊逻辑的规则对模糊集合进行推导，最终得到模糊结论。

模糊逻辑的规则通常由一些模糊推理算法定义，例如模糊关联矩阵、模糊推理系统等。

2.2 模糊推理的应用（1）控制系统：模糊控制是一种基于经验的控制方法，通过建立模糊规则库和模糊推理机制，实现对复杂系统的控制。

（2）决策分析：模糊决策分析可以处理决策问题中的不确定性和模糊性，通过对决策因素进行模糊建模和模糊推理，帮助决策者做出准确的决策。

（3）模式识别：模糊模式识别可以应用于人脸识别、语音识别等领域，通过对模糊集合的特征提取和模糊推理，实现对模糊样本的分类和识别。

三、模糊逻辑在实际问题中的应用案例3.1 模糊控制在自动驾驶中的应用自动驾驶是一个典型的控制问题，传统的控制方法很难解决其中的不确定性和模糊性。

模糊逻辑中的模糊集合与模糊推理的概念与原理模糊逻辑是一种基于模糊集合和模糊推理的数学理论，用于处理存在不确定性和模糊性的问题。

在许多实际应用中，我们常常遇到一些无法精确描述或者没有明确边界的问题，这时候，传统的二值逻辑就显得力不从心了。

模糊逻辑的提出正是为了解决这类模糊和不确定性问题，使我们能够更好地进行推理和决策。

一、模糊集合的概念与原理模糊集合是模糊逻辑的基础，它是一种用来描述模糊性的数学工具。

与传统的集合不同，模糊集合中的元素并不只有两种可能，而是存在程度上的模糊和不确定性。

模糊集合使用隶属度函数来表示每个元素与集合的关系强弱程度。

隶属度函数取值范围在[0,1]之间，表示该元素与集合的隶属度。

隶属度为0表示该元素不属于集合，隶属度为1表示该元素完全属于集合。

模糊集合的运算包括模糊交、模糊并、模糊补等。

模糊交运算是指两个模糊集合相交后得到的模糊集合，其隶属度函数取两个模糊集合对应元素隶属度函数的最小值。

模糊并运算是指两个模糊集合并集后得到的模糊集合，其隶属度函数取两个模糊集合对应元素隶属度函数的最大值。

模糊补运算是指对一个模糊集合中的每个元素的隶属度进行取反，得到的新模糊集合。

二、模糊推理的概念与原理模糊推理是模糊逻辑的关键部分，它是通过模糊集合的运算和推理规则来推导出模糊结论的过程。

模糊推理的基本框架是模糊推理机，它由模糊集合和模糊规则库组成。

模糊规则库是一组由若干种模糊条件和结论组成的规则集合。

每条规则包含一个或多个模糊条件和一个模糊结论。

通过对输入的模糊条件进行匹配，模糊推理机可以得出一组模糊结论，然后通过模糊集合的运算来合并这些模糊结论，最终得到一个模糊输出。

模糊推理的主要方法有模糊推理法则和模糊推理网络。

模糊推理法则是一种基于模糊规则的推理方法，通过将输入的模糊条件与规则库中的规则进行匹配，得到一组模糊结论，然后通过运算得到最终的输出。

模糊推理网络是一种基于神经网络的推理方法，通过对输入信号的加权求和和激活函数的处理，得到最终的模糊输出。

非经典逻辑中的模糊推理与模糊集合模糊推理和模糊集合作为非经典逻辑的重要分支，对于处理不确定性和模糊性的问题具有重要的意义。

本文将介绍模糊推理和模糊集合的基本概念、特点以及在实际应用中的作用。

一、模糊推理模糊推理是用来处理模糊信息的一种推理方法。

与传统的经典逻辑推理方式不同，模糊推理允许信息的不确定性和模糊性存在。

在模糊推理中，我们将不确定的信息转化为模糊集合，利用模糊集合的运算和推理规则进行推理。

通过模糊推理，我们可以得到一些模糊性较低的结论。

模糊推理的基本框架为模糊推理系统，它包括了模糊推理的输入、模糊推理的处理和模糊推理的输出三个部分。

在输入部分，我们将模糊信息通过模糊化的方式转换为模糊集合；在处理部分，我们利用模糊集合的运算和推理规则进行推理；在输出部分，我们将推理结果通过反模糊化的方式转换为具体的结论。

模糊推理在人工智能、控制理论和决策支持系统等领域有着广泛的应用。

例如，在智能交通系统中，我们可以利用模糊推理来实现车辆的自动驾驶和交通信号的优化控制；在医疗诊断系统中，我们可以利用模糊推理来对患者的病情进行判断和诊断。

二、模糊集合模糊集合是指在一个特定的空间中，每个元素都具有一定的隶属度，表示该元素属于该集合的程度。

与经典集合不同，模糊集合允许元素的隶属度为一个介于0和1之间的实数。

在模糊集合中，我们通过隶属函数来描述元素与模糊集合之间的隶属关系。

模糊集合具有以下几个特点：模糊性、隶属度、包容性和运算规则。

模糊性表示了元素的隶属度可以是一个连续的区间，而不仅仅是一个确定的值；隶属度表示了元素属于模糊集合的程度，它可以用来度量元素与模糊集合之间的相似度；包容性表示了一个元素可以同时属于多个模糊集合；运算规则包括了模糊集合的并、交和补运算等。

模糊集合在模糊推理、模式识别和人工智能等领域有着重要的应用。

例如，在模式识别中，我们可以利用模糊集合来描述模式的不确定性和模糊性，提高系统对于复杂模式的识别能力；在人工智能领域，我们可以利用模糊集合来表示知识的不确定性和模糊性，提高系统的推理和决策能力。