高等数学 第一章 第二节 数列的极限

高等数学说课稿《数列极限》（精选5篇）第一篇：高等数学说课稿《数列极限》《数列极限》说课稿袁勋这次我说课的内容是由盛祥耀主编的《高等数学》（上册）第一章第二节极限概念中的数列极限。

这部分内容在课本第18页至20页。

下面我把对本节课的教学目的、过程、方法、工具等方面的简单认识作一个说明。

一、关于教学目的的确定：众所周知，对极限这个概念的理解是高等数学的学习基础，但由于学生对数列极限概念及其定义的数学语言表述的理解比较困难，这种理解上的困难将影响学生对后继知识的学习，因此，我从知识、能力、情感等方面确定了本次课的教学目标。

1．在知识上，使学生理解极限的概念，能初步利用极限定义确定某些简单的数列极限；2．在能力上，培养学生观察、分析、概括的能力和在探索问题中的，由静态到动态、由有限到无限的辨证观点。

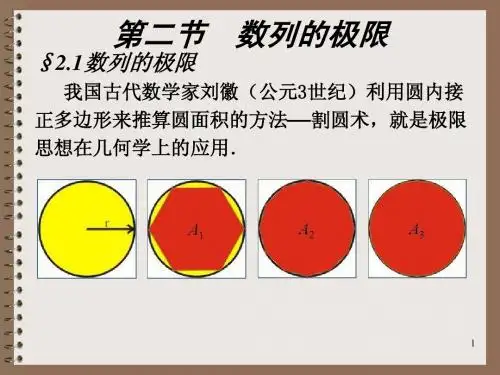
体验‚从具体到抽象，从特殊到一般再到特殊‛的认识过程；3．在情感上，通过介绍我国古代数学家刘徽的成就，激发学生的民族自尊心和爱国主义思想情感，并使他们对数列极限知识有一个形象化的了解。

二、关于教学过程的设计：为了达到以上教学目的，根据两节。

在具体教学中，根据‚循序渐进原则‛，我把这次课分为三个阶段：‚概念探索阶段‛；‚概念建立阶段‛；‚概念巩固阶段‛。

下面我将对每一阶段教学中计划解决的主要问题和教学步骤作出说明。

（一）‚概念探索阶段‛ 1.这一阶段要解决的主要问题在这一阶段的教学中，由于注意到学生在开始接触数列极限这个概念时，总是以静止的观点来理解这个描述变化过程的动态概念，总觉得与以前知识相比，接受起来有困难，似乎这个概念是突然产生的，甚至于不明概念所云，故我在这一阶段计划主要解决这样几个问题：①使学生了解以研究函数值的变化趋势的观点研究无穷数列，从而发现数列极限的过程；②使学生形成对数列极限的初步认识；③使学生了解学习数列极限概念的必要性。

2．本阶段教学安排我采取温故知新、推陈出新的教学过程，分三个步骤进行教学。

第一章 第一节 数列极限A 组 一、选择题：1. 数列{}n x 有界是数列lim n n x →∞存在的【 】A. 充分必要条件B. 充分条件C. 必要条件D. 既非充分条件又非必要条件 2. 下列命题正确的是【 】 A. 有界数列一定收敛 B. 无界数列一定收敛C. 若数列收敛，则极限唯一D. 若函数(sin )y f x =在()f x 处的左右极限都存在，则()f x 在此点处的极限存在3. 下面命题正确的是【 】A. 若{}n u 有界，则{}n u 发散B. 若{}n u 有界，则{}n u 收敛C. 若{}n u 单调，则{}n u 收敛D. 若{}n u 收敛，则{}n u 有界4. 观察下列数列的变化趋势，其中极限是1的数列是【 】A.1n n x n =+ B. 2(1)nn x =-- C. 13n x n=+D. 211n x n =- 5、⎪⎩⎪⎨⎧=-为偶数当为奇数当n n n x n ,10,17则 。

（A ）;0lim =∞→n n x （B ）;10lim 7-∞→=n n x（C ）;,10,,0lim 7⎩⎨⎧=-∞→为偶数为奇数n n x n n (D) 不存在n n x ∞→lim6、下列数列n x 中，收敛的是 。

（A ）n n x nn 1)1(--=（B ）1+=n n x n （C ）2sin πn x n =（D ）nn n x )1(--= 7．下列命题：（1）设a u n n =∞→lim ，b v n n =∞→lim ，且b a >，则必有n n v u >（ ，，，321=n ）；（2）设n n v u >（ ，，，321=n ），且a u n n =∞→lim ，b v n n =∞→lim ，则必有b a >；（3）设n n n v x u ≤≤（ ，，，321=n ），且0)(lim =-∞→n n n v u ，则n n x ∞→lim 必存在． 正确的个数为( ) ． （A ） 零个； （B ） 1个； （C ） 2个； （D ）3个．8、数列{}n x 无界是数列发散的【 】A. 充分必要条件B. 充分条件C. 必要条件D. 既非充分条件又非必要条件10.设n n n x z y ≤≤，且lim()0,lim n n n n n y x z →∞→∞-=则（）(A)存在且等于零 (B)存在但不一定等于零 (C)不一定存在 (D) 一定不存在 11.设=1>0,,nn n kk a n Z S a+∈=∑，则数列{}n a 有界是数列{}n S 收敛的（）(A)充分必要条件 (B)充分非必要条件 （C ）必要非充分条件 （D ）即非充分地非必要条件. 12. 设有两个数列{}{}lim()0n n n n n a b b a →∞-=，，且则（A ）{}{}n n a b ，必都收敛，且极限相等 （B ）{}n a 收敛，{}n b 发散（C ）{}{}n n a b ，必都收敛，且极限不相等 （D ）{}{}n n a b ，可能收敛，也可能发散 13、下列说法正确的是：（A ）如果数列n x 发散，则n x 必是无界数列。

高等数学公式与定理（第六版上册）第一章 函数与极限第一节：初等函数幂函数：a x y =(是常数）R a ∈ 指数函数：x a y =（a >0且)1≠a对数函数：y=x a log (a>0且a ≠1，特别当a=e 时，记为y=lnx) 三角函数: 如y=x sin 等 反三角函数：如y=arctan x 等第二节：数列的极限收敛数列的性质：定理1 (极限的唯一性)如果数列{x n }收敛，那么它的极限唯一。

定理2 (收敛数列的有界性)如果数列{x n }收敛，那么数列{x n }一定有界。

定理3 (收敛数列的保号性)如果,lima x n n =∞→且a>0(或a<0),那么存在正整数N>0，当n>N 时，都有.n x >0(.n x <0)定理 4 (收敛数列与其子数列的关系)如果数列{.n x }收敛于a,那么它的任一子数列也收敛，且极限也是a.第三节 函数的极限函数极限的性质定理1 (函数极限的唯一性) 如果)(limx f xx →存在，那么这极限唯一.定理2 （函数极限的局部有界性）如果)(limx f xx →=A 存在，那么存在常数M>0和δ>0,使得当0<{0x x - }<δ时，有)(x f M≤.定理 3 （函数极限的局部保号性）如果)(limx f xx →=A ，且A>0(或A<0),那么存在常数δ>0，使得δ<-<00x x 时，有0)(>x f （或0)(<x f ）定理3′ 如果)0()(lim 0≠=→A A x f xx ,那么就存在着n x 的某一去心邻域),(00x U 当)(00x U x ∈时，就有2)(0A x f >.推论 如果在0x 的某去心邻域内)0)x 0)(0≤≥（或（f x f ，而且A x f x x =→)(lim 0，那么）或（00≤≥A A定理4 （函数极限与数列极限的关系） 如果极限)(limx f xx →存在，{n x }为函数)(x f 的定义域内任一收敛于0x 的数列，且满足：)(*0N n x x n ∈≠,那么相应的函数数列)(n x f 必收敛，且).(lim )(lim 0x f x f x x n →∞→=第四节 无穷小与无穷大定理 1 在自变量的同义一变化过程0x x →)x (∞→或中，函数)(x f 具有极限A 的充分必要条件是,)(a A x f +=其中a是无穷小。

- 1 -第一章 函数与极限第一节 函数1.区间(interval):介于某两个实数之间的全体实数构成区间.这两个实数叫做区间的端点..,,b a R b a <∈∀且}{b x a x <<开区间),(b a 记作}{b x a x ≤≤闭区间],[b a 记作ox a bo xab}{b x a x <≤}{b x a x ≤<左闭右开区间左开右闭区间),[b a 记作],(b a 记作}{),[x a x a ≤=+∞}{),(b x x b <=-∞o x aoxb注:两端点间的距离称为区间的长度.无穷区间2 邻域.0,>δδ且是两个实数与设a ,叫做这邻域的中心点a .叫做这邻域的半径δ.}{),(δδδ+<<-=a x a x a U xaδ-a δ+a δδ,}{邻域的称为点数集δδa a x x <-记作二、函数的概念1.函数的定义函——信函单值对应多值函数不是函数自变量因变量对应法则(())x )(0x f f xyDW------函数的定义域D 和函数的对应规律f 函数的值域称为派生要素。

2. 函数的两个要素w={y │y=f(x), x ∈D}xaδ- a δ+ a δδ,邻域 的去心的 点 δa) , ( δ a U记作 .}0{),(δδ<-<=a x x a U知识归纳整理- 2 -❖定义域的求法❖在实际问题中，定义域由实际问题的具体条件来确定。

（即使实际问题故意义的取值范围）。

如时光、长度、分量必须大等于0 。

❖对于数学式子表达的函数，如果给出了取值范围就不必再求。

否则，则是使解析式故意义的x的集合（使对应的函数值唯一确定）。

1. 在分式中，分母应不为0；2. 在偶次根式中，被开方数不能为负数；3. 在对数式中，真数不能为0和负数；▪ 4. 在反三角函数式中，要符合反三角函数的定义域；▪ 5. 若函数表达式中含有分式、根式、对数式、反三角函数式等，则应取各部分定义域的交集。

高等数学电子版-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章极限与连续第一节 数列的极限一、数列极限的概念按照某一法则，对于每一个+∈N n ，对应一个确定的实数n x ，将这些实数按下标n 从小到大排列，得到一个序列,,,,21n x x x称为数列，简记为数列}{n x ，n x 称为数列的一般项。

例如： ,1,,43,32,21+n n ,2,,8,4,2n ,21,,81,41,21n ,)1(,,1,1,11+--n ,)1(,,56,43,34,21,21n n n --+ 一般项分别为1+n n ，n 2，n 21，1)1(+-n ，n n n 1)1(--+ 数列}{n x 可看成自变量取正整数n 的函数，即)(n f x n =，+∈N n 设数列n n x n n 1)1(--+=，来说明数列}{n x 以1为极限。

为使100111)1(|1|1<=--+=--n n n x n n ，只需要100>n ，即从101项以后各项都满足1001|1|<-n x ， 为使100000111)1(|1|1<=--+=--n n n x n n ，只需要100000>n ，即从100001项以后各项都满足1000001|1|<-n x ， 为使ε<=--+=--n n n x n n 11)1(|1|1（ε是任意给定的小正数），只需要ε1>n ，即当ε1>n 以后，各项都满足ε<-|1|n x 。

令]1[ε=N ，当N n >时，ε1>n ，因此有ε<-|1|n x ，即任意给定小正数ε，总存在正整数]1[ε=N ，当N n >时的一切n x 都满足ε<-|1|n x ，则 定义：设}{n x 为一数列，如果存在常数a ，对于任意给定的正数ε（不论它多么小），总存在正整数N ，使得当N n >时的一切n x 都满足不等式ε<-||a x n则说常数a 是数列}{n x 的极限，或者说数列}{n x 收敛于a ，记为a x n n =∞→lim 或 a x n →)(∞→n 如果不存在这样的常数a ，则说数列}{n x 没有极限，或者说数列}{n x 发散。