计算水力学第三章

第三章给水排水管道系统水力计算基础本章内容：1、水头损失计算2、无压圆管的水力计算3、水力等效简化本章难点：无压圆管的水力计算第一节基本概念一、管道内水流特征进行水力计算前首先要进行流态的判别。

判别流态的标准采用临界雷诺数Re k，临界雷诺数大都稳定在2000左右，当计算出的雷诺数Re小于2000时，一般为层流，当Re大于4000时，一般为紊流，当Re介于2000到4000之间时，水流状态不稳定，属于过渡流态。

对给水排水管道进行水力计算时，管道内流体流态均按紊流考虑紊流流态又分为三个阻力特征区：紊流光滑区、紊流过渡区及紊流粗糙管区。

二、有压流与无压流水体沿流程整个周界与固体壁面接触，而无自由液面，这种流动称为有压流或压力流。

水体沿流程一部分周界与固体壁面接触，另一部分与空气接触，具有自由液面，这种流动称为无压流或重力流给水管道基本上采用有压流输水方式，而排水管道大都采用无压流输水方式。

从水流断面形式看，在给水排水管道中采用圆管最多三、恒定流与非恒定流给水排水管道中水流的运动，由于用水量和排水量的经常性变化，均处于非恒定流状态，但是，非恒定流的水力计算特别复杂，在设计时，一般也只能按恒定流(又称稳定流)计算。

四、均匀流与非均匀流液体质点流速的大小和方向沿流程不变的流动，称为均匀流；反之，液体质点流速的大小和方向沿流程变化的流动，称为非均匀流。

从总体上看，给水排水管道中的水流不但多为非恒定流，且常为非均匀流，即水流参数往往随时间和空间变化。

对于满管流动，如果管道截面在一段距离内不变且不发生转弯，则管内流动为均匀流；而当管道在局部有交汇、转弯与变截面时，管内流动为非均匀流。

均匀流的管道对水流的阻力沿程不变，水流的水头损失可以采用沿程水头损失公式进行计算；满管流的非均匀流动距离一般较短，采用局部水头损失公式进行计算。

对于非满管流或明渠流，只要长距离截面不变，也没有转弯或交汇时，也可以近似为均匀流，按沿程水头损失公式进行水力计算，对于短距离或特殊情况下的非均匀流动则运用水力学理论按缓流或急流计算。

第三章水动力学基础1、渐变流与急变流均属非均匀流。

( )2、急变流不行能是恒定流。

( )3、总水头线沿流向能够上涨，也能够降落。

( )4、水力坡度就是单位长度流程上的水头损失。

( )5、扩散管道中的水流必定是非恒定流。

( )6、恒定流必定是均匀流，非恒定流必定是非均匀流。

( )7、均匀流流场内的压强散布规律与静水压强散布规律同样。

( )8、测管水头线沿程能够上涨、能够降落也可不变。

( )9、总流连续方程v1A1 = v2 A2 对恒定流和非恒定流均合用。

( )10、渐变流过水断面上动水压强随水深的变化呈线性关系。

( )11、水流老是从单位机械能大的断面流向单位机械能小的断面。

( )12、恒定流中总水头线老是沿流程降落的，测压管水头线沿流程则能够上涨、降落或水平。

( )13、液流流线和迹线老是重合的。

( )14、用毕托管测得的点流速是时均流速。

( )15、测压管水头线可高于总水头线。

( )16、管轴高程沿流向增大的等直径管道中的有压管流，其管轴压强沿流向增大。

( )17、理想液体动中，随意点处各个方向的动水压强相等。

( )2／2g = z2 +p2／g + v22／2g +hw1- 2 ，式中各项代表( )18、恒定总流的能量方程z1+ p1／g + v1(1) 单位体积液体所拥有的能量；(2) 单位质量液体所拥有的能量；(3) 单位重量液体所拥有的能量；(4) 以上答案都不对。

19、图示抽水机吸水管断面A─A 动水压强随抽水机安装高度h 的增大而( )(1) 增大(2) 减小(3) 不变(4) 不定20、在明渠恒定均匀流过水断面上1、2 两点安装两根测压管，如下图，则两测压管高度h1 与h2 的关系为( ) (1) h1 ＞h2 (2) h1 ＜h2 (3) h1 = h2 (4) 没法确立21、对管径沿程变化的管道( )(1) 测压管水头线能够上涨也能够降落(2) 测压管水头线老是与总水头线相平行(3) 测压管水头线沿程永久不会上涨(4) 测压管水头线不行能低于管轴线22、图示水流经过渐缩管流出，若容器水位保持不变，则管内水流属( )(1) 恒定均匀流(2) 非恒定均匀流(3) 恒定非均匀流(4) 非恒定非均匀流23、管轴线水平，管径渐渐增大的管道有压流，经过的流量不变，其总水头线沿流向应( )(1) 渐渐高升(2) 渐渐降低(3) 与管轴线平行(4) 没法确立24、均匀流的总水头线与测压管水头线的关系是( )(1) 相互平行的直线；(2) 相互平行的曲线；(3) 互不平行的直线；(4) 互不平行的曲线。

《水力计算手册》水力计算手册第一章：引言1.1 背景介绍水力计算是水利工程领域中的重要内容，它是设计、建设和维护水利设施的基础。

水力计算手册是为了系统地介绍水力计算的基本原理、方法和应用而编写的。

本手册旨在帮助工程师和技术人员更好地理解和应用水力学知识，提高水力计算的准确性和可靠性。

1.2 基本概念本章将介绍水力计算手册中常用的基本概念，包括水力学、水流特性和水力计算的定义和分类。

第二章：水力学基础2.1 流体力学基础本节将介绍流体力学的基本概念和方程，包括流体静力学和流体动力学的基本原理和公式。

2.2 流体流动特性本节将介绍流体在不同条件下的流动特性，包括稳恒流动和非稳恒流动的特点和计算方法。

2.3 流量计算本节将介绍水力计算中常用的流量计算方法，包括流速计算、流量测量和河流横截面面积计算等。

第三章：水力计算方法3.1 水力元件计算方法本节将介绍水力计算中常用的水力元件计算方法，包括管道流动、水泵和水轮机的计算方法。

3.2 液压计算方法本节将介绍液压计算中的基本原理和方法，包括压力计算、流速计算和水力损失计算等。

3.3 水力模型计算方法本节将介绍水力模型计算中的基本原理和方法，包括模型试验的设计和数据处理等。

第四章：水力计算实例4.1 管道网络计算实例本节将给出管道网络计算的实例，包括水流速度计算、管道阻力计算和管道压力计算等。

4.2 水泵计算实例本节将给出水泵计算的实例，包括水泵性能曲线计算和水泵选型等。

4.3 水轮机计算实例本节将给出水轮机计算的实例，包括水轮机效率计算、水轮机功率计算和水轮机设计等。

第五章：水力计算应用5.1 水利工程设计本节将介绍水力计算在水利工程设计中的应用，包括渠道设计、堤坝设计和船闸设计等。

5.2 水资源管理本节将介绍水力计算在水资源管理中的应用，包括河流流量调控、水库调度和灌溉规划等。

5.3 水环境保护本节将介绍水力计算在水环境保护中的应用，包括水污染控制、水质保护和水生态修复等。

能量方程的运用技巧：
1． 选择基准面
✧ 原则上基准面可以任意选定，一旦确定，则上、下游断面能量值必须针对同一基准面取值。

✧ 一般基准面取在z 值计算较为方便和明确的地方。

✧ 通常对管道取在管出口中心水平面；对容器水体取在水面。

2． 选择上、下游计算断面
✧ 确保计算断面为渐变流；
✧ 计算断面已知运动要素尽可能多同时又含有待求未知数。

通常取水面、管的大气出口、均匀管段等处。

3． 选择断面上计算点
✧ 选择计算点主要是进行断面任一点测压管水头γp
z +的
计算，因此尽可能选在易于求出该值的地方，通常是水面点、管轴中心点。

4． 所有能量值都以水头表示
✧ 一般液体多为水，所以方程各项都为水柱高度，尤其注意压强项必要时需要转换。

5． 等式两边压强表达统一，一般情况采用相对压强
6． 工程实用上一般取12
α1α== 7． 常常和连续方程联解。

第三章 流体运动学本章在连续介质假设下，讨论描述流体运动的方法，根据运动要素的特性对流动进行分类。

本章的讨论是纯运动学意义上的，不涉及流动的动力学因素。

连续方程是质量守恒定律对流体运动的一个具体约束，也在本章的讨论范围之中。

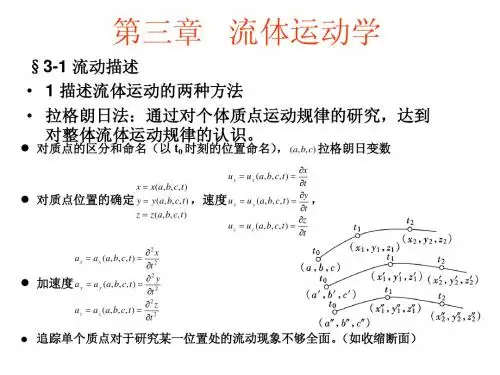
§3—1 描述流动的方法一. 拉格朗日法和欧拉法● 拉格朗日法是质点系法，它定义流体质点的位移矢量为：r r a b c t =(,,,)，其中(,,)(,,,)a b c r a b c t =0是拉格朗日变数，即t 0时刻质点的空间位置，用来对连续介质中无穷多个质点进行编号，作为质点标签。

● 欧拉法是流场法，它定义流体质点的速度矢量场为：u u x y z t =(,,,)，其中(,,)x y z 是空间点（场点）。

流体的其它物理特性和运动要素也都用对应于时间与空间域的场的形式描述。

二. 流体质点的加速度、质点导数● 在拉格朗日观点下，流体质点加速度的求法是比较简单的。

求速度和加速度只须将位移矢量直接对时间求一、二阶导数即可，求导时a,b,c 作为参数不变，意即跟定流体质点。

u r t rt a u t u t r t =====d d ,d d ∂∂∂∂∂∂22.● 欧拉法中流体质点加速度的表达必须特别注意，求加速度需要跟定流体质点，于是 x,y,z均随 t 变，而且),,(d ),,d(z y x u u u tz y x =，所以加速度 u u tz u u y u u x u u t u t z z u t y y u t x x u t u t u a z y x)(d d d d d d d d ∇⋅+=+++=+++==∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂. ● 建立 t 时刻和 t+dt 时刻的流场图，假设一流体质点在 t 时刻位于场点 M ，t + dt 时刻它到达场点M ’，在 t+dt 时刻的流场图上再标上与点M 处于同一位置的场点M 1，此时有另一个流体质点占据该场点。

第三章 液流形态和水头损失考点一 沿程水头损失、局部水头损失及其计算公式1、沿程水头损失和局部水头损失计算公式（1）水头损失的物理概念定义：实际液体运动过程中，相邻液层之间存在相对运动。

由于粘性的作用，相邻流层之间就存在内摩擦力。

液体运动过程中，要克服这种摩擦阻力就要做功，做功就要消耗一部分液流的机械能，转化为热能而散失。

这部分转化为热能而散失的机械能就是水头损失。

分类：液流边界状况的不同，将水头损失分为沿程水头损失和局部水头损失。

（2）沿程水头损失：在固体边界平直的水道中，单位重量的液体自一个断面流至另一个断面损失的机械能就叫做该两个断面之间的水头损失，这种水头损失是沿程都有并随沿程长度增加而增加的，所以称作沿程水头损失，常用h f 表示。

沿程水头损失的计算公式为达西公式对于圆管 gv d L h f 22λ= 对于非圆管 gv R L h f 242λ= 式中，λ为沿程阻力系数，其值与液流的流动形态和管壁的相对粗糙度d /∆有关，其中∆称为管壁的绝对粗糙度，)(Re,df ∆=λ； L 为管长；d 为管径；v 为管道的断面平均流速；R 为水力半径； v 为断面平均流速。

（3）局部水头损失：当液体运动时，由于局部边界形状和大小的改变，液体产生漩涡，或流线急剧变化，液体在一个局部范围之内产生了较大的能量损失，这种能量损失称作局部水头损失，常用h j 表示。

局部水头损失的计算公式为 gv h j 22ζ= 式中，ζ为局部阻力系数；其余符号同前。

（4）总水头损失对于某一液流系统，其全部水头损失h w 等于各流段沿程水头损失与局部水头损失之和，即 ∑∑+=ji fi w h h h2、湿周、水力半径（1）湿周χ：液流过水断面与固体边界接触的周界线，是过水断面的重要的水力要素之一。

其值越大，对水流的阻力和水头损失越大。

（2）水力半径R : 过水断面面积与湿周的比值，即 χAR =单靠过水断面面积或湿周，都不足以表明断面几何形状和大小对水流水头损失的影响。

水力学第三章课后习题答案2.23 已知速度场xu =2t +2x +2y ，yu =t -y +z ，zu =t +x -z 。

试求点（2，2，1）在t =3时的加速度。

解：x x x x xx y z u u u uau u u t x y z∂∂∂∂=+++∂∂∂∂()()2222220t x y t y z =+++⋅+-+⋅+26422t x y z=++++ ()2321t x y z =++++y y y y y xyzu u u u a u u u t x yz∂∂∂∂=+++∂∂∂∂ ()()101t y z t x z =+--+++-⋅12x y z=++-z z z z z x y z u u u ua u u u t x y z∂∂∂∂=+++∂∂∂∂ ()()12220t x y t x z =++++-+-12t x y z=++++()()3,2,2,12332221134x a =⨯⨯+⨯+++=（m/s 2）()3,2,2,112223y a =++-=（m/s 2） ()3,2,2,11324111z a =++++=（m/s 2）2222223431135.86xyza a a a =++=++=（m/s 2）答：点（2，2，1）在t =3时的加速度35.86a =m/s 2。

3.8已知速度场xu =2xy ，y u =–331y ，zu =xy 。

试求：（1）点（1，2，3）的加速度；（2）是几维流动；（3）是恒定流还是非恒定流；（4）是均匀流还是非均匀流。

解：（1）44421033x x x x xx y z u u u u au u u xy xy xy t x y z ∂∂∂∂=+++=-+=∂∂∂∂ 551100033y y y y y xyzu u u u a u u u y y txyz∂∂∂∂=+++=+++=∂∂∂∂ 33312033z z z z z x y z u u u u a u u u xy xy xy t x y z ∂∂∂∂=+++=+-=∂∂∂∂()41161,2,31233x a =⨯⨯=（m/s 2）()51321,2,3233y a =⨯=（m/s 2） ()32161,2,31233x a =⨯⨯=（m/s 2） 22213.06x y z a a a a =++=（m/s 2）（2）二维运动，空间点的运动仅与x 、y 坐标有关；（3）为恒定流动，运动要素与t 无关； （4）非均匀流动。