MATLAB语言在非线性最小二乘估计中的应用

matlab最小二乘法求微分方程系数在Matlab中，可以使用最小二乘法来求解微分方程的系数。

最小二乘法是一种统计方法，用于寻找一组参数，使得这组参数与数据之间的误差平方和最小化。

下面是使用Matlab实现最小二乘法求解微分方程系数的步骤：1. 首先，定义微分方程的形式，如y'(t) = a * y(t) + b *u(t)，其中y'(t)表示y关于t的导数，a和b是待求解的系数，u(t)是输入函数。

2. 生成输入数据u(t)和对应的输出数据y(t)。

将输入数据和输出数据存储在向量中。

3. 创建误差函数，该函数计算模型预测值与实际输出值之间的误差。

根据微分方程的形式，计算预测值y_pred(t) = a * y(t-Δt) + b * u(t-Δt)，其中Δt是时间步长。

4. 使用Matlab的非线性最小二乘函数（如lsqnonlin）来求解最小二乘问题。

将误差函数作为目标函数，并给定初始猜测的参数值，通过迭代优化参数值以最小化误差函数。

5. 获取最优参数值。

下面是使用Matlab实现最小二乘法求解微分方程系数的示例代码：```matlab% 定义微分方程形式 y'(t) = a * y(t) + b * u(t)% 生成输入数据 u(t) 和输出数据 y(t)% 将输入数据和输出数据存储在向量 u 和 y 中% 创建误差函数function error = diff_eqn_coefficients(x, u, y, dt)a = x(1);b = x(2);y_pred = a * y(1:end-1) + b * u(1:end-1);error = y(2:end) - y_pred;end% 给定初始猜测的参数值x0 = [1, 1];% 使用 lsqnonlin 求解最小二乘问题coefficients = lsqnonlin(@(x) diff_eqn_coefficients(x, u, y, dt), x0);% 获取最优参数值a = coefficients(1);b = coefficients(2);```在实际应用中，需根据具体的微分方程形式和数据进行适当的修改和调整。

---------------------------------------------------------------最新资料推荐------------------------------------------------------ matlab最小二乘法的非线性参数拟合（精荐）matlab 最小二乘法的非线性参数拟合 matlab 最小二乘法的非线性参数拟合首先说一下匿名函数：在创建匿名函数时，Matlab 记录了关于函数的信息，当使用句柄调用该函数的时候，Matlab 不再进行搜索，而是立即执行该函数，极大提高了效率。

所以首选匿名函数。

具体拟合时可以使用的方法如下：1 曲线拟合工具箱1 曲线拟合工具箱提供了很多拟合函数，使用简单非线性拟合 nlinfit 函数 clear all; x1=[0.4search 或优化工具箱提供的极小化函数求解。

在 Matlab 中，曲线拟合工具箱也提供了曲线拟合的图形界面操作。

在命令提示符后键入：cftool，即可根据数据，选择适当的拟合模型。

\命令\命令 1.假设要拟合的多项式是：y=a+b*x+c*x.首先建立设计矩阵 X：X=[ones(size(x)) x x]; 执行：para=X\y para 中包含了三个参数：para(1)=a;para(2)=b;para(3)=c; 这种方法对于系数是线性的模型也适应。

1 / 102.假设要拟合：y=a+b*exp(x)+cx*exp(x) 设计矩阵 X 为 X=[ones(size(x)) exp(x) x.*exp(x.)]; para=X\y 3.多重回归(乘积回归) 设要拟合： y=a+b*x+c*t，其中 x 和 t 是预测变量，y 是响应变量。

设计矩阵为 X=[ones(size(x)) x t] %注意 x,t 大小相等！para=X\y polyfit 函数polyfit 函数 polyfit 函数不需要输入设计矩阵，在参数估计中，polyfit 会根据输入的数据生成设计矩阵。

MATLAB中的最小二乘问题求解技巧最小二乘问题是求解一个最优拟合曲线或平面的方法，它在各种科学和工程领域中都有广泛的应用。

在MATLAB中，有很多强大的工具和函数可以用来解决最小二乘问题。

本文将介绍一些MATLAB中常用的最小二乘问题求解技巧，帮助读者更好地利用MATLAB来解决实际问题。

一、线性最小二乘问题求解线性最小二乘问题是最简单的一类最小二乘问题，它对应于求解一个线性方程组。

在MATLAB中，我们可以使用“\”运算符来直接求解线性最小二乘问题。

例如，如果我们有一个包含m个方程和n个未知数的线性方程组Ax=b，其中A是一个m×n的矩阵，b是一个m×1的向量，我们可以使用以下代码来求解该方程组：```matlabx = A\b;```在这个例子中，MATLAB将会利用最小二乘法来计算出一个使得Ax与b之间误差的平方和最小的向量x。

二、非线性最小二乘问题求解非线性最小二乘问题的求解相对复杂一些，因为它不再对应于一个简单的方程组。

在MATLAB中，我们可以使用“lsqcurvefit”函数来求解非线性最小二乘问题。

该函数的基本用法如下：```matlabx = lsqcurvefit(fun,x0,xdata,ydata);```其中，fun是一个函数句柄，表示我们要拟合的目标函数；x0是一个初始值向量；xdata和ydata是实验数据的输入和输出。

lsqcurvefit函数将会尝试找到一个使得目标函数与实验数据之间残差的平方和最小的参数向量。

三、加权最小二乘问题求解加权最小二乘问题是在非线性最小二乘问题的基础上引入权重因子的一种求解方法。

它可以用来处理实验数据中存在的误差或不确定性。

在MATLAB中，我们可以使用“lsqnonlin”函数来求解加权最小二乘问题。

```matlabx = lsqnonlin(fun,x0,[],[],options);```其中，fun、x0、options的含义与lsqcurvefit函数相同。

在MATLAB中，你可以使用`lsqnonlin`函数来实现Levenberg-Marquardt方法。

Levenberg-Marquardt方法是一种非线性最小二乘问题的优化算法，用于求解具有高度非线性的目标函数的最优解。

该方法通过调整参数来平衡最速下降法和高斯-牛顿法之间的权衡，从而实现更快的收敛速度和更好的稳定性。

下面是使用Levenberg-Marquardt方法求解非线性最小二乘问题的基本步骤：1. 定义目标函数：首先需要定义一个非线性函数，表示你想要求解的最小二乘问题。

2. 定义初始参数估计值：根据问题的特点，给出一个初始的参数估计值。

3. 定义残差函数：将目标函数与实际观测数据之间的差异定义为残差函数。

4. 调用`lsqnonlin`函数：使用`lsqnonlin`函数来求解最小二乘问题。

该函数需要输入目标函数、初始参数估计值和残差函数，并返回最优的参数估计值。

以下是一个简单的示例代码，演示如何在MATLAB中使用Levenberg-Marquardt方法求解非线性最小二乘问题：```matlab定义目标函数fun = @(x) x(1)*exp(-x(2)*[1:10]) - [2, 4, 6, 8, 10, 12, 14, 16, 18, 20];定义初始参数估计值x0 = [1; 0.1];定义残差函数residuals = @(x) norm(fun(x));调用lsqnonlin函数求解最小二乘问题options = optimoptions('lsqnonlin', 'Algorithm', 'levenberg-marquardt');x = lsqnonlin(residuals, x0, [], [], options);disp('最优参数估计值:');disp(x);```在上述示例中，我们首先定义了一个目标函数`fun`，然后给出了初始参数估计值`x0`。

1、线性最小二乘拟合最小二乘法（又称最小平方法）是一种数学优化技术，其通过最小化误差的平方和寻找数据的最佳函数匹配。

利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

最小二乘法通过变量的数据来描述变量之间的相互关系。

例如通过()1122m m x ,y ,x ,y ,,x ,y 描述x 、y 之间的相互关系01y =a +a x 。

常见的多项式拟合曲线有：直线01y =a +a x 、多项式01+n n y =a +a x a x + 、双曲线01y =a x+a 、指数曲线*e ^y =a b 。

Matlab 中的最小二乘函数：P=polyfit(x,y,n)（n=1时为01y =a +a x ），[P S mu]=polyfit(x,y,n)，polyval(P,t)返回n 次多项式在t 处的值（plot(t, polyval(P,t)）。

P-返回n 次拟合多项式系数从高到低依次存放于向量P 中，S-包含三个值其中normr 是残差平方和，mu-包含两个值mean （x ）均值，std （x ）标准差。

2、非线性拟合超定方程组（方程组的个数大于未知数的个数），Matlab 中提供lsqcurvefit 和lsqnonlin 两个非线性最小二乘拟合函数，两者的区别在于其定于的函数f (x )不一样。

非线性曲线拟合lsqcurvefit 用以求含参量x （向量）的向量值函数F(x,xdata)=（F （x ，xdata 1），…，F （x ，xdata n ））T 中的参变量x(向量)，使得：()()1,ni ii F x xdata ydata =-∑最小 其输入格式有：(1) x = lsqcurvefit (‘fun’,x0,xdata,ydata);(2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,options);(3) x = lsqcurvefit (‘fun’,x0,xdata,ydata,options,’grad’);(4) [x, options] = lsqcurvefit (‘fun’,x0,xdata,ydata,…);(5) [x, options,funval] = lsqcurvefit (‘fun’,x0,xdata,ydata,…);(6) [x, options,funval, Jacob] = lsqcurvefit (‘fun’,x0,xdata,ydata,…);其中fun 为事先建立的函数F(x,xdata)的M-文件x0为迭代初始值，xdata 、ydata 为已知数据点、options 为无约束优化。

matlab lm算法在MATLAB中，可以使用lm算法（Levenberg-Marquardt算法）来进行非线性最小二乘拟合。

该算法是一种迭代算法，用于优化参数估计，特别适用于解决非线性最小二乘问题。

在lm算法中，通过最小化残差平方和来找到最优参数估计。

算法通过迭代的方式进行，每一次迭代都会更新参数的估计值，直到达到收敛条件。

迭代的过程中，算法会根据当前参数估计值计算出残差的梯度和海森矩阵，然后通过调整参数估计值来减小残差平方和。

在MATLAB中，可以使用'lsqcurvefit'函数来实现lm算法。

这个函数可以通过传入一个自定义的非线性函数来进行拟合。

首先，需要定义一个函数，这个函数描述了要拟合的模型。

然后，使用'lsqcurvefit'函数来调用lm算法进行参数估计。

下面是一个使用lm算法进行数据拟合的示例：```matlab% 定义要拟合的非线性函数fun = @(x,xdata)x(1)*exp(-x(2)*xdata);% 生成带有噪声的数据xdata = linspace(0,10,100);ydata = 2*exp(-0.5*xdata) + 0.1*randn(size(xdata));% 初始化参数估计值x0 = [1, 1];% 使用lm算法进行参数估计x = lsqcurvefit(fun, x0, xdata, ydata);% 输出参数估计值disp('Estimated parameters:')disp(x)% 绘制拟合结果x_fit = linspace(0, 10, 100);y_fit = fun(x, x_fit);figureplot(xdata, ydata, 'o')hold onplot(x_fit, y_fit, 'r')xlabel('x')ylabel('y')legend('原始数据', '拟合结果')```在上面的示例中，我们定义了一个指数衰减函数作为要拟合的模型。

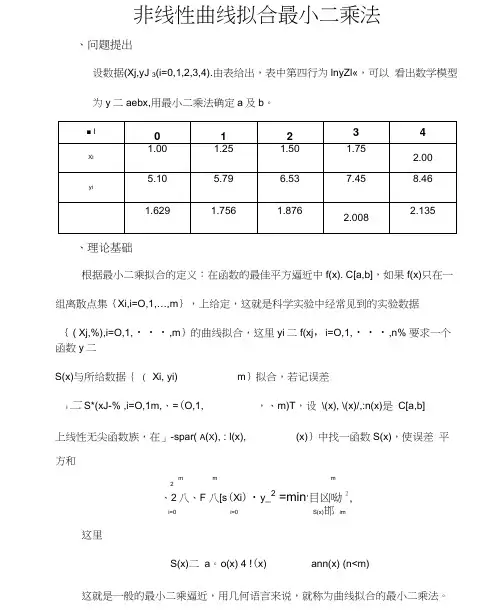
非线性曲线拟合最小二乘法、问题提出设数据(Xj,yJ 3(i=0,1,2,3,4).由表给出，表中第四行为lnyZl«，可以看出数学模型为y二aebx,用最小二乘法确定a及b。

、理论基础根据最小二乘拟合的定义：在函数的最佳平方逼近中f(x). C[a,b]，如果f(x)只在一组离散点集｛Xi,i=O,1,…,m｝，上给定，这就是科学实验中经常见到的实验数据｛ ( Xj,%),i=O,1,・・・,m｝的曲线拟合，这里yi二f(xj，i=O,1,・・・,n% 要求一个函数y二S(x)与所给数据｛ ( Xi, yi) m｝拟合，若记误差i 二 S*(xJ-% ,i=O,1m,、=(O,1, ，、m)T，设\(x), \(x)/,:n(x)是C[a,b]上线性无尖函数族，在」-spar( A(X), : l(x), (x)｝中找一函数S(x)，使误差平方和m m m2、2八、F 八[s(Xi)・y_2 =min,目凶呦2,i=0 i=0 S(x)邯im这里S(x)二a。

o(x) 4 !(x) ann(x) (n<m)这就是一般的最小二乘逼近，用几何语言来说，就称为曲线拟合的最小二乘法。

在建模的过程中应用到了求和命令(sum)、求偏导命令(diff)、化简函数命令(simple)〉用迭代方法解二元非线性方程组的命令(fsolve)，画图命令(plot)等。

三、实验内容用最小二乘法求拟合曲线时，首先要确定S(x)的形式。

这不单纯是数学问题，还与所研究问题的运动规律及所得观测数据( Xi,% )有尖；通常要从问题的运动规律及给定数据描图，确定s(x)的形式，并通过实际计算选出较好的结果。

S(x)的一般表达式为线性形式，若\(x)是k次多项式，S(x)就是n次多项式，为了使问题的提法更有一般性，通常在最小二乘法中2都考虑为加权平方和m：2八(X讥S(Xj) - f(xj]2.i=0这里r(x)_o是[a,b]上的权函数，它表示不同点(Xi, f(xj)处的数据比重不同。

matlab中l-m优化算法
L-M（Levenberg-Marquardt）算法是一种非线性最小二乘优化
算法，用于解决非线性最小化问题。

该算法结合了最速下降法和高
斯-牛顿法的优点，能够在搜索过程中动态调整步长，从而更快地收
敛到最优解。

L-M算法的基本思想是通过不断迭代调整参数，使得目标函数
的值不断减小，直至达到局部最优解。

在每一次迭代中，L-M算法
会根据当前的参数估计值计算出目标函数的梯度和海森矩阵，并结
合这些信息调整参数的取值。

通过这种方式，L-M算法能够有效地
处理非线性最小化问题，并且对初始值的选取不敏感。

在MATLAB中，可以使用内置的lsqnonlin函数来实现L-M算法。

该函数可以通过指定目标函数、初始参数估计值等参数来进行非线
性最小化求解。

此外，MATLAB还提供了许多优化工具箱，其中包括
了更多高级的优化算法和工具，可以帮助用户更方便地进行参数估
计和优化问题的求解。

总的来说，L-M算法是一种非常有效的非线性最小化算法，能
够在MATLAB中得到很好的支持和应用。

通过合理使用MATLAB提供
的工具和函数，可以很方便地对复杂的非线性优化问题进行求解。

希望这个回答能够帮助到你。

matlab中的lsqcurvefit使⽤转⾃：⾮线性曲线拟合是已知输⼊向量xdata和输出向量ydata，并且知道输⼊与输出的函数关系为ydata=F(x, xdata)，但不知道系数向量x。

今进⾏曲线拟合，求x使得输出的如下最⼩⼆乘表达式成⽴：min Σ(F(x,xdatai)-ydatai)^2函数 lsqcurvefit格式 x = lsqcurvefit(fun,x0,xdata,ydata)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)[x,resnorm] = lsqcurvefit(…)[x,resnorm,residual] = lsqcurvefit(…)[x,resnorm,residual,exitflag] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(…)[x,resnorm,residual,exitflag,output,lambda,jacobian] =lsqcurvefit(…)参数说明：x0为初始解向量；xdata，ydata为满⾜关系ydata=F(x, xdata)的数据；lb、ub为解向量的下界和上界lb≤x≤ub，若没有指定界，则lb=[ ]，ub=[ ]；options为指定的优化参数；fun为待拟合函数，计算x处拟合函数值，其定义为 function F = myfun(x,xdata)resnorm=sum ((fun(x,xdata)-ydata).^2)，即在x处残差的平⽅和；residual=fun(x,xdata)-ydata，即在x处的残差；exitflag为终⽌迭代的条件；output为输出的优化信息；lambda为解x处的Lagrange乘⼦；jacobian为解x处拟合函数fun的jacobian矩阵。

matlab中levenberg-marquardt method Matlab中的Levenberg-Marquardt方法引言：在科学和工程应用中，我们经常需要拟合数据并找到与其最匹配的数学模型。

Levenberg-Marquardt方法是一种常用于非线性最小二乘优化问题的算法，它通过迭代寻找能最小化残差平方和的参数。

本文将介绍Matlab 中实现Levenberg-Marquardt方法的基本原理和步骤，帮助读者理解和应用该方法。

第一步：定义问题和目标函数在使用Levenberg-Marquardt算法之前，首先需要定义一个问题并确定优化的目标函数。

以数据拟合问题为例，我们需要知道待拟合的数据集，并选择合适的数学模型来描述这些数据。

假设我们的拟合目标是通过一组参数`theta`最小化残差平方和，那么目标函数可以表示为：F(theta) = sum((y_data - f(x_data, theta)).^2)其中，`y_data`是观测到的数据集，`x_data`是对应的自变量数据，`f(x_data, theta)`是用来拟合数据的数学模型。

在Matlab中，我们需要自定义一个函数来实现该目标函数。

第二步：编写目标函数在Matlab中，我们可以使用function关键字来定义一个函数。

以`F(theta)`为例，我们可以通过如下方式编写目标函数：matlabfunction residual = objective_function(theta, x_data, y_data) residual = y_data - f(x_data, theta);residual = residual(:); 将残差矩阵转化为向量end在上述代码中，`theta`是参数向量，`x_data`和`y_data`是输入的数据集。

函数内部首先计算出真实的y值和拟合模型的输出之间的残差，然后将其转化为向量形式。

MATLAB中lsqcurvefit的用法概述在M AT LA B中，`ls qc u rv ef it`是一个用于非线性最小二乘拟合的函数。

该函数可以求解一组非线性方程或拟合一组数据，以最小化残差平方和。

函数语法```m at la b[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(fu n,x0,x da ta,y da ta,l b,u b,o pt io ns)```参数说明-`fu n`：自定义函数句柄，用于计算模型预测值和实际观测值之间的残差。

该函数应接受参数x和xd at a作为输入，返回模型预测值。

-`x0`：拟合参数的初始猜测值。

-`xd at a`：实际观测值的自变量数据。

-`yd at a`：实际观测值的因变量数据。

-`lb`：拟合参数的下界限制。

-`ub`：拟合参数的上界限制。

-`op ti on s`：可选参数，用于指定拟合过程中的详细设置，如最大迭代次数、收敛容限等。

示例假设我们有一组数据，需拟合出一个指数函数模型。

首先定义自定义函数`e xp Fu nc`，用于计算指数函数的预测值和实际观测值之间的残差。

```m at la bf u nc ti on y=ex pF unc(x,xd at a)y=x(1)*e xp(x(2)*x d at a);e n d```然后，我们准备好数据和初始猜测值，并调用`l sq cu rv ef it`进行拟合。

```m at la bx d at a=[01234];y d at a=[12.66.714.529.6];x0=[11];[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(@e xp Fun c,x0,xd at a,yd ata);```输出结果-`x`：拟合出的参数值。

最小二乘法拟合和优化常用的 matlab 命令及其适用范围
最小二乘法拟合和优化常用的Matlab 命令及其适用范围如下：
1. polyfit：用于多项式拟合的函数，可以通过最小二乘法拟合
一组数据点的多项式曲线。

适用范围：适合进行多项式拟合的情况。

2. lsqcurvefit：用于非线性最小二乘法拟合的函数，可以通过
最小二乘法拟合一组数据点的非线性函数曲线。

适用范围：适合进行非线性函数拟合的情况。

3. fminsearch：用于寻找函数的最小值的函数，可以通过优化
算法寻找最适合数据点的参数值。

适用范围：适合进行简单的参数优化的情况。

4. fmincon：用于带约束条件的优化问题的函数，可以通过优
化算法寻找最适合数据点的参数值，并满足约束条件。

适用范围：适合进行带约束条件的参数优化的情况。

5. lsqlin：用于带等式约束的线性最小二乘法拟合的函数，可
以通过最小二乘法拟合一组数据点的线性函数曲线，并满足等式约束。

适用范围：适合进行带等式约束的线性函数拟合的情况。

通过这些 Matlab 命令，可以进行最小二乘法拟合和优化，并
得到最适合数据的拟合曲线或参数值。

具体使用哪个命令取决于数据的特点和问题的需求。

matlab最小二乘法函数一、概述最小二乘法是一种常见的数学分析方法，用于拟合数据和估计参数。

在实际应用中，我们经常需要通过一些离散的数据点来拟合一个连续的函数或曲线，这时候就可以使用最小二乘法来得到最优的拟合结果。

在Matlab中，有专门的函数可以实现最小二乘法。

本文将详细介绍Matlab中最小二乘法函数的使用方法和注意事项。

二、函数介绍Matlab中最小二乘法函数是“lsqcurvefit”。

该函数可以用于非线性回归分析，即通过已知的自变量和因变量数据点来拟合一个非线性模型，并求出模型参数。

该函数的基本语法如下：x = lsqcurvefit(fun,x0,xdata,ydata)其中，“fun”是自定义的非线性模型函数，“x0”是待求解参数向量的初始值，“xdata”和“ydata”分别是已知的自变量和因变量数据点。

三、使用步骤1. 定义非线性模型函数首先需要定义一个非线性模型函数。

该函数应该包含待求解参数向量、“xdata”自变量向量以及其他可能需要用到的常数或变量。

例如：function y = myfun(x,xdata)y = x(1)*exp(-x(2)*xdata);其中，“x(1)”和“x(2)”是待求解的参数，这里的非线性模型函数是一个指数函数。

2. 准备数据接下来需要准备已知的自变量和因变量数据点。

这里以一个简单的例子为例：xdata = [0,1,2,3,4,5];ydata = [1.8,1.2,0.9,0.6,0.4,0.3];3. 设置初始值为了使用最小二乘法求解模型参数，需要给出待求解参数向量的初始值。

可以根据实际情况设置初始值，一般来说可以通过试验或经验得到一个大致的估计值。

例如：x0 = [1,1];这里设置了两个参数的初始值分别为1。

4. 调用函数最后调用“lsqcurvefit”函数进行拟合：x = lsqcurvefit(@myfun,x0,xdata,ydata);其中，“@myfun”表示使用自定义的非线性模型函数，注意要加上“@”符号。

matlabnlinfit原理Matlabnlinfit是一个非线性拟合函数，用于在MATLAB中进行非线性最小二乘拟合。

通过使用nlinfit，我们可以对非线性模型进行拟合，以获取最佳参数值。

在本篇文章中，我们将介绍nlinfit的原理、使用方法、参数意义以及注意事项。

一、非线性拟合简介拟合是指通过找到最佳参数值，使模型与数据之间的差异最小化。

在非线性拟合中，模型通常是非线性的，因此需要使用适合的非线性拟合函数。

nlinfit是MATLAB中提供的一种非线性拟合函数，它基于MATLAB内置的fmincon函数，适用于求解非线性最小二乘问题。

二、nlinfit函数参数nlinfit函数需要指定以下参数：*xdata：数据点x的坐标值。

*ydata：数据点y的观测值。

*f：目标函数，描述模型与数据的相互作用关系。

*xb：模型参数的初始猜测值。

*fun：目标函数的梯度函数。

*options：nlinfit函数的选项参数，用于控制拟合过程的收敛性和稳定性。

三、nlinfit原理nlinfit函数通过迭代优化算法，不断调整模型参数的值，以最小化目标函数与数据之间的差异。

在每一次迭代中，函数计算目标函数的梯度，并根据梯度信息调整参数值。

如果参数值的改变量小于某个阈值，则认为拟合过程收敛。

拟合过程中，可以通过设置选项参数来控制收敛速度和稳定性。

四、使用方法示例下面是一个简单的示例，展示如何使用nlinfit函数进行非线性拟合：```matlab%生成示例数据x=[1,2,3,4,5];y=[2.2,2.8,3.6,4.5,4.9];x_fit=linspace(x(1),x(end),100);%生成用于拟合的数据点y_fit=curvefit(f,x,y);%使用curvefit进行非线性拟合plot(x,y,'o');%绘制原始数据点holdon;plot(x_fit,y_fit);%绘制拟合曲线legend('原始数据','拟合曲线');```在上述示例中，我们使用curvefit函数进行非线性拟合，并使用nlinfit进行参数优化。

matlab中的一些经典算法在MATLAB中，有许多经典算法可以用于各种数学和工程问题。

以下是一些常见的经典算法：1. 最小二乘法（Least Squares Method），用于拟合数据和解决过定系统的线性方程组。

MATLAB中的`polyfit`和`lsqcurvefit`函数可以实现最小二乘拟合。

2. 快速傅里叶变换（Fast Fourier Transform, FFT），用于信号处理和频域分析。

MATLAB中的`fft`函数可以对信号进行快速傅里叶变换。

3. 线性规划（Linear Programming），用于优化问题的求解，例如最大化/最小化线性目标函数的线性约束问题。

MATLAB中的`linprog`函数可以用于线性规划求解。

4. 非线性最小二乘法（Nonlinear Least Squares），用于拟合非线性模型到数据。

MATLAB中的`lsqnonlin`函数可以用于非线性最小二乘拟合。

5. 最优化算法（Optimization Algorithms），MATLAB提供了许多优化算法，包括梯度下降、共轭梯度、拟牛顿等算法，用于解决无约束和约束优化问题。

6. 插值算法（Interpolation），MATLAB中的`interp1`和`interp2`函数可以用于一维和二维数据的插值。

7. 微分方程求解（Differential Equation Solving），MATLAB中的`ode45`和`ode15s`等函数可以用于求解常微分方程和偏微分方程。

8. 图像处理算法（Image Processing Algorithms），MATLAB提供了丰富的图像处理工具箱，包括滤波、边缘检测、图像分割等经典算法。

以上列举的算法只是 MATLAB 中众多经典算法的一小部分，它们在数学建模、信号处理、优化、图像处理等领域有着广泛的应用。

希望这些信息能够帮助到你。

matlib中用于最小二乘法的函数介绍标题：MATLAB中用于最小二乘法的函数介绍介绍：最小二乘法是一种常用的数学方法，用于寻找能够最优拟合给定数据的函数。

MATLAB提供了一些非常有用的函数，用于执行最小二乘拟合和分析。

本文将深入介绍这些函数的使用方法、功能和一些实例应用，以帮助读者更好地理解和应用最小二乘法。

第一部分：概述最小二乘法在这一部分，将对最小二乘法的基本概念和原理进行概述。

我会解释为什么最小二乘法是一个强大的工具，以及在实际问题中的应用领域。

我将介绍如何将问题转化为最小二乘问题，并解释如何定义目标函数。

第二部分：MATLAB中的最小二乘法函数在这一部分，我将深入研究MATLAB中的几个关键函数，这些函数可用于最小二乘法的实现和分析。

我将逐一介绍这些函数的功能、输入参数和输出结果。

在讲解过程中，我将使用一些实际的数据集来说明这些函数的使用方法。

函数1：polyfit函数polyfit函数是MATLAB中用于进行多项式拟合的函数。

我将解释该函数的语法和用法，并提供一个示例来演示如何使用polyfit函数来拟合数据。

函数2：lsqcurvefit函数lsqcurvefit函数是用于非线性最小二乘拟合的强大函数。

我将详细介绍该函数的使用方法和输入参数，并通过一个拟合非线性函数的实例来演示其功能。

函数3：lsqlin函数lsqlin函数是一个用于执行线性最小二乘拟合的函数。

我将讨论该函数的功能、输入和输出，并提供一个实例来说明如何使用lsqlin函数。

第三部分：总结与回顾在这一部分，我将对前两部分的内容进行总结和回顾。

我会提出一些关键观点和结论，以帮助读者更全面、深刻和灵活地理解最小二乘法在MATLAB中的应用。

观点和理解：最小二乘法是一个非常强大和常用的工具，用于拟合和分析数据。

MATLAB提供了一些方便的函数，用于执行最小二乘拟合，并可以应用于不同类型的问题。

polyfit函数适用于多项式拟合，lsqcurvefit函数适用于非线性函数拟合，而lsqlin函数适用于线性函数拟合。

新乡学院数学与信息科学系实验报告
实验名称插值与拟合Ⅱ
所属课程数学软件与实验
实验类型综合型实验
专业信息与计算科学
班级 2011级1班
学号
姓名李欢丽
指导教师朱耀生老师
4.结论及分析
经多次试验可知分析无误
问题二增加生产、发展经济所依靠的主要因素有增加投资、增加劳动力以及技术革新等，在研究国民经济产值与这些因素的数量关系时，由于技术水平不像资金、劳动力那样容易定量化，作为初步的模型，可认为技术水平不变，只讨论产值和资金、劳动力之间的关系。

在科学技术发展不快时，如资本主义经济发展的前期，这种模型是有意义的。

用Q，K，L分别表示产值、资金、劳动力，要寻求的数量关系。

经过简化假设与分析，在经济学中，推导出一个著名的Cobb-Douglas生产函数：（*）
式中
要由经济统计数据确定。

现有美国马萨诸塞州1900—1926年上述三个经济指数的统计数据，如下表，试用数据拟合的方法，求出式（*）中的参数。

表2
t Q K L t Q K L
1900 1.05 1.04 1.05 1901 1.18 1.06 1.08 1902 1.29 1.16 1.18 1903 1.30 1.22 1.22 1914 2.01 3.24 1.65 1915 2.00 3.24 1.62 1916 2.09 3.61 1.86 1917 1.96 4.10 1.93。

matlab的lsqnonlin函数-回复题目: 详解Matlab中的lsqnonlin函数引言:在Matlab中，lsqnonlin函数是非线性最小二乘问题的求解器之一，用于寻找最小化二次误差的最佳参数。

本文将一步一步深入介绍lsqnonlin 函数的使用方法和技巧，帮助读者更好地理解和应用该函数。

第一步：函数定义和输入参数在Matlab中，我们可以通过以下方式调用lsqnonlin函数：[x, resnorm, residual, exitflag, output, lambda, jacobian] = lsqnonlin(fun,x0,lb,ub,options)其中，各参数的含义如下：- fun: 用户定义的非线性方程组或函数的句柄。

该方程组的形式为f = fun(x)，其中x表示待优化的变量。

- x0: 待优化变量的初始估计值。

- lb: 变量的下界限制，可以为空。

- ub: 变量的上界限制，可以为空。

- options: 优化选项，用于指定算法和收敛条件等，默认为空。

第二步：定义用户自定义的非线性方程组用户需要根据实际问题定义一个函数，作为非线性方程组fun的输入参数。

该函数接受一个向量x作为输入，返回一个向量f。

例如，假设我们要求解以下非线性方程组：f1(x) = x(1)^2 + x(2)^2 - 1f2(x) = exp(x(1)) - x(2)我们可以定义一个名为myFun的函数来表示上述方程组：function f = myFun(x)f(1) = x(1)^2 + x(2)^2 - 1;f(2) = exp(x(1)) - x(2);end在这个函数中，将x(1)和x(2)看作输入向量x的两个元素，并根据方程组的定义将计算结果存储在向量f中。

第三步：定义初始参数估计和边界限制在调用lsqnonlin函数之前，我们需要指定变量的初始估计值x0。

通常，我们可以根据问题的特点来选择初始估计值，确保其足够接近最优解。