运筹学教材编写组《运筹学》课后习题-运输问题(圣才出品)

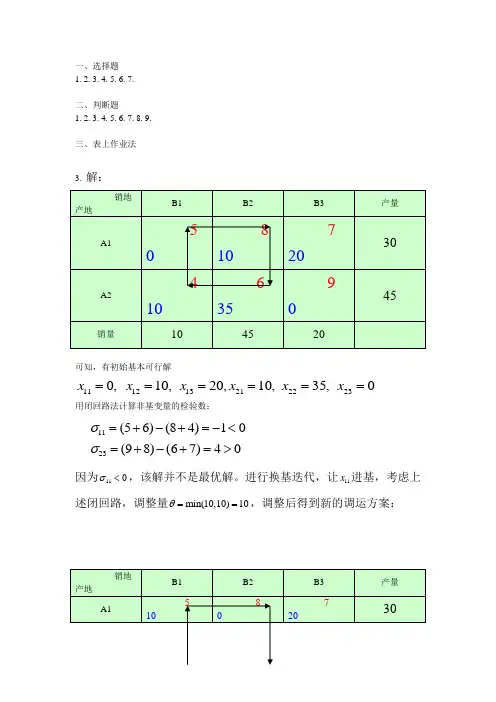
一、选择题1. 2. 3. 4. 5. 6. 7.二、判断题1. 2. 3. 4. 5. 6. 7. 8. 9.三、表上作业法 3. 解：可知，有初始基本可行解1112132122230,10,20,10,35,0x x x x x x ======用闭回路法计算非基变量的检验数：1123(56)(84)10(98)(67)40σσ=+-+=-<=+-+=>因为110σ<，该解并不是最优解。

进行换基迭代，让11x 进基，考虑上述闭回路，调整量min(10,10)10θ==，调整后得到新的调运方案：A2 4 0645945销量10 45 20计算非基变量的检验数得：1223(84)(56)10(95)(47)30σσ=+-+=>=+-+=>故此方案为最优方案，最优解为：11121321222310,0,20,0,45,0x x x x x x ======最优值min 105207456460Z =⨯+⨯+⨯=用电子表格模型求解进行验算：4. 解：用西北角法求得初始基本可行解：1112131421222324313233344,0,0,0;1,2,4,2;0,0,0,4;x x x x x x x x x x x x ============ 用位势法计算检验数：1111212121131322214142233131324323243433333106()210167()861012()9455()12194()731010()47u u v u v v u v u v u u v u v v u v u v v u v u v v u v u v u σσσσσσ=⎧+==-+=⎧⎧⎪=⎪⎪⎪+==-+=⎪⎪⎪=⎪⎪++=-+=⎪⎪⇒=⇒⎨⎨⎨+==-+=-⎪⎪=-⎪⎪+==-+=-=⎪⎪+==-+=⎪⎪⎩=⎩⎪⎪⎪⎪⎪⎩因为3132,σσ小于0，该解不是最优解。

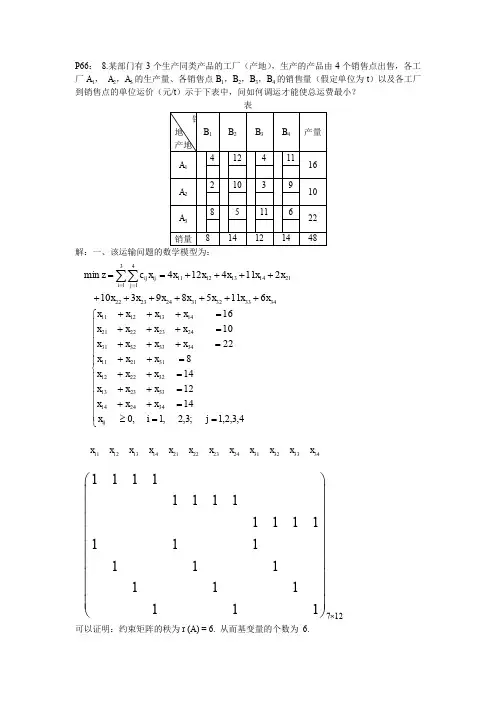
P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？表解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。

此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。

或者说：优先供应罚数最大行（或列）中最小运费的方格，以避免将运量分配到该行（或该列）次小运距的方格中。

第13章存储论13.1 复习笔记1．存储论的基本概念备货时间：从订货到货物进入“存储”往往需要一段时间，我们把这段时间称为备货时间。

备货时间可能很长，也可能很短，可能是随机性的，也可以是确定性的。

提前时间：从另一个角度看，为了在某一时刻能补充存储，必须提前订货，那么这段时间称之为提前时间。

存储策略：决定多少时间补充一次以及每次补充数量的策略称为存储策略。

存储论要解决的问题是：多少时间补充一次，每次补充的数量应该是多少，即存储策略。

2．一些参数的含义K：货物单价；：最佳订货周期；R：需求速度；：最佳订货批量；：单位存储费用；：单位缺货损失；：订购费；：最佳费用；：最佳生产时间；：生产速度；：最大存贮量；：最大缺货量；：最大缺货量。

3．存储策略（1）-循环策略，每隔时间向系统内补充存储量Q。

（2）策略，当存储量时不补充；当时补充存储，补充量(即，将存储量补充到S)。

（3）混合策略，每经过t时间检查存储量，当时不补充；当时，补充存储量使之达到S。

4．确定性存储模型（1）模型一—经典的E.O.Q模型：不允许缺货，备货时间很短，且需求是连续均匀的，即需求速度是一常数；每批订货量不变，订货费用为常数；单位存储费用不变。

已知，求，，（2）模型二：不允许缺货，生产需一定时间，其余条件同模型一。

已知，求，，（3）模型三：允许缺货，备货时间很短，其余条件同模型一。

已知，求，，，最大缺货量（4）模型四：允许缺货（需补足缺货），生产需要一定时间，其余条件同模型一。

已知，求，，简便的记忆方法：①永远成立②记住模型一，，③定义两个因子④与因子的关系与乘以因子，与除以因子模型二乘除，模型三乘除，模型四乘除⑤模型二的，模型三的，模型四的说明：在允许缺货条件下，经过研究而得出的存储策略是：每隔时间订货一次，订货量为，用中的一部分补足所缺货物，剩余部分进入存储。

很明显，在相同的时间段落里，允许缺货的订货次数比不允许缺货时订货次数减少了。

运筹学第3章运输问题第1节运输问题的数学模型第2节表上作业法钱颂迪制作运筹学（第三版）《运筹学》教材编写组第3章运输问题清华大学出版社第3章运输问题第1节运输问题的数学模型第2节表上作业法第3节产销不平衡的运输问题及其求解方法第4节应用举例第1节运输问题的数学模型已知有m个生产地点Ai,i=1,2,…，m。

可供应某种物资，其供应量(产量)分别为ai，i=1，2，…，m，有n个销地Bj，j=1,2,…,n，其需要量分别为bj，j=1,2,…,n，从Ai到Bj运输单位物资的运价(单价)为cij，这些数据可汇总于产销平衡表和单位运价表中，见表3-1，表3-2。

有时可把这两表合二为一。

表3-1销地产地1 2 ┉ n产量12┆mA 1A2┆Am销量B1 B2 ┈ BNn表3-2若用xij表示从Ai到Bj的运量，那么在产销平衡的条件下，要求得总运费最小的调运方案，数学模型这就是运输问题的数学模型。

它包含m×n个变量，(m+n)个约束方程。

其系数矩阵的结构比较松散，且特殊。

该系数矩阵中对应于变量xij的系数向量Pij，其分量中除第i个和第m+j个为1以外，其余的都为零。

即Pij=(0,… ,1,0,…,0,1,0,…,0)T=ei+em+j对产销平衡的运输问题，由于有以下关系式存在：第2节表上作业法表上作业法是单纯形法在求解运输问题时的一种简化方法，其实质是单纯形法。

但具体计算和术语有所不同。

可归纳为：(1) 找出初始基可行解。

即在(m×n)产销平衡表上用西北角法或最小元素法，Vogel法给出m+n-1个数字，称为数字格。

它们就是初始基变量的取值。

(2) 求各非基变量的检验数，即在表上计算空格的检验数，判别是否达到最优解。

如已是最优解，则停止计算，否则转到下一步。

(3) 确定换入变量和换出变量，找出新的基可行解。

在表上用闭回路法调整。

(4) 重复(2)，(3)直到得到最优解为止。

例 1 某公司经销甲产品。

第三章运输问题一、建立下列问题的数学模型1、P119, 3.6某厂按照合同规定须于当年每季度末分别提供10，15，25，20台同一规格的柴油机。

已知该厂各季度的生产能力及生产每台柴油机的成本如表所示。

又如果生产出来的柴油机当季不交货，每台每积压一个季度，存储维护费用0.15万元。

要求在完成合同的情况下，使得全年生产（存储）费用最小的决策。

将此问题归结为运输问题，试建立该问题的产销平衡及单位运价表。

解：以四个季度为产地和销地，建立产销平衡运输表如下：2、P119, 3.7上题中若允许某些季度末交货时发生短缺，但全部合同必须于Ⅳ季度末完成。

又缺货时，每台每晚交一个季度，罚款0.1万元。

为使总的生产、存储和缺货罚款损失费用最小，重新列出用运输问题求解时的产销平衡和单位运价表。

解：以四个季度为产地和销地，建立产销平衡运输表如下：3、P119, 3.8某造船厂在某年算起的连续三年的年末各提供三条规格相同的货轮，已知该厂今后三年的的生产能力及生产成本如下表所示。

已知加班生产时每条货轮成本比正常生产时高70万元，又知造出的货轮如当年不交货，每条每积压一年增加维护费用40万元。

在签订合同时，已有以前积压的两条，该厂希望在第三年末交货后多留一条备用。

问该厂应如何安排生产计划，满足上述要求，并使得总费用最小。

请列出产销平衡表和单位运价表。

解4、P120, 3.9为确保飞行的安全，飞机上的发动机每半年必须强迫更换进行大修。

某维修厂估计某种型号的战斗机从下一个半年起的今后三年内每半年需更换的发动机数量分别为：100,70,80,120,150,140（台）。

更换发动机时，可以换上新的，也可以用经过大修的旧的发动机。

已知每台新发动机的购置费是10万元，而旧发动机的维修方式有两种：快修，每台2万元，半年交货（本期拆下，下期即可用上，半年为一期）；慢修，每台1万元，一年才能交货（本期拆下，下下期可用上）。

该厂新接手该项发动机的更换维修任务，又知三年后这种战斗机将退役，退役后这种发动机将报废。

第3章 运输问题3.1 复习笔记1．运输问题的数学模型运输问题：已知有m 个生产地点,1,2,,i A i m =…，可供应某种物资，其供应量（产量）分别为i a ，1,2,,i m =…，有n 个销地j B ，1,2,,j n =…，其需要量分别为j b ，1,2,,j n =…，从i A 到j B 运输单位物资的运价（单价）为ij c 。

如何安排运输，能使得总运输成本最小？（1）产销平衡运输问题的数学模型1111min ,1,2,,..,1,2,,0m nij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪==⎨⎪⎪≥⎪⎩∑∑∑∑ 模型特点：①该模型包含m n ⨯个变量，()m n +个约束方程；②该系数矩阵中对应于变量ij x 的系数向量ij P ，其分量中除第i 个和第m j +个为1外，其余的都为零。

即(01010)T ij i m j P e e +==+…………③对于产销平衡的运输问题，有以下关系式存在：111111n m n n m m j ij ij i j i j j i i b x x a ======⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑ 所以模型最多只有m+n-1个独立约束方程。

即系数矩阵的秩≤m+n -1。

注意：运输问题的基变量一定是m+n-1个，m+n-1个变量构成基变量的充要条件是它们不构成闭回路。

闭回路的特点：在运输产销平衡表中，每一条边都是水平或垂直的；每一行或每一列至多只有两个闭回路的顶点。

（2）产销不平衡运输问题的数学模型当产大于销，即11m n i j i j a b ==>∑∑时，运输问题的数学模型可写成：1111min ,1,2,,..,1,2,,0m n ij iji j mij j i nij i j ijz c x x b j n s t x a i mx =====⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑∑∑ 当产小于销，即11m n i j i j a b ==<∑∑时，运输问题的数学模型可写成：11min m n ij ij i j z c x ===∑∑11, (1,2,,), (1,2,,)0nij i j mij j i ij x a i m x b j n x ==⎧==⎪⎪⎪≤=⎨⎪⎪≥⎪⎩∑∑……2．表上作业法表上作业法是单纯形法在求解运输问题时的一种简化方法，其实质是单纯形法。