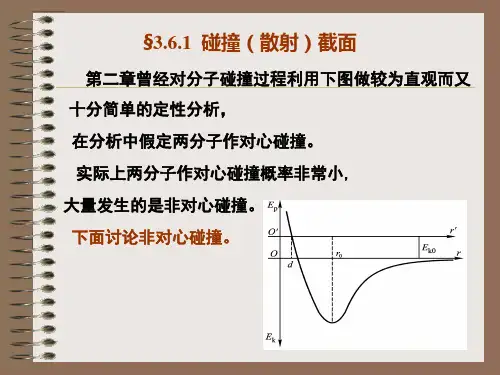
6.1碰撞过程散射截面

场力作用下的高能粒子碰撞散射截面肖 军 （xj5107@ ）我们知道，如果已知两粒子间相互作用势能()V r 的具体形式，由其可求出入射粒子的动能k E 远大于()V r 情形时的微分散射截面[1]是()()()22244sin q rV r Kr dr K μθ+∞=⎰（1）其中2sin 2K k θ⎛⎫= ⎪⎝⎭（2）/k p = ；p是入射粒子的动量。

（1）式就是高能微分散射截面波恩近似表达式。

总散射截面是()()02sin Q q d ππθθθ=⎰ （3）一、核力作用散射截面若两粒子间存在有核力作用势能 //1/()e e r R R r x x c cV r r r----=-=- （4）其中/x r R =, ()/k R m M c E c=++（5）由（1）式则可得到入射粒子以动量p碰撞另一粒子时的微分散射截面是()()()2221/22021e sin 4x xcR q ax dx R J a a μθ+∞--⎛⎫== ⎪⎝⎭⎰ （6） 式中()()1/01e sin x xJ a ax dx a +∞--=⎰((11⎤=⎦ （7）()2sin /2k p a KR m M c E c θ⎛⎫==⎪++⎝⎭（8）把（6）式代入（3）式，可得到总散射截面为()()()2222008sin 32sin sin 22Q R J a d R J a d ππθθπθθπ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭⎰⎰ （9）又由（8）式知()()sin 22//k a a p m M c E c θχ⎛⎫== ⎪++⎝⎭ （10） 其中()()2//k p m M c E c χ=++。

于是，可得到在有核力作用下的总散射截面是()()22232R Q J a ada χπχχ=⎰（11）讨论：1、从（1）式的积分范围可以看出，波恩公式中的V 要满足如下要求，（i ）作用距离r 是从0到无穷大，作用势能V 存在有限的极大值max V ；（ii ）入射粒子的动能k E 要远大于最大作用势能max V 。

话题6：碰撞与散射问题一、两体碰撞在水平面上运动的两个光滑小球发生碰撞时，小球之间的作用力是冲力，作用在小球上的其他力都是常规力，如重力、地面的支撑小球的力等等，一般情况下常规力可以忽略不计。

碰撞分为弹性与非弹性碰撞，也可以分成正碰与斜碰，既可以在实验室坐标系讨论，也可以在质心坐标系分析。

二、两体正碰正碰是是指碰撞前后两个质点的速度均在两质点的连线上的一种碰撞，参碰的两个质点都在一条直线上运动，速度的正负号就表示了速度矢量的方向。

用1m 与2m 表示两个发生碰撞的物体的质量，分别用10v 与20v 表示碰撞前的初速度，碰撞后的速度1v ,2v 是待求的量。

忽略所有常规力，则动量守恒给出初、末速度的关系1102201122m v m v m v m v +=+仅有动量守恒不能求出两个质点的末速度，还需要其他条件，按照不同的类型分别求出末速度。

三、两体正碰压缩过程压缩阶段：两小球接触后，发生微小的压缩形变，物体各部分速度不同。

达到最大压缩后，压缩阶段结束，此时物体各部分都有相同的速度，而且碰撞的两物体速度也相等。

在这一阶段冲击力的冲量称为压缩冲量。

从开始碰撞到两物体达到最大压缩为压缩阶段称为压缩阶段。

四、两体正碰恢复阶段恢复阶段：压缩阶段结束达到最大压缩。

如果两物体之间，两物体质元之间没有力作用两物体不再发生形变，没有恢复阶段。

如果仍然存在力的作用，存在恢复过程。

恢复过程中压缩逐渐变小，恢复过程结束时，两物体之间，两物体内部各质元之间，不再有相互作用力，物体内部各质元之间有相同的速度，两物体之间不再有相互作用力，碰撞过程结束。

五、弹性碰撞------动量守恒----能量守恒201m 2m1、两体正碰-----弹性碰撞机械能守恒压缩形变是弹性形变，如同弹簧那样，形变能完全消除。

发生弹性形变时，两物体之间作用力做功使动能减少转化为弹性势能。

而恢复阶段，相互作用力做功，弹性势能减少，又转化为动能，原来转化为势能的动能又完全恢复为动能。

§6 散射问题在量子力学中，散射现象也称为碰撞现象，主要研究粒子与力场、粒子与粒子的碰撞过程，这有很重要的实际意义。

如研究气体放电、气体分子碰撞、原子内部结构等。

§6.1 一般描述 1. 几个概念弹性散射（弹性碰撞）．．．．．．．．．．：粒子与粒子碰撞过程中，只有动能的交换，粒子内部状态不改变的碰撞。

非弹性散射（非弹性碰撞）．．．．．．．．．．．．：粒子与粒子碰撞过程中粒子内部状态发生改变（如原子被激发或电离）的碰撞。

课程主要讨论弹性碰撞．．．．．．．．．．。

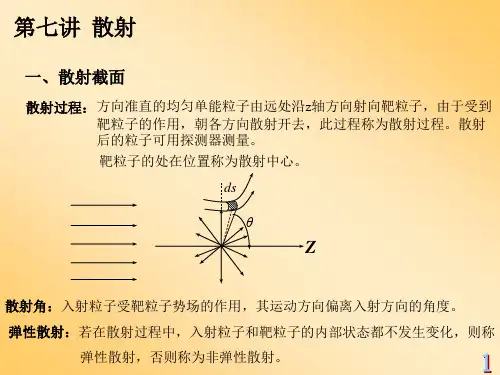
微分散射截面．．．．．．： 设一束粒子沿z 轴入射粒子A ，A 称为散射中心，碰撞引起A 的运动可略去。

粒子被散射后的运动方向与入射方向之间的夹角?称为散射角．．．。

单位时间内散射到垂直于散射方向的小面积元dS 上的粒子数与dS 、入射粒子流强度N 成正比，与dS 到A 的距离r 平方成反比，即Ω=Nd rdSNdn 2~ 引入比例系数)(ϕθ,qΩ=Nd ,q dn )(ϕθ (6.1.1))(ϕθ,q 与入射粒子、散射中心的性质及相互之间的作用和相对动能有关。

量纲关系：22][1][1][L q TL N Tdn =→==)(ϕθ,q 具有面积的量纲，称为微分散射截面．．．．．．。

∫∫∫=Ω=ππϕςθϕθϕθ020sin )()(d d ,q d ,q Q (6.1.2)称为总散射面积．．．．．。

2. 散射面积量子力学解法 以散射中心为坐标原点，)(r U 表示入射粒子与散射中心间的相互作用势能，散射体系的薛定鄂方程为　ψψψµE U =+∇−222h (6.1.3) 令 22222hh p E k ==µ (6.1.4)µµk p v h ==(6.1.5) )(2)(2r r V h µ=(6.1.6) 薛定鄂方程改为　0)]([22=−+∇ψψr V k (6.1.7) 由于探测散射粒子在离散射中心很远处，即→∝r ，此时0)(→r U 。

高能粒子碰撞散射截面肖 军 （xj5107@ ）我们知道，当粒子以动能k E 撞击另一粒子时会发生散射，如果已知两粒子间相互作用势能()V r 的具体形式，由波恩公式可求出入射粒子的动能k E 远大于()V r 情形时的微分散射截面[1]是()()()22244sin q rV r K r dr K μθ+∞=⎰（1）其中2/sin 2K p θ⎛⎫= ⎪⎝⎭（2）p是入射粒子的动量；/2h π= ；h 是普朗克常数。

总散射截面是()()02sin Q q d ππθθθ=⎰（3）笔者认为，场对散射截面的影响主要是在测不准距离m kc r E =（4）内完成，在测不准距离m r 外虽有场作用，但不会改变散射截面，也就是在m r r >时场对散射截面的贡献为零，在m r r <时场对散射截面的贡献是()()()22244sin m r q rV r K r dr K μθ=⎰（5）下面利用（5）式讨论碰撞粒子分别在核力、电场力和弱力作用下的散射截面。

1、核力作用散射截面考虑虚电荷的作用，两粒子间核力作用势能为//()er R R rc V r r --=-（6）式中()/khR m M c E c=++ （7）把（6）式代入（5）式，并令/m x r r = （8）就可得到碰撞粒子在核力作用下的微分散射截面()()222//224esin m r r R R rc q K r dr K μθ--=⎰()()()22221////224esin m m x R r R r xm m c r K r x dx K μ--=⎰（9）若令()m Kr ηηθ==， /m a R r = （10）则有()()224224212//22244esin ()x a a xmmc r c r q x dxJ μμθηηη--==⎰（11）其中()()1//01esin x a a xJ x dx ηηη--=⎰（12）总散射截面为()()02sin Q q d ππθθθ=⎰()()224228sin mc r Jd ππμηθθ=⎰()2242232sin sin 22mc r Jd ππμθθη⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭⎰()2222208mc r Jd pζπμηηη=⎰（13）其中2/m p r ζ=。

散射截面及核阻止本领第三章散射截面及核阻止本领在上一章我们采用经典动力学的方法描述了二体弹性碰撞过程和散射过程。

可以看出，一旦确定了固体中原子之间的相互作用势及入射粒子的能量，原则上说就可以计算出在单个碰撞事件中入射粒子传给靶原子的能量。

然而，我们在描述二体散射时曾引入了碰撞参数这个物理量，见方程(2.2-6)，这是一个随机量。

人们无法精确地确定带电粒子在固体p中发生的单个碰撞事件，而只能给出发生这个碰撞事件的几率。

同时，在等离子体表面改性及合成新型薄膜材料工艺中，将有大量的带电粒子同时辐照到固体的表面。

实验上也不可能确定单个入射粒子在固体中的碰撞过程以及测量在每次碰撞中的能量损失。

因此，有必要对带电粒子在固体中的碰撞过程进行统计性的描述。

本章首先引入微分散射截面的概念，它是描述一个入射粒子散射到单位空间立体角d,,2,sin,d,中的几率，并在小角散射近似条件下给出微分散射截面的约化表示式。

cc其次，借助于这种微分散射截面，我们确定带电粒子在固体中穿行单位长度内用于靶原子核反冲运动所损失的能量，即核阻止本领。

3.1 微分散射截面在研究带电粒子与固体相互作用过程时，通常引入微分散射截面这个概念来描述入射粒子散射进单位空间立体角中的粒子数。

如图3.1所示，设所有入射粒子穿过一个半径为、p,，d,,dp宽度为的圆环，散射到从到的角度间隔内。

那么散射截面的定义为cccd,,2,pdp (3.1-1),它具有面积的量纲。

由上一章的 (2.2-6) 可以看出，散射角是碰撞参数的函数，反过pc,,来我们也可以认为碰撞参数是散射角的函数，即=()。

这样散射截面又可以表pppcc示成,,pdp()()cc, d,d, (3.1-2) ,,dsinccd,d,就是所谓的微分散射截面。

在 (3.1-2) 式中我们使用了的绝对值，主要是dpd,cd,为了保证散射截面的值为正的缘故，因为当碰撞参数的值减小时，散射角的值则p,c增加。

量子力学散射截面量子力学是研究微观粒子行为的物理学分支，其中散射截面是一个重要的概念。

散射截面描述了碰撞过程中粒子的散射行为及其概率。

本文将对散射截面的原理、应用和意义进行详细阐述。

首先，我们来了解散射截面的基本原理。

散射是指在碰撞过程中，入射粒子与靶粒子之间发生的相互作用。

散射截面就是描述散射过程中粒子散射的概率。

具体来说，对于入射粒子与靶粒子的碰撞，我们可以通过测量出射粒子的角度和能量得到散射截面。

散射截面的大小反映了碰撞发生的概率有多大，较大的散射截面意味着较高的碰撞概率。

散射截面的应用非常广泛。

在核物理、粒子物理以及凝聚态物理等领域，散射截面是研究微观粒子相互作用的重要工具。

通过测量散射截面，我们可以了解微观粒子之间相互作用的特性，从而进一步探索物质的组成和性质。

同时，散射截面还可以应用于医学领域，用于放射治疗中的剂量计算和辐射安全的评估。

散射截面的意义在于指导我们理解和解释微观世界中的现象。

通过测量和研究散射截面，我们可以揭示物质的内部结构和相互作用规律，从而深入理解量子力学的基本原理。

散射截面的数值计算和实验测量结果可以与理论模型进行比较，验证理论的正确性，并推动理论的发展。

为了获得准确的散射截面，科学家们开展了大量的实验研究和理论计算。

他们使用各种粒子加速器和探测器设备，通过测量入射粒子和出射粒子的性质，来确定散射截面。

在理论计算方面，科学家们借助量子力学的数学工具，通过计算和模拟，预测和解释散射截面的行为。

总之，散射截面作为量子力学的重要概念，对于揭示微观粒子相互作用的规律具有重要意义。

它在核物理、粒子物理、凝聚态物理等领域的应用广泛，并且为我们理解和解释微观世界的现象提供了重要指导。

通过深入研究散射截面，我们可以进一步推动量子力学的发展，探索物质的奥秘。

第六章 散射§6.1碰撞过程，散射截面散射实验在近代物理学的发展中起了特别重要的作用。

特别是在认识原子、分子、核及粒子的结构性质方面，Rutherford 的粒子散射→原子的结构。

从此揭开了原子结构的新篇章，夫兰克赫兹实验证明了玻尔关于原子有定态的假设，原子很小，很难看到其微观结构，只能通过粒子与其作用，探测其性质，结构,就像用石头探水深，投石问路的方式探测其结构。

散射现象也称为碰撞现象通过散射表现出的宏观现象，研究靶的结构性质Δ散射态是一种非束体态，涉及到体系能谱的连续区部分，人们可以自由地控制入射粒子的能量。

Δ束体态理论主要在于求体系的分立能量本征值，和本征态以及在外界作用下量子态之间的跃迁规律。

Δ散射主要关心散射粒子的角分布及散射过程中粒子各种性质的变化。

Δ散射实验所观测到的都是离靶“很远”地方粒子的行为o r a 因此关心波函数在r →∞的渐近行为。

散射过程的一些基本概念①一粒子与另一粒子碰撞的过程中，只有动能变换，粒子内部状态无改变态，则称为弹性碰撞（散射）若碰撞中粒子内部状态有所改变，如原子被激发或电离，则为非弹性碰撞，注意和经典物理中物体碰撞的比较。

②粒子和另一粒子的散射实质是粒子与力场的作用，微观原子为靶时，实质是粒子与原子的作用，场电、电场、核力确定原子、粒子很小靶粒子称为散射中心，当靶A 的质量能入射粒子质量大得多时，可忽略靶的运动。

这样以来入射粒了受A 的作用偏离原来运动方向，发生散射于原来方向的夹解Q ，为散射角，如以极坐标描述，取入射粒子流方向为∂轴，则Q 用就为散射角。

研究dn单位时间内散射到面积元ds 上的粒子数dn ，当r 一定时，取求面上面积元ds 则，dn dx ∞当r 变化时2ds r ∞∴2ds dn d r∞=Ω即与ds 所张的立体角成正比，同时dn 与入射粒子流强度N 成正比N 定义，单位时间穿过单位横截面的粒子数 d n N d ∞Ω一般情下，不同方向(,)θϕ散射到的粒了数不同 (,)d N q N d θϕ=Ω(,)dn q Nd θϕ=Ω 当N 一定时，单位时间散射到(,)θϕ方向立体角ds 内的粒子数dn 由(,)q θϕ确定，(,)q θϕ与入射粒子，散射中心的性质等有关(,)q θϕ的量纲为2L面积 (,)dnq N d θϕ=Ω(,)q θϕ称为微分散射截面一个粒子(,)q d θϕΩ散到(,)θϕ方向d Ω立体内的几率 N 个粒子 (,)q Nd θϕΩ散到(,)θϕ方向d Ω立体内的个数 N 为单位时间入射粒子则(,)q Nd θϕΩ单位时 个数 将(,)q d θϕΩ对所有方向积分2(,)(,)sin ooQ q d q d dp ππθϕθϕθθ=Ω=⎰⎰⎰称为总截面量子力学如何处理散射？取散射中心为坐标原点，用()U r 表示入射粒子与散射中心之间的相互作用势能，则体系的薛方程为222U E ψψψμ-∇+=式中的μ为入射的质量，E 是它的能量为了方便，定交22222E p kμ==pkv μμ==22()()V r U r μ=hp k λ==2p k πλ==方程变为 22(())0k V r ψψ∇++=我们关心r →∞时ψ的行为，假设r →∞时()0U r →在粒子远离散射中心时，作用超于零，()U r 比1r 更快超于零，对电场不适用。

⾼中物理竞赛_话题6：碰撞与散射问题话题6：碰撞与散射问题⼀、两体碰撞在⽔平⾯上运动的两个光滑⼩球发⽣碰撞时，⼩球之间的作⽤⼒是冲⼒，作⽤在⼩球上的其他⼒都是常规⼒，如重⼒、地⾯的⽀撑⼩球的⼒等等，⼀般情况下常规⼒可以忽略不计。

碰撞分为弹性与⾮弹性碰撞，也可以分成正碰与斜碰，既可以在实验室坐标系讨论，也可以在质⼼坐标系分析。

⼆、两体正碰正碰是是指碰撞前后两个质点的速度均在两质点的连线上的⼀种碰撞，参碰的两个质点都在⼀条直线上运动，速度的正负号就表⽰了速度⽮量的⽅向。

⽤1m 与2m 表⽰两个发⽣碰撞的物体的质量，分别⽤10v 与20v 表⽰碰撞前的初速度，碰撞后的速度1v ,2v 是待求的量。

忽略所有常规⼒，则动量守恒给出初、末速度的关系1102201122m v m v m v m v +=+仅有动量守恒不能求出两个质点的末速度，还需要其他条件，按照不同的类型分别求出末速度。

三、两体正碰压缩过程压缩阶段：两⼩球接触后，发⽣微⼩的压缩形变，物体各部分速度不同。

达到最⼤压缩后，压缩阶段结束，此时物体各部分都有相同的速度，⽽且碰撞的两物体速度也相等。

在这⼀阶段冲击⼒的冲量称为压缩冲量。

从开始碰撞到两物体达到最⼤压缩为压缩阶段称为压缩阶段。

四、两体正碰恢复阶段恢复阶段：压缩阶段结束达到最⼤压缩。

如果两物体之间，两物体质元之间没有⼒作⽤两物体不再发⽣形变，没有恢复阶段。

如果仍然存在⼒的作⽤，存在恢复过程。

恢复过程中压缩逐渐变⼩，恢复过程结束时，两物体之间，两物体内部各质元之间，不再有相互作⽤⼒，物体内部各质元之间有相同的速度，两物体之间不再有相互作⽤⼒，碰撞过程结束。

五、弹性碰撞------动量守恒----能量守恒201m 2m1、两体正碰-----弹性碰撞机械能守恒压缩形变是弹性形变，如同弹簧那样，形变能完全消除。

发⽣弹性形变时，两物体之间作⽤⼒做功使动能减少转化为弹性势能。

⽽恢复阶段，相互作⽤⼒做功，弹性势能减少，⼜转化为动能，原来转化为势能的动能⼜完全恢复为动能。