几种典型路阻函数的特性比较及参数选择研究
- 格式:ppt
- 大小:1.34 MB
- 文档页数:18

二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点之南宫帮珍创作一、 实验目的二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点。
2掌握二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点的测试方法。
二、 实验原理二阶电路是含有立个独立储能元件的电路,描述电路行为的方程是二阶线性常系数微分方程。
应用经典定量分析开关闭合后UC 、i 等零输入响应的变更规律 将如下R 、L 、C 元件的电压电流表达式代入KVL 方程,可得由数学分析可知,要确定二阶微分方程的解,除应知道函数的初始值外,还应知道函数的一阶导数初始值,它可根据下列关系求得 由于ci dt du C -= 所以"+'=u u u C C C 所示二阶微分方程的解可设为特征根为因此 t t C e A e A u 21s 2s 1+= 由初始条件Uc(0+)=Uo,可得 A1+A2=Uo又t t C e A e A dtdu 21s 2s 1+= 可求得⎪⎪⎩⎪⎪⎨⎧--=-=1201212021s s U s A s s U s A (1) C LR 2>,S1和S2为不相等的负实数,暂态属非振荡类型,称电路是过阻尼的。
(2) C LR 2=,S1和S2为两相等的负实数,电路处于临界阻尼,暂态是非振荡的。
(3) C LR 2<,S1和S2为一对共轭复数,暂态属振荡类型,称电路是欠阻尼的。
三、 仿真实验设计与测试 解:800LC 1_)2L R (2L R s2200LC 1_)2L R (2L R s1240010*5.125.022226———特征根程。
,电路为非振荡放电过Ω,=-==+-=>==-C L R C L代入公式可得电流最大值发生的时间tm 为四、结果与误差分析1.结果符合二阶电路响应的基本特性2.误差发生的主要原因可能是因为元件内阻的存在五、设计总结通过这次设计我掌握了EWB电路电子分析仿真软件的使用,通过这款软件验证所学的知识,使我对所学的知识有了更深更直观的理解,同时在计算机上设计模拟电路来验证理论对以后的电路学习也将有莫大的帮忙。

流体力学中的特殊函数逼近在流体力学中,特殊函数是解析和数值求解流动问题中的关键工具。
特殊函数可以近似描述流体流动的复杂动力学行为,提供精确和高效的数值计算方法。
本文将介绍在流体力学中常用的特殊函数及其逼近方法。
一、贝塞尔函数逼近贝塞尔函数是具有重要物理意义的特殊函数之一,广泛应用于流体力学中的边界值问题和振动问题。
贝塞尔函数主要用于描述圆柱坐标系中的流动情况。
对于特定的流动问题,我们可以利用贝塞尔函数的逼近方法来简化求解过程。
贝塞尔函数逼近方法的原理是利用递推关系和级数展开,将复杂的问题转化为求解递推关系的简单问题。
通过对贝塞尔函数的级数展开和截断,我们可以得到一个近似解,该近似解在求解流体力学问题时具有高度精确性和高效性。
二、拉普拉斯函数逼近拉普拉斯函数是另一个在流体力学中常用的特殊函数,它主要用于描述椭圆坐标系中的流动情况。
椭圆坐标系在解析和数值求解流体力学问题中具有独特的优势,可以有效地简化复杂的流动场问题。
拉普拉斯函数逼近方法的基本原理与贝塞尔函数逼近方法相似,通过级数展开和截断得到一个近似解。
需要注意的是,在拉普拉斯函数的逼近过程中,我们需考虑到坐标变换和系数的选择,以确保逼近解在椭圆坐标系中的有效性和准确性。
三、传热中的特殊函数逼近在传热学中,特殊函数的逼近方法被广泛应用于描述边界值问题和传热问题。
例如,在对换热管道中的传热过程进行研究时,我们可以利用伽马函数、巴塞尔函数等特殊函数的逼近方法来简化数值计算过程。
特殊函数逼近方法在传热学中的应用包括对换热系数、传热率以及温度分布等参数的求解。
这些逼近方法不仅可以提供高精度的数值计算结果,还能大大减少计算时间和计算资源的消耗。
四、特殊函数逼近的数值求解方法特殊函数逼近的数值求解方法是一种基于数值计算的近似求解方法。
这种方法通过将特殊函数分解为级数、积分或其他形式的近似表达式,从而得到一个近似解。
特殊函数逼近的数值求解方法可以分为直接求解和迭代求解两种类型。


18 种常见开关电源拓扑结构特点和优缺点对比
本文主要讲了常见的开关电源拓扑结构特点和优缺点对比,常见的拓扑结构有Buck 降压,Boost 升压,Buck-Boost 降压-升压,Flyback 反激,
Forward 正激,Two-Transistor Forward 双晶体管正激等,具体的就随小编来
看看吧。
基本名词
常见的基本拓扑结构
■Buck降压
■Boost升压
■Buck-Boost降压-升压
■Flyback反激
■Forward正激
■Two-Transistor Forward 双晶体管正激
■Push-Pull推挽
■Half Bridge 半桥
■Full Bridge 全桥
■SEPIC
■C’uk
基本的脉冲宽度调制波形
这些拓扑结构都与开关式电路有关。
基本的脉冲宽度调制波形定义如下:
1、Buck 降压。

14交通信息与安全2013年2期第3l卷总175期道路路阻函数模型及适用性研究*周继彪1王露1孟现勇2金袁3(1.长安大学公路学院西安710064;2.山东交院交通司法鉴定中心济南250100;3.北京中领工程咨询有限责任公司北京100034)摘要交通诱导系统中2节点间最优路径的选择是目前的1个难点问题,其中路阻函数的确定是路径优化的核心内容。
针对交通流由畅通状态到拥挤状态、堵塞状态的过程,应用经典交通流理论和实际调查数据,构建交通流诱导系统分段路阻函数模型,以q一10ve h/h为1个单位,对函数进行分段拟合,构建高速公路和城市快速路下的分段路阻函数,并对其适应性进行拟合分析。
应用结果表明:在不同的流量范围内,高速公路和城市快速路分段路阻函数在自由流状态、高密度状态和低密度条件下适合不同的分段函数。
关键词交通工程;路阻函数;交通流理论;道路交通;适应性中图分类号:U491文献标志码:A doi:10.3963/j.i s sn1674—4861.2013.02.0040引吾交通流诱导系统是智能交通系统(i nt el l i gentt r ans por t syst em,I T S)在交通运输领域的1个重要应用,也是目前国内I TS研究方向之一。
其路阻函数是进行公路网规划、交通诱导系统和交通分配的重要函数[1],决定着动态交通诱导和交通分配过程中路径的选择。
路阻函数是指路段行驶时间与路段交通负荷,交叉口延误与交叉口负荷之间的关系[2-a]。
对于动态路径诱导系统,最终的路径诱导结果取决于路网的路阻函数,而路阻函数的计算是基于历史行程时间数据、实时行程时间数据和预测行程时间数据3方面信息[4。
6]。
通常说来,根据准确的预测行程时间得到的优化路径是最有效的,然而交通网络非常复杂,预测的行程时间要满足实时性和准确性两方面要求绝非易事。
1路阻函数模型1.1当前路阻函数模型国际上已经被确定的路阻函数有[7。

实验二之杨若古兰创作二阶电路呼应的三种(欠阻尼、过阻尼及临界阻尼)形态轨迹及其特点一、实验目的1、熟练把握二阶电路微分方程的列写及求解过程;2、把握RLC二阶电路零输入呼应及电路的过阻尼、临界阻尼和欠阻尼形态;3、学会利用MULTISIM仿真软件熟练分析电路,特别是电路中各电压电流的变更波形.二、实验道理用二阶线性常微分方程描述的电路称为二阶电路,二阶电路中至多含有两个储能元件.二阶电路微分方程式一个含有二次微分的方程,由二阶微分方程描述的电路称为二阶电路.分析二阶电路的方法仍然是建立二阶微分方程,并利用初始条件求解得到电路的呼应.二阶方程普通都为齐次方程.齐次方程的通解普通分为三种情况:(RLC串联时)1、为两个不等的实根(称过阻尼形态)此时,,二阶电路为过阻尼形态.2、为相等实根(称临界形态)此时,,二阶电路为临界形态.3、为共轭复根(称欠阻尼形态)此时,二阶电路为欠阻尼形态.这三个形态在二阶电路中式一个主要的数据,它决定了电路中电流电压关系和电流电压波形.三、实验内容电路中开关S闭合已久.t=0时将S打开,并测量.1、欠阻尼形态(R=10Ω,C=10mF,L=50mH)如图所示,为欠阻尼形态时的二阶电路图.波形图展现了欠阻尼形态下的和波形(橙色线条为电容电压衰减波形,红色线条为电感电压衰减波形).2、临界阻尼(R=10Ω,C=10mF,L=0.25mH)如图所示,为临界形态的二阶电路图.图展现了临界形态下的的波形.波形图展现了临界形态下的和波形.3、过阻尼形态(R=10Ω,C=1mF,L=1mH)如图所示,为过阻尼形态下的二阶电路图.波形图展现了临界形态下的和波形图.四、实验分析由道理公式和仿真结果,我们可以验证得出1)当二阶电路为欠阻尼形态时,其特征方程特征根为一对复根,且为共轭复根.2)当二阶电路为过阻尼形态时,其特征方程特征根为两个不等的实根.3)当二阶电路为临界阻尼形态时,其特征方程特征根为相等实根五、实验陈述1、总结、分析实验方法与结果在实验过程中,实验须要进行多次电路的转换.实验时须要当心谨慎,以防止出错.在实验结果中,大部分与理论符合合,但仍存在些微误差(省略定量分析).2、心得体会及其他通过本次实验的进修,我熟悉了二阶电路微分方程的列写及求解过程,熟悉了RLC二阶电路零输入呼应及电路的过阻尼、临界阻尼和欠阻尼形态,更熟练地利用仿真仪器分析电路,这将对当前的仿真实验有主要的基础感化.。
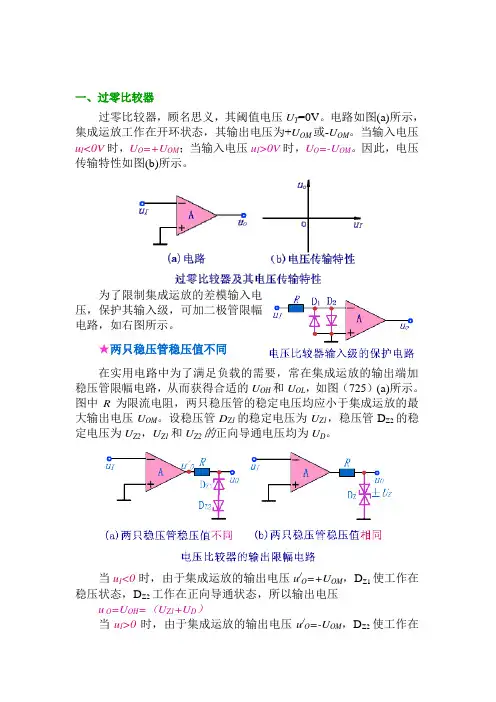
一、过零比较器过零比较器,顾名思义,其阈值电压U T=0V。
电路如图(a)所示,集成运放工作在开环状态,其输出电压为+U OM或-U OM。
当输入电压u I<0V时,U O=+U OM;当输入电压u I>0V时,U O=-U OM。
因此,电压传输特性如图(b)所示。
为了限制集成运放的差模输入电压,保护其输入级,可加二极管限幅电路,如右图所示。
★两只稳压管稳压值不同在实用电路中为了满足负载的需要,常在集成运放的输出端加稳压管限幅电路,从而获得合适的U OH和U OL,如图(725)(a)所示。
图中R为限流电阻,两只稳压管的稳定电压均应小于集成运放的最大输出电压U OM。
设稳压管D Z1的稳定电压为U Z1,稳压管D Z2的稳定电压为U Z2,U Z1和U Z2的正向导通电压均为U D。
当u I<0时,由于集成运放的输出电压u/O=+U OM,D Z1使工作在稳压状态,D Z2工作在正向导通状态,所以输出电压u O=U OH=(U Z1+U D)当u I>0时,由于集成运放的输出电压u/O=-U OM,D Z2使工作在稳压状态,D Z1工作在正向导通状态,所以输出电压u O=U OL=-(U Z2+U D)★两只稳压管稳压值相同若要求,U Z1=U Z2则可以采用两只特性相同而又制作在一起的稳压管,其符号如图(b)所示,稳定电压标为±U Z。
当u I<0时,u O=U OH=U Z;当u I>0时,u O=U OL=-U Z。
★稳压管接在反馈通路中限幅电路的稳压管还可跨接在集成运放的输出端和反相输入端之间,如右图所示。
假设稳压管截止,则集成运放必然工作在开环状态,输出电压不是+U OM,就是-U OM。
这样,必将导致稳压管击穿而工作在稳压状态,D Z构成负反馈通路,使反相输入端为“虚地”,限流电阻上的电流i R等于稳压管的电流i Z,输出电压u O=±U Z。


四种n 型rc 滤波电路模拟电源数字电源0. 1UF 100UI 0. 1UFGND PND阻抗公式:Z=R+i( wL-l/wC) w=2nfR —电阻 wL ——感抗 1/«C ------容抗1.典型II 型RC 滤波电路图7・27所示是典型的II 型RC 淀波电路。
电路中的C 】、C2是两只滤波电容,Ri 是 清波电阻,。
、%和C2构成一节n 型RC 滤波电路.由于这种淀波电路的形式如同字母 II 且采用了电阻、电容,所以称为II 型RCit 波电跖 ADP3211AMNG (集成电路IC) 从电路中可以看出,II 型RC 沌波电路接在整流电路的输出墙,这一电路的温敝原理是:从整流电路输出的电压首先经过G 的滤波,将大部分的交流 成分滤除,见图中的交流电流示意图.H 祓电深图7-27典型的w 型少微交流'll泡经过J 滤波后的电压,再加到由R1和C2构成的it 波电路中,电容C2进一步对交 潦成分进行波波,有少■的交流电流泡过C2到达地线,见图中的电流所示.由于电容C2具有隔直作用.直流电流不能流过电容C2.而只能流过电阻RL见图中所示,所以.R1和C2分压电路对直流电压不存在分压衰减的作用・这样直流对交流电F 而(木变;C2大则滤波效;果好 !电压通过R1输出,_______________________因为C2的容宗很大.容抗很小,所以RI 、C2构成的分压电路对交流成分的衰诚最很大.达到了滤波的目的如大泌波电容C2的容量可以提高滤波效果,这是因为C2容量大容抗小.对交 流成分的衰减量更大。
~~因为流过负载的直流电流流过电阻幻,会在R1上产生很大的直流电压虹 磁R1的阻值不;波电路输出的直流输出电压仁减小RI 的阻攸越大•在R1上的电压降越大,使滤 能太大 !波电路输出的直流电压a 越低;流过负载的直流电流越大时•在R1上的电压降也越!大,使直流输出电压心也越低。

交通建模过程中的路阻函数研究【摘要】路阻函数贯穿于交通建模的出行分布、方式选择和交通分配多个阶段,函数参数的确定需要结合建模方法、建模精度以及参数调用等多方面综合考虑,是影响模型计算精度的关键参数,本文结合交通模型软件的处理方式,研究路阻函数型式、调查、标定和校验方法,并得到了符合济南市出行规律的路阻函数值。
【关键词】交通建模;路阻函数;参数标定1 路阻函数的作用路阻函数包括路段和节点两部分。
路段流量延误函数,用于反映不同等级道路随着路段车流量增加,行程时间延误的增长规律。
节点的控制延误及转向排队延误是行程时间延误中重要部分,是城市模型有别于公路模型的主要区别。
在出行时间中,节点的延误占有一定比重,特别是当节点拥挤或阻塞时,节点延误可能会远远超过路段行驶时间,因此必须对路阻函数进行节点延误的修正。
当转向在网络的连线之间发生时,大部分规划软件程序允许用户应用限制规则、处罚和延迟等。
2 路阻函数的模型使用阶段出行分布阶段常用的重力模型方法被吸引来的交通量是与小区之间的距离有关。
吸引力随着出行时间降低的变化趋势的规律,一方面与出行的目的有关,另一方面与出行的方式有关。
描述这种趋势的就是阻力函数。
方式选择阶段常用的Logit模型方法,基于出行距离、车辆拥有条件、出行费用、出行时间、舒适度、可达性等条件。
不同方式的延误时间,影响方式之间的竞争关系。
交通分配阶段流量延误函数是影响车辆随着路段分配流量增加选择路径的主要依据。
依据查询道路网的最短行程时间判断出行路径的选择。
3 节点路段化延误函数构建在交通分配模型中,采用的路段流量延误函数模型有BPR函数、Akcelik函数、锥形拥堵函数以及IITRP函数。
交通模型中通过在节点进口道添加延误函数的查询索引,将节点处的控制延误和停车延误引入到交通分配中。
节点流量延误函数的形式一般分为两种:一种是根据城市交通调查统计的按照相交道路等级分类的节点平均延误(分级式节点延误),以表格的形式存储;另一种是根据调查数据统计回归得到的节点流量延误函数(联动式节点延误),以函数方程的形式存储。

路阻函数模型1. 概述路阻函数模型是一种用于描述网络流量拥塞传输机制的数学模型。
它通过将网络流量以及路由器、链路等网络设备的行为建模,分析网络中的拥塞行为并预测网络的性能。
路阻函数模型主要用于解决网络拥塞问题,即网络中出现的流量超过网络设备处理能力的情况。
通过建立网络流量和设备行为之间的数学关系,可以评估网络的性能并提供关于拥塞控制的建议。
路阻函数模型基于路阻函数的概念,该函数描述了网络中的拥塞程度与网络流量之间的关系。
在该模型中,路阻函数通常用来估计网络连接的延迟和丢包率。
通过分析路阻函数,可以确定网络中存在的拥塞情况并采取相应的拥塞控制策略,以确保网络的性能和可靠性。
2. 路阻函数的定义路阻函数是指网络中的一种函数,用于描述网络的拥塞传输机制。
它是网络流量和设备行为之间的数学映射关系,通常用于预测和控制网络的拥塞情况。
路阻函数通常由以下几个部分组成:1.流量函数:描述网络中的流量输入和输出之间的关系。
2.节点模型:描述网络节点(如路由器、交换机等)的行为,如队列长度、服务时间等。
3.链路模型:描述网络中的链路(如光纤、无线电链路等)的特性,如带宽、传输速率等。
4.拥塞控制算法:基于路阻函数进行网络拥塞控制的算法,如拥塞避免、拥塞检测、流量控制等。
路阻函数的定义可以根据具体的网络拥塞场景进行定制。
不同的网络拥塞问题可能需要不同的流量函数、节点模型和链路模型来进行描述和建模。
3. 路阻函数模型的用途路阻函数模型在网络拥塞控制和性能优化方面具有广泛的应用。
以下是该模型的几个主要用途:1.拥塞控制:路阻函数模型可以用来评估网络流量和设备行为之间的关系,从而帮助网络管理者采取相应的拥塞控制策略。
通过分析路阻函数的变化,可以确定网络中存在的拥塞情况,如延迟增大、丢包率增加等。
基于这些信息,可以采取一系列的措施,如减少流量量、调整传输速率等,以避免或减轻拥塞。
2.性能优化:路阻函数模型可以帮助优化网络性能,提高传输效率和可靠性。
二阶电路响应的三种欠阻尼过阻尼及临界阻尼状态轨迹
及其特点
1.欠阻尼状态:当阻尼比ξ小于1时,电路呈欠阻尼状态。
在欠阻尼状态下,电路的响应会在一段时间内发生振荡,并最终稳定下来。
欠阻尼状态下的响应特点如下:
a.振荡频率较高:欠阻尼状态下,电路中的振荡频率较高,振荡的周期较短。
b.振幅衰减较慢:由于欠阻尼状态下存在振荡,电路中信号的振幅衰减较慢。
c.最大振幅发生在峰值时间后:欠阻尼状态下,电路的振荡过程中,最大振幅会在峰值时间后达到。
2.临界阻尼状态:当阻尼比ξ等于1时,电路呈临界阻尼状态。
临界阻尼状态下,电路的响应既不会出现振荡,也不会过于迅速地收敛到稳定状态。
临界阻尼状态下的响应特点如下:
a.不出现振荡:临界阻尼状态下,电路的响应不会出现振荡现象。
b.受阻尼作用较快地趋于稳态:相较于欠阻尼状态,临界阻尼状态下电路响应的收敛速度更快。
3.过阻尼状态:当阻尼比ξ大于1时,电路呈过阻尼状态。
过阻尼状态下,电路的响应会迅速地收敛到稳定状态,不会出现振荡。
a.不出现振荡:过阻尼状态下,电路的响应不会出现振荡现象。
b.收敛速度较快:相较于欠阻尼和临界阻尼状态,过阻尼状态下电路响应的收敛速度最快。
c.没有峰值时间:过阻尼状态下,电路的响应不会出现峰值时间,最大振幅会在响应过程中逐渐减小。
总结起来,二阶电路的响应特点与阻尼比ξ的值有关,欠阻尼状态下会出现振荡,并且振荡频率较高;临界阻尼状态下电路响应收敛速度最快,不会出现振荡;过阻尼状态下电路响应迅速地收敛到稳定状态,不会出现振荡。
这些特点对于理解和分析二阶电路的行为和性能非常重要。
三种BPR道路阻抗函数的比较作者:洪进谈少盈石卉史敏来源:《科学与财富》2020年第10期摘要:本文将国内目前主要应用的道路阻抗函数,从车流速度、道路阻抗两个角度分别进行计算,并将所得到的结果与国家城市道路工程设计规范中道路服务水平、拥堵程度数据进行比较,得出启发式BPR函数最能反映我国城市道路人车混流现状尤其是拥堵状态下的实时交通路况,其次是重新标定BPR函数,再是传统BPR函数。
0 引言道路阻抗是直接影响路径规划结果的指向性指标。
道路阻抗函数与实时路况吻合程度如何,直接决定交通诱导和路径选择的合理性与效果情况。
美欧等发达国家由于经济发展较早受到道路交通的困扰,在道路阻抗函数的研究上取得较多的成果。
澳大利亚著名的交通工程学专家W.R.Blunden很早就总结出道路阻抗函数必须具备的三条理论性质[1]。
1964年,美国公路局依托国内的高速路网进行实时交通调查和研究,在非线性回归模型的基础上进行分析和计算,得出著名的BPR函数。
1 三种BPR函数的定义北京工业大学的研究者利用北京的实时道路交通数据对不同的道路阻抗函数进行比较,结果证明美国公路局的BPR函数最接近我国的实际交通路况。
BPR函数的数学表达式是:ti=ti0× [1+α×(Qi/Ci)β]其中,表示车流通过路段i的时间; 表示通过路段i的自由流量通行时间; 表示路段i上的车流量; 表示路段i的通行能力; 、为道路阻抗影响参数,美国联邦公路局推荐的值为 =0.15和=4。
四兵锋等人运用交通流理论,证明传统BPR函数应用于我国人车混流的现状下必须加以改进。
根据改进方法的不同,可以将目前国内正在研究和使用中的BPR函数分为重新标定BPR函数和启发式BPR函数。
通过查阅资料,笔者决定选取文献[1]的传统BPR函数,文献[2]以重新标定的方法改进的BPR函数,文献[1]以启发式的方法改进的BPR函数进行比较。
三者均是在对大连市区主要道路进行大量数据采集基础上,采用SPSS17.0软件进行分类拟合,且在此期间不存在大规模道路基础设施建设改造,可比性强。
阻抗函数值标定过程路段阻抗函数是用数学公式来描述出行时间与路段流量和最大通行能力之间的关系。
BRP 函数是一个最常用的路段性能函数。
BRP 函数将路段出行时间表达为流量与通行能力之比的函数。
其公式为:1f v t t c βα⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦其中:t 为拥挤路段的出行时间; f t 为路段自由流出行时间; v 为路段流量;c 为路段通行能力;α,β为待标定参数,若没有数据进行标定,一般α=0.15,β=4.0;对路段阻抗函数进行参数标定之前,对BRP 函数公式进行对数化处理,得ln 1ln ln f t v t c αβ⎛⎫⎛⎫-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭其中:t ,f t ,v ,c 都是常数,可以从调查中得到;设ln 1f t t ⎛⎫- ⎪ ⎪⎝⎭=b ,ln α=y ,ln v c ⎛⎫⎪⎝⎭=k ,β=x ,则有y kx b =+;即可转化为一元回归分析,利用最小二乘法求出待标定参数α,β。
利用公式:1112211nn n i i i i i i i n ni i i i n x y x y n x x β=====⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭=⎛⎫- ⎪⎝⎭∑∑∑∑∑,y x αβ--=-即可求出待标定参数。
例1:某局部路网包括主干路、次干路及支路,每种类型路段调查3组数据,见表1。
注:数据自己调查进行标定。
此外,该函数也可以对行人阻抗进行标定,如综合交通枢纽中的行人换乘,包括电动扶梯、平面路段、平面通道。
本文档系本人从网络获得,若有侵权,烦请QQ253169161,第一时间处理。