全等三角形总结复习过程

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上，△ABD，△BCE都是等边 三角形，AE交BD于F，DC交BE于G，求证：BF＝BG。
AB
＝
DB
∠ABE ＝ ∠ DBC
BE＝BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3： 已知一边一角（边与角相邻）：
找夹这个角的另一边
AD=CB （SAS）
找夹这条边的另一角
∠ACD=∠CAB（ASA）
找边的对角
∠D=∠（B AAS）
15
如图，已知∠B= ∠E，要识别△ABC≌ △AED，需 要添加的一个条件是--------------
A
D
C
E
思路4：
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中，AE < AB+BE＝AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA， CD过点E，则AB与AC+BD相等吗？请说明理由。
C A
∵ QD⊥OA，QE⊥OB，QD＝QE（已知）． ∴点Q在∠AOB的平分线上．（到角的两边的距
离相等的点在角的平分线上）
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证：点P到三边AB、BC、CA的距离相等

AB=A´B´
BC=B´C´
∴Rt△ABC≌ Rt△A´B´C´(HL)
B
B′
A
C
已知：如图,在△ABC和△ABD中,AC⊥BC,
BD⊥AD,垂足分别为C,D,AC=BD
(1)求证： △ABC≌△BAD.
(2)求证：BC=AD
(1)解： ∵ AC⊥BC, BD⊥AD D
C
∴ ∠C=∠D=90°
在Rt△ABC和 Rt△BAD中
例子1：如图，在△AEC和△ADB中，已 知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。
解：在△AEC和△ADB中
C
_A_E__=__A_D_(已知)
D
∠A= ∠A( 公共角)
A
E
B
_A_C___=_A__B_(已知)
∴ △AEC≌△ADB（ SAS ）
例2：如图，AC=BD，∠CAB= ∠DBA，
用符号语言表达为：
在△ABC和△DEF中
∠A=∠D （已知 ）
AB=DE（已知 ）
∠B=∠E（已知 ）
B
∴ △ABC≌△DEF（ASA）
A
D
CF E
例1： 已知如图，O是AB的中点，∠A=∠B，
求证：△AOC≌△BOD
证明：
∵ O是AB的中点(已知） C
∴ OA=OB(中点定义）
在△AOC和△BOD中 A
,有
AB=AB,
A
B
AC=AD. ∴ Rt△ACB≌Rt△ADB (HL). (2)∵ Rt△ACB≌Rt△ADB (HL). ∴ BC=AD
例2. 如图，AC=AD，∠C，∠D是直角， 将上述条件标注在图中，求证BC=BD

Q
P
B
C
本题源自《教材帮》
深化练习 3
如图，已知△ABC中，AB=AC=10，BC=8，点D为AB的中点，点P在线段BC上以每秒
3个单位长度的速度由点B向点C运动，同时点Q在线段CA上由点C向点A以每秒a个单
位长度的速度运动，设运动时间为t秒.
A
解：（1）由题意得：BP=3t.
∵BC=8，
∴CP=BC-BP=8-3t.
A
∠ACN=∠M+∠N =80° ，∠BCN=∠ACB-∠ACN=20° .
M
C
本题源自《教材帮》
重点解析 6
动脑想一想，动手练一练
6、如图，沿着AM折叠，使得点D落在BC的N点处，如果AD=7cm，DM=5cm，
∠DAM=30°，则AN、NM的长度以及∠NAM的度数分别是多少？
A
D
解：∵△ADM沿着AM折叠得到△ANM，
∴△BCD的面积和△ACE的面积相等.
∴四边形AECD的面积
=△ACD的面积+△ACE的面积
=△ACD的面积+△BCD的面积 =△ABC的面积= 1 ×4×4=8cm2.
2
D
C
B
本题源自《教材帮》
深化练习 1
如图，已知△ABD≌△ACE，点B、D、E、C在同一条直线上.
（1）∠BAE和∠CAD有什么关系？说明理由； A
位长度的速度运动，设运动时间为t秒.
A
（1）求CP的长（用含有t的式子表示）； （2）若以点C、P、Q为顶点的三角形和以点B、D、P 为顶点的三角形全等，且∠B和∠C是对应角，求a和t 的值.
D
Q
P
B
C
本题源自《教材帮》

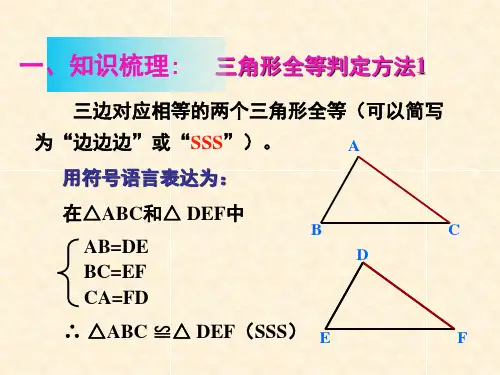
全等三角形知识点总结及复习一、知识网络⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪→⇒⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎨⎩对应角相等性质对应边相等边边边 SSS 全等形全等三角形应用边角边 SAS 判定角边角 ASA 角角边 AAS 斜边、直角边 HL 作图 角平分线性质与判定定理二、基础知识梳理 （一）、基本概念1、“全等”的理解 全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；即能够完全重合的两个图形叫全等形。

同样我们把能够完全重合的两个三角形叫做全等三角形。

全等三角形定义 ：能够完全重合的两个三角形称为全等三角形。

（注：全等三角形是相似三角形中的特殊情况）当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

由此，可以得出：全等三角形的对应边相等，对应角相等。

(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边； (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角； (3)有公共边的，公共边一定是对应边； (4)有公共角的，角一定是对应角；(5)有对顶角的，对顶角一定是对应角； 2、全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等； 3、全等三角形的判定方法（1）三边对应相等的两个三角形全等。

（2）两角和它们的夹边对应相等的两个三角形全等。

（3）两角和其中一角的对边对应相等的两个三角形全等。

（4）两边和它们的夹角对应相等的两个三角形全等。

（5）斜边和一条直角边对应相等的两个直角三角形全等。

4、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上（二）灵活运用定理1、判定两个三角形全等的定理中，必须具备三个条件，且至少要有一组边对应相等，因此在寻找全等的条件时，总是先寻找边相等的可能性。

2、要善于发现和利用隐含的等量元素，如公共角、公共边、对顶角等。

全等三角形的判定复习与总结教学目标：1.复习和巩固全等三角形的判定方法；2.总结全等三角形判定的规律和技巧；3.小组合作，培养学生的合作能力和思维能力。

教学准备：1.教学素材：全等三角形判定题目，活动卡片；2.教学工具：黑板、彩色粉笔、计算器。

教学过程：一、引入课题（5分钟）1.引入话题：今天我们要来复习和总结全等三角形的判定方法。

2.引发思考：请回顾一下，全等三角形的判定条件是什么？二、复习全等三角形的判定法（15分钟）1.复习SSS判定法：如果两个三角形的三条边分别相等，则这两个三角形全等。

2.复习SAS判定法：如果两个三角形的一边和两个角度分别相等（这个边是两个角的夹边），则这两个三角形全等。

3.复习ASA判定法：如果两个三角形的两个角度和一边分别相等（这个边是两个角的边），则这两个三角形全等。

4.复习AAS判定法：如果两个三角形的两个角度和一边分别相等（这个边不是两个角的边），则这两个三角形全等。

三、总结全等三角形判定的规律和技巧（15分钟）1.全等三角形判定的基本规律：要判断两个三角形是否全等，只需对应两边相等且夹角相等即可。

2.技巧一：当给出两个三角形的三个边的长度时，先比较三边的长度是否相等，再比较夹角是否相等。

3.技巧二：当给出两个三角形的两边和夹角时，先比较两边的长度是否相等，再比较夹角是否相等。

四、小组合作活动（30分钟）1.分成若干小组，每组3-4个学生，每组发放一组活动卡片。

2.活动内容：每组成员轮流拿一张卡片，上面写有一组给定的边长和角度。

学生根据卡片上的数据，判断这两个三角形是否全等，并给出理由。

其他组员通过提问和讨论来验证判断的正确性。

3.活动要求：每个学生都要积极参与，提出问题和表达自己的观点；每个小组要有一个组长，负责组织小组讨论和总结。

五、展示与总结（20分钟）1.每个小组派出一位学生上台展示他们分析判断的过程，并给出判断的结果和理由。

2.全班一起讨论和比较不同小组的判断结果和理由，总结全等三角形判定的规律和技巧。

A. ①④
B.①②
C.②③
D.③④
2．如图，ABD ≌ CDB ，且 AB 和 CD 是对应边，下面四个结论中不正确的是（ ）
A. ABD和CDB 的面积相等
A
D
B. ABD和CDB 的周长相等 C. A + ABD = C + CBD
B
C
D.DAD//BC 且 AD=BC
3．如图， ABC ≌ BAD ，A 和 B 以及 C 和 D 分别是对应点，如果
4．全等三角形的判定（一）：三边对应相等的两个三角形全等，简与成“边边边”或“SSS”．
AB = DE 如图，在 ABC 和 DEF 中 BC = EF
AC =
【典型例题】
例1．如图， ABC ≌ ADC ，点 B 与点 D 是对应点， BAC = 26 ，且 B = 20 ， SABC = 1，求 CAD , D, ACD 的度数及 ACD 的面积．
数及 BC 的长．
E
F
A
BC
D
本文来源于网络，如果侵权行为，请联系删除！
精品文档，助力人生，欢迎关注小编！
11．如图，在 ABC与ABD 中，AC=BD，AD=BC，求证： ABC ≌ ABD
D A
C B
全等三角形（一）作业
1．如图， ABC ≌ CDA ，AC=7cm，AB=5cm.，则 AD 的长是（ ）
求证：（1） DE ⊥ AB ； （2）BD 平分 ABC （角平分线的相关证明及性质）
B
A E
D
C
【巩固练习】 1．下面给出四个结论：①若两个图形是全等图形，则它们形状一定相同；②若两个图形的
形状相同，则它们一定是全等图形；③若两个图形的面积相等，则它们一定是全等图形； ④若两个图形是全等图形，则它们的大小一定相同，其中正确的是（ ）

小学生元旦联欢会的主持词精选4篇小学生元旦联欢会主持词篇一主持词要根据活动对象的不同去设置不同的主持词。

我们眼下的社会，各种集会的节目都通过主持人来进行串联，快来参考主持词是怎么写的吧，以下是小编为大家整理的小学生元旦联欢会主持词（精选13篇），仅供参考，希望能够帮助到大家。

小学生元旦联欢会的主持词篇二甲：尊敬的各位领导﹑老师，乙：亲爱的同学们，大家，合：晚上好！甲：我是来自2020级的小鱼。

乙：我是来自2020级的小绿。

丙：我是来自2020级的小黄。

丁：我是来自2020级的小红。

甲：新年的钟声即将敲响，时光的车轮又留下了一道深深的印痕。

满天的雪花，是飞舞的音符，以思念谱成乐章，用祝福奏出所盼。

乙：没有松风的秋，雁去长空；没有飞雪的冬，乍暖还寒。

一夜高风凋碧树，凋不了青春不灭的火焰；满地余寒露凝香，凝不住你绝美的年华。

丙：在这烛光与微笑构成的舞台，在这笑声与歌声汇成的海洋，在这永恒与温馨筑就的圣地，我们欢聚在一起。

丁：光阴茬苒，我们即将迎来新的一年。

今天大家在这里欢聚一堂，迎接元旦的曙光。

这一刻是美好的，这一刻是温馨的，这一刻是充满激情的。

甲：台历翻去最后一页，20--年已经成为历史。

回首时光年轮上又一度春秋寒暑，我们不禁感慨万千。

乙：灿烂辉煌的20--年即将向我们告别，充满希望与奋进的20--年正微笑着向我们走来。

丁：在这辞旧迎新的日子里，就让我们用热情与激情来表达我们的喜悦，传达对新一年的憧憬。

丙：今晚，就让我们踏着歌声的翅膀，向着梦想――启航！甲：现在我宣布20--年庆元旦文艺晚会，合：现在开始！甲：首先请允许我为大家隆重介绍今晚到场的领导和嘉宾，--。

乙：欢迎您的到来！丙：---。

丁：欢迎您的到来！甲：还有我们敬爱的--老师和--老师，乙：让我们用热烈的掌声来欢迎各位老师的到来！丁：今天啊，我们在开场前将会进行第一个抽奖环节的前奏！丙：没错！我们需要在场的观众拿出旁边已经为你们准备好的袋子，里面呢会有一张小纸条，请将你对20--年的新年愿望写在纸上，并写好你的姓名，待会儿会有同学去收集，我们将在晚会的最后从这些小纸条中抽出3位幸运儿，并且由主持人念出这3个新年愿望，而这3位幸运的同学也将获得奖品哦！大家快点动起来吧！甲：OK，相信你们已经写好了自己的新年愿望了吧，我们马上进入今晚的正轨了哟！乙：没错，接下来呢就让我们跟着--和--的歌声走进《下一站天后》。

全等三角形判定复习教案教案：全等三角形判定的复习一、教学目标：1.复习全等三角形的判定方法和性质。

2.掌握使用全等三角形的判定方法解决相关问题。

3.培养学生的逻辑思维能力和分析问题的能力。

二、教学重点：1.全等三角形的判定方法和性质。

2.全等三角形的相关题目解答。

三、教学难点：1.通过给出的条件判定三角形是否全等。

2.通过给出的三角形判定是否全等。

四、教学过程：Step 1：复习全等三角形的判定方法1.提问：回顾一下全等三角形的判定方法有哪些？2.学生回答：欢迎学生回答，教师进行总结。

3.教师解释：全等三角形的判定方法有以下几种：a.SSS判定法：三边相等的两个三角形全等。

b.SAS判定法：两边和夹角相等的两个三角形全等。

c.ASA判定法：两角和边相等的两个三角形全等。

d.AAS判定法：两角和对边相等的两个三角形全等。

e.RHS判定法：直角边和斜边相等的两个三角形全等。

Step 2：练习全等三角形的判定方法1.提问：根据给出的条件，判断以下三角形是否全等。

a.△ABC≌△DEF，AB=DE，BC=EF，∠B=∠E。

b.△ABC≌△DEF，AB=DE，BC=DF，AC=EF。

c.△ABC≌△DEF，AC=DE，∠A=∠D，∠C=∠F。

2.学生回答：请学生根据给出的条件，结合全等三角形的判定方法，回答问题。

3.教师解释和点评：让学生进行回答，并解释判断的依据和结果。

Step 3：复习全等三角形的性质1.提问：回顾一下全等三角形的性质有哪些？2.学生回答：欢迎学生回答，教师进行总结。

3.教师解释：全等三角形的性质包括以下几个方面：a.对应角相等：全等三角形的对应角相等。

b.对应边相等：全等三角形的对应边相等。

c.对应中线相等：全等三角形的对应中线相等。

d.对应角平分线相等：全等三角形的对应角平分线相等。

Step 4：练习全等三角形的性质1.提问：根据给出的全等三角形，判断下列几组线段是否相等。

a.AB≌DE，AC≌DF，∠B≌∠E，∠C≌∠F，AD≌DG，BE≌EH。

7.家长参与题：鼓励家长参与学生的作业过程，与学生一起探讨全等三角形在实际生活中的应用，共同完成作业。增进家长对学校教学的了解，提高学生的学习兴趣。
8.作业批改与反馈：要求学生在完成作业后，进行自我检查和互评，培养自主学习能力。教师应及时批改作业，给予评价和指导，帮助学生发现问题、提高能力。
4.结合实际案例，讲解全等三角形在实际生活中的应用，如建筑设计、工程测量等，增强学生的应用意识。
（三）学生小组讨论
1.将学生分成若干小组，针对全等三角形的判定方法和性质，设计一些讨论题目，让学生在小组内进行讨论交流。
2.每个小组选派一名代表进行汇报，分享本组的讨论成果和心得体会。
3.教师巡回指导，参与学生讨论，解答疑问，引导学生深入探究全等三角形的性质和判定方法。
（一）导入新课
1.利用多媒体展示生活中全等三角形的实例，如剪纸艺术、建筑图案等，引发学生对全等三角形的关注和兴趣。
2.提问：“我们已经学习过全等三角形的基本概念，那么如何判断两个三角形是全等的呢？”让学生回顾全等三角形的判定方法，为新课的学习做好铺垫。
3.通过一个简单的实际问题，如测量不规则图形的面积，引出全等三角形在实际问题中的应用，激发学生的学习兴趣。
5.培养团队合作精神，学会尊重他人，提高人际沟通能力。
本章小结与复习教学设计旨在帮助学生巩固全等三角形的知识，提高解决问题的能力，培养空间观念和几何直观，以及增强数学情感和价值观。在教学过程中，教师应关注学生的个体差异，因材施教，使每位学生都能在原有基础上得到提高。同时，注重启发式教学，引导学生主动探究、发现、总结规律，提高学生的自主学习能力。
5.培养问题解决能力，学会从实际问题中发现全等三角形的问题，并运用所学知识解决。
（三）情感态度与价值观

全等三角形复习[ 知识要点 ]一、全等三角形1．判定和性质一般三角形直角三角形边角边（ SAS）、角边角（ ASA）具备一般三角形的判定方法判定斜边和一条直角边对应相等（ HL ）角角边（ AAS）、边边边（ SSS）对应边相等，对应角相等性质对应中线相等，对应高相等，对应角平分线相等注：①判定两个三角形全等必须有一组边对应相等；② 全等三角形面积相等．2．证题的思路：找夹角（ SAS）已知两边找直角（ HL ）找第三边（ SSS）若边为角的对边，则找任意角（ AAS）找已知角的另一边（SAS）已知一边一角边为角的邻边找已知边的对角（AAS）找夹已知边的另一角（ASA）找两角的夹边（ASA）已知两角找任意一边（AAS）性质1、全等三角形的对应角相等、对应边相等。

2、全等三角形的对应边上的高对应相等。

3、全等三角形的对应角平分线相等。

4、全等三角形的对应中线相等。

5、全等三角形面积相等。

6、全等三角形周长相等。

( 以上可以简称 : 全等三角形的对应元素相等)7、三边对应相等的两个三角形全等。

（SSS)8、两边和它们的夹角对应相等的两个三角形全等。

(SAS)9、两角和它们的夹边对应相等的两个三角形全等。

(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。

(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。

(HL)运用1、性质中三角形全等是条件，结论是对应角、对应边相等。

而全等的判定却刚好相反。

2、利用性质和判定，学会准确地找出两个全等三角形中的对应边与对应角是关键。

在写两个三角形全等时，一定把对应的顶点，角、边的顺序写一致，为找对应边，角提供方便。

3，当图中出现两个以上等边三角形时，应首先考虑用 SAS找全等三角形。

4、用在实际中，一般我们用全等三角形测等距离。

以及等角，用于工业和军事。

有一定帮助。

5、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。

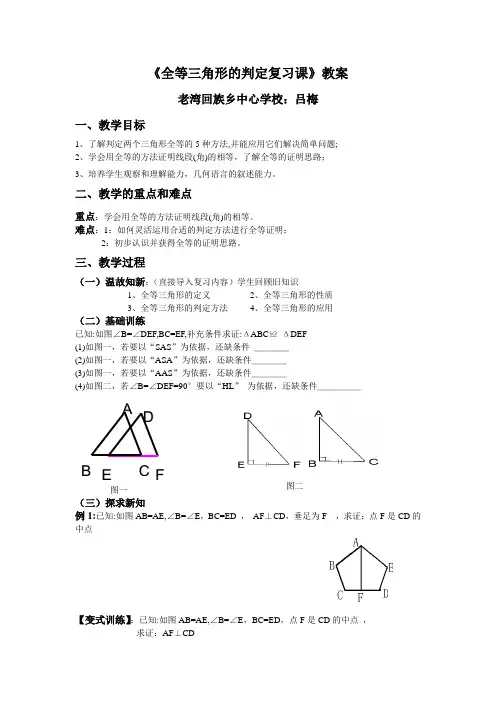
《全等三角形的判定复习课》教案老湾回族乡中心学校：吕梅一、教学目标1、了解判定两个三角形全等的5种方法,并能应用它们解决简单问题;2、学会用全等的方法证明线段(角)的相等，了解全等的证明思路；3、培养学生观察和理解能力，几何语言的叙述能力。

二、教学的重点和难点重点：学会用全等的方法证明线段(角)的相等。

难点：1：如何灵活运用合适的判定方法进行全等证明；2：初步认识并获得全等的证明思路。

三、教学过程（一）温故知新：（直接导入复习内容）学生回顾旧知识1、全等三角形的定义2、全等三角形的性质3、全等三角形的判定方法4、全等三角形的应用（二）基础训练已知:如图∠B=∠DEF,BC=EF,补充条件求证:ΔABC ≌ ΔDEF(1)如图一，若要以“SAS ”为依据，还缺条件 ＿＿＿＿(2)如图一，若要以“ASA ”为依据，还缺条件＿＿＿＿(3)如图一，若要以“AAS ”为依据，还缺条件＿＿＿＿(4)如图二，若∠B=∠DEF=90°要以“HL ” 为依据，还缺条件＿＿＿＿＿图一 （三）探求新知例1:已知:如图AB=AE,∠B=∠E ，BC=ED ， AF ⊥CD ，垂足为F ，求证：点F 是CD 的中点【变式训练】：已知:如图AB=AE,∠B=∠E ，BC=ED ，点F 是CD 的中点 ， 求证：AF ⊥CD F DEA B C 图二例2 已知AD ∥BC ， ∠1=∠2， ∠3=∠4， 直线DC 过点E 交AD 于D ，交BC 于C.求证：AD+BC=AB你还有其它的解题方法吗？【方法归纳】要证明两条线段的和与一条线段相等时常用的两种方法：1、截长法 ：可在长线段上截取与两条线段中一条相等的一段，然后证明剩余的线段与另一条线段相等。

2、补短法 ：将两线段中的一条延长，使延长部分等于另一线段，再证它与较长线段相等。

【变式训练】已知：AC 平分∠BAD ，CE ⊥AB ，垂足为E ，∠B+∠D=180°，求证：AE=AD+BE（四）课堂小结通过本节的学习，谈谈你在全等证明问题中的收获和经验。

全等三角形只是总结及经典例题[知识要点]一、全等三角形一般三角形 直角三角形 判定边角边〔SAS 〕、角边角〔ASA 〕 角角边〔AAS 〕、边边边〔SSS 〕 具备一般三角形的判定方法 斜边和一条直角边对应相等〔HL 〕 性质 对应边相等，对应角相等对应中线相等，对应高相等，对应角平分线相等注：① 判定两个三角形全等必须有一组边对应相等；② 全等三角形面积相等．2．证题的思路：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧）找任意一边（）找两角的夹边（已知两角）找夹已知边的另一角（）找已知边的对角（）找已知角的另一边（边为角的邻边）任意角（若边为角的对边，则找已知一边一角）找第三边（）找直角（）找夹角（已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS 例1如图，∠E=∠F=90。

，∠B=∠C ，AE=AF ，给出下列结论：①∠1=∠2；②BE=CF ；③△ACN ≌△ABM ；④CD=DN ，其中正确的结论是 (把你认为所有正确结论的序号填上)例2在△ABC 中，AC=5，中线AD=4，则边AB 的取值范围是( )A ．1<AB<9B ．3<AB<13C ．5<AB<13D ．9<AB<13例3一张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如下右图形式，使点B 、F 、C 、D 在同一条直线上(1)求证：AB ⊥ED(2)假设PB=BC ，请找出图中与此条件有关的一对全等三角形，并给予证明例4假设两个三角形的两边和其中一边上的高分别对应相等，试判断这两个三角形的第三边所对的角之间的关系，并说明理由例5如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA=BC，EB=AC，FC=AB，∠AFB=51°，求∠DFE的度数1．如图，AD、A′D′分别是锐角△ABC和△A′B′C′中BC，B′C′边上的高，且AB=A′B′，AD=A′D ′，假设使△ABC≌△A′B′C′，请你补充条件(只需要填写一个你认为适当的条件)2．如图，0A=0B，OC=OD，∠O=60°,∠C=25°,则∠BED等于3．如图，把大小为4×4的正方形方格图形分割成两个全等图形，例如图1．请在以下图中，沿着虚线画出四种不同的分法，把4×4的正方形方格图形分割成两个全等图形．4．如图，△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的，假设∠1：∠2：∠3=28：5：3，则∠a的度数为5．如图，已知0A=OB，OC=0D，以下结论中：①∠A=∠B；②DE=CE；③连OE，则0E平分∠0，正确的选项是( )A．①②B。

敷学培fit 方法*»1-2価明三廊形全箸(舍倦段相著、角相等)的几种方法一、三角形全等的判定:① 三组对应边分别相等的两个三角形全等(SSSJo 【最简单，考得也最少，考试过程中没有注意点】② 有两边及其夹角对应相等的两个三角形全等(SAS)。

【最常考，而且考试就考“角是不是两边夹角”】 r 当题目中得出“2对边及1对角相等”时，一定要检査“角是不是两边夹角“。

i ③ E鬲爲反養美另另航蒔京满不三浦花荃,新忑「① 有两角及一角的对边对应相等的两个三角形全等(AAS)o⑤直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL)o F ............................ } j 直角三角形全等的特殊证法。

但当该方法不行时，前面的4种方法也能用来证明直角三角形全等。

： !如何找斜边：斜边是直角所对的边，只要找90。

的角所对的边就能找到斜边: ................................................................................................. J 二、全等三角形的性质： ① 全等三角形的对应边相等；全等三角形的对应角相等。

② 全等三角形的周长、面积相等。

③全等三角形的对应边上的高对应相等。

①全等三角形的对应角的角平分线相等。

⑤全等三角形的对应边上的中线相等。

几种常见全等三箱形的基本图形： 【平移】i 题目中只要得出“1对边及2对角相等"，那就能证明三角\ ；形全等，唯一要做的就是区分好是ASA 还是AAS三、找全等三痢形的方法：①可以从结论出发，看要证明相等的两条线段（或角）分别在哪两个可能全等的三角形中:②可以从己知条件出发，看己知条件可以确定哪两个三角形相等;③从条件和结论综合考虑，看它们能一同确定哪两个三角形全等;①若上述方法均不行，可考虑添加辅助线，构造全等三角形。

全等三角形1.基本定义：⑴全等形：能够完全重合的两个图形叫做全等形.⑵全等三角形：能够完全重合的两个三角形叫做全等三角形.理解：①全等三角形形状与大小完全相等，与位置无关；②一个三角形经过平移、翻折、旋转可以得到它的全等形；③三角形全等不因位置发生变化而改变。

.2.基本性质：理解：①长边对长边，短边对短边；最大角对最大角，最小角对最小角；②对应角的对边为对应边，对应边对的角为对应角。

(3)全等三角形的周长相等、面积相等。

(4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。

3.全等三角形的判定定理：⑴边边边（SSS）：三边对应相等的两个三角形全等.⑵边角边（SAS）：两边和它们的夹角对应相等的两个三角形全等.⑶角边角（ASA）：两角和它们的夹边对应相等的两个三角形全等.⑷角角边（AAS）：两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边（HL）：斜边和一条直角边对应相等的两个直角三角形全等.4.证明两个三角形全等的基本思路：5.角平分线：⑴画法：⑵性质定理：角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.(4)三角形的三条角平分线交于三角形内部一点，并且这点到三边的距离相等6.证明的基本方法：⑴明确命题中的已知和求证.（包括隐含条件，如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系）⑵根据题意，画出图形，并用数字符号表示已知和求证.⑶经过分析，找出由已知推出求证的途径，写出证明过程.7.学习全等三角形应注意以下几个问题：(1)要正确区分“对应边”与“对边”，“对应角”与“对角”的不同含义；(2)表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；(3)“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；通关精选1．如图，△ABC≌△EFD，且AB＝EF，EC＝4，CD＝3，则AC＝() A．3 B．4 C．7 D．8,第1题图)2．如图，AC＝BD，AO＝BO，CO＝DO，∠D＝30°，∠A＝95°，则∠AOB 等于()A．120°B．125°C．130°D．135°,第2题图)3．如图，已知AB∥CD，AD∥CB，则△ABC≌△CDA的依据是() A．SAS B．ASA C．AAS D．SSS,第3题图)4．(2015·六盘水)如图，已知∠ABC＝∠DCB，下列所给条件不能证明△ABC≌△DCB的是()A．∠A＝∠D B．AB＝DC C．∠ACB＝∠DBC D．AC＝BD,第4题图)5．如图，△ABC和△EDF中，∠B＝∠D＝90°，∠A＝∠E，点B，F，C，D在同一条直线上，再增加一个条件，不能判定△ABC≌△EDF的是()A．AB＝ED B．AC＝EF C．AC∥EF D．BF＝DC,第5题图)常考例题精选1.(2015·绥化中考)如图，A，B，C三点在同一条直线上，∠A=∠C=90°，AB=CD，请添加一个适当的条件，使得△EAB≌△BCD.2.(2015·临沂中考)在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE= cm.3.(2015·武汉中考)如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D.6.(2015·昆明中考)已知：如图，AD，BC相交于点O，OA=OD，AB∥CD.求证：AB=CD.7.(2015·大理中考)如图，点B在AE上，点D在AC上，AB=AD，请你添加一个适当的条件，使△ABC≌△ADE(只能添加一个).(1)你添加的条件是.(2)添加条件后，请说明△ABC≌△ADE的理由.8.(2015·随州中考)如图，点F，B，E，C在同一直线上，并且BF=CE，∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC≌△DEF，并给出证明.提供的三个条件是：①AB=DE；②AC=DF；③AC∥DF.9.(2015·河源中考)如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD 的中点，连接OE.(1)求证：△AOB≌△DOC.(2)求∠AEO的度数.7．如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F 在AC上，BE＝FC，求证：BD＝DF.如图，点B，E，C，F在同一条直线上，∠A＝∠D，∠B＝∠DEF，BE＝CF.求证：AC＝DF.。

第17讲全等三角形【考点总汇】一、全等三角形的性质及判定定理 1•性质(1) _________________________ 全等三角形的对应边，对应角 。

(2) ________________________________ 全等三角形的对应边的中线 _______________________ ，对应角平分线 _____________________________________ ，对应边上的高 __________ ，全等三角 形的周长 _________ ，面积 _________ 。

2•判定定理(1)三边分别 _________ 的两个三角形全等(简写“边边边”或“ _______ ”)。

微拨炉：已知两边和一角判定三角形全等时，没有“ SSA ”定理，即不能错用成“两边及一边对角相等的两个三角形全等”。

二、角的平分线1•性质：角的平分线上的点到角的两边的距离 ___________ 。

2•判定：角的内部到角的两边的距离相等的点在 ____________ 。

3•三角形的三条角平分线相交于一点，并且这一点到三条边的距离 微拨炉： 1•三角形的角平分线是一条线段，不是射线。

2•角的平分线的性质定理和判定定理互为逆定理。

注意分清题设和结论。

高频考点1、全等三角形的判定与性质 【范例】如图，在△ ABC 中，AB=CB ，■ ABC =90，D 为AB 延长线上一点，点 E 在BC 边上, 且 BE 二 BD ，连接 AE 、DE 、DC 。

(2)两边和它们的夹角分别________ 的两个三角形全等(简写“边角边”或 ”) (3)两角和它们的夹边分别________ 的两个三角形全等(简写“角边角”或”)(4)斜边和一条直角边分别 的两个直角三角形全等(简写“斜边、直角边”或 ”)(1)求证：△ ABE ◎△ CBD(2)若• CAE =30 ［求• BDC 的度数D得分要领：判定全等三角形的基本思路1•已知两边：（1）找夹角（SAS） ; （2）找直角（HL或SAS） ; （3）找第三边（SSS）。

广州市培贤教育学校升初二数学 （新课）班讲义第五讲 全等三角形的复习[教学过程]一、全等三角形的概念及其性质1、全等三角形的定义：能够完全重合的两个三角形叫做全等三角形。

2、全等三角形性质：①对应边相等 ②对应角相等 ③周长相等 ④面积相等 例1.已知如图（1），∆ABC ≅∆DCB ，其中的对应边： 与 ， 与 ， 与 ，对应角： 与 ， 与 ， 与 。

（图2）例2： 如图（2），∆ABC ≅∆ADE ，BC 的延长线交DA 于F ，交DE 于G ，∠ACB =∠AED =105O ，∠CAD =10O ，∠B =∠D =25O ，求∠DFB 、∠DGB 的度数。

二、全等三角形的判定方法1、三边对应相等的两个三角形全等（SSS ）例1、如图，在∆ABC 中，M 在BC 上，D 在AM 上，AB=AC ，DB=DC 。

求证：MB=MC A EDD DM名师点睛DA（图1）D2、两边和夹角对应相等的两个三角形全等（SAS ）例2：如图，AD 与BC 相交于O ，OC=OD ，OA=OB ，求证：∠CAB =∠DBAB 3、两角和夹边对应相等的两个三角形全等（ASA ）例3、如图，梯形ABCD 中，AB//CD ，E 是BC 的中点，直线AE 交DC 的延长线于F 。

求证：∆ABE ≅∆FCE4、两条和夹边对应相等的两个三角形全等（AAS ）例4、如图，在∆ABC 中，D 、E 分别在BC 、AC 边上。

且∠ADE =∠B =∠C ，AD =DE 。

求证：∆ADB ≅∆DEC5、一条直角边和斜边对应相等的两个直角三角形全等。

（HL ）例5：如图，在∆ABC 中，∠C =90o ，沿过点B 的一条直线BE 折叠∆ABC ，使点C 恰好落在AB 边的中点D 处，则∠A 的度数= 。

三、角平分线角平分线性质定理：角平分线上的点到这个角两边的距离相等。

逆定理：到一个角两边的距离相等的点在这个角的平分线上。

全等三角形知识点总结及复习一、知识网络⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪→⇒⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎨⎩对应角相等性质对应边相等边边边 SSS 全等形全等三角形应用边角边 SAS 判定角边角 ASA 角角边 AAS 斜边、直角边 HL 作图 角平分线性质与判定定理二、基础知识梳理 （一）、基本概念1、“全等”的理解 全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；即能够完全重合的两个图形叫全等形。

同样我们把能够完全重合的两个三角形叫做全等三角形。

全等三角形定义 ：能够完全重合的两个三角形称为全等三角形。

（注：全等三角形是相似三角形中的特殊情况）当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

由此，可以得出：全等三角形的对应边相等，对应角相等。

(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边； (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角； (3)有公共边的，公共边一定是对应边；(4)有公共角的，角一定是对应角；(5)有对顶角的，对顶角一定是对应角；2、全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等；3、全等三角形的判定方法（1）三边对应相等的两个三角形全等。

（2）两角和它们的夹边对应相等的两个三角形全等。

（3）两角和其中一角的对边对应相等的两个三角形全等。

（4）两边和它们的夹角对应相等的两个三角形全等。

（5）斜边和一条直角边对应相等的两个直角三角形全等。

4、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上（二）灵活运用定理1、判定两个三角形全等的定理中，必须具备三个条件，且至少要有一组边对应相等，因此在寻找全等的条件时，总是先寻找边相等的可能性。

2、要善于发现和利用隐含的等量元素，如公共角、公共边、对顶角等。

3、要善于灵活选择适当的方法判定两个三角形全等。