双曲线第一课定义带动画.ppt

x2 a2
by22
1(a,bo)
x2 y2 b2 a2 1(a,bo)
y
y
. .B
A1 o A x
. B.
A1 o A x
B1
B1
关系
c2 = a2 + b 2
例题：
根据下列条件，求双曲线的标准方程：
1、过点 P ( 3 , 15 )、Q ( 16 , 5 ) 且焦点在坐标
4
3
轴上；
2、 c = 6 ，经过点 (－5 , 2 )，焦点在 x 轴上；
的焦点坐标．
3．已知方程
x2
y2
1表示双曲线，求的取值范围．
2m m1
精选
•
例3，证明椭圆
x2 25
+
y2 =1
9
与双曲线x2-15y2=15的焦点相同.
• 变:椭圆与双曲线的一个交点为P， F1是椭圆的左焦点,求|PF1|.
精选
小结
焦点在 x 轴上
焦点在 y 轴上
定义 方程
图象
| | MF1 | － | MF2 | | = 2a ( 2a ＜| F1F2 | )
共性： 1、两者都是平面内动点到两定点的距离问题； 2、两者的定点都是焦点； 3、两者定点间的距离都是焦距。
区别： 椭圆是距离之和； 双曲线是距离之差的绝对值。
求双曲线的标准方程
点击观看动画
精选
1、建系设点。
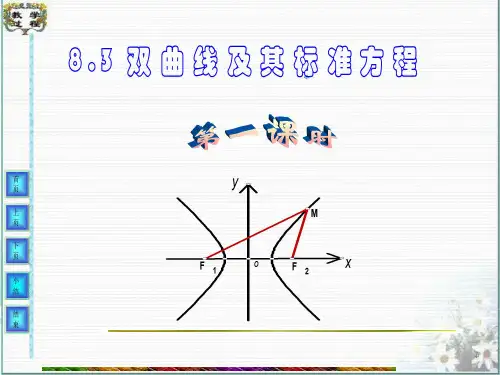
设M（x , y）,双曲线的焦距 为2c（c>0）,F1(-c,0),F2(c,0)
常数=2a
同的符号。
精选
• 例线1，、求如m果的方范程围mx-21+2-ym2 = 1表示双曲 • 解（m-1)(2-m)<0，∴m>2或m<1

（差的绝对值）
上面 两条合起来叫做双曲线
根据实验及椭圆定义，你能给双曲线下定义吗？
回2.忆双椭曲圆线的定义
等值于平（常面大数平内于面（与︱内小F两1与于F个2两︱︱定个）F点1定F的F2点1︱点，F）的F1，2轨的的F迹距点2的叫离的距做的轨离椭差迹的圆的叫和绝做为对双一值曲个线定.
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
M
注意 (1)距离之差的绝对值
| |MF1| - |MF2| | = 2a
F1 o F2
(2)常数要小于|F1F2|大于0
0<2a<2c
ቤተ መጻሕፍቲ ባይዱ
令c2－a2=b2
y
M
F1
o
双曲线的标准方程
y
M
y M
F1 O F2 x
F2 x
O
F1
思考：如何由双曲线的标准方程来判断它的焦点 是在X轴上还是Y轴上？
双曲线第一课定义(带动画)_图文.ppt
北京摩天大楼
巴西利亚大教堂
法拉利主题公园
花瓶
反比例函数的图像
冷却塔
罗兰导航系统原理
画双曲线
演示实验：用拉链画双曲线
①如图(A)， |MF1|-|MF2|=|F2F|=2a
②如图(B)， |MF2|-|MF1|=|F1F|=2a
由①②可得： | |MF1|-|MF2| | = 2a
判断：
与
的焦点位置？
结论：看
前的系数，哪一个为正，则
焦点在哪一个轴上。
双曲线的标准方程与椭圆的 标准方程有何区别与联系?

04 双曲线的标准方程的推导
推导过程
设双曲线上任意一点为$P(x,y)$， 根据双曲线的定义，点$P$到两 个焦点的距离之差为常数，即 $2a$。
利用距离公式和双曲线的定义， 可以得到点$P$到两个焦点的距 离分别为$sqrt{(x+a)^2+y^2}$ 和$sqrt{(x-a)^2+y^2}$。
对称性
01
02
03
对称性
双曲线关于其对称轴对称， 即关于x轴和y轴都对称。
总结词
双曲线关于其对称轴对称， 即关于x轴和y轴都对称。
详细描述
双曲线上的任意一点关于 x轴和y轴的对称点都在双 曲线上。
顶点
顶点
双曲线与对称轴的交点称 为顶点。
总结词
双曲线与对称轴的交点称 为顶点。
详细描述
顶点是双曲线与对称轴的 交点，也是双曲线离准线 最远的点。
比例常数。
性质
双曲线的焦点到任意一点的距离之 差等于常数2a，即|PF1| - |PF2| = 2a。
应用
通过焦点可以计算出双曲线的离心 率和准线方程。
焦距
定义
双曲线的两个焦点之间的距离称 为焦距，记作2c。
性质
焦距与半主轴长a和半次轴长b有 关，关系为c^2 = a^2 + b^2。
应用
通过焦距可以计算出双曲线的离 心率和准线方程。
双曲线的简单性质课件ppt课件
目录
• 双曲线的定义与标准方程 • 双曲线的几何性质 • 双曲线的焦点与焦距 • 双曲线的标准方程的推导 • 双曲线的应用
01 双曲线的定义与标准方程
定义
总结词
双曲线是由两个无限延伸的分支组成的，其形状类似于开口 的抛物线。

按方程形式分类
双曲线方程的对称性 双曲线的标准方程是(x-a)²/b² - (y-b)²/a² = 1，其具有中心对称性，即点 (a, b)为中心。 双曲线的焦距与实轴长度的关系 在双曲线中，焦距c与实轴长度2a有固定的数学关系：c² = a² + b²，此 式被称为双曲线的基本性质之一。
T 双曲线关于其轴和中心点均具有对称性，这是由其定义决定的。 双曲线的渐近线性质 双曲线的渐近线是一条直线，该直线与双曲线交于两个无穷远点，这是双 曲线的重要特性之一。
05 双曲线的实际应用
双曲线的实际应用:物理中的应 用
双曲线的几何特性 双曲线是二次曲线的一种，其 双曲线的几何特性 双曲线是二次曲线的一种，其几何特性包括焦点在两个固定点，且所有到两 焦点距离之和为定长的点的集合。 双曲线的方程式 双曲线的标准方程是(x^2)/a^2 - (y^2)/b^2 = 1，其中a, b > 0, a^2 + b^2 = c^2 双曲线在物理中的应用 双曲线广泛应用于物理学中，如电磁场理论、光学、量子力学等，例如，双 曲线的焦散线就是光学中的一条重要概念。 双曲线与实际问题的联系 双曲线的许多性质，如离心率、焦点等，可以用于解决实际问题，如测量物 体的距离、角度等。
双曲线的图形特征:焦点和准线
双曲线定义 双曲线是平面内到两个定点的距离之差的绝对值等于常数的点的轨迹。 焦点性质 双曲线的两个焦点位于实轴两端，距离实轴相等。 准线特征 双曲线有两条互相垂直的准线，分别交坐标轴于原点和渐近线点。
04 双曲线的性质解析
双曲线的性质解析:主要性质
双曲线的焦点特性 双曲线有两焦点位于其对称轴上，距离中心等距。 双曲线的对称性 双曲线具有旋转对称性和平移对称性。 双曲线的渐近线 双曲线有两个渐近线，分别代表双曲线在x轴和y轴上的极限状态。 实数双曲线的面积 实数双曲线的面积是πab/4。

下
页 ∴ a = 3, c = 5
小
结
∴ b2 = 52-32 =16
结 束
所以所求双曲线的标准方程为： x2 y2 1
2020年10月2日
9 16
8
练习1:如果方程
x2
y2
1表示双曲线，
2m m1
求m的取值范围.
分析:由 (2m )m (1)0
首 页
得 1m2
上 页
下 页
变式一:
小 结
方程
页
上 的范围和焦点坐标。
页
下 分析:
页
小
m 2m100m2
结
结
c 2 (m 1 ) (m 2 ) 2 m 1
束
2020年10月2日 焦 （0， 点 (0 ,2 为 m 23 m )1)
10
练习2:证明椭圆 x2 y与2 双1 曲线
25 9
x2-15y2=15的焦点相同.
首 变式:
页
上 上题的椭圆与双曲线的一个交点为P，
结 束
2020年10月2日
2
①如图(A)， |MF1|-|MF2|=|F2F|=2a
②如图(B)， |MF2|-|MF1|=2a
首 页
由①②可得：
上 页
| |MF1|-|MF2| | = 2a
下
（差的绝对值）
页
小 上面 两条合起来叫做双曲线
结
结 束
2020年10月2日
3
定义:
平面内与两个定点F1，F2的距离的差 的绝对值
+
y2 b2
=
1
首 页
上
y2 a2
+
x2 b2

双曲线的性质及应用
双曲线拥有许多重要的性质和应用。在工程、物理学和金融等领域，双曲线的概念经常被应用于解决实际问题。 让我们深入研究双曲线的性质和应用。
结论及要点
通过本课件的学习，我们回顾了双曲线的定义、标准方程、图像特征以及其 性质和应用。掌握这些知识，可以帮助我们更好地理解曲线的性质和实际应 用。谢谢大家！
双曲线的图像特征
双曲线具有许多独特的图像特征。它的形状、对称性以及与其他曲线的关系使其在几何学和应用数学中具有广 泛的应用价值。
ห้องสมุดไป่ตู้
双曲线的焦点与准线
双曲线的焦点和准线是双曲线的重要属性。它们不仅确定了双曲线的形状， 还对我们理解双曲线的性质和应用起到关键作用。
双曲线的渐近线
双曲线的渐近线是一条特殊的直线，与双曲线的曲线趋势密切相关。了解双 曲线的渐近线有助于我们对双曲线的图像和性质有更深入的理解。
双曲线的定义及标准方程 ppt课件
欢迎来到本次精彩的课程介绍！我们将一起探讨双曲线的定义、标准方程以 及其图像特征。准备好了吗？让我们开始吧！
双曲线的定义
双曲线是数学中一种重要的曲线形式。它由离心率小于1的点构成，并具有特定的几何性质。让我们深入了解 双曲线的定义和性质。
双曲线的标准方程
双曲线可以使用标准方程来表示。这种方程的形式简洁，方便我们对双曲线 进行分析和计算。让我们掌握双曲线的标准方程。

y
B2
A1 F1 O
F2 A2
x
B1
y C3C2 C1
O
x
焦点在x轴上的双曲线图像
y 渐进线方程： b x a
Y x2 y2 1 a2 b2
B2
F1
A1
A2 F2 X B1
离心率对双曲线形状的影响
焦点在y轴上的双曲线图
像
Y
y2 a2
x2 b2
1
F2
A2
B1
O
B2
X
A1
F1
焦点在y轴上的双曲线的几何性质
2、对称性：关于x轴，y轴，
原点对称。 3、顶点 A1(-a,0),A2(a,0)
F1 A1 O
A2 F2
x
4、轴：实轴 A1A2 虚轴 B1B2
B1
|A1A2|=2ca,|B1B2|=2b 5、离心率：e= a
根据以上几何性质能够
根据以上几何性质能否
较准确地画出椭圆的图形？ 较准确地画出双曲线的图形呢？
双曲线标准方程：y 2 x 2 1 双曲线性质： a 2 b2
Y
1、范围：y≥a或y≤-a
F2
2、对称性：关于x轴，y轴，原点对称。
A2
3、顶点 A1（0，-a），A2（0，a）
4、轴：实轴 A1A2 ; 虚轴 B1B2 B1
5、渐近线方程： y a x
o
b
6、离心率：e=c/a
A1
F2
B2 X
Y
F1
B2
F’1 A1 o
B1
X
A2 F’2
F2
证明:(1)设已知双曲线的方程是:
x2 a2
y2 b2
1

立体几何课件（十一）
11.4 双曲线的定 义及标准方程
.
1
[复习] 1、求曲线方程的步骤
一、建立坐标系，设动点的坐标； 二、找出动点满足的几何条件；
三、将几何条件化为代数条件；
四、化简，得所求方程。
.
2
2、椭圆的定义
到平面上两定点F1，F2的距离之和（大于 |F1F2|）为常数的点的轨迹
PF1 PF 2 2a
.
3
3、椭圆的标准方程有几类？
[两类]x2 a2Fra biblioteky2 b2
1(焦点在x轴上)
x2 b2
y2 a2
1(焦点在y轴上)
.
4
；单创:/News/Detail/2019-9-20/442424.htm
；
我也是服了！“ （9）“您就当浪子回头吧，兴许真考上了，您也是积德了。”我回复了微信，也不忘调侃地加了几个坏笑的表情。 （10）之后，因为工作的关系，我离开了那座城市，也与律师楼和老李少了很多的交集。 （11）青海茫崖的矿难，突然成为了这个国家的头条新闻。部分矿务局 领导受贿私自外包矿坑，私人小矿主违规野蛮开采，导致了一次灭顶的矿难。在矿难中死去的矿工遗孀，因为没有基本的合同和安全保险凭据，无法获得赔偿，更无人愿意替他们去争取权利。 （12）就当矿难的悲哀正在褪去的时候，媒体上一个很不起眼报道终于被我看到了。 一个名叫常远的 律师，带领着自己的小团队义务承揽下了所有死难矿工的索赔事务。这条很小的信息，却因为这个熟悉而又陌生的名字而让我震惊。 （13）我立刻致电李信律师的时候，他确认道“没错，就是他，我也很佩服这小子。” （14）“您觉得他接这个案子是为了出名吗？”我问道。 （15）“还真不 是。你记得他曾经在青海一个矿区的酒吧演出过一段时间吧。”老李继 续说道。 “那地方就在茫崖。听常远的爸说，常远在那生活的一段时间，很了解矿工们的生活状况。他自己后来跑回来要继续考律师时就跟他爸说，以后要帮请不起律师的穷人打官司。” （16）我听老李说完这些，沉默了 许久，最后，我发自内心地说了一句：“后生可畏啊！” （17）电话那头老李肯定地重复道：“后生可畏！” （选自《新华文摘》2016年第13期，有删改） （1）文中写到常远的哪些经历？请按顺序补充完整 ﹣﹣﹣被迫备考律师﹣﹣﹣﹣﹣ ﹣﹣﹣﹣ ﹣﹣﹣﹣帮助穷人打官司 （2）读文中 划线句子，完成题目 ①简析第一段中划线句子的描写手法及其表达效果 ②第十二段中划线句子为什么说“我”对常远的名字熟悉而又陌生 （3）联系内容分析，常远的哪些品质让“我”和老李觉得“后生可畏”？ （4）小说主人公是常远，作者却以大部分内容写“我”和老李，这样写有什么 好处？ 代谢：12、（1）想当摇滚乐手 继续备考律师 承揽死难矿工索赔 （2）①这个句子运用了神态与动作描写，形象生动地表现出看书备考的常远心不在焉，为下文“我”和老李对年轻人的感慨作铺垫； ②因为在报上看到常远的名字与事迹之前，我对他的爱好及经历已有所了解，所以说“ 熟悉”；但我所知道的常远是一个不务正业，与父母反叛，不愿作律师的青年，现在他不仅当上了律师，还自愿免费为穷苦人打官司，让我惊讶，所以说“陌生”． （3）①他个性鲜明，有主见．父亲让他当律师，而他却根据自己的爱好选择当一名摇滚乐手．②他有社会责任感，勇于担当．他 到青海茫崖矿区演出，了解到矿工生活状况后，就决定回来考律师，为请不起律师的穷人打官司．③他不计名利，有奉献精神．矿难发生，他带领律师团队，义务为矿工打官司． （4）①“我”和老李的对话构成小说的基本框架．先写我们“上辈人”对他的不满，再写对他的佩服，先抑后扬， 波澜起伏，曲折有致．②通过“我”和老李的叙述侧面描写了常远这个有个性、敢于担当的人物形象，真实可信，给人以宽广的想象空间．③通过“我”和老李的态度变化，表现了要正确看待年轻人这一主题． （2017山东枣庄）8．（15分）阅读下面文章，完成下面各题 嘱托 格?鲍姆特 就在 彼得动身前往华沙参加一九五五年世界青年联欢节的前一晚，有人来敲门。原来是一位邻居。他从衣兜里掏出一个红色的小包包，然后摆在桌面上，摊开来。里头是一张相片、一封信和一张字条。 他讲述了有关这个红小包的一段经历﹣﹣ 一九三九年，第二次世界大战爆发后，德国法西斯的第 一个目标就是波兰。这样，大批的波兰人被弄到德国去。那时候，这位邻居正在一家锯木厂当工人，他曾答应帮助一个波兰囚犯实现他的托付。 一天，锯木厂的一个工棚失火了。人们都在交头接耳，心里明白是囚徒们干的好事，他们想用这样的方式把斗争进行下去。一群身穿黑制服的党卫队员 朝工厂一拥而入，带走了许多做苦工的囚犯。 当党卫队员冲进邻居工作的那个车间时，他正与那位囚犯在干活，这位波兰人迅速地从裤兜里摸出一个红色的小包包，塞到德国工人的手里，“老婆和孩子……多替我问候﹣﹣要是战争完蛋了。”他脸急得煞白，压低嗓门刚说出这几句话，党卫队就 把他带走了，作为对这次纵火的报复。 一九四六年夏天，这位邻居发了一封信给囚犯的太太，她的地址就写在那张纸条上。可是，他并没有得到回音。一年半之后，他又试图再投一信﹣﹣然而，一切依旧是徒劳的。现在好了，终于有了这一天，他可以托人将这个小包包直接带到波兰去。这位邻 居把小红包郑重地递给彼得。 彼得注视着这张相片。相片上是一位妇女，手里抱着一个大约两岁左右的小姑娘。信呢，不言而喻是遇害者留给他家属的最后诀语。在那个小小的纸片上，用大大的字迹写着这样一个地址：“Z和M?尼波耶夫斯卡华沙斯巴索夫斯基大街十八号”。 “一定的，我会去 找她的，并将事情的一切转告她，这件事您完全可以信赖我。”彼得说。 那时候，当这位邻居把这个小红包交给他的时候，彼得觉得一切都很简单：只要去到华沙，把事情一讲，东西一交，不就完了嘛！然而，当彼得后来抵达那条街的时候，十八号的门牌怎样找也找不到。在那块空地上，从前 确实有过十二至二十六号门牌的房子，现在只见一群孩子在空地上踢着足球。在警察所，彼得也得不到一点答复。她们现在究竟住在哪儿呢？这个，彼得反而横下一条心，非找到她们不可了。 来到华沙，彼得有一种难以形容的求知的渴念，他见得越多，什么活动都想参加一下的要求就更大。 大约在联欢节开始后一个星期，他的朋友们建议他去与一些波兰小伙子和姑娘相会一下。开头他想不太好吧，但朋友们干脆连拉带扯地把他推拥走了。跳舞的时候，每个人都得找个舞伴，这时在彼得而前就站着一位姑娘，她羞赧地望着他，并且邀请他跳舞。就这样，德国、波兰的小伙子和姑娘 们相聚在一起。他们尽力地用手势比划着交谈，大伙笑着，欢快地跳着。 自这个晚上邂逅相遇后，彼得与玛留莎每天都要相会。 世界青年联欢节的最后一天终于到来了，整个华沙城都陷入一片欢腾之中，在大广场上，阿拉伯青年与瑞典青年，中国青年与黑人青年，伊朗青年与德国青年都在纵 情地载歌载舞地狂欢，然后他们慢慢地拥向火车站。 彼得伴随玛留莎在火车站站台上来来回回地溜达，广播员用广播催促大家赶快上车，彼得才恋恋不舍地攀上了车厢，将身子从车窗里探出来。他们相互凝视着，一时无言以对。 “地址，”玛留莎突然想起来，她的喊声就象呼救那样。 彼得摸 出笔记本，撕下一页，将他的地址记在上面。这时，他一下子才想起了那个小红包，于是赶忙把它掏出来。 “玛留莎，请帮助找一找，”他说，然后把这个小红包按在她的手心上。 “打开看看！”他大声说，他见她一时还未领悟他的意思。 她打开这个小红包，念起来了。火车慢慢地挪动了。 玛留莎脚下象是生了根似的，粘住了。她几乎要被那些跟着火车而跑的人撞倒。“玛留莎，”彼得喊了她一声。玛留莎抬起头来一望，开始随火车跑起来，接着她停下脚来，摆着手，手里的那块红包纸就象一方告别的红头巾。彼得还在望着她，一时间留给他最深的印象是，她整个脸庞都叫泪水 湿透了。 “为什么她哭得这样厉害？”彼得思忖着，这时他已缩在一个角落里。“我将给她写信，”他这样想着。彼得拿出她的地址来，他念着念着，脸色越变越白，一直白到额头。原来，上面留下这样的名字：“玛留莎?尼波耶夫斯卡”，也就是那个小红包里的纸条上写着的名字。 （1）谈 谈本文以“嘱托”为题的含义。 （2）划线的段落在文中有什么作用？ （3）发挥想象，请将下面句子中省略号的内容补充出来。 “老婆和孩子……多替我问候﹣要是战争完蛋了。” （4）赏析下面句子的表达效果。 ①他脸急得煞白，压低嗓门刚说出这几句话…… ②他念着念着，脸色越变越 白，一直白到额头。 （5）小说的构思富有特色，请简要谈谈你的理解。 【��

-5
(xc)2 y2 (xc)2 y2 2a
.
9
四、化简
代数式化简得： (c2 a2) x2 a2 y2 a2 (c2 a2)
5
P(x,y)
因为三角形F2PF1的两边之差 必小于第三边，所以2a<2c, a<c, a2<c2, c2-a2>0
-5
F2(-c,0)
于是令：c2-a2=b2
一、建立坐标系，设动点的坐标； 二、找出动点满足的几何条件；
三、将几何条件化为代数条件；
四、化简，得所求方程。
.
2
2、椭圆的定义
到平面上两定点F1，F2的距离之和（大于 |F1F2|）为常数的点的轨迹
PF1 PF 2 2a
.
3
3、椭圆的标准方程有几类？
[两类]
x2 a2
y2 b2
1(焦点在x轴上)
-5
.
7
5
二、根据双曲线的定
义找出P点满足的几
P(x,y)
何条件。
-5
F2(-c,0)
| PF2 | | PF1| 2a
F1(c,0)
5
注：P点到两焦点的距
离之差用2a(a>0)表示。
-5
.
8
5
P(x,y)
三、将几何条件化为
代数条件。
-5
F2(-c,0)
F1(c,0)
5
根据两点的间的距离公式得：
请按顺序补充完整被迫备考律师帮劣穷人打官司2读文中划线句子完成题目简析第一段中划线句子的描写手法及其表达效果第十事段中划线句子为什么说我对常进的名字熟悉而又陌生3联系内容分析常进的哪些品质让我和老李觉得后生可畏