下载文档原格式
平面几何部分教学目标：1． 熟练掌握五大面积模型 2. 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比； 如右图12::S S a b =③夹在一组平行线之间的等积变形，如右图ACDBCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、鸟头定理两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形． 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上，E 在AC 上)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵三、蝴蝶定理ba S 2S 1DCBA S 4S 3S 2S 1O DCBA A BCDO ba S 3S 2S 1S 4任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．梯形中比例关系(“梯形蝴蝶定理”)： ①2213::S S a b =②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +． 四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方； ⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半． 相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具． 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形． 五、燕尾定理在三角形ABC 中，AD ，BE ，CF 相交于同一点O ，那么::ABO ACO S S BD DC ∆∆=．OFE DCBA上述定理给出了一个新的转化面积比与线段比的手段，因为ABO∆的形状很象燕子∆和ACO的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用，它的特殊性在于，它可以存在于任何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相联系的途径.典型例题【例 1】如图，正方形ABCD的边长为6，AE=，CF=2．长方形EFGH的面积为．【巩固】如图所示，正方形ABCD的边长为8厘米，长方形EBGF的长BG为10厘米，那么长方形的宽为几厘米【例 2】长方形ABCD的面积为362cm，E、F、G为各边中点，H为AD边上任意一点，问阴影部分面积是多少E【巩固】在边长为6厘米的正方形ABCD内任取一点P，将正方形的一组对边二等分，另一组对边三等分，分别与P点连接,求阴影部分面积．【例 3】如图所示，长方形ABCD内的阴影部分的面积之和为70，8AD=，四AB=，15边形EFGO的面积为．AB【巩固】如图，长方形ABCD的面积是36，E是AD的三等分点，2=，则阴影部分AE ED的面积为．B【例 4】已知ABC为等边三角形，面积为400，D、E、F分别为三边的中点，已知甲、乙、丙面积和为143，求阴影五边形的面积．(丙是三角形HBC)B【例 5】如图，已知5EF=，6FG=，线段AB将图形分成两部分，DE=，15CD=，7左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是．GFE DC BA【例 6】 如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．EDCBA【巩固】如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少EDCBA【巩固】如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍乙甲E DCBA【例 7】 如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．EDCBA【例 8】 如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2， 求平行四边形ABCD 与四边形EFGH 的面积比．HGAB CD EF【例 9】 如图所示的四边形的面积等于多少DC131213131212【例 10】 如图所示，ABC ∆中，90ABC ∠=︒，3AB =，5BC =，以AC 为一边向ABC ∆外作正方形ACDE ，中心为O ，求OBC ∆的面积．【例 11】 如图，以正方形的边AB 为斜边在正方形内作直角三角形ABE ，90AEB ∠=︒，AC 、BD 交于O ．已知AE 、BE 的长分别为3cm 、5cm ，求三角形OBE 的面积．【例 12】 如下图，六边形ABCDEF 中，AB ED =，AF CD =，BC EF =，且有AB 平行于ED ，AF 平行于CD ，BC 平行于EF ，对角线FD 垂直于BD ，已知24FD =厘米，18BD =厘米，请问六边形ABCDEF 的面积是多少平方厘米FEABDC【例 13】 如图，三角形ABC 的面积是1，E 是AC 的中点，点D 在BC 上，且:1:2BD DC =，AD 与BE 交于点F ．则四边形DFEC 的面积等于 ．FED CBA【巩固】如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米x xABFGE D CBA【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)．如果三角形ABD 的面积等于三角形BCD 的面积的13，且2AO =，3DO =，那么CO 的长度是DO 的长度的_________倍．ABCDO【巩固】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形BGC 的面积；⑵:AG GC =B【例 15】 如图，平行四边形ABCD 的对角线交于O 点，CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6．求：⑴求OCF △的面积；⑵求GCE △的面积．OGFEDCBA【例 16】 如图，长方形ABCD 中，:2:3BE EC =，:1:2DF FC =，三角形DFG 的面积为2平方厘米，求长方形ABCD 的面积．ABCDEF G【例 17】 如图，正方形ABCD 面积为3平方厘米，M 是AD 边上的中点．求图中阴影部分的面积．CBA【巩固】在下图的正方形ABCD中，E是BC边的中点，AE与BD相交于F点，三角形BEF 的面积为1平方厘米，那么正方形ABCD面积是平方厘米．AB CDEF【例 18】已知ABCD是平行四边形，:3:2BC CE ，三角形ODE的面积为6平方厘米．则阴影部分的面积是平方厘米．B【巩固】右图中ABCD是梯形，ABED是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是平方厘米．B【巩固】右图中ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是 平方厘米．B【例 19】 如图，长方形ABCD 被CE 、DF 分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形OFBC 的面积为___________平方厘米．?852O A BCD EF【例 20】 如图，ABC ∆是等腰直角三角形，DEFG 是正方形，线段AB 与CD 相交于K 点．已知正方形DEFG 的面积48，:1:3AK KB =，则BKD ∆的面积是多少B【例 21】 下图中，四边形ABCD 都是边长为1的正方形，E 、F 、G 、H 分别是AB ，BC ，CD ，DA 的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn，那么，()m n +的值等于 ．BEE【例 22】 如图， ABC △中，DE ，FG ，BC 互相平行，AD DF FB ==，则::ADEDEGF FGCB S S S =△四边形四边形 ．EGF A D CB【巩固】如图，DE 平行BC ，且2AD =，5AB =，4AE =，求AC 的长．A ED CB【巩固】如图， ABC △中，DE ，FG ，MN ，PQ ，BC 互相平行，AD DF FM MP PB ====，则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 ．【例 23】 如图，已知正方形ABCD 的边长为4，F 是BC 边的中点，E 是DC 边上的点，且:1:3DE EC =，AF 与BE 相交于点G ，求ABG S △Q E GNMF PADCBGFAEDCB【例 24】 如图所示，已知平行四边形ABCD 的面积是1，E 、F 是AB 、AD 的中点， BF交EC 于M ，求BMG ∆的面积．MHGF E DCBA【例 25】 如图，ABCD 为正方形，1cm AM NB DE FC ====且2cm MN =，请问四边形PQRS 的面积为多少CA【例 26】 如右图，三角形ABC 中，:4:9BD DC =，:4:3CE EA =，求:AF FB ．O F EDCBA【巩固】如右图，三角形ABC 中，:3:4BD DC =，:5:6AE CE =，求:AF FB .O F EDCBA【巩固】如右图，三角形ABC 中，:2:3BD DC =，:5:4EA CE =，求:AF FB .O F EDCBA【例 27】 如右图，三角形ABC 中，:::3:2AF FB BD DC CE AE ===，且三角形ABC 的面积是1，则三角形ABE 的面积为______，三角形AGE 的面积为________，三角形GHI 的面积为______．I HGFEDCBA【巩固】 如右图，三角形ABC 中，:::3:2AF FB BD DC CE AE ===，且三角形GHI 的面积是1，求三角形ABC 的面积．IH G FEDCBA【巩固】如图，ABC ∆中2BD DA =，2CE EB =，2AF FC =，那么ABC ∆的面积是阴影三角形面积的 倍．B【巩固】如图在ABC △中，12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值． IHG FEDCBA【例 28】 如图，三角形ABC 的面积是1，BD DE EC ==，CF FG GA ==，三角形ABC 被分成9部分，请写出这9部分的面积各是多少GFE D CBA【巩固】如图，ABC ∆的面积为1，点D 、E 是BC 边的三等分点，点F 、G 是AC 边的三等分点，那么四边形JKIH 的面积是多少K JI HABC D EF G【例 29】 右图，ABC △中，G 是AC 的中点，D 、E 、F 是BC 边上的四等分点，AD 与BG 交于M ，AF 与BG 交于N ，已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米，则ABC △的面积是多少平方厘米N M GA BCD EF【例 30】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.GCB【例 31】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBA课后练习：练习1. 已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．FED CBA练习2. 如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．H GFED CB A练习3. 正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF 的面积是 平方厘米．H GFEDC BA练习4. 如图，已知4cm AB AE ==，BC DC =，90BAE BCD ∠=∠=︒，10cm AC =，则S ABC ACE CDE S S ∆∆∆++= 2cm ．DCEBA练习5. 如图，正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF 的面积是_____平方厘米．ED练习6. 如图，ABC ∆中，点D 是边AC 的中点，点E 、F 是边BC 的三等分点，若ABC∆的面积为1，那么四边形CDMF 的面积是_________．FABCDE MN练习7. 如右图，三角形ABC 中，:::4:3AF FB BD DC CE AE ===，且三角形ABC 的面积是74，求角形GHI 的面积．IH G FEDCBA备选【备选1】 按照图中的样子，在一平行四边形纸片上割去了甲、乙两个直角三角形．已知甲三角形两条直角边分别为2cm 和4cm ，乙三角形两条直角边分别为3cm 和6cm ，求图中阴影部分的面积．【备选2】 如图所示，矩形ABCD 的面积为36平方厘米，四边形PMON 的面积是3平方厘米，则阴影部分的面积是 平方厘米．【备选3】 如图，已知3BD DC =，2EC AE =，BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几OE DCBA【备选4】 如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使12CE BC =，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少A BCDEF【备选5】 如图，:2:3BD DC =,:5:3AE CE =,则:AF BF =GF EDCBA【备选6】 如图在ABC △中，13DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值． IHG FEDCBA。
图形与几何的知识点一、基本概念图形与几何是数学中的一个重要分支，研究物体的形状、大小、位置和运动等方面。
在这个领域里，有一些基本的概念和术语我们需要了解。
1. 点：在几何中，点是最基本的概念，没有形状和大小，只有位置。
2. 线段：线段是由两个点确定的一段连续的直线。
3. 直线：直线是由一条连续的线段无限延伸而成的。
4. 射线：射线是由一个端点和一条连续的直线段组成。
5. 角：角是由两条射线共享一个端点而形成的图形。
6. 边：多边形是由线段构成的，每个线段被称为一个边。
二、图形的分类图形可以根据各种属性进行分类，以下是几个常见的分类方式：1. 几何图形：几何图形是平面上的图形，包括点、线、面等。
2. 二维图形：二维图形是在平面上具有宽度和高度的图形，如长方形、正方形、三角形等。
3. 三维图形：三维图形是在空间中具有宽度、高度和深度的图形，如立方体、圆柱体、球体等。
4. 凸多边形和凹多边形：凸多边形是没有内角大于180度的多边形，凹多边形是至少有一个内角大于180度的多边形。
5. 等边图形：等边图形是指具有相等边长的图形，比如等边三角形。
三、图形的性质图形具有一些共同的性质，这些性质有助于我们理解和比较不同的图形。
1. 对称性：图形在某个轴线或点处可以被分成两个相等的部分。
2. 平行性：两条直线在平面上没有点重合，但始终保持相同的间距。
3. 垂直性：两条直线相交，且相交的角为直角（90度）。
4. 相似性：两个图形的形状相似，但大小可能不同。
5. 定理：几何学中有很多定理，如勾股定理、正弦定理、余弦定理等，它们可以用来解决各种几何问题。
四、常见图形的计算公式图形的计算涉及到面积、周长、体积等方面，以下是几个常见图形的计算公式：1. 矩形的面积公式：面积 = 长 ×宽2. 三角形的面积公式：面积 = 底边长 ×高 ÷ 23. 圆的面积公式：面积= π × 半径^24. 圆的周长公式：周长= 2 × π × 半径5. 立方体的体积公式：体积 = 长 ×宽 ×高五、实际应用图形与几何的知识点在实际生活中有许多应用。
数学奥赛教练员培训班讲义（1）第一讲 平面几何平面几何是数学竞赛中的一个基本内容。
它以严密的逻辑结构、灵活的证题方法，在发展学生的逻辑思维能力和空间想象能力等方面起着特殊的作用。
因此在数学竞赛中平面几何的内容占有十分突出的地位。
平面几何主要研究度量关系的证明、位置关系的证明、面积关系解题、几何量的计算、轨迹问题等。
一、与三角形有关的重要定理1.梅涅劳斯定理一直线分别截△ABC 的边BC 、CA 、AB （或其延长线）于D 、E 、F ，则1=∙∙FBAF EA CE DC BD 。
说明：（1）结论的图形应考虑直线与三角形三边交点的位置情况，因而本题图形应该有两个。
（2）结论的结构是三角形三边上的6条线段的比，首尾相连，组成一个比值为1的等式。
（3）其逆定理为：如果D 、E 、F 分别在△ABC 的边BC 、CA 、AB （或其延长线上），并且1=∙∙FBAF EA CE DC BD ，那么D 、E 、F 三点在同一条直线上。
（4）梅氏定理及其逆定理不仅可以用来证明点共线问题，而且是解决许多比例线段问题的有力工具。
用梅氏定理求某个比值的关键，在于恰当地选取梅氏三角形和梅氏线。
2.塞瓦定理设O 是△ABC 内任意一点，AO 、BO 、CO 分别交对边于D ，E ，F ，则1=∙∙FBAF EA CE DC BD 。
说明：（1）该定理可借助于梅氏定理来证明（也可用面积法来证明）。
如果O 点在三角形外，结论仍然是成立的。
（2）其逆定理为：分别在△ABC 三边（所在直线）BC 、CA 、AB 上各取一点D 、E 、F ，若有1=∙∙FBAF EA CE DC BD ，则AD 、BE 、CF 平行或共点。
（3）塞瓦定理及其逆定理是证明三直线交于一点（线共点）问题的重要定理，应用塞瓦定理很容易证明三角形中的主要线段的共点问题。
3.三角形的五心三角形的三条中线共点，三条角平分线共点，三条高线共点，三条中垂线共点。
平面几何基础平面几何是几何学的重要分支之一，研究了在平面上的点、线、角以及图形的性质和关系。
它是我们理解和解决实际问题中经常用到的一种数学工具。
本文将介绍平面几何的基础知识，包括点、线、角和图形的特征与性质。
一、点的性质与关系1. 点的定义与表示：在平面几何中，点是最基本的概念，通常用大写字母表示，如"A"、"B"、"C"等。
点没有大小和形状，只有位置。
2. 点的相对位置：在平面上，点的相对位置可以用坐标来表示。
我们可以用直角坐标系或极坐标系来确定点的位置，其中直角坐标系由x 轴和y轴组成，而极坐标系由原点、极径和极角组成。
3. 点的连线：两个点之间可以用线段连接起来，形成一个直线。
直线是经过两个点的最短路径。
4. 点的投影：当点在平面上与另一个物体重叠时，它的投影就是它在平面上的垂直投影点。
投影是判断物体位置和大小的重要工具。
二、线的性质与关系1. 线的定义与表示：线是通过两个点或多个点上的连续点组成的。
可以用小写字母表示线，如"l"、"m"、"n"等。
2. 线的分类：根据线的位置和形状，我们可以将线分为水平线、垂直线、直线、曲线等。
3. 线的相对位置：在平面上，两条线可以相交、平行或重合。
相交的两条线称为交线，平行的两条线永不相交，重合的两条线完全重合。
4. 线的性质：两条平行线上的任意两个点到另一条平行线的距离是相等的。
两条垂直线的斜率乘积为-1。
这些性质在解决实际问题中起着重要的作用。
三、角的性质与关系1. 角的定义与表示：角是由两条线或线段的端点共同确定的，通常用大写字母表示，如"A"、"B"、"C"等，其中顶点位于两条边的交点处。
2. 角的度量：角可以用度数或弧度表示。
度数是常用的度量单位，360度是一个完整的角。
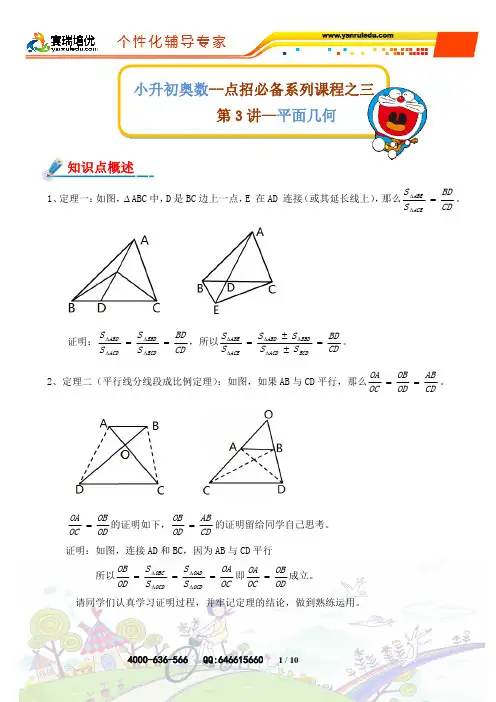
几何概念复习1、角（角的概念）（1）n边形内角和为（），其外角和为（），正n边型的内角为（）。
（2）等角模型（3）聚角模型（请证明公式）∠A+∠B=∠ACD ∠A+∠B+∠C=∠D ∠A+∠B=∠C+∠D例题1、如图, ∠E=30°,AF∥ED,求∠A+∠B+∠C+∠D+∠E+∠+F=?例题2、求标有数字的12个角的度数之和？例题3、每个50分的硬币是一个正12边形，当两个硬币以这样角度竖立，则图中∠X=（）。
2、求面积图形的若干一半模型（用阴影画出）3、求复杂图形的面积（1）、毕克定理正方形格点S=(N+L/2-1)·单三角形格点S=(2N+L-2)·单例1、例题1、正方形格点的面积为1，求⊿ACD的面积。
（2）平移和旋转（全等三角形）（3）空白和阴影对比法，结合和差公式。
（4）特殊四边形的面积例2、如图，如果长方形ABCD的面积为56 cm2，那么四边形MNPQ的面积为（）cm2。
例3、如图，甲乙丙丁四个长方形拼成一个正方形EFGH，中间阴影为正方形。
已知甲乙丙丁四个长方形的面积和为54 cm2，四边形ABCD的面积为37 cm2，求正方形EFGH的面积及甲、乙、丙、丁四个长方形的周长总和。
2、三角形三角形的内角和为（），外角和为（）。
等腰三角形的特点：（1）（2）（3）直角三角形：（1）、勾股定理：。
（2）、勾股定理逆定理：。
（3）、特殊直角三角形：【巩固1】、如图，RTΔABC，AB=AC,AD=BD,斜边AB=a，则ΔABC的面积为多少？【巩固2】如图，RTΔABC，∠A=30°, AD=BD,斜边AB=a，则ΔABC的面积为多少？【巩固3】已知一个直角三角形的两边长分别为5和12，则第三边长的平方是多少？巧求多边形的周长和面积【巩固3】正方形的边长为10，E、F、G、H分别是边长的中点，则阴影部分的面积为（）。
【巩固4】一个正方形，边长增加8 cm，其面积就增加256 cm2，问原来这个正方形的面积是多少？【巩固5】如图，RT⊿ABC中，AB=3，AC=4，点D、E、F、G、N、I都在长方形KLMJ上，且ABED、ACNI、BCGF都是正方形，则KLMJ面积为( ).【巩固5】有一个正方形（如图），把它分成8个小长方形，它们的周长之和为120cm，那么这个正方形的面积是多少？【巩固6】3.用4个相同的等腰直角三角形相互交迭拼成下图，阴影正方形的面积是（）平方厘米。
平面几何知识点总结大全一、基本图形。
1. 点。
- 点是平面几何中最基本的元素，没有大小、长度、宽度或厚度。
它通常用一个大写字母表示，如点A。
2. 线。
- 直线。
- 直线没有端点，可以向两端无限延伸。
直线可以用直线上的两个点表示，如直线AB；也可以用一个小写字母表示，如直线l。
- 经过两点有且只有一条直线（两点确定一条直线）。
- 射线。
- 射线有一个端点，它可以向一端无限延伸。
射线用表示端点的字母和射线上另一点的字母表示，端点字母写在前面，如射线OA。
- 线段。
- 线段有两个端点，有确定的长度。
线段用表示两个端点的字母表示，如线段AB；也可以用一个小写字母表示，如线段a。
- 两点之间，线段最短。
3. 角。
- 由公共端点的两条射线组成的图形叫做角，这个公共端点是角的顶点，这两条射线是角的两条边。
角通常用三个大写字母表示（顶点字母写在中间），如∠AOB；也可以用一个大写字母表示（这个大写字母表示顶点，且以这个顶点为顶点的角只有一个时），如∠ O；还可以用一个数字或希腊字母表示，如∠1、∠α。
- 角的度量单位是度、分、秒，1^∘=60'，1' = 60''。
- 角的分类：- 锐角：大于0^∘而小于90^∘的角。
- 直角：等于90^∘的角。
- 钝角：大于90^∘而小于180^∘的角。
- 平角：等于180^∘的角。
- 周角：等于360^∘的角。
二、相交线与平行线。
1. 相交线。
- 对顶角。
- 两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做对顶角。
对顶角相等。
- 邻补角。
- 两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。
邻补角互补，即和为180^∘。
- 垂直。
- 当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。
- 在同一平面内，过一点有且只有一条直线与已知直线垂直。
平面几何知识点总结平面几何是数学中一个重要的分支，它研究的是平面内图形的性质和关系。
下面我们来详细总结一下平面几何的主要知识点。
一、点、线、面点是没有大小和形状的，是最基本的几何元素。
线是由无数个点组成的，直线没有端点，可以无限延伸；射线有一个端点，向一端无限延伸；线段有两个端点，有固定的长度。
面是由线围成的，平面没有边界，可以无限延展。
二、角角是由两条有公共端点的射线组成的几何图形。
角的度量单位是度，用“°”表示。
1、角的分类锐角：小于 90 度的角。
直角：等于 90 度的角。
钝角：大于 90 度小于 180 度的角。
平角：等于 180 度的角。
周角：等于 360 度的角。
2、角的性质同角或等角的余角相等，同角或等角的补角相等。
对顶角相等。
三、三角形三角形是由三条线段首尾顺次相接组成的封闭图形。
1、三角形的分类按角分类：锐角三角形、直角三角形、钝角三角形。
按边分类：等边三角形、等腰三角形、不等边三角形。
2、三角形的性质三角形内角和为 180 度。
三角形任意两边之和大于第三边，任意两边之差小于第三边。
3、三角形的特殊线段中线：连接三角形顶点和它对边中点的线段。
高线：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段。
角平分线：三角形一个内角的平分线与这个角的对边相交，这个角的顶点与交点之间的线段。
4、全等三角形全等三角形的性质：全等三角形的对应边相等，对应角相等。
全等三角形的判定：SSS（边边边）、SAS（边角边）、ASA（角边角）、AAS（角角边）、HL（斜边、直角边）。
四、四边形四边形是由不在同一直线上的四条线段首尾顺次相接组成的封闭图形。
1、平行四边形性质：对边平行且相等，对角相等，对角线互相平分。
判定：两组对边分别平行的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形。
2、矩形性质：四个角都是直角，对角线相等。
平面几何部分教学目标：1．熟练掌握五大面积模型2. 掌握五大面积模型的各种变形知识点拨一、等积模型①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；如右图12::S S a b =③夹在一组平行线之间的等积变形，如右图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、鸟头定理两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形． 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比． 如图在ABC △中，,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上，E 在AC 上)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图⑴ 图⑵三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者132S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．梯形中比例关系(“梯形蝴蝶定理”)： b a S 2S 1D C B A A B C D O b a S 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =；③S 的对应份数为()2a b +． 四、相似模型(一)金字塔模型 (二) 沙漏模型 ①AD AE DE AF AB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方；⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具． 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．五、燕尾定理在三角形ABC 中，AD ，BE ，CF 相交于同一点O ，那么::ABO ACO S S BD DC ∆∆=． 上述定理给出了一个新的转化面积比与线段比的手段，因为ABO ∆和ACO ∆的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用，它的特殊性在于，它可以存在于任何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相联系的途径.典型例题【例 1】 如图，正方形ABCD 的边长为6，AE =1.5，CF =2．长方形EFGH 的面积为 ．【巩固】如图所示，正方形ABCD 的边长为8厘米，长方形EBGF 的长BG 为10厘米，那么长方形的宽为几厘米？【例 2】 长方形ABCD 的面积为362cm ，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？【巩固】在边长为6厘米的正方形ABCD 内任取一点P ，将正方形的一组对边二等分，另一组对边三等分，分别与P 点连接,求阴影部分面积． _A _B_G _C _E_F _D _A _B _ G _C _E _F_DO F E D CB A【例 3】 如图所示，长方形ABCD 内的阴影部分的面积之和为70，8AB =，15AD =，四边形EFGO 的面积为 ．【巩固】如图，长方形ABCD 的面积是36，E 是AD 的三等分点，2AE ED =，则阴影部分的面积为 ．【例 4】 已知ABC 为等边三角形，面积为400，D 、E 、F 分别为三边的中点，已知甲、乙、丙面积和为143，求阴影五边形的面积．(丙是三角形HBC )【例 5】 如图，已知5CD =，7DE =，15EF =，6FG =，线段AB 将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG 的面积是 ．【例 6】 如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．【巩固】如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE的面积等于1，那么三角形ABC 的面积是多少？【巩固】如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？【例 7】 如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．【例 8】 如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2， 求平行四边形ABCD 与四边形EFGH 的面积比．【例 9】 如图所示的四边形的面积等于多少？【例 10】 如图所示，ABC ∆中，90ABC ∠=︒，3AB =，5BC =，以AC 为一边向ABC ∆外作正方形ACDE ，中心为O ，求OBC ∆的面积．【例 11】 如图，以正方形的边AB 为斜边在正方形内作直角三角形ABE ，90AEB ∠=︒，AC 、BD 交于O ．已知AE 、BE 的长分别为3cm 、5cm ，求三角形OBE 的面积．【例 12】 如下图，六边形ABCDEF 中，AB ED =，AF CD =，BC EF =，且有AB 平行于ED ，AF 平行于CD ，BC 平行于EF ，对角线FD 垂直于BD ，已知24FD =厘米，18BD =厘米，请问六边形ABCDEF 的面积是多少平方厘米？【例 13】 如图，三角形ABC 的面积是1，E 是AC 的中点，点D 在BC 上，且:1:2BD DC =，AD 与BE 交于点F ．则四边形DFEC 的面积等于 ．【巩固】如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米?【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)．如果三角形ABD 的面积等于三角形BCD 的面积的13，且2AO =，3DO =，那么CO 的长度是DO 的长度的_________倍．【巩固】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知， 求：⑴三角形BGC 的面积；⑵:AG GC =？【例 15】 如图，平行四边形ABCD 的对角线交于O 点，CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6．求：⑴求OCF △的面积；⑵求GCE △的面积．【例 16】 如图，长方形ABCD 中，:2:3BE EC =，:1:2DF FC =，三角形DFG 的面积为2平方厘米，求长方形ABCD 的面积．【例 17】 如图，正方形ABCD 面积为3平方厘米，M 是AD 边上的中点．求图中阴影部分的面积．【巩固】在下图的正方形ABCD 中，E 是BC 边的中点，AE 与BD 相交于F 点，三角形BEF的面积为1平方厘米，那么正方形ABCD 面积是 平方厘米．【例 18】 已知ABCD 是平行四边形，:3:2BC CE =，三角形ODE 的面积为6平方厘米．则阴影部分的面积是 平方厘米．【巩固】右图中ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是 平方厘米．【巩固】右图中ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是 平方厘米．【例 19】 如图，长方形ABCD 被CE 、DF 分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形OFBC 的面积为___________平方厘米．【例 20】 如图，ABC ∆是等腰直角三角形，DEFG 是正方形，线段AB 与CD 相交于K点．已知正方形DEFG 的面积48，:1:3AK KB =，则BKD ∆的面积是多少？【例 21】 下图中，四边形ABCD 都是边长为1的正方形，E 、F 、G 、H 分别是AB ，BC ，CD ，DA 的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n，那么，()m n +的值等于 ． 【例 22】 如图， ABC △中，DE ，FG ，BC 互相平行，AD DF FB ==， 则::ADE DEGF FGCB S S S =△四边形四边形 ．【巩固】如图，DE 平行BC ，且2AD =，5AB =，4AE =，求AC 的长．【巩固】如图， ABC △中，DE ，FG ，MN ，PQ ，BC 互相平行，AD DF FM MP PB ====，则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 ．【例 23】 如图，已知正方形ABCD 的边长为4，F 是BC 边的中点，E 是DC 边上的点，且:1:3DE EC =，AF 与BE 相交于点G ，求ABG S △【例 24】 如图所示，已知平行四边形ABCD 的面积是1，E 、F 是AB 、AD 的中点， BF交EC 于M ，求BMG ∆的面积．【例 25】 如图，ABCD 为正方形，1cm AM NB DE FC ====且2cm MN =，请问四边形PQRS 的面积为多少？【例 26】 如右图，三角形ABC 中，:4:9BD DC =，:4:3CE EA =，求:AF FB ．【巩固】如右图，三角形ABC 中，:3:4BD DC =，:5:6AE CE =，求:AF FB .【巩固】如右图，三角形ABC 中，:2:3BD DC =，:5:4EA CE =，求:AF FB .【例 27】 如右图，三角形ABC 中，:::3:2AF FB BD DC CE AE ===，且三角形ABC 的面积是1，则三角形ABE 的面积为______，三角形AGE 的面积为________，三角形GHI 的面积为______．【巩固】 如右图，三角形ABC 中，:::3:2AF FB BD DC CE AE ===，且三角形GHI 的面积是1，求三角形ABC 的面积．【巩固】如图，ABC ∆中2BD DA =，2CE EB =，2AF FC =，那么ABC ∆的面积是阴影三角形面积的 倍．【巩固】如图在ABC △中，12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值． 【例 28】 如图，三角形ABC 的面积是1，BD DE EC ==，CF FG GA ==，三角形ABC 被分成9部分，请写出这9部分的面积各是多少?【巩固】如图，ABC ∆的面积为1，点D 、E 是BC 边的三等分点，点F 、G 是AC 边的三等分点，那么四边形JKIH 的面积是多少？【例 29】 右图，ABC △中，G 是AC 的中点，D 、E 、F 是BC 边上的四等分点，AD 与BG 交于M ，AF 与BG 交于N ，已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米，则ABC △的面积是多少平方厘米？【例 30】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.【例 31】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.课后练习：练习1. 已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积． 练习2. 如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．练习3. 正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF 的面积是 平方厘米．练习4. 如图，已知4cm AB AE ==，BC DC =，90BAE BCD ∠=∠=︒，10cm AC =，则S ABC ACE CDE S S ∆∆∆++= 2cm ．练习5. 如图，正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF 的面积是_____平方厘米．练习6. 如图，ABC ∆中，点D 是边AC 的中点，点E 、F 是边BC 的三等分点，若ABC∆的面积为1，那么四边形CDMF 的面积是_________． 练习7. 如右图，三角形ABC 中，:::4:3AF FB BD DC CE AE ===，且三角形ABC 的面积是74，求角形GHI 的面积．备选【备选1】 按照图中的样子，在一平行四边形纸片上割去了甲、乙两个直角三角形．已知甲三角形两条直角边分别为2cm 和4cm ，乙三角形两条直角边分别为3cm 和6cm ，求图中阴影部分的面积．【备选2】 如图所示，矩形ABCD 的面积为36平方厘米，四边形PMON 的面积是3平方厘米，则阴影部分的面积是 平方厘米．【备选3】 如图，已知3BD DC =，2EC AE =，BE 与CD 相交于点O ,则ABC △被分成的4部分面积各占ABC △ 面积的几分之几？【备选4】 如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使12CE BC =，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？【备选5】 如图，:2:3BD DC =,:5:3AE CE =,则:AF BF =【备选6】 如图在ABC △中，13DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值． 【备选7】。
小学六年级奥数知识：几何初步认识（平面图形）这篇关于小学六年级奥数知识：几何初步认识（平面图形），是特地为大家整理的，希望对大家有所帮助！二、平面图形1、长方形（1）特征对边相等，4个角都是直角的四边形。
有两条对称轴。
（2）计算公式c=2(a+b)s=ab2、正方形（1）特征：四条边都相等，四个角都是直角的四边形。
有4条对称轴。
（2）计算公式c=4as=a23、三角形（1）特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
（2）计算公式s=ah/2（3）分类按角分锐角三角形：三个角都是锐角。
直角三角形：有一个角是直角。
等腰三角形的两个锐角各为45度，它有一条对称轴。
钝角三角形：有一个角是钝角。
按边分不等边三角形：三条边长度不相等。
等腰三角形：有两条边长度相等；两个底角相等；有一条对称轴。
等边三角形：三条边长度都相等；三个内角都是60度；有三条对称轴。
4、平行四边形（1）特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等，相邻的两个角的度数之和为180度。
平行四边形容易变形。
（2）计算公式s=ah5、梯形（1）特征只有一组对边平行的四边形。
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
（2）公式s=(a+b)h/2=mh6、圆（1）圆的认识平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o 表示。
半径：连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里，有无数条半径，每条半径的长度都相等。
直径：通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有无数条直径，所有的直径都相等。
同一个圆里，直径等于两个半径的长度，即d=2r。
圆的大小由半径决定。
圆有无数条对称轴。
（2）圆的画法把圆规的两脚分开，定好两脚间的距离（即半径）；把有针尖的一只脚固定在一点（即圆心）上；把装有铅笔尖的一只脚旋转一周，就画出一个圆。
（3）圆的周长围成圆的曲线的长叫做圆的周长。
平面图形与几何知识汇总1.四边形：（1）四边形的特征：有4条直的边，有4个角，是封闭图形。
（2）长方形和正方形的特征：长方形特征：4个角都是直角，对边相等，较长的边叫做长，较短的边叫做宽。
正方形的特征：4个角都是直角，每条边都相等，每条边的长叫做边长。
图形的周长：封闭图形一周的长度，是它的周长。
2.周长的求法：（1）测直边物体和图形的周长：用直尺分别测量出每条边的长度，再计算长度之和。
（2）测量圆形物体的周长：①绕绳法：用一根绳绕圆的边缘一周，剪去多余的部分，再拉直，量出它的长度即得到圆的周长。
②滚动法：把圆放在直尺上滚动一周，直接量出圆的周长。
（3）测量不规则物体的周长：用细线绕树叶周围一圈，拉直后测量细线的长度。
3. 长方形的周长＝长＋宽＋长＋宽长方形周长的计算方法长方形的周长＝长×2＋宽×2长方形的周长＝（长＋宽）×2正方形周长的计算方法正方形的周长＝边长＋边长＋边长＋边长正方形的周长＝边长×44.用相同的小正方形拼长方形和正方形，拼成正方形时周长最短，摆成一排拼成长方形时周长最长。
5.面积：物体的表面或封闭图形的大小，就是它们的面积。
周长与面积的区别：周长是指封闭图形一周的长度，面积是指物体所占平面大小。
6.常用面积单位：（1）平方厘米（cm2）：边长1厘米的正方形，面积是1平方厘米。
（2）平方分米（dm2）：边长1分米的正方形，面积是1平方分米。
（3）平方米（m2）：边长1米的正方形，面积是1平方米。
7.面积公式：长方形面积 = 长×宽正方形面积 = 边长×边长8.平行与垂直：同一个平面内的两条直线的位置关系只有两种不相交——平行相交垂直不垂直平行：在同一平面内不相交的两条直线叫做平行线，也可以说这两条直线互相平行。
垂直：两条直线相交成直角，就说这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。
拓展：①“在同一个平面内”是确定两条直线是不是平行关系的前提。
如果不在同一个平面内，有些直线虽然不相交，但也不能称为互相平行。
②在同一个平面内，如果两条直线都和第三条直线平行，这两条直线也互相平行。
如果a∥b，b∥c，那么a∥c。
③在同一个平面内，如果两条直线都和第三条直线垂直，那么这两条直线互相平行。
如果a⊥b，b⊥c，那么a∥c。
9.垂直的画法：（1）在画互相垂直的两条直线时，可以借助三角尺或量角器来画。
（2）过直线上一点画已知直线的垂线的方法：①把三角尺的一条直角边与已知直线重合。
②沿着直线移动三角尺，使三角尺的直角顶点和直线上的已知点重合。
③沿着三角尺的另一条直角边画一条直线（三角尺的直角顶点是垂足），这条直线就是已知直线的垂线。
④标出直角符号。
（3）过直线外一点画已知直线的垂线的方法：①把三角尺的一条直角边与已知直线重合。
②沿着直线移动三角尺，使三角尺的另一条直角边过直线外的一点。
③沿着三角尺的另一条直角边画一条直线（三角尺的直角顶点是垂足），这条直线就是已知直线的垂线。
④标出直角符号。
10.点到直线的距离：(1)从直线外一点到这条直线所画的垂直线段最短，它的长度叫做这点到直线的距离。
(2)平行线间的距离处处都相等。
11.画长方形的方法：(1)先画出长方形的长；(2)再以这条长的两个端点为垂足，向同一个方向画两条长度相等且与这条长垂直的线段作为长方形的两条宽；(3)最后把这两条宽的另外两个端点连接起来，画出长方形的另一条长。
12.平行四边形：两组对边分别平行的四边形，叫做平行四边形。
特征：两组对边分别平行且相等。
平行四边形的底和高：从平行四边形一条边上的一点向对边引一条垂线，这点和垂足之间的线段叫做平行四边形的高，垂足所在的边叫做平行四边形的底。
平行四边形特性：易变形，具有不稳定性。
13.梯形：只有一组对边平行的四边形，叫做梯形。
梯形各部分的名称：特殊梯形：①等腰梯形：两腰相等的梯形叫做等腰梯形。
（如图1）②直角梯形：有一个角是直角的梯形叫做直角梯形。
（如图2）画梯形高的方法：在梯形的底上选一点向对边画一条垂线，这点和垂足之间的线段就是梯形的高。
（通常从上底的一个端点向它的对边画高。
）14.补充：（1）.平行四边形和梯形画高的注意事项：①要用虚线表示。
②一定要画直角符号。
③一般把高画在图形内。
（2）.四边形之间的关系（3）.比较各种四边形的特征：四边形 边数对边是否平行对边是否相等对角是否相等正方形长方形平行四边形梯形15.平行四边形的面积平行四边形 长方形转化的数学思想长方形的面积＝ 长 × 宽 平行四边形的面积 ＝ 底 × 高平行四边形的面积＝底×高S ＝ah注意：①求平行四边形的面积，要先找到底和其相对应的高，再计算。
②平行四边形底不变，高扩大到原来的n 倍，则面积扩大到原来的n 倍；平行四边形底不变，高缩小到原来的1n ，则面积缩小到原来的1n 。
平行四边形高不变，底扩大到原来的n 倍，则面积扩大到原来的n 倍； 平行四边形高不变，底缩小到原来的1n，则面积缩小到原来的1n。
平行四边形的底扩大到原来的n 倍，高缩小到原来的1n，面积不变。
16.三角形的面积三角形 平行四边形 或 长方形两个完全相同的三角形可以拼成一个平行四边形，拼成一个平行四边形的两个三底a高h 底=平行四边形的面积÷高高=平行四边形的面积÷底 a ＝S ÷hh ＝S ÷a底高 底高 底高底高底高底底角形完全相同。
三角形的底 ＝ 平行四边形的底 三角形的高 ＝ 平行四边形的高 每个三角形的面积 ＝ 平行四边形的面积÷2＝ 平行四边形的底×平行四边形的高÷2＝ 三角形的底×三角形的高÷ 2 （相对应的底和高）三角形的面积 ＝ 底×高÷2S ＝ ah ÷217.梯形的面积梯形 平行四边形两个完全相同的梯形可以拼成一个平行四边形。
梯形的（上底+下底）＝ 平行四边形的底梯形的高 ＝ 平行四边形的高 每个梯形的面积 ＝ 平行四边形的面积÷2＝ 平行四边形的底×平行四边形的高÷2 ＝ （梯形的上底+梯形的下底）×梯形的高÷2梯形的面积 ＝ （上底＋下底）×高÷2 S ＝（a ＋b ）×h ÷2底 ＝ 三角形的面积×2÷高高 ＝ 三角形的面积×2÷底 a ＝2S ÷h h ＝2S ÷a 底a高h上底 ＋下底 ＝ 梯形的面积×2÷高高 ＝ 梯形的面积×2÷（上底＋下底）a ＋b ＝ 2S ÷h h ＝ 2S ÷（a ＋b ）下底b高h 上底a18.圆的认识（1）圆：一条线段绕着它固定的一端在平面上旋转一周时，它的另一端就会画出一条封闭的曲线，这条封闭曲线叫做圆。
（2）圆规画圆的方法。
①把圆规的两脚分开，定好两脚之间的距离；→定半径②把带有针尖的角固定在一点上；→定圆心③把装有铅笔的脚旋转一周，就画出了一个圆。
→画圆（3）圆的认识。
①圆心：用圆规画圆时，针尖所在的点叫圆心。
用字母O表示。
→决定圆的位置②半径：连接圆心和圆上任意一点的线段叫半径。
用字母r表示。
③直径：通过圆心，并且两端都在圆上的线段叫做直径。
用字母d表示。
半径（直径）越长，圆越大；半径（直径）越短，圆越小。
④等圆：半径相等的两个圆叫做等圆。
等圆经过平移可以完全重合。
⑤同心圆：圆心重合，半径不相等的两个圆叫做同心圆。
⑥在同圆或等圆中：2dr=或2d r=半径扩大到原来的几倍，直径也扩大到原来的几倍；半径缩小到原来的几分之一，直径也缩小到原来的几分之一。
⑦圆是轴对称图形，直径所在的直线都是圆的对称轴，圆有无数条对称轴。
19.圆的周长圆的周长。
（1）圆的周长：围成圆的曲线的长是圆的周长。
（2）测量方法：滚动法、绕绳法、直接测量法。
（3）圆周率是任意一个圆的周长和它直径的比值。
这个比值是一个固定数，用π表示。
决定圆的大小等圆同心圆它是一个无限不循环小数，π=3.1415926535……通常取π≈3.14。
（4）圆的周长圆周率直径圆的周长=圆周率直径圆的周长⨯=圆周率直径圆的周长⨯=半径×2 拓展：圆的半径或直径扩大到原来的几倍，它的周长也扩大到原来的几倍。
圆的半径或直径缩小到原来的几分之一，它的周长也缩小到原来的几分之一。
② 111222r d C r d C ==③ C 圆周长的一半12r d ππ==；C 半圆=C 圆周长的一半+直径122r r d d ππ=+=+20.圆的面积公式推导 （1）圆的面积定义：圆所占平面的大小叫做圆的面积。
圆的面积的大小与半径（直径）的长短有关。
（2）圆的面积公式：把圆等分成若干份，用这些接近于等腰三角形的小图形拼成学过的图形来进行推导。
3.14圆周率（π）直径圆的周长≈=⋯⋯=1415926535.3无限不循环小数，π圆周率半径圆的周长⨯⨯=2C dπ=2C rπ=发现：把圆平均分成的份数越多，每一份就会越小，拼成的图形就会越接近于一个长方形。
圆的面积＝长方形的面积＝长×宽＝2C×r＝rπ×r＝2 r π梯形的（上底+下底）→圆的三角形的底→圆的梯形的高→圆的三角形的高→圆的21.圆的半径、直径、周长、面积之间的关系。
①圆的半径扩大到原来的a倍，则它的直径扩大到原来的a倍，它的周长扩大到原来的a倍，它的面积扩大到原来的a2倍。
例如：圆的半径扩大到原来的3倍，则它的直径扩大到原来的（）倍，周长扩大到原来的（）倍，面积扩大到原来的（）倍。
②圆的半径缩小到原来的1a，则它的直径缩小到原来的1a，它的周长缩小到原来的1a，长方形的宽近似于圆的半径长方形宽长长方形的长近似于圆的周长的一半2S rπ=2()2dSπ=2()2CSππ=它的面积缩小到原来的2211()a a=。
例如：圆的半径缩小到原来的13，则它的直径缩小到原来的（ ），周长缩小到原来的（ ），面积缩小到原来的（ ）。
③ 111222C r d C r d == 2222111112222222()()S r r d d S r r d d ====22.圆环的面积圆环（环形）：两个半径不相等的同心圆之间的部分叫做圆环，也叫做环形。
外圆：圆环中较大的圆。
外圆的半径用字母“R ”表示。
内圆：圆环中较小的圆。
内圆的半径用字母“r ”表示。
环宽：两个圆之间的宽度。
环宽＝外圆半径－内圆半径，用字母“L ”表示，即L ＝R －r 。
