11.3 旋转对称图形和中心对称图形

初二数学讲义第三讲 旋转对称图形与中心对称图形一、主要知识点1．把—个图形绕旋转中心旋转一定(小于周角)角度后，所得图形能够与自身重合，这种图形称为旋转对称图形。

2．中心对称图形是绕某一中心点旋转180°后能与自身重合的旋转对称图形，这个中心点叫做对称中心；3．中心对称图形是旋转对称图形的特例。

4．中心对称的特征：如果两个图形成中心对称，那么对称中心在对应点的连线上且平分这条线段．两个图形的对应角相等，对应线段平行且相等，两个图形的形状和大小都一样。

5．中心对称与中心对称图形：中心对称与中心对称图形是两个不同的概念，它们既有区别又有联系。

区别：(1)中心对称是指两个图形的关系，中心对称图形是指一个具有某种性质的图形。

(2)成中心对称的两个图形的对称点分别在两个图形上，中心对称图形的对称点在一个图形上。

联系：若把中心对称图形的两部分看成两个图形，则它们成中心对称，若把中心对称的两个图形看成—个整体，则成为中心对称图形。

6．常见的中心对称图形有：①线段；②相交直线；③平行四边形；④矩形；⑤菱形；⑥正方形；⑦圆。

既是轴对称图形，又是中心对称图形的有：①线段；②相交直线；④矩形；⑤菱形；⑥正方形；⑦圆。

二、例题与练习例1．下列旋转对称图形中绕哪一个点旋转多少度与自身重合？答：例2．如图所示，该图按顺时针绕旋转中心旋转，可与自身重合的度数是 （ ） （A ）60°； （B ）180°； （C ）120°； （D ）320°。

答：（1）（3） （4） （5）例3．如图，△ABC 为等边三角形，D 为△ABC 内一点，△ABD 经过旋转后到达△ACE 的位置。

（1）旋转中心是点 ；（2）旋转角度是 ；（3）△ADE 是 三角形。

例4、如图，已知△ABC 和点O ，画出△A ’B ’C ’，使△A ’B ’C ’和△ABC 关于点O 成中心对称。

解：（1）连结 并延长 到 ，使 = ，于是得到点 的对称点 ；（2）同样画出点 和点 的对称点 和 ； （3）顺次连结 、 、 。

旋转对称知识点总结旋转对称的基本概念旋转对称是指物体围绕一个中心点旋转一定角度后，仍然能够保持原来的形状。

在二维空间中，旋转对称主要涉及到平面图形的旋转对称。

而在三维空间中，旋转对称则涉及到立体物体的旋转对称。

在平面几何中，对于一个平面图形，如果把它围绕一个点旋转某个角度后，仍然能够和原来的图形完全重合，那么我们就称这个图形具有旋转对称性。

旋转对称的性质和相关定理旋转对称具有一些独特的性质，以及一些重要的定理。

下面将对旋转对称的性质和相关定理进行详细的总结。

1. 旋转对称的中心：对于一个具有旋转对称性的图形，其旋转对称的中心就是围绕哪个点进行旋转后能够保持图形不变。

在平面几何中，如果一个图形具有旋转对称性，那么它的旋转对称中心是唯一的，并且通常位于图形的中心位置。

2. 旋转对称的角度：对于一个具有旋转对称性的图形，其旋转对称的角度就是围绕旋转对称中心进行旋转的角度。

一般来说，旋转对称的角度通常是以360度为周期的。

3. 旋转对称图形的周期性：具有旋转对称性的图形通常具有周期性。

也就是说，只要围绕旋转对称中心旋转一定的角度，就能够得到一个新的重合图形。

这个角度通常就是旋转对称图形的周期。

4. 旋转对称的定理：在平面几何中，有一些重要的旋转对称定理，例如：旋转对称定理、旋转对称的逆定理、旋转对称的合成定理等。

这些定理为我们理解和运用旋转对称提供了重要的理论支撑。

旋转对称的应用旋转对称不仅是数学和几何中的一种重要性质，同时也有着广泛的应用。

下面将对旋转对称的应用进行总结。

1. 旋转对称的图案设计：在设计艺术和工艺品中，常常会使用旋转对称性来设计图案和纹样。

旋转对称的图案通常具有优美的几何形状和艺术效果。

2. 旋转对称的雕塑和建筑：在雕塑和建筑中，也常常会运用旋转对称性来设计和构造物体的形状。

旋转对称的雕塑和建筑作品通常具有对称美感和动感。

3. 旋转对称的数学模型：在数学建模和科学研究中，旋转对称也有着重要的应用。

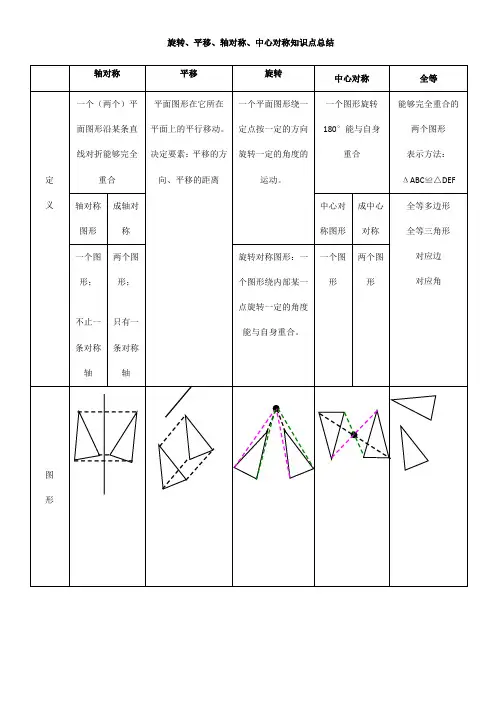
旋转、平移、轴对称、中心对称知识点总结对应点间的连线平行且相等（或在同一条直线上）对应边平行且相等（或在同一条直线上），对应角相等，图形的形状和大小不改变。

图形上每一点都绕同一点按相同的方向和角度旋转对应点到旋转中心的距离相等对应边相等，对应角相等，图形的性状大小不改变旋转180°能否与自身重合对应点间的连线是否经过同一点，并被这一点平分找对称轴：找一组对应点连线，做其垂直平分线。

找两组对应点连线，过两条中点的直线找对称中心：找一组对应点连线找其中点两组对应点连线的交点找关键点过每个关键点做对称轴的垂线截取与之相等的距离，标出对应找关键点过每个关键点做平移方向的平行线截取与之相等的距离，标出对应点找关键点连接关键点与旋转中心，将这条线段按方向和角度旋转，标出对应点找关键点连接关键点与对称中心，延长并截取相等的长度，标出对应点点连接对应点。

连接对应点。

连接对应点。

连接对应点。

线段是轴对称图形，对称轴是它的垂直平分线。

角是轴对称图形，对称轴是它的角平分线。

垂直平分线的性质：垂直平分线上任意一点到线段两端的距离相等。

④角平分线的性质：角平分线上任意一点到叫两边的距离相等。

⑤对称轴垂直平分对称点间的连线。

多次平移相当于一次平移两条对称轴平行时，两次轴对称相当于一次平移线段旋转90°后与原来的位置垂直两条对称轴相交时，两次轴对称相当于一次旋转。

中心对称一定是旋转对称，旋转对称不一定是中心对称。

任何通过中心对称图形的对称中心的直线都将这个图形分成面积相等的两部分。

两条对称轴互相垂直时，两次轴对称相当于一次中心对称一个图形经过轴对称、平移或选转等变换得到的新图形一定与原图形全等两个全等的图形总能经过轴对称、平移或旋转等变换后重合。

11.3旋转对称图形与中心对称图形班级学号姓名知识点归纳：（1）在平面内，把一个图形绕着______________后,与___________________图形重合,这种图形叫做_______________________.这个定点叫做_____________. 旋转的角度叫做_______________________.(旋转角______________________). （2）如果把一个图形绕着____________________后,与___________________图形重合,这种图形叫做__________________________.这个点叫做___________. 即:中心对称图形是特殊的旋转对称图形,旋转角是_________度的旋转对称图形是中心对称图形.注意:旋转对称图形与中心对称图形都是指一个图形内部因素之间的关系.预习下列图形旋转一定角度后能与自身重合吗?分别指出相应的旋转角度是多少?旋转度数:______________________________________________________旋转度数:______________________________________________________旋转度数:______________________________________________________旋转度数:______________________________________________________上述图形中是中心对称图形的请打 “√ ”号练习1、观察下列图形，其中不是旋转对称图形的有（ ）(1) (2)(3)C(4)X2、如下图，它们绕哪一个点至少旋转多少度能与自身重合？（右图考虑颜色）3、请尝试设计一个至少旋转720后能与自身重合的图形。

练习1、下列图形不是旋转图形的是（）A、线段B、等腰三角形C、等边三角形D、圆2、四边形ABCD是旋转对称图形，点_______是旋转中心，•旋转了_____度后能与自身重合，则AD=_____，DC=_____，AO=_____，BO=_____．3、三叶电风扇叶片是一个旋转对称图形，其最小旋转角度的度数是（）A.60B.120C.180D.2404、下列图不是旋转对称图形的是_______。

第一讲图形的旋转、中心对称与中心对称图形1.1 图形的旋转一、知识点1．旋转的概念：在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。

这个定点叫做旋转中心，转动的角度叫做旋转角。

2．旋转的性质：（1）旋转前后图形的大小和形状没有改变，旋转前后的图形全等；（2）对应点到旋转中心的距离相等；（3）对应线段的长度、对应角的大小相等3．旋转作图：旋转三要素：旋转中心、旋转方向、旋转角。

二、典型例题例1．下列各组图中，图形甲变成图形乙，既能用平移，又能用旋转的是（）例2．如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过一次逆时针旋转后到△ACP的位置,则旋转中心是______,旋转角等于______△ADP是______三角形。

例3．如图，将△ ABC 绕点 C 顺时针方向旋转 40 °得△ A ′ B ′ C ，若 AC ⊥ A ′ B ′，则∠ BAC等于（）A. 50 °B. 60 °C. 70 °D. 80 °例4．△ABC在方格中的位置如图所示．（1）请在方格纸上建立平面直角坐标系,使得A 、B 两点的坐标分别为A （2,﹣1）、B （1,﹣4）．并求出C 点的坐标。

（2）作出△ABC 关于横轴对称的△A 1 B 1 C 1 ,再作出△ABC 以坐标原点为旋转中心、旋转180°后△A 2 B 2 C 2 ,并写出C 1 ,C 2 两点的坐标。

例5．如图,在直角坐标系中,已知点A(−3,0),B(0,4)，对△OAB 连续作旋转变换，依次得到三角形①，②，③， ④…，则三角形⑩的直角顶点的坐标为_________________．三、课堂练习1．下列现象属于旋转的有（ ）个．（1）方向盘的转动；（2）钟摆的运动；（3）荡秋千运动；（4）传送带的移动． A.1 B.2 C.3 D.42．如图，这是一个正面为黑，反面为白的未拼完的拼木盘，给出如下四块正面为黑、反面为白的拼木，现欲拼满拼木盘并使其颜色一致，请问应选择的拼木是（ ）A ．B ．C ．D ．3．一个图形无论经过平移还是旋转，有以下说法（ ）①对应线段平行；②对应线段相等；③对应角相等；④图形的形状和大小都没有发生变化． A.①②③ B.①②④ C.①③④ D.②③④4．如图，该图形绕点O 按下列角度旋转后，不能与其自身重合的是（ ） A.72° B.108° C.144° D.216°5．如图,将正方形图案绕中心O 旋转180°后,得到的图案是( )第（4）题图6．正方形绕中心至少旋转________度后能与自身重合．7．如图，在等边三角形ABC 中，AB=6，D 是BC 上一点，且BC=3BD ，△ABD 绕点A 旋转后得到△ACE ，则CE 的长度为________．8．如图所示，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形（图中的阴影部分）绕中心O 至少经过________次旋转而得到，每一次旋转_______度．9．如图，把Rt △ABC 绕点A 逆时针旋转40°，得到Rt △AB ′C ′，点C ′恰好落在边AB上，连接BB ′，则∠BB ′C ′=________度．10．如图，在△ABC 中，∠CAB=75°，在同一平面内，将△ABC 绕点A 旋转到△AB ′C ′的位置，使得CC ′∥AB ，则∠BAB ′=________. 四、课堂小结五、课后作业1．如图,△ABC 以点A 旋转中心,按逆时针方向旋转60∘得到△AB ′C ′,则△ABB ′是（ ）三角形。

§11.3旋转对称图形与中心对称图形
教学目标：
1．在探究旋转对称图形和中心对称图形的概念过程中，感受从一般到特殊的研究问题方法．2．理解旋转对称图形和中心对称图形的区别和联系．
3．感受旋转对称图形和中心对称图形在生活中的应用，体会数学的价值．
教学重点和难点：
探究旋转对称图形和中心对称图形的概念形成过程．
二、新知探索
师：我们把具有这个特征的图形叫做旋
转对称图形．
问：你能说出什么是旋转对称图形吗？
师生共同总结：
归纳：请比较旋转对称图形和中心对称图形的异同．
练习：课本P102第2、3题
三、拓展应用
1．在一次游戏当中，小明将下面图(1)的四张扑克牌中的一张旋转180o后，得到图(2)，小亮看完，很快知道小明旋转了哪一张扑克，你知道为什么吗？
图(1)
(2)
．如图是由两个等边三角形拼成的图形．
这个图形是不是旋转对称图形
是中心对称图形?若是指出对称中心．若三角形ACD旋转后能与三角形
重合．那么图形所在的平面上可以作为
哪些
称图形，
中
形？
图形（2）是旋转对称图形，
也是中心对称图形．它的旋
转中心是对角线的交点O
图形（3）是旋转对称图形，
也是中心对称图形．它的旋
转中心是对角线的交点O
图形（4）是旋转对称图形，
但不是中心对称图形．它的
解答
答：这个图形是旋转对称图
形，最小的旋转角是120︒．旋转对称图形和旋转角
3．如图，如果四边形CDEF
ABCD重合，那么图
2．画一个旋转角是的旋转对称图形．。

DB1、旋转的定义：把一个平面图形绕平面内 转动 就叫做图形的旋转。

旋转的三要素：旋转 ；旋转 ；旋转旋转的基本性质：（1）对应点到 的距离相等。

（2）每一组对应点与旋转中心所连线段的夹角相等都等于 （3）旋转前后的两个图形是 2、 旋转作图基本步骤： ○1明确旋转三要素：______________、______________、_______________○2找出原图形中的各顶点在新图形中的对应点的位置。

○3按原图形中各顶点的排列规律，将这些对应点连成一个新的图形。

3、中心对称：把一个图形绕着某一个点旋转︒180，如果它能够与 重合， 那么就说 关于这个点对称或中心对称。

这个点叫做对称中心。

性质：（1）中心对称的两个图形，对称点所连线段都经过 ，而且被对称中心 。

（2）中心对称的两个图形是 图形。

4、中心对称图形：把一个图形绕着某一个点旋转︒180，如果旋转后的图形能够与 完全重合，那么这个图形叫做中心对称图形。

中心对称、中心对称图形是两个不同的概念，它们既有区别又有联系。

区别：中心对称是针对 图形而言的，而中心对称图形指是 图形。

联系：把中心对称的两个图形看成一个“整体”，则成为 。

把中心对称图形的两个部分看成“两个图形”，则它们 。

5、 利用尺规作关于中心对称的图形：○1明确对称中心的位置○2利用“对应点的连线被对称中心平分”的特性，分别找出原图形中各个关键点的对应点○3按原图形中各点的次序，将各对应点连接起来 6、点（x ，y ）关于x 轴对称后是（ , ） 点（ , ）关于y 轴对称后是（-x ，y ） 点（x ，y ）关于原点对称后是（ ， ）1如图1，P 是正△ABC 内的一点，若将△PBC 绕点B 旋转到△P BA ，则∠PBP ’的度数是 （ ）A ．45°B ．60°C ．90°D ．120°2、 如图，∠AOB ＝90°，∠B ＝30°，△A ’OB ’可以看作是由△AOB 绕点O 顺时针旋转α角度得到的，若点A ’在AB 上，则旋转角α的大小可以是 （ ） A ．30°B ．45°C ．60°D ．90°3、如图所示，在方格纸上建立的平面直角坐标系中，将△ABO 绕点O 按顺时针方向旋转90°，得A B O ''△ ，则点A '的坐标为 （ ）．A ．（3，1）B ．（3，2）C ．（2，3）D ．（1，3） 4、下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A ．等腰梯形B ．平行四边形C ．正三角形D ．矩形5、单词NAME 的四个字母中，是中心对称图形的是 （ ） A ．N B ．A Ｃ．M D ．E6、某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种方案，你认为符合条件的是（ ） x y 12 43 0 -1 -2 -3 1 2 3 AB7、下列图形中，既是轴对称图形，又是中心对称图形的是 ( )8、已知如图1所示的四张牌，若将其中一张牌旋转180O 后得到图2，则旋转的牌是 （ ）9、下列各组图中，图形甲变成图形乙，既能用平移，又能用旋转的是（ ）例题1、如图，根据要求画图．（1）把△ABC 向右平移5个方格，画出平移的图形．（2）以点B为旋转中心，把△ABC 顺时针方向旋转90度，画出旋转后的图形．分析：（1）找出平移后的点A 、B 、C 的对应点的位置，然后顺次连接即可； （2）找出旋转变换后的点A 、C 的对应点的位置，然后顺次连接即可． 解：如图所示，（1）△A′B′C′即为平移后的图形； （2）△A″BC″即为旋转后的图形．图1图2A ．B ．C ．D ．甲乙甲乙A ．B ．C ．D．甲乙甲乙例题2、如图，已知P是正方形ABCD内一点，PA=1，PB=2，PC=3，以点B为旋转中心，将△ABP沿顺时针方向旋转，使点A与点C重合，这时P点旋转到G点．（1）请画出旋转后的图形，并说明此时△ABP以点B为旋转中心旋转了多少度？（2）求出PG的长度；（3）请你猜想△PGC的形状，并说明理由．例题1、如图，在画有方格图的平面直角坐标系中，△ABC的三个顶点均在格点上．（1）填空：△ABC是________三角形，它的面积等于_______平方单位；（2）将△ACB绕点B顺时针方向旋转90°，在方格图中用直尺画出旋转后对应的△A′C′B，则A′点的坐标是（，），C′点的坐标是（，）．【变式练习】1、如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别为A （-2，-1）、B （-1，1）、C （0，-2）．（1）点B 关于坐标原点O 对称的点的坐标为_______ （2）将△ABC 绕点C 顺时针旋转90°，画出旋转后得到的△A 1B 1C ； （3）求过点B 1的反比例函数的解析式．2、如图所示，每个小方格都是边长为1的正方形，以O 点为坐标原点建立平面直角坐标系.(1)画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1，并写出点B 1的坐标是 . (2)画出四边形OABC 绕点O 顺时针方向旋转90°后得到的四边形OA 2B 2C 23、如图，在由边长为1的小正方形组成的方格纸中，有两个全等的三角形，即111A B C △和222A B C △．（1）请你指出在方格纸内如何运用平移、旋转变换，将111A B C △重合到222A B C △上； （2）在方格纸中将111A B C △经过怎样的变换后可以与222A B C △成中心对称图形？画出变换后的三角形并标出对称中心．2C2B2A例题2、如图，在Rt △ABC 中，∠ABC=90°，点D 在BC 的延长线上，且BD=AB ，过点B 作BE ⊥AC ，与BD 的垂线DE 交于点E ． （1）求证：△ABC ≌△BDE ；（2）△BDE 可由△ABC 旋转得到，利用尺规作出旋转中心O （保留作图痕迹，不写作法）．【变式练习】1、如图，已知△ABC 和△A″B″C″及点O ． ⑴画出△ABC 关于点O 对称的△A′B′C ′；⑵若△A″B″C″与△A′B′C′关于点O ′对称，请确定点O′的位置； ⑶探究线段OO′与线段CC″之间的关系，并说明理由．2、如图，已知AD 是△ABC 的中线，画出以点D 为对称中心，与△ABC 成中心对称的三角形．C″B″A ″图 10CBA例题3、△ABC是等边三角形，D是BC上一点，△ABD经旋转后到达△ACE的位置．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若M是AB的中点，那么经过上述旋转后，点M转到了什么位置？【变式练习】1、如图，四边形ABCD的∠BAD=∠C=90º,AB=AD,AE⊥BC于E,BEA∆∆旋转后能与DFA 重合。