浦东中考一对一补习 初中数学 1对1 概率 压轴题

2017上海浦东新区智康教育一对一辅导初中奥数有吗？智康简介智康1对1，帮孩子持续提升!智康内涵:积极快乐智慧健康智康理念:延续家庭的关怀，见证孩子成长每一步，帮孩子持续提升。

"智康1对1"是教育旗下专注1对1的品牌，依托强大的品牌优势:于2010年10月20日在美国纽约证券交易上市，成功融资1.2亿美元。

据百度搜索数据研究中心发布的"中小学课外辅导品牌"专题报告显示，教育以17.3%的关注度领跑排行榜，成为中国网民搜索关注度第一的中小学教育培训机构品牌。

在新浪网的2009中国教育年度盛典中，教育被评为"2009年度家长信赖课外教育机构"。

智康1对1自2007年创建以来，在北京开设18个校区、上海开设分校区4个，广州、深圳、天津分校相继开业。

南京，杭州，武汉，西安，成都等十个城市分校。

精准的含义是精确、精密、可衡量的。

精准学习有三个层面的含义:☆第一、发现和建立精准的学习目标。

☆第二、匹配精准的学习资源，包括施教者、学习手段和材料。

☆第三、建立和实施精准的考核体系。

智康1对1名师团队选拔严格，仅为4%，80%来自国内一流名校，90%以上为专职教师。

我们特别采用高标准化的1对1模式，打造适合学员自身的个性化教学方案，为每位学员量身定制教学讲义，重点透析，考点破解，使每个学员都能在充分认识自身学习问题基础上，快速提高成绩。

定期提供学习讲座、升学资讯、报考指导与心理咨询，及时为学员及家长解读新的教育信息与心理问题，帮助学员考试、升学以及拥有更好的生活态度一臂之力。

率先推出的讲义教研团队，在同行业内可谓。

智康1对1教育网站以科学系统的管理模式为依托，提供在线答疑，随时解除学生及家长的疑虑，增强学员的学习效果。

2010年，智康1对1再次刷新辉煌战绩:高考总分600分以上71人，18名学员考入清华北大，中考500分以上442人，15名学员单科成绩满分，小升初95%升入重点，迎春杯获奖率95%，走美杯获奖率97%……2010年8月，智康搜课系统上线，中小学一对一辅导行业创新――"名师网上选快速提高分"，让家长自由挑选老师，师资更透明、效果更有保障。

初三数学期末测试卷（时间100分钟）一、选择题：（本大题共6题）1.下列图形，一定相似的是（）A.两个直角三角形B.两个等腰三角形C.两个等边三角形D.两个菱形2.己知抛物线()2213y x =-+，那么它的顶点坐标是（）A.(1,3)- B.(1,3)C.(2,1)D.(2,3)3.在Rt ABC 中，90B Ð=°，如果A α∠=，BC a =，那么AC 的长是（）A.tan a αB.cot a αC.cos aa D.sin a a4.小杰在一个高为h 的建筑物顶端，测得一根高出此建筑物的旗杆顶端的仰角为30︒，旗杆与地面接触点的俯角为60︒，那么该旗杆的高度是（）A.23h B.45h C.43h D.54h 5.已知二次函数2y ax bx c =++的图像如图所示，那么点(,)P a b 在（）A.第一象限B.第二象限C.第三象限D.第四象限6.如图，DF AC ∥，DE BC ∥，下列各式中正确的是（）A.BD ABCE AC= B.AD BFBD FC= C.AD CEDE BD= D.AE BFCE CF=二、填空题：（本大题共12题）7.如果23a b =，那么b aa b -=+__________．8.如果两个相似三角形的面积比是4：9，那么它们对应高的比是________9.已知点P 是线段MN 的黄金分割点，>MP PN ，如果8MN =，那么PM 的长是_____．10.如果在比例尺为1：1000000的地图上，A 、B 两地的图上距离是3.4厘米，那么A 、B 两地的实际距离是_____千米．11.两个相似三角形的对应边上中线之比为2:3，周长之和为20cm ，则较小的三角形的周长为__________．12.将抛物线241y x x =+-向右平移3个单位后，所得抛物线的表达式是_______________．13.如图，已知AD ∥BE ∥CF ．如果 4.8AB =， 3.6DE =， 1.2EF =，那么AC 的长是_____．14.已知一条斜坡的长度是10米，高度是6米，那么坡角的角度约为_______．（备用数据tan31°=cot59°≈0.6，sin37°=cos 53°≈0.6)15.在Rt ABC △中，90A ∠=︒，已知1AB =，2AC =，AD 是BAC ∠的平分线，那么AD 的长是_____．16.如图，点E 、F 分别在边长为1的正方形ABCD 的边AB 、AD 上，2BE AE =、2AF FD =，正方形A B C D ''''的四边分别经过正方形ABCD 的四个顶点，已知A D EF ''∥，那么正方形A B C D ''''的边长是_____．17.在ABC 中，2A B ∠=∠，如果4AC =，5AB =，那么BC 的长是_____．18.如图，正方形ABCD 的边长为5，点E 是边CD 上的一点，将正方形ABCD 沿直线AE 翻折后，点D 的对应点是点D ¢，联结CD '交正方形ABCD 的边AD 于点F ，如果AF CE =，那么AF 的长是______________．三、解答题：（本大题共7题）19.计算：cot 454sin 452tan 30cos30cos 60︒︒-︒︒+︒20.如图，在ABC 中，BE 平分ABC ∠，DE BC ∥，3AD =，2DE =．（1）求:AE AC 的值；（2）设AB a =，BC b = 求向量BE （用向量a b 、表示）．21.如图，在Rt EAC 中，90EAC ∠︒＝，45E ∠︒＝，点B 在边EC 上，BD AC ⊥，垂足为D ，点F 在BD 延长线上，5FAC EAB BF ∠∠＝，＝，tan AFB ∠＝34．求：（1）AD 的长；（2）cot DCF ∠的值．22.某地一段长为50米的混泥土堤坝，堤坝的横断面ABCD 是等腰梯形（如图所示），坝顶AD 宽为8米，坝高为4米，斜坡AB 的坡度为1:1.5．（1）求横断面ABCD 的面积；（2）为了提高堤坝的防洪能力，现需将原堤坝按原堤坝要求和坡度加高1米，求加高堤坝需要多少立方米的混泥土？（堤坝的体积=横断面的面积×堤坝的长度）23.如图，在ABC 中，点D 、F 分别是边BC 、AB 上的点，AD 和CF 交于点E ．（1）如果BF AB BD BC =，求证：EF CE DE AE =；（2）如果2AE BF AF DE =，求证：AD 是ABC 的中线．24.如图，在平面直角坐标系xOy 中，抛物线23y ax bx =++与x 轴的正、负半轴分别交于点B 、A ，与y 轴交于点C ，已知5AB =，tan 3CAB ∠=，:3:4OC OB =．（1）求该抛物线的表达式；（2）设该抛物线的对称轴分别与x 轴、BC 交于点E 、F ，求EF 的长；（3）在（2）的条件下，联结CE ，如果点P 在该抛物线的对称轴上，当CEP △和CEB 相似时，求点P 的坐标25.如图，在Rt ABC △中，90ABC ∠=︒，10AC =，3tan 4C =，点D 是斜边AC 上的动点，连接BD ，EF 垂直平分BD 交射线BA 于点F ，交边BC 于点E ．（1）如图，当点D 是斜边AC 上的中点时，求EF 的长；（2）连接DE ，如果DEC 和ABC 相似，求CE 的长；（3）当点F 在边BA 的延长线上，且2AF =时，求AD 的长．初三数学期末测试卷（时间100分钟）一、选择题：（本大题共6题）1.下列图形，一定相似的是（）A.两个直角三角形B.两个等腰三角形C.两个等边三角形D.两个菱形【答案】C【分析】根据相似图形的定义，结合图形，对选项一一分析，利用排除法求解．【详解】解：A .两个直角三角形，不一定有锐角相等，故不一定相似；B .两个等腰三角形顶角不一定相等，故不一定相似；C .两个等边三角形，角都是60°，故相似；D ..任意两个菱形的对应边的比相等，但对应角不一定相等，故不一定相似；故选C ．【点睛】本题考查的是相似图形的概念，掌握对应角相等，对应边的比相等的多边形，叫做相似多边形是解题的关键．2.己知抛物线()2213y x =-+，那么它的顶点坐标是（）A.(1,3)-B.(1,3)C.(2,1)D.(2,3)【答案】B【分析】根据二次函数的顶点式的特点即可得出答案．【详解】解：由抛物线的顶点式()2213y x =-+可得：该抛物线的顶点坐标为(1,3)，故选：B ．【点睛】本题主要考查抛物线的顶点式，关键是要牢记抛物线的顶点式的特点．3.在Rt ABC 中，90B Ð=°，如果A α∠=，BC a =，那么AC 的长是（）A.tan a αB.cot a αC.cos aa D.sin a a【答案】D【分析】画出图形，根据锐角三角函数的定义求出即可．【详解】如图：在Rt ABC 中，AC sin BC A =sin aα=．故选：D ．【点睛】本题考查解直角三角形，解题的关键是熟练掌握直角三角形边角之间的关系．4.小杰在一个高为h 的建筑物顶端，测得一根高出此建筑物的旗杆顶端的仰角为30︒，旗杆与地面接触点的俯角为60︒，那么该旗杆的高度是（）A.23h B.45h C.43h D.54h 【答案】C【分析】过A 作AE BC ⊥于E ，在Rt ACE △中，已知了CE 的长，可利用俯角CAE ∠的正切函数求出AE 的值；进而在Rt ABE △中，利用仰角BAE ∠的正切函数求出BE 的长；从而可得答案．【详解】解：如图，过A 作AE BC ⊥于E ，则四边形ADCE 是矩形，CE AD h ==．∵在Rt ACE △中，CE h =，60CAE ∠=︒，∴3tan 603CE AE h ==︒，∵在Rt ABE △中，30BAE ∠=︒，∴331tan 30333BE AE h h =︒=⨯=，∴1433BC BE CE h h h =+=+=．即旗杆的高度为43h ．故选C ．【点睛】本题考查了解直角三角形的应用--仰角俯角问题，首先构造直角三角形，再运用三角函数的定义解题，是中考常见题型，解题的关键是作出高线构造直角三角形．5.已知二次函数2y ax bx c =++的图像如图所示，那么点(,)P a b 在（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【分析】根据对称轴的位置、开口方向、即可判断出a 、b 符号，进而求出(,)P a b 的位置．【详解】解：∵抛物线开口向下，∴a<0，又∵对称轴在y 轴右侧，∴02ba->，∴>0b ，∴(,)P a b 在第二象限故选：B【点睛】本题考查的是二次函数2y ax bx c =++系数符号的确定．根据对称轴的位置、开口方向、与y 轴的交点的位置判断出a 、b 、c 的符号是解题的关键．6.如图，DF AC ∥，DE BC ∥，下列各式中正确的是（）A.BD ABCE AC= B.AD BFBD FC= C.AD CEDE BD= D.AE BFCE CF=【答案】A【分析】由平行线分线段成比例可判断A ，B ，D ，证明四边形DFCE 是平行四边形，ADE DBF ∽，可得AD BDDE BF =，再利用等线段代换也不能证明AD CE DE BD=，可判断C ，从而可得答案．【详解】解：∵DE BC ∥，∴BD CEAB AC=，∴BD ABCE AC=，故A 符合题意；∵DF AC ∥，∴AD CFBD BF=，故B 不符合题意；∵DF AC ∥，DE BC ∥，∴四边形DFCE 是平行四边形，BDF A ∠=∠，ADE B ∠=∠，∴CE DF =，DE CF =，ADE DBF ∽，∴AD BDDE BF=，故C 不符合题意；∵DE BC ∥，DF AC ∥∴AE ADEC BD =，BF BD CF AD=，∴AE BFCE CF≠，故D 不符合题意；故选A ．【点睛】本题考查的是平行四边形的判定与性质，平行线分线段成比例，相似三角形的判定与性质，熟练的利用平行线与相似三角形的性质证明成比例的线段是解本题的关键．二、填空题：（本大题共12题）7.如果23a b =，那么b aa b -=+__________．【答案】15【分析】设a=2k ，得到b=3k ，代入b aa b-+化简即可求解．【详解】解：设a=2k ，∵23a b =，∴b=3k ，∴3213255b a k k k a b k k k --===++．故答案为：15【点睛】本题主要考查了比例化简求值，理解比例的意义，用含k 的式子分别表示a 、b 是解题关键．8.如果两个相似三角形的面积比是4：9，那么它们对应高的比是________【答案】2：3##23【详解】解：∵两个相似三角形的面积比是4：9，两个相似三角形的相似比是2：3，∴它们对应高的比是2：3．故答案为：2：3．9.已知点P 是线段MN 的黄金分割点，>MP PN ，如果8MN =，那么PM 的长是_____．【答案】4##4-+【分析】根据黄金分割点的概念列式求解即可．【详解】解：∵点P 是线段MN 的黄金分割点，>MP PN ，8MN =，∴51518422PM MN --==⨯=-，故答案为：4．【点睛】此题考查了黄金分割点的概念，解题的关键是熟练掌握黄金分割点的概念．把一条线段分成两部分，使其叫做黄金比．10.如果在比例尺为1：1000000的地图上，A 、B 两地的图上距离是3.4厘米，那么A 、B 两地的实际距离是_____千米．【答案】34【分析】根据地图上的距离与实际距离的比等于比例尺，即可求解．【详解】解：设A 、B 两地的实际距离为cm x 则：3.4:1:1000000x =解得3400000cm 34x ==千米A 、B 两地的实际距离为34千米故答案为：34【点睛】本题考查了比例线段，熟练掌握比例尺=图上距离：实际距离是解题的关键．11.两个相似三角形的对应边上中线之比为2:3，周长之和为20cm ，则较小的三角形的周长为__________．【答案】8cm【分析】根据相似三角形的性质，相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比来解答．【详解】解：因为该相似比为2：3，而周长比也等于相似比，则较小的三角形周长为20×25=8cm ，故答案为：8cm【点睛】本题考查对相似三角形性质的理解：①相似三角形周长的比等于相似比；②相似三角形面积的比等于相似比的平方；③相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．12.将抛物线241y x x =+-向右平移3个单位后，所得抛物线的表达式是_______________．【答案】224y x x =--【分析】利用二次函数图像的平移规律：左加右减，上加下减，从而可得答案．【详解】解：由题意可知，将抛物线向右平移3个单位后得：()()23435y x x =-+-+2694121x x x -++--=224x x =--，故答案为224y x x =--．【点睛】本题主要考查二次函数图像的平移，掌握函数的平移规律是解题的关键．13.如图，已知AD ∥BE ∥CF ．如果 4.8AB =， 3.6DE =， 1.2EF =，那么AC 的长是_____．【答案】6.4##325【分析】根据三条平行线截两条直线，所得对应线段成比例，列出比例式解答即可．【详解】解：∵AD BE CF ∥∥，∴AB DEBC EF =，∵AB ＝4.8，DE ＝3.6，EF ＝1.2，∴4.8 3.61.2BC =，解得 1.6BC =，∴ 4.8 1.6 6.4AC AB BC =+=+=．故答案为：6.4．【点睛】本题考查了平行线分线段成比例定理，解题的关键是掌握定理并灵活运用列出正确的比例式．14.已知一条斜坡的长度是10米，高度是6米，那么坡角的角度约为_______．（备用数据tan31°=cot59°≈0.6，sin37°=cos 53°≈0.6)【答案】37°．【分析】画出图形，设坡角为α，根据sinα=ABAC，可求得α的度数．【详解】由题意，作出图形，设坡角为α，∵sina=AB AC即sina=0.6∴a=37°故答案为:37°.【点睛】本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，解直角三角形.15.在Rt ABC △中，90A ∠=︒，已知1AB =，2AC =，AD 是BAC ∠的平分线，那么AD 的长是_____．【答案】223【分析】过B 作BE AB ⊥交AD 的延长线于E ，先证ABE 是等腰直角三角形，推出1BE AB ==，AE ==，再证ACD EBD ∽，推出AC ADBE DE=，代入数值即可求解．【详解】解：过B 作BE AB ⊥交AD 的延长线于E ，90BAC ∠=︒，AD 是BAC ∠的平分线，∴45BAE ∠=︒，∴ABE 是等腰直角三角形，∴1BE AB ==，∴AE ==， 90BAC ∠=︒，BE AB ⊥，∴AC BE ∥，∴BED CAD ∠=∠，又 BDE CDA ∠=∠，∴ACD EBD ∽，∴AC AD BE DE=，∴21=，∴3AD =，故答案为：3．【点睛】本题考查等腰三角形的判定，勾股定理，相似三角形的判定与性质等，解题的关键是正确添加辅助线，构造相似三角形．16.如图，点E 、F 分别在边长为1的正方形ABCD 的边AB 、AD 上，2BE AE =、2AF FD =，正方形A B C D ''''的四边分别经过正方形ABCD 的四个顶点，已知A D EF ''∥，那么正方形A B C D ''''的边长是_____．【答案】355【分析】根据边长为1的正方形ABCD 中，2BE AE =、2AF FD =，得到23BE AF ==，13AE DF ==，根据勾股定理得到3EF ==，根据A D EF ''∥，得到A AB AEF '∠=，结合90A EAF ∠=∠='︒，推出A AB AEF '∽，得到AA AB AE EF '=，求出55A A '=，同理求出：255AD '=，推出355A D ''=．【详解】解：∵2BE AE =、2AF FD =，1AB AD ==，∴23BE =，13AE =，23AF =，13=DF ，∴EF==3，∵A D EF ''∥，∴A AB AEF ∠=∠'，又∵90A EAF ∠=∠='︒，∴A AB AEF '∽，∴'A A AB AE EF=，∴A A '=1331⨯=同理可求：255AD '=，∴A D ''=355，∴正方形A B C D ''''的边长为355．故答案为：355．【点睛】本题主要考查了正方形，相似三角形，勾股定理等，解决问题的关键是熟练掌握正方形性质，相似三角形判定和性质，勾股定理解直角三角形．17.在ABC 中，2A B ∠=∠，如果4AC =，5AB =，那么BC 的长是_____．【答案】6【分析】过C 作CH AB ⊥，垂足为H ，在AB 上取点D ，连接CD ，使4CD AC ==，然后根据等腰三角形的性质和三角形外角的性质得出AH 的值，最后根据勾股定理即可求解．【详解】过C 作CH AB ⊥，垂足为H ，在AB 上取点D ，连接CD ，使4CD AC ==，∵4CD AC ==，∴2A CDA B ∠=∠=∠，∴B BCD ∠=∠，∴4BD CD ==，∴541AD AB AD =-=-=，∴10.52DH AH AD ===，∴2223154CH AC AH =-=，∵222BC BH CH =+，∴2234.5154BC =+，即6BC =，故答案为：6．【点睛】本题考查了等腰三角形的性质、三角形外角的性质和勾股定理，画出图形，合理构建辅助线是解题的关键．18.如图，正方形ABCD 的边长为5，点E 是边CD 上的一点，将正方形ABCD 沿直线AE 翻折后，点D 的对应点是点D ¢，联结CD '交正方形ABCD 的边AD 于点F ，如果AF CE =，那么AF 的长是______________．【答案】5-##5-+【分析】连接DD '，由折叠的性质及直角三角形的性质可得D DE DAE '∠=∠，再可证明ADE CDF V V ≌，则可得点D ¢是CF 的中点，设DF x =，则可得DD '，再可证明D DE DCD ''∽，由相似三角形的性质建立关于x 的方程，解方程即可求得x ，从而求得结果．【详解】解：连接DD '，如图，四边形ABCD 是正方形，AD CD ∴=，90ADC ∠=︒，90AED DAE ∴∠+∠=︒，由折叠的性质得：DE D E '=，AE DD '⊥，90D DE AED '∴∠+∠=︒，D DE DAE '∴∠=∠，AF CE = ，AD AF CD CE ∴-=-，即DF DE =，90ADE CDF ∠=∠=︒ ，AD CD =，(SAS)ADE CDF ∴△≌△，DCF DAE ∴∠=∠，D DE DCF '∴∠=∠，CD DD ''∴=，90DCF CFD ∠+∠=︒ ，90D DE D DF ''∠+∠=︒，CFD D DF '∴∠=∠，D D D F CD '''∴==，即点D ¢是CF 的中点，设DF x =，则12DD CF '=，222225CF CD DF x =+=+ ，221(25)4DD x '∴=+，DE D E '= ，CD DD ''=，D DE DCF DD E ''∴∠=∠=∠，D DE DCD ''∴∽，DD DE CD CD '∴='，CD DD ''= ，2DD CD DE '∴=⋅，即21(25)54x x +=解得：110x =-210x =+（舍去），5(105AF AD DF ∴=-=--=故答案为：5-．【点睛】本题考查了折叠的性质，正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，解一元二次方程，直角三角形的性质等知识，利用相似三角形的性质建立一元二次方程是本题的关键与难点．三、解答题：（本大题共7题）19.计算：cot 454sin 452tan 30cos30cos 60︒︒-︒︒+︒【答案】【详解】试题分析：将特殊三角函数的值代入，利用实数的混合运算计算即可.解：原式=4×22-2×33×32+112-1+21.20.如图，在ABC 中，BE 平分ABC ∠，DE BC ∥，3AD =，2DE =．（1）求:AE AC 的值；（2）设AB a = ，BC b = 求向量BE （用向量a b 、表示）．【答案】（1）35AE AC =（2）3255BE b a =- 【分析】（1）先证明DEB EBC ∠=∠，ADE ABC △△∽，结合角平分线的定义可得DBE CBE ∠=∠，证明2DB DE ==，结合相似三角形的性质可得答案；（2）先求解AC AB BC a b =+=+ ，结合（1）可得25CE AC =，可得222555EC AC a b ==+ ，再利用BE BC EC =- ，从而可得答案．【小问1详解】解：∵BE 平分ABC ∠，∴DBE CBE ∠=∠，∵DE BC ∥，∴DEB EBC ∠=∠，ADE ABC △△∽，∴DBE DEB ∠=∠，而2DE =，∴2DB DE ==，而3AD =，∴5AB AD BD =+=，∵ADE ABC △△∽，∴35AE AD AC AB ==．【小问2详解】∵AB a = ，BC b =，∴AC AB BC a b =+=+ ，∵35AE AC =，∴25CE AC =，∴222555EC AC a b ==+ ，∴22325555BE BC EC b a b b a =-=--=- ．【点睛】本题考查了平面向量、相似三角形的判定与性质，注意熟练掌握相似三角形判定的方法，难度一般．21.如图，在Rt EAC 中，90EAC ∠︒＝，45E ∠︒＝，点B 在边EC 上，BD AC ⊥，垂足为D ，点F 在BD 延长线上，5FAC EAB BF ∠∠＝，＝，tan AFB ∠＝34．求：（1）AD 的长；（2）cot DCF ∠的值．【答案】（1）125（2）916【分析】（1）由各角之间的关系得出90BAF ∠=︒，再由正切函数及勾股定理求解得出34AB AF ==，，最后利用三角形等面积法求解即可；（2）由等面积法得出95BD =，结合图形得出95DC BD ==，再由余切函数的定义求解即可．【小问1详解】解：∵90EAC ∠=︒，∴90EAB BAC ∠∠+=︒，∵FAC EAB ∠∠=，∴90FAC BAC ∠∠+=︒，∴90BAF ∠=︒，∵3tan 4AB AFB AF ∠==，令3AB x =，则4AF x =，∵222BF AB AF =+，∴()()22234BF x x =+，∴55BF x ==，∴1x =，∴3344AB x AF x ====，，∵··2ABF BF AD AB AF S=＝，∴53412AD =⨯=，∴125AD =；【小问2详解】在Rt ABF 中，AD BF ⊥，∴2·AB BD BF =，∴95BD =，∴95BD =，∴165DF BF BD =-=，∵9045EAC E ∠∠=︒=︒，，∴45BCD ∠=︒，∴45DBC ∠=︒，∴95DC BD ==，∴9cot 16DC DCF DF ∠==．【点睛】本题主要考查三角函数解三角形及勾股定理解三角形，理解题意，找准各角之间的关系是解题关键．22.某地一段长为50米的混泥土堤坝，堤坝的横断面ABCD 是等腰梯形（如图所示），坝顶AD 宽为8米，坝高为4米，斜坡AB 的坡度为1:1.5．（1）求横断面ABCD 的面积；（2）为了提高堤坝的防洪能力，现需将原堤坝按原堤坝要求和坡度加高1米，求加高堤坝需要多少立方米的混泥土？（堤坝的体积=横断面的面积×堤坝的长度）【答案】（1）横断面ABCD 的面积为256m ．（2）加高堤坝需要的混泥土为：3325m ．【分析】（1）如图，过A 作AE BC ⊥于E ，过D 作DF BC ⊥于F ，再证明8AD EF ==，6BE CF ==，再利用梯形面积公式进行计算即可；（2）先画出图形，如图，过G 作GK AD ⊥于K ，过H 作HL AD ⊥于L ，结合题意可得：1KG HL ==，斜坡AG 的坡度是1:1.5，四边形GADH ，四边形GBCH 都是等腰梯形，同理可得：AK DL =，GH KL =，再求解1.5AK DL ==，5KL GH ==，可得四边形GADH 的面积为：213m 2，从而可得答案．【小问1详解】解：如图，过A 作AE BC ⊥于E ，过D 作DF BC ⊥于F ，由等腰梯形是轴对称图形可得：4AE DF==，BE CF =，四边形AEFD 是矩形，∴8AD EF ==，∵斜坡AB 的坡度为1:1.5，∴11.5AE BE =，∴4 1.56BE CF =⨯==，∴20BC BE EF CF =++=，∴横断面ABCD 的面积为()()21820456m 2+⨯=．【小问2详解】如图，过G 作GK AD ⊥于K ，过H 作HL AD ⊥于L ，结合题意可得：1KG HL ==，斜坡AG 的坡度是1:1.5，四边形GADH ，四边形GBCH 都是等腰梯形，同理可得：AK DL =，GH KL =，由斜坡AG 的坡度是1:1.5，∴11.5GK AK =，∴ 1.5AK DL ==，∴8 1.5 1.55KL AD AK DL GH =--=--==，∴四边形GADH 的面积为：()()21135+81m 22⨯=，∴加高堤坝需要的混泥土为：()31350325m 2⨯=．【点睛】本题考查的是等腰梯形的性质，坡度的应用，堤坝体积的计算，理解题意，作出符合题意的图形，利用数形结合的方法解题是关键．23.如图，在ABC 中，点D 、F 分别是边BC 、AB 上的点，AD 和CF 交于点E ．（1）如果BF AB BD BC =，求证：EF CE DE AE =；（2）如果2AE BF AF DE =，求证：AD 是ABC 的中线．【答案】（1）见解析（2）见解析【分析】（1）先将等式化为比例式，可得到BF BC BD AB=，再根据角相等，证得ABD CBF ∽△△、∽AEF CED △△，从而能证得EF CE DE AE =；（2）过D 作DG AB ∥交CF 于G ，则DEG FEA △∽△，再根据比例式的代换得到12CD BC =，从而得出结论．【小问1详解】证明：∵BF AB BD BC =，∴BF BC BD AB=，∵B B ∠=∠，∴ABD CBF ∽△△，∴BAD BCF ∠=∠，又∵AEF CED ∠=∠，∴∽AEF CED △△，∴EF AE ED CE=,∴EF CE DE AE =；【小问2详解】过D 作DG AB ∥交CF 于G ，则DEG AEF ∽，∴AE AF ED DG=，∵2AE BF AF DE =，∴2AE AF ED BF =，∴2AF AF DG BF=，即122DG AF FB AF ==，∵CD DG BC FB=，∴12CD BC =，∴D 为BC 的中点，AD 是ABC 的中线．【点睛】本题考查了相似三角形的判定和性质，熟练掌握其判定定理及性质是解题的关键．24.如图，在平面直角坐标系xOy 中，抛物线23y ax bx =++与x 轴的正、负半轴分别交于点B 、A ，与y 轴交于点C ，已知5AB =，tan 3CAB ∠=，:3:4OC OB =．（1）求该抛物线的表达式；（2）设该抛物线的对称轴分别与x 轴、BC 交于点E 、F ，求EF 的长；（3）在（2）的条件下，联结CE ，如果点P 在该抛物线的对称轴上，当CEP △和CEB 相似时，求点P 的坐标【答案】（1）239344y x x =-++（2）158EF =（3）P 的坐标为：3,52⎛⎫⎪⎝⎭或39,24⎛⎫ ⎪⎝⎭．【分析】（1）先利用抛物线的解析式求解C 的坐标，再求解B 的坐标，A 的坐标，设设抛物线为()()14y a x x =+-，把()0,3C 代入即可；（2）先求解抛物线的对称轴为直线14322x -+==，再求解直线BC 为334y x =-+，可得F 的坐标，从而可得答案；（3）如图，过E 作EH BC ⊥于H ，证明32EO EH ==，可得OCE BCE ∠=∠，而OC EF ∥，可得OCE CEF ∠=∠，则BCE CEF ∠=∠，当CEP △和CEB 相似时，显然CO 与对称轴没有交点，P 不在E 的下方，只能在E 的上方，且CEP ∠与BCE ∠是对应角，再分两种情况分别求解即可．【小问1详解】解：∵抛物线23y ax bx =++，当0x =，则3y =，即()0,3C ，∵:3:4OC OB =，∴4OB =，即()4,0B ，∵5AB =，∴1OA =，即()1,0A -，设抛物线为()()14y a x x =+-，把()0,3C 代入得：43a -=，解得：34a =-，∴抛物线的解析式为：()()2339143444y x x x x =-+-=-++．【小问2详解】∵()1,0A -，()4,0B ，∴抛物线的对称轴为直线14322x -+==，∵()4,0B ，()0,3C ，设直线BC 为3y kx =+，∴430k +=，解得：34k =-，∴直线BC 为334y x =-+，当32x =时，33153428y =-⨯+=，即315,28F ⎛⎫ ⎪⎝⎭，∴158EF =．【小问3详解】如图，过E 作EH BC ⊥于H ，∵()4,0B ，()0,3C ，3,02E ⎛⎫ ⎪⎝⎭，∴5BC ==，2CE ==，35422BE =-=，3sin 5ABC ∠=，∴35EH BE =，则32EH =，∴32EO EH ==，而90COE CHE ∠=∠=︒，∴OCE BCE ∠=∠，而OC EF ∥，∴OCE CEF ∠=∠，∴BCE CEF ∠=∠，当CEP △和CEB 相似时，显然CO 与对称轴没有交点，∴P 不在E 的下方，只能在E 的上方，且CEP ∠与BCE ∠是对应角，当CEB ECP ∽时，∴1BC CE EP CE==，∴5EP BC ==，∴3,52P ⎛⎫ ⎪⎝⎭，当CEB EPC ∽，∴CE BC EP CE=，∴2352PE =，解得：94PE =，∴39,24P ⎛⎫ ⎪⎝⎭．综上：P 的坐标为：3,52⎛⎫ ⎪⎝⎭或39,24⎛⎫ ⎪⎝⎭．【点睛】本题考查的是利用待定系数法求解抛物线的解析式，求解一次函数的解析式，锐角三角函数的应用，相似三角形的判定与性质，角平分线的判定与性质，勾股定理的应用，熟练的证明CEP ∠与BCE ∠是对应角是解（3）的关键．25.如图，在Rt ABC △中，90ABC ∠=︒，10AC =，3tan 4C =，点D 是斜边AC 上的动点，连接BD ，EF 垂直平分BD 交射线BA 于点F ，交边BC 于点E．（1）如图，当点D 是斜边AC 上的中点时，求EF 的长；（2）连接DE ，如果DEC 和ABC 相似，求CE 的长；（3）当点F 在边BA 的延长线上，且2AF =时，求AD 的长．【答案】（1）12524EF =（2）327CE =或5CE =（3）16665AD =【分析】（1）如图，记BD ，EF 的交点为K ，证明52BK DK ==，BFK DBC C ∠=∠=∠，再利用锐角三角函数分别求解EK ，FK 即可；（2）先求解AB ，BC ，由DEC 和ABC 相似，分两种情况讨论即可；（3）如图，连接DF ，过F 作FT AD ⊥交DA 的延长线于T ，由4tan tan 3CB FAT CAB AB ∠=∠==，可得43FT AT =，求解85FT =，65AT =，结合垂直平分线的性质可得：8FD FB AF AB ==+=，由勾股定理可得TD ==，从而可得答案．【小问1详解】解：如图，记BD ，EF 的交点为K ，∵10AC =，点D 是斜边AC 上的中点，90ABC ∠=︒，∴152BD CD AC ===，∴∠=∠DBC C ，∵EF 垂直平分BD ∴52BK DK ==，90BKF BKE ABC ∠=∠=︒=∠，∴90BFK BEK BEK EBK ∠+∠=︒=∠+∠，∴BFK DBC C ∠=∠=∠，∵3tan 4C =，∴3tan 4EK EBK BK ∠==，3tan 4BK BFK FK ∠==，∴3515428EK =⨯=，5410233FK =⨯=，∴151********EF EK FK =+=+=．【小问2详解】∵90ABC ∠=︒，10AC =，3tan 4C =，∴3tan 4AB C BC==，设3AB m =，则4BC m =，∴510AC m ==，解得：2m =，∴6AB =，8BC =，∵DEC 和ABC 相似，如图，当DEC ABC △∽△时，∴DE CE AB CB=，由垂直平分线的性质可得：8BE DE CE ==-，∴868CE CE -=，解得：327CE =，如图，当DEC BAC ∽△△时，∴DE CE AB AC=，∴8610CE CE -=，解得：5CE =．【小问3详解】如图，连接DF ，过F 作FT AD ⊥交DA 的延长线于T ，∵4tan tan 3CB FAT CAB AB ∠=∠==，∴43FT AT =，而2AF =，同理可得：85FT =，65AT =，由垂直平分线的性质可得：8FD FB AF AB ==+=，∴TD ==∴6166655AD DT AT -=-==．【点睛】本题考查的是线段的垂直平分线的性质，勾股定理的应用，相似三角形的判定与性质，锐角三角函数的应用，清晰的分类讨论，作出适当的辅助线构建相似三角形与直角三角形都是解本题的关键．。

中考解答题 专题训练二一、22．（本题满分10分）如图，等腰梯形ABCD 中，AD ∥BC ，点E 是AD 延长线上一点，DE = BC.（1）求证：∠E =∠DBC ；（2）若等腰梯形ABCD 的中位线长为6，∠E =︒30，求等腰梯形ABCD 的对角线的长。

答案：22．（1）证明：∵AD ∥BC ，DE = BC ，∴四边形BCED 是平行四边形.……………(1分)∴∠E =∠DBC .……………………(1分)（2）∵ 等腰梯形ABCD 的中位线长为6，∴ AD + BC = 2×6 = 12，∴ AE = 12.……………(1分) ∵ 四边形BCED 是平行四边形， ∴ DB = CE . …………………………(1分) ∵DB = AC .∴ AC = CE . …………………………(1分)过点C 作CH ⊥AE ，垂足为H ，…………………………(1分) 则AH = EH =21 AE = 6. …………………………(1分)在Rt △EHC 中，cos ∠E =EC EH ，∴cos ︒30= EC6， ∴EC623=，…………………………(1分)∴34=EC.…………………………(1分)∴ DB = AC = 34.…………………………(1分)∴等腰梯形ABCD 的对角线的长是34.C（第22题图）D ABC（第22题EH二、23．（本题满分12分）某公司急需用车，但暂时无力购买，于是准备与出租车公司签订租车合同：（以每月行驶路程x千米计算）甲出租车公司的月租车费y甲是：每月基本租费为1000元，再加每千米行驶费为0.5元；乙出租车公司的月租车费y乙是：每千米行驶费为1元；（1）写出y甲、y乙与x的函数关系式；（2）每月行驶多少路程时，两家公司的租车费相同？（3）如果每月用车的路程约为3000千米，那么租用哪家的车合算？请说明理由。

答案：23．解：（1）y甲= 0. 5x + 1000 …………………………(2分)y乙= x . …………………………(2分)（2）当y甲= y乙，即0. 5x + 1000 = x……………………(2分)x= 2000…………………………(1分)所以，当每月行驶2000千米路程时，两家公司的租车费相同.…………………………(1分)（3）当x = 3000时，y甲= 0. 5×3000 + 1000= 2500元………………(1分) 当x = 3000时，y乙= 3000元…………………………(1分)此时，y甲＜y乙…………………………(1分)所以，每月用车的路程约为3000千米，租用甲出租车公司的车合算.…………………………(1分)三、24．（本题满分12分）已知O为原点，点A的坐标为（4，3），圆A的半径为2，过A 作直线l平行于x轴，点P在直线l上运动.（1）当点P在圆A上时，请你直接写出它的坐标；（2）在（1）的条件下，过O、P两点作直线，求直线OP与圆A相交所得的弦的长.x第24题图答案：24．解：（1）P （2，3）或（6，3）. …………………………(1分) （2）设直线OP 与圆A 的另一个交点为Q ，作AC ⊥PQ 于C ，则PQ = 2PC . …………………………(1分)设直线l 与y 轴的交点为B ，则B （0，3）. …………………(1分)①当P （2，3）时，PB = 2，OB = 3， ∴PO =133222=+…………(1分)易证△PAC ∽△POB ，POPA PBPC =，…………………(1分)∴1322=PC ，∴13134=PC ，…………………………(1分)∴13138=PQ .…………………………(1分)②当P （6，3）时，PB = 6，OB = 3， ∴PO =536322=+.…………………………(1分)易证△PAC ∽△POB ，∴POPA PBPC =，…………………………(1分)∴5326=PC ，∴554=PC ，…………………………(1分)∴558=PQ .…………………………(1分)答：直线OP 与圆A 相交所得的弦长为13138或558.…………(1分)x四、25．（本题满分14分）已知∠MON = 60°，OT 是∠MON 的平分线，P 是射线OT 上一个动点，射线PB 交射线ON 于点B ，（1）如图甲，若射线PB 绕点P 顺时针旋转120°后与射线OM 交于点A ．①求证：PA = PB ；②若点C 是AB 与OP 的交点 , 且PC =23PB ，求△POB 与△PBC 的面积之比．（2）若OB = 2，射线PB 绕点P 顺时针旋转120°后与直线OM 交于点A （点A 不与点O 重合），直线PA 交射线ON 于点D ，且满足ABO PBD ∠=∠．请直接写出OP 的长．答案：25．（1）证明：如图甲，作PF ⊥OM 于F ，作PG ⊥ON 于G ，………(1分)∵OP 平分∠MON ，∴PF =PG ，…………(1分) ∵∠MON = 60°，∴∠FPG = 360°– 60°– 90°– 90°= 120° 又∵∠APB =120°，∴∠APF = ∠BPG ，…………………………(1分) ∴△PAF ≌△PBG ，…………………………(1分) ∴PA = PB ．…………………………(1分) （2）解：由（1）得：PA = PB ，∠APB =120°，∴∠PAB = ∠PBA = 30°，…………………………(1分) ∵∠MON = 60°，OP 平分∠MON ，∴∠TON = 30°，…………………………(1分) ∴∠POB = ∠PBC ，…………………………(1分) 又∠BPO = ∠OPB ，∴△POB ∽△PBC ，…………………………(1分) ∴34)23()(22===∆∆PBPB PCPB S S PBCPOB ；…………………………(1分)∴△POB 与△PBC 的面积之比为4∶3．MONTPA B甲COMNT（备用图） OMNT（备用图）第25题图OM N TPAB 图甲CFG（3）解：①当点A在射线OM上时（如图乙1），易求得：∠BPD = ∠BOA = 60°，∵ABOPBD∠=∠，而∠PBA = 30°，∴∠OBA = ∠PBD = 75°，作BE⊥OT于E，∵∠NOT = 30°，OB = 2，∴BE =1，OE = 3，∠OBE = 60°，∴∠EBP = ∠EPB = 45°，∴PE = BE =1，∴OP = OE + PE =3+ 1；…………………………(2分)②当点A在射线OM的反向延长线上时（如图乙2），此时∠AOB= ∠DPB= 120°，∵ABOPBD∠=∠，而∠PBA = 30°，∴∠OBA = ∠PBD = 15°，作BE⊥OT于E，∵∠NOT = 30°，OB = 2，∴BE =1，OE = 3，∠OBE = 60°，∴∠EBP = ∠EPB = 45°，∴PE = BE =1，∴OP = 3－1. …………………………(2分)OMNT图乙1APDBEOMNT图乙2PABED五、24．（本题12分）据统计，某小区2007年底拥有家庭小桥车64辆，2009年底家庭小桥车拥有量达到100辆.（1）若该小区2007年底到2010年底家庭小桥车拥有量的年平均增产率都相同，求该小区到2010年底家庭小桥车将达到多少辆？（2）为缓解停车矛盾，该小区决定投资15万元再建造若干个停车位.据测算，建造费用分别为室内车位5000元/个，露天车位1000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，求该小区最多可建两种车位各多少个？试写出所有可能的方案.答案：24．解：(1) 设家庭小桥车拥有量的年平均增产率为x ，则有 100)1(642=+x ……………………………………3分 解得 49%,254121-===x x （不合题意，舍去）……1分所以 100（1+25%）=125……………………………………1分 答：该小区到2010年底家庭小桥车将达到125辆. ……………1分(2) 设该小区可建室内车位a 个，露天车位b 个，则151.05.0=+b a ，得a b 5150-=……………………………1分 又因为a b a 5.22≤≤，……………………………………1分 所以有a a a 5.251502≤-≤，解之得715020≤≤a .………1分因为a 为正整数，所以a =20或a =21.当a =20时，b =50; 当a =21时，b =45. …………………………2分答：方案1：建室内车位20个，露天车位50个；方案2：建室内车位21个，露天车位45个. ……………………………………1分六、24．（本题满分12分，第（1）小题4分，第（2）小题5分，第（3）小题3分）如图，在△ABC 中，AB =6，BC =4，点D 在边BC 的延长线上，∠ADC =∠BAC ，点E 在边BA 的延长线上，∠E =∠DAC ． （1） 找出图中的相似三角形，并证明； （2） 设AC=x,DE=y ，求y 关于x 的函数解析式，并写出定义域； （3） △AED 能否与△ABC 相似？如果能够，请求出B cos 的值；如果不能，请说明理由．答案：24．解：（1）△ABC ∽△DBA ，△CAD ∽△AED ．………………………………（2分）证明如下：∵∠B =∠B ，∠ADC =∠BAC ，∴△ABC ∽△DBA ．………（1分）∵∠BAC +∠DAC =∠BAD =∠ADE +∠E ，∠DAC =∠E ，∴∠BAC = ∠ADE =∠ADC ，∴△CAD ∽△AED ．………………………（1分） （2）∵△ABC ∽△DBA ，∴,DAAC BABC BDBA ==∴2346x x BCBA AC DA =⋅=⋅=，（1分）∴.94362===BCBA BD ∴CD =5．…………………………………………（1分）ABCDE(第24题图)∵△CAD ∽△AED ，∴CDDA DADE =．∴2DA CD DE =⋅，………………（1分）∴2)23(5x y =，∴函数解析式为2209x y =，定义域为2<x <10．………（2分）（3）△AED 能与△ABC 相似．∵∠BAC = ∠ADE =∠ADC ，∠BCA >∠ADC =∠ADE ，∠BCA >∠CAD =∠E ， ∴只有∠B =∠E =∠DAC 时，△AED 与△ABC 相似．…………………（1分） 这时，由于∠B +∠BAC +∠CAD +∠ADC =180º，∴∠BAC +∠DAC =90º，∴∠ACB =∠BAD =90º．………………………（1分） ∴cos B =3264==ABBC .………………………………………………………（1分）七、24．（本题满分12分，每小题满分各4分）某果农承包果园若干亩，投资7800元种果树2000棵，其成活率为90%，08年首次开始结果，在摘果时，随意摘下10棵果树的水果，称得重量如下（单位：千克）：8，9，12，13，8，9，11，10，12，8（1）根据样本平均数估计该果农在08年水果的总产量是多少？（2）此水果在市场每千克售1.3元，在果园每千克售1.1元，该果农用农用车将水果拉到市场出售，平均每出售1000千克，需8人帮助，每人每天付工资25元.若两种方式都可在一天内售完全部水果，选择哪种方式合理？为什么？（3）根据08年的纯收入（纯收入=总收入-总支出），若该农户计划还用两年时间到2010年度合计纯收入达到57000元，求2009年、2010年平均每年的纯收入增长率是多少？答案：24.解 （1）101010010812101198131298==+++++++++ ------2分18000%90200010=⨯⨯（千克）----------2分（2）①果园出售收入：18000×1.1=19800（元）. ----------1分用人工资：18000÷1000×8×25=3600（元）----------1分实际收入：23400-3600=19800（元）. ----------1分故在果园出售合理，因为市场出售，还要支付农用车费用. ----------1分 （3）设2009、2010年的平均增产率为x ， 08年纯收入19800-7800=12000（元），----------1分 依题意得 12000()[]570001112=++++x x ----------1分整理得 071242=-+x x解之得 5.3,5.021-==x x ----------1分 因为 x =-3.5不合题意，舍去，所以x =0.5=50%. 答：2009、2010年的平均增产率为50%.----------1分八、25．（本题满分14分，第（1）小题满分6分，第（2）、（3）小题满分4分）某商场计划用9万元从厂家购进50台电视机，已知该厂家生产三种不同型号的电视机，出厂价分别为甲种每台1500元，乙种每台2100元，丙种每台2500元.（1）若商场同时购进其中两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案.（2）若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元，在同时购进两种不同型号电视机的方案中，为使销售获利最多，你选择哪种进货方案？（3）若商场准备用9万元同时购进三种不同型号的电视机50台，请你设计进货方案.答案：25.解：（1）分三种情况①设购甲种电视机x 台，乙种电视机y 台， 则有⎩⎨⎧==⇒⎩⎨⎧=+=+;25,259000021001500,50y x y x y x ----------2分②设购甲种电视机x 台，丙种电视机z 台， 则有⎩⎨⎧==⇒⎩⎨⎧=+=+;15,359000025001500,50z x z x z x ----------2分③设购乙种电视机y 台，丙种电视机z 台， 则有⎩⎨⎧-==⇒⎩⎨⎧=+=+5.37,5.879000025002100,50z y z y z y (舍去) ----------2分（2）①当购甲种25台，乙种25台时，可获利150×25+200×25=8750（元）. -2分 ②当购甲种35台，丙种15台时，可获利150×35+250×15=9000（元）. -2分（3）设购甲种电视机x 台，乙种电视机y 台，丙种电视机z 台.则有y x z y x z y x 523590000250021001500,50-=⇒⎩⎨⎧=++=++--------2分 当y =5时，x =33，z =12; y =10时，x =31，z =9; y =15时，x =29，z =6; y =20时，x =27，z =3.--------1分 答：（1）有两种进货方案：购甲种25台和乙种25台或购甲种35台和丙种15台. （2）选购甲种35台，丙种15台时获利最多.（3）有四种方案：甲33台，乙5台，丙12台；甲31台，乙10台，丙9台；甲29台，乙15台，丙6台；甲27台，乙20台，丙3台；--------1分提高题部分：【行程问题】1．难度：★★★两地相距900米，甲、乙二人同时、同地向同一方向行走，甲每分钟走80米，乙每分钟走100米，当乙到达目标后，立即返回，与甲相遇，从出发到相遇共经过多少分钟？【解答】甲、乙二人开始是同向行走，乙走得快，先到达目标．当乙返回时运动的方向变成了相向而行，把相同方向行走时乙用的时间和返回时相向而行的时间相加，就是共同经过的时间．乙到达目标时所用时间：900100=9(分钟)，甲9分钟走的路程：80*9=720(米)，甲距目标还有：900-720=180(米)，相遇时间：180（100+80）=1(分钟)，共用时间：9+1 =10(分钟)．另解：观察整个行程，相当于乙走了一个全程，又与甲合走了一个全程，所以两个人共走了两个全程，所以从出发到相遇用的时间为：900*2（100+80）=10分钟．2．难度：★★★★李经理的司机每天早上7点30分到他家接他去公司上班，有一天，李经理7点从家出发步行去公司，路上遇到按时来接他的车，乘车去公司，结果早到5分钟．问李经理什么时间遇上汽车？汽车速度是步行速度的___________倍．【分析】汽车比平时少走5分钟，往返各为=2.5分钟，30-2.5=27.5(分钟)，所以相遇时是7点27分30秒．汽车走2.5分钟的路程等于人走27.5分钟的路程．根据路程相等，速度比等于时间的反比，所以车与人的速度比等于人与车的时间比，即27.5:2.5=11:1，所以汽车速度是步行速度的11倍．3．难度：★★★学校组织军训，甲、乙、丙三人步行从学校到军训驻地．甲、乙两人早晨7点一起从学校出发，甲每小时走6千米，乙每小时走5千米，丙上午9点才从学校出发，下午5点甲、丙同时到达军训驻地．问：丙在何时追上乙？10【分析】先看丙和甲的追及问题，追及路程为甲走9-7=2(小时)的路程，为：6*2=12(千米)，追及时间为上午9点到下午5点，共17-9=8(小时)，所以丙的速度为：128+6=7.5(千米/时)．再看丙和乙的追及问题．丙追及乙的追及路程为乙先走9-7=2(小时)的路程，为5*2=10(千米)，两人的速度差为：7.5-5=2.5(千米／时)，追及时间为：10 2.5=4(小时)，此时为下午1点．4．难度：★★★★甲、乙、丙三人依次相距280米，甲、乙、丙每分钟依次走90米、80米、72米．如果甲、乙、丙同时出发，那么经过几分钟，甲第一次与乙、丙的距离相等？【分析】甲与乙、丙的距离相等有两种情况：一种是乙追上丙时；另一种是甲位于乙、丙之间．⑴乙追上丙需：280（80-72）=35(分钟)．⑵甲位于乙、丙之间且与乙、丙等距离，我们可以假设有一个丁，他的速度为乙、丙的速度的平均值，即（80+72）2=76(米/分)，且开始时丁在乙、丙之间的中点的位置，这样开始时丁与乙、丙的距离相等，而且无论经过多长时间，乙比丁多走的路程与丁比丙多走的路程相等，所以丁与乙、丙的距离也还相等，也就是说丁始终在乙、丙的中点．所以当甲遇上丁时甲与乙、丙的距离相等，而甲与丁相遇时间为：（280+2802）（90-76）=30(分钟)．经比较，甲第一次与乙、丙的距离相等需经过30分钟．。

浦东一对一培训机构 初中数学 恒高1对1 24题强化训练
初中用的较多的是用几何问题去解决直角坐标系中的函数问题，对于初中生，尽可能从图形着手去解决，比如求点的坐标，可以通过往坐标轴作垂线，把它转化为求线段的长，再结合基本的相似全等三角比解决，尽可能避免用两点间距离公式列方程组，所以遇到此类题目，切记先用几何方法，实在做不出再用解析法。

5.
6.（2012上海） 在平面直角坐标系中，二次函数y =ax 2+6x +c 的图象经过点A (4，0)、B (-1，
0)，与y 轴交于点C ，点D 在线段OC 上，OD =t ，点E 在第二象限，∠ADE =90°，tan ∠DAE =
12
，EF ⊥OD ，垂足为F .（1）求这个二次函数的解析式；（2）求线段EF 、OF 的长(用含t 的代数式表示)；
（3）当∠ECA =∠OAC 时，求t 的值.
7、。

浦东中考一对一补习初中数学恒高教育平行四边形的存在性问题(一)平行四边形的存在性问题-------已知平行四边形三定点+1动点
【方法：动点坐标错误！未找到引用源。

：相对顶点横坐标之和相等,纵坐标之和相等】(二)平行四边形的存在性问题-------已知平行四边形2定点+2动点
【方法：以固定的一边作为平行四边形的一边或对角线进行分类讨论】
例1、
二、梯形的存在性问题
例2、
已知A(-1，m)与B(2，m+3)是反比例函数图象上的两个点．
(1)求k的值；
(2)若点C(-1，0)，则在反比例函数图象上是否存在点D，使
得以A，B，C，D四点为顶点的四边形为梯形？若存在，求出点D的
坐标；若不存在，请说明理由．
三、动点产生的面积问题
例4、
例5、
如图，已知等腰直角三角形ABC中，∠C=90°，AC=2，M是边AC上一点，过点M的直线交CB的延长线于点N，交边AB于点P，且AM=BN．
（1）求证：MP=NP；
（2）设AM=x，AP=y, 求y与x的函数解析式;
(3) 设AM=x，四边形MCBP的面积为y，求y与x的函数解析式，并写出函数的定义域；。

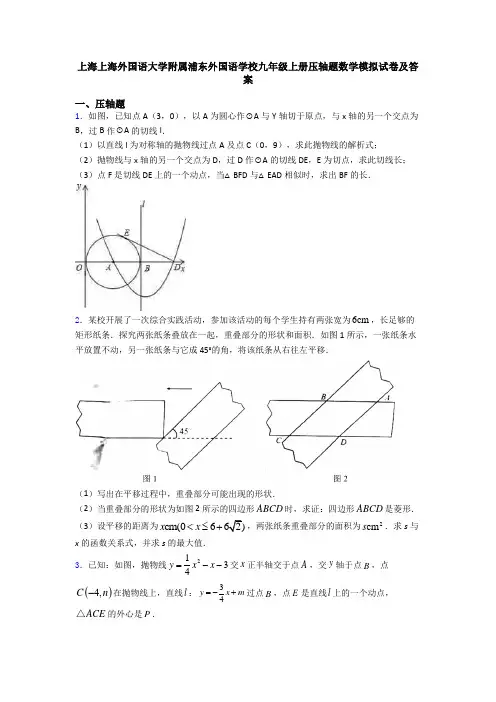
上海上海外国语大学附属浦东外国语学校九年级上册压轴题数学模拟试卷及答案一、压轴题1．如图，已知点A （3，0），以A 为圆心作⊙A 与Y 轴切于原点，与x 轴的另一个交点为B ，过B 作⊙A 的切线l ．（1）以直线l 为对称轴的抛物线过点A 及点C （0，9），求此抛物线的解析式；（2）抛物线与x 轴的另一个交点为D ，过D 作⊙A 的切线DE ，E 为切点，求此切线长； （3）点F 是切线DE 上的一个动点，当△BFD 与△EAD 相似时，求出BF 的长．2．某校开展了一次综合实践活动，参加该活动的每个学生持有两张宽为6cm ，长足够的矩形纸条．探究两张纸条叠放在一起，重叠部分的形状和面积．如图1所示，一张纸条水平放置不动，另一张纸条与它成45°的角，将该纸条从右往左平移．（1）写出在平移过程中，重叠部分可能出现的形状．（2）当重叠部分的形状为如图2所示的四边形ABCD 时，求证：四边形ABCD 是菱形． （3）设平移的距离为cm(0662)x x <≤+，两张纸条重叠部分的面积为2cm s ．求s 与x 的函数关系式，并求s 的最大值．3．已知：如图，抛物线2134y x x =--交x 正半轴交于点A ，交y 轴于点B ，点()4,C n -在抛物线上，直线l ：34y x m =-+过点B ，点E 是直线l 上的一个动点，ACE △的外心是P ．（1）求m，n的值．（2）当点E移动到点B时，求ACE△的面积．（3）①是否存在点E，使得点P落在ACE△的边上，若存在，求出点E的坐标，若不存在，请说明理由．②过点A作直线AD x轴交直线l于点D，当点E从点D移动到点B时，圆心P移动的路线长为_____．（直接写出答案）4．如图，过原点的抛物线y=﹣12x2+bx+c与x轴交于点A（4，0），B为抛物线的顶点，连接OB，点P是线段OA上的一个动点，过点P作PC⊥OB，垂足为点C．（1）求抛物线的解析式，并确定顶点B的坐标；（2）设点P的横坐标为m，将△POC绕着点P按顺利针方向旋转90°，得△PO′C′，当点O′和点C′分别落在抛物线上时，求相应的m的值；（3）当（2）中的点C′落在抛物线上时，将抛物线向左或向右平移n（0＜n＜2）个单位，点B、C′平移后对应的点分别记为B′、C″，是否存在n，使得四边形OB′C″A的周长最短？若存在，请直接写出n的值和抛物线平移的方向，若不存在，请说明理由．5．如图①是一张矩形纸片，按以下步骤进行操作：(Ⅰ)将矩形纸片沿DF折叠，使点A落在CD边上点E处，如图②；(Ⅱ)在第一次折叠的基础上，过点C再次折叠，使得点B落在边CD上点B′处，如图③，两次折痕交于点O；(Ⅲ)展开纸片，分别连接OB、OE、OC、FD，如图④．（探究）（1）证明：OBC≌OED；（2）若AB ＝8，设BC 为x ，OB 2为y ，是否存在x 使得y 有最小值，若存在求出x 的值并求出y 的最小值，若不存在，请说明理由．6．如图1，抛物线221y x x =-+-的顶点A 在x 轴上，交y 轴于B ，将该抛物线向上平移，平移后的抛物线与x 轴交于,C D ，顶点为()1,4E ．（1）求点B 的坐标和平移后抛物线的解析式；（2）点M 在原抛物线上，平移后的对应点为N ，若OM ON =，求点M 的坐标； （3）如图2，直线CB 与平移后的抛物线交于F ．在抛物线的对称轴上是否存在点P ，使得以,,C F P 为顶点的三角形是直角三角形？若存在，直接写出点P 的坐标；若不存在，请说明理由．7．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是 ，位置关系是 ；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．8．如图，⊙O 经过菱形ABCD 的三个顶点A 、C 、D ，且与AB 相切于点A ．（1）求证：BC 为⊙O 的切线；（2）求∠B 的度数．（3）若⊙O 半径是4，点E 是弧AC 上的一个动点，过点E 作EM ⊥OA 于点M ，作EN ⊥OC 于点N ，连接MN ，问：在点E 从点A 运动到点C 的过程中，MN 的大小是否发生变化？如果不变化，请求出MN 的值；如果变化，请说明理由．9．如图1，平面直角坐标系xOy 中，等腰ABC ∆的底边BC 在x 轴上，8BC =，顶点A 在y 的正半轴上，2OA =，一动点E 从(3,0)出发，以每秒1个单位的速度沿CB 向左运动，到达OB 的中点停止．另一动点F 从点C 出发，以相同的速度沿CB 向左运动，到达点O 停止．已知点E 、F 同时出发，以EF 为边作正方形EFGH ，使正方形EFGH 和ABC ∆在BC 的同侧．设运动的时间为t 秒（0t ≥）．（1）当点H 落在AC 边上时，求t 的值；（2）设正方形EFGH 与ABC ∆重叠面积为S ，请问是存在t 值，使得9136S =？若存在，求出t 值；若不存在，请说明理由；（3）如图2，取AC 的中点D ，连结OD ，当点E 、F 开始运动时，点M 从点O 出发，以每秒25OD DC CD DO ---运动，到达点O 停止运动．请问在点E 的整个运动过程中，点M 可能在正方形EFGH 内（含边界）吗？如果可能，求出点M 在正方形EFGH 内（含边界）的时长；若不可能，请说明理由．10．⊙O 是四边形ABCD 的外接圆，OB AC ⊥，OB 与AC 相交于点H ，21012BC AC CD ===，．（1）求⊙O 的半径；（2）求AD 的长；（3）若E 为弦CD 上的一个动点，过点E 作EF//AC ，EG//AD ． EF 与AD 相交于点F ，EG 与AC 相交于点G ．试问四边形AGEF 的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．11．在平面直角坐标系中，经过点()0,2A 且与33y x =-平行的直线，交x 轴于点B ，如图1所示．（1）试求B 点坐标，并直接写出ABO ∠的度数；（2）过()1,0M 的直线与AB 成45︒夹角，试求该直线与AB 交点的横坐标；（3）如图2，现有点(,)C m n 在线段AB 上运动，点,(320)D m -+在x 轴上，N 为线段CD 的中点．①试求点N 的纵坐标y 关于横坐标x 的函数关系式；②直接写出N 点的运动轨迹长度为 ．12．在锐角△ABC 中，AB=AC ，AD 为BC 边上的高，E 为AC 中点．（1）如图1，过点C 作CF ⊥AB 于F 点，连接EF ．若∠BAD =20°，求∠AFE 的度数；（2）若M 为线段BD 上的动点（点M 与点D 不重合），过点C 作CN ⊥AM 于N 点，射线EN ，AB 交于P 点．①依题意将图2补全；②小宇通过观察、实验，提出猜想：在点M 运动的过程中，始终有∠APE =2∠MAD ． 小宇把这个猜想与同学们进行讨论，形成了证明该猜想的几种想法：想法1：连接DE ，要证∠APE =2∠MAD ，只需证∠PED =2∠MAD ．想法2：设∠MAD =α，∠DAC =β，只需用α，β表示出∠PEC ，通过角度计算得∠APE =2α．想法3：在NE 上取点Q ，使∠NAQ =2∠MAD ，要证∠APE =2∠MAD ，只需证△NAQ ∽△APQ ．……请你参考上面的想法，帮助小宇证明∠APE =2∠MAD ．（一种方法即可）13．如图，在平面直角坐标系中，直线y=12x+2与x 轴交于点A ，与y 轴交于点C ，抛物线y=12x 2+bx+c 经过A 、C 两点，与x 轴的另一交点为点B ．（1）求抛物线的函数表达式； （2）点D 为直线AC 上方抛物线上一动点；①连接BC 、CD ，设直线BD 交线段AC 于点E ，△CDE 的面积为S 1， △BCE 的面积为S 2， 求12S S 的最大值； ②过点D 作DF⊥AC，垂足为点F ，连接CD ，是否存在点D ，使得△CDF 中的某个角恰好等于∠BAC 的2倍？若存在，求点D 的横坐标；若不存在，请说明理由14．对于⊙C 与⊙C 上的一点A ，若平面内的点P 满足：射线．．AP 与⊙C 交于点Q （点Q 可以与点P 重合），且12PA QA≤≤，则点P 称为点A 关于⊙C 的“生长点”． 已知点O 为坐标原点，⊙O 的半径为1，点A （-1，0）．（1）若点P 是点A 关于⊙O 的“生长点”，且点P 在x 轴上，请写出一个符合条件的点P 的坐标________；（2）若点B 是点A 关于⊙O 的“生长点”，且满足1tan BAO 2∠=，求点B 的纵坐标t 的取值范围；（3）直线3y x b =+与x 轴交于点M ，与y 轴交于点N ，若线段MN 上存在点A 关于⊙O 的“生长点”，直接写出b 的取值范围是_____________________________．15．已知在矩形ABCD 中，AB=2，AD=4．P 是对角线BD 上的一个动点（点P 不与点B 、D 重合），过点P 作PF⊥BD，交射线BC 于点F ．联结AP ，画∠FPE=∠BAP，PE 交BF 于点E ．设PD=x ，EF=y ．（1）当点A 、P 、F 在一条直线上时，求△ABF 的面积；（2）如图1，当点F 在边BC 上时，求y 关于x 的函数解析式，并写出函数定义域；（3）联结PC ，若∠FPC=∠BPE，请直接写出PD 的长．16．如图，正方形ABCD 中，对角线AC 、BD 交于点O ，E 为OC 上动点(与点O 不重合)，作AF ⊥BE ，垂足为G ，交BO 于H ．连接OG 、CG ．(1)求证：AH=BE ；(2)试探究：∠AGO 的度数是否为定值？请说明理由；(3)若OG ⊥CG ，BG=32，求△OGC 的面积．17．如图所示，在Rt ABC ∆中，90B ∠=︒，43BC =，30C ∠=︒，点D 从点C 出发沿CA 方向以每秒2个单位长度的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以每秒1个单位长度的速度向点B 匀速运动，当其中一点到达终点时，另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(0)t >，过点D 作DF BC ⊥于点F ，连接DE 、EF .（1）求证：AE DF =；（2）四边形AEFD 能够成为菱形吗？若能，求出t 的值；若不能，请说明理由； （3）当t =________时，DEF ∆为直角三角形.18．如图，在直角坐标系中，点C 在第一象限，CB x ⊥轴于B ，CA y ⊥轴于A ，3CB =，6CA =，有一反比例函数图象刚好过点C ．（1）分别求出过点C 的反比例函数和过A ，B 两点的一次函数的函数表达式；（2）直线l x ⊥轴，并从y 轴出发，以每秒1个单位长度的速度向x 轴正方向运动，交反比例函数图象于点D ，交AC 于点E ，交直线AB 于点F ，当直线l 运动到经过点B 时，停止运动．设运动时间为t （秒）．①问：是否存在t 的值，使四边形DFBC 为平行四边形？若存在，求出t 的值；若不存在，说明理由；②若直线l 从y 轴出发的同时，有一动点Q 从点B 出发，沿射线BC 方向，以每秒3个单位长度的速度运动．是否存在t 的值，使以点D ，E ，Q ，C 为顶点的四边形为平行四边形；若存在，求出t 的值，并进一步探究此时的四边形是否为特殊的平行四边形；若不存在，说明理由．19．我们规定：有一组邻边相等，且这组邻边的夹角为60︒的凸四边形叫做“准筝形”．（1）如图1，在四边形ABCD 中，270A C ∠+∠=︒，30D ∠=︒，AB BC =，求证：四边形ABCD 是“准筝形”；（2）如图2，在“准筝形”ABCD 中，AB AD =，60BAC BCD ∠=∠=︒，4BC =，3CD =，求AC 的长；（3）如图3，在ABC 中，45A ∠=︒，120ABC ∠=︒，33AB =-，设D 是ABC 所在平面内一点，当四边形ABCD 是“准筝形”时，请直接写出四边形ABCD 的面积．20．如图①，在ABC 中，AB AC =，BAC α∠=，点D 、E 分别在边AB 、AC 上，AD AE =，连接BE ，点M 、P 、N 分别为DE 、BE 、BC 的中点．（1）观察猜想：图①中，线段PM 与PN 的数量关系是_____________，用含α的代数式表示MPN ∠的度数是________________________；（2）探究证明：把ADE 绕点A 顺时针方向旋转到图②的位置，连接MN ，BD ，CE ，当120α=︒时，判断PMN 的形状，并说明理由；（3）拓展延伸：把ADE 绕点A 在平面内任意旋转，若90α=︒，3AD =，7AB =，请直接写出线段MN 的最大值和最小值．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）21(6)33y x =--；（2）3）32【解析】试题分析：（1）已知了抛物线的顶点坐标，可将抛物线的解析式设为顶点坐标式，然后将C 点坐标代入求解即可．（2）由于DE 是⊙A 的切线，连接AE ，那么根据切线的性质知AE ⊥DE ，在Rt △AED 中，AE 、AB 是圆的半径，即AE=OA=AB=3，而A 、D 关于抛物线的对称轴对称，即AB=BD=3，由此可得到AD 的长，进而可利用勾股定理求得切线DE 的长．（3）若△BFD 与EAD △相似，则有两种情况需要考虑：①△AED ∽△BFD ，②△AED ∽△FBD ，根据不同的相似三角形所得不同的比例线段即可求得BF 的长． 试题解析：（1）设抛物线的解析式为y=a （x-6）2+k ；∵抛物线经过点A （3，0）和C （0，9）， ∴90{369a k a k +=+=， 解得：1 {33a k ==-∴y=13（x-6）2-3． （2）连接AE ；∵DE 是⊙A 的切线，∴∠AED=90°，AE=3，∵直线l 是抛物线的对称轴，点A ，D 是抛物线与x 轴的交点，∴AB=BD=3，∴AD=6；在Rt △ADE 中，DE 2=AD 2-AE 2=62-32=27，∴（3）当BF ⊥ED 时；∵∠AED=∠BFD=90°，∠ADE=∠BDF ，∴△AED ∽△BFD ， ∴AE AD BF BD =， 即363BF =， ∴BF=32；当FB ⊥AD 时，∵∠AED=∠FBD=90°，∠ADE=∠FDB ， ∴△AED ∽△FBD ， ∴AE EDBF BD=， 即BF=33333⨯=； ∴BF 的长为32或3．考点：二次函数综合题．2．（1）三角形，四边形（梯形、菱形），五边形；（2）见解析；（3）221(06)2618(662)1[(62)]2(6262)22(62)x x x x s x x x ⎧<⎪⎪-<⎪=⎨⎪--++<+⎪⎪=-⎩，s 的最大值为2362cm ． 【解析】 【分析】（1）根据平移过程中，重叠部分四边形的形状判定即可；（2）分别过点B 、D 作BE CD ⊥于点E 、DF CB ⊥于点F ，再根据纸条的特点证明四边形ABCD 是平行四边形，再证明邻边相等即可证明；（3）分06x <≤、662x <、62<662x <+x=62+s 与x 的函数关系式，然后再求最大值即可． 【详解】解：（1）在平移过程中，重叠部分的形状分别为：三角形，四边形（梯形、菱形），五边形；（2）证明：分别过点B 、D 作BE CD ⊥于点E 、DF CB ⊥于点F ， ∴90BEC DFC ∠=∠=︒ ∵两张纸条等宽，∴6BE DF ==．在BCE 和DCF 中45BCE DCF ∠=∠=︒， ∴2266=62BC DC ==+， ∵两张纸条都是矩形，， ∴//AB CB //BC AD ． ∴四边形ABCD 是平行四边形， 又∵BC DC =， ∴四边形ABCD 是菱形；（3）Ⅰ、如图：当06x <≤时，重叠部分为三角形，如图所示， ∴212S x =， ∴018S <．最大值为218cm ．Ⅱ、如图：当662x <时，重叠部分为梯形，如图所示，梯形的下底为cm x ，上底为(6)cm x -，∴()1666182S x x x =+-⋅=-，当62x =s 取最大值2(36218)cm ．Ⅲ、当62662x <<+时，重叠部分为五边形，2211=626(662)[(662)]36222S S S x x -=⨯-+-=--++五边形菱形三角形．此时36218362S -<<五边形．Ⅳ、当662x =+时，重叠部分为菱形， ∴2362cm S =菱形．∴221(06)2618(662)1[(662)]2(62662)2362(662)x x x x s x x x ⎧<⎪⎪-<⎪=⎨⎪--++<+⎪⎪=-⎩ ∴s 的最大值为2362cm ． 【点睛】本题考查了平移变换、等腰直角三角形的性质、菱形的判定以及运用二次函数求最值，考查知识点较多，因此灵活运用所学知识成为解答本题的关键．3．（1）3,5m n =-=；（2）30ACES=；（3）①点E 的坐标为：1653,1122⎛⎫-- ⎪⎝⎭或6415,1111E ⎛⎫- ⎪⎝⎭或3660,1111E ⎛⎫- ⎪⎝⎭； ②圆心P 移动的路线长 【解析】 【分析】 （1）令2130,4y x x =--=求出点A （6，0），把点C （-4，n ）代入在抛物线方程，解得：n=5，把点B （0，-3）代入34y x m =-+，从而可得答案；（2）记AC 与y 轴的交点为H ，利用()1.2ACEA C SBH x x =••-即可求解； （3）①分当点P 落在CA 上时，点P 落在AE 上时，点P 落在CE 上时三种情况讨论即可； ②分E 在D 和B 点两种情况，求出圆心12,P P 点的坐标，则圆心P 移动的路线长=12PP ，即可求解． 【详解】 解：（1）令2130,4y x x =--= 24120,x x ∴--=()()260,x x ∴+-= 122,6,x x ∴=-=∴ 点A （6，0），把点C （-4，n ）代入在抛物线方程， 解得：()()214435,4n =⨯----= ()4,5C ∴-，把点B （0，-3）代入34y x m =-+，解得：3m =-， 则：直线l ：334y x =--，…① 3,5,m n ∴=-=（2）由（1）知：A （6，0）、B （0，-3）、C （-4，5）、 AC 中点为51,,2⎛⎫⎪⎝⎭设AC 为：,y kx b =+6045k b k b +=⎧∴⎨-+=⎩解得：123k b ⎧=-⎪⎨⎪=⎩AC ∴所在的直线方程为：132y x =-+， 如图，AC 与y 轴交点H 坐标为：（0，3），()1161030.22ACEA C SBH x x ∴=••-=⨯⨯=（3）如下图： ①当点P 落在CA 上时， 圆心P 为AC 的中点51,,2⎛⎫⎪⎝⎭其所在的直线与AC 垂直，1,2AC k =-AC ∴的垂直平分线即圆心P 所在的直线方程为：2,y x a =+把51,2⎛⎫ ⎪⎝⎭代入得：52,2a =+ 1,2a ∴=122y x ∴=+…②，334122y x y x ⎧=--⎪⎪∴⎨⎪=+⎪⎩①②解得：11,5322y ⎪⎪⎨⎪=-⎪⎩E 的坐标为1653,1122⎛⎫-- ⎪⎝⎭； 当点P 落在AE 上时， 设点3,3,4E m m ⎛⎫-- ⎪⎝⎭则点P 的坐标633,282m m +⎛⎫-- ⎪⎝⎭， 则PA=PC ，2222633633645282282m m m m ++⎛⎫⎛⎫⎛⎫⎛⎫∴-++=++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭解得：64,11m =- 故点6415,.1111E ⎛⎫-⎪⎝⎭ 当点P 落在CE 上时， 则PC=PA ， 同理可得：36,11m = 故点3660,1111E ⎛⎫-⎪⎝⎭ 综上，点E 的坐标为：1653,1122⎛⎫-- ⎪⎝⎭或6415,1111E ⎛⎫- ⎪⎝⎭或3660,1111E ⎛⎫- ⎪⎝⎭；②当E 在D 点时，作AD 的垂直平分线交AC 的垂直平分线于1P 点， 则156,2D ⎛⎫-⎪⎝⎭，1P 的纵坐标为15,4- 代入②式，解得：11715,,84P ⎛⎫-- ⎪⎝⎭ 同理当当E 在B 点时， 作AB 的垂直平分线交AC 的垂直平分线于2P 点，()()6,0,0,3,A B -AB ∴的中点为：33,2⎛⎫- ⎪⎝⎭，设AB 为：y ex f =+，603e f f +=⎧∴⎨=-⎩解得：23f ⎨⎪=-⎩∴ AB 直线方程为：132y x =-， 设AB 的垂直平分线方程为：12,y x b =-+1323,2b ∴-⨯+=-192b ∴=， ∴ AB 的垂直平分线方程为：92,2y x =-+122922y x y x ⎧=+⎪⎪∴⎨⎪=-+⎪⎩解得：152x y =⎧⎪⎨=⎪⎩251,,2P ⎛⎫∴ ⎪⎝⎭则圆心P 移动的路线长=221217515251 5.8248PP ⎛⎫⎛⎫=+++= ⎪ ⎪⎝⎭⎝⎭故答案为：8【点评】本题是二次函数的综合题，考查了二次函数与x 轴的交点坐标，利用待定系数法求解一次函数的解析式，三角形的外心的性质、一次函数的交点问题，勾股定理的应用，综合性很强，是难度较大类题目．4．（1）2122y x x =-+，点B （2，2）；（2）m=2或209m =；（3）存在；n=27时，抛物线向左平移． 【解析】 【分析】（1）将点A 和点O 的坐标代入解析式，利用待定系数法即可求得二次函数的解析式，然后利用配方法可求得点B 的坐标；（2）由点A 、点B 、点C 的坐标以及旋转的性质可知△△PDC 为等腰直角三角形，从而可得到点O′坐标为：（m ，m ），点C′坐标为：（32m ，2m），然后根据点在抛物线上，列出关于m 的方程，从而可解得m 的值；（3）如图，将AC′沿C′B 平移，使得C′与B 重合，点A 落在A′处，以过点B 的直线y=2为对称轴，作A′的对称点A″，连接OA″，由线段的性质可知当B′为OA″与直线y=2的交点时，四边形OB′C″A 的周长最短，先求得点B′的坐标，根据点B 移动的方向和距离从而可得出点抛物线移动的方向和距离． 【详解】解：（1）把原点O （0，0），和点A （4，0）代入y=12-x 2+bx+c ． 得040c b b c =⎧⎨-++=⎩，∴02c b =⎧⎨=⎩．∴22112(2)222y x x x =-+=--+． ∴点B 的坐标为（2，2）． （2）∵点B 坐标为（2，2）． ∴∠BOA=45°．∴△PDC 为等腰直角三角形． 如图，过C′作C′D ⊥O′P 于D ．∵O′P=OP=m．∴C′D=12O′P=12m．∴点O′坐标为：（m，m），点C′坐标为：（32m，2m）．当点O′在y=12-x2+2x上．则−12m2+2m＝m．解得：12m=，20m=（舍去）．∴m=2．当点C′在y=12-x2+2x上，则12-×(32m)2+2×32m＝12m，解得：120 9m=，20m=（舍去）．∴m=20 9（3）存在n=27，抛物线向左平移．当m=209时，点C′的坐标为（103，109）．如图，将AC′沿C′B平移，使得C′与B重合，点A落在A′处．以过点B的直线y=2为对称轴，作A′的对称点A″，连接OA″．当B′为OA″与直线y=2的交点时，四边形OB′C″A的周长最短．∵BA′∥AC′，且BA′=AC′，点A（4，0），点C′（103，109），点B（2，2）．∴点A′（83，89）．∴点A″的坐标为（83，289）．设直线OA″的解析式为y=kx，将点A″代入得：828 39k=，解得：k=76．∴直线OA″的解析式为y=76 x．将y=2代入得：76x=2，解得：x=127，∴点B′得坐标为（127，2）．∴n=2122 77 -=．∴存在n=27，抛物线向左平移．【点睛】本题主要考查的是二次函数、旋转的性质、平移的性质、路径最短等知识点，由旋转的性质和平移的性质求得点点O′坐标为：（m，m），点C′坐标为：（32m，2m）以及点B′的坐标是解题的关键．5．（1）见解析；（2）x=4，16【解析】【分析】（1）连接EF，根据矩形和正方形的判定与性质以及折叠的性质，运用SAS证明OBC≌OED即可；（2）连接EF、BE，再证明△OBE是直角三角形，然后再根据勾股定理得到y与x的函数关系式，最后根据二次函数的性质求最值即可．【详解】（1）证明：连接EF．∵四边形ABCD是矩形，∴AD＝BC，∠ABC＝∠BCD＝∠ADE＝∠DAF＝90°由折叠得∠DEF＝∠DAF，AD＝DE∴∠DEF＝90°又∵∠ADE ＝∠DAF ＝90°，∴四边形ADEF 是矩形又∵AD ＝DE ，∴四边形ADEF 是正方形∴AD ＝EF ＝DE ，∠FDE ＝45°∵AD ＝BC ，∴BC ＝DE由折叠得∠BCO ＝∠DCO ＝45°∴∠BCO ＝∠DCO ＝∠FDE ．∴OC ＝OD ．在△OBC 与△OED 中，BC DE BCO FDE OC OD =⎧⎪∠=∠⎨⎪=⎩，，， ∴△OBC ≌△OED （SAS ）；（2）连接EF 、BE ．∵四边形ABCD 是矩形，∴CD ＝AB ＝8．由（1）知，BC ＝DE∵BC ＝x ，∴DE ＝x∴CE ＝8－x由（1）知△OBC ≌△OED∴OB ＝OE ，∠OED ＝∠OBC ．∵∠OED ＋∠OEC ＝180°，∴∠OBC ＋∠OEC ＝180°．在四边形OBCE 中，∠BCE ＝90°，∠BCE ＋∠OBC ＋∠OEC ＋∠BOE ＝360°，∴∠BOE ＝90°．在Rt △OBE 中，OB 2＋OE 2＝BE 2．在Rt △BCE 中，BC 2＋EC 2＝BE 2．∴OB 2＋OE 2＝BC 2＋CE 2．∵OB 2＝y ，∴y ＋y ＝x 2＋(8－x)2．∴y ＝x 2－8x ＋32∴当x=4时，y 有最小值是16．【点睛】本题是四边形综合题，主要考查了矩形和正方形的判定与性质、折叠的性质、全等三角形的判定、勾股定理以及运用二次函数求最值等知识点，灵活应用所学知识是解答本题的关键．6．（1）B 点坐标(0，-1)，平移后的抛物线为2y=-x +2x+3；（2）点M 的坐标为(1+2，或(1-2，；（3）存在，1P (1,1)，2P (1,6)-，3P (12)，，4P (1,8)-，详解见解析．【解析】【分析】（1）将x=0代入抛物线公式2y=-x +2x-1求出y 值，即可得到抛物线与y 轴交点B 的坐标，平移后的抛物线的顶点为E(1,4)，可根据顶点式求出平移后抛物线的解析式；（2）因为抛物线向上平移4个单位，所以MN=4，又因为OM=ON ，可知点M 的纵坐标为-2，将y=-2代入原抛物线2y=-x +2x-1，即可求出x 值，点M 的坐标就可以表示出来． （3）要使C 、F 、P 为顶点的三角形为直角三角形，可以画一个以C 、F 为直径的圆（直径对应圆周角为直角），交抛物线对称轴x=-1可得点1P 、2P 的坐标解，另外可以使∠PCF=90°或∠CFP=90°，可分别得出点3P 、4P 的坐标解．【详解】解：（1）抛物线2y=-x +2x-1与y 轴相交于点B ，将x=0代入，求得y=-1，∴B 点坐标(0，-1)．∵设平移后的抛物线为2y=-(x-h)+k ，顶点为E(1,4)，即h=1，k=4，∴2y=-(x-1)+4，即平移后的抛物线为22y=-(x-1)+4=-x +2x+3．（2）如上图所示，∵原坐标顶点A(1，0)，平移后抛物线顶点为E(1,4)，∴抛物线向上平移了4个单位，即MN //y 轴，MN ⊥x 轴，又∵OM=ON ，MN=4，∴点O 在垂直平分线上，点M 、N 关于x 轴对称，∴M 点的纵坐标为–2，将y=-2代入2y=-x +2x-1，得：222-x +2x-1=-2-(x -2x+1)=-2(x-1)=2x=12± 解得：x=12±，∴点M 的坐标为(1+2-2)，或(1-2-2)，． （3）存在，且1P (1,1)，2P (1,6)-，3P (12)，，4P (1,8)-． 如图所示，点P 一共有四种结果，∵C 点为平移后的解析式与x 轴的左交点，将y=0代入2y=-x +2x+3，得x=-13或， ∴C(-1，0)，且点B(0，-1)，将点B(0，-1)、C(-1，0)代入直线BC 解析式为：y=kx+b ， ∴-k+b=0b=-1⎧⎨⎩，解得：k=-1b=-1⎧⎨⎩，即直线BC 解析式：y=-x-1， 根据题意可知，直线BC 与平移后的解析式相交于点F ，∴2y=-x-1y=-x +2x+3⎧⎨⎩，解得：x=-1（舍）或4，y=-5，即F(4，-5)， ∵要使C 、F 、P 为顶点的三角形为直角三角形，可以画一个以C 、F 为直径的圆，该圆与抛物线对称轴x=-1交点即为点P （因为圆的直径对应的圆周角为90°，即∠CPF=90°）∴以C 、F 为直径的圆，圆心为线段CF 的中点(32，5-2)，直径为线段CF 的长∴圆的方程为：22235x-+y+=22()()，将x=1代入圆的方程，得：y=1或-6， 即1P (1,1)，2P (1,6)-， ∵直线CF 解析式：y=-x-1，即斜率k=-1，即直线CF 与x 轴夹角为45°，要使C 、F 、P 为顶点的三角形为直角三角形，则使∠PCF=90°，直线CP 与x 轴夹角也为45°，即直线CP 斜率为1，直线CP 的解析式为：y=x+1，此时该直线与抛物线对称轴x=1的交点为3P (1,2)，又∵直线CF 解析式：y=-x-1，即斜率k=-1，即直线CF 与x 轴夹角为45°，要使C 、F 、P 为顶点的三角形为直角三角形，则使∠CFP=90°，直线FP 与x 轴夹角也为45°，即直线FP 斜率为1，直线FP 的解析式为：y=x-9，此时该直线与抛物线对称轴x=1的交点为4P (1,-8)．【点睛】本题考查了一元二次函数与坐标轴、直线的交点，一元二次函数的平移及应用，圆的直径所对应的圆周角为直角等知识点，该题有一定的难度，所以一定要结合图形进行分析，这样才不会把解遗漏．7．（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492． 【解析】【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =， 点P ，M 是CD ，DE 的中点， //PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =， 利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=，在Rt ABC ∆中，10AB AC ==，52AN =225272MN ∴=最大222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大． 方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大． 【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．8．（1）见解析；（2）60°；（3）不变，MN=23【解析】【分析】（1）连接AO、CO、BO、BD，根据菱形的性质得到AB=CB，然后根据SSS即可证明两三角形全等；（2）首先根据全等的性质得到O、B、D共线，然后根据三角形外角的性质得到∠BOC＝2∠ODC＝2∠OBC，最终根据余角的性质即可求解；（3）延长EM、EN交⊙O于F、G，连接FG、OF、OG，过点O作OH垂直于FG于点H，根据垂径定理和三角形中位线的性质得到MN=12FG，根据（2）问结论结合圆周角定理求得∠FOH＝60°，最后根据含30°的直角三角形的边角关系即可求解．【详解】（1）如图，连接AO、CO、BO、BD．∵AB是⊙O的切线，∴OA⊥AB∴∠BAO＝90°．∵四边形ABCD是菱形∴AB＝CB又∵AO＝CO，BO＝BO∴△BAO≌△BCO（SSS）∴∠BCO＝∠BAO＝90°，即OC⊥BC∴BC为⊙O的切线（2）∵△ABO≌△CBO∴∠ABO＝∠CBO∵四边形ABCD是菱形∴BD平分∠ABC，CB＝CD∴点O在BD上∵∠BOC＝∠ODC＋∠OCD，OD＝OC∴∠ODC＝∠OCD∴∠BOC＝2∠ODC∵CB＝CD∴∠OBC＝∠ODC∴∠BOC＝2∠OBC∵∠BOC＋∠OBC＝90°∴∠OBC＝30°∴∠ABC＝2∠OBC＝60°即∠B=60°；（3）不变延长EM、EN交⊙O于F、G，连接FG、OF、OG．过点O作OH垂直于FG于点H．∵EM⊥OA、EN⊥OC．∴M、N是EF、EG的中点．∴MN是△EFG的中位线∴MN=12 FG．由（2）知∠ABC＝60°∴∠AOC＝120°∴∠FOG＝∠AOC＝120°∴∠MEN＝12∠FOG＝60°，∴∠FOH＝60°，∴OH=2，FH=23∴FG=43∴MN=12FG=23【点睛】本题考查了菱形的性质，三角形全等的判定和性质，垂径定理，圆周角定理，正确的引出辅助线，熟练利用三角形和圆的知识点求解是本题的关键．9．（1）t=1；（2）存在，143t=，理由见解析；（3）可能，3455t≤≤或4533t≤≤或35t≤≤理由见解析【解析】【分析】（1）用待定系数法求出直线AC的解析式，根据题意用t表示出点H的坐标，代入求解即可；（2）根据已知，当点F运动到点O停止运动前，重叠最大面积是边长为1的正方形的面积，即不存在t，使重叠面积为9136S=，故t﹥4,用待定系数法求出直线AB的解析式，求出点H 落在BC 边上时的t 值，求出此时重叠面积为169﹤9136，进一步求出重叠面积关于t 的表达式，代入解t 的方程即可解得t 值； （3）由已知求得点D （2，1），AC=结合图形分情况讨论即可得出符合条件的时长．【详解】（1）由题意，A(0，2)，B(-4，0)，C(4，0)，设直线AC 的函数解析式为y=kx+b ，将点A 、C 坐标代入，得：402k b b +=⎧⎨=⎩，解得：122k b ⎧=-⎪⎨⎪=⎩， ∴直线AC 的函数解析式为122y x =-+， 当点H 落在AC 边上时，点E(3-t ，0)，点H （3-t ，1），将点H 代入122y x =-+，得： 11(3)22t =--+，解得：t=1； （2）存在，143t =，使得9136S =． 根据已知，当点F 运动到点O 停止运动前，重叠最大面积是边长为1的正方形的面积，即不存在t ，使重叠面积为9136S =，故t ﹥4， 设直线AB 的函数解析式为y=mx+n ，将点A 、B 坐标代入，得：402m n n -+=⎧⎨=⎩，解得：122m n ⎧=⎪⎨⎪=⎩， ∴直线AC 的函数解析式为122y x =+， 当t ﹥4时，点E （3-t ，0）点H （3-t ，t-3），G(0，t-3)， 当点H 落在AB 边上时，将点H 代入122y x =+，得： 13(3)22t t -=-+，解得：133t =； 此时重叠的面积为221316(3)(3)39t -=-=，∵169﹤9136，∴133﹤t ﹤5， 如图1，设GH 交AB 于S ，EH 交AB 于T,将y=t-3代入122y x =+得：1322t x -=+， 解得：x=2t-10，∴点S(2t-10，t-3)， 将x=3-t 代入122y x =+得：11(3)2(7)22y t t =-+=-， ∴点T 1(3,(7))2t t --，∴AG=5-t ，SG=10-2t ，BE=7-t ，ET=1(7)2t -， 211(7)24BET S BE ET t ∆==-, 21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-， 由2527133424t t -+-=9136得：1143t =，29215t =﹥5(舍去)， ∴143t =；（3）可能，35≤t≤1或t=4． ∵点D 为AC 的中点，且OA=2,OC=4，∴点D （2，1），AC=255易知M 点在水平方向以每秒是4个单位的速度运动； 当0﹤t ﹤12时，M 在线段OD 上，H 未到达D 点，所以M 与正方形不相遇； 当12﹤t ﹤1时， 12+12÷（1+4）=35秒，∴t =35时M 与正方形相遇，经过1÷（1+4）=15秒后，M 点不在正方行内部，则3455t ≤≤； 当t=1时，由（1）知，点F 运动到原E 点处，M 点到达C 处；当1≤t≤2时，当t=1+1÷（4-1）=43秒时，点M 追上G 点，经过1÷（4-1）=13秒，点M 都在正方形EFGH 内（含边界），4533t ≤≤ 当t=2时，点M 运动返回到点O 处停止运动，当 t=3时，点E 运动返回到点O 处, 当 t=4时，点F 运动返回到点O 处,当35t ≤≤时，点M 都在正方形EFGH 内（含边界），综上，当3455t ≤≤或4533t ≤≤或35t ≤≤时，点M 可能在正方形EFGH 内（含边界）．【点睛】本题考查了一次函数与几何图形的综合，涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识，解答的关键是认真审题，提取相关信息，利用待定系数法、数形结合法等解题方法确定解题思路，进而推理、探究、发现和计算．10．（1）⊙O 的半径为10，（2）AD 长为19.2，（3）存在，四边形AGEF 的面积的最大值为34.56．【解析】【分析】（1）如图1利用垂径定理构造直角三角形解决问题．（2）如图2在（1）基础上利用圆周角和圆心角的关系证明△OCH∽△DCK，求出Dk，再据垂径定理求得AD．（3）如图3以平行四边形AGEF的面积为函数，以AG边上的高为自变量，列出一个二次函数，利用二次函数的最值求解．【详解】（1）如图1连接OC ，因为OB AC ⊥,根据垂径定理知 HC=1112622AC =⨯= 在RT △BCH 中∵210BC = ∴由勾股定理知：2222BH (210)62BC HC =-=-=∴OH=OB-BH=OB-2又∵OB=OC所以在RT △OCH 中，由勾股定理可得方程：2222)6OC OC -+=（解得OC=10．（2）如图2，在⊙O 中：∵AC=CD ，∴OC ⊥AD （垂径定理）∴AD=2KD ，∠HCK=∠DCK又∵∠DKC=∠OHC=90°∴△OCH ∽△DCK∴KD DC HO OC= ∴DC 1248KD=8105HO OC =⨯==9.6 ∴AD=2KD=19.2．。

图1固体能否传声A真空能否传声B音调与频率的关系C响度与振幅的关系D 中考冲刺一一、基础训练（12min）1．在原子中，不带电的粒子是（）A质子B中子C电子D核子2．端午节，小明给奶奶剥粽子时闻到粽子的香味，这个现象说明（）A 分子间存在作用力B 分子间有空隙C分子由原子组成D分子在不停地运动3．研究牛顿第一定律时运用了实验和推理的方法，在图1所示声现象的探究中运用该方法的是（）4．图2所示的四种现象中，属于光的反射现象的是（）5．小刚学习了磁的知识后，标出了如图3四种情况磁体的磁极（小磁针的黑端为N 极），其中正确的是（）6．用测力计两次拉动重为G 的物体竖直向上运动，两次运动的s —t 图像如图4所示，则下列判断中正确的是（）A 第一次测力计的示数一定大于第二次测力计的示数B 第一次测力计的示数可能小于第二次测力计的示数C 运动相同时间，第一次通过的路程一定大于第二次通过的路程D运动相同时间，第一次通过的路程可能小于第二次通过的路程t /秒12图4图3图2桥在水中形成“倒影”放大镜把文字放大鸽子在沙滩上形成影子筷子好像在水面处“折断”ABCD7．在图5所示的电路中，电源电压保持不变。

电键S 闭合后，发现只有一个电压表的指针位置发生了变化。

若电路中只有一处故障，且只发生在电阻R 或灯泡L 处，则可能是（）A 灯泡L 发光，电阻R 短路B 灯泡L 发光，电阻R 断路C 灯泡L 不发光，电阻R 短路D灯泡L 不发光，电阻R 断路8．甲、乙两个实心立方体分别放在水平地面上（ρ甲＜ρ乙），它们对水平地面的压强相等。

若沿竖直方向将甲、乙两个立方体各切除一部分，且使甲、乙两个立方体剩余部分的厚度相同，再将切除部分分别叠放在各自剩余部分上面，则水平地面受到甲、乙的压强（）A p 甲＞p 乙Bp 甲＝p 乙Cp 甲＜p 乙D以上情况均有可能二、填空题9．我国家庭电路中用电器正常工作的电压为伏，电键与它所控制的用电器之间是连接的（选填“串联”或“并联”），各用电器消耗的电能是用表来测量的。

上海吴淞初级中学七年级数学压轴题专题一、七年级上册数学压轴题1．已知数轴上点A对应的数为6-，点B在点A右侧，且,A B两点间的距离为8．点P为数轴上一动点，点C在原点位置．（1）点B的数为____________；（2）①若点P到点A的距离比到点B的距离大2，点P对应的数为_________；②数轴上是否存在点P，使点P到点A的距离是点P到点B的距离的2倍？若存在，求出点P对应的数；若不存在，请说明理由；（3）已知在数轴上存在点P，当点P到点A的距离与点P到点C的距离之和等于点P到点B的距离时，点P对应的数为___________；2．如图，在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a、c 满足|a+2|+（c﹣7）2=0．（1）a=，b=，c=；（2）若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；（3）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C 之间的距离表示为BC．则AB=，AC=，BC=．（用含t的代数式表示）（4）请问：3BC﹣2AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．3．“数形结合”是重要的数学思想．请你结合数轴与绝对值的知识回答下列问题：（1）一般地，数轴上表示数m和数n的两点之间的距离等于│m－n│．如果表示数a和－2的两点之间的距离是3，记作│a－(－2)│＝3，那么a＝．（2）利用绝对值的几何意义，探索│a＋4│＋│a－2│的最小值为______，若│a＋4│＋│a－2│＝10，则a的值为________．（3）当a＝______时，│a＋5│＋│a－1│＋│a－4│的值最小．（4）如图，已知数轴上点A表示的数为4，点B表示的数为1，C是数轴上一点，且AC＝8，动点P从点B出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t>0)秒．点M是AP的中点，点N是CP的中点，点P在运动过程中，线段MN的长度是否发生变化?若变化，请说明理由；若不变，求线段MN的长度．4．如图，在数轴上点A表示的数是－3，点B在点A的右侧，且到点A的距离是18；点C在点A 与点B 之间，且到点B 的距离是到点A 距离的2倍． （1）点B 表示的数是；点C 表示的数是；（2）若点P 从点A 出发，沿数轴以每秒4个单位长度的速度向右匀速运动；同时，点Q 从点B 出发，沿数轴以每秒2个单位长度的速度向左匀速运动．设运动时间为t 秒，当P 运动到C 点时，点Q 与点B 的距离是多少？（3）在（2）的条件下，若点P 与点C 之间的距离表示为PC ，点Q 与点B 之间的距离表示为QB ．在运动过程中，是否存在某一时刻使得PC+QB ＝4？若存在，请求出此时点P 表示的数；若不存在，请说明理由．5．数轴上有,,A B C 三点，给出如下定义；若其中一个点与其他两个点的距离恰好满足2倍的数量关系，则称该点是其它两个点的：“关联点”（1）例图，数轴上点,,A B C 三点所表示的数分别为1,3,4，点B 到点A 的距离AB = ，点B 到点C 的距离是 ，因为AB 是BC 的两倍，所以称点B 是点,A C的“关联点”．（2）若点A 表示数2,-点B 表示数1，下列各数1,2,4,6-所对应的点分别是1234,,,C C C C ，其中是点,A B 的“关联点”的是 ；（3）点A 表示数10-，点B 表示数为15,P 数轴上一个动点；若点P 在点B 的左侧，且点P是点AB 、的“关联点”，求此时点Р表示的数；若点P 在点B 的右侧，点P A B 、、中，有一个点恰好是其它两个点的“关联点”．请直接写出此时点Р表示的数6．已知，A ，B 在数轴上对应的数分用a ，b 表示，且()220100a b -++=，数轴上动点P 对应的数用x 表示.(1)在数轴上标出A 、B 的位置，并直接写出A 、B 之间的距离； (2)写出x a x b -+-的最小值；(3)已知点C 在点B 的右侧且BC ＝9，当数轴上有点P 满足PB ＝2PC 时， ①求P 点对应的数x 的值；②数轴上另一动点Q 从原点开始第一次向左移动1个单位长度，第二次向右移动3个单位长度，第三次向左移动5个单位长度，第四次向右移动7个单位长度，…点Q 能移动到与①中的点P 重合的位置吗？若都不能，请直接回答.若能，请直接指出，第几次移动可以重合。

上海民办浦东交中初级中学八年级上册压轴题数学模拟试卷及答案一、压轴题1．已知：如图1，直线//AB CD ，EF 分别交AB ，CD 于E ，F 两点，BEF ∠，DFE ∠的平分线相交于点K ．（1）求K ∠的度数；（2）如图2，BEK ∠，DFK ∠的平分线相交于点1K ，问1K ∠与K ∠的度数是否存在某种特定的等量关系？写出结论并证明；（3）在图2中作1BEK ∠，1DFK ∠的平分线相交于点2K ，作2BEK ∠，2DFK ∠的平分线相交于点3K ，依此类推，作n BEK ∠，n DFK ∠的平分线相交于点1n K +，请用含的n 式子表示1n K ∠+的度数．（直接写出答案，不必写解答过程）2．在《经典几何图形的研究与变式》一课中，庞老师出示了一个问题：“如图1，等腰直角三角形的三个顶点分别落在三条等距的平行线1l ，2l ，3l 上，90BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长度”.在研究这道题的解法和变式的过程中，同学们提出了很多想法：（1）小明说：我只需要过B 、C 向1l 作垂线，就能利用全等三角形的知识求出AB 的长. （2）小林说：“我们可以改变ABC 的形状.如图2，AB AC =，120BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长.”（3）小谢说：“我们除了改变ABC 的形状，还能改变平行线之间的距离.如图3，等边三角形ABC 三个顶点分别落在三条平行线1l ，2l ，3l 上，且1l 与2l 之间的距离为1，2l 与3l 之间的距离为2，求AB 的长、”请你根据3位同学的提示，分别求出三种情况下AB 的长度.3．（阅读材科）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，连接AO，下列结论：①BD=EC；②∠BOC=60°；③∠AOE=60°；④EO=CO，其中正确的有．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB=BC，∠ABC=∠BDC=60°，试探究∠A与∠C的数量关系．4．问题情景：数学课上，老师布置了这样一道题目，如图1，△ABC是等边三角形，点D 是BC的中点，且满足∠ADE＝60°，DE交等边三角形外角平分线于点E．试探究AD与DE 的数量关系．操作发现：（1）小明同学过点D作DF∥AC交AB于F，通过构造全等三角形经过推理论证就可以解决问题，请您按照小明同学的方法确定AD与DE的数量关系，并进行证明．类比探究：（2）如图2，当点D是线段BC上任意一点(除B、C外)，其他条件不变，试猜想AD与DE之间的数量关系，并证明你的结论．拓展应用：（3）当点D 在线段BC 的延长线上，且满足CD ＝BC ，在图3中补全图形，直接判断△ADE 的形状(不要求证明)．5．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明． 同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．”小伟：“通过做辅助线构造全等三角形，就可以将问题解决．”......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．6．已知ABC 和ADE 都是等腰三角形，AB AC =，AD AE =，DAE BAC ∠=∠． （初步感知）（1）特殊情形：如图①，若点D ，E 分别在边AB ，AC 上，则DB __________EC ．（填＞、＜或=）（2）发现证明：如图②，将图①中的ADE 绕点A 旋转，当点D 在ABC 外部，点E 在ABC 内部时，求证：DB EC =．（深入研究）（3）如图③，ABC 和ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则CDB ∠的度数为__________；线段CE ，BD 之间的数量关系为__________．（4）如图④，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，点C 、D 、E 在同一直线上，AM 为ADE 中DE 边上的高，则CDB ∠的度数为__________；线段AM ，BD ，CD 之间的数量关系为__________．（拓展提升）（5）如图⑤，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，将ADE 绕点A 逆时针旋转，连结BE 、CD ．当5AB =，2AD =时，在旋转过程中，ABE △与ADC 的面积和的最大值为__________．7．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q 是直线l 上的动点，问是否存在点P ，使得以P C Q 、、为顶点的三角形和ABP ∆全等，若存在求点P 的坐标以及此时对应的点Q 的坐标，若不存在，请说明理由．8．如图（1），AB ＝4cm ，AC ⊥AB ，BD ⊥AB ，AC ＝BD ＝3cm ．点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t （s ）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t ＝1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC ⊥AB ，BD ⊥AB”为改“∠CAB ＝∠DBA ＝60°”，其他条件不变．设点 Q 的运动速度为x /cm s ，是否存在实数x ，使得△ACP 与△BPQ 全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．9．某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并证明．10．问题背景：（1）如图1，已知△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE＝BD＋CE．拓展延伸：（2）如图2，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC．请写出DE、BD、CE三条线段的数量关系．（不需要证明）实际应用：（3）如图，在△ACB中，∠ACB＝90°，AC＝BC，点C的坐标为(－2，0)，点A的坐标为(－6，3)，请直接写出B点的坐标．11．（1）在等边三角形ABC中，①如图①，D，E分别是边AC，AB上的点且AE=CD，BD与EC交于点F，则∠BFE的度数是度；②如图②，D，E分别是边AC，BA延长线上的点且AE=CD，BD与EC的延长线交于点F，此时∠BFE的度数是度；（2）如图③，在△ABC中，AC=BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D ，E 分别在AC ，OA 的延长线上，AE=CD ，BD 与EC 的延长线交于点F ，若∠ACB=α，求∠BFE 的大小．（用含α的代数式表示）．12．已知，如图1，直线l 2⊥l 1，垂足为A ，点B 在A 点下方，点C 在射线AM 上，点B 、C 不与点A 重合，点D 在直线11上，点A 的右侧，过D 作l 3⊥l 1，点E 在直线l 3上，点D 的下方．（1）l 2与l 3的位置关系是 ；（2）如图1，若CE 平分∠BCD ，且∠BCD ＝70°，则∠CED ＝ °，∠ADC ＝ °； （3）如图2，若CD ⊥BD 于D ，作∠BCD 的角平分线，交BD 于F ，交AD 于G ．试说明：∠DGF ＝∠DFG ；（4）如图3，若∠DBE ＝∠DEB ，点C 在射线AM 上运动，∠BDC 的角平分线交EB 的延长线于点N ，在点C 的运动过程中，探索∠N :∠BCD 的值是否变化，若变化，请说明理由；若不变化，请直接写出比值．13．数学活动课上，老师出了这样一个题目：“已知：MF NF ⊥于F ，点A 、C 分别在NF 和MF 上，作线段AB 和CD （如图1），使90FAB MCD ∠-∠=︒．求证：//AB CD ”．（1）聪聪同学给出一种证明问题的辅助线：如图2，过A 作//AG FM ，交CD 于G ．请你根据聪聪同学提供的辅助线（或自己添加其它辅助线），给出问题的证明． （2）若点E 在直线CD 下方，且知30BED ∠=︒，直接写出ABE ∠和CDE ∠之间的数量关系．14．（阅读材料）：（1）在ABC ∆中，若90C ∠=︒，由“三角形内角和为180°”得1801809090A B C ∠︒+∠=-∠︒︒-=︒=．（2）在ABC ∆中，若90A B ∠+∠=︒，由“三角形内角和为180°”得180()1809090C A B ∠=︒-∠+∠=︒-︒=︒．（解决问题）：如图①，在平面直角坐标系中，点C 是x 轴负半轴上的一个动点．已知//AB x 轴，交y 轴于点E ，连接CE ，CF 是∠ECO 的角平分线，交AB 于点F ，交y 轴于点D ．过E 点作EM 平分∠CEB ，交CF 于点M ．（1）试判断EM 与CF 的位置关系，并说明理由；（2）如图②，过E 点作PE ⊥CE ，交CF 于点P ．求证：∠EPC=∠EDP ；（3）在（2）的基础上，作EN 平分∠AEP ，交OC 于点N ，如图③．请问随着C 点的运动，∠NEM 的度数是否发生变化？若不变，求出其值：若变化，请说明理由．15．在△ABC 中，已知∠A ＝α．（1）如图1，∠ABC 、∠ACB 的平分线相交于点D ．求∠BDC 的大小（用含α的代数式表示）；（2）如图2，若∠ABC 的平分线与∠ACE 的平分线交于点F ，求∠BFC 的大小（用含α的代数式表示）；（3）在（2）的条件下，将△FBC 以直线BC 为对称轴翻折得到△GBC ，∠GBC 的平分线与∠GCB 的平分线交于点M （如图3），求∠BMC 的度数（用含α的代数式表示）．16．（1）发现：如图1，ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。

一、选择题1．小明制作了5张卡片，上面分别写了一个条件：①AB BC =；②AB BC ⊥；③AD BC =；④AC BD ⊥，⑤AC BD =．从中随机抽取一张卡片，能判定ABCD 是菱形的概率为（ ）A ．15B ．25C ．35D ．452．由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘，如果一个转盘转出了红色，另一转盘转出了蓝色，游戏者就配成了紫色，下列说法正确的是（ ）A ．两个转盘转出蓝色的概率一样大B ．如果A 转盘转出了蓝色，那么B 转盘转出蓝色的可能性变小了C ．游戏者配成紫色的概率为16D ．先转动A 转盘再转动B 转盘和同时转动两个转盘，游戏者配成紫色的概率不同 3．下列事件中，必然事件是（ ）A ．抛掷1个均匀的骰子，出现6点向上B ．两直线被第三条直线所截，同位角相等C ．366人中至少有2人的生日相同D ．实数的绝对值是非负数4．国学经典《声律启蒙》中有这样一段话：“斜对正，假对真，韩卢对苏雁，陆橘对庄椿”，现有四张卡片依次写有一“斜”、“正”、“假”、“真”，四个字（4张卡片除了书写汉字不同外其他完全相同），现从四张卡片中随机抽取两张，则抽到的汉字恰为相反意义的概率是（ ）A ．12B ．13C ．23D ．145．如果小球在如图所示的地面上自由滚动，并随机停留在某块方砖上，那么它最终停留在黑色区域的概率是（ ）A ．14B ．34C ．12D ．386．下列说法：①“明天的降水概率为80%”是指明天有80%的时间在下雨；②连续抛一枚硬币50次，出现正面朝上的次数一定是25次（ ）A ．只有①正确B ．只有②正确C ．①②都正确D ．①②都错误 7．某一超市在“五•一”期间开展有奖促销活动，每买100元商品可参加抽奖一次，中奖的概率为13．小张这期间在该超市买商品获得了三次抽奖机会，则小张( ) A ．能中奖一次 B ．能中奖两次C ．至少能中奖一次D ．中奖次数不能确定 8．某学校在进行防溺水安全教育活动中，将以下几种在游泳时的注意事项写在纸条上并折好，内容分别是：①互相关心；②互相提醒；③不要相互嬉水；④相互比潜水深度；⑤选择水流湍急的水域；⑥选择有人看护的游泳池．小颖从这6张纸条中随机抽出一张，抽到内容描述正确的纸条的概率是（ ）A ．12B ．13C ．23D ．169．在一个不透明的袋子中，装有红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同．若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15．和0.45，则该袋子中的白色球可能有( )A ．6个B ．16个C ．18个D ．24个10．现有A 、B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P （,x y ），那么他们各掷一次所确定的点P 落在已知抛物线24y x x =-+上的概率为（ ）A ．118B ．112C ．19D ．1611．某班学生做“用频率估计概率”的实验时，给出的某一结果出现的频率折线图，则符合这一结果的实验可能是（ ）A ．抛一枚硬币，出现正面朝上B ．从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数C ．从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球D ．一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃12．在70周年国庆阅兵式上有两辆阅兵车的车牌号如图所示（每辆阅兵车的车牌号含7位数字或字母），则“9”这个数字在这两辆车牌号中出现的概率为（ ）A．37B．314C．326D．11213．罚球是篮球比赛中得分的一个组成部分，罚球命中率的高低对篮球比赛的结果影响很大．如图是对某球员罚球训练时命中情况的统计：下面三个推断：①当罚球次数是500时，该球员命中次数是411，所以“罚球命中”的概率是0.822；②随着罚球次数的增加，“罚球命中”的频率总在0.812附近摆动，显示出一定的稳定性，可以估计该球员“罚球命中”的概率是0.812；③由于该球员“罚球命中”的频率的平均值是0.809，所以“罚球命中”的概率是0.809．其中合理的是（）A．①B．②C．①③D．②③第II卷（非选择题）请点击修改第II卷的文字说明参考答案14．下列说法正确的是（）A．“穿十条马路连遇十次红灯”是不可能事件B．任意画一个三角形，其内角和是180°是必然事件C．某彩票中奖概率为1%，那么买100张彩票一定会中奖D．“福山福地福人居”这句话中任选一个汉字，这个字是“福”字的概率是1 215．下列事件属于不可能事件的是（）A．太阳从东方升起B．1＋1＞3C．1分钟＝60秒D．下雨的同时有太阳二、填空题16．在一个不透明的盒子里装有4个标有1，2，3，4的小球，它们形状、大小完全相同．小明从盒子里随机取出一个小球，记下球上的数字，作为点P的横坐标x，放回然后再随机取出一个小球，记下球上的数字，作为点P的纵坐标y．则点P在以原点为圆心，5为半径的圆上的概率为_____．17．从﹣2，﹣1，0，13，1，2这六个数字中，随机抽取一个数记为a，则使得关于x的方程213axx+=-的解为非负数，且满足关于x的不等式组12321x ax⎧->⎪⎨⎪-+≤⎩只有三个整数解的概率是_____．18．如图，点O为正方形的中心，点E、F分别在正方形的边上，且∠EOF＝90°，随机地往图中投一粒米，则米粒落在图中阴影部分的概率是___________．19．小明、小虎、小红三人排成一排拍照片，小明站在中间的概率是____________．20．重庆市某校初二（3）班同学，在学校组织的语文作文选拔考试中，有三名同学满分，其中有一名男生和两名女生，现在从三名满分同学中随机抽取两名同学参加重庆市优秀作文比赛，则选出来的两名同学刚好是一男一女的概率是_____．21．如图所示的转盘分成8等份，若自由转动转盘一次，停止后，指针落在阴影区域内的概率是_______．22．若一个袋子中装有形状与大小均完全相同有4张卡片,4张卡片上分别标有数字2-,1-,2,3,现从中任意抽出其中两张卡片分别记为x,y,并以此确定点()P x,y,那么点P落在直线y x1=-+上的概率是____.23．某种油菜籽在相同条件下发芽试验的结果如下：每批粒数501003004006001000发芽的频数4596283380571948这种油菜籽发芽的概率的估计值是______．（结果精确到0.01）24．一个盒子中装有标号为1、2、3、4、5的五个小球，这些球除了标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于6的概率为______．25．如图，这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．已知AE=5，BE=3，若向正方形ABCD内随意投掷飞镖（每次均落在正方形ABCD内，且落在正方形ABCD内任何一点的机会均等），则恰好落在正方形EFGH内的概率为__________．26．我市倡导垃圾分类投放，将日常垃圾分成四类，分别投放四种不同颜色的垃圾桶中，在“垃圾分类”模拟活动中，某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中，则这个同学正确分类投放垃圾的概率是______.三、解答题27．某数学小组为调查成都七中万达学校周五放学时学生的回家方式，随机抽取了部分学生进行调查，所有被调查的学生都需从“A：乘坐电动车，B：乘坐普通公交车或地铁，C：乘坐学校的定制公交车，D：乘坐家庭汽车，E：步行或其他”这五种方式中选择最常用的一种，随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图，请结合统计图回答下列问题．（1）本次调查中一共调查了名学生；扇形统计图中， E选项对应的扇形心角是度．（2）请补全统计图．（3）若甲、乙两名学生放学时从A、B、C三种方式中随机选择一种，请用列表法或画树状图的方法，求出甲、乙两名学生恰好选择同一种交通工具的概率．28．2019年1月，温州轨道交通1S线正式运营，1S线有以下4种购票方式：A．二维码过闸 B．现金购票 C．市名卡过闸 D．银联闪付（1）某兴趣小组为了解最受欢迎的购票方式，随机调查了某区的若干居民，得到如图所示的统计图，已知选择方式D的有200人，求选择方式A的人数.（2）小博和小雅对A，B，C三种购票方式的喜爱程度相同，随机选取一种方式购票，求他们选择同一种购票方式的概率.（要求列表或画树状图）.29．在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复.下表是活动进行中的一组统计数据：摸球的次数n1001502005008001000摸到白球的次数m5996b295480601摸到白球的频率mna0.640.580.590.600.601（1）上表中的a=________，b=________；（2）“摸到白球的”的概率的估计值是_________（精确到0.1）；（3）如果袋中有12个白球，那么袋中除了白球外，还有多少个其它颜色的球？30．李老师为了解学生完成数学课前预习的具体情况，对部分学生进行了跟踪调查，并将调查结果分为四类，A：很好；B：较好；C：一般；D：较差．制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）李老师一共调查了名同学？（2）C类女生有名，D类男生有名，将下面条形统计图补充完整；（3）为了共同进步，李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．。

一、中考几何压轴题1．已知：60AOC BOC ∠=∠=︒，过平面内一点P 分别向OA 、OB 、OC 画垂线，垂足分别为D 、E 、F ． （问题引入）如图①，当点P 在射线OC 上时，求证：OD OE =．（类比探究）（1）如图②，当点P 在AOC ∠内部，点E 在射线OB 上时，求证：OD OE OF +=．（2）当点P 在AOC ∠内部，点E 在射线OB 的反向延长线上时，在图③中画出示意图，并直接写出线段OD 、OE 、OF 之间的数量关系． （知识拓展）如图④，AB 、CD 、EF 是O 的三条弦，都经过圆内一点P ，且60FPD BPD ∠=∠=︒．判断PA PD PE ++与PB PC PF ++的数量关系，并证明你的结论．2．（发现问题）（1）如图1， 已知CAB ∆和CDE ∆均为等边三角形，D 在AC 上，E 在CB 上， 易得线段AD 和BE 的数量关系是 ．（2）将图1中的CDE ∆绕点C 旋转到图2的位置， 直线AD 和直线BE 交于点F ①判断线段AD 和BE 的数量关系，并证明你的结论． ②图2中AFB ∠的度数是 ．（3）（探究拓展）如图3，若CAB ∆和CDE ∆均为等腰直角三角形，90ABC DEC ∠=∠=，AB BC =，DE EC =， 直线AD 和直线BE 交于点F ， 分别写出AFB ∠的度数， 线段AD 、BE 之间的数量关系 ．3．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．原题：如图1，在平行四边形ABCD 中，点E 是BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G ．若3AFEF =，求CD CG的值．（1）尝试探究在图1中，过点E 作//EH AB 交BG 于点H ，则AB 和EH 的数量关系是_________，CG 和EH 的数量关系是_________，CDCG的值是_________． （2）类比延伸如图2，在原题的条件下，若()0AF m m EF =>，则CD CG的值是_________（用含有m 的代数式表示），试写出解答过程． （3）拓展迁移如图3，梯形ABCD 中，//DC AB ，点E 是BC 的延长线上的一点，AE 和BD 相交于点F ．若ABa CD =，BCb BE=，()0,0a b >>，则AF EF 的值是________（用含a 、b 的代数式表示）．4．（问题发现）（1）如图1所示，在Rt ABC △中，90BAC ∠=︒，4AB AC ==，点D 在BC 边上，且3BD CD =，将线段AD 绕点A 顺时针旋转90°得到线段AE ，连接DE 、BE ，BE BD +的值为______；（类比探究）（2）如图2所示，在（1）的条件下，点P 为AB 的中点，3BD CD =，将线段PD 绕点P 顺时针旋转90°得到PE ，连接BE ，则BE BD +的值会发生改变吗？说明你的理由； （拓展延伸）（3）如图3所示，在钝角ABC 中，AB AC =，BAC α∠=，点P 在边BA 的延长线上，BP k =，连接PD ．将线段PD 绕着点P 顺时针旋转，旋转角EPD α∠=，连接DE ，则BD BE +=______（请用含有k ，α的式子表示）．5．综合与实践 动手操作利用旋转开展教学活动，探究图形变换中蕴含的数学思想方法．如图1，将等腰直角三角形ABC 的AB 边绕点B 顺时针旋转90°得到线段A B '，90ACB ∠=︒，1AC =，连接A C '，过点A '作A H CB '⊥交CB 延长线于点H ．思考探索 （1）在图1中：①求证：ABC A BH '≌△△； ②A BC '的面积为______； ③tan A CB '∠=______． 拓展延伸（2）如图2，若ABC 为任意直角三角形，90ACB ∠=︒．BC 、AC 、AB 分别用a 、b 、c 表示．请用a 、b 、c 表示： ①A BC '的面积：______； ②A C '的长：______；（3）如图3，在ABC 中，AB AC =，AB A B '⊥，10AB =，12BC =，5A B '=，连接A C '．①A BC '的面积为______；②点D 是BC 边的高上的一点，当AD =______时，A D DB '+有最小值______． 6．（1）（操作）如图，请用尺规作图确定圆的圆心P ，保留作图痕迹，不要求写作法；（2）（探究）如图，若（1）中的圆P 的半径为2，放入平面直角坐标系中，使它与x 轴，y 轴分别切于点B 和C ，点A 的坐标为()8,0，过点A 的直线与圆P 有唯一公共点D （与B 不重合）时，求点D 的坐标；（3）（拓展）如图3，点M 从点()8,0A 出发，以每秒1个单位的速度沿x 轴向点O 运动，同时，点N 从原点O 出发，以每秒1个单位的速度沿y 轴向上运动，设运动时间为t （08s t <<），过点M ，N ，O 三点的圆，交第一象限角平分线OG 于点E ，当t 为何值时，MN 有最小值，求出此时OMEN S 四边形，并探索在变化过程中OMEN S 四边形的值有变化吗？为什么？7．（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，点G，F分别在边CD，AB上，GF⊥AE．①求证：DQ＝AE；②推断：GFAE的值为；（2）类比探究：如图（2），在矩形ABCD中，BCAB＝k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF 于点O．试探究GF与AE之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP，当k＝23时，若tan∠CGP＝34，GF＝210，求CP的长．8．在矩形ABCD中，ADkAB（k为常数），点P是对角线BD上一动点（不与B，D重合），将射线PA绕点P逆时针旋转90°与射线CB交于点E，连接AE．（1）特例发现：如图1，当k=1时，将点P移动到对角线交点处，可发现点E与点B重合，则PAPE= ，∠AEP = ；当点P 移动到其它位置时，∠AEP 的大小 （填“改变”或“不变”）；（2）类比探究：如图2，若k ≠1时，当k 的值确定时，请探究∠AEP 的大小是否会随着点P 的移动而发生变化，并说明理由；（3）拓展应用：当k ≠1时，如图2，连接PC ，若PC ⊥BD ，//AE PC ，PC =2，求AP 的长．9．在ABC 中，AB AC =，点D ､E 分别是BC AC ､的中点，将CDE △绕点C 按顺时针方向旋转一定的角度，连接BD AE ､． 观察猜想（1）如图①，当60BAC ∠=︒时，填空： ①AEBD=______________； ②直线BD AE ､所夹锐角为____________； 类比探究（2）如图②，当90BAC ∠=︒时，试判断AEBD的值及直线BD AE ､所夹锐角的度数，并说明理由； 拓展应用（3）在（2）的条件下，若2DE =CDE △绕着点C 在平面内旋转，当点D 落在射线AC 上时，请直接写出2AE 的值． 10．综合与实践 操作探究（1）如图1，将矩形ABCD 折叠，使点A 与点C 重合，折痕为EF ，AC 与EF 交于点G ．请回答下列问题：①与AEG △全等的三角形为______，与AEG △相似的三角形为______．并证明你的结论：（相似比不为1，只填一个即可）：②若连接AF 、CE ，请判断四边形AFCE 的形状：______．并证明你的结论； 拓展延伸（2）如图2，矩形ABCD 中，2AB =，4BC =，点M 、N 分別在AB 、DC 边上，且AM NC =，将矩形折叠，使点M 与点N 重合，折痕为EF ，MN 与EF 交于点G ，连接ME ．①设22m AM AE =+，22n ED DN =+，则m 与n 的数量关系为______； ②设AE a =，AM b =，请用含a 的式子表示b ：______； ③ME 的最小值为______．11．综合与实践——探究特殊三角形中的相关问题 问题情境：某校学习小组在探究学习过程中，将两块完全相同的且含60︒角的直角三角板ABC 和AFE 按如图1所示位置放置，且Rt ABC 的较短直角边AB 为2，现将Rt AEF 绕A 点按逆时针方向旋转α(090)α︒<<︒，如图2，AE 与BC 交于点M ，AC 与EF 交于点N ，BC 与EF 交于点P ．（1）初步探究：勤思小组的同学提出：当旋转角α= 时，AMC 是等腰三角形； （2）深入探究：敏学小组的同学提出在旋转过程中，如果连接AP ，CE ，那么AP 所在的直线是线段CE 的垂直平分线．请帮他们证明； （3）再探究：在旋转过程中，当旋转角30α=︒时，求ABC 与AFE △重叠的面积； （4）拓展延伸：在旋转过程中，CPN 是否能成为直角三角形？若能，直接写出旋转角α的度数；若不能，说明理由．12．△ABC 中，∠BAC=α°，AB=AC ，D 是BC 上一点，将AD 绕点A 顺时针旋转α°，得到线段AE ，连接BE ．（1）（特例感知）如图1，若α=90，则BD+BE 与AB 的数量关系是 ．（2）（类比探究）如图2，若α=120，试探究BD+BE 与AB 的数量关系，并证明．（3）（拓展延伸）如图3，若α=120，AB=AC=4，BD=33，Q为BA延长线上的一点，将QD绕点Q顺时针旋转120°，得到线段QE，DE⊥BC，求AQ的长．13．定义：有一组邻边相等且对角互补的四边形叫做等补四边形．（问题理解）(1)如图1，点A、B、C在⊙O上，∠ABC的平分线交⊙O于点D，连接AD、CD．求证：四边形ABCD是等补四边形；（拓展探究）(2)如图2，在等补四边形ABCD中，AB＝AD，连接AC，AC是否平分∠BCD？请说明理由；（升华运用）(3)如图3，在等补四边形ABCD中，AB＝AD，其外角∠EAD的平分线交CD的延长线于点F．若CD＝6，DF＝2，求AF的长．14．问题提出（1）如图（1），在等边三角形ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边三角形AMN，连接CN，则∠ACN＝ °．类比探究（2）如图（2），在等边三角形ABC中，点M是BC延长线上的任意一点（不含端点C），其他条件不变，（1）中的结论还成立吗？请说明理由．拓展延伸（3）如图（3），在等腰三角形ABC中，BA＝BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰三角形AMN，使AM＝MN，连接CN．添加一个条件，使得∠ABC＝∠ACN仍成立，写出你所添加的条件，并说明理由．15．我们定义：连结凸四边形一组对边中点的线段叫做四边形的“准中位线”．（1）概念理解：如图1，四边形ABCD 中，F 为CD 的中点，90ADB ∠=︒，E 是AB 边上一点，满足DE AE =，试判断EF 是否为四边形ABCD 的准中位线，并说明理由．（2）问题探究：如图2，ABC ∆中，90ACB ∠=︒，6AC =，8BC =，动点E 以每秒1个单位的速度，从点A 出发向点C 运动，动点F 以每秒6个单位的速度，从点C 出发沿射线CB 运动，当点E 运动至点C 时，两点同时停止运动．D 为线段AB 上任意一点，连接并延长CD ，射线CD与点,,,A B E F 构成的四边形的两边分别相交于点,M N ，设运动时间为t ．问t 为何值时，MN 为点,,,A B E F 构成的四边形的准中位线．（3）应用拓展：如图3，EF 为四边形ABCD 的准中位线，AB CD =，延长FE 分别与BA ，CD 的延长线交于点,M N ，请找出图中与M ∠相等的角并证明．16．如图（1），已知点G 在正方形ABCD 的对角线AC 上，,GE BC ⊥垂足为点,E GF CD ⊥，垂足为点F ．（1）证明与推断：①求证：四边形CEGF 是正方形；②推断：AG BE 的值为_ _； （2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转a 角)045(a ︒<<︒，如图（2）所示，试探究线段AG 与BE 之间的数量关系，并说明理由；（3）拓展与运用：若24AB EC ==，正方形CEGF 在绕点C 旋转过程中，当A E G 、、三点在一条直线上时，则BE = ．17．（1）问题情境：如图1，已知等腰直角ABC ∆中，90ABC ∠=︒，6AB =，E 是AC 上的一点，且2CE =，过E 作ED BC ⊥于D ，取AE 中点F ，连接BF ，则BF 的长为_______（请直接写出答案）小明采用如下的做法：延长AB 到H ，使AB BH =，连接EH ，B 为AH 中点，F 为AE 的中点，BF ∴是AEH ∆的中位线……请你根据小明的思路完成上面填空；（2）迁移应用：将图1中的CDE ∆绕点C 作顺时针旋转，当CE AC ⊥时，试探究BF 、AC 、CE 的数量关系，并证明你的结论．（3）拓展延伸：在旋转的过程中，当A 、C 、D 三点共线时，直接写出线段BF 的长． 18．问题呈现：已知等边三角形ABC 边BC 的中点为点D ，120EDF ∠=︒，EDF ∠的两边分别交直线AB ，AC 于点E ，F ，现要探究线段BE ，CF 与等边三角形ABC 的边长BC 之间的数量关系．（1）特例研究：如图1，当点E ，F 分别在线段AB ，AC 上，且DE AB ⊥，DF AC ⊥时，请直接写出线段BE ，CF 与BC 的数量关系：________；（2）问题解决：如图2，当点E 落在射线BM 上，点F 落在线段AC 上时，（1）中的结论是否成立？若不成立，请通过证明探究出线段BE ，CF 与等边三角形ABC 的边长BC 之间的数量关系；（3）拓展应用：如图3，当点E 落在射线BA 上，点F 落在射线AC 上时，若2CD =，45CDF ∠=︒62sin CFD -∠=，请直接写出BE 的长和此时DEF ∆的面积． 19．（1）观察发现：如图1，在ABC ∆中，AC BC =，90ACB ∠=︒，点D 是ACB ∠的平分线CM 上一点，将线段CD 绕点C 逆时针旋转90°到CE ，连结BE 、BD ，DE 交BC 于F ．填空：①线段BD 与BE 的数量关系是_________；②线段BC 与DE 的位置关系是_________．（2）拓展探究：如图2，在ABC ∆中，AC BC =，ACB α∠=，点D 是边AB 的中点，将CD 绕点C 逆时针旋转α到CE ，连结BE 、DE ，DE 交BC 于F ．（1）中的结论是否仍然成立？请说明理由．（3）拓展应用：如图3，在ABC ∆中，AB AC =，60BAC ∠=︒，2BC =，ACB ∠的平分线交AB 于D ，点E 是射线CD 上的一点，将CE 绕点C 顺时针旋转60°到CF ，连结AE 、AF 、EF ，EF 与AC 相交于G ，若以A 、F 、G 为顶点的三角形与ADE ∆全等，直接写出EF 的长．20．综合与实践数学活动课上，老师让同学们结合下述情境，提出一个数学问题：如图1，四边形ABCD 是正方形，四边形BEDF 是矩形．探究展示：“兴趣小组”提出的问题是：“如图2，连接CE ．求证：AE ⊥CE ．”并展示了如下的证明方法：证明：如图3，分别连接AC ，BD ，EF ，AF ．设AC 与BD 相交于点O ．∵四边形ABCD 是正方形，∴OA =OC =12AC ，OB =OD =12BD ，且AC =BD ．又∵四边形BEDF 是矩形，∴EF 经过点O ，∴OE =OF =12EF ，且EF =BD ．∴OE=OF，OA=OC．∴四边形AECF是平行四边形．（依据1）∵AC=BD，EF=BD，∴AC=EF．∴四边形AECF是矩形．（依据2）∴∠CEA=90°，即AE⊥CE．反思交流：（1）上述证明过程中“依据1”“依据2”分别是什么？拓展再探：（2）“创新小组”受到“兴趣小组”的启发，提出的问题是：“如图4，分别延长AE，FB交于点P，求证：EB=PB．”请你帮助他们写出该问题的证明过程．（3）“智慧小组”提出的问题是：若∠BAP=30°，AE1，求正方形ABCD的面积．请你解决“智慧小组”提出的问题．【参考答案】***试卷处理标记，请不要删除一、中考几何压轴题1．【问题引入】见解析；【类比探究】（1）见解析；（2）图见解析，；【知识拓展】，证明见解析【分析】[问题引入]利用AAS证明△POE≌△POD，即可得出结论；[类比探究]（1）过点F作FN解析：【问题引入】见解析；【类比探究】（1）见解析；（2）图见解析，OD OE OF-=；【知识拓展】PA PD PE PB PC PF++=++，证明见解析【分析】[问题引入]利用AAS证明△POE≌△POD，即可得出结论；[类比探究]（1）过点F作FN⊥OB，FM⊥OA，垂足分别为N、M，FM与PE交于点Q，先证明△PFQ为等边三角形，得出FG=PH，再运用矩形性质得出OM=12OF，ON=12OF，即可证得结论；（2）作FN⊥OB于点N，FM⊥OA于点M，射线FM交PE于点Q，作PH⊥FQ于点H，FG⊥PQ于点G，同（1）可证：NE=FG=PH=MD，ON=OM=12OF，即可得出结论；[知识拓展]过点O 作OM ⊥AB ，ON ⊥EF ，OQ ⊥CD ，垂足分别为M 、N 、Q ，利用垂径定理可得出PB -PA =2PM ，PF -PE =2PN ，PD -PC =2PQ ，再运用[类比探究]得：PM +PN =PQ ，从而证得结论．【详解】[问题引入]证明：∵AOC BOC ∠=∠，PE OB ⊥，PD OA ⊥，∴90OEP ODP ∠=∠=︒．∵OC OC =，∴OEP ODP ≅△△．∴OD OE =．[类比探究]（1）过点F 作FN OB ⊥，FM OA ⊥，垂足分别为N 、M ，FM 与PE 交于点Q ．∵60AOC BOC ∠=∠=︒，PE OB ⊥，PD OA ⊥，则PFQ △为等边三角形，FQ 、PQ 边上的高相等，即FG PH =．在矩形EGFN 、矩形DPHM 中，有NE FG =，MD PH =，∴EN MD =．∴OD OE OM ON +=+．∵90FMO ∠=︒，60FOM ∠=︒， ∴1cos 2OM OF FOM OF =⋅∠=， 同理，12ON OF =， ∴OM ON OF +=，∴OD OE OF +=．（2）结论：OD OE OF -=．作FN OB ⊥于点N ，FM OA ⊥于点M ，射线FM 与PE 的交点为Q ，作PH FQ ⊥于点H ，FG PQ ⊥于点G ，同（1）可证NE FG PH MD ===，12ON OM OF ==， ∴OF OM ON OD MD NE OE OD OE =+=-+-=-．[知识拓展]数量关系：PA PD PE PB PC PF ++=++．理由如下：过点O 作OM AB ⊥，ON EF ⊥，OQ CD ⊥，垂足分别为M 、N 、Q ．由垂径定理可得AM BM =．∴()()2PB PA PM MB MA PM PM -=+--=．同理2PF PE PN -=，2PD PC PQ -=，由[类比探究]得PM PN PQ +=，∴222PM PN PQ +=，∴PB PA PF PE PD PC -+-=-．∴PA PD PE PB PC PF ++=++．【点睛】本题是圆的综合题，考查了全等三角形判定和性质，等边三角形判定和性质，角平分线性质，矩形性质，垂径定理等，熟练掌握全等三角形判定和性质及垂径定理等相关知识是解题关键．2．（1）；（2）①，证明见解析；②；（3），【分析】（1）由等腰三角形的性质，结合等量代换即可求解；（2）①根据SAS 证明，然后根据全等三角形的性质即可证明；②由全等三角形的性质得，然后利用等解析：（1）AD BE =；（2）①AD BE =，证明见解析；②60；（3）45AFB ∠=︒，2AD BE =【分析】（1）由等腰三角形的性质，结合等量代换即可求解；（2）①根据SAS 证明ACD BCE ≅∆∆，然后根据全等三角形的性质即可证明； ②由全等三角形的性质得ACD CBF ∠=∠，然后利用等量代换即可求解；（3）首先证明ACD BCE ∆∆，然后根据相似三角形的性质得到AD AC BE BC =，和CBF CAF ∠=∠，即可求解．【详解】（1）∵CAB ∆和CDE ∆均为等边三角形∴CA=CB ，CD=CE∴AC-CD=BC-CE ，即AD=BE ∴AD=BE ；（2）①AD=BE证明：∵CAB ∆和CDE ∆均为等边三角形∴CA=CB ，CD=CE ，60ACB DCE ∠=∠=︒∴ACD BCE ∠=∠∴ACD BCE ≅∆∆∴AD=BE②∵ACD BCE ≅∆∆∴ACD CBF ∠=∠设BC 和AF 交于点O ，如图2∵AOC BOF ∠=∠∴60BFO ACO ∠=∠=︒，即60AFB ∠=︒∴60AFB ∠=︒；（3）结论45AFB ∠=︒，2AD BE =证明：∵90ABC DEC ∠=∠=，AB=BC ，DE=EC∴45ACD BCD BCE ∠=︒+∠=∠，2AC DC BC EC=∴ACD BCE ∆∆∴AD ACBE BC ==CBF CAF ∠=∠ ∴AD =∵AFB CBF ACB CAF ∠+∠=∠+∠∴45AFB ACB ∠=∠=︒【点睛】本题考查了几何变换综合，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形，关键证明全等和相似，并且分类讨论．3．（1）；；；（2）；（3）．【分析】（1）本问体现“特殊”的情形，是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最解析：（1）3AB EH =；2CG EH =；32；（2）2m ；（3）ab ． 【分析】（1）本问体现“特殊”的情形，3AF EF =是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最后求得比值；（2）本问体现“一般”的情形，AF m EF =不再是一个确定的数值，但（1）问中的解题方法依然适用，如答图2所示．（3）本问体现“类比”与“转化”的情形，将（1）（2）问中的解题方法推广转化到梯形中，如答图3所示．【详解】解：（1）依题意，过点E 作//EH AB 交BG 于点H ，如图1所示．则有ABF EHF ， ∴3AB AF EH EF==， ∴3AB EH =． ∵ABCD ，//EH AB ， ∴//EH CD ，又∵E 为BC 中点，∴EH 为BCG 的中位线，∴2CG EH =．3322CD AB EH CG CG EH ===． 故答案为：3AB EH =；2CG EH =；32．（2）如图2所示，作//EH AB 交BG 于点H ，则EFH AFB △△． ∴AB AF m EH EF ==， ∴AB mEH =．∵AB CD =，∴CD mEH =．∵////EH AB CD ，∴BEHBCG △△． ∴2CG BC EH BE==， ∴2CG EH =． ∴22CD mEH m CG EH ==． 故答案为：2m ． （3）如图3所示，过点E 作//EH AB 交BD 的延长线于点H ，则有////EH AB CD ． ∵//EH CD ，∴BCD BEH △△，∴=CD BC b EH BE=， ∴CD bEH =． 又AB a CD =， ∴AB aCD abEH ==．∵//EH AB ，∴ABF EHF ， ∴==AF AB abEH ab EF EH EH=． 故答案为：ab ．【点睛】本题的设计独特：由平行四边形中的一个特殊的例子出发（第1问），推广到平行四边形中的一般情形（第2问），最后再通过类比、转化到梯形中去（第3问）．各种图形虽然形式不一，但运用的解题思想与解题方法却是一以贯之：即通过构造相似三角形，得到线段之间的比例关系，这个比例关系均统一用同一条线段来表达，这样就可以方便地求出线段的比值．本题体现了初中数学的类比、转化、从特殊到一般等思想方法，有利于学生触类旁通、举一反三．4．（1）；（2）BE+BD 的值不会发生改变，理由见解答；（3）2k•sin【分析】（1）只要证明，即可解决问题；（2）如图2中，作交于，过点作交于．利用（1）中结论即可解决问题； （3）如图③中解析：（1）422）BE +BD 的值不会发生改变，理由见解答；（3）2k •sin2α 【分析】（1）只要证明BAE CAD ∆≅∆，即可解决问题；（2）如图2中，作//DM AC 交AB 于M ，过点P 作//PN BC 交MD 于N ．利用（1）中结论即可解决问题；（3）如图③中，作//PH AC 交BC 的延长线于H ，作PM BC ⊥于M ．只要证明EPB DPH ∆≅∆，可证BD BE BH +=，即可解决问题．【详解】解：（1）如图1中，90EAD BAC ∠=∠=︒，BAE CAD ∴∠=∠，AD AE =，AB AC =，()BAE CAD SAS ∴∆≅∆，BE DC ∴=，BE BD BD DC BC ∴+=+=，4AB AC ==，90BAC ∠=︒， 42BC ∴=，42BE BD ∴+=，故答案为：42． （2）BE BD +的值不会发生改变，理由如下：作//DM AC 交AB 于M ，过点P 作//PN BC 交MD 于N ，AB AC =，90BAC ∠=︒，45ABC C ∴∠=∠=︒，//MD AC ，90BMD BAC ∴∠=∠=︒，BMD ∴∆是等腰直角三角形，DM BM ∴=，//PN BC ，45MPN ABC ∴∠=∠=︒，PMN ∴∆是等腰直角三角形，PM NM ∴=，BM PM DM NM ∴-=-，PB DN ∴=，由（1），知42BC =3BD CD =，32BD ∴=， cos453BM BD ∴=⋅︒=，P 为AB 边上的中点，122AP BP AB ∴===， 321MN PM BM BP ∴==-=-=，222PN MN PM ∴=+=，90BPE DPM ∠+∠=︒，90PDM DPM ∠+∠=︒，BPE PDM ∴∠=∠，PD PE =，()PBE DNP SAS ∴∆≅∆，2BE PN ∴==，23242BE BD ∴+=+=；（3）如图3中，作//PH AC 交BC 的延长线于H ，作PM BC ⊥于M ．//AC PH ，ACB H ∴∠=∠，BPH BAC α∠=∠=，AB AC =，ABC ACB ∴∠=∠，PBH H ∴∠=∠，PB PH ∴=，EPD BPH α∠=∠=，BPE HPD ∴∠=∠，PE PD =，PB PH =，()EPB DPH SAS ∴∆≅∆，BE DH ∴=，BE BD BD DH BH ∴+=+=，=PB PH ，PM BH ⊥，BM MH ∴=，BPM HPM ∠=∠，sin 2BM MH BP α∴==⋅．2sin 2BD BE BH k α∴+==⋅．故答案为：2sin 2k α⋅． 【点睛】 本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．5．（1）①见解析；②；③；（2）①；②；（3）①24；②，【分析】（1）①由旋转的性质，，然后利用AAS ，即可得到结论成立；②求出，即可求出面积；③求出，即可求出答案；（2）①过点作交延长线解析：（1）①见解析；②12；③12；（2）①22a ；②2222a ab b ++；（3）①24；②558，265 【分析】（1）①由旋转的性质，AB A B '=，然后利用AAS ，即可得到结论成立；②求出1AC A H '==，即可求出面积；③求出2CH =，即可求出答案；（2）①过点A '作A H CB '⊥交CB 延长线于点H ，由（1）可知ABC A BH '≌△△，求出A H '的长度，即可求出答案；②求出CH 的长度，利用勾股定理，即可求出答案；（3）①过点A 作AE ⊥BC ，过点A '作A H CB '⊥交CB 延长线于点H ，然后证明ABE BA H '△△，求出A H '，CH 的长度，即可求出面积；②点C 是点B 关于AE 的对称点，则BD =CD ，设A C '与AE 的交点为点D ，使得A D DB '+有最小值为，为线段A C '的长度，然后利用勾股定理求出A C '，再利用平行线分线段成比例求出DE 的长度即可．【详解】解：（1）如图：①由旋转的性质，则AB A B '=，90ABA '∠=︒，∵90ACB A HB '∠=∠=︒，∴90ABC A ABC A BH '∠+∠=∠+∠=︒，∴A A BH '∠=∠，∴ABC A BH '≌△△（AAS ）；②∵1AC BC ==，∴1A H BH '==，∴A BC '的面积为111122⨯⨯=； 故答案为：12．③在直角三角形A CH '中，∵112CH =+=，1A H '=，∴1tan 2A H A CB CH ''∠==； 故答案为：12．（2）①过点A '作A H CB '⊥交CB 延长线于点H ，由（1）可知，ABC BA H '≌△△， ∴A H BC a '==，BH AC b ==，∴A BC '的面积为：211222a BC A H a a '•=••= 故答案为：22a ； ②∵CH BC BH ab =+=+，由勾股定理，则222222()22A C CH A H a b a a ab b ''=+=++=++；故答案为：2222a ab b ++；（3）①过点A 作AE ⊥BC ，过点A '作A H CB '⊥交CB 延长线于点H ，如图与（1）同理，可证BAE A BH '∠=∠，∵90AEB A HB '∠=∠=︒，∴ABE BA H '△△， ∴AB BE AE BA A H BH ==''， ∵AB AC =，10AB =，12BC =，5A B '=， ∴1112622BE BC ==⨯=； ∴221068AE =-=， ∴10685A H BH=='， ∴3A H '=，4BH =，∴12416CH BC BH =+=+=，∴A BC '的面积为：11•1231822CB A H =⨯⨯'=；故答案为：18．②由题意，点C 是点B 关于AE 的对称点，则BD =CD ，设A C '与AE 的交点为点D ，则此时A D DB '+有最小值，如图：此时A D DB '+的最小值为线段A C '的长度，∵22316265A C '+∵AE ∥A H '，∴CE DE CH A H ='，即6163DE =， ∴98DE =， ∴955888AD =-=， ∴当558AD =时，A D DB '+265． 故答案为：558265 【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，旋转的性质，勾股定理，最短路径问题等知识，解题的关键是熟练掌握所学的知识，正确的作出辅助线，从而进行解题．6．（1）见解析；（2）；（3）当时，有最小值，此时；的值不变，见解析【分析】（1）在圆上任意取两条弦AC 、BC ，作AC 、BC 的垂直平分线，则它们的交点为P 点；（2）由题意得与相切于点，根据切线长解析：（1）见解析；（2）1618,55D ⎛⎫ ⎪⎝⎭；（3）当4t =时，MN 有最小值，此时16OMEN S =四边形；OMEN S 四边形的值不变，见解析【分析】（1）在圆上任意取两条弦AC 、BC ，作AC 、BC 的垂直平分线，则它们的交点为P 点； （2）由题意得AE 与P 相切于点D ，根据切线长定理和勾股定理求得10AE =，再证明ADF AEO ∽△△，利用相似三角形的性质即可求解；（3）根据勾股定理得()2228MN t t =-+22216642(4)32t t t =-+=-+，得到当4t =时，2MN 有最小值，即MN 有最小值．四边形OMEN 是正方形，即可求得此时OMEN S 四边形，根据MON MEN OMEN S S S =+四边形△△利用三角形面积公式，即可求解．【详解】（1）如图，点P 即为所作；（2）如图，过点D 作DF x ⊥轴于点F ，连接PC ，PB ，由题意得：P 与坐标轴相切，∴90OBP OCP COB ∠=∠=∠=︒，∴四边形OBPC 是矩形，∵2PC PB ==，∴四边形OBPC 是正方形，∴2OC OB ==，则6AB =，由题意得AE 与P 相切于点D ，∴6AB AD ==，设EC ED x ==，在Rt OAE △中，90AOE ∠=︒，8AO =，2EO x =+，6AE x =+，由勾股定理得：222OE OA AE +=，即：()()222286x x ++=+，解得4x =，∴10AE =， 由题意可得ADF AEO ∽△△， ∴AD DF AF AE EO AO==， 即：61068DF AF ==， ∴185DF =，245AF =， 则2416855OF =-= ∴161855D ⎛⎫ ⎪⎝⎭，； （3）如图，在Rt OMN △中，90MON ∠=︒，8OM t =-，ON t =，则()2228MN t t =-+22216642(4)32t t t =-+=-+，当4t =时，2MN 有最小值，即MN 有最小值．此时，4OM ON ==，∵OG 平分第一象限，∴∠EON =∠EOM =45︒，∴△EON ≅△EOM ，∴∠ENO =∠EMO ，∵四边形OMEN 是圆内接四边形，∴∠ENO +∠EMO =180︒，∴∠ENO =∠EMO =90︒，又OM =ON ，∴四边形OMEN 是正方形，∴4416OMEN S =⨯=四边形；在这个变化过程中，16OMEN S =四边形没有变化，理由如下：∵OG 平分第一象限，∴EMN 是等腰直角三角形， ∴NE ME = 则()()2222221118222NE MN OM ON t t ⎡⎤==+=-+⎣⎦， ∴MON MEN OMEN S S S =+四边形△△21122ON OM NE =⋅+ ()()2211188222t t t t ⎡⎤=-+⨯-+⎣⎦16 ．【点睛】本题考查了坐标与图形，圆的切线的性质，相似三角形的判定和性质，二次函数最值的求解，解答本题的关键是明确题意，找出所求问题需要的条件，学会利用参数构建方程解决问题．7．（1）①见解析；②1；（2）＝k ，理由见解析；（3）【分析】（1）①由正方形的性质得AB ＝DA ，∠ABE ＝90°＝∠DAH ．所以∠HAO+∠OAD ＝90°，又知∠ADO+∠OAD ＝90°，所以∠解析：（1）①见解析；②1；（2）FG AE ＝k ，理由见解析；（3【分析】（1）①由正方形的性质得AB ＝DA ，∠ABE ＝90°＝∠DAH ．所以∠HAO +∠OAD ＝90°，又知∠ADO +∠OAD ＝90°，所以∠HAO ＝∠ADO ，于是△ABE ≌△DAH ，可得AE ＝DQ ．②证明四边形DQFG 是平行四边形即可解决问题．（2）结论：FG AE＝k ．如图2中，作GM ⊥AB 于M ．证明：△ABE ∽△GMF 即可解决问题．（3）如图2中，作PM ⊥BC 交BC 的延长线于M ．利用相似三角形的性质求出PM ，CM 即可解决问题．【详解】解：（1）①证明：∵四边形ABCD 是正方形，∴AB ＝DA ，∠ABE ＝90°＝∠DAQ ．∴∠QAO +∠OAD ＝90°．∵AE ⊥DQ ，∴∠ADO +∠OAD ＝90°．∴∠QAO ＝∠ADO ．∴△ABE ≌△DAQ （A S A ），∴AE ＝DQ ．②解：结论：GF AE ＝1． 理由：∵DQ ⊥AE ，FG ⊥AE ，∴DQ ∥FG ，∵FQ ∥DG ，∴四边形DQFG 是平行四边形，∴FG ＝DQ ，∵AE ＝DQ ，∴FG ＝AE ，∴GFAE＝1．故答案为1．（2）解：结论：FGk AE=．理由：如图2中，作GM⊥AB于M．∵AE⊥GF，∴∠AOF＝∠GMF＝∠ABE＝90°，∴∠BAE+∠AFO＝90°，∠AFO+∠FGM＝90°，∴∠BAE＝∠FGM，∴△ABE∽△GMF，∴GFAE ＝GMAB，∵∠AMG＝∠D＝∠DAM＝90°，∴四边形AMGD是矩形，∴GM＝AD，∴GF AD BC kAE AB AB===．（3）解：如图2中，作PM⊥BC交BC的延长线于M．∵FB∥GC，FE∥GP，∴∠CGP＝∠BFE，∴tan∠CGP＝tan∠BFE＝34BE BF =，∴可以假设BE ＝3k ，BF ＝4k ，EF ＝AF ＝5k ， ∵FGAE ＝23，FG ＝， ∴AE ＝∴（3k ）2+（9k ）2＝（2，∴k ＝1或﹣1（舍弃），∴BE ＝3，AB ＝9，∵BC ：AB ＝2：3，∴BC ＝6，∴BE ＝CE ＝3，AD ＝PE ＝BC ＝6，∵∠EBF ＝∠FEP ＝∠PME ＝90°，∴∠FEB +∠PEM ＝90°，∠PEM +∠EPM ＝90°，∴∠FEB ＝∠EPM ，∴△FBE ∽△EMP ， ∴EF PE ＝BF EM ＝BE PM ， ∴5436EM PM==， ∴2418,55EM PM ==， ∴249553CM EM EC =-=-=，∴PC ==【点睛】本题属于相似形综合题，考查了正方形的性质，矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．8．（1）1，45°，不变；（2）∠AEP 的大小不变，理由见解析；（3）．【分析】(1)当点P 为对角线交点时，根据正方形的性质可得出结论，当点P 移动到其它位置时，过点P 分别作AB ，BC 的垂线，垂足分解析：（1）1，45°，不变；（2）∠AEP 的大小不变，理由见解析；（3．【分析】(1)当点P 为对角线交点时，根据正方形的性质可得出结论，当点P 移动到其它位置时，过点P 分别作AB ，BC 的垂线，垂足分别为M ，N ．证△PAM ≌△PEN ，可得∠AEP 的大小不变；(2)类似（1），过点P 分别作AB ，BC 的垂线，垂足分别为M ，N ．证△PAM ∽△PEN ，可得∠AEP 的大小不变；(3)利用（2）的结论，证BE = EC ．再证△ABE ∽△BCD ，利用比例式求出k ，再利用三角函数求出AP 的长．【详解】解：（1）如图，∵k =1，∴在矩形ABCD 是正方形，∵点P 移动到对角线交点处，∴PA=PE ，∠AEP=45°， 故=1PA PE，如图，当点P 移动到其它位置时，过点P 分别作AB ，BC 的垂线，垂足分别为M ，N ． ∴∠PMA =∠PMB =∠PNB =∠PNC =90°．∵四边形ABCD 是正方形，∴∠MBN =90°，PN =PM ，∴四边形PMBN 是正方形，∴∠MPN =90°，∵∠APE =90°，∴∠APM ＋∠MPE =∠EPN ＋∠MPE =90°，∴∠APM =∠EPN ．又∵∠PMA =∠PNB ，∴△PAM ≌△PEN ，∴PA=PE ， ∴∠AEP=45°，故=1PA PE，∠AEP 的大小不变； 故答案为：1，45°，不变；（2）∠AEP的大小不变．理由如下：过点P分别作AB，BC的垂线，垂足分别为M，N．∴∠PMA=∠PMB=∠PNB=∠PNC=90°．∵四边形ABCD是矩形，∴∠MBN=∠BAD=∠BCD=90°，∴四边形PMBN是矩形，∴∠MPN=90°，PN=BM，又∵∠APE=90°，∴∠APM＋∠MPE=∠EPN＋∠MPE=90°，∴∠APM=∠EPN．又∵∠PMA=∠PNB，∴△PAM∽△PEN，∴PAPE =PM PN．在Rt△PBM和Rt△BAD中，tan∠ABD=PM ADk BM AB==．在Rt△APE中，tan∠AEP=PA PM PMk PE PN BM===．∵k为定值，∴∠AEP的大小不变．（3）∵PC⊥BD，∠BCD=90°，∴∠PBC＋∠PCB=∠PBC＋∠BDC=∠BPE＋∠EPC=90°．∵AE∥PC，∴∠AEB=∠PCB，∠AEP=∠EPC．∵tan∠AEP=k，tan∠ABD=k，∴∠AEP=∠ABD．∵四边形ABCD 是矩形，∴AB =CD ，AD =BC ，AB ∥CD ，∴∠ABD =∠BDC ，∴∠AEB =∠PCB =∠BDC =∠AEP =∠EPC ，∠PBC =∠BPE ，∴BE =PE =EC ．∵∠AEB =∠BDC ，∠ABE =∠BCD ，∴△ABE ∽△BCD ， ∴AB BE BC CD =，即12BC AB BC AB=， ∴BC 2=2AB 2， ∴2AD BC AB =，k 2在Rt △BPC 中，tan ∠PCB =PB PC=tan ∠AEP =k 2 ∴PB 2PC =22 由勾股定理得22222(22)23BC PC PB +=+∴PE =12BC 3∴PA 26．【点睛】本题考查了矩形的性质与判定，正方形的判定与性质，相似三角形判定与性质，解直角三角形，解题关键是恰当作辅助线，构建全等三角形或相似三角形，利用解直角三角形的知识求解． 9．（1）①1，②；（2）直线所夹锐角为，见解析；（3）满足条件的的值为【分析】（1）①②延长BD 交AE 的延长线于T ，BT 交AC 于O ．证明即可解决问题． （2）如图②中，设AC 交BD 于O ，AE 交BD解析：（1）①1，②60︒；（2）直线BD AE ､所夹锐角为45︒，见解析；（3）满足条件的2AE 的值为1042±【分析】（1）①②延长BD 交AE 的延长线于T ，BT 交AC 于O ．证明()BCD ACE SAS ≌即可解决问题．（2）如图②中，设AC 交BD 于O ，AE 交BD 于T ．证明BCD ACE ∽△△，推出。

上海市浦东新区2019-2020学年中考数学第二次押题试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．如图是抛物线y=ax 2+bx+c （a≠0）的图象的一部分，抛物线的顶点坐标是A （1，4），与x 轴的一个交点是B （3，0），下列结论：①abc ＞0；②2a+b=0；③方程ax 2+bx+c=4有两个相等的实数根；④抛物线与x 轴的另一个交点是（﹣2.0）；⑤x （ax+b ）≤a+b ，其中正确结论的个数是（ ）A ．4个B ．3个C ．2个D ．1个2．在以下四个图案中，是轴对称图形的是（ ）A ．B ．C ．D ．3．如图，在平面直角坐标系中，⊙P 的圆心坐标是（3，a ）（a ＞3），半径为3，函数y ＝x 的图象被⊙P 截得的弦AB 的长为42，则a 的值是（ ）A ．4B ．3＋2C ．32D ．33+4．在实数﹣3 ，0.21，2π，18，0.001 ，0.20202中，无理数的个数为（ ）A ．1B ．2C ．3D ．45．如图，已知正方形ABCD 的边长为12，BE=EC ，将正方形边CD 沿DE 折叠到DF ，延长EF 交 AB 于G ，连接DG ，现在有如下4个结论：①ADG V ≌FDG △；②2GB AG =；③∠GDE=45°；④DG=DE 在以上4个结论中，正确的共有( )个A．1个B．2 个C．3 个D．4个6．估计8-1的值在（）A．0到1之间B．1到2之间C．2到3之间D．3至4之间7．如图,在△ABC中,∠ACB=90°, ∠ABC=60°, BD平分∠ABC ,P点是BD的中点,若AD=6, 则CP的长为( )A．3.5 B．3 C．4 D．4.58．数据”1,2,1,3,1”的众数是( )A．1 B．1.5 C．1.6 D．39．下列图形中，既是中心对称图形，又是轴对称图形的是（）A．B．C．D．10．将抛物线y＝x2﹣x+1先向左平移2个单位长度，再向上平移3个单位长度，则所得抛物线的表达式为（）A．y＝x2+3x+6 B．y＝x2+3x C．y＝x2﹣5x+10 D．y＝x2﹣5x+411．某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是()A．0.15 B．0.2 C．0.25 D．0.312．如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，那么小巷的宽度为( )A．0.7米B．1.5米C．2.2米D．2.4米二、填空题：（本大题共6个小题，每小题4分，共24分．）13．某班有54名学生，所在教室有6行9列座位，用（m ，n ）表示第m 行第n 列的座位，新学期准备调整座位，设某个学生原来的座位为（m ，n ），如果调整后的座位为（i ，j ）,则称该生作了平移[a,b]=[m - i,n - j]，并称a+b 为该生的位置数.若某生的位置数为10，则当m+n 取最小值时，m•n 的最大值为_____________. 14．若反比例函数2ky x-=的图象位于第二、四象限，则k 的取值范围是__. 15．已知一个斜坡的坡度1:3i =，那么该斜坡的坡角的度数是______．16．若将抛物线y=﹣4（x+2）2﹣3图象向左平移5个单位，再向上平移3个单位得到的抛物线的顶点坐标是_____．17．分解因式：3ax 2﹣3ay 2＝_____． 18．如图所示，点C 在反比例函数ky (x 0)x=>的图象上，过点C 的直线与x 轴、y 轴分别交于点A 、B ，且AB BC =，已知AOB V 的面积为1，则k 的值为______．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）已知，数轴上三个点A 、O 、P ，点O 是原点，固定不动，点A 和B 可以移动，点A 表示的数为a ，点B 表示的数为b .（1）若A 、B 移动到如图所示位置，计算+a b 的值.（2）在（1）的情况下，B 点不动，点A 向左移动3个单位长，写出A 点对应的数a ，并计算b a -. （3）在（1）的情况下，点A 不动，点B 向右移动15.3个单位长，此时b 比a 大多少？请列式计算.20．（6分）已知：二次函数2y ax bx =+满足下列条件：①抛物线y=ax 2+bx 与直线y=x 只有一个交点；②对于任意实数x ，a （-x+5）2+b （-x+5）=a （x-3）2+b （x-3）都成立． （1）求二次函数y=ax 2+bx 的解析式；（2）若当-2≤x≤r （r≠0）时，恰有t≤y≤1.5r 成立，求t 和r 的值．21．（6分）某数学教师为了解所教班级学生完成数学课前预习的具体情况，对该班部分学生进行了一学期的跟踪调查，将调查结果分为四类并给出相应分数，A ：很好，95分；B ：较好75分；C ：一般，60分；D ：较差，30分．并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（Ⅰ）该教师调查的总人数为 ，图②中的m 值为 ； （Ⅱ）求样本中分数值的平均数、众数和中位数． 22．（8分）解分式方程：21133x x x-+=--． 23．（8分）如图，在Rt △ABC 的顶点A 、B 在x 轴上，点C 在y 轴上正半轴上，且 A(－1，0)，B(4，0)，∠ACB ＝90°. (1)求过A 、B 、C 三点的抛物线解析式；(2)设抛物线的对称轴l 与BC 边交于点D ，若P 是对称轴l 上的点，且满足以P 、C 、D 为顶点的三角形与△AOC 相似，求P 点的坐标；(3)在对称轴l 和抛物线上是否分别存在点M 、N ，使得以A 、O 、M 、N 为顶点的四边形是平行四边形，若存在请直接写出点M 、点N 的坐标；若不存在，请说明理由.图1 备用图 24．（10分）如图，已知抛物线21322y x x n =--（n ＞0）与x 轴交于A ，B 两点（A 点在B 点的左边），与y 轴交于点C 。