福建省晋江市永春县第一中学2016-2017学年高二数学3月月考试题理

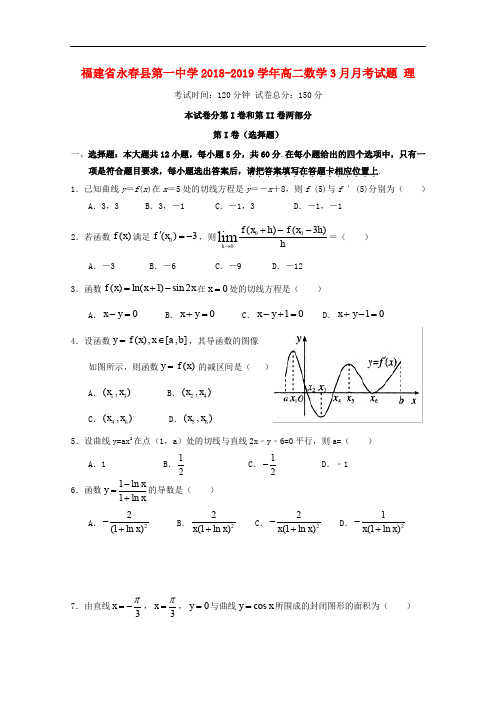
福建省永春县第一中学2018-2019学年高二数学3月月考试题 理考试时间：120分钟 试卷总分：150分 本试卷分第I 卷和第II 卷两部分第I 卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．. 1．已知曲线y ＝f (x )在x ＝5处的切线方程是y ＝－x ＋8，则f (5)与f ′(5)分别为（ ）A ．3，3B ．3，－1C ．－1，3D ．－1，－1 2．若函数()f x 满足0()3f x '=-，则000()(3)limh f x h f x h h→+--＝（ ）A ．－3B ．－6C ．－9D ．－123．函数()ln(1)sin 2f x x x =+-在0x =处的切线方程是（ ）A ．0x y -=B ．0x y +=C ．10x y -+=D ．10x y +-= 4．设函数(),[,]y f x x a b =∈，其导函数的图像如图所示，则函数()y f x =的减区间是（ ） A ．13(,)x x B ．24(,)x x C ．46(,)x x D ．56(,)x x5．设曲线y=ax 2在点（1，a ）处的切线与直线2x ﹣y ﹣6=0平行，则a=（ ）A ．1B ．12C ．12- D ．﹣1 6．函数1ln 1ln xy x-=+的导数是（ ）A ．22(1ln )x -+B ．22(1ln )x x +C ．22(1ln )x x -+D ．21(1ln )x x -+7．由直线3x π=-，3x π=，0y =与曲线cos y x =所围成的封闭图形的面积为（ ）A ．12 B ．1 C ．2D 8．函数y ＝2x 3－2x 2在[－1,2]上的最大值为（ ）A ．－5B ．0C ．－1D ．89．方程x 3－6x 2－15x －10=0的实根个数是（ ）A ．3B ．2C ．1D ．0 10．已知R 上可导函数()f x 的图像如图所示，则不等式2(23)()0x x f x '-->的解集为（ ）A ．(,1)(3,)-∞-+∞B ．(,2)(1,2)-∞-C ．(,1)(1,0)(2,)-∞--+∞D ．(,1)(1,1)(3,)-∞--+∞11．设曲线1()n y xn N +*=∈在（1，1）处的切线与x 轴的交点的横坐标为x n ，则201412014220142013log log log x x x +++的值为（ ）A ．－1B ．2014log 2013-C ．1D ．12014(log 2013)-12．已知点P 为函数()ln f x x =的图像上任意一点，点Q 为圆221[()]1x e y e-++=上任意一点，则线段PQ 的长度的最小值为（ ）A B ．11e e +- 第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．请把答案填在答题卡的横线上．．．．．．．．．．．．．。

一、单选题福建省永春县第一中学2016-2017学年高二3月月考物理试题相似题纠错收藏详情加入试卷1. 如图甲所示，长直导线与闭合金属线框位于同一平面内长直导线中的电流i 随时间t 的变化关系如图乙所示．在时间内直导线中电流向上，则在时间内线框中感应电流的方向与所受安培力情况是（）A ．感应电流方向为顺时针，线框受安培力的合力方向向左B ．感应电流方向为逆时针，线框受安培力的合力方向向右C ．感应电流方向为顺时针，线框受安培力的合力方向向右D ．感应电流方向为逆时针，线框受安培力的合力方向向左2. 如图所示，一个有弹性的金属圆环被一根橡皮绳吊于通电直导线的正下方，直导线与圆环在同一竖直面内，当通电直导线中电流增大时，弹性圆环的面积S 和橡皮绳的长度L 将()A ．S 增大，L 变长B ．S 减小，L 变短C ．S 增大，L 变短D ．S 减小，L 变长3. 如图甲所示，为一种调光台灯电路示意图，它通过双向可控硅电子器件实现了无级调节亮度．给该台灯接220 V 的正弦交流电后加在灯管两端的电压如图乙所示，则此时交流电压表的示数为() A ．220 V B ． V C ．110V D ． V 4. 在变电站里，经常要用交流电表监测电网上的强电流。

所用的器材叫电流互感器，如下图所示中，能正确反映其工作原理的是（ ）A ．B ．C ．D ．5. 图甲所示电路中，A 1、A 2、A 3为相同的电流表，C 为电容器，电阻R 1、R 2、R 3的阻值相同，线圈L 的电阻不计．在某段时间内理想变压器原线圈内磁场的变化如图乙所示，则在t 1～t 2时间内() D ．电流表的示数都不为零C ．电流表A 1和A 2的示数相同B ．电流表A 2的示数比A 3的小A ．电流表A 1的示数比A 2的小6. “西电东输”工程中为减少输电损耗，必须提高输电电压，从西部某电站向华东某地区输送的电功率为106kW ，输电电压为1000kV ，输电线电阻为100Ω.若改用超导材料作为输电线，则可减少电损耗的功率为( )A ．105 kW B ．104 kW C ．106 kW D ．103 kW7. 如图所示,在匀强磁场中放置一个电阻不计的平行金属导轨,导轨跟大线圈M 相连，导轨上放一根导线ab ，磁感线垂直于导轨所在平面，欲使M 所包围的小闭合线圈N 产生顺时针方向的感应电流,则导线的运动情况可能是( )。

俯视图2016-2017年度高二理科寒假作业一必修一、必修二综合测试班级 座号 姓名 等级一、选择题:1、设集合A=｛4,5，7，9｝,B=｛3，4,7，8，9｝，全集U=A B ，则集合()u C A B ⋂中的元素共有( ）A. 3个 B.4个 C 。

5个 D. 6个 2、直线310x +=的倾斜角是( ）A 。

30︒ B. 60︒ C 。

120︒D. 150︒3、直线20ax y +=平行于直线1x y +=,则a 等于( ) A 。

2- B. 1- C. 1 D. 24、函数()22()x x f x x R -=+∈的图像关于（ ）对称 A 。

原点 B. x 轴 C 。

y 轴 D 。

直线y x =5、如图，在正方体1111-ABCD A B C D 中，直线1A B 和直线1B C 所成的角的大小为（ ). A 。

30 B.45 C 。

60 D 。

90 6、圆心在y 轴上，半径为1，且过点（1，2）的圆的方程为( )A.22(2)1x y +-=B.22(2)1x y ++=C.22(1)(3)1x y -+-=D.22(3)1x y +-= 7、光线由点P (2，3）射到x 轴后，经过反射过点Q （1,1），则反射光线方程是（ ） A ．450x y +-= B ．430x y --= C ．3210x y --= D ．2310x y -+= 8、已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是（ ） A ．,,m n m n αα若则‖‖‖B ．,,αγβγαβ⊥⊥若则‖C ．,,m m αβαβ若则‖‖‖D ．,,m n m n αα⊥⊥若则‖9、一个几何体的三视图如右图所示（单位长度： cm), 则此几何体的表面积是（ A 。

2(24cm + B 。

2(22cm C ．2(28cm + D ．2(26cm 10、已知ABC ∆中，AB=2，BC =1，90ABC ︒∠=,平面ABC 外一点P 满足PA=PB=PC=32，则三棱锥P —ABC 的体积是（ ） A ．1B ．13CDAA 1BCD B 1C 1D 111、定义在R 上的函数()x f 是奇函数,且(1)2f =，(2)()(2)f x f x f +=+，则(7)f = （ ） A ．8B ．10C ．12D ．1412、计算机中常用16进制,采用数字0～9和字母A ～F 共16个计数符号与10进制得对应关系如下表:16进制 0 1 2 3 4 5 6 7 8 9 ABCDEF10进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15例如用16进制表示D+E ＝1B ，则A ×B=( ) A 6E B 7C C 5F D B0二、填空题:13、计算552log 10log 0.25+的值为14、三棱锥P ABC -中，2,23,1PA PB AC BC AB PC ======,则二面角P AB C --的平面角大小为 15、若圆224610x y x y +++-=的圆心到直线340x y a ++=的距离为2 ，则a = 16、如图，正方体1111ABCD A B C D -，则下列四个命题：①P 在直线1BC 上运动时，三棱锥1A D PC -的体积不变；②P 在直线1BC 上运动时，直线AP 与平面ACD 1所成角的大小不变； ③P 在直线1BC 上运动时，二面角1P AD C --的大小不变； ④M 是平面1111A B C D 上到点D 和1C 距离相等的点，则M 点的轨迹是过1D 点的直线.其中真命题的编号是 .（写出所有真命题的编号） 三、解答题:17、已知ABC ∆的顶点()3,1A ，()1,3B -()2,1C -求：(1）AB 边上的中线所在的直线方程（2)AC 边上的高BH 所在的直线方程.18、已知函数212()log (23)f x x x =-++（1）求)(x f 的定义域；（2）求)(x f 的值域.19、如图，在直三棱柱（侧棱与底面垂直的三棱柱)111ABC A B C -中，8AB =,6AC =，10BC =,D 是BC 边的中点。

考试时间：120分钟试卷总分：150分本试卷分第I卷和第II卷两部分第I卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．。

1．不等式组(2)0,1x xx+>⎧⎪⎨<⎪⎩的解集为 ( )A．{x|－2＜x＜－1} B．{x|－1＜x＜0} C．{x|0＜x＜1} D．{x|x＞1}2．曲线的参数方程为(是参数)，则曲线是( )A.线段B.射线C.双曲线的一支D.圆3. 对于任意实数a，b，c，d，以下四个命题中正确的有 ( )①若ac2>bc2，则a>b；②若a>b，c>d，则a＋c>b＋d；③若a>b，c>d，则ac>bd；④若a>b，则11a b .A．1个 B．2个 C．3个 D．4个4. 对于常数、，“”是“方程的曲线是椭圆”的 ( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5．不等式|x－3|－|x－1|≤a2－3a对任意实数x恒成立，则实数a的取值范围为 ( ) A．(－∞，－2]∪[5，＋∞) B．(－∞，－1]∪[4，＋∞)C．[1，2] D．(－∞，1]∪[2，＋∞)6．在极坐标系中，点到直线的距离是 ( )A. 1B. 2C.D.7. 已知a >0，b >0，下列四个不等式中，所有正确的序号是 ( )①22ab a b a b +≤+2a b +≤；③2a b +≤22b a a b a b +≥+.A ．②B ．②③C ．①②③D ．①②③④8． 函数,为的导函数, 若, 则( )A．3 B．-3 C．-2 D．29．已知动圆：，则圆心的轨迹是 ( )A.直线B.圆C.椭圆D.抛物线的一部分10．点在椭圆上，则的最大值为 ( ) A．5 B．6 C．7 D．811．已知为椭圆的左、右焦点，是椭圆上异于顶点的任意一点，点是内切圆的圆心，过作于，是坐标原点，则的取值范围为 ( )A . B.C.D.12．已知函数对任意的满足（其中是函数的导函数），则下列不等式成立的是( )A．B．C.D．二、填空题：本大题共4小题，每小题5分，共20分，请把答案填在答题卡的横线上．．．．．．．．．．．．．。

永春一中高二年（上)期中考数学(理)科试卷 (2016。

11）命题：李金进 审核：郭文伟 考试时间：120分钟 试卷总分：150分本试卷分第I 卷和第II 卷两部分第I 卷（选择题、填空题)一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中,只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．。

1.设R ,,∈c b a ，且b a >，则（ )A ．bc ac >B 。

22+<+b a C ．22b a> D ．33b a>2.数列{}n a :,249,157,85,1--的一个通项公式是（）A ．)N (13)1(*21∈+--=+n n n n a n nB ．)N (1212)1(*21∈++-=-n n n a n n C ．)N (22)1(*21∈++-=+n n n n a n nD ．)N (212)1(*21∈++-=-n n n n a n n3.已知点),(b a P 和点)2,1(Q 分别在直线0823:=-+y x l 的两侧，则( ）. A 。

0823=-+b aB. 0823<-+b aC. 0823>-+b aD.023<+b a4.在等比数列{}na 中，已知5127=a a ，则111098a a a a 等于（ ）．A ．10B ．25C ．50D ．755.已知不等式062<--x x 的解集为A ，不等式0452<+-x x 的解集是B ,B A 是不等式02<++b ax x的解集，则=-b a （）.A 。

7- B. 5- C. 1 D 。

56.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱，令上二人所得与下三人等．问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列．问五人各得多少钱？”（“钱”是古代的一种重量单位）．这个问题中，甲所得为（ ）。

福建省晋江市永春县第一中学2016-2017学年高二数学上学期期末考试试题文第I 卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．。

1．命题“x R ，2220x x ”的否定是（）A ．x R ，2220x x B ．0x R ，20220x x C ．xR ，2220xxD．x R ，2022xx 2．命题“若21x，则11x ”的逆否命题是（）A ．若21x ，则1x或1x B．若11x ，则21x C ．若1x 或1x，则21xD．若1x 或1x，则21x 3．一物体做竖直上抛运动，它距地面的高度()h m 与时间()t s 间的函数关系式为2()4.910h t tt ，则1t 的瞬时速度（m /s ）为（）A．－0.98 B．0.2 C．－0.2 D．－0.494．椭圆22132yx的焦距为（）A ．1B ．2 C．23 D．225．函数()xf x xe 在点A （0，f （0））处的切线斜率为（） A．0 B．－1 C．1 D．e6．若p ，q 为简单命题，则“p 且q 为假”是“p 或q 为假”的（）A ．充分不必要条件B．必要不充分条件C ．充要条件 D ．既不充分也不必要条件7．已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为31812343yxx ，则使该生产厂家获取最大年利润的年产量为()A ．13万件B ．11万件 C．9万件 D．7万件8．若双曲线22221x y ab的一条渐近线方程为73yx ，它的一个顶点到较近焦点的距离为1，则双曲线的方程为（）A ．22179xyB．221169xyC．22197xyD．221916xy9．已知圆A 1：22(2)12x y和点A 2（2，0），则过点A 2且与圆A 1相切的动圆圆心P 的轨迹方程为（）A ．2213xy B．2213xyC ．222xyD．221128xy10．函数1()ln f x x x的图像大致为（）11．若函数22()(1)ln f x kx x 在区间（1，）上是减函数，则实数k 的取值范围是（）A ．[－1，1]B ．[2，2] C ．(,1][1,) D ．(,2][2,)12．已知双曲线22221x y ab（0a ，0b ）与函数y x 的图像交于点P ，若函数yx的图像在点P 处的切线过双曲线的左焦点F （－2，0），则双曲线的离心率是（）A ．512B ．2 C．312D ．32第II 卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分，请把答案填在答题卡的横线上．．．．．．．．．．．．．。

2016-2017年度高二数学理科寒假作业三选修2-1综合测试1班级 座号 姓名 等级一、选择题(12×5=60分)1.已知集合A=﹛x ︱x 2–6x+5＜0,x ∈R ﹜,B=﹛x ︱3＜x ＜8,x ∈R ﹜,则A ∩B= ( )A.﹛x ︱1＜x ＜8,x ∈R ﹜B. ﹛x ︱1＜x ＜5,x ∈R ﹜C.﹛x ︱3＜x ＜5,x ∈R ﹜ C. ﹛x ︱5＜x ＜8,x ∈R ﹜ 2．已知抛物线x 2=-12y,则它的准线方程是( ) A.y=-18 B.y=18 C.x=18 D. x=-183.已知命题P:∀x∈R,sinx ≤1,则( )A. P ⌝:∃ x ∈R,sinx ≥1 B.P ⌝:∀x ∈R, sinx ≥1 C. P ⌝:∃ x ∈R, sinx ＞1 D.P ⌝: ∀x ∈R, sinx ＞1 4.在等差数列﹛a n﹜中,a 1+a 9=10,则a 5=( )A.10B.8C.6D.5 5.设p,q 都是简单命题,且命题“p ∧q ”为假命题,则以下一定为真命题的是 ( )A.p ⌝B.q ⌝C.p ⌝∨q ⌝ D q ⌝∧p ⌝6.已知方程22121x y m m -=++表示双曲线,则m 的取值范围是( )A.(-∞,-2)∪(-1,+ ∞)B.(-∞,-2)C.(-1,+ ∞)D.(-2,-1) 7.“tan α=1”是“α=4π”的 ( ) A.充分不必要条件 B. 必要不充分条件 C.充要条件 D.非充分非必要条件8.设变量x,y满足约束条件,则z=5x+y的最大值为( )A.6B.5C.4D.39.已知双曲线的实轴长是虚轴长的2倍,则双曲线的的离心率为 ( )A.2210.已知F1,F2分别是椭圆221169x y+=的左右焦点,P点为椭圆上一点,则⊿P F1F2的周长为( )A. 3+B. 4+C. 6+8+11.等轴双曲线C的中心在原点,焦点在x轴上,与抛物线y2=16x的准线交于A,B两点,且|AB|=,则C的实轴长为( )B.12.已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),则|PA|+|PF|的最小值是（）A.52B.72C.5D.7二、填空题(4×5=20分)13.已知x＞0,则x+2x的最小值是;14.在空间直角坐标系0xyz中有两点A(2,5,1)和B(2,4,-1),则︱AB︱= ；15.抛物线y2=12x上与焦点的距离等于9的点的坐标是;16.下列四个命题，其中为真命题的是；（写出所有的真命题序号）①方程2x2+4x+y=0表示的曲线一定经过坐标原点，②不等式x2+4x+5≤0的解集为空集，③方程xy=0表示的曲线关于直线y=x对称，④若sinα=sinβ,则α=β；三、解答题（解答应写文字说明、证明过程或演算过程）17．（本小题满分10分）如图，在⊿ABC 中,AC=3,AB=5,∠A=1200; (1)求BC 的长；(2) 求⊿ABC 的边BC 上的高AM 的长18．（本小题满分12分）已知双曲线22221x y a b-=(a ＞0,b ＞0)的一条渐近线方程是x,它的一个焦点与抛物线y 2=16x 的焦点相同，求双曲线的方程．19. （本小题满分12分）已知椭圆的两焦点为F 1，F 2，离心率.(１)求椭圆的标准方程；(２)设直线L：y=x+m,若直线L与椭圆相交于P、Q两点，且|PQ|等于椭圆的短轴长，求m 的值。

永春一中高二年月考（理）科数学试卷 （2017.06）命题：颜智清 审核:郭文伟 考试时间：120分钟 试卷总分：150分本试卷分第I 卷和第II 卷两部分第I 卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．。

1．已知随机变量X ＋η＝8，若X ～B (10,0.6)，则E (η)，D (η)分别是( )A ．6,2.4B ．2,2.4C ．2,5.6D ．6,5.62．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X 表示这10个村庄中交通不方便的村庄数，下列概率中等于C 47C 68C 15的是( )A ．P （X ＝2）B ．P （X ≤2）C ．P (X ＝4)D ．P (X ≤4) 3．已知某批零件的长度误差(单位：毫米)服从正态分布N (0，32)，从中随机取一件，其长度误差落在区间(3,6)内的概率为( )(附：若随机变量ξ服从正态分布N (μ，σ2)，则P (μ－σ<ξ<μ＋σ)＝68.26%，P (μ－2σ<ξ<μ＋2σ)＝95.44%.)A ．4.56%B ．13.59%C ．27.18%D ．31.74%4．用5种不同的颜色，把图中A ，B ，C ，D 四块区域分开，允许用同一种颜色涂不同区域，但相邻区域不能涂同一种颜色，不同的涂法种数为( )A ．260B ．240C ．350D ．3605．袋中装有标号为1,2,3的三个小球，从中任取一个，记下它的号码，放回袋中，这样连续做三次．若抽到各球的机会均等，事件A 表示“三次抽到的号码之和为6”，事件B 表示“三次抽到的号码都是2”，则P (B |A )＝( )A ．17B ．27C ．16D ．7276．北京《财富》全球论坛期间，某高校有14名志愿者参加接待工作．若每天排早、中、晚三班，每班4人，每人每天最多值一班，则开幕式当天不同的排班种数为（ ） A ．124414128C A AB ．124414128C C CC ．12441412833C C C AD ．12443141283C C C A 7．用1,2,3,4,5,6组成数字不重复的六位数，满足1不在左、右两端，2,4,6三个偶数中有且只有两个偶数相邻，则这样的六位数的个数为( )A ．423B ．288C ．216D ．1448．代数式225(425)(1)x x x ++-的展开式中，含4x 的项的系数是（ ） A ．30B ．20C ．－20D ．－309．122331010101909090C C C -+-+ (101010)90C +除以88的余数是 （ ） A ． －1 B ．－87 C ． 1 D ．8710．掷一枚质地均匀的骰子n 次，设出现k 次点数为6的概率为Pn(k)，若n=20时，则当Pn(k)取最大值时，k 为（ ）A ．10B ．8C ．4D ．3．11．三对夫妻站成一排照相，则仅有一对夫妻相邻的站法总数是（ ）A ．288B ．240C ．144D ．7212．已知集合A ＝{x |x ＝a 0＋a 1×3＋a 2×32＋a 3×33}，其中a i ∈{0,1,2}(i ＝0,1,2,3)且a 3≠0，则A 中所有元素之和等于( )A ．3 240B ．3 120C ．2 997D ．2 889第Ⅱ卷（非选择题，共90分）本卷包括必考题和选考题两个部分。

福建省晋江市永春县第一中学2016-2017学年高二数学上学期期末考试试题 理考试时间：120分钟 试卷总分：150分 本试卷分第I 卷和第II 卷两部分第I 卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．. 1．设集合{|03}M x x =≤<，集合2{|20}N x x x =+-<，则MN 等于（ ）A. {|01}x x ≤<B. {|02}x x ≤<C. {|01}x x ≤≤D. {|02}x x ≤≤ 2. 抛物线24y x =的焦点坐标为（ ）A. (1,0)B. (0,1)C. 1(,0)16D.1(0,)16 3. 已知命题p ：若0x >，则12x x +≥；命题q ：若11x<，则1x >．则下列命题为真命题的是（ ）A ．p q ∧B ．p q ⌝∧C ．p q ∧⌝D ．p q ⌝∧⌝4. 命题“若1x <，则21x <”的逆命题、否命题、逆否命题中，真命题的个数是（ ）A ．0B ．1C ．2D ．35. “双曲线的方程为221916x y -=”是“双曲线的渐近线方程为43y x =±”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件6．已知△ABC 的内角,,A B C 所对的边分别为,,a b c .若2a =，b =，30A =，则B 等于（ ）A ．30B ．60C ．30或150D ．60或1207．若x ,y 满足2x -y £0x +y £3x ³0ìíïîï，则2x +y 的最大值为（ ）A. 0B. 3C. 4D. 58．空间四边形OABC 中，点M 在OA 上，且12OM MA =，点N 为BC 的中点．若OA =a ，OB =b ，OC =c ，则MN 等于（ ）A ．111322--a b c B ．111322-++a b c C ．111222--a b c D ．111222-++a b c9. 已知12,F F 分别为双曲线221x y -=的左，右焦点，点P 在双曲线上．若1260F PF ∠=，则△12PF F 的面积为（ ）A ．2 B D ．10. 若,m n 为两个不相等的非零实数，则方程0mx y n ++=与221x y m n+=所表示的曲线可能是（ ）11. 已知12,F F 分别为椭圆2212516x y +=的左，右焦点．若M 为椭圆上的一点，且△12MF F 的内切圆的周长等于3π，则满足条件的点M 的个数为（ ） A ．0B ．1C ．2D ．412．在我国古代著名的数学专著《九章算术》里有一段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里.良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，二马相逢. 问：几日相逢？（ ） A ．8日B ．9日C ．12日D ．16日 第Ⅱ卷二、填空题：本大题共4小题，每小题5分，13. 双曲线22169144x y -=的离心率为________ ． 14．图中是抛物线形拱桥，当水面在l 时，拱顶离水面2m ， 水面宽4m ．水位上升1m 后，水面宽________ m ．15．在平行六面体1111ABCD A B C D -中，4AB =，3AD =，14AA =，90BAD ∠=，1160BAA DAA ∠=∠=，则1AC 的长等于 ．16．设△ABC 的内角A 、B 、C 所对的边a 、b 、c 成等比数列，则b aa b+的取值范围为_______．三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知等差数列{}n a 的首项12a =，公差0d ≠，且139,,a a a 成等比数列． （Ⅰ）求数列{}n a 的通项公式； （Ⅱ）2nn n a b =，求数列{}n b 的的前n 项和为n T ．18．（本小题满分12分）如图，在正方体1111ABCD A B C D -中，,E F 分别是111,CC B C 的中点． （Ⅰ）求1A F 与1AD 所成角的余弦值； （Ⅱ）求证：1A F //平面1AD E .F E C 1D 1B 1A 1D CBA19．（本小题满分12分）已知动圆C 过定点(1,0)F 且与定直线l ：1x =-相切，动圆圆心C 的轨迹为曲线E ． （Ⅰ）求曲线E 的方程；（Ⅱ）过点F 作倾斜角为60的直线m ，交曲线E 于,A B 两点，求△AOB 的面积．20．（本小题满分12分）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，侧面PAD ⊥底面ABCD，AB =，2AD =，PA PD =．（Ⅰ）求证：PB AC ⊥；（Ⅱ）设AC 与平面PCD 所成的角为45，求二面角A PB C --的余弦值.21．（本小题满分12分）已知过点(2,0)D -的直线l 与椭圆2212x y +=交于不同的,A B 两点，点M 是AB 的中点.DCBAP（Ⅰ）若四边形OAPB 是平行四边形，求点P 的轨迹方程； （Ⅱ）求||||MA MD 的取值范围.22．（本小题满分10分）已知函数()|1|f x x =-．（Ⅰ）解不等式()(3)5f x f x ++≤；（Ⅱ）||1a >，||1b >，0a ≠，求证：()||()b f ab a f a>．永春一中高二数学（理）期末试卷 参考答案13.5314． 15 16． 17．解：（Ⅰ）因为139,,a a a 成等比数列，所以2319a a a =，即2(22)2(28)d d +=⋅+，220d d -=，0d ≠，2d =，2(1)22n a n n =+-⋅=，数列{}n a 的通项公式为n a n =．（Ⅱ）由（Ⅰ）得2n a n =，则12n n nb -=，122123112222n n n n n T ---=+++++，23111231222222n n n n n T --=+++++， 所以 1231111111222222n n n n T -=+++++-，12111112(1)2222n n n n T --=++++-111()221212nn n --=⋅--1242n n -+=-． 18．解：不妨设正方体的棱长为1，以1,,DA DC DD 为单位正交基底建立空间直角坐标系Dxyz ，如图所示．则(1,0,0)A ，1(1,0,1)A ，1(0,0,1)D ，1(0,1,)2E ，1(,1,1)2F . （Ⅰ）解：11(,1,0)2A F =-，1(1,0,1)AD =-，15||2A F =，1||2AD = 1111(1)100122A F AD ⋅=-⨯-+⨯+⨯=.所以1111111cos ,10||||5A F AD A F AD A F AD ⋅<>===⋅. 因此，1A F 与1AD 所成角的余弦值是10. （Ⅱ）证明：方法一：取1AD 的中点M ，连接ME ，则11(,0,)22M ，1(,1,0)2ME =-.所以1A F ME =，即1A F //ME ， 又1A F ⊄平面1AD E ，ME ⊂平面1AD E ，因此1A F //平面1AD E . 方法二：11(,1,0)2A F =-，1(1,0,1)AD =-，1(1,1,)2AE =-，1112A F AD AE =-+，即1A F 与1AD ，AE 共面，又1A F ⊄平面1AD E ，因此1A F //平面1AD E .方法三：1(1,0,1)AD =-，11(0,1,)2D E =-，设(,,)n x y z =是平面1AD E 的一个法向量，则1n AD ⊥，1n D E ⊥，1100n AD n D E ⎧⋅=⎪⎨⋅=⎪⎩，0102x z y z -+=⎧⎪⎨-=⎪⎩，令2z =，得2x =，1y =，(2,1,2)n=.又11(,1,0)2A F =-，故11(2,1,2)2()112002n A F ⋅==⨯-+⨯+⨯=，所以1n A F ⊥. 又1A F ⊄平面1AD E ，因此1A F //平面1AD E .19．解：（Ⅰ）依题意知，点C 到定点F 和直线l 的距离相等， 所以点C 的轨迹是以点F 为焦点，以直线l 为准线的抛物线， 设抛物线的方程为22y px =（0p >），由12p=，得2p =， 故曲线E 的方程为24y x =． （Ⅱ）直线m的方程为1)y x =-，由21)4y x y x⎧=-⎪⎨=⎪⎩消去x整理得23120y --=， 设11(,)A x y ，22(,)B x y，则12y y +=，124y y =-， 121||||2AOB S OF y y ∆=⨯⨯-112=⨯12== 所以，△AOB20．（Ⅰ）证明：分别取AD ，BC 的中点O ，E ，连接,PO OE ，由P A P D =，得P O A D ⊥， 因为侧面PAD ⊥底面ABCD ，侧面PAD底面ABCD AD =， PO ⊂平面PAD ，所以PO ⊥底面ABCD .在矩形ABCD 中，OE AD ⊥，则,,OA OE OP 两两互相垂直. 以O 为原点，分别以,,OA OE OP 的方向为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系Oxyz ，如图所示． 则(1,0,0)A，B，(C -， 设(0,0,)P t （0t >），所以(AC =-，)PB t =-，所以1(2)()00PB AC t ⋅=⨯-+-⨯=， 因此PB AC ⊥，得PB AC ⊥．（Ⅱ）解法一：(1,0,0)D -，DC =，(1,0,)DP t =．设(,,)m x y z =是平面PCD 的一个法向量，则m DC ⊥，m DP ⊥，00m DC m DP ⎧⋅=⎪⎨⋅=⎪⎩，00x tz +=⎧⎪=，令x t =，得0y =，1z =-，(,0,1)m t =-．又(AC =-，cos ,AC m <>||||AC m AC m ⋅=⋅2||||AC m AC m t ⋅==⋅． 因为AC 与平面PCD 所成的角为45，所以sin45|cos ,|AC m =<>，|2=，t =P ，AB =，PB =， 设1111(,,)n x y z =是平面PAB 的一个法向量，则1n AB ⊥，1n PB ⊥，1100n ABn PB ⎧⋅=⎪⎨⋅=⎪⎩，111100x =-=⎪⎩，令1x ，得10y =，11z =，1(3,0,1)n =．(2,0,0)BC =-，PB =，设2222(,,)n x y z =是平面PAB 的一个法向量，则2n BC ⊥，2n PB ⊥，2200nBC n PB ⎧⋅=⎪⎨⋅=⎪⎩，222220x x -=⎧⎪⎨+=⎪⎩，令2y =，得20x =，2z =，2n =．所以121212cos ,||||n n n n n n⋅<>=⋅==． 因此，二面角A PB C --的余弦值为. 解法二：作AF PD ⊥，垂足为F ，连接CF ，如图所示． 设(,0,)F x z ，则(1,0,)AF x z =-，DC =，(1)0000AF DC x z ⋅==-⨯+⨯=，AF DC ⊥，即AF DC ⊥，又PDDC D =，所以AF ⊥平面PCD ，FC 为AC 在平面PCD 上的射影，故ACF ∠是AC 与平面PCD 所成的角，45ACF ∠=，由||6AC =，得||3AF =，在Rt △ADF 中，2AD =，则1DF =，60ADF ∠=， △PAD为等边三角形，因此P ． 作AG PB ⊥，垂足为G ，连接CG . 在Rt △PAB中，PB =AG =3DG =，13DG DP =，故2(,33G，(C -，B ，GC=5(,33-，PB=，GC PB ⋅=51((033-⨯+⨯=， GC PB ⊥，GC PB ⊥，故A G C ∠为二面角A P B C--的平面角，GA=13(,)33-，cos AGC ∠=cos ,10||||GA GC GA GC GA GC ⋅<>==-⋅. 因此，二面角A PB C --的余弦值为10-. 21． 解法一：（Ⅰ）设直线l 的方程为(2)y k x =+，由22(2)12y k x x y =+⎧⎪⎨+=⎪⎩消去y 整理得2222(12)8820k x k x k +++-=， 2222(8)4(12)(82)0k k k ∆=-+->，212k <， 设11(,)A x y ，22(,)B x y ，则2122812k x x k +=-+，21228212k x x k -=+，12y y +=12(2)(2)k x k x +++12()4k x x k =++2412kk =+，四边形OAPB 是平行四边形，OP OA OB =+，设(,)P x y ，则12x x x =+，12y y y =+，222812412k x k k y k ⎧=-⎪⎪+⎨⎪=⎪+⎩，消去k 整理得22240x y x ++=，由212k <，得20x -<≤， 故点P 的轨迹方程为22240x y x ++=（20x -<≤）. （Ⅱ）不妨设12x x <，21x x -==设(,)M M M x y ，1||||2M M x x MA MD x -=+1212112122422x x x x x x x x x +--==++++2412k =-++=.由2102k ≤<，得||0||2MA MD <≤，即||||MA MD的取值范围为(0,2. 解法二：（Ⅰ）设(,)P x y ，11(,)A x y ，22(,)B x y ，则(,)22x y M ，221122221212x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩，2222121202x x y y -+-=， 12x x ≠，AB k =12121212122y y x x xx x y y y-+=-=--+，222DMyk x =+. 由,,,D A M B 四点共线，得AB DM k k =，2222y x x y -=+，22240x y x ++=. 又(,)22x y M 在椭圆2212x y +=内，22()2()122x y +<，22028x y ≤+<，048x ≤-<，20x -<≤.故点P 的轨迹方程为22240x y x ++=（20x -<≤）. （Ⅱ）同解法一．22．解：（Ⅰ）不等式()(3)5f x f x ++≤可化为|1||2|5x x -++≤．小初高K12教育学习资料小初高K12教育学习资料 当2x <-时，(1)(2)5x x ---+≤，解得3x ≥-，所以32x -≤<-； 当21x -≤≤时，(1)(2)5x x --++≤，所以21x -≤≤；当1x >时，(1)(2)5x x -++≤，解得2x ≤，所以12x <≤． 综上，不等式的解集为[3,2]-．（Ⅱ）()|1|f ab ab =-，||()|||1|||b b a f a a b a a=-=-， 因为||1a >，||1b >，所以22|1|||ab a b ---=222()21(2)ab ab a ab b -+--+ 222()1ab a b =--+22(1)(1)0a b =-->，|1|||ab a b ->-， 故()||()b f ab a f a>．。