2011年丰台区中考一《数学》模试题及答案

ABCDE 122010~2011学年九年级综合水平质量调研数学试卷 2011.3学校___________________班级_______________姓名________________学号_____________ 考 生 须 知1． 本试卷共8页，共五道大题，25道小题，满分120分，考试时间120分钟. 2． 在试卷和答题卡上准确填写学校．班级．姓名．学号. 3． 试题答案一律填涂或书写在答题卡上，在试卷上作答无效. 4． 考试结束，请将本试卷和答题卡一并交回.注意事项 1． 考生要按规定的要求在机读答题卡上作答，题号要对应，填涂要规范. 2． 考试结束后，试卷和机读答题卡由监考人一并收回.第一卷（机读卷32分）一 选 择 题 本 题32分， 每 小 题 4 分1. 4的算术平方根是A ．2B ．±2C ．16D ．±16 2. 如图，已知△ABC 为直角三角形，∠C =90°，若沿图中虚线剪去∠C ， 则∠1+∠2等于 A . 90° B . 135° C . 150°D . 270°第2题图3.布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任 意摸出一个球，摸出的球是白球．．的概率是 A ．13 B ．16 C ．12 D ． 564.某班的9名同学的体重分别是（单位：千克）： 61，59， 70，59，65，67，59， 63，57，这组数据的众数和中位数分别是A ．59，61B ．59，63C ．59，65D ． 57，615.全球可被人类利用的淡水总量仅占地球上总水量的0.00003，因此珍惜水、保护 水，是我们每一位公民义不容辞的责任．其中数字0.00003用科学记数法表示为 A ．4103-⨯ B ．5103-⨯ C ．4103.0-⨯ D ．5103.0-⨯6.如图，模块①－⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成. 现从模块①－⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为3的大正方体. 则下列选择方案中，能够完成任务的为A．模块②，④，⑤B．模块①，③，⑤C．模块①，②，⑤D．模块③，④，⑤一选择题本题32 分，每小题4分7. 如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD=13，PC=4，则两圆组成的圆环的面积是A．16π B．36π C．52π D．81π8. 矩形ABCD中，8cm6cmAD AB==，．动点E从点C开始沿边CB向点B以2cm/s的速度运动至点B停止，动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止．如图可得到矩形CFHE，设运动时间为x（单位：s），此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位：2cm)，则y与x之间的函数关系用图象表示大致是下图中的第8题图第7题图注意事项1．第Ⅱ卷包括4道填空题和13道解答题，共8页.答题前要认真审题，看清题目要求，按要求认真作答.2．答题时字迹要工整，画图要清晰，卷面要整洁.3．考生除画图可以用铅笔外，答题必须用蓝色或黑色钢笔、圆珠笔.第二卷（非机读卷88分）二填空题本题共16分，每小题4分9.若分式2x4x2--的值为0，则x的值为．10. 如图，点A、B、C是半径为6的⊙O上的点，30B∠=︒,则的长为_____________.第10题图11. 如图，在△ABC中，D、E分别AB、AC边上的点，DE∥BC．若AD＝3，DB＝5，DE＝1.2，则BC＝．第11题图12. 如图，在ABC∆中，α=∠A，ABC∠的平分线与ACD∠的平分线交于点1A，得1A∠，则1A∠= ．BCA1∠的平分线与CDA1∠的平分线交于点2A，得2A∠，……，BCA2009∠的平分线与CDA2009∠的平分线交于点2010A，得2010A∠，则2010A∠= ．第12题图ACOABCCAEDB三解答题本题共30分，每小题5 分13. （本小题5分）(31)4sin6027-+-14. （本小题5分）解不等式组31422xx x->-⎧⎨<+⎩，并把它的解集表示在数轴上．15. （本小题5分）如图，E F、是平行四边形ABCD对角线AC上两点，BE DF∥，求证：AF CE=。

2011年九年级教学质量检测数 学 试 题注意事项：本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷为选择题，36分；第Ⅱ卷为非选择题,84分；共120分．考试时间为120分钟．第Ⅰ卷 选择题 (共36分)一、选择题 (本题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来填入题后的括号内，每小题选对得3分.) 1.下列根式中与18是同类二次根式的是( ). A .321 B .27 C .6 D .32.抛物线y ＝2x 2＋4x －3的顶点坐标是（ ）.A ．（1，－5）B ．（－1，－5）C ．（－1，－4）D ．（－2，－7） 3.国家游泳中心——“水立方”是2008年北京奥运会标志性建筑之一，其工程占地面积为62828平方米，将62828用科学记数法表示是（保留三个有效数字）（ ）. A .62.8×103 B .6.28×104 C .6.2828×104 D .0.62828×105 4.数据0，-1，6，1，x 的众数为-1，则这组数据的方差是（ ）. A ．2B ．534C ．2D ．5265.如图，⊙O 的直径为10，弦AB 的长为6，M 是弦AB 上的一动点，则线段OM 的长的取值范围是（ ）. A .3≤OM ≤5 B .4≤OM ≤5 C .3＜OM ＜5 D .4＜OM ＜56.小明随机地在如图所示的正三角形及其内部区域投针，则针扎 到其内切圆(阴影)区域的概率为（ ）. A .21 B .π63C .π93 D .π33第6题图第11题图7.如图，□ABCD 中，对角线AC 和BD 相交于点O ， 如果AC =12，BD =10，AB =m ，那么m 的取值范围是( ).A ．1＜m ＜11B ．2＜m ＜22C ．10＜m ＜12D ．5＜m ＜68.如图，P 1、P 2、P 3是双曲线上的三点．过这三点分别 作y 轴的垂线，得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O ， 设它们的面积分别是S 1、S 2、S 3，则( )． A .S 1<S 2<S 3 B .S 2<S 1<S 3 C .S 1<S 3<S 2 D .S 1=S 2=S 39.直线1l ：1y k x b =+与直线2l ：2y k x =在同一平面直角坐标系中的图象如图所示，则关于x 的不等式12k x b k x +>的解为（ ）.A .1x >-B .1x <-C .2x <-D .无法确定10.如图，将A B C △沿D E 折叠，使点A 与B C边的中点F 重合，下列结论中①EF AB ∥且12E F A B =；②BAF C AF ∠=∠；③DE AF 21S ADFE∙=四边形；④2B D F F E C B A C ∠+∠=∠， 一定正确的个数是（ ）. A ．1B ．2C ．3D .411.若关于x 的一元二次方程ax 2+2x -5=0的两根中有且仅有一根在0和1 之间（不含0和1），则a 的取值范围是（ ）. A .a ＜3 B .a ＞3 C .a ＜-3 D .a ＞-312.如图，⊙O 是△ABC 的内切圆，切点分别是D 、E 、F ，已知∠A = 100°，∠C = 30°，则∠DFE 的度数是 （ ）.A .55°B .60°C .65°D .70°DABCO第7题图xb +x第9题图第8题图第12题图第16题图第Ⅱ卷 非选择题（共84分）二、填空题（本题共5小题，共15分．只要求填写最后结果，每小题填对得3分．） 13.当m = 时，关于x 的分式方程213x m x +=--无解.14.已知关于x 的不等式组⎩⎨⎧--≥-0125a ＞x x 无解，则a 的取值范围是 .15.已知关于的一元二次方程012)1(2=-++x x k 有两个不相同的实数根，则k 的取值范围是 .16.如图，梯形ABCD 中，BC AD //，1===AD CD AB ，︒=∠60B直线MN 为梯形ABCD 的对称轴，P 为MN 上一点，那么PD PC +的最小值是 .17.在实数的原有运算法则中我们补充定义新运算“⊕”如下：当a ≥b 时，a ⊕b ＝b 2；当a ＜b 时，a ⊕b ＝a ．则当x ＝2时，（1⊕x ）－（3⊕x ）的值为 ． 三、解答题（本题共7小题，共69分．解答应写出文字说明、证明过程或推演步骤．）18.（本题满分8分）据《生活报》报道，有关部门要求各中小学要把“每天锻炼一小时”写入课表．为了响应这一号召，某校围绕着“你最喜欢的体育活动项目是什么？（只写一项）”的问题，对在校学生进行了随机抽样调查，从而得到一组数据．图1是根据这组数据绘制的条形统计图．请结合统计图回答下列问题： （1）该校对多少名学生进行了抽样调查？（2）本次抽样调查中，最喜欢篮球活动的有多少人？占被调查人数的百分比是多少？（3）若该校九年级共有200名学生，图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图，请你估计全校学生中最喜欢跳绳活动的人数约为多少？图2图1最喜欢的体育活 动项目的人数/人育活动项目19.（本题满分9分）某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w （千克）随销售单价x （元/千克）的变化而变化，具体关系式为：w ＝－2x ＋240．设这种绿茶在这段时间内的销售利润为y （元），解答下列问题： （1）求y 与x 的关系式； （2）当x 取何值时，y 的值最大？（3）如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？20.（本题满分9分）经过江汉平原的沪蓉(上海—成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①，一测量员在江岸边的A 处测得对岸岸边的一根标杆B 在它的正北方向，测量员从A 点开始沿岸边向正东方向前进100米到达点C 处，测得∠ACB=68°.（1）求所测之处江的宽度（.48.268tan ,37.068cos ,93.068sin ≈≈≈ ）； （2）除(1)的测量方案外，请你再设计一种测量江宽的方案，并在图②中画出图形.21.（本题满分10分）如图，B D 为圆O 的直径，A B A C =，A D 交B C 于E ，2A E =，4E D =．（1）求证：A B E A D B △∽△，并求A B 的长；（2）延长D B 到F ，使B F B O =，连接F A ，那么直线F A 与⊙O 相切吗？为什么？22.（本题满分10分）荣昌公司要将本公司100吨货物运往某地销售，经与春晨运输公司协商，计划租用甲、乙两种型号的汽车共6辆，用这6辆汽车一次将货物全部运走，其中每辆甲型汽车最多能装该种货物16吨，每辆乙型汽车最多能装该种货物18吨．已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元；租用2辆甲型汽车和1辆乙型汽车共需费用2450元，且同一种型号汽车每辆租车费用相同．（1）求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元？（2）若荣昌公司计划此次租车费用不超过5000元．通过计算求出该公司有几种租车方案？请你设计出来,并求出最低的租车费用．C23.(本题满分11分)如图，等腰梯形ABCD中，AD∥BC，AB=DC，AC⊥BD，过D点作DE∥AC 交BC的延长线于E点.（1）求证：四边形ACED是平行四边形；（2）若AD=3，BC=7，求梯形ABCD的面积.24.（本题满分12分）如图所示，在平面直角坐标系中，⊙M 经过原点O ，且与x 轴、y轴分别相交于A (-6，0)，B （0，-8）两点．（1）请求出直线AB 的函数表达式；（2）若有一抛物线的对称轴平行于y 轴且经过点M ，顶点C 在⊙M 上，开口向下，且经过点B ，求此抛物线的函数表达式；（3）设（2）中的抛物线交x 轴于D ，E 两点，在抛物线上是否存在点P ，使得115PDE ABCS S =△△？若存在，请求出点P 的坐标；若不存在，请说明理由．数学参考答案一、选择题1.A2.B3.B4.B5.B6.C7.A8.D9.B10.B11.B12.C 二、填空题13.-6 14.a ≥3 15.k ＞-2，且k ≠-1 16.3 17.-318.解：（1）由图1知：4810181050++++=（名）………2分 答：该校对50名学生进行了抽样调查．（2）本次调查中，最喜欢篮球活动的有18人．………………3分x181003650⨯=％％………………………………………….4分∴最喜欢篮球活动的人数占被调查人数的36％． （3）1(302624)20-++=％％％％ 20020100÷=％ （人）…6分8100100016050⨯⨯=％ （人）答：估计全校学生中最喜欢跳绳活动的人数约为160人．………8分 19.解：⑴ y ＝(x －50)∙ w ＝(x －50) ∙ (－2x ＋240)＝－2x 2＋340x －12000，∴y 与x 的关系式为：y ＝－2x 2＋340x －12000．.......3分 ⑵ y ＝－2x 2＋340x －12000＝－2 (x －85) 2＋2450，∴当x ＝85时，y 的值最大． ……………………………6分 ⑶ 当y ＝2250时，可得方程 －2 (x －85 )2＋2450＝2250． 解这个方程，得 x 1＝75，x 2＝95． 根据题意，x 2＝95不合题意应舍去．∴当销售单价为75元时，可获得销售利润2250元．…………9分20.解：（1）在BAC Rt ∆中， 68=∠ACB ，∴24848.210068tan =⨯≈⋅= AC AB （米）答：所测之处江的宽度约为248米…………………………………3分 （2）从所画出的图形中可以看出是利用三角形全等、三角形相似、解直角三角形的知识来解决问题的，只要正确即可得分……………9分21.（1）证明：A B A C = ，ABC C ∴=∠∠，C D = ∠∠，ABC D ∴=∠∠．又BAE D AB = ∠∠，ABE AD B ∴△∽△．A B A E A D A B∴=． AB 2=AD ·AE=（AE+ED ）·AE=（2+4）×2=12.AB ∴=． ……………………………………………………5分（2）直线F A 与⊙O 相切．理由如下： 连接O A ．BD 为⊙O 的直径，∴∠．BD ∴====1122B F B O B D ∴===⨯=AB = ，BF BO AB ∴==．90OAF ∴= ∠．∴直线F A 与⊙O 相切． ……………………………………10分22.解：（1）设租用一辆甲型汽车的费用是元，租用一辆乙型汽车的费用是元．由题意得解得答：租用一辆甲型汽车的费用是800元，租用一辆乙型汽车的费用是850元．……………………………………………………………3分 （2）设租用甲型汽车辆，则租用乙型汽车辆．由题意得解得……………………………………………………6分由题意知，为整数，或或共有3种方案，分别是：方案一：租用甲型汽车2辆，租用乙型汽车4辆； 方案二：租用甲型汽车3辆，租用乙型汽车3辆； 方案三：租用甲型汽车4辆，租用乙型汽车2辆． 方案一的费用是（元）； 方案二的费用是（元）；方案三的费用是（元），所以最低运费是4900元．……………9分答：共有3种方案，分别是：方案一：租用甲型汽车2辆，租用乙型汽车4辆； 方案二：租用甲型汽车3辆，租用乙型汽车3辆； 方案三：租用甲型汽车4辆，租用乙型汽车2辆．最低运费是4900元．……………………………………………10分 23.证： ⑴∵AD ∥BC ∴AD ∥CE 又∵DE ∥AC∴四边形ACED 是平行四边形……………… 3分 ⑵过D 点作DF ⊥BE 于F 点 ……………………4分∵DE ∥AC ，AC ⊥BD ∴DE ⊥BD ，即∠BDE=90° 由⑴知DE=AC ，CE=AD=3∵四边形ABCD 是等腰梯形∴AC=DB ………………………………………7分 ∴DE=DB ……………………………………8分∴△DBE 是等腰直角三角形，∴△DFB 也是等腰直角三角形 ∴DF=BF=21(7－3)+3=5……………………9分(也可运用：直角三角形斜边上的中线等于斜边的一半)()2553721DF BC)(AD 21S ABCD=⨯+=∙+=梯形……11分注：⑴过对角线交点O 作OF ⊥BC 于F ，延长FO 交AD 于H ，于是OH ⊥AD由△ABC ≌△DCB ，得到△OBC 是等腰直角三角形，OF=21BC=27同理OH=21AD=23，高HF=52327=+⑵过A 作AF ⊥BC 于F ，过D 作DH ⊥BC 于H ，由△AFC ≌△DHB得高AF=FC=21(AD+BC)=5⑶DOA COD BOC AOB ABCD S S S S S ∆∆∆∆+++=梯形(进行计算)24. 解：（1）设直线AB 的函数表达式为(y kx b k =+∵直线AB经过(60)(08)A B --，，，，∴由此可得60,8.k b b -+=⎧⎨=-⎩解得4,38.k b ⎧=-⎪⎨⎪=-⎩∴直线AB的函数表达式为483y x =--． (4)分（2）在R t AO B △中，由勾股定理，得10AB ===，x∵圆M 经过O A B ，，三点，且90AO B ∠=°，AB∴为圆M 的直径，∴半径5M A =，设抛物线的对称轴交x 轴于点N ，M N x ⊥∵，∴由垂径定理，得132A N O N O A ===．在R t A M N △中，4M N ===，541C N M C M N ∴=-=-=，∴顶点C 的坐标为(31)-，， 设抛物线的表达式为2(3)1y a x =++， 它经过(08)B -，，∴把0x =，8y =-代入上式，得28(03)1a -=++，解得1a =-，∴抛物线的表达式为22(3)168y x x x =-++=---．…………8分（3）如图，连结A C ，B C ，35213521ON MC 21AN MC 21S S S BMC AMC ABC ⨯⨯+⨯⨯=∙+∙=+=∆∆∆ =15在抛物线268y x x =---中，设0y =， 则2680x x ---=， 解得12x =-，24x =-．D E ∴，的坐标分别是(40)-，，(20)-，， 2D E ∴=；设在抛物线上存在点()P x y ，，使得111511515P D E A B C S S =⨯=△△＝，则1y 221y DE 21S PDE =⨯⨯=∙=∆，1y ∴=±，当1y =时，2681x x ---=，解得123x x ==-，1(31)P ∴-，；当1y =-时，2681x x ---=-，解得13x =-+，23x =--2(3)P ∴-+-1，3(3)P ---1．综上所述，这样的P 点存在，且有三个，1(31)P -，，2(3)P -+-1，3(31)P ---．…………………….12分。

2011年北京市高级中等学校招生考试数 学 试 卷学校______________ 姓名______________ 准考证号_________________考生须知1．本试卷共6页，共五道大题，25道小题，满分120分．考试时间120分钟． 2．在试卷和答题卡上准确填写学校名称、姓名和准考证号． 3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效． 4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答． 5．考试结束，将本试卷、答题卡和草稿纸一并交回．一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的 1．34-的绝对值是A ．43- B ．43C ．34-D ．342．我国第六次全国人口普查数据显示，居住在城镇的人口总数达到665 575 306人，将665 565 306用科学记数法表示（保留三个有效数字）约为 A ．766.610⨯ B ．80.66610⨯ C ．86.6610⨯ D ．76.6610⨯ 3．下列图形中，既是中心对称图形又是轴对称图形的是 A ．等边三角形 B ．平行四边形 C ．梯形 D ．矩形4．如图，在梯形A B C D 中，A D B C ∥，对角线A C 、B D 相交于点O ，若1A D =，3B C =，则A O C O 的值为 A ．12B ．13C ．14D ．195．北京市今年6月某日部分区县的最高气温如下表：区县大兴通州平谷顺义杯柔门头沟延庆昌平 密云 房山最高气温（℃）32 32 30 32 30 32 29 32 30 32则这10个区县该日气温的众数和中位数分别是 A ．32，32 B ．32，30 C ．30，32 D ．32，31 6．一个不透明的盒子中装有2个白球、5个红球和8个黄球，这些球除颜色外，没有任何其他区别，现从这个盒子中随机摸出一个球，摸到红球的概率为 A ．815B ．13C ．215D ．1157．抛物线265y x x =-+的顶点坐标为 A ．(34)-， B ．(34)， C ．(34)--， D ．(34)-，8．如图，在R t A B C △中，90A C B ∠=︒，30B A C ∠=︒，2AB =，D 是A B 边上的一个动点（不与点A 、B 重合），过点D 作C D 的垂线交射线C A 于点E ．设A D x =，C E y =，则下列图象中，能表示y 与x 的函数关系的图象大致是ODCBACE DBAxyy yxxy111111122OOOxy DCBAO21二、填空题（本题共16分，每小题4分） 9．若分式8x x-的值为0，则x 的值等于_____________．10．分解因式：321025a a a -+=____________．11．若右图是某几何体的表面展开图，则这个几何体是_________． 12．在右表中，我们把第i 行第j 列的数记为i j a ，（其中i ，j 都是不大于5的正整数），对于表中的每个数i j a ，规定如下： 当i j≥时，1i ja =，；当i j<时，0i ja =，．例如：当2i=，1j=时，211i ja a ==，，．按此规定，13a =，_______；表中的25个数中，共有______个1；计算111122133144155i i i i i a a a a a a a a a a ⋅+⋅+⋅+⋅+⋅，，，，，，，，，，的值为__________．三、解答题（本题共30分，每小题5分）13．计算：()112c o s 30272π2-⎛⎫-++- ⎪⎝⎭。

y C y x =2y x =(1,1)丰台区2011年高三年级第二学期统一练习（一）数 学（理科）2011.3 一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合U =R ，2{560}A x x x =-+≥，那么U A =ð(A) {2x x <或3}x > (B) {23}x x << (C) {2x x ≤或3}x ≥ (D) {23}x x ≤≤2．6x x的展开式中常数项是 (A) -160(B) -20(C) 20(D) 1603．已知平面向量a ，b 的夹角为60°，3,1)=a ，||1=b ，则|2|+=a b(A) 27(C)23(D)274．设等差数列{}n a 的公差d ≠0，14a d =．若k a 是1a 与2k a 的等比中项，则k = (A) 3或-1 (B) 3或1(C) 3 (D) 1 5．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题： ① 若m β⊂，αβ⊥，则m α⊥； ② 若α//β，m α⊂，则m //β；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥． 其中正确命题的序号是 (A) ①③ (B) ①②(C)③④ (D) ②③6．已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x )，则实数x 的取值范围是(A) (,1)(2,)-∞-⋃+∞(B) (,2)(1,)-∞-⋃+∞(C) (1,2)-(D) (2,1)-7．从如图所示的正方形OABC 区域内任取一个点(,)M x y ，则点M 取自阴影部分的概率为(A)12(B)13(C) 14(D)168．对于定义域和值域均为[0，1]的函数f (x )，定义1()()f x f x =，21()(())f x f f x =，…，1()(())n n f x f f x -=，n =1，2，3，…．满足()n f x x =的点x ∈[0，1]称为f 的n 阶周期点．设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是(A) 2n(B) 2(2n -1)(C) 2n(D) 2n 2二、填空题：本大题共6小题，每小题5分，共30分．9．如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ， 点A 的纵坐标为45，则cos α= ． 10．双曲线的焦点在x 轴上，实轴长为4，离心率为3，则该双曲线的标准方 程为 ，渐近线方程为 ． 11．已知圆M ：x 2+y 2-2x -4y +1=0，则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）的距离为 ．12．如图所示，过⊙O 外一点A 作一条直线与⊙O 交于C ，D 两点，AB 切⊙O 于B ，弦MN 过CD 的中点P ．已知AC =4，AB =6，则MP ·NP = ． 13．对某种花卉的开放花期追踪调查，调查情况如下：则这种卉的平均花期为___天． 14．将全体正奇数排成一个三角形数阵： 1 3 5 7 9 11 13 15 17 19 ……按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为 ．NBAαxy O三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ． （Ⅰ）求角A 的大小； （Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC 的形状．16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD． （Ⅰ）若点M 是棱PC 的中点，求证：PA // 平面BMQ ； （Ⅱ）求证：平面PQB ⊥平面PAD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值 ．17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖． （Ⅰ）求分别获得一、二、三等奖的概率；PABCD QM（Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．18.（本小题共13分） 已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数． （Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值； （Ⅱ）若函数()'()axg x e f x -=⋅，求函数()g x 的单调区间．19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P 满足||||PA PB +=P 的轨迹为W ． （Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．20.（本小题共13分）已知123{(,,,,)n n S A A a a a a ==L ，0i a =或1，1,2,,}i n =L (2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值； （Ⅱ）令0(0,0,0,,0)n W =L 14243个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥；（Ⅲ）令123(,,,,)n U a a a a =L ，若n V S ∈，求所有(,)d U V 之和．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011年高三年级第二学期数学统一练习（一）数 学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．35- 10．221432x y -=，y =± 11．2 12．25413．16天（15.9天给满分） 14．n 2-n +5 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ． （Ⅰ）求角A 的大小； （Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC 的形状．解：（Ⅰ）在△ABC 中，因为b 2+c 2-a 2=bc ，由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =12．(余弦定理或公式必须有一个，否则扣1分) ……3分∵ 0<A <π ， （或写成A是三角形内角） ……………………4分∴3A π=． ……………………5分（Ⅱ）PA BCDQM2cos 2cos 2sin 3)(2xx x x f +=11sin cos 222x x =++ ……………………7分1sin()62x π=++， ……………………9分∵3A π= ∴2(0,)3B π∈∴5666B πππ<+<（没讨论，扣1分） …………………10分∴当62B ππ+=，即3B π=时，()f B 有最大值是23． ……………………11分 又∵3A π=， ∴3C π=∴△ABC 为等边三角形． ……………………13分16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD． （Ⅰ）若点M 是棱PC 的中点，求证：PA // 平面BMQ ； （Ⅱ）求证：平面PQB ⊥平面PAD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值 ． 证明：（Ⅰ）连接AC ，交BQ 于N ，连接MN ． ……………………1分∵BC ∥AD 且BC =12AD ，即BC //AQ ． ∴四边形BCQA 为平行四边形，且N 为AC 中点， 又∵点M 在是棱PC 的中点，∴ MN // PA ……………………2分 ∵ MN ⊂平面MQB ，PA ⊄平面MQB ，…………………3分 ∴ PA // 平面MBQ ． ……………………4分 （Ⅱ）∵AD // BC ，BC =12AD ，Q 为AD 的中点， ∴四边形BCDQ 为平行四边形，∴CD//BQ ． ……………………6分∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ． 又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD ， ……………………7分∴BQ ⊥平面PAD ． ……………………8分∵BQ ⊂平面PQB ， ∴平面PQB ⊥平面PAD ． ……………………9分 另证：AD // BC ，BC =12AD ，Q 为AD 的中点 ∴ BC // DQ 且BC = DQ ，∴ 四边形BCDQ 为平行四边形，∴CD // BQ ． ∵ ∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ． ……………………6分∵ PA =PD ， ∴PQ ⊥AD ． ……………………7分∵ PQ ∩BQ =Q ，∴AD ⊥平面PBQ ． ……………………8分∵ AD ⊂平面PAD ， ∴平面PQB ⊥平面PAD ． ……………………9分 （Ⅲ）∵PA =PD ，Q 为AD 的中点， ∴PQ ⊥AD ．∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD=AD ， ∴PQ ⊥平面ABCD ．……………10分（不证明PQ ⊥平面ABCD 直接建系扣1分）如图，以Q 为原点建立空间直角坐标系．则平面BQC的法向量为(0,0,1)n =r；(0,0,0)Q ，P ，B，(C -分设(,,)M x y z ，则(,,PM x y z =-u u u u r ，(1,)MC x y z =---u u uu r ， ∵PM tMC =u u u u r u u u u r ，∴(1))(x t x y t y z t z =--⎧⎪=⎨⎪-=-⎩）， ∴1t x t y z ⎧=-⎪+⎪⎪=⎨⎪⎪=⎪⎩ ……………………12分 在平面MBQ中，QB =u u u r，(1t QM t =-+u u u u r ， ∴平面MBQ法向量为)m t =u r． ……………………13分∵二面角M -BQ -C 为30°，cos302n m n m ︒⋅===r u r r u r ∴3t =． ……………………14分17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖． （Ⅰ）求分别获得一、二、三等奖的概率； （Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．解：（Ⅰ）设“摸到一等奖、二等奖、三等奖”分别为事件A ，B ，C ． ……1分则P (A )=111114444256⨯⨯⨯=，（列式正确，计算错误，扣1分） ………3分 P (B )33341-A =2565= （列式正确，计算错误，扣1分） ………5分三等奖的情况有：“生，生，意，兴”；“生，意，意，兴”；“生，意，兴，兴”三种情况． P (C )222444111*********()()()444444444444A A A =⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯964=．…7分（Ⅱ）设摸球的次数为ξ，则1,2,3ξ=． ……8分1(1)4P ξ==， 313(2)4416P ξ==⨯=，3319(3)44464P ξ==⨯⨯=，27(4)1(1)(2)(3)64P P P P ξξξξ==-=-=-==．（各1分）故取球次数ξ的分布列为139271234 2.754166464E ξ=⨯+⨯+⨯+⨯=．(约为2.7) …13分18.（本小题共13分） 已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数． （Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值； （Ⅱ）若函数()'()axg x e f x -=⋅，求函数()g x 的单调区间．解：（Ⅰ）∵3211()(0)32f x x ax x b a =+++≥， ∴2'()1f x x ax =++． ……………………1分∵()f x 在(1,0)处切线方程为33y x =-， ∴'(1)3(1)0f f =⎧⎨=⎩， ……………………3分 ∴1=a ，611-=b ． （各1分） ……………………5分（Ⅱ）'()()ax f x g x e=21axx ax e ++=()x R ∈．'()g x =22(2)(1)()ax axax x a e a x ax e e +-++2[(2)]ax x ax a e -=-+-． ……………………7分①当0a =时，'()2g x x =，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞． ……………………9分②当a >时，令'()0g x =，得x =或2x a a=- ……………………10分（ⅰ）当20a ->，即0a <<()g x 的单调递增区间为22(0,)a a -，单调递减区间为(,0)-∞，22(,)a a-+∞；……11分（ⅱ）当20a a-=，即a ='()g x =2220x x e -=-≤， 故()g x 在(,)-∞+∞单调递减； ……12分（ⅲ）当20a -<，即a >()g x 在22(,0)a a-上单调递增，在(0,)+∞，22(,)a a --∞上单调递 ………13分 综上所述，当0a=时，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞；当0a<<时，()g x 的单调递增区间为22(0,)a a-，单调递减区间为(,0)-∞， 当a =()g x 的单调递减区间为(,)-∞+∞；当a >时，()g x的单调递增区间为22(,0)a a-，单调递减区间为(0,)+∞，22(,)a a--∞． （“综上所述”要求一定要写出来）19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P 满足||||PA PB +=P 的轨迹为W ． （Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．解：（Ⅰ）由椭圆的定义可知，动点P 的轨迹是以A ，B 为焦点，长轴长为2分∴1c =，a =22b =． ……3分W 的方程是22132x y +=． …………4分 （另解：设坐标1分，列方程1分，得结果2分）（Ⅱ）设C ，D 两点坐标分别为11(,)C x y 、22(,)D x y ，C ，D 中点为00(,)N x y ．由221132y kx x y =+⎧⎪⎨+=⎪⎩ 得 22(32)630k x kx ++-=． ……6分所以122632k x x k +=-+ …………7分 ∴12023232x x k x k +==-+， 从而0022132y kx k =+=+． ∴MN 斜率2002232332MN y k k k x m m k +==---+． ………9分 又∵CM DM =， ∴CD MN ⊥， ∴222132332k k k m k +=---+ 即 232k m k =-+ …10分 当0k =时，0m =； ……11分当0k ≠时，212323k m k k k=-=-++]126,0()0,126[⋃-∈． ……13分 故所求m 的取范围是]126,126[-． ……14分 （可用判别式法）20.（本小题共13分） 已知123{(,,,,)n n S A A a a a a ==L ， 0i a =或1，1,2,}i n =L (2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值； （Ⅱ）令0(0,0,0,,0)n W =L 14243个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥； （Ⅲ）令123(,,,,)n U a a a a =L ，若n V S ∈，求所有(,)d U V 之和．解：（Ⅰ）2510C =； ………3分（Ⅱ）证明：令123(,,)n u a a a a =……，123(,,)n v b b b b =……∵0i a =或1，0i b =或1；当0i a =，0i b =时，||i a +||0i b =||i i a b =-当0i a =，1i b =时，||i a +||1i b =||i i a b =-当1i a =，0i b =时，||i a +||1i b =||i i a b =- 当1i a =，1i b =时，||i a +||2i b =||0i i a b ≥-= 故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++L ++123()n b b b b +++L ++ 123(||||||)n a a a a =++L |++|123(||||||)n b b b b +++L |++| 112233(||||||)n n a b a b a b a b ≥-+-+--L |++|(,)d u v = ………8分（Ⅲ）解：易知n S 中共有2n 个元素，分别记为(1,2,,2)n k v k =L 123(,,)n v b b b b =……∵0i b =的k v 共有12n -个，1i b =的k v 共有12n -个．∴21(,)nk k d u v =∑ =∴21(,)n kk d u v =∑=12n n -g ．法二：根据（Ⅰ）知使(,)k d u v r =的k v 共有r n C 个∴21(,)n k k d u v =∑=012012n n n n n C C C n C ++++g g g L g 21(,)n kk d u v =∑=120(1)(2)0n n n n n n n n C n C n C C --+-+-++g g g L g两式相加得21(,)n k k d u v =∑=12n n -g（若用其他方法解题，请酌情给分）。

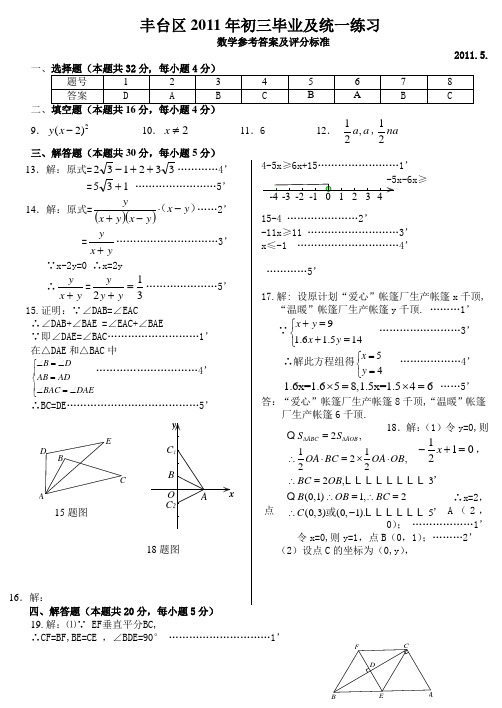
EDCBA AB CDEF丰台区2011年初三毕业及统一练习数学参考答案及评分标准2011.5.9．2(2)y x - 10．2≠x 11．6 12． 1,2a a ,12na 三、解答题（本题共30分，每小题5分） 13．解：原式=332132++-…………4’ =135+ ……………………5’14．解：原式=()()）（y x y x y x y-⋅-+……2’=yx y+…………………………3’ ∵x-2y=0 ∴x=2y ∴y x y +=312=+y y y …………………5’ 15.证明：∵∠DAB=∠EAC∴∠DAB+∠BAE =∠EAC+∠BAE∵即∠DAE=∠BAC ………………………1’ 在△DAE 和△BAC 中B DAB ADBAC DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩…………………………4’ ∴BC=DE …………………………………5’15题图18题图16．解：4-5x ≥6x+15……………………1’≥15-4 …………………2’-11x ≥11 ………………………3’ x ≤-1 …………………………4’…………5’17.解: 设原计划“爱心”帐篷厂生产帐篷x 千顶,“温暖”帐篷厂生产帐篷y 千顶. ………1’ ∵⎩⎨⎧=+=+145.16.19y x y x ……………………3’ ∴解此方程组得⎩⎨⎧==45y x ………………4’ 1.6x=1.658,1.5x=1.546⨯=⨯= ……5’ 答：“爱心”帐篷厂生产帐篷8千顶,“温暖”帐篷厂生产帐篷6千顶.18．解：（1）令y=0,则0121=+-x ， ∴x=2，点A （2，0）； ………………1’令x=0,则y=1，点B （0，1）；………2’（2）设点C 的坐标为（0,y ），四、解答题（本题共20分，每小题5分） 19.解：⑴∵ EF 垂直平分BC,∴CF=BF,BE=CE ，∠BDE=90° …………………………1’2,112,222,3(0,1)1,2(0,3)(0,1).5’或’∆∆=∴⋅=⨯⋅∴=∴=∴=∴-Q L L L L L L L L Q L L L L L L ABC AOB S S OA BC OA OB BC OB B OB BC CFEDABC O FE DCB A 321又∵ ∠ACB=90°∴EF ∥AC∴E 为AB 中点， 即BE=AE ………………………………2’ ∵CF=AE ∴CF=BE∴CF=FB=BE=CE …………………………………………3’ ∴四边形是BECF 菱形. …………………………………4’ ⑵当∠A= 45°时，四边形是BECF 是正方形. …………5’20.（1）直线FC 与⊙O 的位置关系是_相切_；………………1’ 证明：联结OC∵OA=OC ，∴∠1=∠2，由翻折得，∠1=∠3，∠F=∠AEC=90°∴∠3=∠2 ……………………………………………………2’ ∴OC ∥AF ，∴∠F=∠OCD=90°，∴FC 与⊙O 相切 …………3’ （2）在Rt △OCD 中，cos ∠COD=OC 1OD 2∴∠COD=60° …………………………4’在Rt △OCD 中，CE=OC ·sin ∠3………………………5’21. 解：(1)2010年；年均增长率为13%；6696元 …………3’(2)见图；……………………………………………………4’(3)140. ……………………………………………………5’22．解：（1）………………… 正确画出一个图形给1分，共2’（2）符合要求的矩形最多可以画出 3 个，它们面积之间的数量关系是 相等 ；………4’ (3) 不相等 ． …………………………………………………………………………………5’五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23．⑴反比例函数解析式：1y x=………………………………1’ ⑵∵已知B(1,1),A(2,0) ∴△OAB 是等腰直角三角形 ∵顺时针方向旋转135°，∴B ’2), A’(22) ∴中点P 为(-22, -2)．………………………………………2’ ∵（-22）·（2）=1 ………………………………………3’ ∴点P 在此双曲线上． ……………………………………………4’ ⑶∵EH=n , 0M=m ∴S △OEM =EH OM ⋅21=mn 21=22，∴m=2n ………………5’ 又∵F(m ，312m -) 在函数图象上 ∴)123(-m m =1．………………………………………………6’ 将m =2n 代入上式，得2)2(23n -2n=1∴2n 2n 3∴2n 2n 33-7’24．解：（1）∵在□ABCD 中∴EH=FG=2 ，G （0，－1）即OG=1………………………1’ ∵∠EFG=45°∴在Rt △HOG 中，∠EHG=45° 可得OH=1∴H （1，0）……………………………………………………2’ （2）∵OE=EH-OH=1 ∴E （－1，0），设抛物线1C 解析式为1y =2ax +bx+c ∴代入E 、G 、H 三点，∴a =1 ，b=0,，c=－1∴1y =2x －1……………………………………………………3’依题意得，点F 为顶点，∴过F 点的抛物线2C 解析式是2y =2(+2x ）－1…………………4’（3）∵抛物线2C 与y 轴交于点A ∴A （0，3），∴AG=4 情况1：AP=AG=4E 过点A 作AB ⊥对称轴于B ∴AB=2在Rt △PAB 中，BP=∴1P(-2,3+或2P(-2,3-……………………………6’ 情况2：PG=AG=4同理可得：3P(-2,-1+或4P(-2,-1-…………………8’ ∴P 点坐标为(-2,3+或(-2,3-或(-2,-1+或(-2,-1-.25．解：（1）33；…………………………………………1’（2）2363 ； …………………………………………2’（3）以点D 为中心，将△DBC 逆时针旋转60°，则点B 落在点A ，点C 落在点E.联结AE,CE ，∴CD=ED ，∠CDE=60°，AE=CB= a ， ∴△CDE 为等边三角形，∴CE=CD. …………………………………………4’当点E 、A 、C 不在一条直线上时，有CD=CE<AE+AC=a +b ； 当点E 、A 、C 在一条直线上时， CD 有最大值，CD=CE=a +b ；此时∠CED=∠BCD=∠ECD=60°，∴∠ACB=120°，……………………7’ 因此当∠ACB=120°时，CD 有最大值是a +b .。

第9题图2cm215cm 2011年北京市解密预测中考模拟数学试题卷11. 本试卷分试题卷和答题卷两部分。

满分120分, 考试时间120分钟.2．答题时, 应该在答题卷密封区内写明校名, 姓名和学号。

3．考试时不能使用计算器，所有答案都必须做在答题卷标定的位置上，请务必注意试题序号和答题序号相对应.4．考试结束后, 上交答题卷.试题卷一、仔细选一选（本大题有10小题，每小题3分，共30分。

请选出各题中一个符合题意的正确选项，不选、多选、错选，均不得分）1．下列四个数中，比0小的数是（▲）A．23B．．π D．12．2009年初甲型H1N1流感在墨西哥爆发并在全球蔓延，研究表明，甲型H1N1流感球形病毒细胞的直径约为0.00000156 m，用科学记数法表示这个数是（▲）A．0.156×510- m B．0.156×510 m C．1.56×610- m D．1.56×610 m 3．下列运算正确的是（▲）A．236·a a a= B．11()22-=- C4=± D．|6|6-=4．解方程组23739x yx y+=⎧⎨+=⎩，①－②得（▲）A．32x= B. 32x=- C. 2x= D. 2x=-5．把不等式组110xx+⎧⎨-≤⎩>0,的解集表示在数轴上，如下图，正确的是（▲）6．已知二次函数131232+-=xxy，则函数值y的最小值是（▲）A. 3B. 2C. 1D. -17．小明中午放学回家自己煮面条吃，有下面几道工序：（1）洗锅盛水2分钟；（2）洗菜3分钟；（3）准备面条及佐料2分钟；（4）用锅把水烧开7分钟；（5）用烧开的水煮面条和菜要3分钟。

以上各工序除（4）外，一次只能进行一道工序，小明要将面条煮好，最少用（▲）A. 14分钟B. 13分钟 C . 12分钟 D . 11分钟8．由左图所示的地板砖各两块所铺成的下列图案中，既是轴对称图形，又是中心对称图形的是（▲）①②主视图 俯视图左视图A ．B ．C ．D ．9．如图是一个高为，底面半径为2cm 的圆锥形无底纸帽，现利用这个纸帽的侧面纸张裁剪出一个圆形纸片（不考虑纸帽接缝），这个圆形纸片的半径最长可以是（ ▲ ） （计算结果保留3个有效数字。

NM L M NL 2011年丰台区中考一模数学试卷一、选择题 （本题共32分，每小题4分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1．3-的倒数是（ ）．A ．3-B ．3C ．13D ．13-2．2010年某市启动了历史上规模最大的轨道交通投资建设项目，预计某市轨道交通投资将达到51800000000元人民币．将51800000000用科学记数法表示正确的是（ ）． A ．105.1810⨯ B ．951.810⨯ C ．110.51810⨯ D ．851810⨯3．下列立体图形中，侧面展开图是扇形的是（ ）．4．若130x y -++=，则x y -的值是（ ）．A ．1B ．1-C ．4D ．4-5．某射击队要从四名运动员中选拔一名参加比赛，选拔赛中，每名队员的平均成绩x 与方差2S 如下表所示．如果要选择一个平均成绩高且发挥稳定的人参赛，那么这个人应是（ ）．甲 乙 丙 丁 x 8 9 9 8 2S111．21．3A ．甲B ．乙C ．丙D ．丁6．已知关于x 的一元二次方程22x m x -=有两个不相等的实数根，则m 的取值范围是（ ）． A ．1m >- B ．2m <- C ．1m -≥ D ．1m <7．在九张大小质地都相同的卡片上分别写有数字4-、3-、2-、1-、0、1、2、3、4，任意抽取一张卡片，则所抽卡片上数字的绝对值小于2的概率是（ ）．A ．19B ．13C ．12D ．238．一电工沿着如图所示的梯子NL 往上爬，当他爬到中点M 处时，由于地面太滑，梯子沿墙面与地面滑下，设点M 的坐标为(,)x y (0)x >，则y 与x 之间的函数关系用图象表示大致是（ ）．A ．B ．C ．D ．OD CBAx xxxyyyyO OOO图3图2图1B 1C 1C 2B 2B n -1C n-1Cn Bn ABCB 2C 2A BCB 1C 1C 1B 1CBAA ．B ．C ．D ．二、填空题（本题共16分，每小题4分） 9．分解因式：244x y xy y -+= ．10．在函数12y x =-中，自变量x 的取值范围是 ．11．如图，AB 为⊙O 的弦，⊙O 的半径为5，OC AB ⊥于点D ，交⊙O 于点C ，且1CD =，则弦AB 的长是 ．12．已知在ABC △中，BC a =．如图1，点1B 、1C 分别是AB 、AC 的中点，则线段11B C 的长是_______；如图2，点1B 、2B ，1C 、2C 分别是AB 、AC 的三等分点，则线段1122B C B C +的值是__________；如图3，点1B 、2B 、L L n B ，1C 、2C 、L L n C ，分别是AB 、AC 的(1)n +等分点，则线段1122n n B C B C B C +++L L 的值是 ______．三、解答题（本题共30分，每小题5分）13．计算：011122011()3tan 602-++︒-（-）．14．已知20x y -=，求122y x y x y ÷--的值．EDCBAxy B AO-4-3-2-10432115．已知：如图，B D ∠=∠，DAB EAC ∠=∠，AB AD =． 求证：BC DE =．16．解不等式453(25)x x -+≥，并把它的解集在数轴上表示出来．17．列方程或方程组解应用题：“爱心”帐篷厂和“温暖”帐篷厂原计划每周生产帐篷共9千顶，现某地震灾区急需帐篷14千顶，两厂 决定在一周内赶制出这批帐篷．为此，全体职工加班加点，“爱心”帐篷厂和“温暖”帐篷厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍，恰好按时完成了这项任务．求在赶制帐篷的一周内，“爱心”帐篷厂和“温暖”帐篷厂各生产帐篷多少千顶？18．如图，在平面直角坐标系中，一次函数112y x =-+的图象与x 轴、y 轴分别交于A 、B 两点．（1）求点A 、B 的坐标； （2）点C 在y 轴上，当2ABC AOB S S ∆∆=时，求点C 的坐标．A B C D E FO A B C D E F四、解答题（本题共20分，每小题5分）19．已知：如图，在四边形ABFC 中，90ACB ∠=︒，BC 的垂直平分线EF 交BC 于点D ，交AB 于点E ，且CF AE =．（1）求证：四边形BECF 是菱形；（2）当A ∠的大小为多少度时，四边形BECF 是正方形？20．在Rt AFD △中，90F ∠=︒，点B 、C 分别在AD 、FD 上，以AB 为直径的半圆O 过点C ，连结AC ，将AFC △沿AC 翻折得AEC △，且点E 恰好落在直径AB 上． （1）判断：直线FC 与半圆O 的位置关系是_______________；并证明你的结论． （2）若2OB BD ==，求CE 的长．21．“十一五”期间，尽管我国经历了雪冻、干旱、洪涝、地震等自然灾害，以及受国际金融危机冲击等影响，但在政府的各种强农、惠农、扩大内需、促进消费的政策措施下，农村居民收入保持较快增长态势．在农村居民收入较快增长的基础上，农村居民消费整体呈现较强增势，生活消费水平稳定提高，生活质量明显改善．根据国家统计局公布的20062010-年农村居民纯收入及增长情况的相关数据绘制的图表如下：图1 图2ABCABC图3表1 2010年农村居民家庭生产经营人均纯收入分项统计表纯收入分项项目第一产业生产经营 得到的纯收入第二产业生产经营 得到的纯收入第三产业生产经营 得到的纯收入金额（元）2240420请根据以上信息解答下列问题：（1）“十一五”期间，农村居民人均纯收入年增长最快的是 年，计算这五年农村居民人均纯收入的平均增长率是 （精确到1%）．根据此平均增长率预测2011年农村居民纯收入人均约为__________元（精确到个位）；（2）请将图2中的空缺部分补充完整（补图所用数据精确到个位）； （3）填写表1中的空缺部分．22．认真阅读下列问题，并加以解决：问题1：如图1，ABC △是直角三角形，90C ∠=︒．现将ABC △补成一个矩形．要求：使ABC △的两个顶点成为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．请将符合条件的所有矩形在图1中画出来；图1 图2问题2：如图2，ABC △是锐角三角形，且满足BC AC AB >>，按问题1中的要求把它补成矩形．请问符合要求的矩形最多可以画出 个，并猜想它们面积之间的数量关系是 （填写“相等”或“不相等”）；问题3：如果ABC △是钝角三角形，且三边仍然满足BC AC AB >>，现将它补成矩形．要求：ABC △有两个顶点成为矩形的两个顶点，第三个顶点落在矩形的一边上，那么这几个矩形面积之间的数量关系是 （填写“相等”或“不相等”）．xy O H G F E五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23．已知：反比例函数()0ky k x=≠经过点(1,1)B ． （1）求该反比例函数解析式； （2）连结OB ，再把点(2,0)A 与点B 连结，将OAB △绕点O 按顺时针方向旋转135︒得到''OA B △，写出''A B 的中点P 的坐标，试判断点P 是否在此双曲线上，并说明理由； （3）若该反比例函数图象上有一点3(,1)2F m m -）（其中0m >），在线段OF 上任取一点E ，设E 点的纵坐标为n ，过F 点作FM x ⊥轴于点M ，连结EM ，使OEM △的面积是22，求代数式2223n n +-的值．24．已知：如图，在平行四边形EFGH 中，点F 的坐标是(2,1)--，45EFG ∠=︒． （1）求点H 的坐标；（2）抛物线1C 经过点E 、G 、H ，现将1C 向左平移使之经过点F ，得到抛物线2C ，求抛物线2C 的解析式；（3）若抛物线2C 与y 轴交于点A ，点P 在抛物线2C 的对称轴上运动．请问：是否存在以AG 为腰的等腰AGP △？若存在，求出点P 的坐标；若不存在，请说明理由．D C B A A B C DA BC D 25．已知：在ABC △中，BC a =，AC b =，以AB 为边作等边ABD △．探究下列问题：（1）如图1，当点D 与点C 位于直线AB 的两侧时，3a b ==，且60ACB ∠=︒，则CD = ；（2）如图2，当点D 与点C 位于直线AB 的同侧时，6a b ==，且90ACB ∠=︒，则CD = ；（3）如图3，当ACB ∠变化，且点D 与点C 位于直线AB 的两侧时，求CD 的最大值及相应的ACB ∠的度数．图1 图2 图3EDCBA-4-3-2-104321 2011年丰台区中考一模数学试卷答案一、选择题（本题共32分， 每小题4分）题号1 2 3 4 5 6 7 8 答案 D A B C BABC二、填空题（本题共16分，每小题4分）9．2(2)y x - 10．2x ≠ 11．6 12．12a ，a ，12na三、解答题（本题共30分，每小题5分） 13．解：原式=231233-++ =531+．14．解：原式()()=yx y x y x y ⋅-+-（） =yx y+． ∵20x y -=， ∴2x y =， ∴y x y +1=23y y y =+．15．证明：∵DAB EAC ∠=∠∴DAB BAE EAC BAE ∠+∠=∠+∠ ∵即DAE BAC ∠=∠ 在DAE △和BAC △中 B D AB ADBAC DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BC DE =．16．解：45615x x -+≥， 56154x x ---≥， 1111x -≥， 1x -≤．17．解：设原计划“爱心”帐篷厂生产帐篷x 千顶，“温暖”帐篷厂生产帐篷y 千顶． ∵91.6 1.514x y x y +=⎧⎨+=⎩O FE DCB A321AB CDEFxy C 2AB C 1O ∴解此方程组得54x y =⎧⎨=⎩ 1.6 1.658x =⨯=，1.5 1.546y =⨯=．答：“爱心”帐篷厂生产帐篷8千顶，“温暖”帐篷厂生产帐篷6千顶．18．解：（1）令0y =，则1102x -+=，∴2x =，点(2,0)A ；令0x =，则1y =，点(0,1)B ； （2）设点C 的坐标为(0,)y ， ∵2ABC AOB S S =△△∴11222OA BC OA OB ⋅=⨯⋅ ∵2BC OB = ∵(0,1)B ∴1OB = ∴2BC =∴(0,3)C 或(0,1)-．四、解答题（本题共20分，每小题5分） 19．解：（1）∵EF 垂直平分BC ， ∴CF BF =，BE CE =，90BDE ∠=︒又∵90ACB ∠=︒∴EF AC ∥ ∴E 为AB 中点， 即BE AE = ∵CF AE =∴CF BE =∴CF FB BE CE ===∴四边形是BECF 菱形．（2）当45A ∠=︒时，四边形是BECF 是正方形． 20．（1）直线FC 与⊙O 的位置关系是相切； 证明：连结OC ， ∵OA OC =，∴12∠=∠，由翻折得，13∠=∠，90F AEC ∠=∠=︒∴32∠=∠ ∴OC AF ∥，∴90F OCD ∠=∠=︒， ∴FC 与⊙O 相切．（2）在Rt OCD △中，1cos 2OC COD OD ∠==F ED A BC ∴60COD ∠=︒在Rt OCD △中，sin 3CE OC COD =⋅∠=．21．解：（1）2010年；年均增长率为13%；6696元；（2）见图；（3）140．22．解：（1）（2）符合要求的矩形最多可以画出3个，它们面积之间的数量关系是相等； （3）不相等．五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．（1）反比例函数解析式：1y x= （2）∵已知(1,1)B ，(2,0)A ∴OAB △是等腰直角三角形 ∵顺时针方向旋转135︒， ∴'(0,2)B -，'(2,2)A -- ∴中点P 为2(,2)2--． ∵2()(2)12-⨯-=， ∴点P 在此双曲线上． （3）∵EH n =，OM m =∴112222OEM S OM EH mn =⋅==△，∴2m n=． 又∵3(,1)2F m m -）在函数图象上∴3(1)12m m -=． 将2m n=代入上式，得2322()12n n -=， ∴223n n +=， ∴22233n n +-=-．24．解：（1）∵在平行四边形ABCD 中∴2EH FG ==，(0,1)G -即1OG =∵45EFG ∠=︒∴在Rt HOG △中，45EHG ∠=︒可得1OH =∴(1,0)H ．（2）∵1OE EH OH =-=∴(1,0)E -，设抛物线1C 解析式为21y ax bx c =++∴代入E 、G 、H 三点，∴1a =，0b =，1c =-∴211y x =-．依题意得，点F 为顶点，∴过F 点的抛物线2C 解析式是22(2)1y x =+-．（3）∵抛物线2C 与y 轴交于点A∴(0,3)A ，∴4AG =情况1：4AP AG ==过点A 作AB ⊥对称轴于B∴2AB =在Rt PAB △中，23BP = ∴1(2,323)P -+或2(2,323)P --．情况2：4PG AG == 同理可得：3(2,123)P --+或4(2,123)P --- ∴P 点坐标为(2,323)-+或(2,323)--或(2,123)--+或(2,123)---．25．解：（1）33；（2）3632-；（3）以点D 为中心，将DBC △逆时针旋转60︒，则点B 落在点A ，点C 落在点E ．连结AE ，CE ，∴CD ED =，60CDE ∠=︒，AE CB a ==，∴CDE △为等边三角形，E D CB A D A BC E ∴CE CD =．当点E 、A 、C 不在一条直线上时，有CD CE AE AC a b =<+=+；当点E 、A 、C 在一条直线上时，CD 有最大值，CD CE a b ==+；此时60CED BCD ECD ∠=∠=∠=︒，∴120ACB ∠=︒，因此当120ACB ∠=︒时，CD 有最大值是a b +．2011年丰台区中考一模数学试卷答案部分解析一、选择题1. 【答案】D【解析】3-的倒数是13-，故选D ．2. 【答案】A【解析】51800000000用科学记数法表示为105.1810⨯，故选A ．3. 【答案】B【解析】侧面展开图是扇形的是圆锥，长方体侧面展开图可能是长方形也可能是正方形，圆柱侧面展开图是长方形，棱锥侧面展开图是三角形，故选B ．4. 【答案】C 【解析】130x y -++=，1x =，3y =-，=1(3)4x y ---=，故选C ．5. 【答案】B【解析】选择一个平均成绩高且发挥稳定的人参赛，即平均成绩较高，方差较小的乙参赛，故选B ．6. 【答案】A【解析】一元二次方程22x m x -=有两个不相等的实数根，220x x m --=，=4+40m >V ，1m >-，故选A ．7. 【答案】B【解析】绝对值小于2的数有1-、0、1共3个数，故概率为31=93，故选B ．8. 【答案】C【解析】直角三角形斜边中线等于斜边一半，梯子NL 长度不变，故M 点到直角顶点的距离不变，即M 点的轨迹是以原点为圆心的一段圆弧．故选C ．二、填空题9. 【答案】2(2)y x -【解析】分解因式：22244(44)(2)x y xy y y x x y x -+=-+=-．故答案为：2(2)y x -．10. 【答案】2x ≠ 【解析】函数12y x =-有意义，分母不为0，即20x -≠，2x ≠． 故答案为：2x ≠．11. 【答案】6 【解析】由垂径定理可知AD BD =，⊙O 的半径为5，1CD =，4OD =，由勾股定理可知3AD BD ==，6AB =．故答案为：6．12. 【答案】12a ，a ，12na 【解析】依题意知，根据中位线性质可知111122B C BC a ==； 图2中，111=3B C BC ，222=3B C BC ，112212=33B C B C a a a ++=； 图3中，111=+1B C BC n ，222=1B C BC n +，L L ，=1n n n B C BC n +； 11221231(1)1=1212n n n n n B C B C B C BC BC na n n ++++++++=⨯⨯=++L L L ． 故答案为：12a ，a ，12na ．。

丰台区2010—2011学年度第一学期期末练习初三数学 2011.011. 如图，在ABC ∆中，D ，E 两点分别在AB 、AC 边上，且BC DE //，若3:2:=BC DE ，则ABC ADE S S ∆∆:的值为( ) A. 9:4B. 4:9C. 3:2D. 2:32. 将抛物线23x y =向下平移1个单位得到新的抛物线，则新抛物线的解析是( )A. 132+=x yB. 132-=x yC. 2)1(3+=x yD. 2)1(3-=x y3. 在小正方形组成的网络中，直角三角形的位置如图所示，则αtan 的值是( )A.53B.54 C. 34 D. 434. 在半径为18的圆中，︒120的圆心角所对的弧长是( ) A. π12 B. π10 C. π6 D. π35. 抛物线)3)(1(+-=x x y 的对称轴是直线( )A. 1=xB. 1-=xC. 3-=xD. 3=x6. 如图，矩形ABOC 的面积为3，反比例函数)0(≠=k xky 的图象过点A ，则k 的值为( )A. 3B. 5.1-C. 6-D. 3-7. 如图，一个圆形转盘被等分成七个扇形区域，上面分别标有数字1、2、3、4、5、6、7，转盘指针的位置固定，转动转盘后自由停止。

转动转盘一次，当转盘停止转到时，记指针指向标有偶数所在区域的概率为P （偶数），指针指向标有奇数所有区域的概率为P （奇数），则P （偶数）与P （奇数）的大小关系是( ) A. P （偶数）> P （奇数） B. P （偶数）= P （奇数） C. P （偶数）< P （奇数） D. P （偶数）≤ P （奇数）8. 如图，在梯形ABCD 中，BC AD //，︒=∠90B ，1=AD ，23=AB ，2=AB ，点P 是BC 边上的一个动点（点P 与点B 不重合），AP DE ⊥于点E ，设x AP =，y DE =，在下列图象中，能正确反映y 与x 的函数关系的是( )9. 已知四条线段a 、b 、c 、d 之间有如下关系：d c b a ::=，且12=a ，8=b ，15=c ，则线段d =_____10. 已知01cos 2=-α，则锐角=α________11. 已知A ，B 是⊙O 上的两点，如果︒=∠60AOB ，C 是⊙O 上不与A ，B 重合的任一点，那么ACB∠的度数为_______12. 如图，⊙O 的半径为2, 1C 是函数的221x y =的图象，2C 是函数的221x y -=的图象，3C 是函数的x y =的图象，则阴影部分的面积是______13. 计算：︒-︒+︒60tan 45sin 30cos 214. 如图，在ABC ∆中，D 、E 两点分别在AC ，AB 两边上，ADE ABC ∠=∠，3=AD ，7=AB ，7.2=AE ，求AC 的长。

2010~2011年丰台区中考数学一模试题分析
北京中考研究中心施佳辰一、整体难度
本试卷题目比较简单，考查内容比较基础，选择填空最后一道题的难度系数相对历年中考属于比较高的，包括最后一道压轴题考察的也是几何三大变换中相对简单的旋转变换。

本试卷的难点基本集中在后四道大题，之所以说难只是说需要学生对于基本模型与基本方法有一个比较扎实的把握，例如第24题中对于构造等腰三角形的讨论方法，25题中对于有可能涉及到旋转的模型的认识，都需要学生有清醒的认识。

总体上，这张试卷难度不大，但是想要的高分，需要对于基础知识掌握到位。

二、难度与分值分布
80
70
60
50
40
30
20
10
简单中等难
难易分布
三、难点、易错点分析
四、总结分析
几何方面，本张试卷比较突出的一点就是考察同学们对于基本模型的掌握程度，例如有关中点的几种模型，三角形n等分点模型，双垂直模型，构造等腰三角形的几种模型，以及两条共顶点的等长线段模型。

这些模型往往是学生的易错点和题目中的难点，所以同学们需要特别强化自己对于基本知识，基本方法，基本模型的掌握。

代数方面，几种函数图象的性质，以及图像上的点的坐标与函数解析式的联系是常考的考点，同时考生们还应在接下来的时间里加强对于代数式变形中用到的换元法、整体带入法、配方法等常用方法的熟练程度。

阅读使人充实，会谈使人敏捷，写作使人精确。

——培根百日质量活动知识答题1.公司的质量方针是：持续改进、创一流品质，竭诚服务、让顾客满意2.质量信息的特征为：价值性、适时性、正确性、等级性、可追索性3.质量是一组固有特性满足要求的程度4.质量改进是致力于增强满足质量要求的能力5.质量改进包括：防守型改进进攻型改进6.质量问题处理时一般遵循二个原则：一是必须坚持三不放过原则二是执行逐级上拆原则7.QC小组分为：管理型、现场型、攻关型、服务型四种类型8.质量改进的措施有：纠正措施、预防措施9.对策表又叫措施计划表，是针对质量问题的主要原因而制定的应采取措施的计划表10.流程图是将一个过程的步骤用图的形式表示出来的一种技术11.质量改进是质量管理的一部分，致力于增强满足质量要求的能力12.质量改进消除系统性的问题，对现有的质量水平在控制的基础上加以提高，使质量达到一个新的水平，新的高度13.质量改进是通过不断采取纠正和预防措施来增强企业的质量管理水平14.质量问题是以质量损失的形式表现出来的，大多数损失往往是由几种不合格引起的，这些不合格往往是又是由少数原因引起的15.质量管理的发展，大致经历了质量检验阶段、统计质量控制阶段、全面质量管理阶段三个阶段。

16.管理体系文件分为以下四个层次：一、管理手册；二、程序文件；三、管理制度和作业指导书；四、记录。

17.质量管理八项原则分别是：以顾客为关注焦点、领导作用、全员参与、过程方法、管理的系统方法、持续改进、基于事实的决策方法、与供方互利的关系。

18.质量管理体系对公司的意义是：公司实施质量管理的必备条件；使公司得到发展；是拓展市场的基础；提高公司产品质量水平和能力19.PDCA的模式分别是指：策划、实施、检查、处置20.管理评审应该由总经理来主持二、判断题1.（×）质量管理体系审核是指有资格的第三方对组织质量管理体系的符合性、有效性、充分性进行的系统的检查活动。