山东省邹平双语学校2015届高三上学期第一次月考数学(理)试题

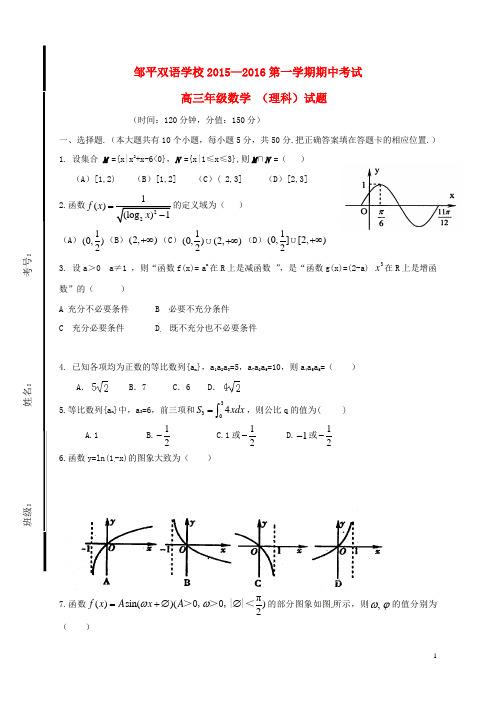
邹平双语学校2015—2016第一学期期中考试高三年级数学 （理科）试题（时间：120分钟，分值：150分）一、选择题.（本大题共有10个小题，每小题5分，共50分.把正确答案填在答题卡的相应位置.） 1. 设集合 M ={x|x 2+x-6<0}，N ={x|1≤x ≤3},则M ∩N =（ ） （A ）[1,2) （B ）[1,2] （C ）( 2,3] （D ）[2,3] 2.函数()f x 的定义域为（ ）（A ）1(0,)2（B ）(2,)+∞（C ）1(0,)(2,)2+∞（D ）1(0,][2,)2+∞3. 设a ＞0 a ≠1 ，则“函数f(x)= a x在R 上是减函数 ”，是“函数g(x)=(2-a) 3x 在R 上是增函数”的（ ）A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件4. 已知各项均为正数的等比数列{a n }，a 1a 2a 3=5，a 7a 8a 9=10，则a 4a 5a 6=（ ）A ．B ．7C ．6D ．5.等比数列{a n }中，a 3=6，前三项和3304S xdx =⎰，则公比q 的值为( )A.1B.12-C.1或12-D.1-或12-6.函数y=ln(1-x)的图象大致为（ ）7.函数π()sin()()2f x A x A ωω=+∅∅＞0,＞0,||＜的部分图象如图所示，则,ωϕ的值分别为（ ）班级：____________ 姓名：_____________ 考号：________________________A.1，0B.1，π4 C.2，-π3D.2，π68. 函数f （x ）=x 2﹣bx+a 的图象如图所示，则函数g （x ）=ln x+f′（x ）的零点所在的区间是（ ）A ．（，）B ．（，1）C ．（1，2）D ．（2，3） 9.在△ABC 中，有命题 ①； ②；③若，则△ABC 为等腰三角形；④若，则△ABC 为锐角三角形．上述命题正确的是（ ）A ．①②B ．①④C ．②③D ．②③④10. 已知函数f （x ）=，函数g （x ）=αsin （）﹣2α+2（α＞0），若存在x 1，x 2∈[0，1]，使得f （x 1）=g （x 2）成立，则实数α的取值范围是（ ）A ．[]B ．（0，]C ．[] D ．[，1]二、填空题.（本大题共有5个小题，每小题5分，共25分.把正确答案填在答题卡的相应位置.） 11. 在△ABC 中，a=4，b=5，c=6，则= ．12.在等差数列{}n a 中，若1594a a a π++=，则46tan()a a +=___________13. 在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知△ABC 的面积为3，b ﹣c=2，cosA=﹣，则a 的值为 ．14．设函数⎪⎩⎪⎨⎧≥<=-1,1,)(311x x x e x f x 则使得f(x)≤2成立的x 的取值范围是________．15.下列五个函数中：①2x y =；②2log y x =；③y ；④y =；⑤cos 2y x =，当1201x x <<<时，使()()121222f x f x x x f ++⎛⎫>⎪⎝⎭恒成立的函数是________（将正确的序号都填上）.三、解答题（本大题共75分，请写出必要的文字说明） 16.（本小题满分12分））已知函数f （x ）=sin 2x ﹣sin 2（x ﹣），x ∈R ．（Ⅰ）求f （x ）的最小正周期； （Ⅱ）求f （x ）在区间[﹣，]内的最大值和最小值．17. （本小题满分12分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且bcosC=3acosB ﹣ccosB ． （Ⅰ）求cosB 的值； （Ⅱ）若，且，求a 和c 的值．18. （本小题满分12分） 等差数列{a n }中，a 7=4，a 19=2a 9， （Ⅰ）求{a n }的通项公式； （Ⅱ）设b n =，求数列{b n }的前n 项和S n ．19. （本小题满分12分）已知S n是等比数列{a n}的前n项和，a1＞0，S1，S2，S3成等差数列，16是a2和a8的等比中项．（Ⅰ）求{a n}的通项公式；（Ⅱ）若等差数列{b n}中，b1=1，前9项和等于27，令c n=2a n•b n，求数列{c n}的前n项和T n．20. （本小题满分13分）某商店预备在一个月内分批购入每张价值为20元的书桌共36台，每批都购入x台（x是正整数），且每批均需付运费4元，储存购入的书桌一个月所付的保管费与每批购入书桌的总价值（不含运费）成正比，若每批购入4台，则该月需用去运费和保管费共52元，现在全月只有48元资金可以用于支付运费和保管费.f x（Ⅰ）求该月需用去的运费和保管费的总费用();（Ⅱ）能否恰当地安排每批进货的数量，使资金够用？写出你的结论，并说明理由.21. （本小题满分14分）己知函数f（x）=e x﹣x﹣1（Ⅰ）求函数y=f（x）在点（1，f（1））处的切线方程：（Ⅱ）若方程f（x）=a，在[﹣2，ln 2]上有唯一零点，求实数a的取值范围；（Ⅲ）对任意x≥0，f（x）≥（t﹣1）x恒成立，求实数t的取值范闱．邹平双语学校2015—2016第一学期期中考试高三 年级数学（理科）试题答案（时间：120分钟，分值：150分）把正确答案填在答题卡的相应位置.）二、填空题.（本大题共有5个小题，每小题5分，共25分.把正确答案填在答题卡的相应位置.） 13.8 14.(,8] 15.①②三、解答题（共75分）16.（本大题12分） 解：（Ⅰ）化简可得f （x ）=sin 2x ﹣sin 2（x ﹣）=（1﹣cos2x ）﹣[1﹣cos （2x ﹣）]=（1﹣cos2x ﹣1+cos2x+sin2x ）=（﹣cos2x+sin2x ）=sin （2x ﹣）∴f （x ）的最小正周期T==π；（Ⅱ）∵x ∈[﹣，]，∴2x ﹣∈[﹣，]， ∴sin （2x ﹣）∈[﹣1，]，∴sin （2x ﹣）∈[﹣，]， ∴f （x ）在区间[﹣，]内的最大值和最小值分别为，﹣17. （本大题12分）（I ）由正弦定理得a=2RsinA ，b=2RsinB ，c=2RsinC ， 则2RsinBcosC=6RsinAcosB ﹣2RsinCcosB ， 故sinBcosC=3sinAcosB ﹣sinCcosB ， 可得sinBcosC+sinCcosB=3sinAcosB ， 即sin （B+C ）=3sinAcosB ，可得sinA=3sinAcosB ．又sinA≠0， 因此．（6分）（II ）解：由，可得accosB=2，班级：____________ 姓名：_____________ 考号：________________________，由b2=a2+c2﹣2accosB，可得a2+c2=12，所以（a﹣c）2=0，即a=c，所以．（12分）18. （本大题12分）解：（I）设等差数列{a n}的公差为d∵a7=4，a19=2a9，∴解得，a1=1，d=∴=（II）∵==∴s n===19．（本大题12分）解：（Ⅰ）设数列{a n}的公比为q，已知S n是等比数列{a n}的前n项和，a1＞0，S4，S2，S3成等差数列，则：2S2=S3+S4解得：q=﹣2或1（舍去）由于：16是a2和a8的等比中项解得：a1=1所以：（Ⅱ）等差数列{b n}中，设公差为d，b1=1，前9项和等于27．则：解得：d=所以：令c n=2a n b n==（n+1）（﹣2）n﹣1T n =c 1+c 2+…+c n ﹣1+c n =2•（﹣2）0+3•（﹣2）1+…+（n+1）（﹣2）n ﹣1①﹣2T n =2•（﹣2）1+3•（﹣2）2+…+（n+1）（﹣2）n② ①﹣②得：3]﹣（n+1）（﹣2）n解得：20. （本大题13分） 解：（1）设题中比例系数为k ，若每批购入x 台，则共需分36x批，每批价值为20x 元，由题意 36()420f x k x x=⋅+⋅ ………………………………………………4分 由 4x =时，52y = 得 161805k == ………………………………………………6分 *144()4(036,)f x x x x x∴=+<≤∈N ……………………………………………8分 （2）由（1）知*144()4(036,)f x x x x x=+<≤∈N()48f x ∴≥=（元） ………………………………………………11分 当且仅当1444x x=，即6x =时，上式等号成立. 故只需每批购入6张书桌，可以使资金够用. ………………………………………13分21. （本大题14分）解：（Ⅰ）∵f（x ）=e x﹣x ﹣1，∴f′（x ）=e x﹣1．…（1分） ∴f′（1）=e ﹣1，f （1）=e ﹣2， ∴求函数y=f （x ）在点（1，f （1））处的切线方程是y ﹣（e ﹣2）=（e ﹣1）（x ﹣1）． 化简得所求切线的方程为y=（e ﹣1）x ﹣1．…（3分）（Ⅱ）f′（x ）=e x﹣1，当x ∈（﹣2，0）时，f′（x ）≤0，f （x ）单调递减；当x ∈（0，ln2）时，f′（x ）≥0，f （x ）单调递增．…（5分），f （ln2）=1﹣ln2．…（6分）∵f（﹣2）＞f （ln2）．函数f （x ）=a ，在[﹣2，ln2]上有唯一零点，等价于，f （ln2）＜a≤f（﹣2）或a=f （0）， 即或a=0．∴实数a 的取值范围是或a=0．…（8分）（Ⅲ）令g （x ）=f （x ）﹣（t ﹣1）x=e x﹣1﹣tx ，则g′（x ）=e x﹣t ．∵x≥0，∴e x≥1．…（10分）（ i ）当t≤1时，g′（x ）≥0，g （x ）在区间[0，+∞）上是增函数，所以g （x ）≥g（0）=0．即f（x）≥（t﹣1）x恒成立．…（11分）（ ii）当t＞1时，e x﹣t=0，x=lnt，当x∈（0，lnt）时，g′（x）≤0，g（x）单调递减，当x∈（0，lnt）时，g（x）＜g（0）=0，此时不满足题设条件．…（13分）综上所述：实数t的取值范围是t≤1．…（14分）第页，共页第页，共页。

2015-2016第一学期期中考试(3区) 高一 年级 数学(连读班）试题（时间：120分钟，分值：150分）一、选择题(共10道小题,每道小题5分，共50分。

请将正确答案填涂在答题卡上)1、数列1，2，4，8，16，32，…的一个通项公式是（ ）A 、21na n =- B 、 12n n a -= C 、2n na= D 、12n na+=2、由11,3ad ==确定的等差数列{}n a 中，当298n a =是，序号n 等于（）A 、99 C 、96 C 、100 D 、1013、已知ABC ∆的面积为23，且2,AC AB ==A ∠等于 （ )A 、30 B 、30150或 C 、60 D 、60120或4、若实数,x y 满足约束条件222x y x y ≤⎧⎪≤⎨⎪+≥⎩，则目标函数2z x y =+的取值范围为（ )A 、［2,6]B 、［2,5］C 、[3,6]D 、［3，5］ 5、直线cos 10x y α+-=的倾斜角的范围是 ( ）A 、3,,4224ππππ⎡⎫⎛⎫⎪⎪⎢⎣⎭⎝⎭ B 、30,,44πππ⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭ C 、30,4π⎡⎫⎪⎢⎣⎭D 、3,44ππ⎡⎤⎢⎥⎣⎦ 6、已知等比数列0>na,前n 项和为n S ，且56,8641==+S a a ，则公比为( )A ．2B ．3-C ．2或3-D ．2或3 w.w.w..c7、若两直线02)2(4:,022:21=+-+=-++y m x l m y mx l 互相平行，则常数m 等于（ ）A 。

－2B 。

4 C.－2或4 D 。

0班级：____________ 姓名：_____________ 考号：________________________ 班级：____________ 姓名：_____________ 考号：________________________A 、0B 、1C 、2D 、49、在等差数列{}na 中，10110,0a a <>,1110a a >且，nS 为数列{}na 的前n 项和，则使0nS >的n 的最小值为 （ ）A 、10B 、11C 、20D 、2110、点P （－2， －1）到直线l ： (1+3λ)x +（1+2λ)y =2+5λ的距离为d , 则d 的取值范围是 （ ） A. 0≤d ≤13 B. d ≥0 C 。

邹平双语学校2014——2015学年度第一学期第一次测评高三年级（文科班）数 学试卷（时间：120分钟 满分：150分）一.选择题：（每题5分，共50分）】1.设集合A ＝{1,2,3,4}，B ＝{0,1,2,4,5}，全集U ＝A ∪B ，则集合∁U (A ∩B )中的元素共有( )A ．3个B ．4个C ．5个D ．6个2.下列四个函数中，与y ＝x 表示同一函数的是 ( )A ．y ＝(x )2B ．y ＝3x 3C ．y ＝x 2D ． y ＝x 2x3.下列函数中，最小正周期为π，且图象关于直线x ＝π3对称的是 （ ） A ．y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π6 B ．y ＝sin ⎝⎛⎭⎪⎫2x ＋π3 C ．y ＝sin ⎝ ⎛⎭⎪⎫2x －π3 D ．y ＝sin ⎝⎛⎭⎪⎫2x －π6 4.如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则 ( )A..AD →＋BE →＋CF →＝0B..BD →－CF →＋DF →＝0C..AD →＋CE →－CF →＝0D..BD →－BE →－FC →＝05. 下列各式中，对任何实数x 都成立的一个式子是（ ）A ．()2lg 1lg 2x x +≥B ．212x x +>C ．2111x ≤+D ．12x x+≥ 6.已知a ＝(cos 40°，sin 40°)，b ＝(sin 20°，cos 20°)，则a·b 等于 ( )A ．1 B.32 C.12 D.227.下列命题错误的是( )A ．命题“若m ≤0，则方程x 2＋x ＋m ＝0有实数根”的逆否命题为：“若方程x 2＋x ＋m ＝0无实数根，则m >0”B ．“x ＝2”是“x 2－x －2＝0”的充分不必要条件C ．若p ∧q 为假命题，则p ，q 中必有一真一假D ．对于命题p ：∃x ∈R ，x 2＋x ＋1<0，则綈p ：∀x ∈R ，x 2＋x ＋1≥08.在△ABC 中，已知222c bc b a ++=，则角A 为（ ） A. 3π B. 6π C. 32π D. 3π或32π 9.若函数f (x )＝e x sin x ，则此函数图象在点(4，f (4))处的切线的倾斜角为 ( )A.π2B ．0C ．钝角D ．锐角 10..函数y ＝lg|x |x的图象大致是 ( )二.填空题：（每题5分，共25分）11.已知向量a ＝(2，－1)，b ＝(－1，m )，c ＝(－1， 2)，若(a ＋b )∥c ，则m ＝________.12.在△ABC 中，若B=︒30，AB=32，AC=2，则△ABC 的面积是13.关于x 的不等式x 2＋(a ＋1)x ＋ab>0的解集是{x|x<－1或x>4}，则实数a 、b 的值分别为________．14.已知对不同的a 值，函数f (x )＝2＋a x －1(a >0，且a ≠1)的图象恒过定点P ，则P 点的坐标是________．15.已知向量a ，b 满足|a |＝1，|b |＝2，a 与b 的夹角为60°，则|a －b |＝________.三．解答题（共75分）16.（12分）已知A ＝{a ＋2,2a 2＋a }，若3∈A ，求a 的值．17.。

2015-2016学年度邹平双语学校12月月考卷考试时间：120分钟总分：150第I卷（选择题）一、选择题（每小题五分，共50分）1．已知集合，则（）A．B．C．D．2．下列结论正确的个数是（）①若，则恒成立；②命题“”的否定是“”；③“命题为真”是“命题为真”的充分不必要条件．A．1个B．2个C．3个D．4个3．已知等差数列前项为，若，则（）A．B．C．D．4．正三角形ABC内一点M满足，，则的值为（）A．B．C．D．5．已知数列，给定，若对任意正整数，恒有，则的最小值为（）A．1 B．2 C．3 D．46．已知函数 f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜）的部分图象如图所示，为了得到g（x）=sin2x的图象，则只需将f （x）的图象（）A．向右平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向左平移个长度单位7．如图是一个几何体的三视图，根据图中的数据，计算该几何体的表面积为A．B．C．D．8．函数 f（x）=（x2﹣2x）e x的图象大致是（）A．B．C．D．9．已知点的坐标满足，点的坐标为，点为坐标原点，则的最小值是（）A．B．C．D．10．设函数．若存在的极值点满足，则m 的取值范围是（）A．B．C．D．第II卷（非选择题）二、填空题（每小题五分，共20分）11．与向量垂直且模长为的向量为．12．已知递增的等差数列满足，则．13．在中，角的对边分别为，已知，且，则为．14．一个球的内接圆锥的最大体积与这个球的体积之比为．15．已知函数则满足的实数a的取值范围是.三、解答题16．（本小题满分10分）在中，角对边分别为，且．（Ⅰ）求角；（Ⅱ）若，求周长的取值范围．17．（本小题满分12分）已知向量，满足，，函数·．（Ⅰ）将化成的形式；（Ⅱ）求函数的单调递减区间；（Ⅲ）求函数在的值域．18．（本小题满分12分）已知数列的前项和（），数列的前项和（）．（Ⅰ）求数列的前项和；（Ⅱ）求数列的前项和．19．如图，在三棱柱中，四边形都为矩形.（I）设D是AB的中点，证明：直线平面;（II）在中，若，证明：直线平面.20．（本小题满分12分）已知函数（1）求的单调区间和极值；（2）若对于任意的，都存在，使得，求的取值范围．21．函数.（I）函数在点处的切线与直线垂直，求a的值；（II）讨论函数的单调性；（III）不等式在区间上恒成立，求实数a的取值范围.。

邹平双语学校2015-2016第一学期第一次月考高二年级数学试卷（普通理科）（时间90分钟，满分120分）一、选择题（共10题，每题5分，共50分） 1．下列语句不是命题的有( )①若a >b ，b >c ，则a >c ；②x >2；③3<4；④函数y ＝a x(a >0，且a ≠1)在R 上是增函数． A ．0个 B ．1个 C ．2个D ．3个2．命题甲：动点P 到两定点A ，B 的距离之和|PA |＋|PB |＝2a (a >0，常数)；命题乙：P 点轨迹是椭圆．则命题甲是命题乙的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件3.设命题p ：∀x ∈R ，x 2＋1>0，则p ⌝为( )A ．∃x 0∈R ，x 20＋1>0B ．∃x 0∈R ，x 20＋1≤0 C ．∃x 0∈R ，x 20＋1<0 D ．∀x ∈R ，x 2＋1≤0 4．椭圆1422=+y x 的离心率为 ( )A ．21 B ．23 C ． ±21D ．±235. 双曲线19422=-y x 的渐近线方程是 （ ） A ．x y 23±= B ．x y 32±= C ．x y 49±= D ．x y 94±= 6．如果方程x 2a 2＋y 2a ＋6＝1表示焦点在x 轴上的椭圆，则实数a 的取值范围是( )A ．a >3B ．a <－2C ．a >3或a <－2D ．a >3或－6<a <－27、椭圆x 225＋y 29＝1上的一点M 到左焦点F 1的距离为2，N 是MF 1的中点，则|ON |等于( )学区： 班级： 姓名： 考号：A ．2B ．4C ．8 D.328、抛物线24(0)y ax a =<的焦点坐标是（ ）A.1(,0)4a B.1(0,)16a C.1(0,)16a - D. 1(,0)16a9．过点(0,2)与抛物线28y x =只有一个公共点的直线有（ ） A.1条 B.2条 C.3条 D.无数多条10.设12,F F 为双曲线2214x y -=的两个焦点，点P 在双曲线上，且满足120PF PF ⋅=u u u r u u u u r ，则12F PF ∆的面积是（ ）A.1B. 2C. 3D.2二、填空题（共5题，每题5分，共25分）11.设命题p ：2x ＋y ＝3，q ：x －y ＝6，若p ∧q 为真命题，则x ＝________，y ＝________．12.若∀x ∈R ，f (x )＝(a 2－1)x是单调减函数，则a 的取值范围是________．13.动圆C 经过定点F(0，2)且与直线y+2=0相切，则动圆的圆心C 的轨迹方程是________．14.双曲线22a x -22by =1的两条渐近线互相垂直，那么它的离心率 ．15.已知直线x －y =2与抛物线y 2=4x 交于A 、B 两点，那么线段AB 的中点坐标是三、解答题(每15分，共45分)16.已知p ：2x 2－3x －2≥0，q ：x 2－2(a －1)x ＋a (a －2)≥0，若p 是q 的充分不必要条件，求实数a 的取值范围．17.设21,F F 分别为椭圆C ：)0(12222>>=+b a by a x 的左右两个焦点，椭圆上的点A （1，23）到21,F F 两点的距离之和等于4，求：①写出椭圆C 的方程和焦点坐标②过1F 且倾斜角为30°的直线，交椭圆于A,B 两点，求△AB 2F 的周长18.已知动点P 与平面上两定点(2,0),(2,0)A B -连线的斜率的积为定值12-. （Ⅰ）试求动点P 的轨迹方程C.（Ⅱ）设直线1:+=kx y l 与曲线C 交于M 、N 两点，当|MN |=324时，求直线l 的方程.邹平双语学校2015-2016第一学期第一次月考高二年级数学答题纸（普通理科） （时间90分钟，满分120分）题号12345678910考号：答案二、填空题（共5题，每题5分，共25分）11. ． 12. __________. 13.__________.14. ． 15. ．三、解答题(共45分，每题15分)16.17.18.邹平双语学校2015-2016第一学期第一次月考高二年级数学答案（普通理科） （时间90分钟，满分120分）一、选择题（共10题，每题5分，共50分）答案 B B B B A D B BCA二、填空题（共5题，每题5分，共25分）11. 3,-3 ． 12. ()()2,11,2Y --. 13. y x 82=.14.2 ． 15. (4,2) ．三、解答题(共45分，每题15分) 16.令M ＝{x |2x 2－3x －2≥0}＝{x |(2x ＋1)(x －2)≥0}＝⎩⎨⎧⎭⎬⎫x |x ≤－12或x ≥2， N ＝{x |x 2－2(a －1)x ＋a (a －2)≥0}＝{x |(x －a )[x －(a －2)]≥0} ＝{x |x ≤a －2或x ≥a }， 由已知p ⇒q 且q ⇒/p ，∴⎩⎪⎨⎪⎧a －2≥－12，a <2或⎩⎪⎨⎪⎧a －2>－12，a ≤2⇔32≤a <2或32<a ≤2⇔32≤a ≤2，即所求a 的取值范围是⎣⎢⎡⎦⎥⎤32，2. 17.①1422=+y x ，F （±3，0）②周长为4a ＝8 18..解：设点(,)P x y ，则依题意有1222x x ⋅=-+-， 整理得.1222=+y x 由于2x ≠±，所以求得的曲线C的方程为221(2).2x y x +=≠± （Ⅱ）由.04)21(:.1,122222=++⎪⎩⎪⎨⎧+==+kx x k y kx y y x 得消去解得x 1=0, x 2=212,(214x x k k +-分别为M ，N 的横坐标）由,234|214|1||1||22212=++=-+=kk k x x k MN .1:±=k 解得 所以直线l 的方程x －y +1=0或x +y －1=0。

邹平双语学校2015-2016第一学期第一次月考高三年级数学试卷（理科班）（时间120分钟，满分150分）一、选择题（共10题，每题5分，共50分）1.若集合M ＝{x ∈R|－3＜x ＜1}，N ＝{x ∈Z|－1≤x ≤2}，则M ∩N ＝ ( )A.{0}B.{－1,0}C.{－1,0,1}D.{－2，－1,0,1,2} 2.已知a ，b 是实数，则“a >0且b >0”是“a ＋b >0且ab >0”的 ( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 3.函数y=x ln （1－x ）的定义域为（ ）A ．（0,1） B.[0,1) C.(0,1] D.[0,1]4.5.2(sin 22.5cos 22.5)︒+︒的值为（ ）A ．212-B ．212+C ．21-D ．26.已知函数f(x)为奇函数,且当x>0时, f(x) =x 2+1x,则f(-1)= ( ) （A ）-2 （B ）0 （C ）1 （D ）2 7.函数()3sin 2cos 2f x x x =+（ ） A ．在(,)36ππ--单调递减 B ．在(,)63ππ单调递增C ．在(,0)6π-单调递减 D ． ()f x 在(0,)6π单调递增8.函数)20)(sin()(πϕϕω<>+=，A x A x f 其中的图象如图所示，为了得到x x g 2sin )(=的图象，则只需将)(x f 的图象（ ）（A ）向右平移6π个长度单位 （B ）向右平移3π个长度单位（C ）向左平移6π个长度单位（D ）向左平移3π个长度单位9.已知函数y ＝e x的图像与函数y ＝f (x )的图像关于直线y ＝x 对称，则( )A ．f (2x )＝e 2x(x ∈R ) B ．f (2x )＝ln2ln x (x >0) C ．f (2x )＝2e x (x ∈R ) D ．f (2x )＝ln x ＋ln2(x >0)学区： 班级： 姓名： 考号：10.设a ∈R ，函数f (x )＝e x ＋a ·e －x的导函数是f ′(x )，且f ′(x )是奇函数．若曲线y ＝f (x )的一条切线的斜率是32，则切点的横坐标为 ( )A ．ln 2B ．－ln 2 C.ln 22 D.－ln 22二、填空题（共5题，每题5分，共25分）11.令p (x )：ax 2＋2x ＋1＞0，若对∀x ∈R ，p (x )是真命题，则实数a 的取值范围是 . 12.已知)(x f 是定义在R 上的奇函数.当0>x 时，x x x f 4)(2-=，则不等式x x f >)(的解集用区间表示为 .13.设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为____. 14.已知向量a ＝(x 2，x ＋1)，b ＝(1－x ，t )，若函数f (x )＝a ·b 在区间(－1,1)上是增函数，则实数t 的取值范围是________．15.函数f (x )＝3x －x 3在区间(a 2－12，a )上有最小值，则实数a 的取值范围是________． 三、解答题（共75分）16.(本小题满分12分)设集合A ＝{－4,2a －1，a 2}，B ＝{9，a －5，1－a }，且A ∩B ＝{9}，求实数a 的值.17.(本小题满分12分)已知函数()2cos 6f x x πω⎛⎫=+ ⎪⎝⎭(其中0ω>x ∈R )的最小正周期为10π.(Ⅰ)求ω的值;(Ⅱ)设α、0,2πβ⎡⎤∈⎢⎥⎣⎦,56535f απ⎛⎫+=- ⎪⎝⎭,5165617f βπ⎛⎫-= ⎪⎝⎭,求()cos αβ+的值.18.(本小题满分12分)已知向量(sin ,1),(3cos ,cos 2)(0)3Am x n x x A ==>u r r ,函数()f x m n=⋅u r r 的最大值为6.(Ⅰ)求A ;(Ⅱ)将函数()y f x =的图象向左平移12π个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数()y g x =的图象.求()g x 在5[0,]24π上的值域.19.(本小题满分12分)设函数f (x )＝ax 3＋bx ＋c (a ≠0)为奇函数，其图像在点(1，f (1))处的切线与直线x －6y －7＝0垂直，导函数f ′(x )的最小值为－12.(1)求a ，b ，c 的值；(2)求函数f (x )的单调递增区间，并求函数f (x )在[－1,3]上的最大值和最小值．20.(本小题满分13分)设函数22()(1)f x ax a x =-+，其中0a >，区间{()>0}I x f x =（Ⅰ）求区间I 的长度（注：区间(,)αβ的长度定义为βα-）；（Ⅱ）给定常数(0,1)k ，当时，求长度的最小值。

邹平双语学校2015-2016第一学期第一次月考高三年级数学试卷（文科）（时间120分钟，满分150分）一、选择题（本题共10小题，每题5分，共50分）1．α是第一象限角，tan α＝34，则sin α等于( )A.45B.35 C ．－45 D ．－352．函数y ＝sin ⎝⎛⎭⎪⎫2x ＋π3图象的对称轴方程可能是 ( ) A ．x ＝－π6 B ．x ＝－π12C ．x ＝π6D ．x ＝π123．要得到函数y ＝sin)34(π-x 的图象，可以把函数y ＝sin 4x 的图象( ) A ．向左平移12π个单位B ．向右平移12π个单位C ．向左平移3π个单位D ．向右平移3π个单位4.如图所示的是某函数图象的一部分，则此函数是 ()A ．y ＝sin ⎝⎛⎭⎪⎫x ＋π6B ．y ＝sin ⎝⎛⎭⎪⎫2x －π6 C ．y ＝cos ⎝⎛⎭⎪⎫4x －π3 D ．y ＝cos ⎝⎛⎭⎪⎫2x －π6 5．函数f (x )＝sin 2x －cos 2x 的最小正周期是 ( )A.π2B ．πC ．2πD ．4π 6．在△ABC 中，若A ＝60°，BC ＝43，AC ＝42，则角B 的大小为( )A ．30°B ．45°C ．135°D ．45°或135°7．如图，设A 、B 两点在河的两岸，一测量者在A 的同侧，在所在的河岸边选定一点C ，测出AC 的距离为50 m ，∠ACB ＝45°，∠CAB ＝105°后，就可以计算出A 、B 两点的距离为 ( )A ．50 2 mB ．50 3 mC ．25 2 mD.2522m8.设向量)4,2(=与向量)6,(x =共线，则实数=x （ ） A.2 B.3 C.4 D. 69.在Y ABCD 中，AB ＝a ，AD ＝b ，AN ＝3NC ，M 为BC 的中点，则等于 ( )A ．－14a ＋14bB ．－12a ＋12bC ．a ＋12bD ．－34a ＋34b10．已知函数f (x )＝3sin ⎝⎛⎭⎪⎫ωx －π6 (ω>0)和g (x )＝2cos(2x ＋φ)＋1的图象的对称轴完全相同． 若x ∈⎣⎢⎡⎦⎥⎤0，π2，则f (x )的取值范围是( )A ⎥⎦⎤⎢⎣⎡-3,21 B.[]2,1- C ⎥⎦⎤⎢⎣⎡-3,23 D ⎥⎦⎤⎢⎣⎡-2,23二、填空题（本题共5题，每题5分，共25分）11．在平面直角坐标系xOy 中，四边形ABCD 的边AB ∥DC ，AD ∥BC .已知A (－2,0)，B (6,8)，C (8，6)，则D 点的坐标为________．12．已知α是第二象限的角，tan α＝－12，则cos α＝________13．已知)2,0(,53)2sin(πααπ∈=+，则=+)sin(απ ________14.已知向量),3(),3,1(m b a ==,若向量b a ,的夹角为6π，则实数m = ________15．设a ，b 是任意的两个向量，λ∈R ，给出下面四个结论： ①若a 与b 共线，则b ＝λa ； ②若b ＝－λa ，则a 与b 共线； ③若a ＝λb ，则a 与b 共线；④当b ≠0时，a 与b 共线的充要条件是有且只有一个实数λ＝λ1，使得a ＝λ1b . 其中正确的结论有________三、解答题（本题共5题，共75分）16. （12分）已知α是三角形的内角，且sin α＋cos α＝15.(1)求tan α的值；(2)把1cos 2α－sin 2α用tan α表示出来，并求其值．17. （12分）已知函数2sin 32sin )(2π-=x x f（1）求)(x f 的最小正周期（2）求)(x f 在区间【0，32π】上的最小值18. （12分）设ABC ∆的内角A,B,C 所对应的长分别为c b a ,,，且,1,3==c b ABC ∆的面积为2，求A cos 与a 的值19．（14分）已知向量a ＝(sin x ，23sin x )，b ＝(2cos x ，sin x )，定义f (x )＝a·b － 3.(1)求函数y ＝f (x )，x ∈R 的单调递减区间；(2)若函数y ＝f (x ＋θ) (0<θ<π2)为偶函数，求θ的值．20. （13分）已知)4,3(),1,3(),4,2(----C B A ，设c CA b BC a AB ===,,，且c CM 3=，b CN 2-= （1）求c b a 33-+（2）求满足c n b m a +=的实数m 、n 的值 （3）求N M ,的坐标以及向量MN 的坐标21. （12分）如图，A ，B 是海面上位于东西方向相距5(3＋3)海里的两个观测点，现位于A 点北偏东45°，B 点北偏西60°的D 点有一艘轮船发出求救信号，位于B 点南偏西60°且与B 点相距203海里的C 点的救援船立即前往营救，其航行速度为30海里/时，该救援船到达D 点需要多长时间？邹平双语学校2015-2016第一学期第一次月考高三年级数学答题纸（文科） （时间120分钟，满分150分）二、填空题（共5题每空5分，共25分）11 .12 .13 .14 .15 .三、解答题16.(12分)17.（12分）18.（12分）19.（14分）20.（13分）21.（12分）邹平双语学校2015-2016第一学期第一次月考高三年级数学答案（文科） （时间120分钟，满分150分）一、选择题（共10题，每题5分，共50分）题号 1 2 3 4 5 6 7 8 9 10 答案BDBD BBABAC二、填空题（共5题，每题5分，共25分） 11. )2,0(-12. 552-13. 54-14. 3 15. 2.3.4三、解答题16.（12分）解 (1)联立方程⎩⎨⎧sin α＋cos α＝15， ①sin 2α＋cos 2α＝1， ②由①得cos α＝15－sin α，将其代入②，整理得25sin 2α－5sin α－12＝0.[2分]∵α是三角形的内角，∴⎩⎨⎧sin α＝45cos α＝－35，[4分]∴tan α＝－43.[6分](2)1cos 2α－sin 2α＝sin 2α＋cos 2αcos 2α－sin 2α＝sin 2α＋cos 2αcos 2αcos 2α－sin 2αcos 2α＝tan 2α＋11－tan 2α，[8分] ∵tan α＝－43，∴1cos 2α－sin 2α＝tan 2α＋11－tan 2α[10分]＝⎝ ⎛⎭⎪⎫－432＋11－⎝ ⎛⎭⎪⎫－432＝－257.[12分]17.（12分）解析:(1)因为3cos 3sin )(-+=x x x f=3)3sin(2-+πx所以)(x f 的最小正周期为π2（2）因为320π≤≤x ，所以πππ≤+≤33x当ππ=+3x ，即32π=x 时，)(x f 取得最小值 所以)(x f 在区间【0，32π】上的最小值为3)32(-=πf18.（12分）解析：由三角形面积公式，得2sin 1321=•⨯⨯A ，故322sin =A 因为1cos sin 22=+A A所以31981sin 1cos 2±=-±=-±=A A①当31cos =A 时，由余弦定理得83131213cos 22222=⨯⨯⨯-+=-+A bc c a所以22=a②当31cos -=A 时，由余弦定理得 12)31(31213cos 22222=-⨯⨯⨯-+=-+A bc c a所以32=a19．（14分）解 f (x )＝2sin x cos x ＋23sin 2x － 3＝sin 2x ＋23·1－cos 2x2－ 3＝sin 2x －3cos 2x ＝2sin ⎝⎛⎭⎪⎫2x －π3.………………………………………………………(4分) (1)令2k π＋π2≤2x －π3≤2k π＋3π2，k ∈Z ，解得单调递减区间是⎣⎢⎡⎦⎥⎤k π＋5π12，k π＋11π12，k ∈Z .……………………………………………………………………………………………(8分)(2)f (x ＋θ)＝2sin ⎝⎛⎭⎪⎫2x ＋2θ－π3. 根据三角函数图象性质可知，y ＝f (x ＋θ) ⎝⎛⎭⎪⎫0<θ<π2在x ＝0处取最值， ∴sin ⎝ ⎛⎭⎪⎫2θ－π3＝±1， ∴2θ－π3＝k π＋π2，θ＝k π2＋5π12，k ∈Z .……………………………………………………(12分)又0<θ<π2，解得θ＝5π12.…………………………………………………………………(14分)20.（13分）解析：由已知得)8,1(),3,6(),5,5(=--=-=c b a（1）c b a 33-+=)42,6()24315,3615()8,1(3)3,6()5,5(3-=-----=---+- （2）)5,5()83,6(-=+-+-=+n m n m c n b m Θ⎩⎨⎧-=+-=+-∴58356n m n m解得⎩⎨⎧-=-=11n m（3）设O 为坐标原点c OC OM CM 3=-=Θ)20,0()4,3()24,3(3=--+=+=∴OC c OM )20,0(M ∴又b OC ON CN 2-=-=Θ)2,9()4,3()6,12(2=--+=+-=∴OC b ON )2,9(N ∴)18,9(-=∴MN21.（12分）解 由题意知AB ＝5(3＋3)海里，∠DBA ＝90°－60°＝30°，∠DAB ＝90°－45°＝45°，∴∠ADB ＝180°－(45°＋30°)＝105°.在△DAB 中，由正弦定理，得DB sin ∠DAB ＝ABsin ∠ADB，∴DB ＝AB ·sin∠DAB sin ∠ADB ＝5(3＋3)·sin 45°sin 105°＝5(3＋3)·sin 45°sin 45°cos 60°＋cos 45°sin 60°＝103(海里)．又∠DBC＝∠DBA＋∠ABC＝30°＋(90°－60°)＝60°，BC＝203(海里)，在△DBC中，由余弦定理，得CD2＝BD2＋BC2－2BD·BC·cos∠DBC＝300＋1 200－2×103×203×12＝900，∴CD＝30(海里)，∴需要的时间t＝3030＝1(小时)．故救援船到达D点需要1小时．。

邹平双语学校2015—2016第一学期期中考试高三年级数学（春考班）试题（时间：120分钟，分值：120分）一、 选择题（本大题共20个小题，每小题3分，共60分，把正确答案写在答题纸的相应位置） 1. 设U ={2，5，7，8}，A ={2，5，8}，B ={2，7，8}，则U （A ∪B ）等于（ ）(A) {2，8} (B) ∅ (C) {5，7，8} (D) {2，5，7，8}2. x >0是| x | >0的（ ）(A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件(D) 既不充分也不必要条件 3. 已知f （e x）= x ，则f （5）=（ ）A 、e5B 、5C 、ln5D 、log 5 e4. 设命题p ：∅＝0，q ：2∈ R ，则下列结论正确的是（ ）(A) p q ∧为真 (B) p q ∨为真 (C) p 为真 (D) q ⌝为真 5. 若a,b 是任意实数,且a ＞b,则（ ）（A ）a 2＞b 2（B ）b a ＜1 （C ）lg(a-b)＞0 （D ）(12)a ＜(12)b6. 下列算式正确的是（ ）A ．26+22=28B ．26﹣22=24C ．26×22=28D ．26÷22=237. 数列{}n a 满足,,11n S a n ==则=2012a （ ） A 、1 B 、2010 C 、2011 D 、20128. 已知奇函数f(x)在（0，+∞）上是增函数，偶函数g(x)在（0，∞）上是减函数，则在（－∞，0）上，有（ ）A 、f(x)为减函数，g(x)为增函数；B 、f(x)为增函数，g(x)为减函数；C 、f(x)、g(x)都是增函数；D 、f(x)、g(x)都是减函数9. 若2a＝4，则log a 12的值是（ ）(A) －1 (B) 0(C) 1 (D) 1210. 在等比数列}{n a 中，若a 2⋅a 6＝8，则lo g 2(a 1⋅a 7)等于（ ）班级：____________ 姓名：_____________ 考号：________________________(A) 8 (B) 3 (C) 16 (D) 2811. 函数f (x )= 1x －1＋lg (x ＋1)的定义域为( ) (A) (－∞，－1) (B) (1，＋∞) (C) (－1，1)∪(1，＋∞) (D) R12. 在同一坐标系中，当a >1时，函数 y ＝( 1a)x与 y ＝log a x 的图像可能是（ ）(A ) (B) (C) (D)13. 设a=1，b=0.35，c=50.3，则下列不等式中正确的是（ ） A ．a ＞b ＞c B ．b ＞a ＞c C ．c ＞a ＞b D ．a ＞c ＞b14．如果函数y=2x 2+(2a-b)x+b ，当y ＜0时，有1＜x ＜2，则a 、b 的值为（ ） A 、a=-1,b=-4 B 、a=-12 ,b=2 C 、a=-1,b=4 D 、a=1,b=-415. 已知函数f （x ）=2x+2，则f （1）的值为（ ） A ．2B ．3C ．4D ．616. 已知数列，则是它的第（ ）项．A ．19B ．20C ．21D ．2217. 已知{a n }是公差为1的等差数列；S n 为{a n }的前n 项和，若S 8=4S 4，则a 10=（ ） A ． B ．C ．10D ．1218. 设实数y x ,满足⎪⎩⎪⎨⎧≥-≤-+.0,0,042＞y y x y x 则y x 2-的最大值为( )A 、2B 、4C 、6D 、819. 函数3xy =是（ ）A.奇函数，在（0，+∞）上是减函数B. 奇函数，在（0，+∞）上是增函数C. 偶函数，在（0，+∞）上是减函数D. 偶函数，在（0，+∞）上是增函数20. 我国轿车进入家庭是时代发展的必然，随着车价的逐年降低，购买轿车将不是一件难事，如果每隔3年车价将降低13 ，那么现价为18万元的小轿车6年后的车价是（ ）A 、2万元B 、4万元C 、8万元D 、16万元二、填空题（本大题共5个小题，每小题4分，共20分，把正确答案写在答题纸的相应位置）21. 函数y =的定义域为__ __22. 已知集合A={1，2，3}，B={2，4，5}，则集合A∪B 中元素的个数为 ．23. 不等式x 2﹣3x ﹣10＜0的解集为 ．24. 已知函数f （x ）为奇函数，且当x ＞0时，f （x ）=x 2+，则f （﹣1）= ． 25.某种洗衣机，洗一次去污34，要使一件衣服去污99%以上，至少应洗 次 三、解答题（本大题共5个小题，共40分，请在答题卡．．．相应的题号处写出解答过程） 26．（7分）已知等差数列{}n a 中，公差0d >，且2a 、6a 是一元二次方程2181402x x -+=的根．(1) 求数列{}n a 的通项公式n a ． (2)求数列{}n a 的前10项和．27．（7分）光明商店销售某种商品，每件商品的进价是60元，销售过程中发现：当每件商品售价75元时，每天可售出85件，如果每件商品售价90元时，则每天可售出70件．假设每天售出的商品件数p （件）与每件售价x （元）之间的函数关系为p kx b =+（每件售价不低于进价，且货源充足）．（1）求出p 与x 之间的函数关系式．（2）设每天的利润是y （元），若不考虑其他费用，则每件定价为多少时每天的利润最大，最大利润是多少？28．（8分）设集合P={x|x 2-x-6＜0 }，Q={x|x-a ≥0 } （1）P ∩Q=∅，求实数a 的取值范围.（2）若P ∩Q={x|0≤x ＜3}，求实数a 的取值范围.29．（8分）关于x 的一元二次方程2(2)2x m x m --+-=0有两个不相等的实数根，试求m 的取值范围.30．（10分）一元二次不等式ax 2+bx+c ＞0的解集为{x|x ＜-2或x ＞4}，求： （1）函数f （x ）=ax 2+bx+c 的单调区间. （2）比较f （2），f （-1），f （5）的大小.邹平双语学校2015—2016第一学期期中考试高三年级数学（春考）试题答案（时间：120分钟，分值：120分）二、填空题.（本大题共有5个小题，每小题4分，共20分.把正确答案填在下面的横线上.） 21. [1,2) 22. 5 23. (-2,5) 24. -2 25. 4三、解答题（本大题共5个小题，共40分，请在答题卡．．．相应的题号处写出解答过程） 26.（7分）解：（1）由题意得：一元二次方程2181402x x -+=的根为2，14 ∵公差0d >∴22a =，614a =……………………………………………………1分即112514a d a d +=⎧⎨+=⎩ …………………………………………………2分解得：11a =-， 3d =…………………………………………………3分 ∴通项公式()11334n a n n =-+-⨯=-………………………………5分 （2）()1010910131252S ⨯=⨯-+⨯=…………………………………7分27.（7分）解：（1）由题意得：75859070k b k b +=⎧⎨+=⎩…………………………………………2分解得：1160k b =-⎧⎨=⎩……………………………………………………3分所以p 与x 之间的函数关系式为()16060p x x =-+≥………4分班级：____________ 姓名：_____________ 考号：________________________（2）由题意得：()()60160y x x =--+……………………………5分 22209600x x =-+-()21102500x =--+……………………………6分 当110x =时，max 2500y =；所以每件售价110元时，取得的利润最大，为2500元…………7分28.（8分） 解：（1）∵P ∩Q=∅，∴a ≥3.（2）∵若P ∩Q={x|0≤x ＜3}，∴a=0.29.（8分）解：∵2(2)2x m x m --+-=0有两个不相等的实数根，∴△＞0， 即2[(2)]4(2)m m ----＞0，∴（m-2）（m-6）＞0， ∴m＜2或m ＞6. 30.（10分）解：∵一元二次不等式ax 2+bx+c ＞0的解集为{x|x ＜-2或x ＞4}，∴函数f （x ）=ax 2+bx+c 是开口向上的抛物线，且与x 轴交于点（-2，0），（4，0）.∴函数f （x ）=ax 2+bx+c 的对称轴方程为直线x=1，∴函数f （x ）在（-∞，1]上单调递减，在[1，+∞）上单调递增. （2）f （5）＞f （-1）＞f （2）.。

2014-2015学年山东省滨州市邹平县双语学校高三（上）第一次月考数学试卷（理科）一、选择题（共10道每题5分）1．集合M={y|y=x2﹣1，x∈R}，集合N={x|y=，x∈R}，则M∩N=( )A．{t|0≤t≤3} B．{t|﹣1≤t≤3} C．{（﹣，1），（，1）} D．∅2．下列四个命题中，其中为真命题的是( )A．∀x∈R，x2+3＜0 B．∀x∈N，x2≥1 C．∃x∈Z，使x5＜1 D．∃x∈Q，x2=33．下列函数中，与函数y=x相同的函数是( )A．y=B．y=C．y=lg10x D．y=2log2x4．下列命题中的真命题是( )A．若a＞b，c＞d，则ac＞bd B．若|a|＞b，则a2＞b2C．若a＞b，则a2＞b2 D．若a＞|b|，则a2＞b25．不等式y≥|x|表示的平面区域为( )A．B．C．D．6．如图，阴影部分的面积是( )A．2 B．﹣2C．D．7．f（x）=2x3﹣6x2+a在[﹣2，2]上有最大值3，那么在[﹣2，2]上f（x）的最小值是( ) A．﹣5 B．﹣11 C．﹣29 D．﹣378．如图，一个正五角星薄片（其对称轴与水面垂直）匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S′（t）的图象大致为( )A．B．C．D．9．已知，函数y=f（x+φ）的图象关于直线x=0对称，则φ的值可以是( )A．B．C．D．10．定义在R上的偶函数f（x）在[0，+∞）上递增，，则满足的取值范围是( )A．B．（0，+∞）C．D．二、填空题（共5道小题，每小题5分，共25分）11．“lg x＞lg y”是“10x＞10y”的__________条件．12．已知向量，满足||=1，||=2，与的夹角为60°，则|﹣|=__________．13．已知f（3x）=4xlog23+233，则f（2）+f（4）+f（8）+…+f（28）的值等于__________．14．已知函数在区间[1，2]上是增函数，则实数a的取值范围是__________．15．下列关于函数f（x）=（2x﹣x2）e x的判断正确的是__________（填写所有正确的序号）．①f（x）＞0的解集是{x|0＜x＜2}；②f（﹣）是极小值，f（）是极大值；③f（x）没有最小值，也没有最大值．三、解答题（共6小题，共75分）16．已知A={x||x﹣a|＜4}，B={x||x﹣2|＞3}．（I）若a=1，求A∩B；（II）若A∪B=R，求实数a的取值范围．17．已知向量=（sinx，2sinx），=（2cosx，sinx），定义f（x）=•﹣（1）求函数y=f（x），x∈R的单调递减区间；（2）若函数y=f（x+θ）（0＜θ＜）为偶函数，求θ的值．18．设f（x）=x3﹣x2﹣2x+5．（1）求函数f（x）的单调递增、递减区间；（2）当x∈[﹣1，2]时，f（x）＜m恒成立，求实数m的取值范围．19．已知函数f（x）=x3﹣2ax2+3x（x∈R）．（1）若a=1，点P为曲线y=f（x）上的一个动点，求以点P为切点的切线斜率取最小值时的切线方程；（2）若函数y=f（x）在（0，+∞）上为单调增函数，试求满足条件的最大整数a．20．（13分）某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？21．（14分）函数f（x）的定义域为D={x|x≠0}，且满足对于任意x1、x2∈D，有f（x1•x2）=f（x1）+f（x2）．（1）求f（1）的值；（2）判断f（x）的奇偶性并证明；（3）如果f（4）=1，f（3x+1）+f（2x﹣6）≤3，且f（x）在（0，+∞）上是增函数，求x 的取值范围．2014-2015学年山东省滨州市邹平县双语学校高三（上）第一次月考数学试卷（理科）一、选择题（共10道每题5分）1．集合M={y|y=x2﹣1，x∈R}，集合N={x|y=，x∈R}，则M∩N=( )A．{t|0≤t≤3} B．{t|﹣1≤t≤3} C．{（﹣，1），（，1）} D．∅【考点】交集及其运算．【专题】计算题．【分析】求出集合M中函数的值域得到集合M，求出集合N中函数的定义域得到集合N，求出两集合的交集即可．【解答】解：由集合M中的函数y=x2﹣1，可得y≥﹣1，所以集合M={y|y≥﹣1}；由集合N中的函数y=，得到9﹣x2≥0，即（x+3）（x﹣3）≤0，解得：﹣3≤x≤3，所以集合N={x|﹣3≤x≤3}，则M∩N={t|﹣1≤t≤3}．故选B【点评】此题属于以函数的定义域和值域为平台，考查了交集的运算，是一道基础题．2．下列四个命题中，其中为真命题的是( )A．∀x∈R，x2+3＜0 B．∀x∈N，x2≥1 C．∃x∈Z，使x5＜1 D．∃x∈Q，x2=3【考点】四种命题的真假关系．【分析】借助x2≥0这个结论判断A和B，再由数学常识判断C和D．【解答】解：由于∀x∈R都有x2≥0，因而有x2+3≥3，所以命题“∀x∈R，x2+3＜0”为假命题；由于0∈N，当x=0时，x2≥1不成立，所以命题“∀x∈N，x2≥1”是假命题；由于﹣1∈Z，当x=﹣1时，x5＜1，所以命题“∃x∈Z，使x5＜1”为真命题；由于使x2=3成立的数只有±，而它们都不是有理数，因此没有任何一个有理数的平方能等于3，所以命题“∃x∈Q，x2=3”为假命题，故选C．故选C．【点评】本题考查四种命题真假的判断，解题时要合理运用x2≥0这个结论．3．下列函数中，与函数y=x相同的函数是( )A．y=B．y=C．y=lg10x D．y=2log2x【考点】判断两个函数是否为同一函数．【专题】计算题．【分析】由相同函数的定义需要函数的定义域、值域和对应关系全相同．A、B、D的定义域均不为R，可用排除法选出答案．【解答】解：A中分母不为0，故A的定义域为{x|x≠0}，B中为根式，被开方数大于或等于0，B的定义域为[0，+∞），C中，10x＞0，则其定义域为R，D中x为真数，故应大于0，故D的定义域为（0，+∞），而y=x的定义域为R，故排除A、B和D，故选C【点评】本题考查函数的三要素：定义域、值域和对应关系，属基本题型的考查．4．下列命题中的真命题是( )A．若a＞b，c＞d，则ac＞bd B．若|a|＞b，则a2＞b2C．若a＞b，则a2＞b2 D．若a＞|b|，则a2＞b2【考点】复合命题的真假．【分析】本题真假命题的判断与不等式性质有关，故可采用特值法．【解答】解：A中取a=﹣1，b=﹣1，c=1，d=2可判断A为假命题；取a=1，b=﹣2可判断B、C为假命题；D中由a＞|b|，可得a＞|b|≥0⇒a2＞b2．故选D【点评】本题考查命题真假的判断和不等式的性质，特值法是一种常用方法．5．不等式y≥|x|表示的平面区域为( )A．B．C．D．【考点】二元一次不等式（组）与平面区域．【专题】计算题．【分析】取点（0，1），满足不等式y≥|x|，从而点（0，1）在不等式y≥|x|表示的平面区域，结合选项即可选出正确答案．【解答】解：取点（0，1），满足不等式y≥|x|故点（0，1）在不等式y≥|x|表示的平面区域故选A．【点评】本题主要考查了二元一次不等式（组）与平面区域，常用取点法进行判定，属于基础题．6．如图，阴影部分的面积是( )A．2 B．﹣2C．D．【考点】定积分在求面积中的应用．【专题】导数的综合应用．【分析】利用定积分的几何意义表示出阴影部分的面积，然后计算．【解答】解：由题意，结合图形，得到阴影部分的面积是=（3x﹣）|=；故选C．【点评】本题考查了利用定积分求封闭图形的面积；关键是正确利用定积分表示面积，然后计算．7．f（x）=2x3﹣6x2+a在[﹣2，2]上有最大值3，那么在[﹣2，2]上f（x）的最小值是( ) A．﹣5 B．﹣11 C．﹣29 D．﹣37【考点】利用导数求闭区间上函数的最值．【专题】计算题；压轴题．【分析】本题需要先根据条件：f（x）有最大值3来求出参数a的值，再进一步求出f（x）的最小值来．【解答】解：由已知f′（x）=6x2﹣12x，令f′（x）＞0得x＜0或x＞2，又因为x∈[﹣2，2]因此f（x）在[﹣2，0]上是增函数，在[0，2]上是减函数，所以f（x）在区间[﹣2，2]的最大值为f（x）max=f（0）=a=3由以上分析可知函数的最小值在x=﹣2或x=2处取到，又因为f（﹣2）=﹣37，f（2）=﹣5，因此函数的最小值为﹣37．故应选D【点评】本题考查了函数的导数的应用，以三次的多项式类型函数为模型进行考查，以同时考查函数的单调性为辅，紧扣大纲要求，模型典型而又考查全面，虽是基础题，却是一个非常好的题目．8．如图，一个正五角星薄片（其对称轴与水面垂直）匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S（t）（S（0）=0），则导函数y=S′（t）的图象大致为( )A．B．C．D．【考点】函数的图象．【专题】压轴题；创新题型．【分析】本题利用逐一排除的方法进行判断，结合选项根据最初零时刻和最后终点时刻没有变化，导数取零，以及总面积一直保持增加，没有负的改变量，考虑到导数的意义，判断此时面积改变为突变，产生中断进行判定即可．【解答】解：最初零时刻和最后终点时刻没有变化，导数取零，排除C；总面积一直保持增加，没有负的改变量，排除B；考察A、D的差异在于两肩位置的改变是否平滑，考虑到导数的意义，判断此时面积改变为突变，产生中断，选择A．故选A．【点评】本题考查函数图象、导数图、导数的实际意义等知识，重点考查的是对数学的探究能力和应用能力．9．已知，函数y=f（x+φ）的图象关于直线x=0对称，则φ的值可以是( )A．B．C．D．【考点】y=Asin（ωx+φ）中参数的物理意义；运用诱导公式化简求值；图形的对称性．【专题】计算题．【分析】化简函数的表达式，函数y=f（x+φ）的图象关于直线x=0对称，说明是偶函数，求出选项中的一个φ即可．【解答】解：=2sin（x+），函数y=f（x+φ）=2sin（x+φ+）的图象关于直线x=0对称，函数为偶函数，∴φ=故选D．【点评】本题考查y=Asin（ωx+φ）中参数的物理意义，运用诱导公式化简求值，图形的对称性，考查计算能力，是基础题．10．定义在R上的偶函数f（x）在[0，+∞）上递增，，则满足的取值范围是( )A．B．（0，+∞）C．D．【考点】复合函数的单调性；对数函数的单调性与特殊点．【分析】先根据将题中关系式转化为，再由f（x）是偶函数且在[0，+∞）上递增可得关于x的不等式．【解答】解：由题意得，因为f（x）为R上的偶函数且在[0，+∞）增可得或解得：0或x＞2故选A．【点评】本题重要考查函数的基本性质﹣﹣单调性、奇偶性．对于不知道解析式求自变量x 的范围的题一般转化为单调性求解．二、填空题（共5道小题，每小题5分，共25分）11．“lg x＞lg y”是“10x＞10y”的充分不必要条件．【考点】必要条件、充分条件与充要条件的判断．【专题】函数的性质及应用；简易逻辑．【分析】分析命题“lg x＞lg y”，“10x＞10y”的充分性和必要性，综合可得答案．【解答】解：当“lg x＞lg y”时，“x＞y＞0”，“10x＞10y”成立，故“lg x＞lg y”是“10x＞10y”的充分条件；当“10x＞10y”时，“x＞y”，“lg x＞lg y”不一定成立，故“lg x＞lg y”是“10x＞10y”的不必要条件；故“lg x＞lg y”是“10x＞10y”的充分不必要条件；故答案为：充分不必要．【点评】判断一个条件是另一个条件的什么条件，应该先确定出条件角色，然后两边互推，利用充要条件的有关定义得到结论，12．已知向量，满足||=1，||=2，与的夹角为60°，则|﹣|=．【考点】向量的模．【专题】计算题；数形结合．【分析】根据题意和根据向量的减法几何意义画出图形，再由余弦定理求出||的长度．【解答】解：如图，由余弦定理得：||===故答案为：．【点评】本题考查的知识点有向量的夹角、向量的模长公式、向量三角形法则和余弦定理等，注意根据向量的减法几何意义画出图形，结合图形解答．13．已知f（3x）=4xlog23+233，则f（2）+f（4）+f（8）+…+f（28）的值等于2008．【考点】对数函数图象与性质的综合应用；对数的运算性质．【专题】计算题；压轴题．【分析】本题考查的知识点是函数解析式的求法，因为f（3x）=4xlog23+233，利用换元法容易求出函数f（x）的解析式，结合对数的运算性质，不难求出答案．【解答】解：∵f（3x）=4xlog23+233=4log23x+233∴f（x）=4log2x+233，∴f（2）+f（4）+f（8）+…+f（28）=8×233+4（log22+2log22+3log22+…+8log22）=1864+144=2008．故答案为：2008．【点评】求解析式的几种常见方法：①代入法：即已知f（x），g（x），求f（g（x））用代入法，只需将g（x）替换f（x）中的x即得；②换元法：已知f（g（x）），g（x），求f（x）用换元法，令g（x）=t，解得x=g﹣1（t），然后代入f（g（x））中即得f（t），从而求得f （x）．当f（g（x））的表达式较简单时，可用“配凑法”；③待定系数法：当函数f（x）类型确定时，可用待定系数法．④方程组法：方程组法求解析式的实质是用了对称的思想．一般来说，当自变量互为相反数、互为倒数或是函数具有奇偶性时，均可用此法．在解关于f （x）的方程时，可作恰当的变量代换，列出f（x）的方程组，求得f（x）．14．已知函数在区间[1，2]上是增函数，则实数a的取值范围是（1，2）．【考点】函数单调性的性质；对数函数的单调性与特殊点．【专题】计算题．【分析】观察函数形式，是一个复合函数，欲求a的范围，需要依据复合函数的单调性判断规则将区间上的单调性问题转化为参数不等式，求解参数的范围．【解答】解：因为在区间[1，2]上是增函数，所以在区间[1，2]上是增函数，且g（1）＞0．于是a﹣2＜0，且2a﹣2＞0，解得1＜a＜2．故应填（1，2）【点评】本题考查复合函数单调性的判断规则，利用复合函数的判断规则将单调性转化为关于参数的不等式解参数的范围，复合函数的判断规则：看各层中减函数的个数，若其个数是奇数，则复合函数是减函数，否则是增函数．15．下列关于函数f（x）=（2x﹣x2）e x的判断正确的是①②（填写所有正确的序号）．①f（x）＞0的解集是{x|0＜x＜2}；②f（﹣）是极小值，f（）是极大值；③f（x）没有最小值，也没有最大值．【考点】命题的真假判断与应用．【专题】导数的综合应用；简易逻辑．【分析】①由e x＞0，f（x）＞0化为2x﹣x2＞0，即x（x﹣2）＜0，解出即可得出；②f′（x）=e x（2﹣x2），分别令f′（x）＞0，f′（x）＜0，解出即可得出单调性极值；③由②可知：x→+∞时，f（x）→﹣∞；x→﹣∞时，f（x）→0．即可判断出．【解答】解：①∵e x＞0，∴f（x）＞0化为2x﹣x2＞0，即x（x﹣2）＜0，解得0＜x＜2．其解集为{x|0＜x＜2}，因此正确；②f′（x）=e x（2﹣x2），令f′（x）＞0，解得，此时函数f（x）单调递增；令f′（x）＜0，解得或x，此时函数f（x）单调递减．∴当x=﹣时，f （x）取得极小值；当x=时，f（x）取得极大值．∴②正确．③由②可知：x→+∞时，f（x）→﹣∞；x→﹣∞时，f（x）→0．可知：f（x）没有最小值，但是有最大值．因此不正确．综上可得：①②正确．故答案为：①②．【点评】本题考查了利用导数研究函数的单调性集极值与最值、一元二次不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于难题．三、解答题（共6小题，共75分）16．已知A={x||x﹣a|＜4}，B={x||x﹣2|＞3}．（I）若a=1，求A∩B；（II）若A∪B=R，求实数a的取值范围．【考点】交、并、补集的混合运算．【专题】计算题；数形结合．【分析】（I）把a=1代入绝对值不等式|x﹣a|＜4求出解集，再求解|x﹣2|＞3的解集，再求出A∩B；（II）先求解|x﹣a|＜4得出集合A，再由A∪B=R画出数轴，由图列出关于a的不等式，注意等号是否取到，求出a范围．【解答】解：（I）当a=1时，则由|x﹣1|＜4，即﹣4＜x﹣1＜4，解得﹣3＜x＜5，由|x﹣2|＞3，即x﹣2＞3或x﹣2＜﹣3，解得x＜﹣1或x＞5，∴A={x|﹣3＜x＜5}．B={x|x＜﹣1或x＞5}．∴A∩B={x|﹣3＜x＜﹣1}．（II）由|x﹣a|＜4得，a﹣4＜x＜a+4，则A={x|a﹣4＜x＜a+4}，因B={x|x＜﹣1或x＞5}，且A∪B=R，用数轴表示如下：∴，解得1＜a＜3，∴实数a的取值范围是（1，3）．【点评】本题的考点是集合的交集和并集的求法，考查了绝对值不等式得解法，借助于数轴求出a的范围，注意端点处的值是否取到，这是易错的地方．17．已知向量=（sinx，2sinx），=（2cosx，sinx），定义f（x）=•﹣（1）求函数y=f（x），x∈R的单调递减区间；（2）若函数y=f（x+θ）（0＜θ＜）为偶函数，求θ的值．【考点】平面向量数量积的运算；余弦函数的图象．【专题】计算题；函数的性质及应用；三角函数的图像与性质；平面向量及应用．【分析】（1）运用向量的数量积的坐标表示和二倍角公式及两角差的正弦公式，结合正弦函数的减区间，解不等式即可得到所求区间；（2）运用余弦函数为偶函数，以及诱导公式，解方程即可求得．【解答】解：（1）向量=（sinx，2sinx），=（2cosx，sinx），则f（x）=•﹣=2sinxcosx+2sin2x﹣=sin2x﹣cos2x=2sin（2x﹣），令2k≤2x﹣≤2k，k∈Z，解得，kπ+≤x≤kπ+，即有f（x）的单调减区间为[kπ+，kπ+]，k∈Z；（2）函数y=f（x+θ）（0＜θ＜）为偶函数，即有y=2sin（2x+2）为偶函数．可令2=kπ+，k∈Z，解得，θ=+，k∈Z．由诱导公式可得，y=2sin（2x+2）=2sin（2x+kπ+）=±2cos2x，即为偶函数．则有θ=+，k∈Z．【点评】本题考查平面向量的数量积的坐标表示，考查二倍角公式和两角差的正弦公式，考查正弦函数的单调性和余弦函数的奇偶性的运用，考查运算能力，属于中档题．18．设f（x）=x3﹣x2﹣2x+5．（1）求函数f（x）的单调递增、递减区间；（2）当x∈[﹣1，2]时，f（x）＜m恒成立，求实数m的取值范围．【考点】利用导数求闭区间上函数的最值．【专题】导数的综合应用．【分析】（1）由已知得f′（x）=3x2﹣x﹣2，令f′（x）=0，得x=1或x=﹣，由此利用导数性质能求出函数f（x）的单调递增、递减区间．（2）由已知得只需使x∈[﹣1，2]时，f（x）的最大值小于m即可．【解答】解：（1）∵f（x）=x3﹣x2﹣2x+5，∴f′（x）=3x2﹣x﹣2，令f′（x）=0，得x=1或x=﹣，当x∈（﹣∞，﹣）时，f′（x）＞0，f（x）为增函数；当x∈（﹣，1）时，f′（x）＜0，f（x）为减函数；当x∈（1，+∞）时，f′（x）＞0，f（x）为增函数．∴f（x）的增区间为（﹣∞，﹣）和（1，+∞），f（x）的减区间为（﹣，1）．（2）当x∈[﹣1，2]时，f（x）＜m恒成立，只需使x∈[﹣1，2]时，f（x）的最大值小于m即可，=f（﹣）=5，f（2）=7，由（1）知f（x）极大值∴f（x）在x∈[﹣1，2]中的最大值为f（2）=7，∴m＞7．【点评】本题重点考查利用导数研究函数的性质，利用函数的性质解决不等式、方程问题．重点考查学生的代数推理论证能力，分类讨论等综合解题能力，解题时要认真审题，注意导数性质的合理运用．19．已知函数f（x）=x3﹣2ax2+3x（x∈R）．（1）若a=1，点P为曲线y=f（x）上的一个动点，求以点P为切点的切线斜率取最小值时的切线方程；（2）若函数y=f（x）在（0，+∞）上为单调增函数，试求满足条件的最大整数a．【考点】利用导数研究曲线上某点切线方程；利用导数研究函数的单调性．【专题】综合题．【分析】（1）设出切线的斜率k，得到k等于f′（x）并把a=1代入到f（x）中求出解析式，根据二次函数求最小值的方法，求出k的最小值，然后把x=1代入到f（x）中求出f（1）的值即可得到切点坐标，根据斜率和切点坐标写出切线方程即可；（2）求出f′（x），要使f（x）为单调递增函数，必须满足f'（x）＞0，即对任意的x∈（0，+∞），恒有f′（x）大于0，解出a小于一个关系式，利用基本不等式求出这个关系式的最小值，得到关于a的不等式，求出解集即可得到a的取值范围，在范围中找出满足条件的最大整数即可．【解答】解：（1）设切线的斜率为k，则k=f′（x）=2x2﹣4x+3=2（x﹣1）2+1，当x=1时，k min=1．把a=1代入到f（x）中得：f（x）=x3﹣2x2+3x，所以f（1）=﹣2+3=，即切点坐标为（1，）∴所求切线的方程为y﹣=x﹣1，即3x﹣3y+2=0．（2）f′（x）=2x2﹣4ax+3，因为y=f（x）为单调递增函数，则对任意的x∈（0，+∞），恒有f′（x）＞0，f′（x）=2x2﹣4ax+3＞0，∴a＜=+，而+≥，当且仅当x=时，等号成立．所以a＜，则所求满足条件的最大整数a值为1．【点评】此题是一道综合题，要求学生会根据导数求出切线的斜率，掌握不等式恒成立时所取的条件，利用会利用基本不等式求函数的最小值及会求二次函数的最小值．20．（13分）某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？【考点】简单线性规划的应用．【专题】计算题；不等式的解法及应用．【分析】设投资人分别用x万元、y万元投资甲、乙两个项目，确定不等式与目标函数，作出平面区域，即可求得结论．【解答】解：设投资人分别用x万元、y万元投资甲、乙两个项目，由题意知目标函数z=x+0.5y．上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域．作直线l0：x+0.5y=0，并作平行于直线l0的一组直线x+0.5y=z，z∈R，与可行域相交，其中有一条直线经过可行域上的M点，且与直线x+0.5y=0的距离最大，这里M点是直线x+y=10和0.3x+0.1y=1.8的交点．由，可得x=4，y=6∵7＞0，∴当x=4，y=6时，z取得最大值．答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大．【点评】本题考查线性规划知识，考查利用数学知识解决实际问题，考查学生分析解决问题的能力，属于中档题．21．（14分）函数f（x）的定义域为D={x|x≠0}，且满足对于任意x1、x2∈D，有f（x1•x2）=f（x1）+f（x2）．（1）求f（1）的值；（2）判断f（x）的奇偶性并证明；（3）如果f（4）=1，f（3x+1）+f（2x﹣6）≤3，且f（x）在（0，+∞）上是增函数，求x 的取值范围．【考点】奇偶性与单调性的综合．【专题】计算题；证明题；转化思想．【分析】（1）赋值，令x1=x2=1，有f（1×1）=f（1）+f（1），由此可解得f（1）的值；（2）方法同（1）赋值求出f（﹣1）=0，再令x1=﹣1，x2=x，有f（﹣x）=f（﹣1）+f（x）构造出f（﹣x）与f（x）的方程研究其间的关系．得出奇偶性，解答本题时注意做题格式，先判断后证明；（3）由题设条件f（4）=1与函数的恒等式，将f（3x+1）+f（2x﹣6）≤3转化为f[（3x+1）（2x﹣6）]≤f（64），再由f（x）在（0，+∞）上是增函数与f（x）是偶函数的性质将此抽象不等式转化为一元二次不等式，求解x的范围．【解答】（1）解：令x1=x2=1，有f（1×1）=f（1）+f（1），解得f（1）=0．（2）证明：令x1=x2=﹣1，有f[（﹣1）×（﹣1）]=f（﹣1）+f（﹣1）．解得f（﹣1）=0．令x1=﹣1，x2=x，有f（﹣x）=f（﹣1）+f（x），∴f（﹣x）=f（x）．∴f（x）为偶函数．（3）解：f（4×4）=f（4）+f（4）=2，f（16×4）=f（16）+f（4）=3．∴f（3x+1）+f（2x﹣6）≤3即f[（3x+1）（2x﹣6）]≤f（64）．（*）∵f（x）在（0，+∞）上是增函数，∴（*）等价于不等式组或或或解得3＜x≤5或﹣≤x＜﹣或﹣＜x＜3．∴x的取值范围为{x|﹣≤x＜﹣或﹣＜x＜3且x≠0或3＜x≤5}．【点评】本题考点是奇偶性与单调性的综合，解答本题易出现如下思维障碍：（1）无从下手，不知如何脱掉“f”．解决办法：利用函数的单调性．（2）无法得到另一个不等式．解决办法：关于原点对称的两个区间上，奇函数的单调性相同，偶函数的单调性相反．。

2015-2016三区上学期第一次月考高一年级数学试题(连读) （时间 120 分钟，满分 150 分） 一、选择题（本题共10小题，每小题5分，共50分.只有一个正确选项，将其选项填入答题纸上的表格中.） 1.在△ABC 中，a ＝3，b ＝5，sin A ＝13，则sin B ＝( ) A.15 B.59．1 2．在△ABC 中，若∠A ＝60°，∠B ＝45°，BC＝AC ＝( ) A．．3.等差数列{a n }中，a 3=5，a 5=3，则该数列的前10项的S 10等于（ ） A. 24 B. 25 C. 27 D.284.在△ABC 中，B=60°，b 2=ac ，则△ABC 一定是（ ） A.等腰三角形 B.等边三角形 C.锐角三角形 D.钝角三角形5. 在等比数列{a n }中，a 2，a 6是方程x 2－34x+64=0的两根，则a 4等于（ ） A. 8 B. ﹣8 C. ±8 D.以上都不对6. 等比数列{a n }的前n 项和为S n ，且4a 1，2a 2，a 3成等差数列．若a 1＝1，则S 4等于( ) A ．7 B ．8 C ．15 D ．167. 在数列{a n }中，a 1＝2，a n ＋1＝a n ＋ln(1＋1n )，则a n ＝( ) A ．2＋ln n B ．2＋(n －1)ln n C ．2＋n ln n D ．1＋n ＋ln n8. 已知{a n }为等差数列，a 1＋a 3＋a 5＝105，a 2＋a 4＋a 6＝99.以S n 表示{a n }的前n 项和，则使得S n 达到最大值的n 是( ) A ．21 B ．20 C ．19 D ．18 9.在△ABC 中，a 、b 、c 分别为∠A、∠B、∠C 的对边，如果a 、b 、c 成等差数列，∠B=30°，△ABC 的面积为0.5，那么b 为（ ） A.1D. 210.已知△ABC 的三内角A ，B ，C 所对边的长分别为a ，b ，c ，设向量p ＝(a ＋c ，b )，q ＝(b －a ，c －a )，若p ∥q ，则角C 的大小为( ) A. 6π B. 3π C. 2π D. 23π二、填空题（共5个小题，每小题5分，共25分，请将答案填写的答题纸的相应位置.）11．在等比数列{a n }中，若a 1＋a 2＋a 3＝8，a 4＋a 5＋a 6＝－4，则789a a a ++＝ .12.设公比为q （q ＞0）的等比数列{a n }的前n 项和为S n ，若S 2=4a 2+3，S 4=4a 4+3，则q= ．13.如果一个等差数列中，前三项和为34，后三项和为146，所有项的和为390，则数列的项数是 ___________.14．已知△ABC 三边满足a 2＋b 2＝c 2－3ab ，则此三角形的最大内角为________．15．已知等差数列{}n a 的前n 项和n S 能取到最大值，且满足：9111011+30,0,a a a a <⋅<对于以下几个结论：①数列{}n a 是递减数列；②数列{}n S 是递减数列； ③数列{}n S 的最大项是10S ；④数列{}n S 的最小的正数是19S ．其中正确的结论的个数是___________三、解答题（共75分）.16．(本小题满分12分)(1)在△ABC 中，已知∠C ＝45°，∠A ＝60°，b ＝2，求此三角形最小边的长及a 与∠B 的值．(2)在△ABC 中，已知∠A ＝30°，∠B ＝120°，b ＝5，求∠C 及a 、c 的值．17. （本小题满分12分）已知A 、B 、C 为△ABC 的三个内角，他们的对边分别为a 、b 、c ，且cosBcosC －sinBsinC=12. （1）求A ;（2）若a=b ＋c=4.求bc 的值，并求△ABC 的面积.18. （本题满分12分）设△ABC 的内角A ，B ，C 所对边分别为a ，b ，c ，且有2sin B cos A ＝sin A cos C ＋cos A sin C .(1)求角A 的大小；(2)若b ＝2，c ＝1，D 为BC 的中点，求AD 的长．19. （本题满分12分）缉私艇发现在方位角45°方向，距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜，若缉私艇的速度为14海里/小时，缉私艇沿方位角45°+α的方向追去，若要在最短的时间内追上该走私船，求追击所需时间和α角的正弦．（注：方位角是指正北方向按顺时针方向旋转形成的角，设缉私艇与走私船原来的位置分别为A 、C ，在B 处两船相遇）．20.（本小题满分13分）数列}{n a 满足11=a ，121+=+n n n a a a （*N n ∈）. （1）求证1n a ⎧⎫⎨⎬⎩⎭是等差数列；（2） 求数列}{n a 的通项公式; （3）若T n =++3221a a a a …1++n n a a ，求证: 21<n T 21.（本小题满分14分） 已知数列{}n a 中，122,3a a ==，其前n 项和n S 满足1121(2,*)n n n S S S n n N +-+=+≥∈． （Ⅰ）求证：数列{}n a 为等差数列，并求{}n a 的通项公式； （Ⅱ）设2n n n b a =⋅，求数列{}n b 的前n 项和n T ； 三区上学期第一次月考高一年级数学答题纸(连读)11．；12．；13．；14. ；15. ；三、解答题（共75分）16.（12分）17.（12分）18.（12分）19.（12分）20.（13分）21.（14分）。