12年图论试题
- 格式:docx
- 大小:209.24 KB
- 文档页数:5



图论试题及答案解析图片一、选择题1. 图论中,图的基本元素是什么?A. 点和线B. 点和面C. 线和面D. 点和边答案:A2. 在无向图中,如果两个顶点之间存在一条边,则称这两个顶点是:A. 相邻的B. 相连的C. 相等的D. 相异的答案:A3. 在有向图中,如果从顶点A到顶点B有一条有向边,则称顶点A是顶点B的:A. 父顶点B. 子顶点C. 邻接顶点D. 非邻接顶点答案:B4. 一个图的度是指:A. 图中顶点的总数B. 图中边的总数C. 一个顶点的边数D. 图的连通性答案:C5. 一个图是连通的,当且仅当:A. 图中任意两个顶点都是相邻的B. 图中任意两个顶点都可以通过边相连C. 图中任意两个顶点都可以通过路径相连D. 图中任意两个顶点都可以通过子顶点相连答案:C二、填空题1. 在图论中,一个顶点的度数是该顶点的________。
答案:边数2. 如果一个图的任意两个顶点都可以通过边相连,则称该图为________。
答案:完全图3. 一个图中,如果存在一个顶点到其他所有顶点都有边相连,则称该顶点为________。
答案:中心顶点4. 图论中,最短路径问题是指在图中找到两个顶点之间的________。
答案:最短路径5. 如果一个图的任意两个顶点都可以通过有向路径相连,则称该图为________。
答案:强连通图三、简答题1. 请简述图论中的欧拉路径和哈密顿路径的定义。
答案:欧拉路径是指在图中经过每条边恰好一次的路径,而哈密顿路径是指在图中经过每个顶点恰好一次的路径。
2. 什么是图的着色问题?答案:图的着色问题是指将图中的顶点用不同的颜色进行标记,使得相邻的两个顶点颜色不同。
四、计算题1. 给定一个无向图G,顶点集为{A, B, C, D, E},边集为{AB, BC, CD, DE, EA},请画出该图,并计算其最小生成树的权重。
答案:首先画出图G的示意图,然后使用克鲁斯卡尔算法或普里姆算法计算最小生成树的权重。
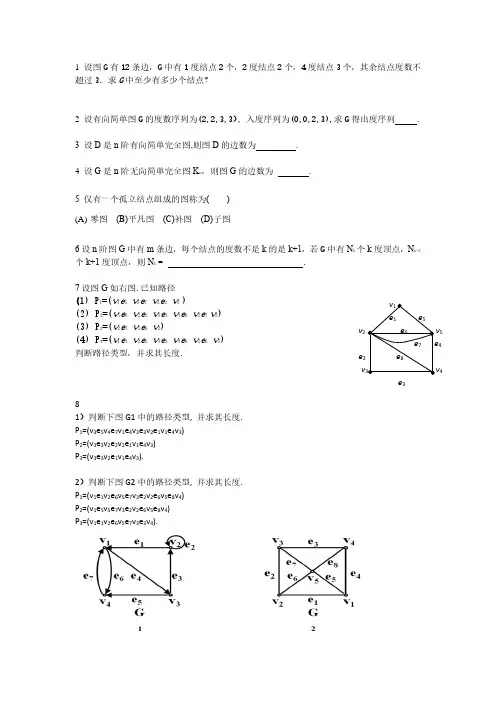
1 设图G有12条边,G中有1度结点2个,2度结点2个,4度结点3个,其余结点度数不超过3.求G中至少有多少个结点?2 设有向简单图G的度数序列为(2,2,3,3), 入度序列为(0,0,2,3),求G得出度序列 .3 设D是n阶有向简单完全图,则图D的边数为 .4设G是n阶无向简单完全图K n,则图G的边数为 .5 仅有一个孤立结点组成的图称为( )(A)零图(B)平凡图(C)补图(D)子图6设n阶图G中有m条边,每个结点的度数不是k的是k+1,若G中有N k个k度顶点,N k+1个k+1度顶点,则N k = .7设图G如右图.已知路径(1) P1=(v1e5 v5e7 v2e2 v3 )(2) P2=(v5e6 v2e2 v3e3 v4e8 v2e7 v5)(3) P3=(v2e7 v5e6 v2)(4) P4=(v1e1 v2e2 v3e3 v4e8 v2e6 v5)判断路径类型,并求其长度.81)判断下图G1中的路径类型, 并求其长度. P1=(v3e5v4e7v1e4v3e3v2e1v1e4v3)P2=(v3e3v2e2v2e1v1e4v3)P3=(v3e3v2e1v1e4v3).2)判断下图G2中的路径类型, 并求其长度. P1=(v1e1v2e6v5e7v3e2v2e6v5e8v4)P2=(v1e5v5e7v3e2v2e6v5e8v4)P3=(v1e1v2e6v5e7v3e3v4).v1e1e5v2e65e7e4 e2e8v3 4e3v e v1 设图G 有12条边,G 中有1度结点2个,2度结点2个,4度结点3个,其余结点度数不超过3.求G 中至少有多少个结点? 至少9个2 设有向简单图G 的度数序列为(2,2,3,3), 入度序列为(0,0,2,3),求G 得出度序列 (2,2,5,6) .3 设D 是n 阶有向简单完全图,则图D 的边数为 )1(−n n .4 设G 是n 阶无向简单完全图K n ,则图G 的边数为 m =n (n -1)/2 .5 仅有一个孤立结点组成的图称为( B ) (A) 零图 (B)平凡图 (C)补图 (D)子图6设n 阶图G 中有m 条边,每个结点的度数不是k 的是k+1,若G 中有N k 个k 度顶点,N k+1个k+1度顶点,则N k = N k =(k+1)n-2m . 7设图G 如右图.已知路径 (1) P 1=(v 1e 5 v 5e 7 v 2e 2 v 3 ) (2) P 2=(v 5e 6 v 2e 2 v 3e 3 v 4e 8 v 2e 7 v 5) (3) P 3=(v 2e 7 v 5e 6 v 2)(4) P 4=(v 1e 1 v 2e 2 v 3e 3 v 4e 8 v 2e 6 v 5)判断路径类型,并求其长度. (1) 初级通路;3 (2) 简单回路;5 (3) 初级回路;2 (4) 简单通路. 5 81)判断下图G1中的路径类型, 并求其长度. P 1=(v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3) P 2=(v 3e 3v 2e 2v 2e 1v 1e 4v 3) P 3=(v 3e 3v 2e 1v 1e 4v 3).2)判断下图G2中的路径类型, 并求其长度. P 1=(v 1e 1v 2e 6v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 2=(v 1e 5v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 3=(v 1e 1v 2e 6v 5e 7v 3e 3v 4).解:在图G 1中,v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3是一条长度为6的回路,但既不是简单回路,也不是初级回路; v 3e 3v 2e 2v 2e 1v 1e 4v 3是一条长度为4的简单回路,但不是初级回路; v 3e 3v 2e 1v 1e 4v 3是一条长度为3的初级回路。


图论期末考试题库及答案一、单项选择题1. 图论的创始人是()。
A. 欧拉B. 莱布尼茨C. 牛顿D. 高斯答案:A2. 在图论中,一个图的顶点集合为空,但边集合不为空的图称为()。
A. 空图B. 完全图C. 树D. 多重图答案:A3. 如果一个图的任意两个顶点之间都存在一条路径,则称该图为()。
A. 连通图B. 强连通图C. 弱连通图D. 无环图答案:A4. 在图论中,一个图的边的集合可以划分为若干个不相交的路径,使得图中的每个顶点恰好属于其中一条路径,这样的图称为()。
A. 欧拉图B. 哈密顿图C. 树答案:C5. 图论中,一个图的边的集合可以划分为若干个不相交的回路,使得图中的每个顶点恰好属于其中一条回路,这样的图称为()。
A. 欧拉图B. 哈密顿图C. 树D. 环答案:A二、多项选择题1. 下列哪些是图论中的基本术语()。
A. 顶点B. 边D. 权重答案:ABCD2. 在图论中,以下哪些图是无向图()。
A. 完全图B. 树C. 多重图D. 有向图答案:ABC3. 图论中,以下哪些图是连通图()。
A. 完全图B. 树C. 多重图D. 空图答案:ABC三、填空题1. 图论中,一个图的顶点集合为V,边集合为E,那么图可以表示为G=()。
答案:(V, E)2. 如果一个图的任意两个顶点之间都存在一条路径,则称该图为()。
答案:连通图3. 在图论中,一个图的边的集合可以划分为若干个不相交的路径,使得图中的每个顶点恰好属于其中一条路径,这样的图称为()。
答案:树四、简答题1. 请解释什么是图论中的“完全图”?答案:完全图是指图中每一对不同的顶点之间都恰好有一条边相连的图。
在完全图Kn中,n个顶点两两相连,共有n(n-1)/2条边。
2. 请解释什么是图论中的“欧拉路径”和“欧拉回路”?答案:欧拉路径是指图中存在一条路径,该路径恰好经过每条边一次。
欧拉回路是指图中存在一条回路,该回路恰好经过每条边一次。
五、计算题1. 给定一个图G=(V, E),其中V={A, B, C, D, E},E={(A, B), (B, C), (C, D), (D, E), (E, A), (A, C)},请判断该图是否为连通图,并说明理由。

图论考试试题图论考试试题在计算机科学领域中,图论是一门重要的学科。
它研究的是图的性质和图上的算法。
图由节点和边组成,节点表示对象,边表示对象之间的关系。
图论可以应用于网络分析、社交网络、路径规划等领域。
图论的考试试题可以帮助学生加深对图论的理解和应用能力。
一、基本概念题1. 什么是图?答:图是由节点和边组成的数据结构。
节点表示对象,边表示对象之间的关系。
2. 图的分类有哪些?答:图可以分为有向图和无向图。
有向图的边有方向,无向图的边没有方向。
另外,图还可以分为加权图和非加权图。
加权图的边具有权重,非加权图的边没有权重。
3. 什么是路径?答:路径是图中连接两个节点的边的序列。
4. 什么是连通图?答:连通图是指图中的任意两个节点之间都存在路径。
二、算法题1. 广度优先搜索算法(BFS)是如何工作的?答:广度优先搜索算法从起始节点开始,逐层遍历图中的节点。
它首先访问起始节点的所有邻居节点,然后依次访问邻居节点的邻居节点,直到遍历完所有可达节点。
2. 深度优先搜索算法(DFS)是如何工作的?答:深度优先搜索算法从起始节点开始,沿着一条路径一直向下访问直到无法继续为止,然后回溯到上一个节点,选择另一条路径继续访问,直到遍历完所有可达节点。
3. 如何判断一个图是否是二分图?答:二分图是指可以将图中的节点分为两个独立的集合,使得同一集合中的节点之间没有边相连。
判断一个图是否是二分图可以使用染色法。
从任意一个节点开始,将其染成红色,然后将其邻居节点染成蓝色,再将邻居节点的邻居节点染成红色,以此类推。
如果在染色过程中发现相邻节点颜色相同,则该图不是二分图。
三、应用题1. 在社交网络中,如何找到两个人之间的最短路径?答:可以使用广度优先搜索算法来找到两个人之间的最短路径。
从一个人开始,逐层遍历其朋友圈中的人,直到找到目标人。
在遍历过程中,可以记录路径,最后得到最短路径。
2. 在电信网络中,如何找到两个城市之间的最短路径?答:可以使用迪杰斯特拉算法来找到两个城市之间的最短路径。

作业解答练习题2 利用matlab编程FFD算法完成下题:设有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。
解答一:function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD(降序首次适应)算法求解:先将物体按长度从大到小排序,%然后按FF算法对物体装箱%输入参数w为物品体积,capacity为箱子容量%输出参数num为所用箱子个数,s为元胞数组,表示装箱方案,s{i}为第i个箱子所装%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:nfor j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endendends = s(1:num);解答二:clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) endoutput:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三:function box_count=FFD(x)%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:nj=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;endendif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入:>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v i= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, 122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w i = {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32, 22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。


图论练习题一、基本题1、设G是由5个顶点构成的完全图,则从G中删去(A)边可以得到树。
A.6 B.5 C.8 D.42、下面哪几种图不一定是树(A)。
A.无回路的连通图B.有n个结点,n-1条边的连通图C.对每对结点间都有通路的图D.连通但删去任意一条边则不连通的图3、5阶无向完全图的边数为(B)。
A.5 B.10 C.15 D.204、设图G有n个结点,m条边,且G中每个结点的度数不是k,就是k+1,则G中度数为k的节点数是()A.n/2 B.n(n+1) C.nk-2m D.n(k+1)-2m 5、设G=<V,E>为有向图,V={a,b,c,d,e,f},E={<a,b>,<b,c>,<a,d>,<d,e>,<f,e>}是(B)。
A.强连通图B.单向连通图C.弱连通图D.不连通图6、在有n个结点的连通图中,其边数(B)A.最多有n-1条B.至少有n-1条C.最多有n条D.至少有n条7、设无向简单图的顶点个数为n,则该图最多有(C)条边。
A.n-1 B.n(n-1)/2 C. n(n+1)/2 D.n28、要连通具有n个顶点的有向图,至少需要(A )条边。
A.n-l B.n C.n+l D.2n9、n个结点的完全有向图含有边的数目(B)。
A.n*n B.n(n+1) C.n/2 D.n*(n-l)10、在一个无向图中,所有顶点的度数之和等于所有边数(B)倍。
A.1/2 B.2 C.1 D.411、在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的(C)倍。
A.1/2 B.2 C.1 D.412、连通图G是一棵树,当且仅当G中(B)A.有些边不是割边B.所有边都是割边C.无割边集D.每条边都不是割边13、4个顶点的完全图G,其生成树个数是()。
A.4 B.8 C.16 D.64二、应用题题1、判断下图是否能一笔画出,并说明理由。
1、B2、B3、A4、C5、D6对7对8 错9 对10 对11 标准化(用对偶单纯型法解)MAX Z=-5X1 -2X2 -4X3ST-3X1-X2-2X3+X4 = -4-6X1-3X2-5X3 +X5 = -10X1…X5>=0B (-4,-10) 含负数,不是最优解确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X2单纯型表迭代B (-2/3,10/3) 含负数,不是最优解再迭代一次确定离基变量MIN (X4,X2)=MIN(-2/3,-10/3)=-2/3 所以X4 为离基确定进基MIN()=MIN(Zi/x5)=2/3 所以进基X1单纯型表迭代先X2行除以A11=-1每行-AI1*X1Z’=-26/3 所以Z=26/3 X=(2/3,10/3,0,0,0)对偶问题MAX W=4Y1+10Y2ST3Y1+6Y2<5Y1+3Y2<=2Y1+5Y2<=4Y1,Y2>=0最优解就是松弛变量Y1=2 Y2=4/312题表作业法此题是产销平衡问题检验σ不能小于0A11 =4-4+3-2=1A24=9-3+4-11=-1 24不通过,不是最优解检验31,没有标记的格子A31=8-5+6-11+4-3+2=1检验22,没有标记的格子A22=10-3+4-11+6-5=1最小的σ24=-1,需要变换对奇数转角变量减去A14 ,对偶数转角变量加上A14,本身不变于是运费为2×8+2×3+4×12+5×14+6×8+11×4。
习 题 11. 证明在n 阶连通图中(1) 至少有n -1条边。
(2) 如果边数大于n -1,则至少有一条闭通道。
(3) 如恰有n -1条边,则至少有一个奇度点。
证明 (1) 若对∀v ∈V(G),有d(v)≥2,则:2m=∑d(v)≥2n ⇒ m ≥n >n-1,矛盾! 若G 中有1度顶点,对顶点数n 作数学归纳。
当n=2时,G 显然至少有一条边,结论成立。
设当n=k 时,结论成立,当n=k+1时,设d(v)=1,则G-v 是k 阶连通图,因此至少有k-1条边,所以G 至少有k 条边。
(2) 考虑v 1→v 2→⋯→v n 的途径,若该途径是一条路,则长为n-1,但图G 的边数大于n-1,因此存在v i ,v j ,使得v i adgv j ,这样,v i →v i+1→⋯→v j 并上v i v j 构成一条闭通道;若该途径是一条非路,易知,图G 有闭通道。
(3) 若不然,对∀v ∈V(G),有d(v)≥2,则:2m=∑d(v)≥2n ⇒ m ≥n >n-1,与已知矛盾! 2. 设G 是n 阶完全图,试问(1) 有多少条闭通道?(2) 包含G 中某边e 的闭通道有多少? (3) 任意两点间有多少条路?答 (1) (n-2)! (2) (n-1)!/2 (3) 1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n -2)…1.3. 证明图1-27中的两图不同构:证明 容易观察出两图中的点与边的邻接关系各不相同,因此,两图不同构。
4. 证明图1-28中的两图是同构的证明 将图1-28的两图顶点标号为如下的(a)与(b)图图1-27 图1-28作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明,对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知,图1-27的两个图是同构的。
电子科技大学研究生试卷
(测试时间:至,共__2_小时)
课程名称图论及其使用教师学时60 学分
教学方式讲授考核日期_2012__年___月____日成绩 考核方式:(学生填写)
一、填空题(填表题每空1分,其余每题2分,共30分)
1.n 阶k 正则图G 的边数()m G =___
___2
nk
; 2.3个顶点的不同构的简单图共有___4___个;
3.边数为m 的简单图G 的不同生成子图的个数有__2___m 个;
4. 图111(,)G n m =和图222(,)G n m =的积图12G G ⨯的边数为1221____n m n m +;
5. 在下图1G 中,点a 到点b 的最短路长度为__13__;
6. 设简单图G 的邻接矩阵为A ,且
23
112012*********
102001202A ⎛⎫
⎪
⎪
⎪= ⎪ ⎪
⎪⎝⎭
,则图G 的边数为
__6__; 7. 设G 是n 阶简单图,且不含完全子图3K ,则其边数一定不会超过2___4n ⎢⎥
⎢⎥⎣⎦;
8.3K 的生成树的棵数为__3__;
9. 任意图G 的点连通度()k G 、边连通度()G λ、最小度()G δ之间的关系为
__()()()____k G G G λδ≤≤;
10. 对下列图,试填下表(是⨯⨯类图的打〝√ 〞,否则打〝⨯〞)。
① ② ③
学号姓名学院
……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………
4 5 6 6 4 1 1 2 7 2
4
3 a
b G 1
能一笔画的图 Hamilton 图 偶图 可平面图 ① ⨯ √ ⨯ √ ② ⨯ ⨯ ⨯ √ ③
⨯
√
√ √
二、单项选择(每题2分,共10分)
1.下面命题正确的是(B )
对于序列(7,5,4,3,3,2),下列说法正确的是:
(A) 是简单图的度序列;
(B) 是非简单图的度序列; (C) 不是任意图的度序列; (D)是图的唯一度序列.
2.对于有向图,下列说法不正确的是(D)
(A) 有向图D 中任意一顶点v 只能处于D 的某一个强连通分支中; (B) 有向图D 中顶点v 可能处于D 的不同的单向分支中;
(C) 强连通图中的所有顶点必然处于强连通图的某一有向回路中; (D)有向连通图中顶点间的单向连通关系是等价关系。
3.下列无向图可能不是偶图的是( D ) (A) 非平凡的树;
(B)无奇圈的非平凡图; (C) n (1)n ≥方体;
(D) 平面图。
4.下列说法中正确的是( C )
(A)连通3正则图必存在完美匹配;
(B)有割边的连通3正则图一定不存在完美匹配; (C)存在哈密尔顿圈的3正则图必能1因子分解; (D)所有完全图都能作2因子分解。
5. 关于平面图,下列说法错误的是( B )
(A) 简单连通平面图中至少有一个度数不超过5的顶点; (B)极大外平面图的内部面是三角形,外部面也是三角形;
(C) 存在一种方法,总可以把平面图的任意一个内部面转化为外部面; (D) 平面图的对偶图也是平面图。
三、 (10分)设G 和其补图G 的边数分别为12,m m ,求G 的阶数。
解:设G 的阶数为n 。
因12(1)
2n n m m -+=…………………………………4分
所以:212220n n m m ---=……………………..2分
得:12118()
m m n +++=
………………………..4分
四、(10分)求下图的最小生成树(不要求中间过程,只要求画出最
()16w T =
五、(10分) (1). 求下图G 的k 色多项式;(2). 求出G 的点色数χ;
(3). 给出一种使用χ种颜色的着色方法。
G
解:(1)图G 的补图为:(2分)
1(,)h H x x =………………………………………………..1分
对于2H :12340,2,4,1r r r r ====,所以,其伴随多项式为: 2342(,)24h H x x x x =++……………………………………..1分 所以:345(,)24h G x x x x =++………………………………1分 于是色多项式[][][]345()24G P x k k k =++
2(1)(2)4(1)(2)(3)(1)(2)(3)(4)k k k k k k k k k k k k =--+---+----
= k (k -1) (k-2)[2+4(k -3) +(k-3) (k-4)] = k (k -1)2 (k-2)2
2分
V 7
v 6
v 5
v 4
v 3
v 2
v 1
v v
v 6 5
4 3
5 1
6 24 1 2 3 V 7
v 6
v 5
v 4
v 3
v 2
v 1
v
v
v 6 5
4 3
5 1
6 24
1 2 3
H 1
H 2
解法2()(1)k P G k =- 2分
=(k -1) 3分
=(k -1)[ k (k -1) (k-2)2] = k (k -1)2 (k-2)2
2分 (2)由于123()()0,()12P G P G P G ===,所以,点色数χ=3; 2分
(3)χ点着色: 1分
六、(10分)5个人,,,,A B C D E 被邀请参加桥牌比赛。
桥牌比赛规则是每一场比赛由两个2人组进行对决。
要求每个2人组{},X Y 都要和其它2人组{},W Z (W ,Z ∉{X ,Y })进行对决。
若每个人都要和其他任意一个人组成一个2人组,且每个组在同一天不
能有多余一次的比赛,则最少安排多少天相应的一个时间安排表。
()
解:(1)、建模:5个人能够组成10个2人组:AB, AC, AD, AE, BD, BC,
BE, CD , CE, DE 。
以每个2人组作为顶点,因要求每个2人组{},X Y 都和其它2人组{},W Z 比赛,所以,得到比赛状态图如下:
AB AC
AD BD BE
CD
CE DE AE
(2)、最少安排多少天比赛转化为求状态图的边色数χ'。
因为彼得森图不可1因子分解,于是可推出4χ'≥,又可用4种色对其正常边着色(见下图),所以:4χ'≤。
(3)、安排时间表: 第一天:AB---DE, AE---BC, AC---BE, AD---CE; 第二天:AB---CE, AC---DE,
AE---BD, AD---BC, BE---CD; 第三天:AB---CD, BC---DE, BD---CE; 第四天:AC---BD, AD---BE, AE---CD 。
4分 七、(10分) 由于在测试中获得好成绩,6名学生,,,,,A B C D E F 将获得下列书籍的奖
G
1
2
3
AB AC AD BC BD BE CD CE DE AE
1 1
2 2 2 1 2 2
3 3
3 4 4 4 ⎝⎛ ⎪⎪⎪⎪
⎪⎭⎫+
励,分别是:代数学(a),微积分(c),微分方程(d),几何学(g),数学史(h),规划学(p),拓扑学(t)。
每门科目只有1本书,而每名学生对书的喜好是:
A :d, h, t ;
B : h, t ;
C :d, h ;
D :d, t ;
E :a, c, d ; F::c, d, p, g 。
每名学生是否都可以得到他喜欢的书?为什么?(用图论方法求解) 解:由题意,得模型图:(4分)
B C D E F
a c d g h p t
A
问题转化为是否存在饱和A,B,C,D,E,F 的匹配存在。
2分 取顶点子集合{},,,S A B C D =,因{}(),,N S d h t =,所以()N S S <
由霍尔定理知:不存在饱和A,B,C,D,E,F 的匹配。
故每名学生不能都得到他喜欢的书。
4分
八、(10分)若n 为偶数,且单图G 满足:()12
n
G δ≥+,求证:G 中有3因子。
证明:因单图G 满足:()12
n
G δ≥+,所以G 中存在哈密尔顿圈n C 。
2分
又因n 为偶数,所以,n C 可分解为两个1因子12,H H ,它们显然也是图G 的两
个1因子。
3分 考虑11G G H =-,则1()2
n
G δ≥,于是,1G 中存在哈密尔顿圈n
C '。
2分 作1
n
H H C '=,则H 为G 的一个3因子。
3分。