第三章 证明三 练习题 (北师大版初三上) (3)

一、填空题1.如图，ABCD，则AB=_____，______=AD，∠A=________，________=∠D，若此时∠B+∠D=128°,则∠B=_______度，∠C=_______度.80 cm ，且相邻两边之比为1∶3，则长边=______cm，短边=______cm.3.如下左图，ABCD,∠C的平分线交AB于点E，交D A延长线于点F，且AE=3 cm，E B=5 cm,则ABCD的周长为__________.4.如上中图，ABCD，AB＞BC，AC⊥AD，且AB∶BC=2∶1，则DC∶AD=__________,∠DCA=__________度，∠D=∠B=__________度，∠DAB=∠BCD=__________度.5.如上右图，ABCD的对角线AC，BD交于点O，则图中全等三角形有__________对.二、选择题1.ABCD中，∠A∶∠D=3∶6,则∠C 的度数是° B.120 C.90°°ABCD中，∠A∶∠B∶∠C∶∠D的可能情况是∶7∶2∶∶2∶7∶7∶7∶7∶∶3∶4∶53.如下左图，从等腰△ABC底边上任意一点D，作DE∥AC交AB于E，DF∥AB交AC于F，则AEDF的周长4.如上右图，ABCD中，BC∶AB=1∶2，M为AB 的中点，连结MD、M C，则∠DMC等于°°°°5.以不共线的三点为顶点，可以作平行四边形6.平行四边形具有，但一般四边形不具有的性质是°°7.如下左图，在ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠D A E等于° B.25°C.30°°§证明(三)三、解答题 1.已知：如上右图ABCD 的周长是20 cm,△ADC 的周长是16 cm.求：对角线AC 的长.2.求证：平行四边形的对角线互相平分.3.如下图,ABCD 中，BD 是ABCD 的对角线，AE ⊥BD 于E ，CF ⊥BD 于F . （1）在图中补全图形； （2）求证：AE =CF .一、判断题1.一组对边平行，另一组对边相等的四边形是平行四边形( )2.两组对边分别相等的四边形是平行四边形( )3.对角线相等的四边形是平行四边形( )4.有两组对角分别相等的四边形是平行四边形( )5.对角线互相垂直的四边形是平行四边形( )6.邻边互相垂直的四边形是平行四边形( )7.如果一条对角线将四边形分成两个全等三角形,那么这个四边形是平行四边形( )8.对角线互相平分的四边形是平行四边形( )9.一组对边平行,一组对角相等的四边形是平行四边形( )二、填空题1.如果一个四边形的每对相邻内角都互补，那么这个四边形是__________.△ABC 的中线AD 到E ，使AE =2AD ，则四边形ABEC 是__________.3.如果一个四边形以其对角线交点为中心，在平面内旋转180°，与原四边形重合，则这个四边形是__________。

数学初三上北师大版第三章证明（三）单元突破2时间：1、不能判断四边形ABCD 是平行四边形的是( )、 A 、AB ＝CD ，AD ＝BC B 、AB ＝CD ，AB ∥CD C 、AB ＝CD ，AD ∥BC D 、AB ∥CD ，AD ∥BC2、如图，在△MBN 中，BM ＝6，点A 、C 、D 分别在MB 、NB 、MN 上，四边形ABCD 为平行四边形，∠NDC ＝∠MDA ，那么□ABCD 的周长是( )、A 、12B 、16C 、18D 、24(第2题) (第3题) (第4题)3、如图，在□ABCD 中，添加以下条件不能判定□ABCD 是菱形的是( ) 、 A 、AB ＝BC B 、AC ⊥BD C 、BD 平分∠ABC D 、AC ＝BD4、把一张长方形的纸片按如下图的方式折叠，EM 、FM 为折痕，折叠后的C 点落在 B ′M 或B ′M 的延长线上，那么∠EMF 的度数是( )、 A 、85° B 、90° C 、95° D 、100°5、将n 个边长都为1 cm 的正方形按如下图摆放，点A 1，A 2，…，A n 分别是正方形的中心，那么n 个正方形重叠形成的重叠部分的面积和为( )、 A 、14 cm 2 B 、n 4 cm 2 C 、n －14 cm 2 D 、(14)n cm2(第5题) (第6题) (第7题)6、如图，等腰梯形ABCD 中，AD ∥BC ，AB ＝DC ＝1，BD 平分∠ABC ，BD ⊥CD ，那么AD ＋BC 等于( )、 A 、2 B 、3 C 、4 D 、57、如图，在菱形ABCD 中，E 、F 分别是AB 、AC 的中点，假如EF ＝2，那么ABCD 的周长是( )、 A 、4 B 、8 C 、12 D 、16 A 、两条对角线相等的四边形是矩形B 、两条对角线互相垂直且相等的四边形是正方形C 、两条对角线互相平分的四边形是平行四边形D 、两条对角线互相垂直的四边形是菱形9、如图(1)，将一块正方形木板用虚线划分成36•个全等的小正方形，然后，按其中的实线切成七块形状不完全相同的小木片，制成一副七巧板，用这副七巧板拼成如图(2)所示的图案，那么图(2)中的阴影部分的面积是整个图案面积的()、A 、122B 、14C 、17D 、18(第9题)(第10题)10、如图，四边形ABCD 中，AC ＝A ，BD ＝b ，且AC ⊥BD ，顺次连接四边形ABCD 各边中点，得到四边形A 1B 1C 1D 1，再顺次连接四边形A 1B 1C 1D 1各边中点，得到四边形A 2B 2C 2D 2……，如此进行下去，得到四边形A n B n C n D n 、以下结论：①四边形A 2B 2C 2D 2是矩形;②四边形A 4B 4C 4D 4是菱形;③四边形A 5B 5C 5D 5的周长A ＋b 4；④四边形A n B n C n D n 的面积是Ab2n ＋1，正确的有()、 A 、①②B 、②③C 、②③④D 、①②③④ 【二】填空题(3×8＝24分)11、如图，□ABCD 中，E 是BA 延长线上一点，AB ＝AE ，连结CE 交AD 于点F ，假设CF 平分∠BCD ，AB ＝3，那么BC 的长为、12、如图，在等腰梯形ABCD 中，AB ∥CD ，AD ＝BC ，AC ⊥BC ，∠B ＝60°，BC ＝2cm，那么上底DC 的长是_______cm 、(第11题)(第12题)(第13题)(第14题)13、如图，梯形ABCD 中，AD ∥BC ，∠C ＝90°，且AB ＝AD ，连结BD ，过A 点作BD 的垂线，交BC 于点E 、假如EC ＝3cm ，CD ＝4cm ，那么，梯形ABCD 的面积是_______cm 2、14、如图，在四边形ABCD 中，AB ＝BC ＝CD ＝DA ，对角线AC 与BD •相交于点O ，假设不增加任何字母与辅助线，要使得四边形ABCD 是正方形，那么还需增加的一个条件是_______、 15、如图，在等腰梯形ABCD 中，AD ∥BC ，AB ≠AD ，对角线AC 、BD •相交于点O ，如下四个结论：①梯形ABCD 是轴对称图形；②∠DAC ＝∠DCA ；③△AOB ≌△DOC ；④△AOD ∽△BOC 、请把其中正确结论的序号填在横线上：________、16、将完全相同的平行四边形和完全相同的菱形镶嵌成如下图的图案、设菱形中较小角为x 度，平行四边形中较大角为y 度，那么y 与x 的关系式是、(第15题)(第16题)(第17题)(第18题)17、如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝2，AB ＝42，BC ＝4，点E 在AB 边上，且CE 平分∠BCD ，DE 平分∠ADC ，那么点E 到CD 的距离为、ABDCE18、如图，在直线m 上摆放着三个正三角形：△ABC ，△HFG ，△DCE ，BC ＝12CE ，F 、G 分别是BC 、CE 的中点，FM ∥AC ，GN ∥DC 、•设图中三个平行四边形的面积依次是S 1、S 2、S 3，假设S 1＋S 3＝10，那么S 2＝______、 【三】解答题(共46分)19、如图，在□ABCD 中，BE ⊥AC 于点E ，DF ⊥AC 于点F 、 求证：AE ＝CF 、(第19题)20、如图，直角梯形纸片ABCD 中，AD ∥BC ，∠A ＝90°，∠C ＝30°、折叠纸片使BC 通过点D 、点C 落在点E 处，BF 是折痕，且BF ＝CF ＝8、 (1)求∠BDF 的度数； (2)求AB 的长、(第20题)21、如图，在梯形ABCD 中，AD //BC ，AB ＝DC ，过点D 作DE ⊥BC ，垂足为E ，并延长DE 至F ，使EF ＝DE 、连结BF 、CF 、AC 、(1)求证：四边形ABFC 是平行四边形；(2)假如DE 2＝BE ·CE ，求证四边形ABFC 是矩形、(第21题)22、如图，在梯形纸片ABCD 中，AD ∥BC ，AD >CD ，将纸片沿过点D 的直线折叠，使点C 落在AD 上的点C ′处，折痕DE 交BC 于点E ，连结C ′E 、 (1)求证：四边形CDC ′E 是菱形；(2)假设BC ＝CD ＋AD ，试判断四边形ABED 的形状，并加以证明、(第22题)23、：如图，在梯形ABCD 中，AD ∥BC ，AB ＝DC ，点E 、F 、G •分别在边AB 、BC 、CD 上，AE ＝GF ＝GC 、(1)求证：四边形AEFG 是平行四边形；(2)当∠FGC ＝2∠EFB 时，求证：四边形AEFG 是矩形、(第23题)24、：如图〔1〕，O 为正方形ABCD 的中心，分别延长OA 到点F ，OD 到点E ，使OF ＝2OA ，OE ＝2OD ，连结EF ，将△FOE 绕点O 逆时针旋转α角得到△F ´OE ´(如图〔2〕)、 (1)探究AE ′与BF'的数量关系，并给予证明； (2)当α＝30°时，求证：△AOE ′为直角三角形、(第24题)25、以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形，直角顶点分别为E 、F 、G 、H ，顺次连结这四个点，得四边形EFGH 、 (1)如图〔1〕，当四边形ABCD 为正方形时，我们发明四边形EFGH 是正方形；如图〔2〕，当四边形ABCD 为矩形时，请判断：四边形EFGH 的形状(不要求证明)； (2)如图〔3〕，当四边形ABCD 为一般平行四边形时，设∠ADC ＝α(0°＜α＜90°)， ①试用含α的代数式表示∠HAE ； ②求证：HE ＝HG ；③四边形EFGH 是什么四边形？并说明理由、第三章综合达标训练卷(B 卷)1、C2、A3、D4、B5、C6、B7、D8、C9、D10、C11、612、213、2614、答案不唯一，如AC ＝BD 或∠BAD ＝90°15①③④16、y ＝90＋12x 17、2 218、4提示：设S △ABC ＝S ，那么S 1＝S △ABC －2S △BMF ＝S －2×94S ＝12S ，S 2＝94S －14S －S ＝S ，S 3＝4S－2S ＝2S 、因为S 1＋S 3＝10，即12S ＋2S ＝10，解得S ＝4、因此S 2＝S ＝4、 19、∵四边形ABCD 是平行四边形，A BCDH EF G (2)(第25题)E BFG D HA C (3)(1)ABCDH EFGFEDCBA（第21∴AB ∥CD ，AB ＝CD (平行四边形对边平行且相等)、 ∴∠BAE ＝∠DCF (两直线平行，内错角相等)、 ∵BE ⊥AC 于点E ，DF ⊥AC 于点F ， ∴∠AEB ＝∠CFD ＝90°(垂直定义)、 ∴∠ABE ＝∠CDF (等角的余角相等)、 ∴△ABE ≌△CDF (ASA )，∴AE ＝CF (全等三角形的对应边相等)、 20、(1)∵BF ＝CF ，∠C ＝30°， ∴∠FBC ＝30°，∠BFC ＝120°、 又由折叠可知∠DBF ＝30º、 ∴∠BDF ＝90°、(2)在Rt △BDF 中，∵∠DBF ＝30°，BF ＝8， ∴BD ＝43、∵AD ∥BC ，∠A ＝90°， ∴∠ABC ＝90°、又∠FBC ＝∠DBF ＝30°， ∴∠ABD ＝30°、在Rt △BDA 中，∵∠ABD ＝30°，BD ＝43， ∴AB ＝6、21、(1)连接BD 、∵DE ⊥BC ，EF ＝DE ， ∴BD ＝BF ，CD ＝CF 、∵在梯形ABCD 中，AD //BC ，AB ＝DC ， ∴四边形ABCD 是等腰梯形、 ∴BD ＝AC 、∴AC ＝BF ，AB ＝CF 、∴四边形ABFC 是平行四边形、 (2)∵DE 2＝BE ·CE ，EF ＝DE ，∴EF 2＝BE ·CE 、∴EF BE ＝CE EF 、 又DE ⊥BC ，∴∠CEF ＝∠FEB ＝90°、 ∴△CEF ∽△FEB 、 ∴∠CFE ＝∠FBE 、∵∠FBE ＋∠BFE ＝90°， ∴∠CFE ＋∠BFE ＝90°、即∠BFC ＝90°、由(1)知四边形ABFC 是平行四边形， ∴四边形ABFC 是矩形、22、(1)依照题意可得CD ＝C ′D ，∠C ′DE ＝∠CDE ，CE ＝C ′E ，∵AD ∥BC ，∴∠C ′DE ＝∠CED 、 ∴∠CDE ＝∠CED 、 ∴CD ＝CE ，∴CD ＝C ′D ＝C ′E ＝CE ， ∴四边形CDC ′E 为菱形、(2)当BC ＝CD ＋AD 时，四边形ABED 为平行四边形、 理由：由(1)知CE ＝CD ， 又BC ＝CD ＋AD ，∴BE ＝AD 、 又AD ∥BC ，∴四边形ABED 为平行四边形、 23、(1)∵GF ＝GC ， ∴∠GFC ＝∠GCF 、 ∵AD ∥BC ，AB ＝DC ， ∴∠GCF ＝∠B 、 ∴∠GFC ＝∠B ，∴GF ∥AB ，即GF ∥AE 、 ∵AE ＝GF ，∴四边形AEFG 是平行四边形、(2)在△GFC 中，∠FGC ＝180°－2∠GFC 、 ∵∠FGC ＝2∠EFB ，∴2∠EFB ＝180°－2∠GFC ， ∴∠EFB ＋∠GFC ＝90°、∴∠EFG ＝180°－(∠EFB ＋∠GFC )＝90°、 24、(1)AE ′＝BF 、证明如下：∵在正方形ABCD 中，AC ⊥BD ， ∴∠F ′OE ′＝∠AOD ＝∠AOB ＝90°、即∠AOE ′＋∠AOF ′＝∠BOF ′＋∠AOF ′、 ∴∠AOE ′＝∠BOF ′、又OA ＝OB ＝OD ，OE ′＝2OD ，OF ′＝2OA ， ∴OE ′＝OF ′、∴△OAE ′≌△OBF ′、 ∴AE ′＝BF ′、(2)作△AOE ′的中线AM ，如图， 那么OE ′＝2OM ＝2OD ＝2OA ，∴OA ＝OM 、 ∵α＝30°， ∴∠AOM ＝60°， ∴△AOM 为等边三角形、∴ MA ＝MO ＝ME ′，∠AE ′M ＝∠E ′AM 、又∠AE ′M ＋∠E ′AM ＝∠AMO ， 即2∠AE ′M ＝60°， ∴∠AE ′M ＝30°、∴∠AE ′M ＋∠AOE ′′＝30°＋60°＝90°、 ∴△AOE ′为直角三角形、25、(1)四边形EFGH 是正方形、 (2)①∠HAE ＝90°＋A 、 在□ABCD 中，AB ∥CD ，∴∠BAD ＝180°－∠ADC ＝180°－A 、 ∵△HAD 和△EAB 基本上等腰直角三角形，∴∠HAD ＝∠EAB ＝45°，∴∠HAE ＝360°－∠HAD －∠EAB －∠BAD＝360°－45°－45°－(180°－A )＝90°＋A 、 ②∵△AEB 和△DGC 基本上等腰直角三角形，∴AE ＝22AB ，DG ＝22CD ，在□ABCD中，AB＝CD，∴AE＝DG、∵△HAD和△GDC基本上等腰直角三角形，∴∠DHA＝∠CDG＝45°，∴∠HDG＝∠HAD＋∠ADC＋∠CDG＝90°＋A＝∠HAE、∵△HAD是等腰直角三角形，∴HA＝HD，∴△HAE≌△HDG，∴HE＝HG、③四边形EFGH是正方形、由②同理可得：GH＝GF，FG＝FE、∵HE＝HG(已证)，∴GH＝GF＝FG＝FE，∴四边形EFGH是菱形、∵△HAE≌△HDG(已证)，∴∠DHG＝∠AHE、又∠AHD＝∠AHG＋∠DHG＝90°，∴∠EHG＝∠AHG＋∠AHE＝90°，∴四边形EFGH是正方形、。

【九年级】九年级上册第三章证明（三）单元试题（北师大附答案）第三章证明（三）检测题【本试卷满分为100分，考试时间为90分钟】一、（每小题3分，共30分）1.如图所示，在平行四边形ABCD中，对角线AC和BD在点O处相交。

如果BD和AC 之和为18C，CD？da=2？3.如果△ AOB是13C，那么BC的长度是（）a.6cb.9cc.3cd.12c2.如果等腰梯形的两个底部之间的差值为12，高度为6，则等腰梯形的锐角为（）a.30°b.45°c.60°d.75°3.以下判断是正确的（）a.对角线互相垂直的四边形是菱形b、角相等的四边形是等腰梯形c.四边相等且有一个角是直角的四边形是正方形d、两条对角线相等且相互垂直的四边形是正方形4.如图，梯形中，∥，∠∠90°，分别是的中点，若c，c，那么（）c.a、 4b。

5c。

6.5d。

九5.直角梯形的两个直角顶点到对腰中点的距离（）a、 B.不相等C.可能相等，也可能不相等D.无法比较6.正方形具备而菱形不具备的性质是（）a、对角线被一分为二。

对角线相互垂直c.对角线相等d.每条对角线平分一组对角7.从钻石的钝角顶点到对角线的两侧画一条垂直线，垂直脚正好是边的中点，那么钻石内角的钝角为（）a.150°b.135°c.120°d.100°8.将四边形每边的中点依次连接起来，得到一个矩形，则以下四边形满足条件为（）①平行四边形;②菱形;③等腰梯形;④对角线互相垂直的四边形.A.①③B②③C③④D②④9.在平行四边形、菱形、矩形、正方形中，能够找到一个点，使该点到各顶点距离相等的图形是（）a、平行四边形和菱形B.菱形和矩形c.矩形和正方形d.菱形和正方形10.矩形的边长为10C和15C。

一个内角的角平分线分为两部分，这两部分的长度分别为（）a.6c和9cb.5c和10cc、 4C和11CD 7C和8C二、题（每小题3分，共24分）11.考虑到钻石的周长为40摄氏度，对角线的长度为16摄氏度，钻石的面积为12.如图，ef过平行四边形abcd的对角线的交点o，交ad于点e，交bc于点f，已知ab=4，bc=5，oe=1.5，那么四边形efcd的周长是.13.如图所示，在平行四边形ABCD中，ab=12，ab侧的高度为3，BC侧的高度为6，则平行四边形ABCD的周长为14.在矩形abcd中，对角线ac、bd交于点o，若∠，则∠oab=.15.已知钻石的内角为120°，将内角平分的对角线长度为8C，则钻石的周长为16.如图，把两个大小完全相同的矩形拼成“l”型图案，则∠________，∠________.17.对于边长的正方形，在一个角切割边长的正方形，剩余图形的周长为18.顺次连接四边形各边中点，所得的图形是.顺次连接对角线_______的四边形的各边中点所得的图形是矩形.顺次连接对角线的四边形的各边中点所得的四边形是菱形.顺次连接对角线的四边形的各边中点所得的四边形是正方形.三、回答问题（共46分）19.（7分）如图，在四边形中，，⊥，⊥，垂足为，，求证：四边形是平行四边形.20.（7分）如图所示△, ∠, ⊥二等分∠, 相交，相交，⊥ 在中，验证四边形是菱形21.（7分）如图，已知正方形，过作∥，∠，交于点，求证：22.（8分）已知：如图，△中，是∠的平分线，∥，∥.求证：四边形是菱形.小明证明了这个问题：证明：∵平分∠，∴∠1＝∠2（角平分线的定义）.∥, ∧∠ 2 = ∠ 3（两条直线平行且内部偏移角相等）∴∠1＝∠3（等量代换）.‡（等角到等边）同样可以证明，∴四边形是菱形（菱形定义）.老师说小明的证明过程是错误的。

第三章 证明（Ⅲ）目标检测题班级 姓名 学号 成绩一、选择题（每题4分，共40填在括号内. 1、如图1，在□ABCD 中,O 为对角线AC 、BD 的交点，则图中共有相等的角（ ）A 、4对B 、5对C 、6对D 、8对 2、如图2，已知E 、F 分别为□ABCD 的中点， 连接AE 、CF 所形成的四边形AECF 的面积与□ABCD 的面积的比为（ ） A 、1:1 B 、1:2 C 、1:3 D 、1:4 3、过四边形ABCD 的顶点A 、B 、C 、D 作BD 、AC 的平行线围成四边形EFGH,若EFGH是菱形,则四边形ABCD 一定是( ) A 、平行四边形 B 、菱形C 、矩形D 、对角线相等的四边形 4、在菱形ABCD 中，,,CD AF BC AE ⊥⊥ 且E 、F 分别是BC 、CD 的中点， 那么=∠EAF （ ）A 、075B 、055C 、450D 、0605、矩形的一条长边的中点与另一条长边构成等腰直角三角形，已知矩形的周长是36，则矩形一条对角线长是（ ） A 、56 B 、55 C 、54 D 、356、矩形的内角平分线能够组成一个（ ）A 、矩形B 、菱形C 、正方形D 、平行四边形7、以正方形ABCD 的一组邻边AD 、CD 向形外作等边三角形ADE 、CDF ，则下列结论中错误的是（ ） A 、BD 平分EBF ∠ B 、030=∠DEF C 、BD EF ⊥ D 、045=∠BFD 8、已知正方形ABCD 的边长是10cm ，APQ ∆是等边三角形，点P 在BC 上，点Q 在CD 上，则BP 的边长是（ ） A 、55cm B 、3320cm C 、)31020(-cm D 、)31020(+cm 9、若两个三角形的两条中位线对应相等且两条中位线与一对应边的夹角相等，则这两个三角形的关系是（ ）A 、全等B 、周长相等C 、不全等D 、不确定 10、正方形具有而菱形不具有的性质是（ ）A 、四个角都是直角B 、两组对边分别相等C 、内角和为0360 D 、对角线平分对角 二、填空题（每空1分，共11分）1、平行四边形两邻边上的高分别为32和33，这两条高的夹角为060，此平行四边形的周长为 ，面积为 .2、等腰梯形的腰与上底相等且等于下底的一半，则该梯形的腰与下底的夹角为 .3、三角形三条中位线围成的三角形的周长为19，则原三角形的周长为 .4、在ABC ∆中，D 为AB 的中点，E 为AC 上一点，AC CE 31=，BE 、CD 交于点O ，cm BE 5=，则=OE .5、顺次连接任意四边形各边中点的连线所成的四边形是 .6、将长为12，宽为5的矩形纸片ABCD 沿对角线AC 对折后，AD 与BC 交于点E ，则DE的长度为 .7、从矩形的一个顶点作一条对角线的垂线，这条垂线分这条对角线成1:3两部分，则矩形的两条对角线夹角为 . 8、菱形两条对角线长度比为1:3,则菱形较小的内角的度数为 .9、正方形的一条对角线和一边所成的角是 度. 10、已知四边形ABCD 是菱形，AEF ∆是正三角形，E 、F 分别在BC 、CD 上，且CD EF =，则=∠BAD .三、解答题（第1、2小题各10分，第3、4小题各5分，共30分） 1、如图3，AB//CD ，090=∠ACB ，E 是AB 的中点，CE=CD ，DE 和AC 相交于点F. 求证：（1）AC DE ⊥；（2）ACE ACD ∠=∠.2、如图4，ABCD 为平行四边形，DFEC 和BCGH 为正方形.求证：EG AC .图43、证明：如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.4、从菱形钝角的顶点向对边作垂线，且垂线平分对边，求菱形各角的度数？图5四、（第1、2小题各6分，第3小题7分，共19分）1、如图5，正方形纸片ABCD 的边BC 上有一点E ，AE=8cm ，若把纸片对折，使点A 与点E 重合，则纸片折痕的长是多少？2、如图6，在矩形ABCD 中，E 是BC 上一点且AE=AD ，又AE DF ⊥于点F ，证明：EC=EF.3、如图7，已知P 是矩形ABCD 的内的一点.求证：2222PD PB PC PA +=+.图5答案:一、选择题1、D ；2、B ；3、D ；4、D ；5、A ；6、C ；7、B ；8、C ；9、A ；10、A ； 二、填空题1、20；312。

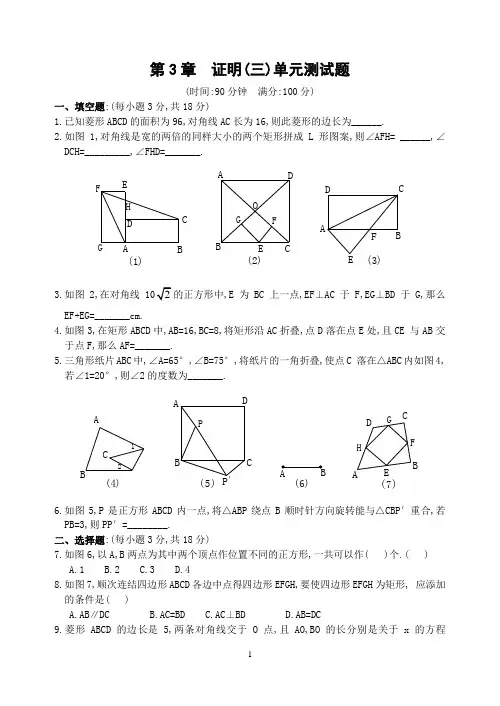
第3章 证明(三)单元测试题(时间:90分钟 满分:100分)一、填空题:(每小题3分,共18分)1.已知菱形ABCD 的面积为96,对角线AC 长为16,则此菱形的边长为______.2.如图1,对角线是宽的两倍的同样大小的两个矩形拼成L 形图案,则∠AFH= ______,∠DCH=_________,∠FHD=_______.EDBA (1)GC HFE CB(2)GDAFODBA(3)ECF3.如图2,在对角线的正方形中,E 为BC 上一点,EF ⊥AC 于F,EG ⊥BD 于G,那么EF+EG=_______cm.4.如图3,在矩形ABCD 中,AB=16,BC=8,将矩形沿AC 折叠,点D 落在点E 处,且CE 与AB 交于点F,那么AF=_______.5.三角形纸片ABC 中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C 落在△ABC 内如图4,若∠1=20°,则∠2的度数为_______.BA (4)12CBA(5)DCPP 'B (6)E CBA(7)GDHF6.如图5,P 是正方形ABCD 内一点,将△ABP 绕点B 顺时针方向旋转能与△CBP ′重合,若PB=3,则PP ′=________.二、选择题:(每小题3分,共18分)7.如图6,以A,B 两点为其中两个顶点作位置不同的正方形,一共可以作( )个.( ) A.1 B.2 C.3 D.48.如图7,顺次连结四边形ABCD 各边中点得四边形EFGH,要使四边形EFGH 为矩形, 应添加的条件是( )A.AB ∥DCB.AC=BDC.AC ⊥BDD.AB=DC9.菱形ABCD 的边长是5,两条对角线交于O 点,且AO,BO 的长分别是关于x 的方程x 2+(2m-1)x+m 2+3=0的两根,则m 的值是( ) A.-3 B.5 C.5或-3 D.-5或310.已知四边形ABCD 的对角线AC 与BD 相交于点O,若S △AOB =4,S △COD =9, 则四边形ABCD 的面积的最小值为( )A.21B.25C.26D.3611.将一长方形纸片按如图8的方式折叠,BC 、BD 为折痕,则∠CBD 的度数为( ) A.60° B.75° C.90° D.95°C B A(8)EDE 'A 'CBA(9)E DF12.如图9,在正方形ABCD 中,E 是BC 边的中点,F 是CD 上一点,AE ⊥EF.则下列结论正确的是( ) A.∠BAE=30° B.CE 2=AB ·CF C.CF=13CD D.△ABE ∽△AEF 三、解答题:(共64分)13.(9分)已知:在正方形ABCD 中,F 是AD 的中点,BF 与AC 交于点G,求△BGC 与四边形CGFD 的面积之比.GCBD AF14.(9分)如图,在平行四边形ABCD 中,延长BA 至E,使AE=AB,连结CE 交AD 于F 点, (1)求证:AF=DF;(2)若ABCD S =12,求AEF S .CBA E DF15.(9分)如图,DE 是YABCD 的∠ADC 的平分线,EF ∥AD 交DC 于F.(1)求证:四边形AEFD 是菱形;(2)如果∠A=60°,AD=5,求菱形AEFD 的面积.CBA12EDF16.(9分)一组线段AB 和CD 把正方形分成形状相同,面积相等的四部分,现给出四种分法,如图所示,请你找出线段AB 、CD 的位置及关系存在的规律, 符合这种规律的线段共有多少组?(不要添加辅助线和其它字母)CBA DC BA DCBADCBA D17.(9分)已知:如图,矩形ABCD.(1)作出点C 关于BD 所在直线的对称点C ′(用尺规作图,不写作法,保留作图痕迹) (2)连结C ′B 、C ′D,若△C ′BD 与△ABD 重叠部分的面积等于△ABD 面积的23, 求∠CBD 的度数.CBAD18.(9分)如图,它是由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G 是小正方形的顶点,以这七个点中的任意三个点为顶点,可组成多少个面积为1 的三角形?请你写出所有这样的三角形?DCBA E GF19.(10分)已知正方形ABCD 中,M 是AB 的中点,E 是AB 延长线上一点,MN ⊥DM 且交∠CBE 的平分线于N(如图甲).(1)求证:MD=MN;(2)若将上述条件中的“M 是AB 中点”改为“M 是AB 上任意一点”其余条件不变(如图乙),则结论“MD=MN ”还成立吗?如果成立,请证明;如果不成立,请说明理由.甲D CB AENM乙D CBAENM单元测试题答案1.102.45°,15°,105°3.54.105.60° 7.C 8.C 9.A 10.B 11.C 12.BD 13.4:5 14.(1)先证△AEF≌△DCF (2)S△AEF=315.(1)证略 (2)S菱形AEFD16.AB、CD的位置及关系的规律是:①AB⊥CD;②AB与CD 均过正方形的中心③符合这种规律的线条有无数多组.17.(1)略.(2)∠CBD=30°18.共十四个,具体有:△ADE △BDE △AFE △BEF △BFG △AFG △ABD △ABE△ABF △ABG △DCF △ECG △BCF △ACG19.(1)取AD中点F,连MF,证△DFM≌△MBN;(2)结论DM=MN仍成立,在AD上截取AF=AM,连FM.证△DFM≌△MBN.。

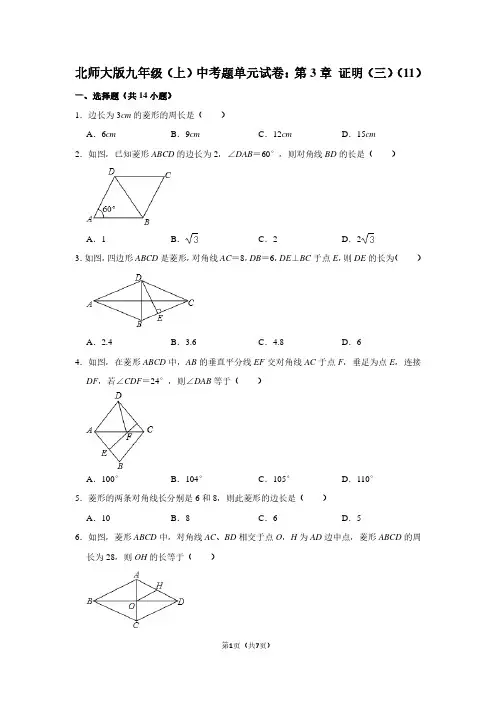
北师大数学九年级上册第三章证明（三）综合检测试题一、选择题1．若四边形的两条对角线互相垂直，则这个四边形 ( )A ．一定是矩形B ．一定是菱形C ．一定是正方形D ．形状不确定2．如图1所示，设F 为正方形ABCD 上一点，CE ⊥CF 交AB 的延长线于点E ，若正方形ABCD 的面积为64，△CEF 的面积为50，则△CBE 的面积为 （ ） A ．20 B ．24 C ．25 D ．263．如图2所示，AB ∥CD ，AE ⊥CD 交CD 于点E ，AE=12，BD=15，AC=20。

则梯形ABCD 的面积为（ ） A ．130 B ．140 C ．150 D ．160 4．小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料，生产一批形状如图3所示的风筝.点E ，F ，G ，H 分别是四边形ABCD 各边的中点，其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均不计余料）.若生产这批风筝需要甲布料30匹，那么需要乙布料 （ ） A ．15匹 B ．20匹 C ．30匹 D ．60匹 5．如图4所示，在□ABCD 中，已知AD=8㎝，AB=6㎝，DE 平分∠ADC ，交BC 边于点E ，则BE 等于（ ）A ．2㎝B ．4㎝C ．6㎝D ．8㎝6．已知四边形ABCD 是平行四边形，下列结论不一定正确的是 （ ）A ．AB=CDB ．AC=BDC ．当AC ⊥BD 时，它是菱形 D ．当∠ABC=900时，它是矩形7．下列命题错误的是 ( )A ．平行四边形的对角相等B ．等腰梯形的对角线相等C ．两条对角线相等的平行四边形是矩形D ．对角线互相垂直的四边形是菱形8．在矩形ABCD 中，AB=2AD ，E 是CD 上一点，且AE=AB 则∠CBE 的度数是（ ） A ．30° B ．22.5° C ．15° D ．以上都不对9．菱形的周长为20㎝，两邻角的角度之比为1：2，则较长的对角线的长为 （ ）A ．4.5㎝B ．4㎝C ．53㎝D ．43㎝10.顺次连接等腰梯形的四边中点，得到一个四边形，再顺次连接所得四边形四边的中点，得到的图形是（ ）A ．等腰梯形B ．直角梯形C ．菱形D ．矩形二、填空题11．顺次连接对角线相等的四边形的各边中点，所得的四边形是 .12．矩形的周长为48㎝，长比宽多2㎝，则矩形的面积为 2cm .13．若菱形的两条对角线长分别为16㎝和12㎝，则它的边长为 ㎝，面积为 2cm14．已知等边三角形ABE 在正方形ABCD 内，DE 的延长线交CB 于G ，则∠BEG ＝ . 15．如图5所示，在□ABCD 中，AC 与BD 交于点O ，点E 是BC 边的中点，OE =1，则AB 的长是 . 16．如图6所示，在□ABCD 中，AE ⊥BC 于点E ，AF ⊥CD 于点F ，∠ABC ＝750，则∠EAF= . 17．如图7所示，在等腰梯形ABCD 中，AD ∥BC ，∠B ＝600 ，AD ＝4，BC ＝7，则梯形ABCD 的周长是 .18．如图8所示，在□ABCD 中，BD 为对角线，E ，F 分别是AD ，BD 的中点，连接EF ，若EF =3，则CD 的长为 .19．若矩形的一条短边的长为5㎝，两条对角线 的夹角为60°，则它的一条较长的边为 ㎝. 20．如图19-143所示，折叠矩形纸片ABCD ，先折出折痕BD 再折叠，使AD 落在对角线BD 上，得折痕DG ，若AB =2，BC =1，则AG = .三、解答题21．如图所示，在□ABCD 中，点E 是AD 的中点，连接CE 并延长，交BA 的延长线于点F .求证FA ＝AB.图1 图2图3 图4 图5 图6 图7 图8 图922．如图所示，四边形ABCD 是正方形，点G 是BC 上的任意一点，DE ⊥AG 于点E ，BF ∥DE ，交AG 于点F ，求证AF ＝BF+EF.23．如图所示，□ABCD 的对角线AC ，BD 相交于点O ，EF ⊥BD 于点O ，分别交AD ，BC 于点E ，F ，且12AE EO BF ==.求证四边形ABCD 为矩形.24．在等腰梯形ABCD 中，已知AB ∥CD ，AD=BC ，AC 为对角线，且AC 平分∠DAB ，AC ⊥BC. （1）求梯形各内角的度数；（2）当梯形的周长为30时，求各边的长； （3）求梯形的面积.25．某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10m ，20m 的梯形空地上种植花木（如图（1）所示）.（1）他们在△AMD 和△BMC 地带上种植太阳花，单价为8元/㎡，当△AMD 地带种满花后（图形阴影部分），共花了160元.请计算种满△BMC 地带所需的费用；（2）若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/㎡和10元/㎡.应选择哪能种花木种植，可以刚好用完所筹集的资金？（3）若梯形ABCD 为等腰梯形，面积不变（如图（2）所示），请设计一种花坛图案，即在梯形内找一点P ，使△APB ≌△DPC 得，且S △APD =S △PBC ，并说出理由.26．如图所示，在梯形ABCD 中，AD ∥BC ，AB ∥DE ，AF ∥DC ，E ，F 两点在边BC 上，且四边形AEFD 是平行四边形.（1）AD 与BC 有何数量关系？请说明理由； （2）当AB =DC 时，求证四边形AEFD 是矩形.参考答案1．D ［提示：可以是正方形、菱形或等腰梯形.］2．B[提示：易证△BCE ≌△DCF ，∴CE CF =.∵,CE CF ⊥∴21502CE =，∴CE=10.在Rt △BEC 中，BC=8，∴22221086BE EC BC =-=-=，∴S △BCE =12×6×8=24.] 3．C[提示：过点A作AF ∥BD 交CD 的延长线于点F ，则四边形AFDB 是平行四边形，∴15,.AF BD DF AB ===易证S△ADF =S△ABC ，即S△APC =S梯形ABCD .∵222215129EF AF AE =-=-=,22EC AC AE =- 22201216=-=,∴91625,FC EF EC =+=+=∴S △F AC=11251215022FC AE •=⨯⨯=.] 4．C[提示：S 阴影= S 剩余.] 5．A[提示：在ABCD 中，AD ∥BC ，则ADE DEC ∠=∠.又∵ADE CDE ∠=∠，∴,CDE CED ∠=∠∴6EC DC AB ===㎝.又∵8BC AD ==㎝，∴BE BC EC =-=2㎝.]6． B[提示：平行四边形的对角线不一定相等.]7．D[提示：对角线互相垂直的四边形可以为任意四边形.] 8．C[提示：∵1,,2AD AB AB AE ==在Rt △ADE 中，1,2AD AE =∴30AED ∠=.∵AB ∥CD ，∴30EAB AED ∠=∠=.∵AB AE=，∴,ABE AEB ∠=∠∴180180307522EAB ABE -∠-∠===，∴90907515CBE ABE ∠=-∠=-=.]9．C[提示：∵两邻角之比为1：2，∴两邻角的度数分别为60°，120°.∴较短对角线长为5，较长对角线长为22525532⎛⎫⨯-= ⎪⎝⎭（㎝）.]10．D[提示：第一次连接得到的四边形是菱形，第二次连接得到的四边形是矩形.] 11．菱形12．143[提示：设两边长分别为,x y ，则2()48,2x y x y +=-=，∴13,11,x y =⎧⎨=⎩∴S矩形=13×11=143（2cm ）.]13．10 96[提示：边长2216121022⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭（㎝）.]14．45°[提示：AED ADE ∠=∠=75°，∴BEG ∠=180°-75°-60°=45°.] 15．2[提示：由题意知OE 是△ABC 的中位线，∴22AB OE ==.]16．75°[提示：∵ABC ∠=75°，∴C ∠=105°.在四边形AECF 中，EAF ∠=360°-90°-90°-105°=75°.]17．17[提示：如图19-149所示，过点D 作DE ∥AB 交BC 于点E ，则易证四边形ABED 是平行四边形，△CDE 是等边三角形，所以4,743,3BE AD CE BC BE AB CD CE ===-=-====.所以梯形ABCD 的周长为37AB BC CD AD +++=+3417++=，]18．6[提示：因为EF 为△ABD 的中位线，所以26AB EF ==.又因为四边形ABCD 是平行四边形，所以6DC AB ==.]19．53[提示：较长边长=2210553-=（㎝）.] 20．51-[提示：2222215BD AB AD =+=+=，设AG x =，点A 落在对角线BD 上的对应点为A '，则CA x '=，∴51A B BD A D ''=-=-.在Rt △BGA '中，222A G AB GB ''+=，解出方程即可.]21．证明：∵四边形ABCD 是平行四边形，∴,AB DC =AB ∥DC .∴.FAE D F ∠=∠∠ECD =∠.又∵,EA ED =∴△AFE ≌△DCE .∴FA DC =.∴FA AB =.22．证明：∵四边形ABCD 是正方形，∴,90AD AB BAD =∠=.∵,DE AG ⊥∴90DEG AED ∠=∠=，∴90ADE DAE ∠+∠=.又∵BAF DAE BAD ∠+∠=∠=90°，∴ADE BAF ∠=∠.∵BF ∥DE ，∴AFB DEG DEA ∠=∠=∠.在△ABF 与△DAE 中，,,.AFB DEA ADE BAF AD BA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△DAE （AAS ）.∴BF AE =.∵AF=AE+EF ，∴AF=BF+EF .23．证明：因为四边形ABCD 为平行四边形，所以,,AO OC DAC ACB =∠=∠AOE COF ∠=∠，所以△AOE ≌△COF .所以.AE CF =又因为,AD BC =所以BF DE =.因为12AE EO BF ==，所以1,2EO ED =又EF BD ⊥，所以EDO ∠=30°.所以60DEO ∠=.因为,AE OE =所以DAO EOA ∠=∠=30°，所以AO DO =，所以AC BD =，所以四边形ABCD 为矩形.24．解：（1）如图19-150所示，因为AC 平分DAB ∠，所以∠1=∠2.又因为DC ∥AB ，所以∠2=∠3.所以∠1=∠3.设∠1=a ，则∠2=a ，2CBA a ∠=.因为AC BC ⊥，所以90ACB ∠=.所以290B ∠+∠=，即290a a +=，所以a =30°，2a =60°.所以梯形ABCD 各内角的度数分别为120,D DCB ∠=∠=60DAB B ∠=∠=.（2）因为∠1=∠3，所以AD CD =.又因为∠2=30°，90ACB ∠=，所以2AB BC =.因为梯形ABCD 的周长为530AB BC CD DA AD +++==，所以6AD =.所以等腰梯形各边长分别为6,12AD DC BC AB ====. （3）过点C 作CE AB ⊥于点E ，则32AB CDBE -==，所以22226333CE BC BE =-=-=.所以S 梯形ABCD =11()(126)3327322AB CD CE +•=+⨯=.25．提示：（1）∵四边形ABCD 是梯形，∴AD ∥BC ，∴△AMD ~△CMB ，S △AMD ：S △BMC =2210:201:4=，故△BMC 地带花费为160÷8×4×8=640（元）.（2）S 梯形ABCD =180㎡，S △AMB + S △DMC =180-20-80=80（㎡），∴160+640+80×12=1760（元）， 160+640+80×10=1600（元），∴种植茉莉花刚好用完所筹集的资金. （3）由△APB ≌△DPC 可知点P 在AD ，BC 的中垂线上.设△APO 的高为x ，则S △APO =1102x ⨯，S △BPC 1202=⨯(12)x -，∴111020(12)22x x ⨯=⨯-，解得8x =，故当点P 为AD ，BC 的中垂线上且与AD 的距离为8m 时，S △APD = S △BPC . 26．（1）解：13AD BC =.理由如下：∵AD ∥BC ，AB ∥DE ，AF ∥DC ，∴四边形ABED 和四边形AFCD 都是平行四边形，∴,AD BE AD FC ==.又∵四边形AEFD 是平行四边形，∴AD EF =.∴AD BE EF FC ===.∴13AD BC =. （2）证明：∵四边形ABED 和四边形AFCD 都是平行四边形，∴,DE AB AF DC ==.∵,AB DC =∴DE AF =.又∵四边形AEFD 是平行四边形，∴四边形AEFD 是矩形.。

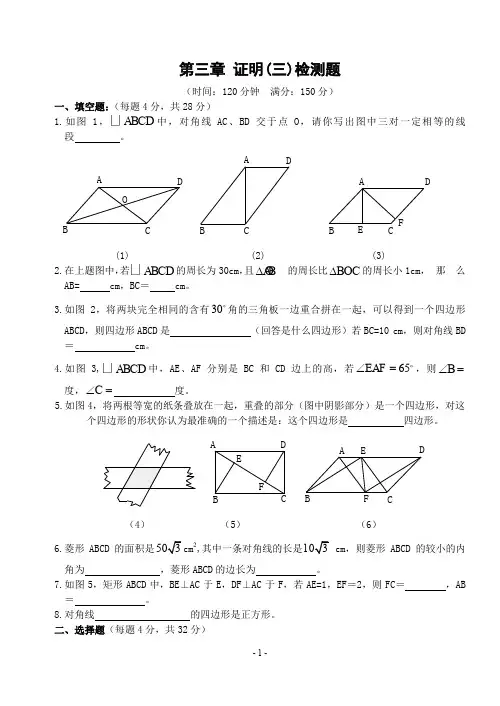
第三章 证明(三)检测题（时间：120分钟 满分：150分）一、填空题：（每题4分，共28分）1.如图1，ABCD 中，对角线AC 、BD 交于点O ，请你写出图中三对一定相等的线 段 。

ODCBADC B A FE DCBA(1) (2) (3) 2.在上题图中，若ABCD 的周长为30cm ，且A O B ∆的周长比BOC ∆的周长小1cm ， 那 么AB= cm ，BC ＝ cm 。

3.如图2，将两块完全相同的含有30角的三角板一边重合拼在一起，可以得到一个四边形ABCD ，则四边形ABCD 是 （回答是什么四边形）若BC=10 cm ，则对角线BD ＝ cm 。

4.如图3,ABCD 中，AE 、AF 分别是BC 和CD 边上的高，若65EAF ∠=，则B ∠=度，C ∠= 度。

5.如图4，将两根等宽的纸条叠放在一起，重叠的部分（图中阴影部分）是一个四边形，对这个四边形的形状你认为最准确的一个描述是：这个四边形是 四边形。

FEDC BAF EDCB A（4） （5） （6）6.菱形ABCD的面积是2,其中一条对角线的长是，则菱形ABCD 的较小的内 角为 ，菱形ABCD 的边长为 。

7.如图5，矩形ABCD 中，BE ⊥AC 于E ，DF ⊥AC 于F ，若AE=1，EF ＝2，则FC ＝ ，AB ＝ 。

8.对角线 的四边形是正方形。

二、选择题（每题4分，共32分）1.如图6，ABCD 中，AE=CF ，则图中的平行四边形的个数是（ ）个 A.2 B.3 C.4 D.52.若第1题的条件中，除原有条件外，再增加FA ＝FD ，则图中的等腰梯形个数是（ ）个 A.2 B.3 C.4 D.53.下列关于平行四边形的判定中正确的是（ ）A.一组对边相等，另一组对边平行的四边形是平行四边形B.一组对边相等，一组对角相等的四边形是平行四边形C.一组对边平行，一组对角相等的四边形是平行四边形D.一组对边平行，一组邻角互补的四边形是平行四边形4.顺次连接对角线互相垂直且相等的四边形各边中点，得到一个四边形，对这个四边形的形状 描述最准确的是（ ）A.平行四边形B.矩形C.菱形D.正方形5.已知菱形ABCD 的面积为96cm 2，对角线AC 的长为16 cm ，则此菱形的边长为（ ）cmA.6.正方形具有而菱形不一定具有的性质是（ ）A. 对角线互相平分B.对角线互相垂直C.对角线相等D. 每一条对角线平分一组对角 7.只用一把刻度尺检查一张四边形纸片是否是矩形，下列操作中最为恰当的是（ ） A.先测量两对角线是否互相平分，再测量对角线是否相等 B. 先测量两对角线是否互相平分，再测量是否有一个直角C. 先测量两组对边是否相等，再测量对角线是否相等D. 先测量两组对边是否互相平行，再测量对角线是否相等 8.如图，梯形ABCD 中，AD ∥BC ，90B C ∠+∠=,E 、F 分别是AD 、BC 的中点，若AD=5cm ，BC=13cm ，那么EF=（ ）cm A.4 B.5 C.6.5 D.9 三、解答题（每小题15分，共90分） 1.（7分）按要求填图下面图中，表达了四边形、平行四边形、矩形、菱形、正方形之间的关系。

第三章 证明（三）单元测试一、填空题（每小题3分，共30分） 1.如图3-29所示，若AC 、BD 、EF 两两互相平分于点O ，则图中共有平行四边形 个； 2.四边形两条对角线互相垂直，顺次连接它的各边中点所成的四边形是 ；3.如图3-30，BD 是 ABCD 的对角线，点E 、F 在BD 上，要使四边形AECF 是平行四边形，还需要增加的一个条件是 （填上你认为正确的一个即可，不必考虑所有可能情形）；4.如图3-31，已知O 是 的对角线交点，AC = 38cm, BD = 24cm, AD = 14cm, 那么△BOC 的周长等于 cm ；5.已知：如图3-32，矩形ABCD 中，对角线AC 、BD 相交于点O ，AC = 10cm ，∠ACB = 30°, 则∠AOB = °，AD = cm ；6.请补充一个条件，使菱形“变成”正方形 ；7.如图3-33，在矩形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，若AB ︰BC = 3︰4, 四边形EFGH 的周长为40cm, 则矩形ABCD 的面积为 ；8.若要使一个平行四边形成为正方形，则需增加的条件是 ； 9.如图3-33，在菱形ABCD 中，∠ABC = 60°，AC = 4，BD 的长为 ；10.如图3-34，E 是边长为1厘米的正方形ABCD 的对角线BD 上一点，且BE = BC . P 为CE 上任意一点，PQ ⊥BC 于点Q ，PR ⊥BE 于点R ，则PQ +PR 的长等于 厘米. 二、选择题（每小题3分，共18分） 11.如图3-35，已知：四边形ABCD 是平行四边形，下列结论中，不一定正确的是（ ）； A. AB = CD B. AC = BDC. 当AC ⊥BD 时，它是菱形D. 当∠ABC = 90°时，它是矩形 12.不能判定四边形ABCD 是平行四边形的题设是（ )；A. AB = CD ，AD = BCB. AB ∥＝ CDC. AB = CD ，AD ∥BCD. AB ∥CD ，AD ∥BC13.如图3-36，顺次连接四边形ABCD 各边的中点，得到四边形EFGH ，在下列条件中，能使四边形EFGH 为矩形的是（ ）；A. AB = CDB. AC = BDC. AC ⊥BDD. AD ∥BC E A B C D图3-29F O F A B C D 图3-30E A BCD 图3-31O 图3-32O B A C D 图3-33D CB A R图3-34ED C B A Q P FG图3-36HE D CBAA BC D 图3-3514.下列条件中，必能判定四边形ABCD 是等腰 梯形的是（ ）；① AD ∥BC ，AD ≠BC ，AB = CD ； ② AD ∥BC ，AD ≠BC ，AC ⊥BD ； ③ AD ∥BC ，AD ≠BC ，AC = BD ；④ ∠A ︰∠B ︰∠C ︰∠D = 1︰2︰3︰4.A. ①②B. ①③C. ②④D. ③④ 15.下列命题中，真命题是（ ）；A.有两边相等的平行四边形是菱形B.有一个角是直角的四边形是矩形C.四个角相等的菱形是正方形D.对角线互相垂直且相等的四边形是正方形16.用长分别为1，4，4，5的四条线段为边作梯形，可作出形状不同的梯形的个数是（ ）.A. 1B. 2C. 3D. 4 三、解答题（第17、18、19、20题各6分，第21题8分，共32分） 17.如图3-37，在梯形ABCD 中，AD ∥BC ，延长CB 到E ，使EB = AD ，连接AE ，若AE = AC . 求证：梯形ABCD 是等腰梯形 .18.如图3-38，在ABCD 中，点E 、F 在对角线AC 上，且AE = CF . 请你以F 为一个端点，和图中已表明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只需证明一组线段相等即可）. （1）连接： .（2）猜想： = .（3）证明： 图3-38A B C D E 图3-3719.如图3-39，将矩形纸片ABCD 对折，设折痕为MN ，再把顶点B 叠在折痕MN 上（图中点B'），已知AB = 3cm ，求折痕AE 的长.20.已知：如图3-40，在梯形ABCD 中，AB ∥CD ，BC = CD ，AD ⊥BD ，E 是AB 的中点. 求证：四边形BCDE 是菱形.21.如图3-41，在Rt △ABC 中，∠A = 90°，AB = AC ，D 是斜边BC 上的一点，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F .（1）求证：四边形AEDF 是矩形；（2）试问：当点D 位于BC 边的什么位置时，四边形AEDF 是正方形？并证明你的结论.测试与评价一、1. 3； 2. 矩形； 3. BF = DE （或AF ∥CE 等）；4. 45； 5. 60°，53； 6. 对角线相等（或有一个角是直角）；7. 192cm 2； 8. 对角线互相垂直且相等（或有一个角是直角且一组邻边相等）； 9. 43； 10. 22. 二、11. B ； 12. C ； 13. C ； 14. B ； 15. C ； 16. B.三、17.略； 18. 略；19. 2cm ； 20. 提示：证△BCD ≌△DEB ； 21.（1）略；（2）D 是BC 的中点.N M B'图3-39EDC B A图3-40E D C BA 图3-41F ED CBA。