苏教版 六年级上册长方体和正方体表面积_题型归纳
- 格式:docx
- 大小:20.28 KB
- 文档页数:2
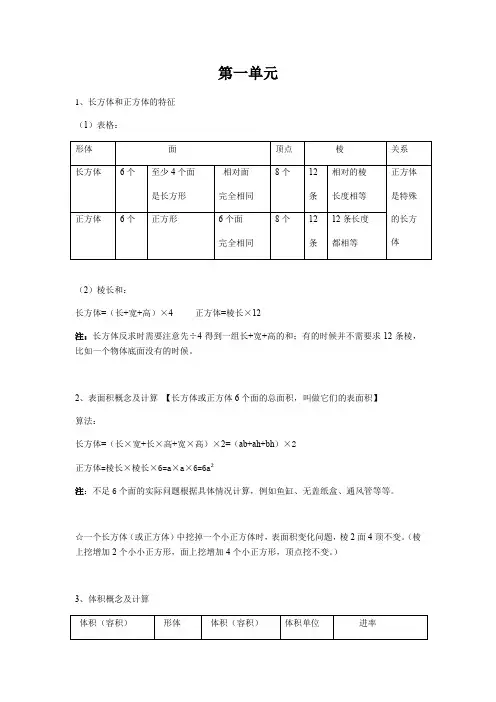
第一单元1、长方体和正方体的特征(1)表格:(2)棱长和:长方体=(长+宽+高)×4 正方体=棱长×12注:长方体反求时需要注意先÷4得到一组长+宽+高的和;有的时候并不需要求12条棱,比如一个物体底面没有的时候。
2、表面积概念及计算【长方体或正方体6个面的总面积,叫做它们的表面积】算法:长方体=(长×宽+长×高+宽×高)×2=(ab+ah+bh)×2正方体=棱长×棱长×6=a×a×6=6a²注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒、通风管等等。
☆一个长方体(或正方体)中挖掉一个小正方体时,表面积变化问题,棱2面4顶不变。
(棱上挖增加2个小小正方形,面上挖增加4个小正方形,顶点挖不变。
)3、体积概念及计算注:长方体(或正方体)的体积=底面积×高=横截面×长4、正方体的棱长扩大n倍,棱长总和扩大n倍,表面积会扩大n²倍,体积会扩大n³倍。
5、正方体涂色问题1面涂色=6(n-2)22面涂色=12(n-2)3面涂色=8 0面涂色=(n-2)3错题整理1、一个长方体长宽高分别是5cm4cm3cm。
一个正方体的棱长总和与该长方体棱长总和相等。
这个正方体的棱长是多少厘米?2、把110cm长的铁丝焊成一个长方体框架。
长是宽的2倍,宽是高的1.5倍,求长方体的长宽高。
3、一个长方体绫长和是72cm,她的长是9cm,宽是6cm,它的表面积是多少平方厘米?4、一个正方体的表面积是30平方厘米,把它锯成大小一样的两个长方体木木块。
每个长方体的表面积是多少?5、一个长方体长宽高分别是11cm、6cm、5cm,如果高增加3cm,那么表面积增加多少平方厘米?6、中学建一个长方体游泳池。
长60米,宽25米,深2米,在游泳池的内壁1.5米高处用白漆画一条水位线,水位线全长多少米?7、一间教室长8米,宽7米,高3.5米。
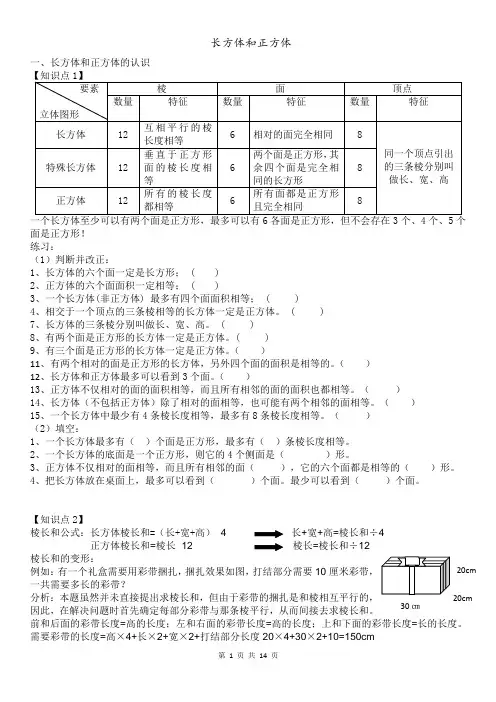
长方体和正方体一、长方体和正方体的认识面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( )13、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( )14、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )15、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
前和后面的彩带长度=高的长度;左和右面的彩带长度=高的长度;上和下面的彩带长度=长的长度。
需要彩带的长度=高×4+长×2+宽×2+打结部分长度20×4+30×2+10=150cm练习:(1)有一个长方体的鱼缸,长50厘米,宽30厘米,高30厘米,需要在用铝合金包裹玻璃连接处,需要( )米的铝合金。
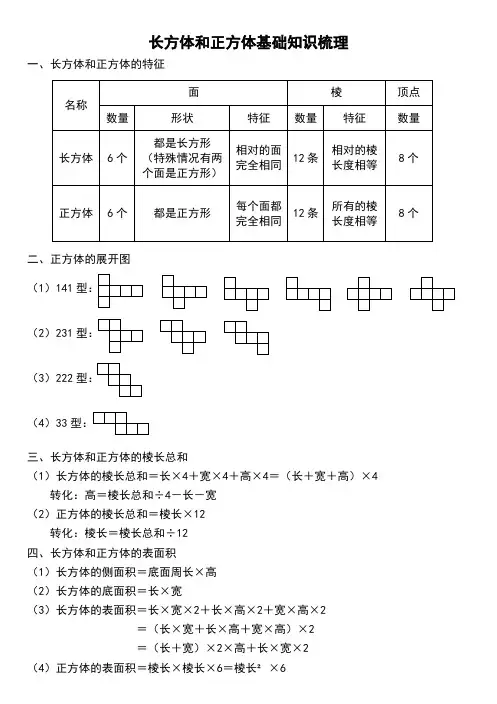
长方体和正方体基础知识梳理一、长方体和正方体的特征二、正方体的展开图(1)141型:(2)231型:(3)222型:(4)33型:三、长方体和正方体的棱长总和(1)长方体的棱长总和=长×4+宽×4+高×4=(长+宽+高)×4 转化:高=棱长总和÷4-长-宽(2)正方体的棱长总和=棱长×12转化:棱长=棱长总和÷12四、长方体和正方体的表面积(1)长方体的侧面积=底面周长×高(2)长方体的底面积=长×宽(3)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2=(长+宽)×2×高+长×宽×2(4)正方体的表面积=棱长×棱长×6=棱长²×6五、长方体和正方体的体积(1)长方体的体积=长×宽×高(2)正方体的体积=棱长×棱长×棱长=棱长³(3)长方体(正方体)的体积=底面积×高(4)体积单位: 1m³=1000dm³ 1dm³=1000cm³ 1m³=1000000cm ³1L=1dm³ 1mL=1cm³六、物体浸没问题(1)完全浸没①物体的体积=容器底面积×水面上升(下降)的高度②水面上升(下降)的高度=物体的体积÷容器底面积③容器底面积=物体的体积÷水面上升(下降)的高度④水面现在的高度=水面原来的高度+水面上升的高度=水面原来的高度-水面下降的高度(2)不完全浸没①水的体积=容器底面积×水面原来的高度②水面现在的高度=水的体积÷(容器底面积-物体底面积)③水面上升的高度=水面现在的高度-水面原来的高度④水的体积=(容器底面积-物体底面积)×水面现在的高度七、表面涂色的正方体一个表面涂色的大正方体,棱长被平均分成n份,变成了若干个小正方体,那么:小正方体的个数:n³3面涂色的个数:82面涂色的个数:12(n-2)1面涂色的个数:6(n-2)²没有涂色的个数:(n-2)³八、表面涂色的长方体一个表面涂色的长方体,长、宽、高分别被平均分成a、b、h份,变成了若干个小正方体,那么:小正方体的个数:a×b×h3面涂色的个数:82面涂色的个数:4(a-2)+4(b-2)+4(h-2)1面涂色的个数:2(a-2)(b-2)+2(a-2)(h-2)+2(b-2)(h-2)没有涂色的个数:(a-2)(b-2)(h-2)。

11、一个正方体木块,若把它切成3个完全相等的长方体后,表面积增加了80平方厘米,这个正方本木块原来的表面积是多少平方厘米?
12、有一个长方体木箱,长0.7米,宽0.5米,高0.3米。
怎样放,这个木箱占地面积最小?最小是多少平方米?
13、有一个长方体的糖盒长和宽都是12厘米,高10厘米,在盒的四周贴上商标纸,这张商标纸的面积至少是多少?
14、李老师在商场买了一盒礼品,礼品盒是一个长10厘米,宽15厘米,高8厘米的长方体。
售货员为他用彩带把礼品盒扎起来(扎法如下图,打结处彩带长2厘米)。
求彩带的长度。

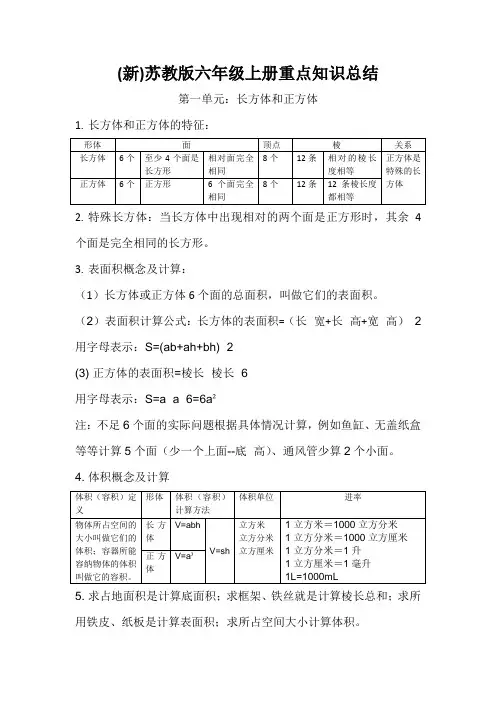
(新)苏教版六年级上册重点知识总结第一单元:长方体和正方体1.长方体和正方体的特征:2.特殊长方体:当长方体中出现相对的两个面是正方形时,其余4个面是完全相同的长方形。
3.表面积概念及计算:(1)长方体或正方体6个面的总面积,叫做它们的表面积。
(2)表面积计算公式:长方体的表面积=(长×宽+长×高+宽×高)×2 用字母表示:S=(ab+ah+bh)×2(3) 正方体的表面积=棱长×棱长×6用字母表示:S=a×a×6=6a²注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等计算5个面(少一个上面--底×高)、通风管少算2个小面。
4. 体积概念及计算5. 求占地面积是计算底面积;求框架、铁丝就是计算棱长总和;求所用铁皮、纸板是计算表面积;求所占空间大小计算体积。
6. 长方体内放正方体或长方体切正方体:(长÷棱长)×(宽÷棱长)×(高÷棱长)=个数(商取整数)7. 长方体的长、宽、高同时扩大n倍,表面积扩大n²倍,体积扩大n³倍。
8. 正方体的棱长扩大n倍,表面积扩大n²倍,体积扩大n³倍。
9. 正方体表面涂色后切成小正方体,每条棱分n份。
三面涂色:数顶点(8个)两面涂色:数棱(n-2)×12一面涂色:数面(n-2)²×610. 长方体上放小正方体(或长方体)(1)表面积=下图表面积+上图四周的面积(2)体积=下图体积+上图体积11. 拼大正方体至少需要8块小正方体。
12. 长方体中最多有2个正方形;最多有4个面完全相同;最多有8条棱长度相等。
最少有2个面完全相同;最少有4条棱长度相等。
13. 长方体中出现相邻的两个面是正方形时是正方体。
14. 扎彩带数长、宽、高各有几条,再计算总和。


苏教版六年级数学(上)长方体正方形经典题型汇总本文档为苏教版六年级数学(上)长方体正方形经典题型的汇总,旨在帮助学生复和掌握相关知识点。
以下是一些常见的题型及其解答。
题型一:长方体的面积计算题目描述:长方体的长、宽、高分别为6cm、4cm、3cm,求其表面积和体积。
解答:长方体的表面积可以通过计算所有面的面积之和来得到。
根据长方体的性质,它的表面包括六个面,分别是底面、顶面、前面、后面、左面和右面。
表面积的计算公式为:$2lw + 2lh + 2wh$,其中$l$为长,$w$为宽,$h$为高。
代入题目给出的数值,可得:表面积 = $2 \times 6 \times 4 + 2 \times 6 \times 3 + 2 \times 4 \times 3 = 72 + 36 + 24 = 132$ 平方厘米长方体的体积计算公式为:$l \times w \times h$。
代入题目给出的数值,可得:体积 = $6 \times 4 \times 3 = 72$ 立方厘米所以,该长方体的表面积为132平方厘米,体积为72立方厘米。
题型二:正方形的周长计算题目描述:求边长为8cm的正方形的周长。
解答:正方形的周长可以通过将所有边的长度相加来得到。
正方形的特点是四条边的长度都相等,所以可以使用以下计算公式得到周长:$4 \times a$,其中$a$为正方形的边长。
代入题目给出的数值,可得:周长 = $4 \times 8 = 32$ 厘米所以,边长为8cm的正方形的周长为32厘米。
题型三:正方形的面积计算题目描述:求边长为5cm的正方形的面积。
解答:正方形的面积可以通过边长的平方来计算。
正方形的特点是四条边的长度都相等,所以可以使用以下计算公式得到面积:$a \times a$,其中$a$为正方形的边长。
代入题目给出的数值,可得:面积 = $5 \times 5 = 25$ 平方厘米所以,边长为5cm的正方形的面积为25平方厘米。

第一单元《长方体和正方体》长方体和正方体的认识(第1页〜5页)1.长方形、正方形、三角形、平行四边形、梯形等是平面图形,只有一个面。
长方体、正方体与平面图形不同,它们占有一定的空间,都是立体图形。
2.把长方体放在桌上,无论从哪个角度观察,最多只能同时看到长方体的三个面。
两个面相交的线叫作棱,三条棱相交的点叫作顶点。
3.长方体的特征:(1)面——有6 个面,都是长方形(特殊情况下有2个相对的面是正方形),相对的面完全相同;(2)棱——有12条棱,分为3组,每组的4条棱长度相等;(3)顶点——有8个。
4.长方体相交于同一顶点的三条棱的长度,分别叫作它的长、宽、高。
长方体有4条长,4条宽,4条高。
5.长方体12条棱的长度和,叫作长方体的棱长总和。
长方体的棱长总和=长×4 + 宽×4 + 高×4,或者长方体的棱长总和=(长+ 宽+ 高)×46.正方体的特征:(1)面——6个面是完全相同的正方形;(2)棱——有12条棱,长度都相等;(3)顶点——有8个。
7.正方体的长、宽、高都相等,都叫作正方体的棱长。
正方体具有长方体的一切特征,正方体是特殊的长方体。
8.正方体12条棱的长度和,叫作正方体的棱长总和。
正方体的棱长总和=棱长×12。
9.正方体的展开图:6个面完全相同,相对的面完全隔开。
10.长方体的展开图:有3组相对的面;相对的面完全相同;相对的面完全隔开。
11.沿着不同的棱剪开正方体或长方体,得到的展开图是不一样的。
长方体和正方体的表面积(第6页~9页)1.物体表面的总面积叫作物体的表面积。
长方体6个面的总面积叫作长方体的表面积。
正方体6个面的总面积叫作正方体的表面积。
2.长方体的表面积=长×宽×2+长×高×2+宽×高×2或=(长×宽+长×高+宽×高)×23.如果用S表示长方体的表面积,用α,b,h分别表示长方体的长、宽、高,那么长方体表面积的计算公式可表示为:S=α×b×2+α×h×2+b×h×2 或S=(α×b+α×h +b×h)×24.正方体的表面积=棱长×棱长×6,如果用S表示正方体的表面积,用α表示长方体的棱长,那么正方体表面积的计算公式可表示为:S=α×α×6 或S=6α2体积(容积)和体积(容积)单位(第10~15页)1.任何物体都占有一定的空间。

第一单元长方体和正方体1.长方体是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
它有6个面、12条棱和8个顶点;在一个长方体中,相对的面完全相同,相对的棱长度相等。
2.把长方体放在桌面上,无论从哪个角度观察,最多只能同时观察到三个面。
3.正方体,有6个完全相同的正方形,12条棱的长度都相等和8个顶点。
正方体是特殊的长方体。
4.长方体6个面的总面积,叫做它的表面积5.长方体的表面积=长×宽×2+长×高×2+高×宽×2=(长×宽+长×高+高×宽)×26.计算公式为S=(ab+ah+bh)×27.正方体的表面积= 6×棱长×棱长计算公式为S=6×a×a(或6×a2)8.体积的意义:物体所占空间的大小叫做物体的体积。
物体大的,占据的空间大,体积就大;物体小的,占据的空间就小,体积就小。
9.容器所能容纳物体的体积,叫做这个容器的容积。
10.常用的体积单位有:立方厘米、立方分米、立方米11.计量液体的体积,常用升和毫升12.1立方分米=1升1立方厘米=1毫升13.长方体的体积=长×宽×高,公式为:V=abh14.正方体的体积=棱长×棱长×棱长,公式为:V=a×a×a(a3)15.长方体或正方体的体积=底面积×高,公式为:V=Sh16.相邻体积单位间的进率是1000.17.1立方米=1000立方分米;18.1立方分米=1000立方厘米(1升=1000毫升)19.把棱长为几厘米的小正方体涂色后切成棱长为1厘米的小正方体,涂色面的规律:●3面涂色的小正方体个数=正方体的顶点个数=8个●2面涂色的小正方体个数=正方体棱的条数乘棱长减2的差=12×(n-2)●1面涂色的小正方体个数=正方体的面数乘棱长减2的差的平方=6×(n-2)2第二单元分数乘法1.分数乘整数的计算方法,先用分数的分子和整数相乘的积作分子,分母不变,再约分;也可以先约分,再计算。

第一单元《长方体和正方体》知识点长方体和正方体的表面积:概念:长方体或正方体6个面的总面积,叫做它们的表面积计算公式:长方体表面积=(长×宽+长×高+宽×高)×2正方体表面积=棱长×棱长×6注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等.体积(容积)单位进率换算:1立方米=1000立方分米 1立方分米=1000立方厘米1m³=1000dm³ 1dm³=1000cm³1升=1000毫升 1立方分米=1升 1立方厘米=1毫升1L=1000mL 1dm³=1L 1cm³=1mL长方体和正方体的体积(容积):概念:物体所占空间的大小叫做它们的体积(容器所能容纳其它物体的体积叫做它的容积).计算公式:长方体体积公式=长×宽×高正方体体积公式=棱长×棱长×棱长长方体和正方体的体积=底面积×高苏教版六年级上册第一单元同步练习及答案一、填空题.1.正方体是( )都相等的长方体,如果用V表示体积,用a表示正方体的棱长,那么V=( ).2.一个长方体,长4分米,宽3分米,高2分米,它的棱长总和是( )分米,它最大的一个面的面积是( )平方分米,表面积是( )平方分米,体积是( )立方分米.3.一个正方体的棱长是2米,它的占地面积是( )平方米,表面积是( )平方米,体积是( )立方米.4.一个正方体的棱长如果扩大到原来的2倍,那么表面积扩大到原来的( )倍,体积扩大到原来的( )倍.5.每瓶医用酒精500毫升,装120瓶需要酒精( )升,如果有3.5立方分米的酒精,可装( )瓶.二、判断题.(对的画“√”,错的画“✕”)1.正方体是特殊的长方体.( )2.体积单位之间的进率是1000.( )3.长方体的6个面不可能有正方形.( )4.瓶子里装了500毫升的水,瓶子的容积是500毫升.( )5.体积单位比面积单位大.( )6.一个正方体的棱长扩大到原来的2倍,它的体积也要扩大到原来的2倍.( )三、选择题.(把正确答案的序号填在括号里)1.一个电饭锅能盛水3( ).A.升B.毫升C.立方米2.把一个长方体放在桌面上,最多可以看到( )个面.A.2B.3C.43.求做一只油桶需要多少铁皮是求( ).A.表面积B.体积C.容积4.把三个棱长是1厘米的正方体拼成一个长方体,这个长方体的表面积比原来3个正方体表面积之和减少了( )平方厘米.A.2B.3C.45.把一个棱长为3厘米的正方体锯成棱长是1厘米的小正方体,可锯成( )个.A.6B.9C.27四、在括号里填上适当的数.1500立方厘米=( )立方分米5立方米=( )立方分米3.5升=( )毫升420立方分米=( )立方米3.5升=( )立方分米=( )毫升五、在括号里填上合适的单位.1.一节火车车厢的容积大约是90( ).2.一台冰箱的体积大约是0.32( ).3.课桌桌面的面积是40( ).4.一瓶胶水310( ).5.一块砖头的体积是1.5( ).六、按要求计算.1.计算下面长方体和正方体的表面积和体积.2.下图是一个长方体的展开图,求围成的长方体的体积.七、解决问题.1.一个正方体的铁皮油箱,棱长是6分米,这个油箱可以盛油多少升?做这个油箱要用多少铁皮?2.一根长方体木料,长2.5米,横截面是一个边长2分米的正方形.这根木料的体积是多少立方米?3.一个通风管的横截面是边长0.4米的正方形,长2.5米.如果用铁皮做这样的通风管20个,需要多少平方米的铁皮?4.用三个棱长为5厘米的正方体拼成一个长方体,这个长方体的表面积是多少平方厘米?5.一间教室的长是8米,宽是6米,高是4米,要粉刷教室的四壁和顶面,除去门窗和黑板面积24平方米,粉刷的面积是多少平方米?6.把一个棱长10厘米的正方体铁块放入一个长50厘米、宽40厘米、高30厘米的玻璃缸中,原来缸中水深20厘米,现在水面升高几厘米?八、动脑筋,做一做.一个长方体的盒子,宽增加3厘米就变成一个正方体,这时表面积增加144平方厘米.这个长方体盒子的体积是多少?参考答案:一、1.长、宽、高 a3 2.36 12 52 24 3.4 24 84.4 85.60 7二、1.√ 2.✕ 3.✕ 4.✕ 5.✕ 6.✕三、1.A 2.B 3.A 4.C 5.C四、1.5 5000 3500 0.42 3.5 3500五、1.立方米 2.立方米 3.平方分米 4.毫升5.立方分米六、1.8100平方厘米 45000立方厘米 29.04平方分米10.648立方分米2. 80立方厘米七、1.6×6×6=216(立方分米) 216立方分米=216升6×6×6=216(平方分米)2.2分米=0.2米 2.5×0.2×0.2=0.1(立方米)3.0.4×2.5×4×20=80(平方米)4.5×3=15(厘米)(15×5+15×5+5×5)×2=350(平方厘米)5.8×6+(8×4+6×4)×2-24=136(平方米)6.10×10×10÷(50×40)=0.5(厘米)八、144÷4÷3=12(厘米) 12-3=9(厘米)12×12×9=1296(立方厘米)。
长方体和正方体基础知识梳理一、长方体和正方体的特征二、正方体的展开图(1)141型:(2)231型:(3)222型:(4)33型:三、长方体和正方体的棱长总和(1)长方体的棱长总和=长×4+宽×4+高×4=(长+宽+高)×4 转化:高=棱长总和÷4-长-宽(2)正方体的棱长总和=棱长×12转化:棱长=棱长总和÷12四、长方体和正方体的表面积(1)长方体的侧面积=底面周长×高(2)长方体的底面积=长×宽(3)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2=(长+宽)×2×高+长×宽×2(4)正方体的表面积=棱长×棱长×6=棱长²×6五、长方体和正方体的体积(1)长方体的体积=长×宽×高(2)正方体的体积=棱长×棱长×棱长=棱长³(3)长方体(正方体)的体积=底面积×高(4)体积单位: 1m³=1000dm³ 1dm³=1000cm³ 1m³=1000000cm ³1L=1dm³ 1mL=1cm³六、物体浸没问题(1)完全浸没①物体的体积=容器底面积×水面上升(下降)的高度②水面上升(下降)的高度=物体的体积÷容器底面积③容器底面积=物体的体积÷水面上升(下降)的高度④水面现在的高度=水面原来的高度+水面上升的高度=水面原来的高度-水面下降的高度(2)不完全浸没①水的体积=容器底面积×水面原来的高度②水面现在的高度=水的体积÷(容器底面积-物体底面积)③水面上升的高度=水面现在的高度-水面原来的高度④水的体积=(容器底面积-物体底面积)×水面现在的高度七、表面涂色的正方体一个表面涂色的大正方体,棱长被平均分成n份,变成了若干个小正方体,那么:小正方体的个数:n³3面涂色的个数:82面涂色的个数:12(n-2)1面涂色的个数:6(n-2)²没有涂色的个数:(n-2)³八、表面涂色的长方体一个表面涂色的长方体,长、宽、高分别被平均分成a、b、h份,变成了若干个小正方体,那么:小正方体的个数:a×b×h3面涂色的个数:82面涂色的个数:4(a-2)+4(b-2)+4(h-2)1面涂色的个数:2(a-2)(b-2)+2(a-2)(h-2)+2(b-2)(h-2)没有涂色的个数:(a-2)(b-2)(h-2)。
苏教版六年级上册数学第三单元长方体与正方体易错题型总结长方体和正方体相关知识点分类复习:1.一个无盖的长方体金鱼缸,长8分米,宽6分米,高7分米。
用后3厘米的玻璃制作这个金鱼缸,一共需要玻璃多少平方分米?这个鱼缸能装多少升水?思路:第一问即是求该长方体的表面积(除去上表面):8*6+(8*7+6*7)*2=244平方分米能装多少水即是求鱼缸体积,这里我们需要考虑玻璃的厚度,分别算出长宽高:3厘米=0.3分米长=8-0.3*2=7.4 宽=6-0.3*2=5.4高=7-0.3=6.7(此处因为上面没有盖子,只需减去底部玻璃的厚度)体积=7.4*5.4*6.7=267.732立方分米=267.732升2.有一个底面积是300平方厘米,高10厘米的长方体,里面盛有5厘米深的水。
现在把一块石头浸没到水里,水面上升2厘米。
这块石头的体积是多少?思路:像这类往水里扔东西或从水里捞出东西,然后看水深变化的问题都是要算这个物体的体积。
题中告诉我们长方体的底面积为300平方厘米,石头放入后水面上升2厘米,其实石头的体积就等于一个底面积为300平方厘米,高2厘米的长方体的体积于是:300*2=6003.一个长方体通风管长2米,侧面是边长为5分米的正方形,做10个这样的通风管需要铁皮多少平方分米?思路:这类通风管道或者在饼干盒四周贴广告纸的问题,实际都是让我们四个侧面积之和。
本题首先注意单位的统一:2米=20分米告诉我们侧面是正方形,实际就是告诉我们宽和高相等,都是5分米。
那么一个侧面面积就为:20*5=100平方分米需要铁皮:100*4*10=4000平方分米4.将一个长8分米,宽6分米,高4分米的长方体木料平均截成两段,表面积增加了多少平方分米?最大增加多少?最小增加多少?思路:首先我们把原长方体或正方体截开表面积会增加,那增加的是多少呢?增加的是两个面的截面积,一定是两个哦(可以那块豆腐在家里多练习,一刀切下去,总会露出两块崭新的面)那么本题没有告诉我们到底怎么切,所以我们有三种方法,就是分别以长宽高的中点截开木料以长的中点切开,增加的是两个左侧面的面积:4*6*2=48平方分米以宽的中点切开,增加的是两个前面的面积:8*4*2=64平方分米以高的中点切开,增加的是两个上面的面积:8*6*2=96平方分米思考:要是讲两个正方体或长方体拼接,表面积变化有什么规律呢?5.一根铁丝,可以做成长8厘米,宽6厘米,高4厘米的长方体框架。
教学内容长方体和正方体题型归类讲解教学目标掌握长方体和正方体各类题型重点长方体和正方体的表面积和体积难点长方体和正方体的表面积和体积教学准备纸、笔教学过程课堂精讲知识梳理:一、长方体和正方体的初步认识知识点1.两个面相交的线叫做棱,三条棱相交的点叫做顶点。
知识点2.形体相同点不同点关系面棱顶点面的形状面的大小棱长长方体 6 12 8一般都是长方形,有时也有两个相对的面是正方形。
相对的面的面积相等平行的四条棱长度相等正方体是特殊的长方体正方体 6 12 8六个面都是正方形六个面的面积相等六条棱长都相等长方体相交于同一顶点的三条棱的长度,分别叫做它的长、宽、高。
长方体的12条棱有3组,每组的四条棱长度相等。
长方体的棱长总和=长×4+宽×4+高×4=(长+宽+高)×4长方体放桌面上,最多只能看到3个面。
例1、礼物包扎(1).如图,用丝带捆扎一种礼品盒,结头处长25cm,要捆扎这种礼品盒,准备()分米的丝带比较合理.例5.把一根长6分米的铁丝,做成一个长6厘米,宽5厘米,高2厘米的长方体后,还剩()厘米。
例6.一个正方体的表面积是384平方厘米,它的棱长是多少?知识点3.正方体的展开(不能出现田字格)1).“141型”,中间一行4个图:作侧面,上下两个各作为上下底面,•共有6种基本图形。
2).“231型”,中间3个作侧面,共3种基本图形。
见下图3).“222”型,两行只能有1个正方形相连。
4).“33”型,两行只能有1个正方形相连。
141型231型222型33型例1.如图:将如图纸片折起来可以做成一个正方体.这个正方体的3号面的对面是()号面.A.2 B.3 C.4 D.1例2.下列图形都是由相同的小正方形组成,哪一个图形不能折成正方体?()A.B. C.例3.如图,有一个无盖的正方体纸盒,下底标有字母“M”,将其剪开展成平面图形,想一想,这个平面图形是()A.B.C.D.例4、如图,是一个正方体展开图,当把它重新折叠成一个正方体时,1与()重合。
苏教版数学六年级上册知识点第一单元:长方体和正方体1、长方体和正方体的特征发现:相对的2个面在展开图中不能相邻。
正方体展开图:(11种)6种:中间四个一连串,两边各一随便放。
简称“一四一”型3种:二三紧连错一个,三一相连一随便,简称“二三一”型1种:两两相连各错一,简称“二二二”型1种:三个两排一对齐简称“三三”型要求:理解并掌握这些情况,能找准哪2个面是相对的面。
3、表面积概念及计算s=(ab+ah+bh)×2=2ab+2ah+2bh正方体表面积= 棱长×棱长×6s= 6×a×a=6a2注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
4、体积概念及计算5、相关例题:(1)已知长方体a=20cm,b=5cm,h=6cm,求体积。
V=abh=20×5×6=600(cm3)(2) 已知长方体S底=100cm2,h=6cm,求体积。
V=S底×h=100×6=600(cm3)(3) 已知长方体S侧=30cm2,a=20cm,求体积。
V=S侧×长=30×20=600(cm3)(4) 已知正方体的棱长是6cm,求表面积和体积。
S表=6a2=6×6×6=216 cm2;V= a3=6×6×6=216 cm3发现:棱长是6厘米的正方体体积和表面积相等。
(×)原因:虽然数值相等,但单位名称不一样。
(5)测P9(5)一张长40厘米、宽30厘米的长方形铁皮,四角各剪去一个边长5厘米的正方形,做成一个深5厘米的无盖长方体铁盒,这个铁盒的容积是多少?30-5-5=20(厘米)40-5-5=30(厘米) 30×20×5=3000(立方厘米)(6)测P11(4)长方体的长是12厘米,高8厘米,阴影部分两个面的面积和是180平方厘米,这个长方体的体积是多少立方厘米?180÷(12+8)=9(厘米) 12×9×8=864(立方厘米)(7)测P16(8)一个密封的长方体玻璃罐,长30厘米,宽18厘米,高12厘米。
苏教版六年级上册长方体和正方体表面积_题型归纳
不夯实基础,难建成高楼。
1. 填一填。
(1)一个正方体木块,棱长为5厘米。
它的表面积是()平方厘米。
(2)工人叔叔做一个长方体不带盖的水箱,长1.5米,宽0.8米,高0.4米。
做这个水箱至少要用()平方米的木板。
(3)楼房外壁用于流水的水管是长方体。
如果每节长15分米,横截面是一个长方形,长1分米,宽0.6分米。
做一节水管,至少要用铁皮()平方分米。
2. 生产50个如图所示的包装袋,一共需多少平方分米的包装纸?
列式:
答:一共需要平方分米的包装纸。
3. 用铁皮焊4个棱长是25厘米的正方体无盖水桶,至少要用多少铁皮?
列式:
答:至少要用平方分米。
4. 有一种长方体食品盒,长与宽都是16厘米,高是22厘米。
如果在四周的侧面贴上一圈商标纸(上、下不贴),那么这张商标纸的面积是多少平方厘米?
列式:
答:这张商标纸的面积是平方厘米。
5. 如图,一个长方体礼品盒长18cm,宽12cm,高7cm,如果围着它的侧面贴一圈包装纸,这张包装纸的面积是多少平方厘米?
列式:
答:这张包装纸的面积是平方厘米。
6. 一根2米长的通风管,横截面是边长为2分米的正方形,制作4根这样的通风管至少需要铁皮多少平方分米?
列式:
答:至少需要铁皮640平方分米。
7. 一个长方体形状的儿童游泳池,长40米、宽14米、深1.2米。
现在要在四壁和池底贴上每块面积为0.16平方米的正方形瓷砖,需要多少块?
列式:
答:需要块。
8. 张老师家客厅的长是6米,宽是4米,高是3米,门窗面积一共8平方米。
(1)要粉刷四周墙壁和屋顶,粉刷的面积是多少平方米?
列式:
答:粉刷的面积是平方米。
(2)如果每平方米用涂料1.5千克,那么一共要用涂料多少千克?
列式:
答:一共要用涂料千克。
(3)如果每平方米粉刷工钱为8元,那么粉刷这个客厅,张老师要付工钱多少元?列式:
答:张老师要付工钱元。