热质交换原理与设备整理版
- 格式:doc
- 大小:263.32 KB
- 文档页数:9




热质交换原理与设备2.1 空气的热湿处理实验2.2.1 实验目的1) 掌握空气混合过程中空气状态点的变化规律。
2) 通过在表冷器中对空气和水的热湿交换过程测试,使学生加深对空气和水间接接触时传热传质过程的理解,并测定表冷器的热工性能;3) 熟悉和掌握有关热工测试的方法。
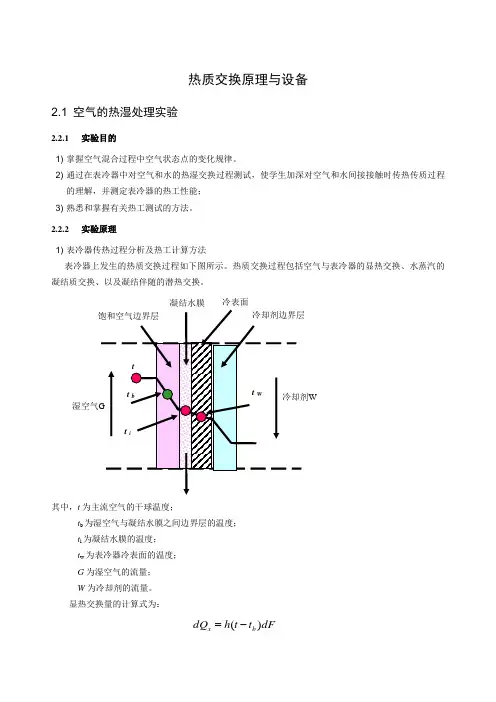
2.2.2 实验原理1) 表冷器传热过程分析及热工计算方法表冷器上发生的热质交换过程如下图所示。
热质交换过程包括空气与表冷器的显热交换、水蒸汽的凝结质交换、以及凝结伴随的潜热交换。
其中,t 为主流空气的干球温度;t b 为湿空气与凝结水膜之间边界层的温度;t i 为凝结水膜的温度;t w 为表冷器冷表面的温度;G 为湿空气的流量;W 为冷却剂的流量。
显热交换量的计算式为:dF t t h dQ b x )(-=凝结水膜湿空气W冷表面式中,h 为显热交换系数,d F 为表冷器的热交换面积。
湿空气的凝结量为:dF d d h dW b md )(-=式中,h md 为传质系数,d 为主流湿空气的含湿量,d b 为湿空气与凝结水膜之间边界层的含湿量。
凝结过程释放的潜热量为:dF d d rh rdW dQ b md q )(-==式中,r 为水蒸汽凝结的潜热释放量。
表冷器空气处理过程的总热交换量为:dF i i h dQ dQ dQ b md q x )(-=+=其中,i 为主流湿空气的焓,i b 为湿空气与凝结水膜之间边界层的焓。
上式即为麦凯尔方程。
而显热传热系数与质交换系数的关系可由刘易斯关系式来表示:pmd c h h =其中,c p 为空气的定压比热。
表冷器对湿空气冷却除湿实际过程与理想过程存在一定的偏差,如下图所示,实际发生的湿空气过程为从状态1到状态2而不能达到饱和状态3。
其中热交换效率可表示为:1w 1211t t t t --=ε 其中,ε1为热交换效率,t w1为冷却剂的入口温度。
上式亦称为表冷器的第一热交换效率。
接触系数为:31212t t t t --=ε其中, 2为接触系数,t3为饱和状态温度。

一当物系中存在速度、温度和浓度的梯度时,则分别发生动量、热量、和质量的传递现象。
二单位体积混合物中某成分的质量称为该组分的质量浓度,以符号ρ表示。
组分的实际速度,称为绝对速度。
相对主体流动速度的移动速度,称为扩散速度。
绝对速度=主体流动速度+扩散速度与热量传递中的导热和对流传热类似,质量传递的方式亦分为分子传质和对流传质。
分子传质又称为分子扩散,简称为扩散,它是由于分子的无规则热运动而形成的物质传递现象。
对流传质是指壁面和运动流体之间,或两个有限互溶的运动流体之间的质量传递。
凭借流体质点的湍流和漩涡来传递物质的现象,称为紊流扩散。
斐克定律:在浓度场不随时间而变化的稳态扩散条件下,当无整体流动时,组成二元混合物中组分A 和组分B 将发生扩散。
其中组分A 向组分B 的扩散通量与组分A 的浓度梯度成正比,这就是扩散基本定律——斐克定律:斐克定律只适用于由于分子无规则热运动引起的扩散过程,其传递的速度即为扩散速度u A -u (或u A -u m )在气体扩散过程中,分子扩散有两种形式,即双向扩散(反方向扩散)和单项扩散(一组分通过另一停滞组分的扩散)。
等分子反方向扩散:设由A 、B 两组分组成的二元混合物中,组分A 、B 进行反方向扩散,若二者扩散的通量相等,则成为等分子反方向扩散。
液体中的稳态扩散过程:液体中的分子扩散速率远远低于气体中的分子扩散速率,其原因是由于液体分子之间的距离较近,扩散物质A 的分子运动容易与邻近液体B 的分子相碰撞,使本身的扩散速率减慢。
常见有两种情况:即组分A 与组分B 的等分子反方向扩散 及 组分A 通过停滞组分B 的扩散。
固体中的稳态扩散过程:固体中的扩散,包括气体、液体、1当物系中存在速度、温度和浓度的梯度时,则分别发生动量、热量、和质量的传递现象。
du dyτμ=- 表示两个作直线运动的流体层之间的切应力正比于垂直运动方向的速度变化率。
不同的流体有不同的传递动量的能力,这种性质用流体的动力黏性系数μ来反映,其物理意义可以理解为,它表征了单位速度梯度作用的切应力,反映了流体黏性滞性的动力性质,因此称它为“动力”黏性系数。
τ,表示单位时间内通过单位面积传递的动量,又称动量通量密度,N/㎡dt q dyλ=-,q 为热量通量密度,或能量通量密度,表示单位时间内通过单位面积传递的热量,J/(㎡.s),负号表示热量传递的方向是温度梯度的负方向,或者说热量是朝温度降低的方向传递的。
A A AB dC mD dy=-,它是指在无总体流动或静止的双组分混合物中,若组分A 的质量分数A C 的分布为一维的,则通过这个式子表示。
A m 为组分A 的质量通量密度,表示单位时间内,通过单位面积传递的组分A 的质量,kg/(㎡.s)动量交换传递的量是运动流体单位容积所具有的动量,热量交换传递的量是物质每单位容积多具有的能量,质量交换传递的量是扩散物质每单位容积所具有的质量也就是浓度。
这些量的速率都分别与各量的梯度成正比。
比例系数均表示了物体具有的扩散性质。
质量浓度ρ:单位体积混合物中某组分的质量称为该组分的质量浓度,以符号ρ表示。
它等于混合物中组分A 的质量A M 与混合物的体积V 之比。
物质的量浓度C :单位体积混合物中某组分的物质的量称为该组分的物质的量浓度,简称浓度。
它等于混合物中组分A 的物质的量,(kmol )与混合物的体积V 之比质量分数a :混合物中某组分的质量与混合物总质量之比称为该组分的质量分数,以符号a 表示组分A 的质量分数,它等于混合物中组分A 的质量A M 与混合物的总质量M 之比。
传质的通量:单位时间通过垂直于传质方向上单位面积的物质的量以绝对速度表示的质量通量:A A A m u ρ=混合物的总质量通量为A B A A B B m m m u u ρρ=+=+混合物的总摩尔通量为A B A A B B m N N N C u C u Cu =+=+= A C 为A 的物质的量浓度 A N 为以绝对速度表示的组分A 的摩尔通量,kmol/(㎡.s)以扩散速度表示的质量通量:扩散速度与浓度的乘积为以扩散速度表示的质量通量以主体流动速度表示的质量通量:主体流动速度与浓度的乘积为以主体流动速度表示的质量通量。
质量传递的方式亦分为分子传质和对流传质分子传质又称为分子扩散,它是由于分子的无规则热运动而形成的物质传递现象。
对流传质是指壁面和运动流体之间,或两个有限互溶的运动流体之间的质量传递。
当流体中存在浓度差时,对流扩散亦必同时伴随分子扩散,分子扩散与对流扩散两者的共同作用称为对流质交换,对流质交换是在流体与液体或固体的两相交界面上完成的。
紊流扩散:分子扩散只有在固体、静止或层流流动的流体内才会单独发生。
在湍流流体中,由于存在大大小小的漩涡运动,而引起各部位流体间的剧烈混合,在有浓度差存在的条件下,物质便朝着浓度降低的方向进行传递。
这种凭借流体质点的湍流和漩涡来传递物质的现象,称为紊流扩散。
斐克定律:在浓度场不随时间而变化的稳态扩散条件下,当无整体流动时,组成二元混合物中组分A 和组分B 将发生互扩散。
其中组分A 向组分B 的扩散通量与组分A 的浓度梯度成正比。
A A AB d j D dzρ=-斐克定律只适用于由于分子无规则热运动引起的扩散过程,其传递的速度即为扩散速度A B u u -。
实际上,在分子扩散的同时经常伴有流体的主流运动。
在气体扩散过程中,分子扩散有两种形式,即双向扩散和单向扩散。
在系统中取1z 和2z 两个平面,设组分A 、B 在平面1z 处的浓度为1A C 和1B C ,2z 处的浓度C 恒定,系统的总浓度C 恒定组分A 通过停滞组分B 扩散时,浓度分布为对数型,在扩散距离的任一点处,A p 和B p 之和为系统总压力p 。
液体中的分子扩散速率远远低于气体中的分子扩散速率,其原因是由于液体分子之间的距离较近,扩散物质A 的分子运动容易与邻近液体B 的分子相碰撞,使本身的扩散速率减慢。
液体扩散也有常见的两种情况,即组分A 和组分B 的等分子方向扩散及组分A 通过停滞组分B 的扩散。
固体中的扩散,包括气体、液体和固体在固体内部的分子扩散。
一般来说,固体中的扩散分为两种类型:一种是与固体内部结构基本无关的扩散,另一种是与固体内部结构基本有关的多孔介质中的扩散。
当气体在固体中扩散时,溶质的浓度常用溶解度S 表示。
在多孔固体中充满了空隙和孔道,当扩散物质在孔道内进行扩散时,其扩散通量除与扩散物质本身的性质有关外,还与孔道的尺寸密切相关。
高压下的气体和常压下的液体,由于其密度较大,因而λ很小,故密度大的气体和液体在多孔固体中的扩散时,一般发生斐克型扩散。
克努森扩散通量:1212()KA A A A D N C C z z =-- 1212()()KA A A A D N p p RT z z =--,故除与低压下的气体在多孔固体中扩散时,一般发生克努森扩散。
扩散系数:扩散系数是沿扩散方向,在单位时间每单位浓度降的条件下,垂直通过单位面积所扩散某物质的质量或摩尔数,A A A A M n D d dC dy dyρ==--,质量扩散系数D 和动量扩散系数v 及热量扩散系数a 具有相同的单位2/m s ,扩散系数的大小主要取决于扩散物质和扩散介质的种类及其温度和压力。
对流传质所涉及的内容即为运动着的流体之间或流体与界面之间的物质传递问题,这种过程既包括由流体位移所产生的对流作用,同时也包括流体分子间的扩散作用,这种分子扩散和对流扩散的总作用称为对流传质。
对流传质是在流体流动条件下的质量传输过程,其中包含着由质点对流和分子扩散两因素决定的传质过程。
对流传质过程与流体的运动特性密切相关,如流体流动的起因、流体的流动性质以及流动的空间条件等等。
固体壁面与流体之间的对流传质速率可定义为:()A m As A N h C C ∞=-,对流传质系数m h 与流体的性质、壁面的几何形状和粗糙度、流体的速度等因素有关。
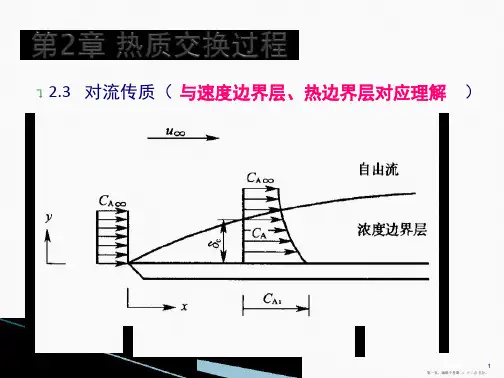
浓度边界层:可以认为质量传递的全部阻力集中于固体表面上一层具有浓度梯度的流体层中,该流体层称为浓度边界层。
流体流过壁面进行传质时,在壁面上会形成两种边界层,即速度边界层与浓度边界层。
浓度边界层厚度为c δ,其定义通常为()/()A As A As C C C C ∞--=0.99时与壁面的垂直距离。
当组分A 进行传递时,首先以分子传质的方式通过该静止流层,然后再向流体主体对流传质。
三种边界层的主要的表现形式:表面摩擦、对流换热以及对流传质,重要的边界层参数分别是摩擦系数f C 、对流换热系数h 以及对流传质系数m h 。
对流传质过程的相关准则数:1 施密特准则数C S 对应于对流传热中的普朗特准则数r P ,r P 准则数为联系动量传输与热量传输的一种相似准则。
与r P 准则数相对应的C S 准则数则相应为联系动量传输与质量传输的相似准则,其值由流体的运动黏度与物体的扩散系数之比构成 2 宣乌特准则数Sh 3 传质的斯坦登准则数m St Re m m h Sh St Sc u==• 渗透理论:当流体流过表面时,有流体质点不断地穿过流体的附壁层向表面迁移并与之接触,流体质点在表面接触之际则进行质量的转移过程,此后流体质点又回到主流核心中去。
可将由无数质点群与表面之间的质量转移,视为流体靠壁薄层对表面的不稳态扩散扩散传质过程。
薄膜理论:当流体靠近物体表面流过时,存在着一层附壁的薄膜,在薄膜的流体侧与具有浓度均匀的主流连续接触,并假定膜内流体与主流不相混合和扰动。
在此条件下,整个传质过程相当于此薄膜上的扩散作用,而且认为在薄膜上垂直于壁面方向上呈线性的浓度分布,膜内的扩散传质过程具有稳态的特性。
流体宏观运动既可导致动量传递,同时也会把热量和质量从流体的一个部分传递到另一个部分,所以温度分布、浓度分布和速度分布是相互联系的。
动量、热量和质量传递类比:当物系中存在速度、温度和浓度的梯度时,则分别发生动量、热量和质量传递现象。
动量、热量和质量的传递,既可以是由分子的微观运动引起的分子扩散,也可以是由漩涡混合造成的流体微团的宏观运动引起的湍流传递。
动量通量密度正比于动量浓度的变化率,能量通量密度正比于能量浓度的变化率,组分A 的质量通量密度正比于组分A 的质量浓度的变化率。
熱质交换类比律:m p Dhhahh c λλρ===,这个关系称为刘伊斯关系式刘伊斯准则数是反映热边界层与浓度边界层厚度关系的准则数。
同一表面上传质过程对传热过程的影响:传质阿克曼修正系数表示传质速率的大小与方向对传热的影响,随着传质方向的不同,0C 值有正有负,当传质的方向是从壁面到流体主流方向时,0C 为正值,反之为负。
传质的存在对壁面导热量和总传热量的影响方向是相反的。