第五章 控制系统的稳定性分析.ppt
- 格式：ppt
- 大小：1.50 MB
- 文档页数：66
下载文档原格式
合集下载
控制工程基础：第五章 控制系统稳定性分析
时，系统闭环后稳定。
2
Nyquist 稳定性判据2
1、若开环传递函数在s右半平面无极点时，当从0变化
时，如果Nyquist曲线不包围临界点(-1, j0)，则系统稳定。
如果Nyquist曲线包围临界点(-1, j0)，则系统不稳定。
❖ 系统稳定性定义：
❖
控制系统处于某一平衡状态下受到扰动作用而偏离了 原来的平衡状态，在干扰消失后系统又能够回到原来的平衡 状态或者回到原平衡点附近，则称该系统是稳定的，否则， 该系统就是不稳定的。
❖
稳定性是系统的一种固有特性，它只取决于系统本身的 结构和参数，而与初始状态和外作用无关。
m
F
F
单摆系统稳定
p(s)
p(s) DK (s)
系统稳定的充要条件:特征方程的根全部具有负实部
（闭环极点均在s平面的左半平面）。
即系统稳定的充要条件为：F(s)的零点都位于s平面 的左半平面。
GB(s)
F(s)
Gk(s)
零点
极点
零点
极点
极点
零点
1、若开环极点均在s平面左半面，则根据米哈伊洛夫定理推论：
arg[
DK
两种特殊情况
1、劳斯阵列表某一行中的第一列元素等于零，但其余各项不 等于零或不全为零 处理方法：
用一个很小的正数 代替该行第一列的零，并据此计算出
阵列中的其余各项。然后令 0 ，按第一列系数进行
判别。
如果零上下两项的符号相同，则系统存在一对虚根，处于临 界稳定状态：如果零上下两项的符号不同，则表明有一个符 号变化，系统不稳定。
0
1
c1
1
b1
a1 b1
a3 110 (7)5 6.43
控制系统的稳定性分析
自动控制原理
其中系数 b1 , b2 , b3 等;根据
下列公式计算：
b1
a1a 2 a 0a 3 a1
b2
a1a 4 a 0a 5 a1
b3
a1a 6 a 0a 7 a1
同样的方法可以计算c;d;e等各行的系数
自动控制原理
注意:
在展开的阵列中;为简化其后的数值计算;可用一个正整数去除 或乘某一个整行;并不影响稳定性结论; 劳斯判据还说明：方程式5 4中;其正实部特征根数;等于劳斯阵列中第一列的系数改变的次数;
自动控制原理
从乃氏图上看;Gjw不包围1;j0点
G ( jw ) 1
稳定
G ( jw )
G ( jw )
不稳定
自动控制原理
2 若开环系统不稳定;有p个零点在右半平面;q的零点在原点;npq个 零点在左半平面 则
argD K(jw)(n2pq)2
如果闭环是稳定的;则
argDb(jw)n 2
故
a r g 1 G (jw ) n ( n 2 p q ) p q
F是新引进的函数;其分母是系统开环特征多项式;分子是闭环特征多 项式;
对于非单位反馈系统;开环传递函数为
GsG' sHsM DK Kss
自动控制原理
2 乃奎斯特队稳定判据 1 若开环是稳定的;则根据米哈依洛夫定理
argDk
jwn
2
如果闭环系统稳定;有
于是
argDb
jwn
2
arg1G (jw )0o
0
0
a n1 0
0
an2 an
自动控制原理
系统稳定的充要条件是：主行列式
式 1,2, n1 ;均大于零;即
控制工程基础 (第12讲) 第五章 乃魁斯特(Nyquist)稳定性判据 PPT课件
如果在s平面上曲线包围k个零点和k个极点(k=0,1,2…)，
即包围的零点数与极点数相同，则在 F(s) 平面上，
相应的封闭曲线不包围 F(s) 平面上的原点。
上述讨论是映射定理的图解说明，奈奎斯特稳 定判据正是建立在映射定理的基础上。
相角（幅角）定理：
如果闭合曲线 s 以顺时针方向为正方向，在 s 平
在右半s平面内的零点数和极点数联系起来的判据。这 种方法无须求出闭环极点，得到广泛应用。
奈奎斯特稳定判据是建立在复变函数理论中的图形映 射基础上的 。
相角（幅角）定理：
如果闭合曲线 S 以顺时针方向为正方向，在[S]平
面上包围了Fs 的 Z 个零点和 P 个极点，但不经过
任何一个零点和极点，那么，对应的映射曲线 F 也以
奈魁斯特稳定判据是利用开环频率特性判别闭环系统的稳 定性。不仅能判断系统的绝对稳定性，而且可根据相对稳定的 概念，讨论闭环系统的瞬态性能，指出改善系统性能的途径。 它从代数判据脱颖而出，故可以说是一种几何判据。
06-7-20
控制系统系统的稳定性分析
2
奈魁斯特稳定判据无需求取闭环系统的特征根，而是利用
F(s) 的轨迹将逆时针方向包围 F(s)平面上原点两次
06-7-20
控制系统系统的稳定性分析
9
s平面
B3
2
1
A0
-1
-2
F -3 -3
-2
-1
j
Im
C
2
1.5
F (s)平面
1 B1
0.5
D
E1
0 C1
F1 -0.5
-1
A
-1.5
D1
第五章_控制系统的稳定性分析
, c2
b1a5 a1b3 b1
, c3
b1a7 a1b4 b1
f1
e1d 2
e1
d1e2
这样可求得n+1行系数
14
这种过程需一直进行到第n行被算完为止，系数 的完整阵列呈现一个倒三角形。
注意：
为简化计算，可用一个正整数去除或乘某一整个 行，并不改变稳定性结论。
15
劳斯稳定判据
劳斯稳定判据是根据所列劳斯表第一列系数符 号的变化，去判别特征方程式根在S平面上的具体 分布，过程如下：
27
5.3.4劳斯-赫尔维茨稳定性判据的应用
判定控制系统的稳定性
[例5-7] 系统的特征方程为：s4 2s3 3s2 4s 5 0 ，判断系统的稳定性。
[解]：排列劳斯阵如下：
s4 1 3 5 s3 2 4 0
因阵第为一，a列i 不0全, (为i 正0，~所4)以，，且系劳统斯
不稳定。
8
0
3
j 2 , j2
S0
16
显然这个系统处于临界稳定状态。
22
5.3.2 劳斯判据的应用
稳定判据只回答特征方程式的根在S平面上的分布 情况，而不能确定根的具体数据。也即也不能保证系 统具备满意的动态性能。换句话说，劳斯判据不能表 明系统特征根在S平面上相对于虚轴的距离。但能判断 是否所有特征根都落在虚轴的左半平面.若用S=Z-1带 入特征方程中,求出的根的实部即为特征根距S=-1垂线 的距离.可判断稳定程度.
s2 1 5 0 由于劳斯阵第一列有两次符号变
2
如果系统不稳定，就会在任何微小的扰动作用下偏离原 来的平衡状态，并随时间的推移而发散。
因此，如何分析系统的稳定性并提出保证系统稳定的措施， 是自动控制理论的基本任务之一。
控制系统的稳定性分析分解课件
控制系统的稳定性分析分 解课件
目 录
• 控制系统稳定性分析方法 • 控制系统稳定性判据 • 控制系统稳定性优化方法 • 控制系统稳定性实例分析 • 控制系统稳定性总结与展望
01 引言
控制系统稳定性概念
01
02
03
稳定性定义
控制系统在受到外部扰动 后，能否恢复到平衡状态 的能力。
稳定性分类
根据系统性质不同，可分 为渐近稳定、指数稳定、 BIBO稳定等。
实例一：机械臂控制系统稳定性分析
01
02
03
04
系统建模
建立机械臂的动力学模型，包 括电机、减速器等组件的动力
学方程。
稳定性判据
应用劳斯判据或奈奎斯特判据 等方法，判断系统的稳定性。
控制器设计
设计合适的控制器，如PID控 制器，以保证系统的稳定性。
仿真与实验
通过仿真和实验验证控制器的 有效性，并对系统稳定性进行
定性。
超前校正优点
03
校正后系统带宽增宽，动态性能提高，对高频噪声有抑制作用。
滞后校正
滞后校正网络
采用RC电路构成的滞后网络，降低系统高频部分的增益，提高 相位裕量。
滞后校正原理
通过牺牲系统带宽来换取更大的相位裕量，从而提高系统稳定性。
滞后校正优点
对低频段增益影响较小，可保持系统稳态精度，同时有效抑制高 频噪声。
稳态误差分析
通过计算系统的稳态误差来分析系 统的稳定性和精度，包括静态误差 系数法、终值定理法等。
动态性能分析
通过分析系统的动态性能指标（如 调节时间、超调量等）来评估系统 的稳定性，常用的方法有相平面法、 时域响应法等。
频域分析法
奈奎斯特稳定判据
目 录
• 控制系统稳定性分析方法 • 控制系统稳定性判据 • 控制系统稳定性优化方法 • 控制系统稳定性实例分析 • 控制系统稳定性总结与展望
01 引言
控制系统稳定性概念
01
02
03
稳定性定义
控制系统在受到外部扰动 后，能否恢复到平衡状态 的能力。
稳定性分类
根据系统性质不同，可分 为渐近稳定、指数稳定、 BIBO稳定等。
实例一：机械臂控制系统稳定性分析
01
02
03
04
系统建模
建立机械臂的动力学模型，包 括电机、减速器等组件的动力
学方程。
稳定性判据
应用劳斯判据或奈奎斯特判据 等方法，判断系统的稳定性。
控制器设计
设计合适的控制器，如PID控 制器，以保证系统的稳定性。
仿真与实验
通过仿真和实验验证控制器的 有效性，并对系统稳定性进行
定性。
超前校正优点
03
校正后系统带宽增宽，动态性能提高，对高频噪声有抑制作用。
滞后校正
滞后校正网络
采用RC电路构成的滞后网络，降低系统高频部分的增益，提高 相位裕量。
滞后校正原理
通过牺牲系统带宽来换取更大的相位裕量，从而提高系统稳定性。
滞后校正优点
对低频段增益影响较小，可保持系统稳态精度，同时有效抑制高 频噪声。
稳态误差分析
通过计算系统的稳态误差来分析系 统的稳定性和精度，包括静态误差 系数法、终值定理法等。
动态性能分析
通过分析系统的动态性能指标（如 调节时间、超调量等）来评估系统 的稳定性，常用的方法有相平面法、 时域响应法等。
频域分析法
奈奎斯特稳定判据
自动控制 控制系统的稳定性分析
例 已知控制系统特征方程,判断系统稳定性。 s6 +2s5 +8s4+12s3+20s2+16s+16=0 解： 劳斯表为: 由为零上一行的元素 s6 1 8 20 16 组成辅助多项式： s5 2 12 16 P(s)=2s4+12s2+16 dP(s)=8s3+24s s4 2 12 16 ds 3 s 代入 0 0 8 24 系统有虚根,不稳定。 2 s 6 16 劳斯表中某行同乘以某正数， s1 8/3 不影响系统稳定性的判断。 0 s 16
第五节 控制系统的稳定性分析
二、劳斯稳定判据
根据稳定的充分与必要条件 , 求得特 征方程的根 , 就可判定系统的稳定性 . 但对 于高阶系统求解方程的根比较困难。 劳斯稳定判据是根据闭环传递函数 特征方程式的各项系数 , 按一定的规则排 列成劳斯表，根据表中第一列系数正负符 号的变化情况来判别系统的稳定性。 下面具体介绍劳斯稳定判据的应用。
第五节 控制系统的稳定性分析
例 已知系统的特征方程,试用劳斯判据确定 方程的根在s平面上的分布。 s3-3s+2=0 解： 方程中的系数有负值，系统不稳定。 ε -2 = -∞ -3 劳斯表为: b31= ε -3 s3 1 b31→ -∞ ε →0 s2 ε0 2 第一列元素的符号变化了 1 s b ∞ 31 两次,有一对不稳定根。 0 s b 241 s3-3s+2=(s-1)2(s+2)=0 通过因式分解验证: s1.2=1 s3=-2
第五节 控制系统的稳定性分析
如果劳斯表中某一行的元素全为零， 表示系统中含有不稳定的实根或复数根。 系统不稳定。 此时，应以上一行的元素为系数，构 成一辅助多项式，该多项式对s求导后， 所得多项式的系数即可用来取代全零行。 同时由辅助方程可以求得这些根。 下面举例说明:
自动控制原理控制系统的稳定性及特性PPT课件
解：由系统的特征方程计算劳斯表如下
劳斯阵中s3行的各项全部为零，为此用不为零的最后一行(s4 行) 的各项组成辅助方程为 F(s) s4 5s2 4 0 将辅助方程对 s 求导数，得导数方程
dF (s) 4s3 10s 0 ds 第24页/共68页
用导数方程的系数取代
s6 1 6 9 4 s5 1 5 4
故有两个实部为正。 的根
第18页/共68页
例 3-8 已知系统的特征方s程3 4s 2 6 0
，
试判断系统的正的特征根的个数。
解：它有一个系数为负的，根据劳斯判据知系统不稳定。
但究竟有几个右根，需列劳斯表：
s3 1 1 s2 4 6 s1 2.5 s0 6
劳斯表中第一列元素符号改变两次，系统有2个 右半平面的根
故系统稳定。
第13页/共68页
3.3.3 稳定判据 1. Routh稳定判据 系统的特征方程为
必要条件:
（1）特征方程的各项系数ai(i=1,2,…,n)都不为零； （2）特征方程的各项系数ai(i=1,2,…,n)具有相同的符号。
充分条件： 劳斯阵列第一列所有元素为正。
第14页/共68页
劳斯阵列
c1
b1an3 an1b2 b1
b2
an1an4 anan5 an1
c2
b1an5 an1b3 b1
第15页/共68页
例3-5 已知系统的特征方程为 (s) s3 3s2 s 55 0
试用劳斯判据判断系统的稳定性。
解：构造劳斯表如下：
s3 1 1 s2 3 55 s1 52 3 0 s0 55 0
控制系统在典型输入信号作用下的动态过程的品质及?系统的稳定性是系统正常工作的首要条件系统的稳定性是系统正常工作的首要条件?系统的稳定性完全由系统自身的结构和参数决定系统的稳定性完全由系统自身的结构和参数决定?系统的稳定性完全由系统自身的结构和参数决定系统的稳定性完全由系统自身的结构和参数决定与系统的输入无关
劳斯阵中s3行的各项全部为零，为此用不为零的最后一行(s4 行) 的各项组成辅助方程为 F(s) s4 5s2 4 0 将辅助方程对 s 求导数，得导数方程
dF (s) 4s3 10s 0 ds 第24页/共68页
用导数方程的系数取代
s6 1 6 9 4 s5 1 5 4
故有两个实部为正。 的根
第18页/共68页
例 3-8 已知系统的特征方s程3 4s 2 6 0
，
试判断系统的正的特征根的个数。
解：它有一个系数为负的，根据劳斯判据知系统不稳定。
但究竟有几个右根，需列劳斯表：
s3 1 1 s2 4 6 s1 2.5 s0 6
劳斯表中第一列元素符号改变两次，系统有2个 右半平面的根
故系统稳定。
第13页/共68页
3.3.3 稳定判据 1. Routh稳定判据 系统的特征方程为
必要条件:
（1）特征方程的各项系数ai(i=1,2,…,n)都不为零； （2）特征方程的各项系数ai(i=1,2,…,n)具有相同的符号。
充分条件： 劳斯阵列第一列所有元素为正。
第14页/共68页
劳斯阵列
c1
b1an3 an1b2 b1
b2
an1an4 anan5 an1
c2
b1an5 an1b3 b1
第15页/共68页
例3-5 已知系统的特征方程为 (s) s3 3s2 s 55 0
试用劳斯判据判断系统的稳定性。
解：构造劳斯表如下：
s3 1 1 s2 3 55 s1 52 3 0 s0 55 0
控制系统在典型输入信号作用下的动态过程的品质及?系统的稳定性是系统正常工作的首要条件系统的稳定性是系统正常工作的首要条件?系统的稳定性完全由系统自身的结构和参数决定系统的稳定性完全由系统自身的结构和参数决定?系统的稳定性完全由系统自身的结构和参数决定系统的稳定性完全由系统自身的结构和参数决定与系统的输入无关
控制系统的稳定性和特性课件
挑战
控制系统面临着诸多挑战，如鲁 棒性、可靠性、稳定性等问题， 需要不断进行研究和改进。
控制系统的未来发展趋势和展望
发展趋势
未来控制系统的发展趋势将包括更加智能化、微型化和网络化，同时还将更加 注重节能和环保。
展望
随着技术的不断进步和发展，控制系统将实现更加高级别的自动化和智能化， 同时还将更加注重安全性和可靠性。未来控制系统将在更多领域得到应用，为 人类带来更加便捷、高效、安全的生活和工作环境。
控制系统的性能指标
01
02
03
04
快速性
控制系统应能迅速对输入信号 做出响应，并达到期望的输出。
准确性
控制系统应能精确地跟随输入 信号，并尽量减少误差。
抗干扰性
控制系统应能对外部干扰做出 正确的响应，并保持稳定的输
出。
鲁棒性
控制系统应能在不同的条件下 保持稳定的性能。
控制系统的时域特性
01
02
03
阶跃响应
控制系统对阶跃输入的响 应，用于分析系统的稳定 性和性能。
脉冲响应
控制系统对脉冲输入的响 应，用于分析系统的动态 性能。
频率响应
控制系统对正弦输入的响 应，用于分析系统的频率 特性。
控制系统的频域特性
奈奎斯特图
通过绘制奈奎斯特图可以 分析控制系统的稳定性、 性能和阻尼特性。
伯德图
通过绘制伯德图可以分析 控制系统的频率响应、相 位和增益裕度。
智能控制理论
基于人工智能和优化算法进行系统 设计，方法包括模糊控制、神经网 络控制等。
控制系统的优化方法
解析优化
使用数学解析方法求解控制系统 的最优解，例如使用拉格朗日乘
数法进行约束优化。
控制系统面临着诸多挑战，如鲁 棒性、可靠性、稳定性等问题， 需要不断进行研究和改进。
控制系统的未来发展趋势和展望
发展趋势
未来控制系统的发展趋势将包括更加智能化、微型化和网络化，同时还将更加 注重节能和环保。
展望
随着技术的不断进步和发展，控制系统将实现更加高级别的自动化和智能化， 同时还将更加注重安全性和可靠性。未来控制系统将在更多领域得到应用，为 人类带来更加便捷、高效、安全的生活和工作环境。
控制系统的性能指标
01
02
03
04
快速性
控制系统应能迅速对输入信号 做出响应，并达到期望的输出。
准确性
控制系统应能精确地跟随输入 信号，并尽量减少误差。
抗干扰性
控制系统应能对外部干扰做出 正确的响应，并保持稳定的输
出。
鲁棒性
控制系统应能在不同的条件下 保持稳定的性能。
控制系统的时域特性
01
02
03
阶跃响应
控制系统对阶跃输入的响 应，用于分析系统的稳定 性和性能。
脉冲响应
控制系统对脉冲输入的响 应，用于分析系统的动态 性能。
频率响应
控制系统对正弦输入的响 应，用于分析系统的频率 特性。
控制系统的频域特性
奈奎斯特图
通过绘制奈奎斯特图可以 分析控制系统的稳定性、 性能和阻尼特性。
伯德图
通过绘制伯德图可以分析 控制系统的频率响应、相 位和增益裕度。
智能控制理论
基于人工智能和优化算法进行系统 设计，方法包括模糊控制、神经网 络控制等。
控制系统的优化方法
解析优化
使用数学解析方法求解控制系统 的最优解，例如使用拉格朗日乘
数法进行约束优化。
机械工程控制基础 第五章 系统的稳定性
相对稳定性
根据根轨迹，我们知道：对于大的K值，系统 是不稳定的。当增益减小到一定值时，系统可能稳 定。
-1
（a）
（b）
相对稳定性的概念
基于Nyquist判剧，当开环传递函数
在s平面右半部无极点时，其开环频率响应 若通过点（-1，j0），则控制系统处于临界稳定边缘
。在这种情况下若控制系统的参数发生漂移，便有可
0变化到＋∞时，开环频率特性
正、
负穿越 平面负实轴上（-1，-∞ ）段的次
数差为 ，这里 是开环传递函数极点中处
于s平面右半部的数目。否则，闭环系统不
稳定。
乃氏判剧-形式Ⅱ例子：如图所示的乃氏曲线中 ，判别哪些是稳定的，哪些是不稳定的。
解：
所以系统稳定 所以系统不稳定 所以系统不稳定
系统稳定
系统不稳定
说明特征方程中存在一些大小相等，但方向相反的根。
改变一次
在这两种情况下, 两个大小相等符号相反的实根
表明系统在复平面内可能存在 两个共轭虚根 以虚轴对称的两对共轭复根,
此时，系统处在不稳定状态或临界稳定状态。
下面通过实例说明这时应如何排劳斯表。若遇到 第一种情况, 可用一个任意小的正数ε代替为零的元 素, 然后继续进行计算, 完成劳斯表。
形式Ⅰ
形式Ⅰ
[F(s)]
[GH(s)]
[s]
[GH(s)]
乃氏图负穿越
在乃氏图上，开环频率特性，从上半部
分穿过负实轴的
段到实轴的下半部
分，称为正穿越；开环频率特性从下半部穿
过负实轴的
段到实轴的上半部分
，称为负穿越；起始于（或终止于）
段的负实轴的正、负穿越称为正负半穿越；
乃氏图负穿越实例1
第五章 控制系统的稳定性
例 5 - 2. 设有下列特征方程 s 4 + 2s 3 + 3s 2 + 4s + 5 = 0
试用Routh判据判别该特征方程正实部根的个数。 判据判别该特征方程正实部根的个数。 试用 判据判别该特征方程正实部根的个数
解 : 列写 劳斯 阵列 : s4 s3 s2 s s
1 0
1 2
2× 3 - 4 2
s3 s2 s s0
1 0≈ε
- 3ε - 2
-3 2 0
改变一次
ε
2
改变一次
∴ 有两实部为正的根。
b.劳斯表某行全为零 说明特征方程中存在一些大小相等，但方向相反的 根。 可用全零行的前一行数值组成辅助方程 A' ( s )，并用 dA' ( s ) / ds 的系数代替全零行的各项，完成劳斯表 ，利用 的系数代替全零行的各项，完成劳斯表， 可解得那些对称根。 辅助方程 A' ( s )可解得那些对称根。
一幅 原 . 角 理 设 (S)是 变 的 项 之 ,除 S平 的 限 奇 复 量 多 式 比 在 面 有 个 F 点 ,为 值 续 则 数又 P为 (S)极 数 , Z为 (S) 外 单 连 正 函 . 设 F 点 目 F 的 点 目 其 包 重 点 重 点 目 以 F(S)的 零 数 , 中 括 极 与 零 数 , 及 全 部 点 零 均 布 S平 的 闭 线 S内 而 S不 过 极 与 点 分 在 面 封 轨 Γ , Γ 通 F(S)的 何 点 零 . 在 种 况 , 当 S以 时 方 任 极 与 点 这 情 下 点 顺 针 向 沿 S 运 , ΓS在 F(S)]平 上 映 ΓF按 时 方 包 原 Γ 动 [ 面 的 射 顺 针 向 围 点 次 的 数 N = Z- P N>0 N<0 N =0 表 ΓF顺 针 围 点 次 示 时 包 原 N 表 ΓF逆 针 围 点 次 示 时 包 原 N 表 ΓF不 围 点 示 包 原
第五章控制系统稳定性分析
第五章 控制系统的稳定性分析5．1 已知开环系统的传递函数如下，试用劳斯判据判别其闭环系统的稳定性。
（1））3)(2()1(10)()(+++=s s s s s H s G特征方程为：01016523=+++s s s10141051610123s s ss 第一列符号为正，故闭环系统稳定（3） ）05600300(100)()(22++=s s s s H s G 特征方程为 010050600300234=+++s s s列劳斯表 10012001005006001005030001234-ss ss s第一列符号为负系统不稳定，根据符号变化的次数可判断系统正根数为2 5．2 已知单位负反馈系统开环传递函数如下)12()(22++=s w ws s K s G nnξ式中s r a d w n /90=，2.0=ξ试确定K 取何值闭环系统稳定。
解：系统特征方程为：0810********3=+++K s s s KK Kss ss 368100810036810010123-⎪⎩⎪⎨⎧<⇒>-⇒>->36036036)36(81000K K K K 360<<K5．3 已知系统开环传递函数为)1()1(10)()(-+=s s s K s H s G 试确定闭环系统稳定时K的临界值。
解：系统闭环特征方程为010)110()()(12=+-+=+K s K s s H s GKK K ss s100110101012-⎩⎨⎧>≥⇒≥-01.00110K K K 1.0≥⇒K 临界值K=0.15.5 设闭环反馈控制系统特征方程如下，试确定有几个根在右半[s]平面 （2）08024102234=++++s s s s801048022428010101234-ss ss s第一列有负号出现系统不稳定，有2个右根 （4） 01249332345=----+s s s ss124.8125.71812001293431012345-------ss s ss s辅助方程为 01293)(24=--=s s s Fs s s F dsd 1812)(3-=0)1)(4(31293)(2224=+-=--=s s s s s F22,1±=s 14,3j s ±= 有1个右根5.6 单位反馈系统开环传递函数为)3)(2()(10)(+++=s s s a s s G ，试确定（1）使系统稳定的a 值（2） 使系统特征根均落在[s]平面中Re=-1这条线左边的a 值。
第五章稳定性分析
第五章稳定性分析第五章：控制系统的稳定性分析3.3.5 控制系统的稳定性分析稳定性的概念线性系统稳定的充要条件线性系统稳定的必要条件代数判据（⼀般情况，特殊情况，劳斯，赫尔维茨）劳斯判据的应⽤（确定稳定域判断稳定性，求系统的极点，设计系统中的参数3.3.5.1 稳定性的概念分析⼩球平衡点的稳定性定义：若线性控制系统在初始扰动的影响下，其过渡过程随着时间的推移逐渐衰减并趋向于零，则称该系统为渐近稳定，简称稳定。
反之，若在初始扰动的影响下，系统的过渡过程随时间的推移⽽发散，则称该系统不稳定。
3.3.5.2线性系统稳定性的充要条件设系统的微分⽅程模型为：分析系统的稳定性是分析在扰动的作⽤下，当扰动消失后系统是否能回到原来的平衡状态的性能，亦系统在作⽤下的性能，亦与系统的输⼊信号⽆关，只与系统的内部结构有关。
对上述微分⽅程描述的系统亦只与等式的左端有关，⽽与右端⽆关，亦：系统的稳定性是由下列齐次⽅程所决定：其稳定性可转化为上述齐次⽅程的解c(t)若则系统稳定，则系统不稳定。
分析齐次⽅程的解的特征。
由微分⽅程解的知识，上述⽅程对应的特征多项式为：设该⽅程有k个实根（i＝1，2，…k）r对复根（i＝1，2，…r）k＋2r＝n 且各根互异（具有相同的根时分析⽅法相同，推导稍繁琐）则上述齐次⽅程的⼀般解为：其中为常数，由式中的决定，分析可见：只有当时，否则。
注：只能是⼩于零，等于或⼤于均不⾏。
等于零的情况为临界稳定，属不稳定。
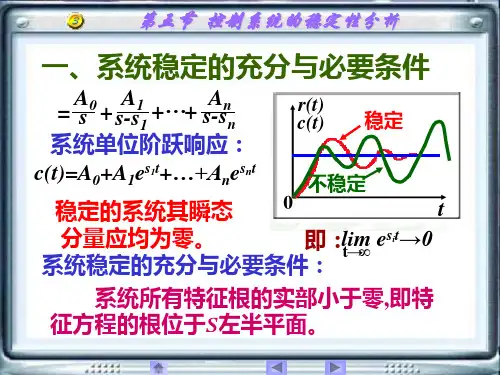
综:线性系统稳定的充要条件（iff）是：其特征⽅程式的所有根均为负实数或具有负的实部。
亦：特征⽅程的根均在根平⾯（复平⾯、s平⾯）的左半部。
亦：系统的极点位于根平⾯（复平⾯、s平⾯）的左半部。
从上⾯的充要条件可以看出：系统稳定性的判断只需计算上系统的极点，看其在s平⾯上的位置，勿需去计算齐次⽅程的解（当系统复杂时的计算可能很繁），勿需去计算系统的脉冲响应。
3.3.5.3 线性系统稳定的必要条件设系统特征⽅程式中所有系数均为实数，并设（若，对特征⽅程两端乘（－1）），可以证明上述特征⽅程中所有系数均⼤于零（即）是该特征⽅程所有根在s平⾯的左半平⾯的必要条件。
第5章控制系统的稳定性分析
设系统闭环传递函数为
Y (s) X (s)
bm sm an s n
bm1sm1 an1sn1
则系统的特征方程为
b1s b0 a1s a0
ansn an-1sn-1 a1s a0 0
（5-5）
例 某单位反馈系统的开环传递函数 G(s) k
则系统的闭环传递函数
s(Ts 1)
（5-7）
a0
an
s1s2 s3 s4
sn2 sn1sn
从式（5-7）可知，要使全部特征根s1， s2，···， sn-1，sn均具有负实部，就必须满足以下两个条件：
（1）特征方程的各项系数ai(i=0，1，2， ···，n) 都不等于零。因为若有一个系数为零，则必出 现实部为零的特征根或实部有正有负的特征根， 才能满足式（5-7） 。此时系统为临界稳定（根 在虚轴上）或不稳定（根的实部为正）。
均不为零。
2. 特征方程的各项系数ai符号一致。
以上只是判定系统稳定的必要条件，而非充要条件， 因为此时还不能排除有不稳定根的存在。
罗斯稳定判据可以用来校验特征方程是否满足系 统稳定的充分条件。罗斯判据的证明比较麻烦， 这里只介绍它的应用。
特征方程系数的罗斯阵列如下：
sn an an-2 an-4 an-6
图示小球处在a点时，是稳定平衡点，因为作用 于小球上的有限干扰力消失后，小球总能回到a 点，而小球处于b、c点时为不稳定平衡点， 因 为只要有干扰力作用于小球，小球便不再回到 点b或c点。
c
b
a 小球的稳定性
上述两个实例说明系统的稳定性反映在干扰消 失后的过渡过程的性质上。这样，在干扰消失 的时刻，系统与平衡状态的偏差可以看作是系 统的初始偏差。
第5章系统的稳定性
经典控制论中，系统稳定性判据
代数判据
Routh（劳斯）判据 Hurwitz（古尔维茨）判据 Nyquist判据 Bode判据
几何判据
5.2 Routh（劳斯）稳定判据
Routh稳定判据
不求解特征方程的根,直接根据特征方程的系 数，判断系统的稳定性，回避了求解高次方程根 的困难。
【例】D(s) s 4 3s3 4s 2 12s 16
【解】：Routh表为： s4 s3 s2 s1 s0 1 3 4 16 12
12 48 48
0( ) 16 12 48 0
很小时，
12
0
16
【结论】：系统不稳定，并有两个正实部根。
【情况2】:
n n n an1 an2 an3 si， si s j， an an an i 1 i j i j k i 1, j 2
(1)
n
s
i 1
n
i
si s j sk，
i 1, j 2, k 3
n a0 n ， (1) si an i 1
系统稳定的必要条件：特征方程中所有项的系数均大 于0，只要有一项等于或小于0，则为不稳定系统。 充分必要条件：Routh表第一列元素均大于0。
必要条件证明
D(s) an s n an1s n1 an1 n1 得：s s an 再展开，得
n
a1s a0 0，两端同除以an，并分解因式， (s sn )
其中N+为：正穿越与半次正穿越次数的和。 其中N-为：负穿越与半次负穿越次数的和。
第五章 控制系统的稳定性分析(含习题答案)
f1 g1
劳斯阵列
注意：如果劳斯阵列第一列元素的符号不全 相同，则该列元素符号变化的次数，就是特 征方程所含实部为正的根的数目。
劳斯判据使用说明： （ 1）用一个正数去乘或除劳斯阵的某一整行，不会改变稳定性的结论。
4 3 2 例5-1 设控制系统的特征方程式为：D s s 8s 17 s 16s 5 0
Bl e
l 1
sin l t l Dr t r e r t sin r t r
r 0
n4 1
n2重实根
s pk
n3对不同的共轭复数根 s l jl
结论：控制系统稳定的充分必要条件：系统特征方程式的根全部具 有负实部。
5. 2 系统稳定的充要条件
s3, 4 2 j
系统特征方程具有两对共轭虚根，系统处于临界稳定。（不稳定，对应的 暂态分量为等幅振荡。)
劳斯判据使用说明：
例 5-3 ： 已知单位反馈控制系统的开环传递函数为：G s 试应用劳斯判据判断预使系统稳定的K的取值范围。 解：根据题意，可得系统的闭环传递函数为：
K s s 2 s 1 s 2
大范围稳定：系统稳定与否，与初始偏差的大小无关。 小偏差稳定：初始偏差不超过一定范围的情况下，系统是稳定的。
5. 2 系统稳定的充要条件
一、系统稳定条件分析
系统扰动输入到输出之间的传递函数：
Xo s G2 s b0 s m b1s m 1 bm 1s bm M s N s 1 G1 s G2 s H s a0 s n a1s n 1 an 1s an D s
C s D s
闭环传递函数的特征方程：D(s)=0，特征方程的根即系统传递函数的极点。
(第12讲) 第五章 劳斯稳定性判据
a 0 s a1 s
n
n 1
a n 1 s a n 0
则该系统稳定的条件为： a. 特征方程的各项系数 a i ( i 0 , , n 1) 都不等于零； b. 特征方程的各项系数 a i 的符号都相同； 此两项为必要条件。
例 如 ： q s s 2 s s 4 s s 2s 8
2
s1 , 2
a1
a1 4 a 2 a 0
2
2a2
只有 a 2 , a 1 , a 0 都大于零，系统才稳定（负实根或实部 为负）。 对于三阶或以上系统，求根是很烦琐的。于是就有了以 下描述的代数稳定性判据。
06-7-20
控制系统的稳定性分析
13
5.3 代数稳定性判据
5.3.1 劳斯稳定性判据 设线性系统的闭环特征方程为：
B：对实际“小偏差线性化”的近似线性系统，偏差达到 一定范围之后，系统不再稳定。 2.稳定性指的是自由震荡之下的稳定性，即输入为零，系 统在初始偏差不为零时的稳定性；也即是讨论自由振荡是收敛 还是发散。
5.2 系统稳定的充要条件
设系统或环节的微分方程为：
y
(n)
( t ) a n 1 y
(m )
06-7-20 控制系统的稳定性分析 2
如果系统不稳定，就会在任何微小的扰动作用下偏离原 来的平衡状态，并随时间的推移而发散。
因此，如何分析系统的稳定性并提出保证系统稳定的措施， 是自动控制理论的基本任务之一。
其他：
一个反馈系统要么是稳定的，要么是不稳定的---绝对稳定性。 具有绝对稳定性的系统称为稳定系统； 若一个闭环系统是稳定的，还可以用相对稳定性来进一步衡 量其稳定程度。例如：飞机越稳定操作起来越困难。但是现代战 斗机的相对不稳定性导致的结果就是良好的可操纵性，因此战斗 机不如商业运输机飞行平稳，但是能够实现快速机动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
个很小的正数 来代替它
例 设控制系统的特征方程为
s4 2 s2 s2 2 s 1 0
用劳斯判据判断其稳定性
自动控制原理
解 由劳斯阵列
s4 1 1 1 s3 2 2 0 s2 0 1
s1 2 2
s0 1
符号改变一次 符号改变一次
由于劳斯阵列第一列元素的符号不一致,系统不稳定,并且符号改 变两次,所以有两个正实部特征根
例 设控制系统的特征方程为
D s s4 2 s3 3 s2 4 s 3 0
试用劳斯判据判断其稳定性
解 首先，由方程系数可知已满足稳定的必要条件。其次，排
劳斯阵列
s4 1 3 3
s3 2 4 0
s2 1 1
s1 2
s0 3
自动控制原理
由劳斯阵列第一列可知，其系数出现负值，因此系统不稳定， 并且符号变化两次，所以有两个正实部特征根。
自动控制原理
§5-3 代数稳定判据
一.劳斯判据 1.系统稳定的必要条件: (1)特征方程的各项系数都不等于零。 (2)特征方程的各项系数都不大于零。 2.系统稳定的充要条件: 设系统稳定的特征方程式为
D s a 0 s n a 1 s n 1 a 2 s n 2 a n 1 s a n 0 5 . 4
自动控制原理
其中系数 b1 , b2 , b3 等，根据
下列公式计算：
b1
a1a 2 a 0a 3 a1
b2
a1a 4 a 0a 5 a1
b3
a1a 6 a 0a 7 a1
同样的方法可以计算c,d,e等各行的系数
自动控制原理
注意:
在展开的阵列中,为简化其后的数值计算,可用一个正整数去除 或乘某一个整行,并不影响稳定性结论。劳斯判据还说明：方程式 (5.4)中,其正实部特征根数,等于劳斯阵列中第一列的系数改变的 次数。
自动控制原理
(2)劳斯阵列出现整排零 例 设控制系统的特征方程为
s 6 2 s 5 8 s 4 1 2 s 3 2 0 s 2 1 6 s 1 6 0
试用劳斯判据判断其稳定性 解 计算劳斯阵列如下
s6 1 8 20 16 s5 2 12 16 0 s4 1 6 8 s3 0 0 0
自动控制原理
式中
p
d dt
，若记
Dpanpnan1pn1 a1pa0
Mpbmpmbm1pm1 b1pb0
并对5.1作拉氏变换，得
X 0s M D s s X is N D ( (s s) )
5 .2
自动控制原理
式中
M D
s s
GБайду номын сангаас
s
为系统的传递函数。
因为是在零初始条件下，有 则
Xi 0
X0
s
N (s) D(s)
自动控制原理 第五章
控制系统的稳定性分析
❖§5-1 系统稳定性的基本概念 ❖§5-2 系统的稳定条件 ❖§5-3 代数稳定判据 ❖§5-4 乃奎斯特判据 ❖§5-5 对数幅相频率特性的稳定判据 ❖§5-6 控制系统的相对稳定性 ❖例题分析 ❖课后习题
自动控制原理
§5-1 系统稳定性的基本概念
如果一个系统受到扰动，偏离了原来的平衡状态，而当扰动取消 后，这个系统又能够逐渐恢复到原来的状态，则称系统是稳定的。否 则这个系统是不稳定的。
2. 控制理论中所讨论的稳定性其实都是指自由振荡下的稳定性, 也就是说,是讨论输入为零,系统仅存在初始偏差不为零时的稳定性, 即讨论自由振荡是收敛还是发散的。
自动控制原理
§5-2 系统的稳定条件
设定常线性系统的微分方程为：
a n p n a n 1 p n 1 a 1 p a 0 x 0 t b m p m b 1 p b 0 x i t 5 . 1
自动控制原理
控制系统稳定性的定义： 若控制系统在任何足够小的初始偏差的作用下，其过渡过程随
着时间的推移，逐渐衰减并趋于零，具有恢复原平衡状态的性能， 则称该系统稳定。否则，称该系统不稳定。
注意： 1. 稳定性是系统自身的固有特性,它取决于系统本身的结构和
参数,而与输入无关；对于纯线性系统来说，系统的稳定与否不与初 始偏差的大小有关。如果，这个系统是稳定的，就叫做大范围稳定。 而经过线性化处理的系统都是“小偏差”稳定。
s3 0 0 0
4 12
s2 3 8
s1 4 /3
s0 8
自动控制原理
x 0t L 1 [X 0s] L 1 N D s s i n 1A ie sit
拉氏反变换，有
5 .3
Resi 0
由上式可知，若系统所有特征根的实部均为负值，即
自动控制原理
这样的系统就是稳定的。
ltim x0 t 0
反之，若特征根中有一个或多个根具有正实部时，则零输入将随时 间的推移发散，即
3.二阶，三阶和四阶系统的劳斯判据
低阶系统的劳斯判据可以化简
(1)二阶系统, a00a10a20 (2)三阶系统,各项系数大于零, a1a2 a0a3 (3)四阶系统,各项系数大于零, a1a2 a0a3 , 4.特殊情况
a1a2a3a0a32a12a40
(1)如果在劳斯判据阵列中任意一行的第一个元素为零,可以用一
在此情况下,可用该行上一行的元素构造一个辅助多项式,并利用这个 多项式方程的导数的系数组成劳斯阵列表中的下一行。利用辅助多 项式够成的辅助方程，解出特征根。
由此可得到辅助多项式
Ass46s28
dA(s) 4s3 12s ds s 6 1 8 2 0 1 6
由此可得到劳斯阵列
s5 2 12 16 0 s4 1 6 8
劳斯判据给出的系统稳定的充分条件是：劳斯阵列中第一列所有项 均为正号。 劳斯阵列是将式的系数排成以下行和列，即为劳斯阵列：
自动控制原理
sn a0 a2 a4 a6
s n1 a1 a 3 a 5 a 7
s n2 b1 b2 b3
b4
s n3 c1 c2 c3
c4
s 2 e1 e2 s1 f1 s0 g
ltim x0 t
这样的系统是不稳定的。
自动控制原理
由此可得以下结论： 1.控制系统稳定的充分必要条件是：系统特征方程式的根全部
具有负实部。系统特征方程式的根就是闭环极点，所以控制系统稳 定的充分必要条件也可以说成是闭环极点全部具有负实部，或说闭 环传递函数的极点全部在[S]平面的左半面。
2.如特征根相同上述结论仍成立。 3.判断稳定性的关键转变为研究系统的特征根是否具有正实部。
例 设控制系统的特征方程为
s4 2 s2 s2 2 s 1 0
用劳斯判据判断其稳定性
自动控制原理
解 由劳斯阵列
s4 1 1 1 s3 2 2 0 s2 0 1
s1 2 2
s0 1
符号改变一次 符号改变一次
由于劳斯阵列第一列元素的符号不一致,系统不稳定,并且符号改 变两次,所以有两个正实部特征根
例 设控制系统的特征方程为
D s s4 2 s3 3 s2 4 s 3 0
试用劳斯判据判断其稳定性
解 首先，由方程系数可知已满足稳定的必要条件。其次，排
劳斯阵列
s4 1 3 3
s3 2 4 0
s2 1 1
s1 2
s0 3
自动控制原理
由劳斯阵列第一列可知，其系数出现负值，因此系统不稳定， 并且符号变化两次，所以有两个正实部特征根。
自动控制原理
§5-3 代数稳定判据
一.劳斯判据 1.系统稳定的必要条件: (1)特征方程的各项系数都不等于零。 (2)特征方程的各项系数都不大于零。 2.系统稳定的充要条件: 设系统稳定的特征方程式为
D s a 0 s n a 1 s n 1 a 2 s n 2 a n 1 s a n 0 5 . 4
自动控制原理
其中系数 b1 , b2 , b3 等，根据
下列公式计算：
b1
a1a 2 a 0a 3 a1
b2
a1a 4 a 0a 5 a1
b3
a1a 6 a 0a 7 a1
同样的方法可以计算c,d,e等各行的系数
自动控制原理
注意:
在展开的阵列中,为简化其后的数值计算,可用一个正整数去除 或乘某一个整行,并不影响稳定性结论。劳斯判据还说明：方程式 (5.4)中,其正实部特征根数,等于劳斯阵列中第一列的系数改变的 次数。
自动控制原理
(2)劳斯阵列出现整排零 例 设控制系统的特征方程为
s 6 2 s 5 8 s 4 1 2 s 3 2 0 s 2 1 6 s 1 6 0
试用劳斯判据判断其稳定性 解 计算劳斯阵列如下
s6 1 8 20 16 s5 2 12 16 0 s4 1 6 8 s3 0 0 0
自动控制原理
式中
p
d dt
，若记
Dpanpnan1pn1 a1pa0
Mpbmpmbm1pm1 b1pb0
并对5.1作拉氏变换，得
X 0s M D s s X is N D ( (s s) )
5 .2
自动控制原理
式中
M D
s s
GБайду номын сангаас
s
为系统的传递函数。
因为是在零初始条件下，有 则
Xi 0
X0
s
N (s) D(s)
自动控制原理 第五章
控制系统的稳定性分析
❖§5-1 系统稳定性的基本概念 ❖§5-2 系统的稳定条件 ❖§5-3 代数稳定判据 ❖§5-4 乃奎斯特判据 ❖§5-5 对数幅相频率特性的稳定判据 ❖§5-6 控制系统的相对稳定性 ❖例题分析 ❖课后习题
自动控制原理
§5-1 系统稳定性的基本概念
如果一个系统受到扰动，偏离了原来的平衡状态，而当扰动取消 后，这个系统又能够逐渐恢复到原来的状态，则称系统是稳定的。否 则这个系统是不稳定的。
2. 控制理论中所讨论的稳定性其实都是指自由振荡下的稳定性, 也就是说,是讨论输入为零,系统仅存在初始偏差不为零时的稳定性, 即讨论自由振荡是收敛还是发散的。
自动控制原理
§5-2 系统的稳定条件
设定常线性系统的微分方程为：
a n p n a n 1 p n 1 a 1 p a 0 x 0 t b m p m b 1 p b 0 x i t 5 . 1
自动控制原理
控制系统稳定性的定义： 若控制系统在任何足够小的初始偏差的作用下，其过渡过程随
着时间的推移，逐渐衰减并趋于零，具有恢复原平衡状态的性能， 则称该系统稳定。否则，称该系统不稳定。
注意： 1. 稳定性是系统自身的固有特性,它取决于系统本身的结构和
参数,而与输入无关；对于纯线性系统来说，系统的稳定与否不与初 始偏差的大小有关。如果，这个系统是稳定的，就叫做大范围稳定。 而经过线性化处理的系统都是“小偏差”稳定。
s3 0 0 0
4 12
s2 3 8
s1 4 /3
s0 8
自动控制原理
x 0t L 1 [X 0s] L 1 N D s s i n 1A ie sit
拉氏反变换，有
5 .3
Resi 0
由上式可知，若系统所有特征根的实部均为负值，即
自动控制原理
这样的系统就是稳定的。
ltim x0 t 0
反之，若特征根中有一个或多个根具有正实部时，则零输入将随时 间的推移发散，即
3.二阶，三阶和四阶系统的劳斯判据
低阶系统的劳斯判据可以化简
(1)二阶系统, a00a10a20 (2)三阶系统,各项系数大于零, a1a2 a0a3 (3)四阶系统,各项系数大于零, a1a2 a0a3 , 4.特殊情况
a1a2a3a0a32a12a40
(1)如果在劳斯判据阵列中任意一行的第一个元素为零,可以用一
在此情况下,可用该行上一行的元素构造一个辅助多项式,并利用这个 多项式方程的导数的系数组成劳斯阵列表中的下一行。利用辅助多 项式够成的辅助方程，解出特征根。
由此可得到辅助多项式
Ass46s28
dA(s) 4s3 12s ds s 6 1 8 2 0 1 6
由此可得到劳斯阵列
s5 2 12 16 0 s4 1 6 8
劳斯判据给出的系统稳定的充分条件是：劳斯阵列中第一列所有项 均为正号。 劳斯阵列是将式的系数排成以下行和列，即为劳斯阵列：
自动控制原理
sn a0 a2 a4 a6
s n1 a1 a 3 a 5 a 7
s n2 b1 b2 b3
b4
s n3 c1 c2 c3
c4
s 2 e1 e2 s1 f1 s0 g
ltim x0 t
这样的系统是不稳定的。
自动控制原理
由此可得以下结论： 1.控制系统稳定的充分必要条件是：系统特征方程式的根全部
具有负实部。系统特征方程式的根就是闭环极点，所以控制系统稳 定的充分必要条件也可以说成是闭环极点全部具有负实部，或说闭 环传递函数的极点全部在[S]平面的左半面。
2.如特征根相同上述结论仍成立。 3.判断稳定性的关键转变为研究系统的特征根是否具有正实部。