反射和折射时的偏振光布儒斯

布儒斯特角原理布儒斯特角原理（Brewster's Angle）是光学中的一个重要概念，它描述了入射光线与介质表面的夹角与反射光线的偏振状态之间的关系。

根据这一原理，当光线以一定角度入射到介质表面时，反射光线将完全偏振为垂直于入射面的偏振态。

本文将详细探讨布儒斯特角原理的基本原理、应用以及实验验证。

布儒斯特角原理是由苏格兰物理学家大卫·布儒斯特（David Brewster）在19世纪初提出的。

他发现，当光线从一个介质垂直入射到另一个介质表面时，存在一个特殊的入射角使得反射光线完全偏振。

这个入射角被称为布儒斯特角，用θ表示。

根据布儒斯特角原理，当入射角等于布儒斯特角时，反射光线的偏振状态为垂直于入射面的偏振态。

布儒斯特角原理的解释基于光的偏振性质和折射定律。

光是一种电磁波，具有电场和磁场振动方向垂直的特性。

当光线从一个介质进入另一个介质时，根据折射定律，入射角和折射角之间存在一定的关系。

而对于特定的入射角，折射光线的偏振态与入射光线的偏振态有关。

在布儒斯特角下，折射光线与反射光线之间的振动方向恰好垂直，因此反射光线完全偏振。

布儒斯特角原理在实际应用中具有重要意义。

例如，它可以用来设计反射镜、滤光片和偏振片等光学元件。

利用布儒斯特角原理，可以选择特定的入射角度，使得反射光线具有所需的偏振态，从而实现对光的控制。

此外，布儒斯特角原理还可以用于测量材料的折射率和表面薄膜的厚度。

为了验证布儒斯特角原理，可以进行简单实验。

首先，选取一个透明的材料作为实验样品，如玻璃或塑料片。

然后，将样品固定在一个可以旋转的支架上，并利用一个光源照射到样品上。

通过调节光源的位置和入射角度，观察反射光线的偏振态变化。

当入射角等于布儒斯特角时，可以观察到反射光线变为完全偏振的现象。

通过测量入射角和折射角，可以计算出样品的折射率，并与理论值进行比较，从而验证布儒斯特角原理的准确性。

布儒斯特角原理是光学中的重要概念，描述了入射光线与介质表面的夹角与反射光线的偏振状态之间的关系。

什么事布儒斯特角
简介
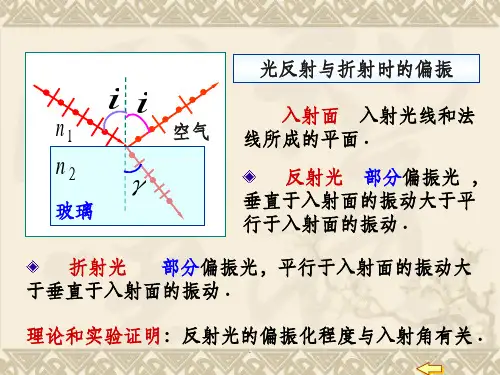
自然光经电介质界面反射后，反射光为线偏振光所应满足的条件。

首先由英国物理学家D.布儒斯特于1815 年发现。

自然光在电介质界面上反射和折射时，一般情况下反射光和折射光都是部分偏振光，只有当入射角为某特定角时反射光才是线偏振光，其振动方向与入射面垂直，此特定角称为布儒斯特角或起偏角，用θb表示。

此规律称为布儒斯特定律。

光以布儒斯特角入射时，反射光与折射光互相垂直。

玻片堆是由许多表面互相平行的玻璃片组成，自然光以布儒斯特角入射时，垂直于入射面的振动分量在每个界面上均要发生反射，而平行于入射面的振动分量则完全不能反射，故从玻片堆透出的光基本上只包含平行分量。

玻片堆可用作起偏器。

自然光在两种各向同性媒质分界面上反射、折射时，反射光和折射光都是部分偏振光。

反射光中垂直振动多于平行振动，折射光中平行振动多于垂直振动。

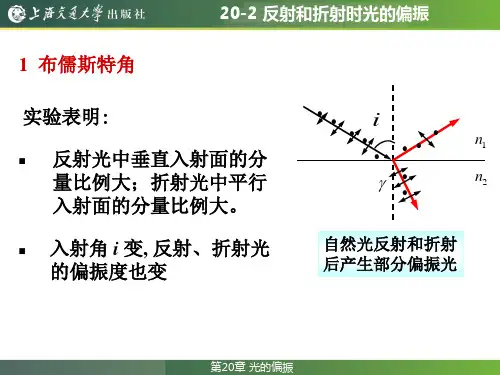
当入射角满足关系式tgi0=n2/n1 时，反射光为振动垂直于入射面的线偏振光，
该式称为布儒斯特定律（Brewster law) ，i0为起偏振角或布儒斯特角。

当光线以起偏振角入射时，反射光和折射光的传播方向互相垂直，即：i0+r=90
编辑本段
求法
布儒斯特角等于两种介质的折光率之比的反正切。

设θ1为入射角，θ2为折射角。

我们有
如果反射角和折射角垂直，则：
整理，得：
其中n1和n2为该两种介质的折射率。

布儒斯特定律的主要内容
布鲁斯特定律主要内容涉及到光的反射和折射现象。

由法国科学家布鲁斯特在19世纪早期提出。

其主要内容包括：
1. 光线的入射角和反射角之间存在一个特定的关系，即光线入射介质的折射率与反射角的正切成正比。

即tan(反射角) = n
（反射介质）/n（入射介质）。

2. 当入射角为特定的角度时，即称为布鲁斯特角（也叫做极化角），入射光线发生完全偏振，只有垂直于某一方向的振动（平行于反射面）。

在此角度上反射的光线呈现为完全偏振光，而反射光中平行于反射面的振动被部分或完全消除。

3. 布鲁斯特角的大小与两个介质的折射率有关，反射面上平行于此面的入射光波高分子极化介质中的极化界面的折射率之比等于与平面垂直入射光波的振幅之比。

4. 布鲁斯特角出现时，反射光线的反射率达到最小值，且此时反射光线与入射光线之间的振幅比为1:n，其中n为入射介质
和反射介质的折射率之比。

布鲁斯特定律的主要内容是描述了当光线从一种介质到另一种介质的界面上发生反射和折射时，光线的入射角、反射角以及反射光线的振幅之间的关系。

反射光的偏振特性—布儒斯特角的测量实验实验科目：光的反射、折射定律，折射率的测量，光的偏振、线偏振光、圆偏振光、椭圆偏振光、1/4波片、反射光的偏振态，布儒斯特角。

反射光的偏振特性与布儒斯特角实验目的：1）用最小偏向角法测量棱镜材料的折射率。

2）测量通过起偏器、1/4波片后的光的偏振特性，了解线偏振光、圆偏振光和椭圆偏振光的特点。

3）通过观察从棱镜材料表面反射回来的光的偏振特性，了解反射光的偏振特性，测量出布儒斯特角。

4）用测量值验证布儒斯特角公式的正确性。

实验原理：一、棱镜材料的折射率的测量当一束光斜入射于棱镜表面时，其光路如下图。

同理出射角γ/ 为sinγ/= sini//n （1）根据几何关系可以证明入射光与出射光之间的夹角为：δ=i＋γ/－A，而且δ有一个极小值δmin ，可以证明：当光束偏转角为δmin时，有i=γ/γ= i/，此时δ=2i－A 即i=（δ＋A）/2而A=γ＋i/=2γγ=A/2由（1）式可得：n=sin[(A+δmin)/2]/sin(A/2)因此，只要我们测量出δmin，就可得到材料相对于该测量光的折射率n。

二、偏振光光是一种横波，它的振动方向是与传播方向相互垂直的。

偏振是指光波的振动方向在空间上的一种相对取向的现象。

当这个振动方向在垂直于传播方向的平面内可取所有可能的方向，并且没有一个方向占优势时，我们称之为自然光或非偏振光。

而如果有某一个方向上的振动占优势时，则称之为部分偏振光。

只有一个单一的振动方向的光叫线偏振光，而在一个振动周期内其振动矢量的端点的轨迹为一个圆或椭圆时，我们称之为圆偏振光或椭圆偏振光。

在我们日常生活和工作中，太阳光、照明用光一般多为自然光。

而自然光经过一些材料的反射和透射后可能变成部分偏振光。

自然光经过一些特殊材料，如偏振片或双折射晶体材料制作的棱镜后，就会变成线偏振光，一些激光器也可产生很好的线偏振光。

线偏振光经过波片后就可能成为椭圆偏振光。

反射光的偏振特性—布儒斯特角的测量实验实验科目：光的反射、折射定律，折射率的测量，光的偏振、线偏振光、圆偏振光、椭圆偏振光、1/4波片、反射光的偏振态，布儒斯特角。

反射光的偏振特性与布儒斯特角实验目的：1）用最小偏向角法测量棱镜材料的折射率。

2）测量通过起偏器、1/4波片后的光的偏振特性，了解线偏振光、圆偏振光和椭圆偏振光的特点。

3）通过观察从棱镜材料表面反射回来的光的偏振特性，了解反射光的偏振特性，测量出布儒斯特角。

4） 用测量值验证布儒斯特角公式的正确性。

实验原理：一、棱镜材料的折射率的测量当一束光斜入射于棱镜表面时，其光路如下图。

Aiγi 'γ'根据光的折射定律其偏转角γ为： sin γ＝sini/nn 为材料的折射率。

同理出射角γ/为sin γ/= sini //n （1）根据几何关系可以证明入射光与出射光之间的夹角为：δ=i ＋γ/－A ，而且δ有一个极小值δmin，可以证明：当光束偏转角为δmin时，有i=γ/ γ= i /，此时 δ=2i －A 即i=（δ＋A ）/2而A=γ＋i /=2γ γ=A/2由（1）式可得：n=sin[(A+δmin)/2]/sin(A/2)因此，只要我们测量出δmin ，就可得到材料相对于该测量光的折射率n 。

二、偏振光光是一种横波，它的振动方向是与传播方向相互垂直的。

偏振是指光波的振动方向在空间上的一种相对取向的现象。

当这个振动方向在垂直于传播方向的平面内可取所有可能的方向，并且没有一个方向占优势时，我们称之为自然光或非偏振光。

而如果有某一个方向上的振动占优势时，则称之为部分偏振光。

只有一个单一的振动方向的光叫线偏振光，而在一个振动周期内其振动矢量的端点的轨迹为一个圆或椭圆时，我们称之为圆偏振光或椭圆偏振光。

在我们日常生活和工作中，太阳光、照明用光一般多为自然光。

而自然光经过一些材料的反射和透射后可能变成部分偏振光。

自然光经过一些特殊材料，如偏振片或双折射晶体材料制作的棱镜后，就会变成线偏振光，一些激光器也可产生很好的线偏振光。

反射光的偏振特性—布儒斯特角的测量实验实验科目：光的反射、折射定律，折射率的测量，光的偏振、线偏振光、圆偏振光、椭圆偏振光、1/4波片、反射光的偏振态，布儒斯特角。

反射光的偏振特性与布儒斯特角实验目的：1）用最小偏向角法测量棱镜材料的折射率。

2）测量通过起偏器、1/4波片后的光的偏振特性，了解线偏振光、圆偏振光和椭圆偏振光的特点。

3）通过观察从棱镜材料表面反射回来的光的偏振特性，了解反射光的偏振特性，测量出布儒斯特角。

4）用测量值验证布儒斯特角公式的正确性。

实验原理：一、棱镜材料的折射率的测量当一束光斜入射于棱镜表面时，其光路如下图。

sini/n同理出射角γ为sinγ= sini/n （1）/可以证明：当光束偏转角为δmin时，有i=γ/γ= i/，此时δ=2i－A 即i=（δ＋A）/2而A=γ＋i/=2γγ=A/2由（1）式可得：n=sin[(A+δmin)/2]/sin(A/2)因此，只要我们测量出δmin，就可得到材料相对于该测量光的折射率n。

二、偏振光光是一种横波，它的振动方向是与传播方向相互垂直的。

偏振是指光波的振动方向在空间上的一种相对取向的现象。

当这个振动方向在垂直于传播方向的平面内可取所有可能的方向，并且没有一个方向占优势时，我们称之为自然光或非偏振光。

而如果有某一个方向上的振动占优势时，则称之为部分偏振光。

只有一个单一的振动方向的光叫线偏振光，而在一个振动周期内其振动矢量的端点的轨迹为一个圆或椭圆时，我们称之为圆偏振光或椭圆偏振光。

在我们日常生活和工作中，太阳光、照明用光一般多为自然光。

而自然光经过一些材料的反射和透射后可能变成部分偏振光。

自然光经过一些特殊材料，如偏振片或双折射晶体材料制作的棱镜后，就会变成线偏振光，一些激光器也可产生很好的线偏振光。

线偏振光经过波片后就可能成为椭圆偏振光。

在本实验中，我们将通过多种实验手段来产生线偏振光和椭圆偏振光（圆偏振光被看成是一个特例）。

布儒斯特定律测折射率用布儒斯特定律测量透明介质折射率 1.实验目的1.观察光在界面上反射和折射时，发生的偏振现象；2.利用布儒斯特定律测量介质的折射率。

2.实验原理2.1光的偏振状态[5]光是一种电磁波,是横波,它的电矢量E和磁矢量 H相互垂直,且垂直于光的传播方向 C（图2.1-1）,偏振现象是横波所独有的特征。

在研究光现象时,通常将 E叫做光矢量,E 的振动叫做光振动。

图2.1-1在光的传播过程中,如果光矢量 E 始终在一个固定的平面沿一个固定的方向振动,这种光称为线偏振光或平面偏振光。

在垂直于传播方向的平面内,沿各方向振动的光矢量的分布各项均匀,而且各方向光振动的振幅都相同,这种光称为自然光。

光的电矢量在某个方向上出现的几率大于其他的方向,即在较长的时间内电矢量在某个方向上较强,这样的光称为部分偏振光。

如图 2.1-2 所示。

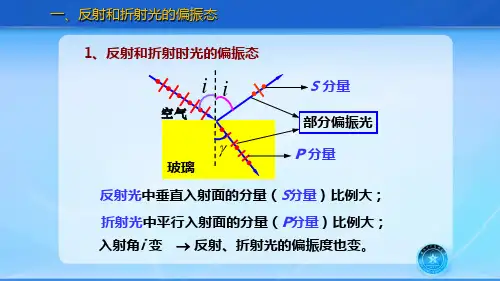
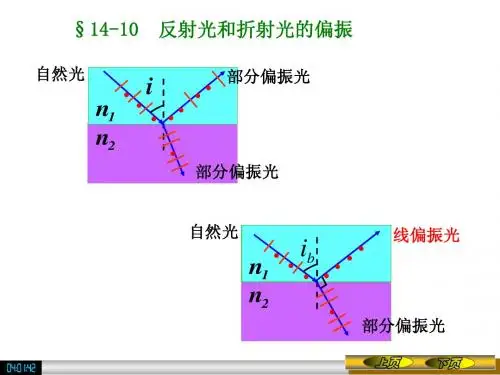
偏振光自然光部分偏振光图 2.1-22.2光在界面上反射和折射时,发生的偏振现象及布鲁斯特定律自然光在两种媒质的分界面上反射和折射时,反射光和折射光都将成为部分偏振光,在特定的情况下,反射光有可能成为完全偏振光。

例如,自然光射到玻璃界面上的反射和折射情况。

现在将自然光分解为两个振幅相等的分振动:其一和入射面入射光与界面法线方向构成的平面垂直,在图 2.2-1中用黑点表示与入射面垂直的振动;其二和入射面平行,在图中用短线表示和入射面平行的振动。

黑点和短线的多少形象地表示上述两个分振动所代表的光波的强弱光波的强弱和振幅平方成正比,在自然光中,黑点和短线是均匀分布的。

根据布儒斯特定律[2],当以布儒斯特角i0入射时,反射光为线偏振光只有垂直于入射面的振动,而折射光为部分偏振光平行于入射面的振动占主要成分,如图 2.2-1。

i0也称为起偏角。

根据布儒斯特定律，有：tan感谢您的阅读，祝您生活愉快。

反射光的偏振特性—布儒斯特角的测量实验实验科目：光的反射、折射定律，折射率的测量，光的偏振、线偏振光、圆偏振光、椭圆偏振光、1/4波片、反射光的偏振态，布儒斯特角。

反射光的偏振特性与布儒斯特角实验目的：1）用最小偏向角法测量棱镜材料的折射率。

2）测量通过起偏器、1/4波片后的光的偏振特性，了解线偏振光、圆偏振光和椭圆偏振光的特点。

3）通过观察从棱镜材料表面反射回来的光的偏振特性，了解反射光的偏振特性，测量出布儒斯特角。

4）用测量值验证布儒斯特角公式的正确性。

实验原理：一、棱镜材料的折射率的测量当一束光斜入射于棱镜表面时，其光路如下图。

同理出射角γ/ 为sinγ/= sini//n （1）根据几何关系可以证明入射光与出射光之间的夹角为：δ=i＋γ/－A，而且δ有一个极小值δmin ，可以证明：当光束偏转角为δmin时，有i=γ/γ= i/，此时δ=2i－A 即i=（δ＋A）/2而A=γ＋i/=2γγ=A/2由（1）式可得：n=sin[(A+δmin)/2]/sin(A/2)因此，只要我们测量出δmin，就可得到材料相对于该测量光的折射率n。

二、偏振光光是一种横波，它的振动方向是与传播方向相互垂直的。

偏振是指光波的振动方向在空间上的一种相对取向的现象。

当这个振动方向在垂直于传播方向的平面内可取所有可能的方向，并且没有一个方向占优势时，我们称之为自然光或非偏振光。

而如果有某一个方向上的振动占优势时，则称之为部分偏振光。

只有一个单一的振动方向的光叫线偏振光，而在一个振动周期内其振动矢量的端点的轨迹为一个圆或椭圆时，我们称之为圆偏振光或椭圆偏振光。

在我们日常生活和工作中，太阳光、照明用光一般多为自然光。

而自然光经过一些材料的反射和透射后可能变成部分偏振光。

自然光经过一些特殊材料，如偏振片或双折射晶体材料制作的棱镜后，就会变成线偏振光，一些激光器也可产生很好的线偏振光。

线偏振光经过波片后就可能成为椭圆偏振光。