幂函数、指数函数、对数函数比较大小
- 格式:ppt
- 大小:183.50 KB
- 文档页数:3


指数函数、对数函数、幂函数作者:来源:《数学金刊·高考版》2013年第03期指数函数、对数函数、幂函数是三类常见的重要函数,在历年的高考题中都占据着重要的地位. 从近几年的高考形势来看,对指数函数、对数函数、幂函数的考查,大多以基本函数的性质为依托,结合运算推理,能运用它们的性质解决具体问题. 题目多以指数函数、对数函数、幂函数为载体的复合函数来考查函数的性质. 若它们与其他知识点交汇命题,则难度会加大.■指数函数与对数函数互为反函数,运算可相互转化,性质可相互理解,方法可相互借鉴.(1)学会指数式与对数式的相互转化;(2)结合指数、对数的“互反”性质记忆有关的概念、图象和性质. (3)若底是参数时,则一定要区分底是大于1还是小于1的情况,与对数有关的问题还要紧扣对数函数的定义域.■■ 若已知函数f(x)=ax,xA. 0,■B. (0,1)C. ■,1D. (0,3)破解思路本题的考查意图:一是解决指数函数的相关问题时,要对底数a进行讨论;二是考虑分段函数的单调性问题,这是学习的一个难点,应紧扣定义理解.经典答案由条件知, f(x)在R上为减函数,则0■ 若已知函数f(x)=log■1-■,其中0(1)证明:f(x)是(a,+∞)上的减函数;(2)解不等式f(x)>1.破解思路证明函数单调性的常用方法有定义法:一般是作差、分解、判断;导数法:若f (x)在某个区间A内有导数,则f ′(x)≥0(x∈A)?圳f(x)在A内为增函数;f ′(x)≤0(x∈A)?圳f(x)在A内为减函数.经典答案(1)任取x1,x2∈(a,+∞),且x10,因此有f(x1)>f(x2),所以f(x)是(a,+∞)上的减函数.(2)由已知01可得log■1-■>logaa,则0■1. 设集合A={x0≤xA. log■■,1B. (log32,1)C. ■,1D. 0,■2. 已知函数f(x)=xlnx.(1)求函数f(x)的单调区间;(2)若函数F(x)=■在[1,e]上的最小值为■,求a的值.。

指数函数、幂函数和对数函数是高中数学中的重要概念,它们在数学和现实生活中都有着重要的应用。
在本篇文章中,我们将深入探讨这三种函数的性质,以及它们之间的比较大小关系。
通过本文的阅读,你将能够更全面地理解这些函数的特点,并从中获得更深入的数学启发。
1. 指数函数指数函数是数学中常见的一种函数,其一般形式可表示为 y = a^x,其中a为常数且不等于1。
指数函数的特点是随着自变量x的增大,函数值y以指数方式增长或者下降。
指数函数在自然科学、工程技术以及金融领域都有着广泛的应用,例如放射性衰变、人口增长模型等都可以使用指数函数来描述。
在指数函数中,底数a的大小决定了函数的增长速度,当a大于1时,函数呈现增长趋势;当a在0和1之间时,函数呈现下降趋势。
2. 幂函数幂函数是指数函数的一种特殊形式,其一般形式可以表示为y = x^a,其中a为常数。
幂函数的特点是自变量x的次幂影响了函数值y的大小,不同的a值会导致函数曲线的形状发生变化。
当a为正数时,幂函数呈现增长趋势;当a为负数时,幂函数呈现下降趋势。
幂函数在物理学、生物学以及经济学中都有着重要的应用,例如牛顿定律中的物体受力情况、生物种群数量增长模型等都可以用幂函数来描述。
3. 对数函数对数函数是幂函数的逆运算,常见的对数函数有以10为底的常用对数函数和以e为底的自然对数函数。
对数函数的一般形式可以表示为 y= loga(x),其中a为底数。
对数函数的特点是能够将幂函数转化为线性函数,便于进行求解和分析。
对数函数在科学领域、信息论以及计算机科学中有着广泛的应用,例如信噪比的计算、数据压缩算法等都离不开对数函数的运算。
指数函数、幂函数和对数函数各自具有独特的特点和应用,它们在数学领域和现实生活中都扮演着重要的角色。
在比较大小方面,一般来说,指数函数增长速度最快,其次是幂函数,对数函数增长速度最慢。
在实际问题中,我们可以根据具体情况选择合适的函数来进行建模和求解。




.指数对数幂函数比拟大小学校 :___________ 姓名: ___________班级: ___________考号: ___________一、单项选择题111.设 alog 11 1 2c1 3〕, b2, 3 ,那么 a, b, c 的大小关系是〔23A.a b cB. c b aC. b c aD. c a b12.设 a=lo g 1 3,b=1,c= 2 3 ,那么()23A. a<b<cB. c<b<aC. c<a<bD. b<a<c3.正数 a 、b 、c 满足 log 2 a log 3blog 5 c 0 ,那么〔〕A.a b cB. a c bC.c a bD. c b a4. 0 a b 1, pa b , q b a , r log b a , 那么p, q, r 的大小关系是A.p q rB.p r qC. r p qD. q p r5. m log 5 , n 5.1 3 , p,那么实数 m , n , p 的大小关系为 〔〕.A.m n pB. m p nC. n m pD. n p m2221,那么 a, b, c 的大小关系是〔6 . alog 2 ,b, c log 〕3 3 21 3A.a b cB. b c aC. c a bD. c b a7. a 2 , b 2 , c2log 5 2 ,那么a,b,c 的大小关系为〔〕A. c b aB. c a bC. b a cD. b c a8.三个数 a 2, b log 2 0.3 , c 2 之间的大小关系是〔〕A. a c bB. a b cC. b a cD. b c a19. 9. alog 2 3 , b log 1 3 , c 3 2 ,那么2A. c b aB. c a bC. a b cD. a c b110. alog 5 2, b log 2 3, c 42,那么〔〕A. a b cB. a c bC. c a bD. c b a'.11. a2 ,b3 , c log 1 3 , 那么 a,b, c 的大小为〔 〕2A.b c a B. a c b C. b a cD. a b c12.假设 a 210 , b log 3, clog 2sin,那么〔〕5A.a b cB. b a cC. c a bD. b c a1 1 11 313.设 a32〕2,b3 , cln,那么〔A.c a b B. c b a C. a b cD. b a c14.假设幂函数的图像过点1, 4 ,那么fx =()2A. 16xB. x 1C. x 2D. x 215. f xlog 2 4 ax 在区间1,3 上是增函数,那么 a 的取值范围〔 〕A.,0B.,0C.4,0D.4,016.函数 y log 1x 2 3x 2 的单调递增区间是〔〕3A.,1B.,3 D.3C. 2,,2217.函数 f xlog 1 x 2 4x 的单调递增区间为3A.,2B.2,C.,0D.4,18.函数 fxlog 1 x 1 , afsin5, b f log 23 , cf2log 2,36那么 a, b, c 的大小关系是〔 〕A.a b c B. b a c C. c b a D. a c b二、填空题19.假设幂函数ym 2 3m 3 x m 2 m 1 的图象不过原点,那么 m 是 __________.20.函数 f xlgx 2 2x 3 的单调递减区间是 __________ ..参考答案1. B【解析】由对数函数的性质可知:11a log213log12 21,0 ,且: b6131 , c 6 21 , 很明显 b0, c12839b 6c 6 , 0 c b 1 ,综上可得:c b a .此题选择 B 选项 .点睛:对于指数幂的大小的比拟, 我们通常都是运用指数函数的单调性, 但很多 时候,因幂的底数或指数不相同, 不能直接利用函数的单调性进行比拟. 这就必 须掌握一些特殊方法.在进行指数幂的大小比拟时,假设底数不同, 那么首先考虑将其转化成同底数, 然后再根据指数函数的单调性进行判断.对于不同底而同指数的指数幂的大小的比 较,利用图象法求解,既快捷,又准确.2. A1【解析】∵ alog 1 3 log 1 1 0 , 0 b1 1 1 ,c23 2012233∴ a b c 应选 A点睛: 此题考查了指数函数的性质和对数函数的性质及其应用, 属于根底题, 解答此题的关键熟记指数函数与对数函数的图象与性质, 利用指数函数与对数函数的性质, 判定 a, b, c 的范围,不明确用中间量“ 1〞, “0〞进行传递比拟,从而得到a,b, c 的大小关系.3. C【解析】给定特殊值,不妨设 log 2 a log 3b log 5c 1 ,那么:a 2,b3,c1, cab .5此题选择 C 选项 .4. A【解析】ab1balogb a ,函数ya xba a, p a , q b , r 递减,那么a, 函数 y x b 递 增 , 那么 a a b a 1 , 函 数 ylog b x 递 减 , 那么 log b a log b b 1 , 故'.a b b a log b a ,即 p q r ,应选 A. 5. A【解析】∵ m log 5log 10 ,0n 5.1 3p ,∴ m n p ,应选 A.6. D【解析】试题分析:0 ,0 b 1,c 11,故c b a.a log 21log122考点:比拟大小. 7. B【解析】B.8. C【解析】∵a 2 1,b 2 22, c 2log5 2 log 5 4 1 , b a c ,应选20.09 1 , b log 2 0.3 log 21 0 , c 2 201∴ b a c应选 C点睛:此题考查了指数函数的性质和对数函数的性质及其应用,属于根底题,解答此题的关键熟记指数函数与对数函数的图象与性质,利用指数函数与对数函数的性质,判定a, b, c的范围,不明确用中间量“1〞,“0〞进行传递比拟,从而得到a,b, c 的大小关系.9. D1【解析】由题意可得: a log2 3 1,b log1 3 0,c 3 20,1 ,2那么: a c b .此题选择 D 选项 .10. B1【解析】∵ a log 5 2, b log 2 3,c 4 21, log 2 31又∵log 51 log5 2 log 55log 2 2 1 , 4 221 2.∴0 a1, b 1, c122∴ a c b应选 B 11. D【解析】 a20,b 30,c log 1 3 0 , a 22,b 30.6 5 33 5 32 2 .2所以 a b c .应选 D. 12. A【解析】∵ a 2100 πππ < log 2 1=0 ,> 2 =1 , 0=log 1< b=log 3<log π =1, c log 2sin5∴a> b >c . 应选 A . 13. B【解析】由 3 1可得 c ln30 ,很明显 a 0, b 0 ,很明显函数 f xlnx 0, e 上单调递增,在区间x1 1ln1ln1故 f f ,即:23 ,231 1 231 1 1那么:11 1 ln 13 ln2 2,据此有:lnln33231 2,1 1131 2b ,结合对数函数的单调性有:3,即 a2综上可得:a b c .此题选择 B 选项 .点睛:对于指数幂的大小的比拟, 我们通常都是运用指数函数的单调性, 但很多时候,因幂的底数或指数不相同, 不能直接利用函数的单调性进行比拟. 这就必须掌握一些特殊方法.在进行指数幂的大小比拟时,假设底数不同, 那么首先考虑将其转化成同底数, 然后再根据指数函数的单调性进行判断. 对于不同底而同指数的指数幂的大小的比拟,利用图象法求解,既快捷,又准确.14. D【解析】设幂函数f x x ,'.图像过点1 , 4 2所以f11 4 ,解得 2 .22所以 f x x 2.应选 D.15. D【解析】令 t4ax ,那么原函数由y f t和 t4ax 复合而成的复合函数,函数f x log24ax 在1,3 上是增函数,{a04 a 0, a 的取值a,解得40范围是4,0,应选 D.16. A【解析】函数的定义域为,12,令 t x23x 2 ,那么y log 1 t3t x23x2在,1上单调递减,在2,上单调递增,y log 1 t 为减函数,3根据“同增异减〞可知:函数 y log 1x2 3x 2 的单调递增区间是,13应选: A点睛::复合函数的单调性的判断口诀为“同增异减〞,即内外层单调性一致为增函数,内外层单调性相反为减函数,易错点忽略了函数的定义域,单调区间必然是定义域的子集. 17. C【解析】函数的定义域为,04,令 t x24x ,那么y log 1t3t x24x 在,0上单调递减,在 4,上单调递增,又 y log 1 t 在定义域上单调递减,根据“同增异减〞可知:3.函数 fxlog 1 x 2 4x 的单调递增区间为,03应选: C点睛: 复合函数的单调性的判断口诀为“同增异减〞, 即内外层单调性一致为增函数,内外层单调性相反为减函数,易错点忽略了函数的定义域,单调区间必然是定义域的子集.18. A【解析】函数 fxlog 1 x 1 关于直线 x1 轴对称,且在,1 上单调递增, 在 1,3上单调递减,afsin5f1 = f3, bf log 23f log 2 3 ,622cf2log 2f π又3log 2 3 πf xlog 1 x 1在1,上单调递减,2,3∴ ab c应选: A19. 1【解析】幂函数ym23m 3 x m 2m 1 的图象不过原点,{ m 2m 1 0 ,解得m 23m 3 1m 1,故答案为 1.20. 1,3【解析】由 x 2 2x 30 ,解得 1 x 3又 x 2 2x 3x 124所以减区间是1,3'.。

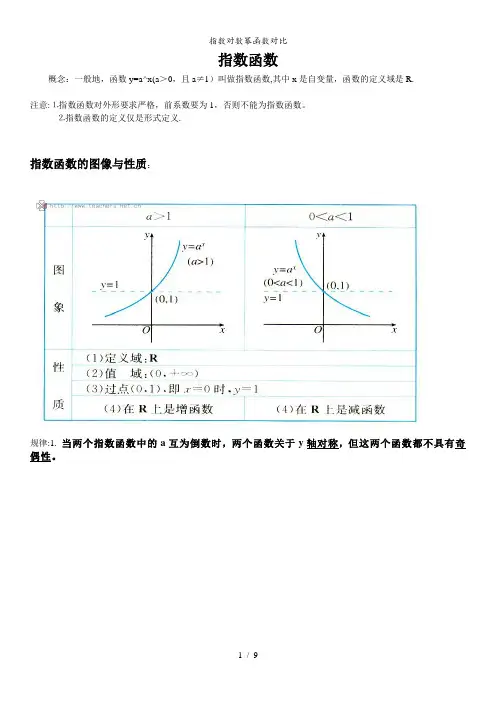
指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义.指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2。
当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴.在y轴右边“底大图高";在y轴左边“底大图低”。
3.四字口诀:“大增小减"。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4。
指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2. 当底数中含有字母时要注意分类讨论;3. 当底数不同,指数也不同时,则需要引入中间量进行比较;4. 对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x 在定义域(—∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x (a >0,a ≠1)的反函数称为对数函数,并记为y=log a x(a >0,a ≠1).因为指数函数y=a x 的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x 的定义域为(0,+∞),值域为(-∞,+∞)。
2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x 。
据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a >0,a ≠1)的性质,我们在同一直角坐标系中作出函数y=log 2x,y=log 10x ,y=log 10x ,y=log 21x ,y=log101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a>0,a≠1)的图像的特征和性质。

[读教材·填要点]1.三种函数的增长特点(1)当a>1时,指数函数y=a x是增函数,并且当a越大时,其函数值的增长就越快.(2)当a>1时,对数函数y=log a x是增函数,并且当a越小时,其函数值的增长就越快.(3)当x>0,n>1时,幂函数y=x n显然也是增函数,并且当x>1时,n越大其函数值的增长就越快.2.三种函数的增长比较在区间(0,+∞)上,尽管函数y=a x(a>1),y=log a x(a>1)和y=x n(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上,幂函数y=x n(n>0),指数函数y=a x(a >1)增长的快慢交替出现,随着x的增大,y=a x(a>1)的增长速度越来越快,会超过并远远大于y=x n(n>0)的增长速度,而y=log a x(a>1)的增长速度则会越来越慢.一般地,若a>1,n>0,那么当x足够大时,一定有a x>x n>log a x.[小问题·大思维]1.2x>log2x,x2>log2x,在(0,+∞)上一定成立吗?提示:结合图像知一定成立.2.2x>x2在(0,+∞)上一定成立吗?提示:不一定,当0<x<2和x>4时成立,而当2<x<4时,2x<x2.[研一题][例1]四个变量y1,y2,y3,y4随变量x变化的数据如下表:关于x呈指数型函数变化的变量是________.[自主解答]以爆炸式增长的变量是呈指数型函数变化的.从表格可以看出,四个变量y1,y2,y3,y4均是从5开始变化,变量y4越来越小,但是减小的速度很慢,则变量y4关于x不呈指数型函数变化;而变量y1,y2,y3都是越来越大,但是增大的速度不同,其中变量y2的增长最快,画出图像可知变量y2关于x呈指数型函数变化.[答案]y2[悟一法]解决该类问题的关键是根据所给出的数据或图像的增长的快慢情况,结合指数函数、幂函数、对数函数增长的差异,从中作出判断.[通一类]1.下面是f(x)随x的增大而得到的函数值列表:试问:(1)随着x的增大,各函数的函数值有什么共同的变化趋势?(2)各函数增长的快慢有什么不同?解:(1)随x的增大,各函数的函数值都在增大;(2)由图表可以看出,各函数增长的快慢不同,其中f(x)=2x增长最快,而且越来越快;增长最慢的是f(x)=log2x,而且增长的幅度越来越小.[研一题][例2]假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?[自主解答]设第x天所得回报是y元.由题意,方案一:y=40(x∈N+);方案二:y=10x(x∈N+);方案三:y=0.4×2x-1(x∈N+).作出三个函数的图像如图:由图可以看出,从每天回报看,在第一天到第三天,方案一最多,在第四天,方案一,二一样多,方案三最少,在第五天到第八天,方案二最多,第九天开始,方案三比其他两个方案所得回报多得多,经验证到第三十天,所得回报已超过2亿元,∴若是短期投资可选择方案一或方案二,长期的投资则选择方案三.通过计算器计算列出三种方案的累积收入表.∴投资一天到六天,应选方案一,投资七天方案一,二均可,投资八天到十天应选方案二,投资十一天及其以上,应选方案三.[悟一法](1)解决应用问题的关键是将应用问题转化成数学问题解决,结合函数图像有助于直观认识函数值在不同范围的大小关系.(2)一般地:指数函数增长模型适合于描述增长速度快的变化规律;对数函数增长模型适合于描述增长速度平缓的变化规律;而幂函数增长模型介于两者之间,适合于描述增长速度一般的变化规律.[通一类]2.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102 kg)与上市时间t(单位:天)的数据如下表:(1)根据表中数据,从下列函数中选取一个函数,描述西红柿种植成本Q 与上市时间t 的变化关系;Q =at +b ,Q =at 2+bt +c ,Q =a ·b t ,Q =a ·log b t .(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本. 解:(1)由表中数据知,当时间t 变化时,种植成本并不是单调的,故只能选择Q =at 2+bt +c .即⎩⎪⎨⎪⎧150=a ×502+b ×50+c ,108=a ×1102+b ×110+c ,150=a ×2502+b ×250+c . 解得Q =1200t 2-32t +4252; (2)Q =1200(t -150)2+4252-2252=1200(t -150)2+100, ∴当t =150天时,西红柿的种植成本最低,为100元/102kg.若x 2<log m x 在x ∈(0,12)内恒成立,求实数m 的取值范围.[巧思] 将不等式恒成立问题转化为两个函数图像在(0,12)内的上下位置关系,再构建不等式求解.[妙解] 设y 1=x 2,y 2=log m x ,作出符合题意的两函数的大致图像(如图),可知0<m <1.当x =12时,y 1=14,若两函数在x =12处相交,则y 2=14.由14=log m 12得m =116,又x 2<log m x 在x ∈(0,12)内恒成立,因此,实数m 的取值范围为116≤m <1.1.下面对函数f (x )=log 1x 与g (x )=(12)x 在区间(0,+∞)上的增减情况的说法中正确的是( )A .f (x )的增减速度越来越慢,g (x )的增减速度越来越快B .f (x )的增减速度越来越快,g (x )的增减速度越来越慢C .f (x )的增减速度越来越慢,g (x )的增减速度越来越慢D .f (x )的增减速度越来越快,g (x )的增减速度越来越快解析:在同一坐标下分别作出函数y =log 12x 和y =(12)x 的图像,由图像知C 正确.答案:C2.下列所给函数,增长最快的是( )A .y =5xB .y =x 5C .y =log 5xD .y =5x 答案:D3.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷,0.4万公顷和0.76万公顷,则沙漠增加数y 关于年数x 的函数关系较为近似的是( )A .y =0.2xB .y =110(x 2+2x )C .y =2x10D .y =0.2+log 16x解析:当x =1时,否定B ;当x =2时,否定D ;当x =3时,否定A. 答案:C4.已知函数f (x )=3x ,g (x )=2x ,当x ∈R 时,f (x )与g (x )的大小关系为________. 解析:在同一直角坐标系中画出函数f (x )=3x ,g (x )=2x 的图像,如图所示,由于函数f (x )=3x 的图像在函数g (x )=2x 图像的上方,则f (x )>g (x ). 答案:f (x )>g (x )5.据报道,青海湖水在最近50年内减少了10%,如果按此规律,设2013年的湖水量为m ,从2013年起,过x 年后湖水量y 与x 的函数关系是________.解析:设湖水量每年为上年的q %,则(q %)50=0.9,∴q%=0.9150,∴x年后湖水量y=m·(q%)x=m·0.9x50.答案:y=0.9x50·m6.函数f(x)=lg x,g(x)=0.3x-1的图像如图所示.(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;(2)比较两函数的增长差异(以两图像交点为分界点,对f(x),g(x)的大小进行比较).解:(1)C1对应的函数为g(x)=0.3x-1,C2对应的函数为f(x)=lg x;(2)当x<x1时,g(x)>f(x);当x1<x<x2时,f(x)>g(x);当x>x2时,g(x)>f(x).一、选择题1.当x越来越大时,下列函数中,增长速度最快的应该是()A.y=10x B.y=lg xC.y=x10D.y=10x解析:由于指数型函数的增长是爆炸式增长,则当x越来越大时,函数y=10x的增长速度最快.答案:D2.某山区为加强环境保护,绿色植被的面积每年都比上一年增长10.4%,那么,经过x年,绿色植被的面积可增长为原来的y倍,则函数y=f(x)的大致图像为()解析:y=f(x)=(1+10.4%)x=1.104x是指数型函数,定义域为{0,1,2,3,4…},由单调性,结合图像知选D.答案:D3.函数y=2x-x2的图像大致是()解析:由图像可知,y =2x 与y =x 2的交点有3个,说明函数y =2x -x 2与x 轴的交点有3个,故排除B 、C 选项,当x <x 0时,有x 2>2x 成立,即y <0,故排除D.答案:A4.当0<x <1时,f (x )=x 2,g (x )=x 12,h (x )=x -2的大小关系是( )A .h (x )<g (x )<f (x )B .h (x )<f (x )<g (x )C .g (x )<h (x )<f (x )D .f (x )<g (x )<h (x )解析:在同一坐标下作出函数f (x )=x 2,g (x )=x 12,h (x )=x -2的图像,由图像知,D 正确.答案:D 二、填空题5.近几年由于北京房价的上涨,引起了二手房市场交易的火爆.房子没有什么变化,但价格却上涨了,小张在2004年以15万元的价格购得一所新房子,假设这10年来价格年膨胀率不变,那么到2014年,这所房子的价格y (万元)与价格年膨胀率x 之间的函数关系式是________.解析:1年后,y =15(1+x );2年后,y =15(1+x )2;3年后,y =15(1+x )3,…,10年后,y =15(1+x )10.答案:y =15(1+x )106.在直角坐标系中,横、纵坐标均为整数的点叫格点.若函数y =f (x )的图像恰好经过k 个格点,则称函数y =f (x )为k 阶格点函数,则下列函数中为一阶格点函数的序号是________.①y =x 2;②y =x -1;③y =e x -1;④y =log 2x .解析:这是一道新概念题,重点考查函数值的变化情况.显然①④都有无数个格点;②有两个格点(1,1),(-1,-1);而③y =e x -1除了(0,0)外,其余点的坐标都与e 有关,所以不是整点,故③符合.答案:③7.若a =(35)x ,b =x 3,c =log 35x ,则当x >1时,a ,b ,c 的大小关系是________.解析:∵x >1,∴a =(35)x ∈(0,1),b =x 3∈(1,+∞),c =log 35x ∈(-∞,0).∴c <a <b .答案:c <a <b8.已知a >0,a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是________.解析:当a >1时,作出函数y 1=x 2,y 2=a x 的图像:要使x ∈(-1,1)时,均有f (x )<12,只要当x =-1时,有(-1)2-a -1≤12,解得a ≤2,∴1<a ≤2.当0<a <1时,同理,只需12-a 1≤12,即a ≥12.∴12≤a <1. 综上所述,a 的取值范围是[12,1)∪(1,2].答案:[12,1)∪(1,2]三、解答题9.一个叫迈克的百万富翁碰到一件奇怪的事.一个叫吉米的人对他说:“我想和你订立个合同,在整整一个月中,我每天给你10万元,而你第一天只需要给我1分钱,以后每天给我的钱数是前一天的两倍”.迈克非常高兴,他同意订立这样的合同. 试通过计算说明,谁将在合同中获利?解:在一个月(按31天计算)的时间里,迈克每天得到10万元,增长的方式是直线增长,经过31天后,共得到31×10=310(万元).而吉米,第一天得到1分, 第二天得到2分, 第三天得到4分, 第四天得到8分,第20天得到219分, ……第31天得到230分,使用计算器计算可得1+2+4+8+16+…+230=2 147 483 647分≈214 7.48(万元). 所以在这份合同中吉米纯获利2 147.48-310=1 837.48(万元).所以吉米将在合同中获利.10.某公司为了实现1 000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,开始按销售利润进行奖励,奖金y (万元)随销售利润x (万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y =0.25x ,y =log 7x +1,y =1.002x ,其中哪个模型能符合公司的要求?解:借助计算器或计算机作出函数y =5,y =0.25x ,y =log 7x +1,y =1.002x 的图像(如图),观察图像发现,在区间[10,1 000]上,模型y =0.25x ,y =1.002x 的图像都有一部分在直线y =5的上方,只有模型y =log 7x +1的图像始终在y =5的下方,这说明只有按模型y =log 7x +1进行奖励时才符合公司的要求,下面通过计算确认上述判断.首先计算哪个模型的奖金总数不超过5万.对于模型y =0.25x ,它在区间[10,1 000]上单调递增,当x ∈(20,1 000)时,y >5,因此该模型不符合要求;对于模型y =1.002x ,由函数图像,并利用计算器,可知在区间(805,806)内有一个点x 0满足1.002x 0=5,由于它在区间[10,1 000]上单调递增,因此当x >x 0时,y >5,因此该模型也不符合要求;对于模型y =log 7x +1,它在区间[10,1 000]上单调递增,而且当x =1 000时,y =log 71 000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.再计算按模型y =log 7x +1奖励时,奖金是否不超过利润的25%,即当x ∈[10,1 000]时,是否有y x =log 7x +1x≤0.25成立.令f (x )=log 7x +1-0.25x ,x ∈[10,1 000]. 利用计算器或计算机作出函数f (x )的图像(如图),由图像可知它是单调递减的,因此f(x)<f(10)≈-0.316 7<0,log7x+1<0.25x.所以,当x∈[10,1 000]时,log7x+1x<0.25.说明按模型y=log7x+1奖励,奖金不会超过利润的25%.综上所述,模型y=log7x+1确实能符合公司要求.更多资源下载地址:/。
指数函数·幂函数·对数函数增长快慢的比较(案例)一.背景:时间:2009年5月地点:西安市远东第一中学参与人员:王军红老师 高一(7)班学生起因:在高一第一学期学完幂函数,指数函数,对数函数后,课本有一节研究性学习课,《指数函数,幂函数,对数函数增长的比较》,本课涉及到画函数图象,比较函数值的大小,但因局部图形的对比难以体现基本关系,且数据计算量很大所以,准备以惠普计算器辅助教学。
我准备用不同的方式对两个班级分别进行教学。
在高一(7)班利用惠普计算器指导学生进行探究,在高一(5)班用常规方法教学,想从学生兴趣,学习效果,学生体会异同几个方面进行教学效果对比。
二.主题:本案例是教师指导学生利用惠普计算器,通过画函数图象,列出函数值表,观察指数函数,幂函数,对数函数增长的快慢,发现,体会“指数爆炸”这一函数值极速增长的现象,培养数形结合的数学思想,激发学生主动探究问题的兴趣,提高自主学习能力,并鼓励学生尝试写出研究小论文。
三.教学过程:提出问题:当a>1时,指数函数y=xa 为增函数;当n>0,x>0时,幂数函数y=n x 为增函数;当a>1时,对数函数y=log a x 为增函数;它们那个增长的较快? 实验一:比较函数212322,,log x y y x y x ===(只考虑x>0的情况)增长的快慢 。
输入函数解析式,画图。
(指导学生动手操作,学生参与积极,并能与他人合作交流。
)引导学生观察图像,发现,对数函数增长显然先快后慢,而幂函数和指数函数增长的快慢则交替出现。
求得2122,x y y x ==的第一个交点是(2,4)。
利用光标跟踪,发现当x>2时,22y x =的图像在12x y =图像的上方,总是如此吗? 引导学生改变坐标单位倍数,求得2122,x y y x ==的第二个交点是(4,16)。
适当对坐标进行缩放:当x>4时,图像观察不是很方便,光标跟踪效果不好,指导学生利用数据表进行比较:观察数据表,学生好奇而惊讶的发现:当x>4时,12x y =的函数值比22y x =的函数值增长的越来越快,直至呈“爆炸”性增长。
指数函数、对数函数比较大小
指数函数对数函数的比较大小问题,在教材上有大量的直接考察习题,而且考点层次要求高,因而高考中已经多次直接进行考察,这一点内容可以不合其他知识点发生关联的情况下直接进行命题,足以可见其重要性。
一般来说,指数、对数比较大小我们采取的思路是:
首先,尽量将不同底数的指数、对数或幂函数,通过公式化成同一底数的,底数相同的指数函数或者对数函数,然后根据底数相同情况下的单调性,进行比较大小;
其次,对于确实不能化成同一底数的,我们尽量将真数或指数化成相同的,然后我们做出图像,也就是说同取一个x值,看不同指数式或者对数式所对应的函数值的大小,主要依据是:
根据指数函数在第一象限内底数越大图像越高;
对数函数在第一象限内绕(1,0)点顺时针排序底数增大(水平向右底数增大);
最后,如果全都不能化成相同的,我们一般先做出图像,观察图像,判断大小,如果图像仍然不能解决问题,那么我们就应该考虑找中间值进行比较,中间值一般取0,-1,1,比如能否确定所要进行比较的数的正负、与1或-1的大小关系。
通过上述方式一般能解决所有比较大小问题。