三角形测试(测试用例)
- 格式:doc
- 大小:241.00 KB
- 文档页数:8
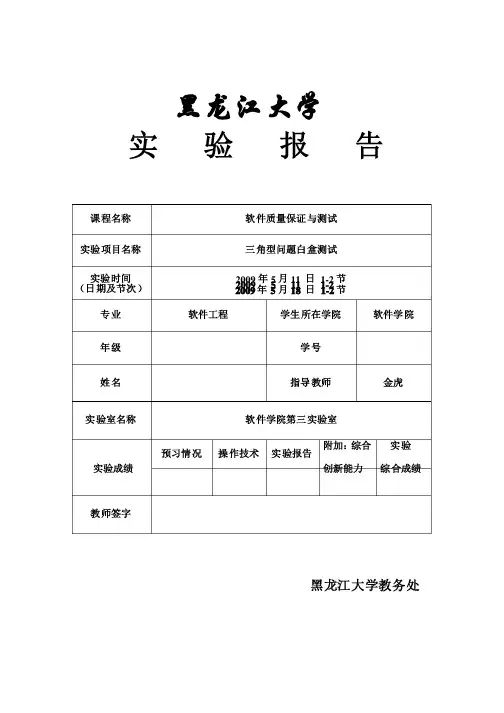
课程名称软件质量保证与测试实验项目名称三角型问题白盒测试实验时间(日期及节次)2009年5月11 日1-2节2009年5月18 日1-2节专业软件工程学生所在学院软件学院年级学号姓名指导教师金虎实验室名称软件学院第三实验室实验成绩预习情况操作技术实验报告附加:综合创新能力实验综合成绩教师签字测试计划(GB8567——88)1引言1.1编写目的1.掌握软件测试技术中白盒测试方法;掌握软件测试技术中白盒测试方法;2.掌握如何进行单元测试。
掌握如何进行单元测试。
1.2背景(三角形形状测试)测试程序名称:triangle(三角形形状测试)任务提出者:金虎老师任务提出者:金虎老师开发者:开发者:用户:用户:测试环境:WINDOWS XP ; VC++6.0 说明:由于程序较小,并且只是作为了解白盒测试的小程序,因此不涉及较高的实验环境,并且测试环境和运行环境在理论上是一样的,因此不存在较大的测试差异。
并且测试环境和运行环境在理论上是一样的,因此不存在较大的测试差异。
1.3定义a:三角型的第一条边三角型的第一条边b:三角型的第二条边三角型的第二条边c:三角型的第三条边三角型的第三条边一般三角形:三边都不相等的三角形一般三角形:三边都不相等的三角形等腰三角形:有任意两边相等的三角形等腰三角形:有任意两边相等的三角形等边三角形:三边都相等的三角形等边三角形:三边都相等的三角形不能构成三角形:因不满足需求条件而不能构成三角形不能构成三角形:因不满足需求条件而不能构成三角形1.4参考资料1.《软件测试教程》.宫云战.机械工业出版社 2008年9月.宫云战. 机械工业出版社2.《软件测试技术》.曲朝阳.中国水利水电出版社 2006年8月.曲朝阳. 中国水利水电出版社3.《软件测试教程》.贺平.电子工业出版社 2005年6月.贺平. 电子工业出版社序号序号 功能功能输入质量指标输入质量指标 输出质量指标输出质量指标 1 判断是否有非整数判断是否有非整数 输入a,b,c 有非整数有非整数 无乱码,输出正确无乱码,输出正确 2 判断是否是三个数判断是否是三个数 输入非三个数输入非三个数 无乱码,输出正确无乱码,输出正确 3 判断是否有数为0 输入a,b,c 为0的数的数无乱码,输出正确无乱码,输出正确 4 判断是否有负数判断是否有负数 输入a,b,c 为负的数为负的数无乱码,输出正确无乱码,输出正确5 判断是否构成三角形判断是否构成三角形输入a,b,c 正整数三边正整数三边 无乱码,输出正确无乱码,输出正确6 判断是否是一般三角形判断是否是一般三角形 输入a,b,c 正整数三边正整数三边 无乱码,输出正确无乱码,输出正确 7 判断是否是等边三角形判断是否是等边三角形 输入a,b,c 正整数三边正整数三边 无乱码,输出正确无乱码,输出正确 8 判断是否是等腰三角形判断是否是等腰三角形 输入a,b,c 正整数三边正整数三边 无乱码,输出正确无乱码,输出正确日期日期 安排安排2010-5-11 熟悉程序代码熟悉程序代码2010-5-18 画控制流图,准备测试数据并测试画控制流图,准备测试数据并测试写测试计划及测试报告写测试计划及测试报告2.3.3测试资料1.《软件测试教程》.宫云战.机械工业出版社 2008年9月.宫云战. 机械工业出版社2.《软件测试技术》.曲朝阳.中国水利水电出版社 2006年8月.曲朝阳. 中国水利水电出版社3.《软件测试教程》.贺平.电子工业出版社 2005年6月.贺平. 电子工业出版社2.3.4测试培训1.《软件测试教程》白盒测试第三章 白盒测试机械工业出版社 2008年9月第三章宫云战 机械工业出版社《软件测试教程》 宫云战2.金虎老师第三张白盒测试PPT课件课件3测试设计说明3.1测试此项测试采用白盒测试方法来测试该功能。

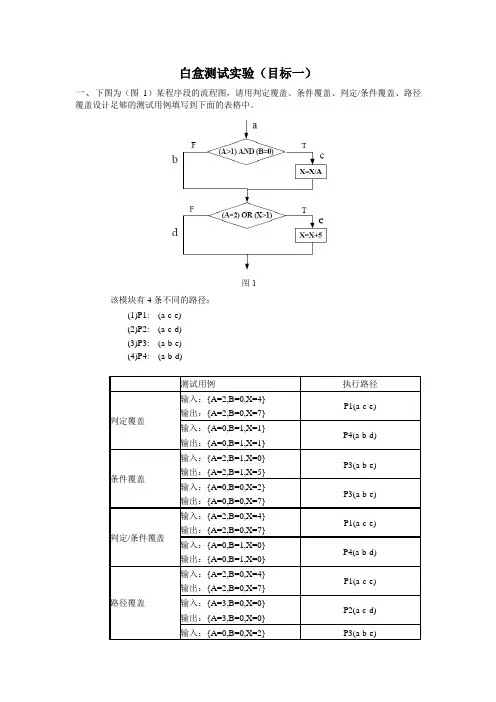
请写出判断三角形的代码,设计用例达到测试效果语句覆盖判定覆盖条件组合覆盖#include<stdio.h>void main(){int a, b, c;printf("please enter three integer:");scanf("%d%d%d", &a, &b, &c);if(0<a && a<200 && 0<b && b<200 && 0<c && c<200){if(a+b>c && a+c>b && c+b>a){if(a==b && b==c && a==c) //这里可以省掉一个判断{printf("1是等边三角形");}else{if(a==b || b==c || a==c){printf("2是等腰三角形");}else{if(a*a+b*b==c*c || a*a+c*c==b*b || b*b+c*c==a*a){printf("3是直角三角形");}else{printf("4是一般三角形");}}}}else{printf("5不能组成三角形");}}else{printf("6某些边不满足限制");}}1.为三角形程序开发判定/条件覆盖和条件组合覆盖的测试用例。
1)判定/条件覆盖对于第一个判定a>0&&b>0&&c>0 :条件a>0 取真值记为T1,取假值记为-T1条件b>0 取真值记为T2,取假值记为-T2条件c>0 取真值记为T3,取假值记为-T3对于第二个判定( a+b>c)&&(a+c>b)&&(b+c>a ):条件a+b>c 取真值记为T4,取假值记为-T4条件a+c>b 取真值记为T5,取假值记为-T5条件b+c>a 取真值记为T6,取假值记为-T62.对下面的流程图用逻辑覆盖法设计测试用例(至少三种)1)..语句覆盖:语句覆盖可以保证程序中的每个语句都得到执行。

黑盒测试三角形简介黑盒测试是一种软件测试方法,通过检查软件的输入和输出,而无需关注内部的实现细节。
本文将介绍如何进行黑盒测试,并以三角形的判定为例进行详细说明。
三角形判定规则在进行三角形测试之前,我们首先需要了解三角形的定义和判定规则。
三角形是由三条边组成的图形,它有以下几个特征: - 三边之和大于第三边 -两边之差小于第三边 - 三边的长度分别为a、b、c,其中a、b、c均大于0根据三角形的三边长度,可以将三角形分为以下几种情况: - 等边三角形:三边长度相等 - 等腰三角形:两边长度相等 - 直角三角形:有一个角为90度 - 钝角三角形:三个角均大于90度 - 锐角三角形:三个角均小于90度黑盒测试方法黑盒测试的目的是检查软件的功能是否按照预期工作,它不关心具体的代码实现,而是从输入和输出的角度出发进行测试。
下面是一些常用的黑盒测试方法:等价类划分等价类划分是一种常用的黑盒测试方法,它将测试用例分为几个等价类,每个等价类代表一个功能的特定条件。
测试用例选择一个等价类进行测试即可,通过这个等价类的测试用例可以代表整个等价类的测试结果。
在三角形判定中,我们可以将输入的三个边长分为以下几个等价类: - 有效等价类:满足三角形判定规则的三个边长组合 - 无效等价类:不满足三角形判定规则的三个边长组合边界值分析边界值分析是一种考虑输入值的边界情况的黑盒测试方法。
通常,边界值是最小输入和最大输入,以及最小输入减去或最大输入加上1的情况。
在三角形判定中,我们可以选择以下边界值进行测试: - 最小输入:三个边均为0 - 边界输入:三个边中有一个边等于1,另外两个边等于最大允许值 - 最大输入:三个边均为最大允许值错误推测法错误推测法是一种根据错误、故障和失败的经验推测可能存在的错误并进行测试的方法。
通过推测错误并进行测试,可以发现软件中可能存在的隐藏错误。
在三角形判定中,我们可以通过错误推测法选择一些可能存在的错误进行测试,例如: - 输入的边长度数据类型错误 - 输入的边长度超出了合理范围 - 输入的边长度顺序错误三角形测试用例根据上述的黑盒测试方法,我们可以选择一些测试用例进行三角形判定的测试。

三角形测试用例设计作者:ღ王正也ღ某程序规定:"输入三个整数a、b、c分别作为三边的边长构成三角形。
通过程序判定所构成的三角形的类型,当此三角形为一般三角形、等腰三角形及等边三角形时,分别作计算… "。
用等价类划分方法为该程序进行测试用例设计。
之前面试了几个地方都问了这个题,网上找了下答案。
不懂测试理论,也不知道啥叫等级类,也不知道哪个答案更准确。
不知道为什么所有答案给出的用例里没有测试边界值,极大的值,负数,小数等等答案1:/godmap/blog/item/12ed690f14cc9c2b6059f3bc. html三角形等价类列表判定类型有效等价类无效等价类一般三角形((a>0) Λ(b>0) Λ(c>0)) Λ (a<=0 V b<=0 V c<=0) Λ(((a+b)>c) V ((a+c)>b) V ((b+c)>a)) (1) (((a+b)<=c) V ((a+c)<=b) V ((b+c)<=a)) (2)等腰三角形(1) Λ (a=b V a=c V b=c) (3) (2) V (a!=b V b!=c V a!=c) (4)等边三角形(1) Λ (a=b=c ) (5) (2) V (a!=b!=c) (6)根据上表组成的测试用例:三角形等价类测试用例ID 输入数据覆盖测试用例输出结果a b c1 3 4 5 (1) 一般三角形2 0 4 5 (2) 非(一般)三角形3 3 0 5 (2)4 3 4 0 (2)5 1 4 5 (2)6 3 8 5 (2)7 3 2 1 (2)8 3 3 5 (3) 等腰三角形9 3 4 310 3 4 411 3 4 9 (4) 非等腰三角形12 3 3 3 (5) 等边三角形13 -1 0 1 (6) 非等边三角形答案2: /?uid-275201-action-viewspace-ite mid-218955分析题目中给出和隐含的对输入条件的要求:(1)整数(2)三个数(3)非零数(4)正数(5)两边之和大于第三边(6)等腰(7)等边如果a、b 、c满足条件( 1 )~ ( 4 ),则输出下列四种情况之一:1)如果不满足条件(5),则程序输出为" 非三角形" 。

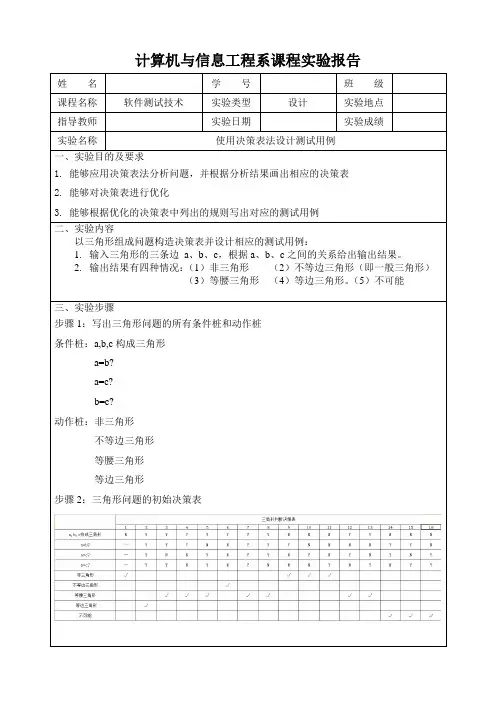
计算机与信息工程系课程实验报告
姓名学号班级
课程名称软件测试技术实验类型设计实验地点
指导教师实验日期实验成绩
实验名称使用决策表法设计测试用例
一、实验目的及要求
1. 能够应用决策表法分析问题,并根据分析结果画出相应的决策表
2. 能够对决策表进行优化
3. 能够根据优化的决策表中列出的规则写出对应的测试用例
二、实验内容
以三角形组成问题构造决策表并设计相应的测试用例:
1.输入三角形的三条边a、b、c,根据a、b、c之间的关系给出输出结果。
2.输出结果有四种情况:(1)非三角形(2)不等边三角形(即一般三角形)
(3)等腰三角形(4)等边三角形。
(5)不可能
三、实验步骤
步骤1:写出三角形问题的所有条件桩和动作桩
条件桩:a,b,c构成三角形
a=b?
a=c?
b=c?
动作桩:非三角形
不等边三角形
等腰三角形
等边三角形
步骤2:三角形问题的初始决策表
步骤3:将初始决策表进行合理的优化,得到简化的决策表
步骤4:写出条件桩修改后的决策表
步骤5:根据决策表设计测试用例
四、实验结果
如上
注:1、实验类型分为:演示、验证、综合、设计研究或其他。
2、附录:可附加源程序代码清单等。

三角形测试用例1. 引言在软件开发中,测试是一个至关重要的环节。
而在测试过程中,测试用例是评估软件功能和性能的关键工具之一。
本文将围绕着三角形的测试用例展开讨论。
三角形是指由三条边组成的图形,它是几何学中最基本的图形之一。
我们将介绍如何编写一组全面且有效的测试用例来验证一个给定的三条边是否可以构成一个有效的三角形。
2. 测试目标我们的目标是编写一组测试用例,通过输入不同长度的三条边来验证是否可以构成一个有效的三角形。
对于给定的三条边a、b和c,我们需要验证以下情况: - a、b和c是否满足构成三角形的条件; - 如果满足条件,那么它是什么类型的三角形(例如等边三角形、等腰三角形或普通三角形); - 如果不满足条件,那么应该返回什么样的错误信息。
3. 测试用例设计3.1 边界值分析在设计测试用例时,我们需要考虑到边界值情况。
以下是一些可能需要考虑到的边界值: - a、b或c为零的情况; - a、b或c为负数的情况; - a、b或c的值非常大的情况。
3.2 等边三角形测试用例等边三角形是指三条边长度相等的三角形。
以下是一些可能需要考虑到的测试用例:- a、b和c均为相等且大于零的值; - a、b和c均为相等且小于零的值; - a、b和c均为相等但其中有一个为零的值。
3.3 等腰三角形测试用例等腰三角形是指两条边长度相等的三角形。
以下是一些可能需要考虑到的测试用例:- a和b相等,且a和b大于零,但c不等于a或b; - a和b相等,且a和b小于零,但c不等于a或b; - a和b相等,且其中一个为零,但c不等于a或b。
3.4 直角三角形测试用例直角三角形是指其中一个内角为90度(直角)的三角形。
以下是一些可能需要考虑到的测试用例: - a^2 + b^2 = c^2 的情况; - a^2 + b^2 ≠ c^2 的情况。
3.5 普通三角形测试用例普通三角形是指没有边相等的三角形。
以下是一些可能需要考虑到的测试用例: - a、b和c均为不相等的正数; - a、b和c均为不相等的负数; - a、b和c均为不相等但其中有一个为零的值。
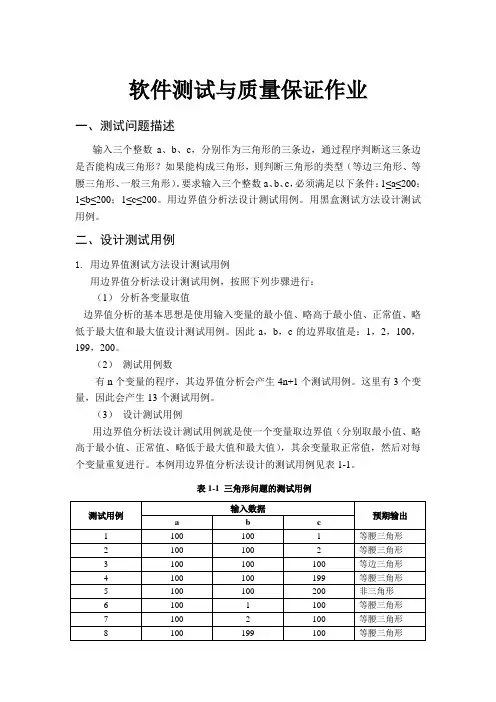
软件测试与质量保证作业一、测试问题描述输入三个整数a、b、c,分别作为三角形的三条边,通过程序判断这三条边是否能构成三角形?如果能构成三角形,则判断三角形的类型(等边三角形、等腰三角形、一般三角形)。
要求输入三个整数a、b、c,必须满足以下条件:1≤a≤200;1≤b≤200;1≤c≤200。
用边界值分析法设计测试用例。
用黑盒测试方法设计测试用例。
二、设计测试用例1. 用边界值测试方法设计测试用例用边界值分析法设计测试用例,按照下列步骤进行:(1)分析各变量取值边界值分析的基本思想是使用输入变量的最小值、略高于最小值、正常值、略低于最大值和最大值设计测试用例。
因此a,b,c的边界取值是:1,2,100,199,200。
(2)测试用例数有n个变量的程序,其边界值分析会产生4n+1个测试用例。
这里有3个变量,因此会产生13个测试用例。
(3)设计测试用例用边界值分析法设计测试用例就是使一个变量取边界值(分别取最小值、略高于最小值、正常值、略低于最大值和最大值),其余变量取正常值,然后对每个变量重复进行。
本例用边界值分析法设计的测试用例见表1-1。
表1-1 三角形问题的测试用例2. 用等价类测试方法设计测试用例(1)首先分析题目中给出的条件和隐含的输入要求,输入条件如下:a)正整数;b)三个数;c)构成一般三角形;d)构成等腰三角形;e)构成等边三角形;f)不能构成三角形(2)根据输入条件的要求划分等价类,列出等价类表并编号,如表1-2所示。
表1-2 三角形问题的等价类注:划分等价类的方式并不唯一,可根据被测对象的具体情况划分等价类。
(3) 设计测试用例,覆盖上表中的等价类,如表1-3表所示。
表1-3三角形问题的测试用例3.用基于判定表的测试方法设计测试用例(1)列出所有的条件桩和动作桩条件桩:C1:a < b + c?C2:b < a + c?C3:c < a + b?C4:a = b?C5:a = c?C6:b = c?动作桩:a1: 非三角形a2: 不等边三角形a3: 等腰三角形a4: 等边三角形a5: 不可能(2)根据输入条件和输出的关系,填写各条规则,画出判定表,如表1-4所示。

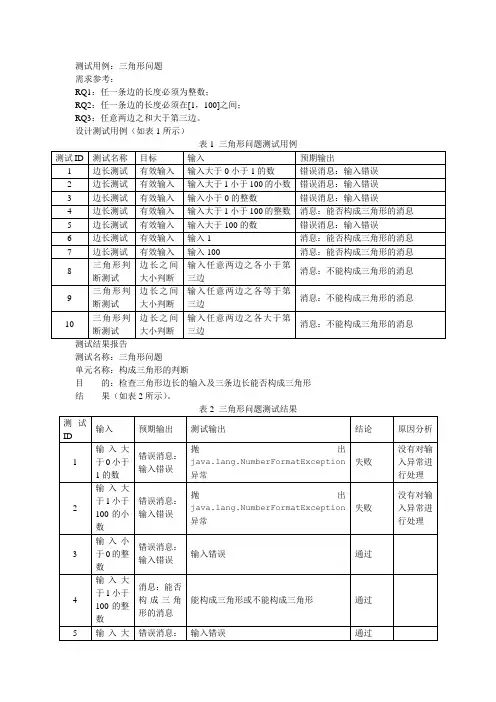
实验六三角形问题的基本路径测试一、实验目的1.掌握程序控制流图的画法。
2.掌握环路复杂度的计算方法。
3.掌握利用基本路径法进行白盒测试的方法。
二、实验任务1.理解三角形问题的命题。
三角形问题是软件测试文献中广泛使用的一个例子。
三角形问题:输入三个整数a、b和c分别作为三角形的三条边,通过程序判断有这三条边构成的三角形类型是:等边三角形、等腰三角形、一般三角形或非三角形。
主要代码如下:1.If (inta >= intb + intc)2. Or (intb >= inta + intc)3. Or (intc >= intb + inta) Then4. strMsg = "非三角形"5.Else6. If (inta = intb)7. And (intb = intc) Then8. strMsg = "等边三角形"9. Else10. If (inta = intb)11. Or (inta = intc)12. Or (intc = intb) Then13. strMsg = "等腰三角形"14. Else15. strMsg = "普通三角形"16. End If17. End If18.End If19.MsgB ox(strMsg, rmation, "三角形问题") //输出判断结果2.利用基本路径测试法对三角形问题进行测试用例设计。
三、实验步骤1.理解三角形问题中各种三角形的判断方法。
2.根据上面的代码画出程序的控制流图。
(注意:复合条件语句,需改复合条件的判断为一系列单个条件的嵌套)3.计算环路复杂度。
4.求出基本路径组合。
5.设计测试用例(按照表1的形式,设计用例)。
表1:用例设计表四、实验报告要求1.实验报告中“实验内容”应包含(1)程序控制流图;(2)环路复杂度计算结果;(3)基本路径集合;(4)测试用例设计(按表1填写)。
软件测试-黑盒测试例子一、等价类划分问:某程序规定:"输入三个整数 a、 b、 c分别作为三边的边长构成三角形。
通过程序判定所构成的三角形的类型,当此三角形为一般三角形、等腰三角形及等边三角形时,分别作计算… "。
用等价类划分方法为该程序进行测试用例设计。
(三角形问题的复杂之处在于输入与输出之间的关系比较复杂。
)解:分析题目中给出和隐含的对输入条件的要求:(1)整数(2)三个数(3)非零数(4)正数(5)两边之和大于第三边(6)等腰(7)等边如果 a、 b 、 c满足条件( 1 ) ~ ( 4 ),则输出下列四种情况之一:1)如果不满足条件(5),则程序输出为 " 非三角形 " 。
2)如果三条边相等即满足条件(7),则程序输出为 " 等边三角形 " 。
3)如果只有两条边相等、即满足条件(6),则程序输出为 " 等腰三角形 " 。
4)如果三条边都不相等,则程序输出为 " 一般三角形 " 。
列出等价类表并编号覆盖有效等价类的测试用例:a b c覆盖等价类号码3 4 5(1)--(7)4 4 5(1)--(7),(8)4 5 5(1)--(7),(9)5 4 5(1)--(7),(10) 4 4 4(1)--(7),(11)覆盖无效等价类的测试用例:二、边界值分析法NextDate函数的边界值分析测试用例在NextDate函数中,隐含规定了变量mouth和变量day的取值范围为1≤mouth≤12和1≤day≤31,并设定变量year的取值范围为1912≤year≤2050 。
三、错误推测法测试一个对线性表(比如数组)进行排序的程序,可推测列出以下几项需要特别测试的情况:I.输入的线性表为空表;II.表中只含有一个元素;III.输入表中所有元素已排好序;IV.输入表已按逆序排好;V.输入表中部分或全部元素相同。
软件测试与质量保证作业一、测试问题描述输入三个整数a b、c,分别作为三角形的三条边,通过程序判断这三条边是否能构成三角形?如果能构成三角形,则判断三角形的类型(等边三角形、等腰三角形、一般三角形)。
要求输入三个整数a、b、c,必须满足以下条件: 1 < a药0 ; 1 < b < 200 ; 1 < c < 200。
用边界值分析法设计测试用例。
用黑盒测试方法设计测试用例。
二、设计测试用例1. 用边界值测试方法设计测试用例用边界值分析法设计测试用例,按照下列步骤进行:(1)分析各变量取值边界值分析的基本思想是使用输入变量的最小值、略高于最小值、正常值、略低于最大值和最大值设计测试用例。
因此a, b , c的边界取值是:1, 2, 100 , 199 , 200。
(2)测试用例数有n个变量的程序,其边界值分析会产生4n+1个测试用例。
这里有3个变量,因此会产生13个测试用例。
(3)设计测试用例用边界值分析法设计测试用例就是使一个变量取边界值(分别取最小值、略高于最小值、正常值、略低于最大值和最大值),其余变量取正常值,然后对每个变量重复进行。
本例用边界值分析法设计的测试用例见表1-1 O2. 用等价类测试方法设计测试用例(1) 首先分析题目中给出的条件和隐含的输入要求,输入条件如下:a) 正整数;b) 三个数;c) 构成一般三角形;d) 构成等腰三角形;e) 构成等边三角形;f) 不能构成三角形(2) 根据输入条件的要求划分等价类,列出等价类表并编号,如表1-2 所示。
表1-2三角形问题的等价类注:划分等价类的方式并不唯一,可根据被测对象的具体情况划分等价类。
(3) 设计测试用例,覆盖上表中的等价类,如表1-3表所示3•用基于判定表的测试方法设计测试用例(1) 列出所有的条件桩和动作桩条件桩C1: a < b + c?C2: b < a + c?C3: c < a + b?C4: a= =b?C5: a= =c?C6: b= =c?动作桩•a1:非三角形a2:不等边三角形a3:等腰三角形a4:等边三角形a5:不可能(2) 根据输入条件和输出的关系,填写各条规则,画出判定表,如表1-4所示(3) 设计测试用例,覆盖判定表中的各条规则。
三角形测试用例
题目:输入三个数a、b、c分别作为三边的边长构成三角形。
通过程序判定所构成的三角形是一般三角形、等腰三角形还是等边三角形时。
用等价类划分方法为该程序设计测试用例。
在三角形计算中,要求三角形的三个边长:ABC。
1、当三边不可能构成三角形时提示错误,可构成三角形时计算三角形周长。
2、若是等腰三角形打印“等腰三角形”,若两个等腰的平方和等于第三边平方和,则打印“等腰直角三
角形”。
3、若是等边三角形,则打印:“等边三角形”。
4、画出程序流程图并设计一个测试用例。
分析一下:
1、构成三角形的条件:任意两边之和大于第三边;
2、构成等腰三角形的条件:任意两边相等;
3、构成等腰直角三角形的条件:任意两边相等,而且两条边的平方和等于第三边的平方和;
4、构成等边三角形的条件:三条边都相等。
那么用什么样的设计方法进行测试用例的设计呢?
一、等价类划分:三角形三条边A、B、C的数据类型不同
二、边界值分析:由于三角形的边长可以是正整数或正小数,所以就不对长度进行测试,那么边界值分析就不用了
三、因果图法:三角形的三条边数据输入组合
我们看一下三角形的流程图:
注:改正一个小错误,在判断是否是等腰直角三角形中A的平方=B的平方+C的平方。
由于画图时,网络
速度问题,导致真或假的值没有标注。
三角形等价类列表
判定类型有效等价类
无效等价类
一般三角形((a>0)Λ(b>0)Λ(c>0))Λ
(a<=0Vb<=0Vc<=0)Λ
(((a+b)>c)V((a+c)>b)V((b+c)>a))(1) (((a+b)<=c)V((a+c)<=b)V((b+c)<=a))(2)
等腰三角形(1)Λ(a=bVa=cVb=c)(3)(2)
V(a!=bΛb!=cΛa!=c)(4)
等边三角形(1)Λ(a=b=c)(5)
(2)V(a!=b!=c)(6)
根据上表组成的测试用例:
三角形等价类测试用例
ID输入数据覆盖测试用例输出结果
abc
1345(1)一般三角形
2045(2)非(一般)三角形
3305(2)
4340(2)
5145(2)
6385(2)
7321(2)
8335(3)等腰三角形
9343
10344
#include<stdio.h>
voidmain()
{
floata,b,c;
printf("请输入三角形三边"); scanf("%f,%f,%f",&a,&b,&c); if(a==b||b==c||a==c)
printf("等腰三角形");
if(a==b&&b==c)
printf("等边三角形");
if(a*a+b*b==c*c||a*a+c*c==b*b||b*b+c*c==a*a) printf("直角三角形");
else
printf("普通三角形");
}
11349(4)非等腰三角形
12333(5)等边三角形
13-101(6)非等边三角形
我们再分析一下三角形的等价类:
有效等价类:
输入3个正整数或正小数:
1、两数之和大于第三数,如A<B+C;B<C+A;C<A+B
2、两数之和不大于第三数
3、两数相等,如A=B或B=C或C=A
4、三数相等,如A=B=C
5、三数不相等,如A!=B,B!=C,C!=A
无效等价类:
1、空
2、负整数
3、非数字
4、少于三个数
三角形测试用例类别输入条件有效等价类无效等价类是否是三角形(A>0)(1)
(B>0)(2)
(C>0)(3)
(A+B>C)(4)
(B+C>A)(5)
(C+A>B)(6)
(A<=0)(7)
(B<=0)(8)
(C<=0)(9)
(A+B<=C)(10)
(B+C<=A)(11)
(C+A<=B)(12)
是否是等腰三角形(A=B)(13)
(B=C)(14)
(C=A)(15)
(A!=B)and(B!=C)and(C!=A)(16)
是否是等腰直角三角形(A=B)and(A2+B2=C2)(17)
(B=C)and(B2+C2=A2)(18)
(C=A)and(C2+A2=B2)(19)
(A!=B)and(B!=C)and(C!=A)(20)
是否是等边三角形(A=B)and(B=C)and(C=A)(21)(A!=B)(22) (B!=C)(23)
(C!=A)(24)
#include<stdio.h>
voidmain()
{
inta,b,c;
printf("PleaseInputa,b,c:");
scanf("%d",&a);
scanf("%d",&b);
scanf("%d",&c);
if(a+b<=c||a+c<=b||b+c<=a)/*判断是否能构成三角形*/ printf("No!\n");
else
{
printf("Yes!\n");
if(a==c||a==b||b==c)/*判断是否为等腰三角形*/
{
printf("Itcanbeanisocelestriangle!\n");
if(a==c&&a==b)/*判断是否为等边三角形*/
printf("Italsocanbeanequilateraltriangle!\n"); else
printf("Butitcannotbeanequilateraltriangle!\n"); }
else
{
printf("Itcan'tbeanisocelestriangle!\n");
}
}
getch();
}
三角形测试用例:
序号[A,B,C]覆盖等价类输出
1[3,4,5](1)(2)(3)(4)(5)(6)是三角形
2[0,1,2](7)非三角形
3[1,0,2](8)非三角形
4[1,2,0](9)非三角形
5[1,2,3](10)非三角形
6[1,3,2](11)非三角形
7[3,1,2](12)非三角形
8[3,3,4](1)(2)(3)(4)(5)(6)(13)等腰三角形
9[3,4,4](1)(2)(3)(4)(5)(6)(14)等腰三角形
10[3,4,3](1)(2)(3)(4)(5)(6)(15)等腰三角形
11[2√2,2√2,4](1)(2)(3)(4)(5)(6)(17)等腰直角三角形12[4,2√2,2√2](1)(2)(3)(4)(5)(6)(18)等腰直角三角形13[2√2,4,2√2](1)(2)(3)(4)(5)(6)(19)等腰直角三角形14[3,4,5]
(1)(2)(3)(4)(5)(6)(16)(20)(22)(23)(24)是三角形
15[3,3,3](1)(2)(3)(4)(5)(6)(16)(21)等边三角形
16[,,,]无效等价类错误提示
17[-3,4,5]无效等价类错误提示18[a,3,@]无效等价类错误提示19[3,4]无效等价类错误提示。