任意角的三角函数2
- 格式:doc
- 大小:321.62 KB
- 文档页数:3


-+-++--+--++y xxy y xOO O任意角的三角函数(2)——三角函数的定义一、课前检测1.设集合M ={α|α=kπ2-π3,k∈Z },N ={α|-π<α<π},则M∩N=________.解析:由-π<kπ2-π3<π得-43<k<83,∵k∈Z ,∴k=-1,0,1,2,故M∩N={-56π,-π3,π6,23π}.答案:{-56π,-π3,π6,23π}2.圆弧长度等于圆内接正三角形的边长,则其圆心角弧度数为( )A.π3B.2π3 C. 3 D .2 解析:选C.二、知识梳理1.1)设α是一个任意角,它的终边与单位圆交于点()y x P ,,那么:xyx y ===αααtan ,cos ,sin . 2)设点()00,y x A 为角α终边上任意一点,那么:(设2020y x r +=)r y 0sin =α,rx0cos =α,00tan x y =α.(解读:特殊与一般的关系)2.αsin ,αcos ,αtan 在四个象限的符号(一全二正弦,三切四余弦,简记为“全s t c ”)3.三角函数线(单位圆中)正弦线:MP; 余弦线:OM; 正切线: AT.4.三角函数的定义域三角函数定义域 x y sin =R x y cos = Rx y tan =⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,2ππ5. 特殊角的三角函数值α的角度︒0 ︒30 ︒45 ︒60 ︒90 ︒120 ︒135 ︒150 ︒180 ︒270 ︒360α的弧度6π 4π 3π 2π 32π 43π 65π π23π π2αsin0 21 22 23 1 23 22 21 0 1- 0 αcos123 22 2121- 22- 23- 1- 01TMA OPxy(3) 若 o<x<2,则sinx<x<tanx(2)(1)|sinx|>|cosx||cosx|>|sinx||cosx|>|sinx||sinx|>|cosx|sinx>cosxcosx>sinx16. 几个重要结论:OOxyxyαtan33 1 3 — 3- 1-33- 0 — 06.诱导公式一:终边相同的角的同一三角函数值相等。

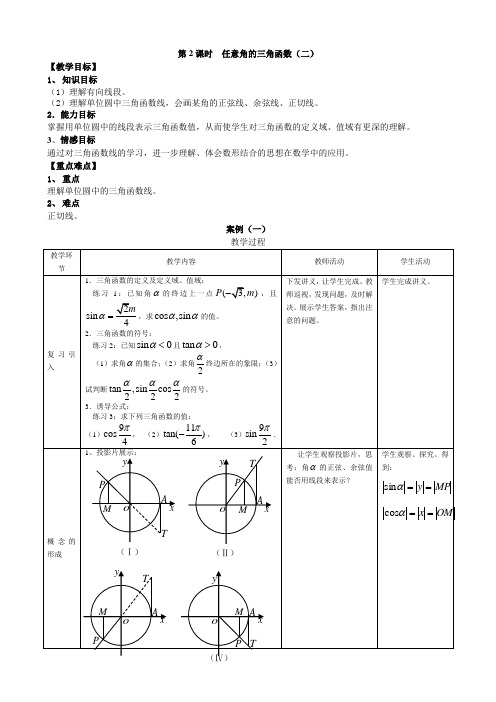
第2课时任意角的三角函数(二)【教学目标】1、知识目标(1)理解有向线段。
(2)理解单位圆中三角函数线,会画某角的正弦线、余弦线、正切线。
2.能力目标掌握用单位圆中的线段表示三角函数值,从而使学生对三角函数的定义域、值域有更深的理解。
3、情感目标通过对三角函数线的学习,进一步理解、体会数形结合的思想在数学中的应用。
【重点难点】1、重点理解单位圆中的三角函数线。
2、难点正切线。
案例(一)教学过程案例(二)教学过程1、观察投影片图1.2-7,角的正弦、余弦值能否用线段来表示? 学生——探究图 1.2-7中(Ⅰ)~(Ⅳ),不难得到(可能有分情况给出的,形式不同):.cos ,sin OM x MP y ====αα教师——提问,了解情况,认可上述结论。
2、为了去掉上述等式中的绝对值符号,能否给线段OM 、MP 规定一个适当的方向,使它们的取值与点P 的坐标一致?教师——请同学们想一下,直角坐标系内的坐标的正负与谁的方向有关?学生——点的坐标与坐标轴的方向有关。
在坐标轴正方向上的为正,负方向上的为负。
教师——根据前面得出的关系如,sin MP y ==α如何规定线段的方向才能将绝对值符号同时拿掉?呈MP y ==αsin 形式?如果实现了这种形式,我们说就给了三角函数的正弦值以几何表示。
学生——观察、思考、回答。
(应该以坐标轴的方向来规定线段的方向。
) 当角α的终边不在坐标轴上时,以O 为始点、M 为终点,规定:当线段OM 与x 轴同向时,OM 的方向为正方向,且有正值x ,当线段OM 与x 轴反向时,OM 的方向为负向,且有负值x 。
其中x 为P 点的横坐标。
这样同,无论哪一种情况都有:αcos ==x OM 。
同理,当角α的终边不在坐标轴上时,以M 为始点、P 为终点,规定:当线段MP 与y 轴同向时,MP 的方向为正方向,且有正值y ;当线段MP 与y 轴反向时,MP 的方向为负方向,且有负值y 。


1 第一章三角函数1.2.1任意角的三角函数(2)
学习目的:
1.复习三角函数的定义、定义域与值域、符号、及诱导公式;
2.利用三角函数线表示正弦、余弦、正切的三角函数值;
3.利用三角函数线比较两个同名三角函数值的大小及表示角的范围。
学习重点:正弦、余弦、正切线的概念。
学习难点:正弦、余弦、正切线的利用。
课堂探究:
一、复习引入:
1.三角函数的定义及定义域、值域:
练习1已知角α
的终边上一点()P m
,且sin 4
α=
,求cos ,sin αα的值。
解:
由题设知x =y m =
,所以2222||(r O P m ==+
,得r =
从而sin 4
α
=
m r ==
,解得0m =
或2
1662m m =+⇒=
当0m =
时,r x =
=
cos 1,tan 0x y
x
αα=
=-=
=;
当m =
r x
==,
cos ,tan 4
x y x
αα=
=-
=
=-
;
当m
=r x ==,
cos ,tan 4
3
x y r x αα=
=-
=
=
.
2.三角函数的符号:
练习2:已知sin 0α<且tan 0α>,
(1)求角α的集合;(2)求角2
α终边所在的象限;(3)试判断tan ,sin cos 2
2
2
ααα
的符号。
3.诱导公式:
练习3:求下列三角函数的值:
(1)9cos 4
π, (2)11tan()
6
π-, (3)9sin 2
π
.
二、讲解新课:
当角的终边上一点(,)P x y 1=时,有三角函数正弦、余弦、正切值的几何表示——三角函数线。
1.单位圆:圆心在圆点O ,半径等于单位长的圆叫做单位圆。
2.有向线段:
坐标轴是规定了方向的直线,那么与之平行的线段亦可规定方向。
规定:与坐标轴方向一致时为正,与坐标方向相反时为负。
3.三角函数线的定义:
设任意角α的顶点在原点O ,始边与x 轴非负半轴重合,终边与单位圆相交与点
P (,)x y ,
过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,它与角α的终边或其反向
2 延长线交与点T .
当角α的终边不在坐标轴上时,有向线段,OM x MP
y ==,于是有
sin 1y y y M P r α====,
c o s 1
x x x O M r α====,
tan y M P A T
A T x O M
O A
α=
===.
我们就分别称有向线段,,MP OM AT 为正弦线、余弦线、正切线。
说明:
①三条有向线段的位置:正弦线为α的终边与单位圆的交点到x 轴的垂直线段;余弦 线在x 轴上;正切线在过单位圆与x 轴正方向的交点的切线上,三条有向线段中两条在单
位
圆内,一条在单位圆外。
②三条有向线段的方向:正弦线由垂足指向α的终边与单位圆的交点;余弦线由原点指向
垂
足;正切线由切点指向与α的终边的交点。
③三条有向线段的正负:三条有向线段凡与x 轴或y 轴同向的为正值,与x 轴或y 轴反向的 为负值。
④三条有向线段的书写:有向线段的起点字母在前,终点字母在后面。
4.例题分析:
例1 作出下列各角的正弦线、余弦线、正切线。
(1)3
π; (2)56
π; (3)23
π-; (4)136
π-.
解:图略。
例2 利用三角函数线比较下列各组数的大小:
1︒ 3
2sin π与5
4sin π 2︒ tan 3
2π与tan 4π 3︒ cot 2π与cot 5
4π
解: 如图可知: 32sin π>5
4sin π
3 tan 32π< tan
54π cot
3
2π >cot
5
4π
例3 利用单位圆寻找适合下列条件的0︒到360︒的角
1︒ sin α≥
2
1 2︒ tan α>
3
3
解:
︒
︒<α<
例4利用单位圆写出符合下列条件的角x 的范围。
(1)1sin 2
x <-
; (2)1cos 2
x >
;
(3)10,sin 2
x x π<<>且1cos 2
x <
;
(4)1|cos |2
x ≤; (5)1sin 2
x ≥
且tan 1x ≤-. 解:(1)71122,6
6
k x k k Z ππππ+<<+∈;(2)22,6
6
k x k k Z π
π
ππ-
+<<+∈;
(3)5,36
x k Z π
π<<∈;(4),6
2
6
2
k x k k Z π
π
π
π
ππ-
+
+<<
+
+∈;
(5)
322,2
4
k x k k Z π
πππ+<<+∈.
三、巩固与练习 四、小 结:
本节课学习以下内容: 1.三角函数线的定义;
2.会画任意角的三角函数线;
3.利用单位圆比较三角函数值的大小,求角的范围。
五、课后作业:
补充:1.利用余弦线比较cos 64,cos 285
的大小;
2.若
42
π
π
θ<<
,则比较sin θ、cos θ、tan θ的大小;
3.分别根据下列条件,写出角θ的取值范围:
(1)cos 2
θ<; (2)tan 1θ>- ; (3)sin 2
θ>-
.。