数理方程：第2讲典型方程的定解条件
- 格式：ppt
- 大小：869.50 KB
- 文档页数：18
下载文档原格式
合集下载
1.2定解条件
•所谓解的存在性，即定解问题有解。 所谓解的存在性，即定解问题有解。 所谓解的存在性 •所谓解的唯一性，即定解问题的解是唯一的。 所谓解的唯一性， 所谓解的唯一性 即定解问题的解是唯一的。 •所谓解的稳定性，即如果定解问题中的已知条件 所谓解的稳定性， 所谓解的稳定性 例如方程或定解条件中的已知函数）有微小变化时， （例如方程或定解条件中的已知函数）有微小变化时， 相应地，解也只有微小的改变。 相应地，解也只有微小的改变。
不适定问题举例
•一般来说，方程的阶数对应于定解 一般来说， 一般来说 条件的个数； 条件的个数； •条件多了，将会破坏解的存在性； 条件多了， 条件多了 将会破坏解的存在性； •条件少了，将会破坏解的唯一性。 条件少了， 条件少了 将会破坏解的唯一性。
二阶线性偏微分方程的分类
F ( x, y , u x , u y , u xx , u yy ) = 0
•第一类边界条件：给出未知函数u 在边界上的值 第一类边界条件：给出未知函数 第一类边界条件 •第二类边界条件：给定未知函数u 在边界上的 第二类边界条件：给定未知函数 第二类边界条件 法向导数值
•第三类边界条件：给出边界上未知数u 及其法向 第三类边界条件：给出边界上未知数 第三类边界条件 导数之间的线性关系
•波动方程：含有对时间的二阶偏导数 ，两个初始条件 波动方程： 波动方程 •传输方程：含有对时间的一阶偏导数 ，一个初始条件 传输方程： 传输方程 •稳定场方程：不随时间变化，没有初始条件 稳定场方程：不随时间变化， 稳定场方程
•边界条件 边界条件——描述系统在边界上的状况 边界条件 描述系统在边界上的状况
•衔接条件 衔接条件
在研究具有不同介质（或跃点处）的问题中， 在研究具有不同介质（或跃点处）的问题中， 在不同介质（或跃点处） 在不同介质（或跃点处）的界面处有衔接条件
不适定问题举例
•一般来说，方程的阶数对应于定解 一般来说， 一般来说 条件的个数； 条件的个数； •条件多了，将会破坏解的存在性； 条件多了， 条件多了 将会破坏解的存在性； •条件少了，将会破坏解的唯一性。 条件少了， 条件少了 将会破坏解的唯一性。
二阶线性偏微分方程的分类
F ( x, y , u x , u y , u xx , u yy ) = 0
•第一类边界条件：给出未知函数u 在边界上的值 第一类边界条件：给出未知函数 第一类边界条件 •第二类边界条件：给定未知函数u 在边界上的 第二类边界条件：给定未知函数 第二类边界条件 法向导数值
•第三类边界条件：给出边界上未知数u 及其法向 第三类边界条件：给出边界上未知数 第三类边界条件 导数之间的线性关系
•波动方程：含有对时间的二阶偏导数 ，两个初始条件 波动方程： 波动方程 •传输方程：含有对时间的一阶偏导数 ，一个初始条件 传输方程： 传输方程 •稳定场方程：不随时间变化，没有初始条件 稳定场方程：不随时间变化， 稳定场方程
•边界条件 边界条件——描述系统在边界上的状况 边界条件 描述系统在边界上的状况
•衔接条件 衔接条件
在研究具有不同介质（或跃点处）的问题中， 在研究具有不同介质（或跃点处）的问题中， 在不同介质（或跃点处） 在不同介质（或跃点处）的界面处有衔接条件
第二章定解问题.
若 f 0
称为弦的自由振动，振动过程中不受外力。
utt a2uxx
齐次波动方程
事实上，除了以上一维波动方程，像薄膜振动（二维），电 磁场方程（三维）等，均属于波动方程：
utt a2u f (x, y, t)
uxx
uyy
2u x2
2u y 2
utt a22u a2 (uxx uyy uzz )
2 2 2 2 x2 y2 z2
三维拉普拉斯算符
补例：电磁场方程（三维波动方程）
已知：电磁场的麦克斯韦方程组的微分形式是
D
(1)
Ε Bt
(2)
B 0
(3)
H j Dt (4)
D E B H j E
(x)utt (x 2x,t) F(x 1x,t)x T ux(x x,t) ux(x,t)
T2 sin 2 T1 sin 1 F(x 1x,t)x (x)utt (x 2x,t)
整理得
utt
(x
2 x, t )
T
Y
Y
F(x,t)
T2
M2
2
M1
1
2、分析：
A x x x
B
X
T1
x
xx
X
（1）确定研究对象：设 u(x,t) 为弦位移，则u满足规律所 求。为了研究u，在x位置处取x小段弦为研究对象。
（2）物理问题的数学抽象：
1）由于弦是“细长”的，所以 (x,t) t
忽略重力
2）由于弦“绷紧”于AB两点，这说明弦中各相邻部分之间有 拉力即“张力”作用；由于弦是“柔软”的，所以相邻小段张 力总是弦线的切线方向；
第一章三类典型方程和定解条件
一个定解问题提的是否符合实际情况，从 数学角度来看，有三方面可以加以检验：
1、解的存在性，看定解问题是否有解。
2、解的唯一性，看是否只有一个解。
3、解的稳定性，看当定解条件有微小
变动时，解是否相应地只有微小的变 动，若确实如此，则称此解是稳定的。
如果一个定解问题存在唯一且稳定的解， 则此问题称为适定的。
用以说明初始状态的条件称为初始条件。 用以说明边界上的约束情况的条件称为边 界条件。
一、初始条件
比如说波动方程（1.3）其初始条件有两 个，一个是参数u，一个是u的一阶导数。 即： u u t 0 及 都已知。 t
t 0
而热传导方程（1.7）其初始条件只有一 个，就是参数u。即：
u t 0 是已知。
2 2 2 2u u u u 2 a ( 2 2 2) 2 t x y z
(1.4)
上式（1.4）称为齐次三维波动方程。
二、热传导方程
若函数u(x,t)关于t是可微的，关于x是二次 连续可微的，并满足：
2 u 2 u a (a为系数) 2 t x
(1.5)
aij ( x), bi ( x), c x , f ( x) 都只是 x1 , x2, 其中， 函数，与未知函数无关。
, xm 的已知
若一个函数具有某偏微分方程中所需 要的各阶连续偏导数，并且代入该方程中 能使它变成恒等式，则此函数称为该方程 的解（古典解）。 初始条件和边界条件都称为定解条件。 把某个偏微分方程和相应的定解条件 结合在一起，就构成了一个定解问题。 只有初始条件，没有边界条件的定解问题 称为始值问题（或柯西问题）。反之，只 有边界条件，没有初始条件的定解问题称 为边值问题。既有初始条件又有边界条件 的定解问题，称为混合问题。
数理方程（ＰＤＦ）
第二章 分离变量法
§ 1 有界弦的自由振动
研究两端固定的弦的自由振动.定解问题为：
⎪⎪⎪⎪⎨⎧u∂∂t2xu2=0
− a2 = 0,
∂2u ∂x 2
u
⎪⎪⎩u t=0 = ϕ(x),
= 0,
= 0,
x=l
∂u ∂t t=0
=ψ
( x),
0< x<l t >0 0< x<l
特点: 方程齐次, 边界齐次.
利用边界条件
⎪⎧ ⎨ ⎪⎩
X X
( 0 )T (l )T
(t) (t)
= =
0 0
…
…
……
…
…
④
④ 成立 ⇔ X (0) = 0, X (l) = 0
则
⎧ ⎨ ⎩
X X
'' + (0)
λX = 0
= 0, X (l
)
=
………………⑤ 0
参数 λ 称为特征值.
特征值问题
函数X(x)称为特征函数
分三种情形讨论特征值问题的求解：
l
+
Bn
sin
nπat
l
n = 1,2,L
所以
u0( x, t) = A0 + B0t
un(
x,
t)
=
(
An
cosnπ
l
at
+
Bn
sin
nπ
l
at)
cosnπ
l
x
故
n =1,2,L
∑ u( x, t )
=
A0
+
B0t
+
∞ n=1
§ 1 有界弦的自由振动
研究两端固定的弦的自由振动.定解问题为：
⎪⎪⎪⎪⎨⎧u∂∂t2xu2=0
− a2 = 0,
∂2u ∂x 2
u
⎪⎪⎩u t=0 = ϕ(x),
= 0,
= 0,
x=l
∂u ∂t t=0
=ψ
( x),
0< x<l t >0 0< x<l
特点: 方程齐次, 边界齐次.
利用边界条件
⎪⎧ ⎨ ⎪⎩
X X
( 0 )T (l )T
(t) (t)
= =
0 0
…
…
……
…
…
④
④ 成立 ⇔ X (0) = 0, X (l) = 0
则
⎧ ⎨ ⎩
X X
'' + (0)
λX = 0
= 0, X (l
)
=
………………⑤ 0
参数 λ 称为特征值.
特征值问题
函数X(x)称为特征函数
分三种情形讨论特征值问题的求解：
l
+
Bn
sin
nπat
l
n = 1,2,L
所以
u0( x, t) = A0 + B0t
un(
x,
t)
=
(
An
cosnπ
l
at
+
Bn
sin
nπ
l
at)
cosnπ
l
x
故
n =1,2,L
∑ u( x, t )
=
A0
+
B0t
+
∞ n=1
定解条件和定解问题
定解条件与定解问题含有未知函数得偏导数得方程叫偏微分方程,常微分方程可以瞧成就是特殊得偏微分方程。
方程得分数就是1得称为方程式,个数多于1得叫做方程组。
方程（组)中出现得未知函数得最高阶偏导数得阶数称为方程(组)得阶数。
如果方程(组)中得项关于未知函数及其各阶偏导数得整体来讲就是线性得，就称方程(组)为线性得,否则就称为非线性得。
非线性又分为半线性、拟线性与完全非线性。
一、定解条件给定一个常微分方程,有通解与特解得概念。
通解只要求满足方程,即满足某种物理定律,而不能完全确定一个物理状态。
特解除了要求满足方程还要满足给定得外加(特殊)条件。
对偏微分方程也就是如此,换句话说，只有偏微分方程还不足以确定一个物理量随空间与时间得变化规律,因为在特定情况下这个物理量还与它得初始状态与它在边界受到得约束有关。
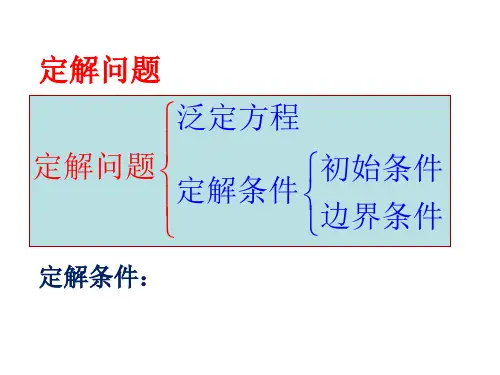
描述初始时刻得物理状态与边界得约束情况,在数学上分别称为初始条件(或初值条件)与边界条件(或边值条件)，她们统称为定解条件。
初始条件：能够用来说明某一具体物理现象初始状态得条件,即描述物理过程初始状态得数学条件。
边界条件:能够用来说明某一具体物理现象边界上得约束情况得条件,即描述物理过程边界状态得数学条件。
定解条件:初始条件与边界条件得统称。
非稳态问题:定解条件包括初始条件与边界条件。
稳态问题:定解条件为边界条件。
1、弦振动方程 ( )初始条件就是指初始时刻(）弦得位移与速度。
若以, 分别表示弦上任意点得初始位移与初始速度，则初始条件为：边界条件就是指弦在两端点得约束情况,一般有三种类型。
(1)第一类边界条件(狄利克雷(Dirichlet)边界条件）:已知端点处弦得位移就是,则边界条件为:或当时,表示在该点处弦就是固定得。
(2)第二类边界条件(诺伊曼(Nｅuｍann)边界条件):已知端点弦所受得垂直于弦线得外力或,则边界条件为:或当,表示弦在端点处自由滑动。
(3）第三类边界条件(混合边界条件或罗宾（Ｒｏbiｎ)边界条件:已知端点处弦得位移与所受得垂直于弦线得外力得与:或,其中表示两端支承得弹性系数,当时,表示弦在该端点处被固定在一个弹性支承上。
2定解条件
而常说恒定表面浓度扩 散，是指硅片表面杂质 浓度维持一定，向内部 扩散。
ut u
t 0
0
0 x l / 2 2lh x 2 h (l x ) l / 2 x l l
t 0
稳定场问题与时间无关，不存在初始条件的问题． 二、边界条件： 研究具体的物理系统，还必须考虑系统
的边界上的物理状况，即边界条件． 常见的线性边界条件有三种。 1、第一类边界条件：直接可写出边界上物理量的表达式。
u s f ( x0 , y0 , z0 , t )
2、第二类边界条件：可写出边界上物理量沿边界法向方向 导数的表达式
u n
f1 ( x0 , y0 , z0 , t )
s
3、第三类边界条件： 可写出边界上物理量沿边界法向方向导数与边界上物理 量的线性组合的表达式
u （ hu) f 2 ( x0 , y0 , z0 , t ) n s
ut ( x, y, z, t ) t 0 ( x, y, z )
从数学角度看，输运过程方程含时间一阶导数，须有一个初始条件， 振动过程含时间二阶导数，须有两个初始条件。 注意：初始状态指的是整个系统的初始状态，而不是系统中个别地点的初
始态．例如：长为L两端固定的弦，用手把它的中点朝横向拨开距离h， 然后放手任其振动.
就时间t这个目变数而论，振动方程是 t的二阶微分程，输运 方程是t的一阶微分方程，所以初始条件的提法有所不 同．对了输运过程(热传导、扩散)，初始状态指的是所研 究物理量 u(温度、浓度)初始分布.
u( x, y, z, t ) t 0 ( x, y, z), 为已知函数。
对于振动过程(弦、杆、膜的振动，传输线上电振动，声振动、 电磁振动)，初始状态包括初始“位移” 和初始“速度” u ( x, y, z , t ) t 0 ( x, y, z )
数理方程：第2讲典型方程的定解条件
弹性力 k u xl
张力
T u x xl
u
u
x
xl
0
( T )
k
(2) 热传导问题（端点自由冷却）
散失的热量
dQ1 h(u u1)dSdt
内部流到边界的热量
dQ2
k
u dSdt n
dQ1 dQ2 k nu h(u u1 )
即
(u
u )
x xl
u1
( k )
h
§3 定解问题
x
, t
0)
的解等于问题(I)和问题(II)的解之和
(I)
utt u t0
a2uxx 0
( x), ut
t0
(
(x)
x
, t
0)Байду номын сангаас
(II) utt a2uxx f ( x, t ) u t0 0, ut t0 0
( x ,t 0)
如
Lu
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u y
c
u
u x
x0
二阶偏微分方程
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u cu y
f
可简写为
L[u] f
叠加原理 1 若ui 满足线性方程 L[ui ] fi ，i 1,2,, n
➢包含初值条件和边界条件的定解问题称为混合问题 (初边值问题)
uutt
0
a2(uxx
(x, y
u yy ,z)
数理方程总结完整版
该方程是非齐次方程。解决该类方程主要用特征函数法来 解决。以本题为例，来介绍一下特征函数法。
1.先求出该题目对应的齐次方程的特征函数， 即时当f（x，t）为零时。该题对应的齐次方 程为左一右一边界条件的齐次的一维波动方 n 程，其特征函数为X(x)=sin x, n 1, 2, 3... l n n 则设u（x，t） = Tn (t ) sin x, f ( x, t ) fn(t ) sin x, l l n 1 n 1 n n ( x) n sin x, ( x) n sin x, n 1, 2, 3... l l n 1 n 1
第二章 分离变量法
本章主要掌握三大类方程的解法，分别是有界弦的
自由振动方程，有限杆上的热传导方程，这两个方 程里包括“左几右几”的边界条件的，齐次或非齐 次边界条件的，齐次或非齐次方程的多种形式。 还有一个就是圆域内或扇形域内的二维拉普拉斯方 程，这类方程相对于比较简单，考试时的类型比较 固定。 1.有界弦的自由振动方程（方程是齐次的）的基本 解：
2 2u 2 u t 2 a x 2 f ( x, t ), 0 x l , t 0, u | x 0 u | x l 0, t 0, u u | t 0 ( x), | t 0 ( x), 0 x l. t
a 2 ( n 1/2) 2 2 t l2
(n 1/ 2) cos x l
④：“左二右二”的齐次边界条件的齐次方程：
2 u 2 u a , 0 x l , t 0, 2 t x u | x 0 0, u | x l 0, t 0, x x
l
1.先求出该题目对应的齐次方程的特征函数， 即时当f（x，t）为零时。该题对应的齐次方 程为左一右一边界条件的齐次的一维波动方 n 程，其特征函数为X(x)=sin x, n 1, 2, 3... l n n 则设u（x，t） = Tn (t ) sin x, f ( x, t ) fn(t ) sin x, l l n 1 n 1 n n ( x) n sin x, ( x) n sin x, n 1, 2, 3... l l n 1 n 1
第二章 分离变量法
本章主要掌握三大类方程的解法，分别是有界弦的
自由振动方程，有限杆上的热传导方程，这两个方 程里包括“左几右几”的边界条件的，齐次或非齐 次边界条件的，齐次或非齐次方程的多种形式。 还有一个就是圆域内或扇形域内的二维拉普拉斯方 程，这类方程相对于比较简单，考试时的类型比较 固定。 1.有界弦的自由振动方程（方程是齐次的）的基本 解：
2 2u 2 u t 2 a x 2 f ( x, t ), 0 x l , t 0, u | x 0 u | x l 0, t 0, u u | t 0 ( x), | t 0 ( x), 0 x l. t
a 2 ( n 1/2) 2 2 t l2
(n 1/ 2) cos x l
④：“左二右二”的齐次边界条件的齐次方程：
2 u 2 u a , 0 x l , t 0, 2 t x u | x 0 0, u | x l 0, t 0, x x
l
定解条件
衔接条件：
在研究区域中出现跳变点，两边不同，两边各写
方程再加上衔接条件。
小结：
(1)边界条件是给出系统与外界“环境”的关系 问题，把握边界的含义，区分边界条件与泛定 方程中的条件； (2)边界条件的多样性与确定性，以及分类问题。 (3)无边界条件与衔接条件的问题。
定解问题的整体性与适定性
1、整体性：必须同时考虑偏微分方程和定解条 件加以联合求解(有特例)；一般不能先求通解再 由定解条件求特解； 2、适定性：表现在三个方面：
u(x，t) x0 N0
u(x，t) xl
N0
第二类(Neumann边界条件)：
u n
边界x0，y0，z0
f
(x0，y0，z0，t)
给出未知函数在边界外法线方向上的方向导数。 例：1、杆作纵振动，x=0或x=l端受沿法线方向的 外力f(t)
(Eun ) x0 S (Eux ) x0 S f (t)
ES
u x
x0
F0
ES u n
xl
ES u x
xl
F0
2、热传导：已知x=l端的热流f(t)
(流出为正，流入为负，这里自身取正值)
kun
xl
f
(t)
un
xl
1 k
f
(t)
若为绝热
ux (x，t) xl 0
3、扩散问题： “限定源”(即只是表层已有的杂
质向硅片深部扩散)
ux (x，t) x0 0 ux (x，t) xl 0 第三类(Robin边界条件)：
(Eun ) xl S
(Eux )
S
xl
f
(t)
对于自由端 f (t) 0，则 ux(x，t) xl 0 注：杨氏模量是描述固体材料抵抗形变能力的物理
数理方程中典型方程和定解条件的推导ppt课件
P5 (1.5) ”是否合理？
结点与节点有区别吗？
Rdx
+
- v(x,t)
Ldx
i(x,t)
Cdx
P● ＋
－
i +di C L– L
GdxC v dv
x
●
图 12
x dx
iC
C
duC dt
di
u L
L
dt 19
梁昆淼先生的做法：
“今考虑一来一往的高频传输线，每单位长一来一往所具有的电阻，电感，电容， 电漏分别记以 R，L，C，G。于是
x1d2x
3、忽略与近似
T cos Tcos 0
(1)
T sin T sin ds g ds utt
(2)
①对于小振动： 0; 0
cos 1 ; cos 1
sin
tg 1 tg2
tg u x
x
sin
tg 1 tg2
tg u x
x dx
于是（1）式变为：
T T
代入（2）式变为：
T sin T sin ds(utt g)
T u x
xdx T
u x
x
ds(ut t g)
②一般说来，ut t g ， 将 g 略去，上式变为
Cdx
Gdx v dv
x
●
x dx
17
电路准备知识 电容元件：
du
i C C
C
dt
q Cu
i dq d(Cu) C du
dt dt
dt
q idt
电感元件：
数理方程第讲
X(x)lX(x)0. (2.5) 6
再利用边界条件(2.2), 由于u(x,t)=X(x)T(t),
X(0)T(t)=0, X(l)T(t)=0. 但T(t)0, 如果T(t)=0, 这种解称为平凡解, 所 以
X(0)=X(l)=0
(2.6)
因此, 要求方程(2.1)满足条件(2.2)的变量分离
由于方程(2.13)与边界条件(2.14)都是齐次的,
所以 u (x,t)C n e- n 2 a 2 tsinnx (2 .2 2 )
n 1
仍满足方程与边界条件. 最后考虑u(x,t)能否
n
xd x
0
10
2
5n 3
3
(1 -
cos
n
)
0, 当 n为偶数 ,
4
5n 3
3
,
当
n 为奇数
.
23
因此, 所求的解为 u(x,t)
543n 0(2n1 1)3sin(2n1 01)xcos10(2n1)t
24
解题中常用到的积分表的内容:
xsin
axd
x
1 a2
sin
ax
-
1 a
x
cosax
x
(2.11)
16
u(x,t) un(x,t) n1
n1Cn
cosnat
l
Dn
sinnl at sinnl
x
(2.11)
将初始条件(2.3)代入上式得:
u(x,t)|t0u(x,0)n1Cnsinnlx(x)
u
t t0
Dn
n1
nasinn
ll
x(x)
17
复习高等数学中周期为2l的傅立叶级数: 如果周期为2l的周期函数f(x)为奇函数, 则有
数学物理方程-典型方程和定解条件名师公开课获奖课件百校联赛一等奖课件
运动时，弦上各点旳运动规律。
简化假设：
(1)柔软：弦上旳任意一点旳张力沿弦旳切线方向； 细：与张力相比可略去重力,弦旳截面直径与长度相比可忽视，弦视为曲
线 均匀：质量是均匀旳，线密度为常数。
(2)横振动：振动发生在同一平面内。若弦旳平衡位置为x轴，横向是指 弦上各点在同一平面内垂直于x轴旳方向运动；
x
x
即x点处的应变为 u(x,t) . x
若略去垂直杆长方向的变形，根据Hooke定律，弹(应)力P与应变 u x
成正比：P E u , E为杆的Young模量,故
x
2u t 2
E
2u x2
,
2u t 2
a2
2u x2
,
（其中a
E）.
例3、热传导方程
热传导现象：当导热介质中各点旳温度分布不均匀时，有 热量从高温处流向低温处。
☆ 特殊函数
在求解某些类型旳数理方程时，采用分离变量法所得到旳方程旳解 是某种特殊函数，例如贝塞尔(Bessel)函数、勒让德(Legendre)函 数等。其中有些特殊函数我们在“微积分”课程中已经学习而且研究 过其性质。在本课程中，我们只讨论它们在数理方程中旳应用问题。
☆ 课程旳内容： 三类方程、 四种求解措施、 二个特殊函数
t1 V
t
M V
S
热场
t2 k2udVdt t2 c udVdt
t1 V
t1 V
t
k2u c u u k 2u a22u （齐次）热传导方程 t t c
如果介质内部有热源，设单位时间内单位体积介质中产生的热量
为Fx, y, z, t ，由能量守恒定律有
t2 k2udVdt t2 FdVdt t2 c udVdt
简化假设：
(1)柔软：弦上旳任意一点旳张力沿弦旳切线方向； 细：与张力相比可略去重力,弦旳截面直径与长度相比可忽视，弦视为曲
线 均匀：质量是均匀旳，线密度为常数。
(2)横振动：振动发生在同一平面内。若弦旳平衡位置为x轴，横向是指 弦上各点在同一平面内垂直于x轴旳方向运动；
x
x
即x点处的应变为 u(x,t) . x
若略去垂直杆长方向的变形，根据Hooke定律，弹(应)力P与应变 u x
成正比：P E u , E为杆的Young模量,故
x
2u t 2
E
2u x2
,
2u t 2
a2
2u x2
,
（其中a
E）.
例3、热传导方程
热传导现象：当导热介质中各点旳温度分布不均匀时，有 热量从高温处流向低温处。
☆ 特殊函数
在求解某些类型旳数理方程时，采用分离变量法所得到旳方程旳解 是某种特殊函数，例如贝塞尔(Bessel)函数、勒让德(Legendre)函 数等。其中有些特殊函数我们在“微积分”课程中已经学习而且研究 过其性质。在本课程中，我们只讨论它们在数理方程中旳应用问题。
☆ 课程旳内容： 三类方程、 四种求解措施、 二个特殊函数
t1 V
t
M V
S
热场
t2 k2udVdt t2 c udVdt
t1 V
t1 V
t
k2u c u u k 2u a22u （齐次）热传导方程 t t c
如果介质内部有热源，设单位时间内单位体积介质中产生的热量
为Fx, y, z, t ，由能量守恒定律有
t2 k2udVdt t2 FdVdt t2 c udVdt
数学物理方程的定解条件
数学物理方程的定解条件数学物理方程是数学物理学中重要的一类问题，它涉及到各种物理现象的建模和解释，是理解物理现象的有用工具。
数学物理方程有一系列特定的定解条件，它们是为了研究物理现象并得到定解而必须遵守的准则。
首先，针对数学物理方程，必须正确理解方程定义以及它表达的物理量的内涵。
在实际求解之前，要了解方程的变量定义以及它与实际物理现象之间的联系，以确保解的准确性。
其次，必须确定定解中的每个变量的取值范围，以便确定方程可以解出多少解。
对于多元一次方程，参数一般被称为“系数”，将其视为未知数，根据它们取值来确定解的存在性或不存在性。
再次，必须解决方程中可能存在的技术和数学问题，如求解方程的函数表达式、求极值、得到非线性方程的精确解等。
这些问题一般需要一定的技术和数学知识来解决，所以解决定解条件有其独特的技术要求。
最后，必须将定解得到的解与实际物理现象进行比较，以确保定解的准确性。
因为物理现象可能比定解器更复杂，所以在实际应用中容易出现偏差，可以通过数值积分和数值近似的方法来消除偏差并更接近实际物理现象。
通过以上步骤，就可以获得数学物理方程的定解了。
补充说明的是，数学物理方程有一系列分析和解决的步骤，除了上述的定解条件外，还包括确定系数、求极限、求精确解等，它们也是重要的步骤，因此要充分理解它们，以达到准确解决数学物理方程的目的。
总之，数学物理方程的定解条件是为了研究物理现象并得到定解而必须遵守的准则，它们包括正确理解方程定义以及它表达的物理量的内涵、确定定解中的每个变量的取值范围、解决方程中可能存在的技术和数学问题，以及将定解得到的解与实际物理现象进行比较。
只有按照这些定解条件准确解决数学物理方程，才能真正理解物理现象。
定解条件和定解问题
定解条件和定解问题含有未知函数的偏导数的方程叫偏微分方程;常微分方程可以看成是特殊的偏微分方程..方程的分数是1的称为方程式;个数多于1的叫做方程组..方程组中出现的未知函数的最高阶偏导数的阶数称为方程组的阶数..如果方程组中的项关于未知函数及其各阶偏导数的整体来讲是线性的;就称方程组为线性的;否则就称为非线性的..非线性又分为半线性、拟线性和完全非线性..一、定解条件给定一个常微分方程;有通解和特解的概念..通解只要求满足方程;即满足某种物理定律;而不能完全确定一个物理状态..特解除了要求满足方程还要满足给定的外加特殊条件..对偏微分方程也是如此;换句话说;只有偏微分方程还不足以确定一个物理量随空间和时间的变化规律;因为在特定情况下这个物理量还与它的初始状态和它在边界受到的约束有关..描述初始时刻的物理状态和边界的约束情况;在数学上分别称为初始条件或初值条件和边界条件或边值条件;他们统称为定解条件..初始条件：能够用来说明某一具体物理现象初始状态的条件;即描述物理过程初始状态的数学条件..边界条件：能够用来说明某一具体物理现象边界上的约束情况的条件;即描述物理过程边界状态的数学条件..定解条件：初始条件和边界条件的统称..非稳态问题：定解条件包括初始条件和边界条件..稳态问题：定解条件为边界条件..1、弦振动方程 2(,),0,0tt xx u a u f x t x l t -=<<>初始条件是指初始时刻0t =弦的位移和速度..若以()x ϕ;()x ψ分别表示弦上任意点x 的初始位移和初始速度;则初始条件为：边界条件是指弦在两端点的约束情况;一般有三种类型.. 1第一类边界条件狄利克雷Dirichlet 边界条件:已知端点()x a a o a l ===或处弦的位移是()a g t ;则边界条件为：(0,)(0,)u t g t = 或 (,)(,)u l t g l t =当0()0()0l g t g t ≡≡或时;表示在该点处弦是固定的..2第二类边界条件诺伊曼Neumann 边界条件：已知端点0x x l ==或处弦所受的垂直于弦线的外力0()g t 或()l g t ;则边界条件为：0(0,)()x Tu t g t -= 或 (,)()x l Tu l x g t =当00()0l g g t ≡≡或时;表示弦在端点0x x l ==或处自由滑动..3第三类边界条件混合边界条件或罗宾Robin 边界条件：已知端点处弦的位移和所受的垂直于弦线的外力的和：000(0,)(0,)g (t),0,x Tu t k u t k -+=>或(,)(,)(),0x l l l Tu l t k u l t g t k +=>;(,0)(),0(,0)(),t u x x x l u x x ϕψ=⎧<<⎨=⎩其中0l k k 和表示两端支承的弹性系数;当0()0()0l g t g t ≡≡或时;表示弦在该端点处被固定在一个弹性支承上..2、热传导方程2(x,t),x ,)nt u a u f t o -=∈Ω⊂>初始条件是指初始时刻物体内的温度分布情况..式中φ x ; y ; z 为已知函数;表示温度在初始时刻的分布..边界条件是指边界上温度受周围介质的影响情况;可分为三种..（1） 第一类边界条件：介质表面温度已知式中;p 为边界面上的点.. 2第二类边界条件：通过介质表面单位面积的热流量己知..3第三类边界条件：边界面与周围空间的热量交换规律已知 由热量守恒定律可知;这个热量等于单位时间内流过单位面积上的热量..3、位势方程泊松方程或拉普拉斯方程对于稳态问题;变量不随时间发生变化..定解条件不含初始条件;只有边界条件..(,,,0)(,,)T x y z x y z ϕ=0(,)S Tp t ϕ==, (,)n ST Tq K const f p t n n ∂∂=-==∂∂0() ()n q T T αα=-为热交换系数0(), (,)ST T K T T hT f p t n n α∂∂⎛⎫-=-+= ⎪∂∂⎝⎭第一边值问题;狄利克莱问题狄氏问题第二边值问题;牛曼问题第三边值问题混合问题鲁宾问题二、 定解问题一个方程匹配上定解条件就构成定解问题..对于定解问题;通常由于定解条件的差异有下面的三种提法：①偏微分方程泛定方程+初始条件+边界条件;称为初边值()S f p ϕ=()Sf p nϕ∂=∂()Sh f p n ϕϕ∂+=∂问题或混合问题；②偏微分方程泛定方程+初始条件;称为初值问题或柯西问题；③偏微分方程泛定方程边界条件;称为边值问题.. 在一个偏微分方程的定解问题中;把不含未知函数及其偏导数的项;称为自由项..如果方程中的自由项为零;则称方程为齐次方程;否则就称为非齐次方程..如果边界条件中的自由项为零;则称边界条件为齐次边界条件;否则就称为非齐次边界条件..例如;对于弦振动方程;当外力等于零时;方程就变为齐次方程;此时也称它为弦的自由振动方程；当弦的两端固定时;边界条件就是齐次边界条件..三、 例题1、长为l 的弦;两端固定于0和l ..在中点位置将弦沿着横向拉开距离h ;如图所示;然后放手任其振动;试写出初始条件..解：初始时刻就是放手的那一瞬间;按题意初始速度为零;即有lxl/2 0==(,)t t u x t 02 0222=⎧∈⎪⎪=⎨⎪-∈⎪⎩[,(,)()[,]t hl x x l u x t h l l x x l l初始位移2、长为l 的杆;上端固定在电梯的顶杆上;杆身竖直;下端自由 ..电梯在下降过程中;当速度为v0 时突然停止..试写出杆振动的定解问题..四、 总结222220,(0,),0(,0)0,(,0),(0,)(0,)(,)0,0t x u u a x l t t x u x u x v x l u t u l t t ⎧∂∂=∈>⎪∂∂⎪⎨==∈⎪⎪==≥⎩王晶1307021066 物理学术班。
数理方程定解问题
数理⽅程定解问题数理⽅程定解问题：1、数理⽅程的分类反应热传导的⽅程类型为：u t=D?u+f其中?=e2ex2+e2ey2+e2ez2，u t=euet，未知数u表⽰温度特征，D表⽰热传导系数，f是与源有关的已知函数，当f=0的时候，相应的⽅程被称为齐次⽅程。
2、⽤数理⽅程研究物理问题的步骤⽤数理⽅程研究物理问题⼀般需经历以下三个步骤（1）导出或写出定解问题，它包括数理⽅程和定解条件两部分（2）求解已导出或写出的定解问题（3）对求得的答案讨论其适定性（即解是否存在、唯⼀且稳定）并作适当的物理解释3、求解数理⽅程的⽅法求解数理⽅程的⽅法⼤致可归纳为如下⼏种（1）⾏波法（d’Alembert解法）（2）分离变量法（3）积分变换法（4）Green函数法（5）保⾓变换法（6）复变函数法（7）变分法定解条件定解条件是确定数理⽅程解中所含的任意函数或常数，使解具有唯⼀性的充分必要条件。
它分为初始条件和边界条件两种。
若所研究的系统是由⼏种不同介质组成的，则在两种介质的交⾯上定解条件还应当有衔接条件。
1、初始条件（1）定义初始条件是物理过程初始状况的数学表达式（2）初始条件的个数关于时间t的n阶偏微分⽅程，要给出n个初始条件才能确定⼀个特解。
热传导⽅程仅需给出⼀个初始条件u x，y，z；t|t=0=φ(x，y，z)2、边界条件（1）定义物理过程边界状况的数学表达式称为边界条件。
（2）边界条件的种类和个数边界条件分为三类。
设f(M，t)为任⼀已知函数，M为边界上的点，则三类边界条件分别为：1 第⼀类边界条件u|边=f(M,t)2 第⼆类边界条件euen |边=f(M,t)3 第三类边界条件[u+heuen ]边=f(M,t)其中u|边表⽰未知函数u在边界⾯上的值，euen|边表⽰未知函数沿边界外法向的导数在边界上的值，h为任意常数。
若f=0，泽以上三类边界条件分别称为第⼀、第⼆、第三类齐次边界条件，否则称作相应的⾮齐次边界条件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
u t0 h
()
u h
u xl / 2 h ( )
0
l
lx
2
正确写法
u t0
2h l
x,
2h (l l
x ),
0 x l 2
l xl 2
二. 边界条件 描述某系统或过程边界状况的约束条件称为边界条件. ➢第一类边界条件
例.长为l的弦，一端固定，一端以 sint 规律运动
u x0 0, u xl sin t
如
Lu
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u y
c
u
u x
x0
二阶偏微分方程
a11
2u x 2
2a12
2u xy
a22
2u y 2
b1
u x
b2
u cu y
f
可简写为
L[u] f
叠加原理 1 若ui 满足线性方程 L[ui ] fi ，i 1,2,, n
i 1
B i
u x
cu
f
0
i
j
i
两个自变量二阶线性偏微分方程的一般形式
A 2u 2B 2u C 2u D u E u Fu f
x 2
xy y2 x y
………
➢ 线性方程的叠加原理
称形如
L
a11
2 x 2
2a12
2 xy
a22
2 y 2
b1
x
b2
y
c
x
x0
的符号为微分算子。
§2 初始条件与边界条件
1. 初始条件
2. 边界条件
一 . 初始条件及Cauchy问题
1、描述某系统或某过程初始状况的条件称为初始 条件；
2、初值条件与对应方程加在一起构成初值问题 (或称Cauchy问题）。
弦振动问题
初始位移、初始速度分别为 ( x), ( x) ,称 u t0 ( x), ut t0 ( x)
u x0 0, ux xl 0
(0 x l,t 0) (0 x l)
波动方程的混合问题
➢只附加边界条件的定解问题称为边值问题. ➢初值条件、边界条件统称为定解条件 . ➢初值问题、边值问题、混合问题统称为定解问题.
➢一般线性二阶偏微分方程（n个自变量）源自nn2ui1 k1
A ik
x
x
n
弹性力 k u xl
张力
T u x xl
u
u
x
xl
0
( T )
k
(2) 热传导问题（端点自由冷却）
散失的热量
dQ1 h(u u1)dSdt
内部流到边界的热量
dQ2
k
u dSdt n
dQ1 dQ2 k nu h(u u1 )
即
(u
u )
x xl
u1
( k )
h
§3 定解问题
➢包含初值条件的定解问题称为初值问题
（Cauchy 问题）
utt u |t0
a 2uxx
(x
)
0
ut |t0 ( x)
( x ,t 0) ( x )
弦振动的Cauchy问题
ut a2uxx 0
u |t0 ( x)
( x ,t 0) ( x )
热传导方程的Cauchy问题
x
, t
0)
的解等于问题(I)和问题(II)的解之和
(I)
utt u t0
a2uxx 0
( x), ut
t0
(
(x)
x
, t
0)
(II) utt a2uxx f ( x, t ) u t0 0, ut t0 0
( x ,t 0)
➢第二类边界条件
u 0 x xl 不受力 自由端
对弦的振动
u x xl
f (t) 表示在x轴方向给出的外力
对热传导方程 u f ( x, y, z,t) 表示单位面积、单 n
位时间沿边外法 线方向流出的热量。
u 0 n 没有热交换 绝热
➢ 第三类边界条件
例 (1) 弦的振动（端点弹性连结）
（或定解条件B[ui ] gi ），
n
则u ci ui 满足方程
i 1 n
L[u] ci fi
i 1 n
（或定解条件B[u] ci gi ），其中ci 为任意常数。
i 1
例 非齐次波动方程的Cauchy问题
utt u t 0
a 2uxx f
( x), ut
( x, t) (
t0 (x)
为波动方程的初值条件。
(x) 0且 (x) 0 齐次初始条件.
热传导方程
u t0 ( x)
称为热传导方程的初值条件
注意 ➢ 不同类型的方程，相应初值条件的个数不同。 ➢ 初始条件给出的应是整个系统的初始状态，而非
系统中个别点的初始状态。
例.长为 l 两端固定的弦，初始时刻将弦的中点拉起 h
➢包含初值条件和边界条件的定解问题称为混合问题 (初边值问题)
uutt
0
a2(uxx
(x, y
u yy ,z)
uzz
)
0
(u u) f ( x, y, z, t )
n
(x, y,z) ,t 0 (x, y,z)
热传导方程的混合问题
utt a2uxx
u t0 ( x),ut t0 ( x)