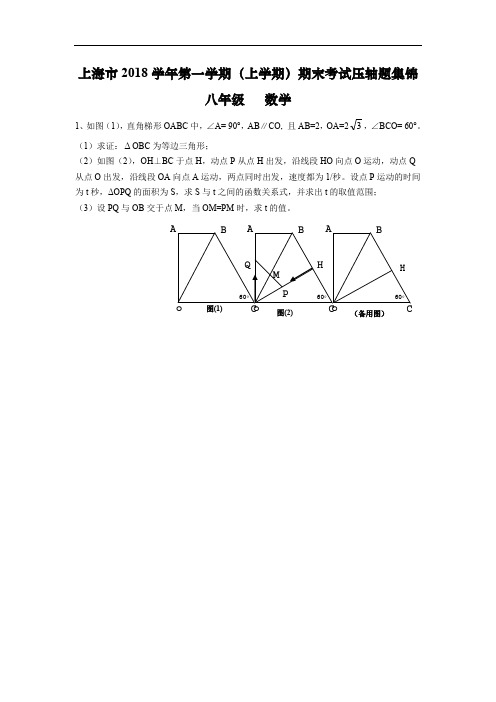
2018年上海市初二期末压轴题图文解析
- 格式:pdf
- 大小:1.77 MB
- 文档页数:64

2018年上海市金山区初二期末数学试卷一、选择题(本大题共10小题,每小题2分,共12分)1. 下列直线与一次函数的图像平行的直线是()A. ;B. ;C. ;D. .【答案】B【解析】【分析】设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.据此可以判断.【详解】A.直线与直线相交,故不能选;B.直线与直线平行,故能选;C.直线与直线重合,故不能选;D.直线与直线相交,故不能选.故选:B【点睛】本题考核知识点:一次函数.解题关键点:熟记一次函数性质.2. 下列方程中是二项方程的是()A. ;B. =0;C. ;D. =1.【答案】C【解析】【分析】二项方程:如果一元n次方程的一边只有含未知数的一项和非零的常数项,另一边是零,那么这样的方程就叫做二项方程.据此可以判断.【详解】A. ,有2个未知数项,故不能选;B. =0,没有非0常数项,故不能选;C. ,符合要求,故能选;D. =1,有2个未知数项,故不能选.故选:C【点睛】本题考核知识点:二项方程.解题关键点:理解二项方程的定义.3. 下列方程中有实数根的是()A. ;B. =;C. ;D. =1+.【答案】B【解析】【分析】根据算术平方根意义或非负数性质以及分式方程的意义,可以判断方程的根的情况.【详解】A. ,算术平方根不能是负数,故无实数根;B. =,两边平方可化为二元一次方程,有实数根,故可以选;C.方程化为,平方和不能是负数,故不能选;D.由=1+得x=1,使分母为0,故方程无实数根.故选:B【点睛】本题考核知识点:方程的根.解题关键点:根据方程的特殊形式判断方程的根的情况.4. 下列事件中是必然事件的是()A. 明天太阳从东边升起;B. 明天下雨;C. 明天的气温比今天高;D. 明天买彩票中奖.【答案】A【解析】【分析】根据必然事件和随机事件的定义进行分析.【详解】A. 明天太阳从东边升起,是必然事件,故可以选;B. 明天下雨,是随机事件,故不能选;C. 明天的气温比今天高,是随机事件,故不能选;D. 明天买彩票中奖,是随机事件,故不能选.故选:A【点睛】本题考核知识点:必然事件和随机事件.解题关键点:理解必然事件和随机事件的定义.5. 下列图形中是中心对称图形,但不是轴对称图形的是()A. 平行四边形;B. 矩形;C. 菱形;D. 正方形.【答案】A【解析】【分析】根据理解中心对称图形和轴对称图形定义,可以判断.【详解】平行四边形是中心对称图形,不是轴对称图形;矩形是中心对称图形,也是轴对称图形;菱形是中心对称图形,也是轴对称图形;正方形是中心对称图形,也是轴对称图形.只有选项A符合条件.故选:A【点睛】本题考核知识点:中心对称图形和轴对称图形.解题关键点:理解中心对称图形和轴对称图形定义.6. 下列说法正确的是()A. 长度相等的两个向量叫做相等向量;B. 只有方向相同的两个向量叫做平行向量;C. 当两个向量不相等时,这两个有向线段的终点一定不相同;D. 减去一个向量相当于加上这个向量的相反向量.【答案】D【解析】【分析】相等向量:长度相等且方向相同的两个向量叫做相等向量; 平行向量(也叫共线向量):方向相同或相反的非零向量; 平行向量包含相等向量的情况.即相等向量一定是平行向量,但是平行向量不一定是相等向量;长度相等且方向相反的两个向量.根据相关定义进行判断.【详解】长度相等且方向相同的两个向量叫做相等向量, 故选项A错误;方向相同或相反的非零向量叫做平行向量, 故选项B错误;当两个向量不相等时,这两个有向线段的终点可能相同,故选项C错误;减去一个向量相当于加上这个向量的相反向量,故选项D正确.故选:D【点睛】本题考核知识点:向量.解题关键点:理解向量的相关定义.二、填空题(本大题共12小题,每小题3分,共36分)7. 方程=8的解是_______【答案】=-2【解析】【分析】求8的立方根可得.【详解】因为23=8,所以,x=2.故答案为:=-2【点睛】本题考核知识点:立方根.解题关键点:求一个数的立方根.8. 方程=2的解是_________【答案】【解析】【分析】方程两边平方可得到整式方程,再解之可得.【详解】方程两边平方可得x2-3x=4,即x2-3x-4=0,解得x1=-1,x2=4故答案为:【点睛】本题考核知识点:二次根式,无理方程. 解题关键点:化无理方程为整式方程.9. 关于的方程+=1的解是_______【答案】【解析】【分析】根据等式性质,将式子变形即可.即用含a的式子表示y.【详解】由+=1,得y(a2+1)=1,因为a2+1≠0,所以,.故答案为:.【点睛】本题考核知识点:解题关键点:10. 一次函数与轴的交点坐标是_______【答案】(-,0)【解析】【分析】令y=0,则0=2x+1,解得x=,可求得交点坐标.【详解】令y=0,则0=2x+1,解得x=,所以,一次函数与轴的交点坐标是(-,0).故答案为:(-,0)【点睛】本题考核知识点:一次函数的图象.解题关键点:熟记一次函数的性质.11. 已知直线在轴上的截距是-2,且与直线平行,那么该直线的解析是______【答案】【解析】【分析】根据一次函数的性质可求得.对于直线在轴上的截距是b;k是斜率,决定直线的位置关系.【详解】因为,已知直线在轴上的截距是-2,所以,b=-2.又直线与直线平行,所以,k=3.故答案为:【点睛】本题考核知识点:一次函数. 解题关键点:熟记一次函数解析式中系数的意义.12. 已知分式方程+=,设,那么原方程可以变形为__________【答案】=【解析】【分析】运用整体换元法可得到结果.【详解】设,则分式方程+=,可以变形为=故答案为:=【点睛】本题考核知识点:分式方程.解题关键点:掌握整体换元方法....... ..................【答案】【解析】【分析】先求出总的情况和对角线相等的情况,再根据概率公式可求得.【详解】因为,出现的图形共有6种情况,对角线相等的有(等腰梯形,正方形,矩形)3这情况,所以,P(对角线相等)=故答案为:【点睛】本题考核知识点:概率.解题关键点:掌握概率的求法.14. 一个多边形的每个内角都是120°,那么这个多边形的边数是_________;【答案】六【解析】【分析】先求出每个外角的度数,再根据多边形的外角和是360°,可求出多边形的边数.【详解】因为,一个多边形的每个内角都是120°,所以每个外角都是180°-120°=60°,因为,多边形的外角和是360°,所以这个多边形的边数是:360°÷60°=6.故答案为:六【点睛】本题考核知识点:多边形的角.解题关键点:理解多边形内角和外角的关系.15. 如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,那么_______;【答案】22.5°【解析】【分析】根据正方形的性质可得到∠DBC=∠BCA=45°又知BP=BC,从而可求得∠BCP的度数,从而就可求得∠ACP的度数.【详解】∵ABCD是正方形,∴∠DBC=∠BCA=45°,∵BP=BC,∴∠BCP=∠BPC=(180°-45°)=67.5°,∴∠ACP度数是67.5°-45°=22.5°.故答案为:22.5°【点睛】本题考核知识点:正方形的性质.解题关键点:熟记正方形的性质,由性质得到角的关系.16. 如图,已知AD是△ABC的中线,,,那么_________;【答案】【解析】【分析】根据向量的加法运算法则可求出结果.【详解】因为AD是△ABC的中线,所以BD=DC,即,又因为-==,所以,. 故答案为:【点睛】本题考核知识点:向量的计算.解题关键点:熟记向量的计算法则.17. 如图,在直角梯形ABCD中,,,,联结BD,若△BDC是等边三角形,那么梯形ABCD的面积是_________;【答案】【解析】【分析】作DE⊥BC,先证四边形ABED是矩形,得AD=BE=3,AB=DE,再根据等边三角形性质得到BC=2BE=6,∠BDE=60°,再利用勾股定理可求得高,再运用梯形面积计算公式可求得结果.【详解】作DE⊥BC,因为四边形ABCD的直角梯形,,,所以,四边形ABED是矩形,所以,AD=BE=3,AB=DE,又因为,三角形BCD是等边三角形,所以,BC=2BE=6,∠BDE=60°,所以,在直角三角形BED中,BD=BC=6,由勾股定理可得DE=,所以,AB=DE=所以,梯形ABCD的面积是:故答案为:【点睛】本题考核知识点:直角梯形.解题关键点:作辅助线,把问题转化为直角三角形解决.18. 如图,矩形ABCD中,,,把矩形ABCD绕点A顺时针旋转,当点D落在射线CB上的点P处时,那么线段DP的长度等于_________.【答案】【解析】【分析】画图,分两种情况:点P在B的右侧或左侧.根据旋转和矩形性质,运用勾股定理,分别求出BP和PC,便可求出PD.【详解】(1)如图,当P在B的右侧时,由旋转和矩形性质得:AP=AD=5,AB=CD=3,在直角三角形ABP中,BP=,所以,PC=BC-BP=5-4=1,在直角三角形PDC中,PD=,(2)如图,当点P在B的左侧时,由旋转和矩形性质得:AP=AD=5,AB=CD=3,在直角三角形APB中,PB=,所以,PC=BC+PB=5+4=9,在在直角三角形PDC中,PD=,所以,PD的长度为故答案为:【点睛】本题考核知识点:矩形,旋转,勾股定理. 解题关键点:由旋转和矩形性质得到边边相等,由勾股定理求边长.三、解答题(本大题共7题,19-22题每题6分,23-24题每题8分,25题12分,满分52分)19. 解方程:【答案】【解析】【分析】方程两边同时平方可把根号化去,逐渐化为整式方程,可求出解.【详解】解:移项,得两边平方,得x+2=1+x+2移项整理,得1=2两边平方,得4x=1所以,x=故答案为:【点睛】本题考核知识点:二次根式,无理方程.解题关键点:方程两边同时平方把根号化去.20. 解方程组【答案】,【解析】【分析】先将②式左边因式分解,再将①式代入,可求出x,再分别代入①式求出y.【详解】解:由②得,③,把①代入③,得,即:,所以,x+2=2或x+2=-2所以,x1=-4,x2=0,把x1=-4,x2=0,分别代入①,得y1=-3,y2=1.所以,方程组的解是,【点睛】本题考核知识点:解二元二次方程组.解题关键点:用代入法解方程组.21. 如图,在梯形中,,,点分别是边的中点,作交于点,,求线段的长度.【答案】24【解析】【分析】先证,再由梯形中位线性质证,利用含有30角的直角三角形性质,可求PC的长度,再利用三角形中位线性质求GF.【详解】解:点分别是边的中点,【点睛】本题考核知识点:梯形,平行四边形,中位线. 解题关键点:灵活运用平行四边形性质,三角形中位线性质和含有30角的直角三角形性质.22. 某中学八年级学生到离学校15千米的青少年营地举行庆祝十四岁生日活动,先遣队与大部队同时出发,已知先遣队的行进速度是大部队行进速度的1.2倍,预计先遣队比大部队早0.5小时到达目的地,求先遣队与大部队的行进速度。

2017—2018学年八年级(下)期末数学试卷一、选择题:(本大题共6题,每题3分,满分18分)[每小题只有一个正确选项,在答题纸相应题号的选项上用2B铅笔正确填涂]1.下列函数中,是一次函数的是()A.B.y=x+2 C.y=x2+2 D.y=kx+b2.用换元法解分式方程,如果设,那么原方程可以化为()A.y2+y﹣5=0 B.y2﹣5y+1=0 C.5y2+y+1=0 D.5y2+y﹣1=0 3.下列四个方程中,有一个根是x=2的方程是()A.B.C.D.4.下列说法错误的是()A.确定事件的概率是1B.不可能事件的概率是0C.必然事件的概率是1D.随机事件的概率是大于0且小于1的一个数5.下列关于向量的等式中,正确的是()A.B.﹣=C.D.6.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是()A.BA=BC B.AC、BD互相平分C.AC=BD D.AB∥CD二、填空题(本大题共12题,每小题2分,满分24分)[在答题纸相应题号后的空格内直接填写答案]7.直线y=x﹣2的截距是.8.已知一次函数y=(m﹣1)x﹣2的函数值y随着自变量x的值的增大而增大,那么m的取值范围是.9.关于x的方程ax﹣4x﹣2=0(a≠4)的解是.10.方程2x3﹣16=0的根是.11.方程的根是.12.一个二元二次方程的一个解是,写出符合要求的方程(只需写一个即可).13.已知▱ABCD,设,,那么用向量、表示向量=.14.一个正多边形的每一个外角都是72°,那么这个多边形是边形.15.在▱ABCD中,如果∠A+∠C=200°,那么∠B的度数是度.16.矩形ABCD的两条对角线AC、BD相交于点O,已知AC=12,∠ACB=30°,那么△DOC 的周长是.17.如果菱形的两条对角线长分别为6和8,那么这个菱形一边上的高是.18.在▱ABCD中,AB=5,BC=7,对角线AC和BD相交于点O,如果将点A绕着点O顺时针旋转90°后,点A恰好落在平行四边形ABCD的边AD上,那么AC的长是.三、解答题(共8题,满分58分)[将下列各题的解答过程做在答题纸的相应位置上19.解方程:=﹣1.20.解方程组:.21.一个不透明的布袋中装了分别标有数字1、2、3、4的四个小球,这些小球除标记数字不同外其余均相同.(1)如果从中任意摸出两个小球,用树形图法或列表法展现所有等可能的结果;(2)如果从中任意摸出两个小球,求摸到的两个小球上的数字之和是5的概率.22.已知:如图,在梯形ABCD中,DC∥AB,AD=BC=2,∠A=60°,对角线BD平分∠ABC.(1)求对角线BD的长;(2)求梯形ABCD的面积.23.某项研究表明:人的眼睛疲劳系数y与睡眠时间t之间成函数关系,它们之间的关系如图2所示.其中,当睡眠时间不超过4小时(0≤t≤4)时,眼睛疲劳系数y是睡眠时间t 的反比例函数;当睡眠时间不少于4小时(4≤t≤6)时,眼睛疲劳系数y是睡眠时间t的一次函数,且当睡眠时间达到6小时后,眼睛疲劳系数为0.根据图象,回答下列问题:(1)求当睡眠时间不少于4小时(4≤t≤6)时,眼睛疲劳系数y关于睡眠时间t之间的函数关系式;(2)如果某人睡眠了t(1<t<3)小时后,再连续睡眠了3小时,此时他的眼睛疲劳系数恰好减少了3,求t的值.24.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,过A点作AF∥BC,且交CE的延长线于点F,联结BF.(1)求证:四边形AFBD是平行四边形;(2)当AB=AC时,求证:四边形AFBD是矩形.25.如图,在平面直角坐标系xOy中,直线y=x﹣2与x轴、y轴分别相交于点A和点B,点C在y轴的正半轴上,且OC=2OB.(1)求线段BC的长度;(2)如果点D在直线AB上,且以B、C、D、E为顶点的四边形为菱形,请直接写出点E 的坐标.26.已知:在正方形ABCD中,AB=2,点P是射线AB上的一点,联结PC、PD,点E、F 分别是AB和PC的中点,联结EF交PD于点Q.(1)如图1,当点P与点B重合时,△QPE的形状是(2)如图2,当点P在AB的延长线上时,设BP=x,EF=y,求y关于x的函数关系式,并写出定义域;(3)当点Q在边BC上时,求BP的长.参考答案与试题解析一、选择题:(本大题共6题,每题3分,满分18分)[每小题只有一个正确选项,在答题纸相应题号的选项上用2B铅笔正确填涂]1.下列函数中,是一次函数的是()A.B.y=x+2 C.y=x2+2 D.y=kx+b【考点】一次函数的定义.【分析】直接利用一次函数的定义分析得出答案.【解答】解:A、y=+2,不符合一次函数的定义,故此选项错误;B、y=x+2,是一次函数,故此选项正确;C、y=x2+2,是二次函数,故此选项错误;D、y=kx+b(k≠0),故此选项错误;故选:B.2.用换元法解分式方程,如果设,那么原方程可以化为()A.y2+y﹣5=0 B.y2﹣5y+1=0 C.5y2+y+1=0 D.5y2+y﹣1=0【考点】换元法解分式方程.【分析】直接把化为y即可.【解答】解:设,则原方程化为5y﹣+1=0,去分母得,5y2+y﹣1=0.故选D.3.下列四个方程中,有一个根是x=2的方程是()A.B.C.D.【考点】无理方程;分式方程的解.【分析】可以先将各个选项的方程解出来,然后看看哪个方程的其中一个根是x=2,从而可以解答本题.【解答】解:当x=2时,方程中的分母x﹣2=0,故x=2不是方程的根,故选项A错误;,解得x=2,故的根是x=2,不符合题意,故选项B错误;=2,解得x=10,故选项C错误;,解得x=2或x=3,故方程,有一根是x=2,故选项D正确;故选D.4.下列说法错误的是()A.确定事件的概率是1B.不可能事件的概率是0C.必然事件的概率是1D.随机事件的概率是大于0且小于1的一个数【考点】概率的意义.【分析】确定事件包括必然事件和不可能事件,必然事件的概率为1,不可能事件的概率为0.不可能发生的事件就是一定不会发生的事件,因而概率为0.必然发生的事件就是一定发生的事件,因而概率是1.不确定事件就是随机事件,即可能发生也可能不发生的事件,发生的概率>0并且<1.【解答】解:A、确定事件包括必然事件和不可能事件,必然事件的概率为1,不可能事件的概率为0,选项正确;B、不可能发生的事件概率为0,选项错误;C、必然发生的事件发生的概率为1,选项错误;D、随机事件发生的概率介于0和1之间,选项正确.故选A.5.下列关于向量的等式中,正确的是()A.B.﹣=C.D.【考点】*平面向量.【分析】根据平面向量的平行四边形法则和三角形法则对各选项分析判断即可得解.【解答】解:A、+=,而不是等于0,故本选项错误;B、﹣=,故本选项错误;C、+=,故本选项错误;D、∵+=,∴++=,故本选正确.故选D.6.如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是()A.BA=BC B.AC、BD互相平分C.AC=BD D.AB∥CD【考点】菱形的判定.【分析】已知四边形的对角线互相垂直,可依据“对角线互相垂直且平分的四边形是菱形”的判定方法,来选择条件.【解答】解:四边形ABCD中,AC、BD互相垂直,若四边形ABCD是菱形,需添加的条件是:AC、BD互相平分;(对角线互相垂直且平分的四边形是菱形)故选B.二、填空题(本大题共12题,每小题2分,满分24分)[在答题纸相应题号后的空格内直接填写答案]7.直线y=x﹣2的截距是﹣2.【考点】一次函数的性质.【分析】把x=0代入一次函数的解析式求出y即可.【解答】解:把x=0代入y=x﹣2得:y=﹣2,故答案为:﹣2.8.已知一次函数y=(m﹣1)x﹣2的函数值y随着自变量x的值的增大而增大,那么m的取值范围是m>1.【考点】一次函数图象与系数的关系.【分析】由题意y=(m﹣1)x﹣2,y随x的增大而增大,可得自变量系数大于0,进而可得出m的范围.【解答】解:∵y=(m﹣1)x﹣2中,y随x的增大而增大,∴m﹣1>0,∴m>1.故答案为:m>1;9.关于x的方程ax﹣4x﹣2=0(a≠4)的解是.【考点】一元一次方程的解.【分析】根据解一元一次方程的方法可以求得方程ax﹣4x﹣2=0(a≠4)的解,本题得以解决.【解答】解:ax﹣4x﹣2=0(a≠4)移项及合并同类项,得(a﹣4)x=2,系数化为1,得x=,故答案为:.10.方程2x3﹣16=0的根是x=2.【考点】高次方程.【分析】求出x3=8,两边开立方根,即可求出x.【解答】解:2x3﹣16=0,2x3=16,x3=8,x=2,故答案为:2.11.方程的根是x=3.【考点】无理方程.【分析】方程两边平方,转化为一元二次方程,解一元二次方程并检验.【解答】解:方程两边平方,得x2=2x+3,即x2﹣2x﹣3=0,解得x1=3,x2=﹣1,代入原方程检验可知x=3符合题意,x=﹣1舍去.故答案为:x=3.12.一个二元二次方程的一个解是,写出符合要求的方程xy=2(只需写一个即可).【考点】高次方程.【分析】分析:方程的解是二元二次方程有很多,如:xy=2;x2+y=5等等.【解答】解:xy=2等13.已知▱ABCD,设,,那么用向量、表示向量=﹣.【考点】*平面向量;平行四边形的性质.【分析】根据=+即可解决问题【解答】解:如图,∵四边形ABCD是平行四边形,∴==,∵=+=﹣+=﹣,故答案为﹣14.一个正多边形的每一个外角都是72°,那么这个多边形是5边形.【考点】多边形内角与外角.【分析】由一个多边形的外角为360°和每一个外角都是72°,可求得其边数.【解答】解:∵一个多边形的每一个外角都是72°,多边形的外角和等于360°,∴这个多边形的边数为:360÷72=5,故答案为:5.15.在▱ABCD中,如果∠A+∠C=200°,那么∠B的度数是80度.【考点】平行四边形的性质.【分析】由在▱ABCD中,如果∠A+∠C=200°,即可求得∠A的度数,又由平行四边形的邻角互补,求得答案.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A+∠C=200°,∴∠A=100°,∵AD∥BC,∴∠B=180°﹣∠A=80°.故答案为:80.16.矩形ABCD的两条对角线AC、BD相交于点O,已知AC=12,∠ACB=30°,那么△DOC 的周长是18.【考点】矩形的性质.【分析】直接利用矩形的性质得出∠OCD=60°,DO=CO=6,进而得出△OCD是等边三角形,即可得出答案.【解答】解:如图所示:∵矩形ABCD的两条对角线AC、BD相交于点O,AC=12,∠ACB=30°,∴∠OCD=60°,DO=CO=6,∴△OCD是等边三角形,∴△DOC的周长是:18.故答案为:18.17.如果菱形的两条对角线长分别为6和8,那么这个菱形一边上的高是.【考点】菱形的性质.【分析】根据对角线的长度即可计算菱形的面积,根据菱形对角线互相垂直平分的性质,可以求得△AOB为直角三角形,根据AO,BO可以求得AB的值,根据菱形的面积和边长即可解题.【解答】解:由题意知AC=6,BD=8,则菱形的面积S=×6×8=24,∵菱形对角线互相垂直平分,∴△AOB为直角三角形,AO=3,BO=4,∴AB==5,∴菱形的高h==.故答案为:.18.在▱ABCD中,AB=5,BC=7,对角线AC和BD相交于点O,如果将点A绕着点O顺时针旋转90°后,点A恰好落在平行四边形ABCD的边AD上,那么AC的长是或.【考点】旋转的性质;平行四边形的性质.【分析】如图,过O点作OE⊥AD于E,过C点作CF⊥AD于F,根据旋转的性质可得△AOA′是等腰直角三角形,△AA′C是等腰直角三角形,再根据勾股定理可求AA′,再根据等腰直角三角形的性质即可求解.【解答】解:如图,过O点作OE⊥AD于E,过C点作CF⊥AD于F,∵将点A绕着点O顺时针旋转90°后,点A恰好落在平行四边形ABCD的边AD上,∴△AOA′是等腰直角三角形,∴△AA′C是等腰直角三角形,设AA′=x,则CF=x,DF=7﹣x,在Rt△CDF中,x2+(7﹣x)2=52,解得x1=4,x2=3,在Rt△CFA中,AC=或.故答案为:或.三、解答题(共8题,满分58分)[将下列各题的解答过程做在答题纸的相应位置上19.解方程:=﹣1.【考点】解分式方程.【分析】观察可得最简公分母是(x+2)(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:去分母,得4=(x+2)﹣(x+2)(x﹣2),整理,得x2﹣x﹣2=0,解得x1=﹣1,x2=2.经检验:x1=﹣1是原方程的根,x2=2是增根.故原方程的根为x=﹣1.20.解方程组:.【考点】高次方程.【分析】先由①得:(x﹣2y)(x﹣3y)=0,求出x=2y或x=3y,再分别代入②,求出x,y的值即可.【解答】解:,由①得:(x﹣2y)(x﹣3y)=0,则x=2y或x=3y,将x=2y代入②得y=,x=,将x=3y代入②得y=,x=,则方程组的解是:,.21.一个不透明的布袋中装了分别标有数字1、2、3、4的四个小球,这些小球除标记数字不同外其余均相同.(1)如果从中任意摸出两个小球,用树形图法或列表法展现所有等可能的结果;(2)如果从中任意摸出两个小球,求摸到的两个小球上的数字之和是5的概率.【考点】列表法与树状图法.【分析】(1)画树状图展示所有12种等可能的情况;(2)找出摸到的两个小球上的数字之和为5的结果数,然后根据概率公式求解.【解答】解:(1)画树状图:共有12种等可能的情况;(2)摸到的两个小球上的数字之和为5的结果数为4,所以摸到摸到的两个小球上的数字之和为5的概率==.22.已知:如图,在梯形ABCD中,DC∥AB,AD=BC=2,∠A=60°,对角线BD平分∠ABC.(1)求对角线BD的长;(2)求梯形ABCD的面积.【考点】梯形.【分析】(1)根据等腰梯形的同一底上的两个底角相等,即可求得∠B的度数,根据三角形的内角和定理证明△ABD是直角三角形,利用直角三角形的性质以及勾股定理即可求解;(2)过点D、C分别作DH⊥AB,CG⊥AB,垂足为点H、G,在直角△ADB中求得DH 和AH的长,则AB即可求得,然后利用梯形的面积公式求解.【解答】解:(1)∵DC∥AB,AD=BC,∴∠A=∠ABC.∵BD平分∠ABC,∠A=60°,∴∠ABD=∠ABC=30°.∴∠ADB=90°.∵AD=2,∴AB=2AD=4.∴BD=.(2)过点D、C分别作DH⊥AB,CG⊥AB,垂足为点H、G.∵DC∥AB,BD平分∠ABC,∴∠CDB=∠ABD=∠CBD.∵BC=2,∴DC=BC=2.在RT△ADH和RT△BCG中,,∴RT△ADH≌RT△BCG.∴AH=BG.∵∠A=60°,∴∠ADH=30°.∴AH=AD=1,DH=.∵DC=HG=2,∴AB=4.∴.23.某项研究表明:人的眼睛疲劳系数y与睡眠时间t之间成函数关系,它们之间的关系如图2所示.其中,当睡眠时间不超过4小时(0≤t≤4)时,眼睛疲劳系数y是睡眠时间t 的反比例函数;当睡眠时间不少于4小时(4≤t≤6)时,眼睛疲劳系数y是睡眠时间t的一次函数,且当睡眠时间达到6小时后,眼睛疲劳系数为0.根据图象,回答下列问题:(1)求当睡眠时间不少于4小时(4≤t≤6)时,眼睛疲劳系数y关于睡眠时间t之间的函数关系式;(2)如果某人睡眠了t(1<t<3)小时后,再连续睡眠了3小时,此时他的眼睛疲劳系数恰好减少了3,求t的值.【考点】反比例函数的应用.【分析】(1)根据图象经过的两点利用待定系数法确定函数的解析式即可;(2)首先利用待定系数法确定反比例函数的解析式,根据“某人睡眠了t(1<t<3)小时后,再连续睡眠了3小时,此时眼睛疲劳系数恰好减少了3”列方程求解.【解答】解:(1)根据题意,设当4≤t≤6时,眼睛疲劳系数y关于睡眠时间t的函数关系式为:y=kt+b(k≠0).∵它经过点(4,2)和(6,0),∴,解得:.…(2分)∴当睡眠时间不少于4小时,眼疲劳系数y关于睡眠时间t的函数关系式是y=﹣t+6.当睡眠时间不超过4小时(0≤t≤4)时,眼睛疲劳系数y是睡眠时间t的反比例函数,设这个反比例函数为:,∵它经过点(4,2),∴,∵某人睡眠了t(1<t<3)小时后,再连续睡眠了3小时,此时眼睛疲劳系数恰好减少了3,∴,整理得:t2﹣6t+8=0.解得:t1=2,t2=4,经检验:t1=2,t2=4是原方程的解,t2=4不符合题意舍去,∴t的值是2.24.如图,在△ABC中,点D是BC边的中点,点E是AD的中点,过A点作AF∥BC,且交CE的延长线于点F,联结BF.(1)求证:四边形AFBD是平行四边形;(2)当AB=AC时,求证:四边形AFBD是矩形.【考点】矩形的判定;平行四边形的判定与性质.【分析】(1)首先证明△AEF≌△DEC(AAS),得出AF=DC,进而利用AF BD得出答案;(2)利用等腰三角形的性质,结合矩形的判定方法得出答案.【解答】证明:(1)∵AF∥BC,∴∠AFC=∠FCD.在△AFE和△DCE中,∴△AEF≌△DEC(AAS).∴AF=DC,∵BD=DC,∴AF=BD,∴四边形AFBD是平行四边形;(2)∵AB=AC,BD=DC,∴AD⊥BC.∴∠ADB=90°.∵四边形AFBD是平行四边形,∴四边形AFBD是矩形.25.如图,在平面直角坐标系xOy中,直线y=x﹣2与x轴、y轴分别相交于点A和点B,点C在y轴的正半轴上,且OC=2OB.(1)求线段BC的长度;(2)如果点D在直线AB上,且以B、C、D、E为顶点的四边形为菱形,请直接写出点E 的坐标.【考点】一次函数图象上点的坐标特征;菱形的性质.【分析】(1)可先求得B点坐标,再结合OC=2OB,可求得BC的长度;(2)分BC为边和对角线,①当BC为边时有两种情况,BD为边或BD为对角线,当BD 为边时,则BD=BC,可先求得D点坐标,再根据DE∥BC且DE=BC可求得E点坐标;当BD为对称线时,则四边形为正方形,可求得E点坐标;②当BC为对角线时,则DE为BC的垂直平分线,可先求得D点坐标,利用对称性可求得E点坐标【解答】解:(1)∵直线y=x﹣2与x轴、y轴分别相交于点A和点B,∴点A(2,0),点B(0,﹣2),∴OB=2,∵OC=2OB,∴OC=4,点C(0,4),∴BC的长度是6;(2)①当BC为边时,有两种情况,BD为边或BD为对称线,当BD为边时,则有BD=BC=6,设D点坐标为(x,x﹣2),则=6,解得x=3或x=﹣3,∴D点坐标为(3,3﹣2)或(﹣3,﹣3﹣2),∵DE=BC=6,且DE∥BC,∴E点坐标为(,3+4)或(,﹣3+4);当BD为对角线时,则∠CBD=∠EBD=45°,如图1,则∠EBC=90°,∴四边形BCDE为正方形,∴BE=BC=6,且BE∥x轴,∴E点坐标为(6,﹣2);②当BC为对角线时,则有DE⊥BC,如图2,设BC与DE交于点F,则F为BC的中点,∴F(0,1),∴D点纵坐标为1,代入直线AB解析式可得1=x﹣2,解得x=3,∴D点坐标为(3,1),又D、E关于BC对称,∴E点坐标为(﹣3,1);综上可知点E的坐标可以为(,3+4)或(,﹣3+4)或(6,﹣2)或(﹣3,1).26.已知:在正方形ABCD中,AB=2,点P是射线AB上的一点,联结PC、PD,点E、F 分别是AB和PC的中点,联结EF交PD于点Q.(1)如图1,当点P与点B重合时,△QPE的形状是等腰直角三角形(2)如图2,当点P在AB的延长线上时,设BP=x,EF=y,求y关于x的函数关系式,并写出定义域;(3)当点Q在边BC上时,求BP的长.【考点】相似形综合题.【分析】(1)根据正方形的性质得到AB=BC,∠ABC=90°,根据等式的性质得到PE=PF,即可得到结论;(2)延长BA到点M,使得AM=BP,连接CM,根据已知条件得到EM=EP,根据三角形的中位线的性质得到EF=MC,根据正方形的性质得到∠MBC=90°,AB=BC,由已知条件得到BM=2+x.根据勾股定理得到MC==,于是得到结论;(3)当点Q在边BC上时,根据平行线的性质得到∠M=∠QEB,根据全等三角形的性质得到∠M=∠APD,推出QE=QP,根据等腰三角形的性质即可得到结论.【解答】解:(1)△QPE的形状是等腰直角三角形,理由:在正方形ABCD中,∵AB=BC,∠ABC=90°,∵点P与点B重合,∴AP=PC,∠APC=90°,∵点E、F分别是AB和PC的中点,∴PE=AP,PF=PC,∴PE=PF,∴△QPE是等腰直角三角形;故答案为:等腰直角三角形;(2)延长BA到点M,使得AM=BP,连接CM,∵AE=BE,∴AE+AM=BE+BP,即EM=EP,∵PF=CF,∴EF=MC,∵四边形ABCD是正方形,∴∠MBC=90°,AB=BC,∵AB=2,BP=AM=x,∴BM=2+x.∴MC==,∴EF=,∴y=(x>0);(3)当点Q在边BC上时,由(2)可知EF∥MC,∴∠M=∠QEB,∵在△ADP和△BCM中,,∴△ADP≌△BCM,∴∠M=∠APD,∴∠QEB=∠APD,∴QE=QP,∵QB⊥PE,∴BP=BE=AB=1.。


2018-2019学年八年级下学期期末数学试卷一、选择题1.下列函数中,是一次函数的是( ) A .11y x=- B .2y x =C .2y x =D .(y kx b k =+、b 是常数) 2.下列方程2240x x --=,10x x ++=,1111x x x -=-+,2240x x --=中无理方程的个数是( ) A .1B .2C .3D .43.把直线2y x =-进行上下平移,使得平移后直线的截距是3,那么平移的过程是( ) A .向上平移5个单位 B .向下平移5个单位C .向上平移1个单位D .向下平移1个单位4.下列事件中,属于随机事件的是( ) A .方程101x =-在实数范围内有解 B .在平面上画一个矩形,这个矩形一定是轴对称图形 C .在一副扑克牌中抽取一张牌,抽出的牌是黑桃A D .十边形有15条对角线5.已知矩形ABCD ,下列条件中不能判定这个矩形是正方形的是( ) A .AC BD ⊥B .AC BD =C .AC 平分BAD ∠ D .ADB ABD ∠=∠6.如图,已知在ABCD Y 中,对角线AC 、BD 相交于点O ,下列向量计算结果等于AD u u u r的是( )A .AB AC +u u u r u u u rB .AB AC -u u u r u u u rC .AO DO +u u u r u u u rD .BO CO -u u u r u u u r二、填空题(本题共12小题)7.一次函数23y x =-的图象不经过第 象限.8.直线112y x =-+在x 轴下方的点的横坐标的取值范围是x .9.方程310x +=的根是 . 10.方程110x x -+=g 的解是 .11.关于x 、y 的二元二次方程组x y axy b +=⎧⎨=⎩的一个解是1112x y =⎧⎨=-⎩;那么这个方程组的其余的解是 .12.一个多边形的每个内角都是160︒,这个多边形是 边形.13.菱形ABCD 的边长为5,一条对角线长为6,则该菱形的面积为 .14.如图,四边形ABCD 是平行四边形,适当选取它的边或对角线作向量,记AB m =u u u r r ;BC n =u u u r r,那么图中等于m n -r r的向量是 .15.掷一枚质地均匀的骰子,掷得的点数是合数的概率为 .16.ABCD Y 的对角线AC 、BD 相交于点O ,如果ABCD Y 的周长为20,ABO ∆的周长比BCO ∆的周长大2,那么AB = .17.梯形ABCD 中,//AD BC ,6AB AD DC ===,BD DC ⊥,那么BD = . 18.如图,正方形ABCD 的边长为1,把这个正方形绕点A 旋转,得到正方形AB C D ''';且点C '在直线AD 上,那么△C D D ''的面积是 .三、简答题19.解方程:2239x x +-=. 20.解方程:2412x x x x--=-. 21.解方程组:224525x y x y ⎧-=⎨-=⎩22.已知一次函数的图象经过(2,2)M ,且平行于直线21y x =--,求这个函数图象与坐标轴围成的三角形面积.23.已知:如图,ABCD Y 中,AE 、CF 分别是BAD ∠和BCD ∠的角平分线,分别交边DC 、AB 于点E 、F ,求证:AE CF =.四、解答题(本大题共3题)24.梯形ABCD 中,//AD BC ,AB CD =,E 、F 分别是腰AB 、CD 的中点,过点F 作//FG AB ,交BC 于点G .(1)求证:四边形AEGF 为平行四边形;(2)联结DG ,如果DGE B ∠=∠,求证:四边形AEGF 是矩形.25.某校八(1)班的学生开展“行走在春天”郊野徒步活动,学生步行出发一段时间后,小明骑自行车按相同的路线,以每小时比学生步行快9千米的速度追赶,如果学生步行的时间为t 小时,离开出发点的路程为1S 千米,小明离开出发点的路程为2S 千米,1S 和2S 关于t 的函数图象如图所示.(1)从图中可以得到,学生出发 小时后小明出发; (2)求学生步行的速度.26.如图,矩形ABCD 中,6AB =,8BC =,P 是射线BC 上一个动点(点P 和点B 不重合),E 、F 分别是线段BP 、DP 的中点,联结CF 、EF .(1)在点P运动的过程中,CEF∆中有没有长度保持不变的边,如果有,指出是哪一条边并求出其长度;如果没有,请说明理由.(2)当点P在线段BC上时,设BP x∆的面积为y,求y关于x的函数关系式,=,CEF并写出定义域.(3)在点P运动的过程中,如果CEF∆是等腰三角形,求线段BP的长.参考答案一、选择题:(本大题共6题)1.下列函数中,是一次函数的是( ) A .11y x=- B .2y x =C .2y x =D .(y kx b k =+、b 是常数)解:A 、1y +与x 成反比例关系,不是一次函数,故本选项错误; B 、是正比例函数,属于一次函数,故本选项正确; C 、自变量次数为2,故不是一次函数,故本选项错误;D 、当0k =时不是一次函数,故本选项错误.故选:B .2.下列方程240x -=0x =111x -=-,240x -=中无理方程的个数是( ) A .1B .2C .3D .4解:方程240x -=0x +=111x -=-,240x --=中无理方程是0x +=,111x =-,240x --=, 故选:C .3.把直线2y x =-进行上下平移,使得平移后直线的截距是3,那么平移的过程是( ) A .向上平移5个单位 B .向下平移5个单位C .向上平移1个单位D .向下平移1个单位解:Q 把直线2y x =-进行上下平移,使得平移后直线的截距是3, ∴平移后直线的解析式为3y x =+,3(2)5--=Q ,∴平移的过程是把直线2y x =-向上平移5个单位.故选:A .4.下列事件中,属于随机事件的是( ) A .方程101x =-在实数范围内有解 B .在平面上画一个矩形,这个矩形一定是轴对称图形C .在一副扑克牌中抽取一张牌,抽出的牌是黑桃AD .十边形有15条对角线 解:A .方程101x =-在实数范围内有解,是确定事件; B .在平面上画一个矩形,这个矩形一定是轴对称图形,是确定事件; C .在一副扑克牌中抽取一张牌,抽出的牌是黑桃A ,是随机事件;D .十边形有15条对角线,是确定事件.故选:C .5.已知矩形ABCD ,下列条件中不能判定这个矩形是正方形的是( ) A .AC BD ⊥B .AC BD =C .AC 平分BAD ∠ D .ADB ABD ∠=∠解:Q 四边形ABCD 是矩形,AC BD ⊥, ∴矩形ABCD 是正方形;Q 四边形ABCD 是矩形, //AD BC ∴, DAC BCA ∴∠=∠, AC Q 平分BAD ∠, BAC DAC ∴∠=∠, BAC ACB ∴∠=∠, AB BC ∴=,∴矩形ABCD 是正方形;ADB ABD ∠=∠Q , AB AD ∴=,Q 四边形ABCD 是矩形 ∴矩形ABCD 是正方形;故选:B .6.如图,已知在ABCD Y 中,对角线AC 、BD 相交于点O ,下列向量计算结果等于AD u u u r的是( )A .AB AC +u u u r u u u rB .AB AC -u u u r u u u rC .AO DO +u u u r u u u rD .BO CO -u u u r u u u r解:在平行四边形ABCD 中,//AB CD =,//AD BC =,AO OC =,BO OD =. A 、AB AC AD +≠u u u r u u u r u u u r,故本选项错误. B 、AB AC CB DA -==u u u r u u u r u u u r u u u r ,故本选项错误.C 、AO DO OC DO DC AD +=+=≠u u u r u u u r u u u r u u u r u u u r u u u r,故本选项错误. D 、BO CO OD OA AD -=-=u u u r u u u r u u u r u u u r u u u r,故本选项正确.故选:D .二、填空题(本题共12小题,每小题2分,满分24分)(第6题图)【请将结果直接填入答题纸的相应位置上】7.一次函数23y x =-的图象不经过第 二 象限. 解:Q 一次函数23y x =-中,20k =>, ∴此函数图象经过一、三象限,30b =-<Q ,∴此函数图象与y 轴负半轴相交,∴此一次函数的图象经过一、三、四象限,不经过第二象限.故答案为:二.8.直线112y x =-+在x 轴下方的点的横坐标的取值范围是x 2> .解:112y x =-+Q ,∴当0y =时,2x =,该函数y 随x 的增大而减小,∴直线112y x =-+在x 轴下方的点的横坐标的取值范围是2x >,故答案为:2>.9.方程310x +=的根是 1- . 解:由310x +=得,31x =-,3(1)1-=-Q ,1x ∴=-.故答案为:1-.100=的解是 1x = . 解:Q0=,∴0=且10x -…,10x +…, 210x ∴-=且1x …, 解得,1x =,经检验,x ,1=是原方程的根, 故答案为:1x =.11.关于x 、y 的二元二次方程组x y axy b +=⎧⎨=⎩的一个解是1112x y =⎧⎨=-⎩;那么这个方程组的其余的解是 2221x y =-⎧⎨=⎩ .解:把1112x y =⎧⎨=-⎩代入方程组得:12a b =-⎧⎨=-⎩,方程组为12x y xy +=-⎧⎨=-⎩,则这个方程组的其余解是2221x y =-⎧⎨=⎩,故答案为:2221x y =-⎧⎨=⎩12.一个多边形的每个内角都是160︒,这个多边形是 18 边形. 解:180(2)160n n -= 解得:18n =. 故答案为:1813.菱形ABCD 的边长为5,一条对角线长为6,则该菱形的面积为 24 . 解:如图,当6BD =时,Q 四边形ABCD 是菱形,AC BD ∴⊥,AO CO =,3BO DO ==, 5AB =Q ,224AO AB BO ∴=-=,8AC ∴=,∴菱形的面积是:68224⨯÷=,故答案为:2414.如图,四边形ABCD 是平行四边形,适当选取它的边或对角线作向量,记AB m =u u u r r ;BC n =u u u r r,那么图中等于m n -r r的向量是 DB u u u r .解:Q 四边形ABCD 是平行四边形, //AD BC ∴,AD BC =,∴BC AD =u u u r u u u r , Q AB m =u u u r r ;BC n =u u u r r , ∴m n BC AD DB -===u u ur u u u r u u u r r r .故答案是:DB u u u r.15.掷一枚质地均匀的骰子,掷得的点数是合数的概率为3. 解:掷一枚质地均匀的骰子,掷得的点数可能是1、2、3、4、5、6中的任意一个数, 共有六种可能,其中4、6是合数,所以概率为21 63 =.故答案为:13.16.ABCDY的对角线AC、BD相交于点O,如果ABCDY的周长为20,ABO∆的周长比BCO∆的周长大2,那么AB= 6 .解:如图所示:Q四边形ABCD是平行四边形,OA OC∴=,OB OD=,AB CD=,AD BC=,ABCDQ Y的周长为20cm,10BC AB cm∴+=①,AOB∆Q的周长比COB∆的周长大2c,()()2OB OA AB OB OC BC cm∴++-++=,2AB BC cm∴-=②,①+②得:212AB cm=,6AB cm∴=;故答案为:6.17.梯形ABCD中,//AD BC,6AB AD DC===,BD DC⊥,那么BD=63.解:如图,取BC的中点E,连接DE,BD DC⊥Q,BE ED EC∴==,DBE BDE∴∠=∠,又//AD BC,ADB DBE ∴∠=∠,ADB BDE ∴∠=∠,AB AD =Q ,ABD ADB ∴∠=∠,BDE ABD ∴∠=∠,//DE AB ∴,又//AD BC Q ,即//AD BE ,∴四边形ABED 为平行四边形,6BE AD ∴==,12BC ∴=, 由勾股定理得:222212663BD BC CD =-=-=. 故答案为:63.18.如图,正方形ABCD 的边长为1,把这个正方形绕点A 旋转,得到正方形AB C D ''';且点C '在直线AD 上,那么△C D D ''的面积是 224+或224- .解:如图,过点D '作D E AD '⊥,Q 把这个正方形绕点A 旋转,得到正方形AB C D ''';1AD AD CD C D '''∴====222AC D A C D ''''∴=+=D E '∴=当点C '在AD 延长线上时,11)2C D D S ''=⨯-=V当点C '在DA 延长线上时,11)2C D D S ''=⨯+=V三、简答题(本大题共5题,每题6分,满分30分19.解方程:29x +=.解:29x +=Q∴92x =-,22381364x x x ∴-=-+,2438840x x ∴-+=,2219420x x ∴-+=,(27)(6)0x x ∴--=,解得,1 3.5x =,26x =,经检验,6x =时,原分式无意义, 3.5x =是方程的根,故原方程的根时 3.5x =.20.解方程:2412x x x x --=-. 解:设2x y x =-, 方程变形为:21y y-=, 去分母得:220y y --=,即(2)(1)0y y -+=,解得:2y =或1y =-, ∴22x x =-或12x x =--, 解得:4x =或1x =,经检验1x =与4x =都为分式方程的解.21.解方程组:224525x y x y ⎧-=⎨-=⎩解:原方程组化为()()22525x y x y x y ⎧+-=⎨-=⎩①②, 将②代入①,得25x y +=③联立②③,2125x y x y +=⎧⎨-=⎩, 解得3x =,1y =-,所以原方程组的解为31x y =⎧⎨=-⎩22.已知一次函数的图象经过(2,2)M ,且平行于直线21y x =--,求这个函数图象与坐标轴围成的三角形面积.解:Q 一次函数的图象平行于直线21y x =--∴可设该一次函数解析式为:2y x b =-+又Q 点(2,2)M 在此函数图象上222b ∴=-⨯+6b ∴=∴该一次函数解析式为:26y x =-+;当0x =时,6y =;当0y =时,3x =∴该一次函数图象与两坐标轴交点为(3,0),(0,6)∴这个函数的图象与两坐标轴围成的三角形的面积为:13692⨯⨯=. 23.已知:如图,ABCD Y 中,AE 、CF 分别是BAD ∠和BCD ∠的角平分线,分别交边DC 、AB 于点E 、F ,求证:AE CF =.解:Q 四边形ABCD 是平行四边形,DAB DCB ∴∠=∠,D B ∠=∠,AD BC =.AE Q 、CF 分别是BAD ∠和BCD ∠的角平分线,DAE BCF ∴∠=∠.()ADE CBF ASA ∴∆≅∆.AE CF ∴=.四、解答题(本大题共3题,满分28分)24.梯形ABCD 中,//AD BC ,AB CD =,E 、F 分别是腰AB 、CD 的中点,过点F 作//FG AB ,交BC 于点G .(1)求证:四边形AEGF 为平行四边形;(2)联结DG ,如果DGE B ∠=∠,求证:四边形AEGF 是矩形.【解答】(1)证明:Q 梯形ABCD 中,//AD BC ,AB CD =,B C ∴∠=∠,//AB FG Q ,FGC B ∴∠=∠,FGC C ∴∠=∠,FG FC ∴=,AB CD =Q ,E 、F 分别是腰AB 、CD 的中点,AE CF ∴=,AE FG ∴=,∴四边形AEGF 是平行四边形;(2)解:FG DF CF ==Q ,90DGC ∴∠=︒,90DGE BGE ∴∠+∠=︒,DGE B ∠=∠Q ,90B BGE ∴∠+∠=︒,90AEG BEG ∴∠=∠=︒,∴四边形AEGF 是矩形.25.某校八(1)班的学生开展“行走在春天”郊野徒步活动,学生步行出发一段时间后,小明骑自行车按相同的路线,以每小时比学生步行快9千米的速度追赶,如果学生步行的时间为t 小时,离开出发点的路程为1S 千米,小明离开出发点的路程为2S 千米,1S 和2S 关于t 的函数图象如图所示.(1)从图中可以得到,学生出发 0.5 小时后小明出发;(2)求学生步行的速度.解:(1)由图象知当20S =时,0.5t =∴学生出发0.5小时后小明出发故答案为:0.5(2)设当t x =时,125S S ==千米则有:5590.5x x +=- 解得:13x =-(不符合题意,舍去)或56x = 经检验:56x =是原方程的解 ∴学生步行的速度为:5566÷=千米/小时 答:学生步行的速度为6千米/小时.26.如图,矩形ABCD 中,6AB =,8BC =,P 是射线BC 上一个动点(点P 和点B 不重合),E 、F 分别是线段BP 、DP 的中点,联结CF 、EF .(1)在点P 运动的过程中,CEF ∆中有没有长度保持不变的边,如果有,指出是哪一条边并求出其长度;如果没有,请说明理由.(2)当点P 在线段BC 上时,设BP x =,CEF ∆的面积为y ,求y 关于x 的函数关系式,并写出定义域.(3)在点P 运动的过程中,如果CEF ∆是等腰三角形,求线段BP 的长. 解:(1)有,线段EF 的长度不变. 理由:如图,连接BD .PE EB =Q ,PF FD =,12EF BD ∴=, Q 四边形ABC 都是矩形,90A ∴∠=︒,8AD BC ==,22226810BD AB AD ∴=+=+=, 152EF BD ∴==.(2)PE EB =Q ,PF FD =, 12EF BD ∴=,//EF BD , PEF PBD ∴∆∆∽, ∴21()2PEF PBD S S ∆∆=, 14PEF PBD S S ∆∆∴=, DF PF =Q ,12PFC DFC S S ∆∆∴=, 111136(8)612(0)42224PEF PDC y S S x x x x ∆∆∴=+=+-=-+>g g g g g g .(3)由题意:当点E 在线段BC 上时,5EF =,11(8)822EC PC PE x x x =+=-+=-,22116(8)22CF PD x ==+-g ,当EF EC =时,1582x =-,解得6x =.当EF CF =时,22156(8)2x =+-g ,解得0x =(舍弃)或16(舍弃).当CF EC =时,221186(8)22x x -=+-g ,解得394x =(舍弃),当点E 在BC 阿德延长线上时,5EF =,182EC BE BC x =-=-,22116(8)22CF PD x ==+-g ,当EF EC =时,1582x =-,解得26x =.当EF CF =时,22156(8)2x =+-g ,解得0x =(舍弃)或16.当CF EC =时,221186(8)22x x -=+-g ,解得394x =,综上所述,满足条件的x 的值为6或26或16或394.。

解析版】2018-2019学年上海市黄浦区八年级上期末数学试卷2019-2020学年上海市黄浦区八年级(上)期末数学试卷一、选择题:(每题2分,共12分)1.在二次根式$\sqrt{a}+\sqrt{b}+\sqrt{c}$中,最简二次根式的个数是()。
A。
1个 B。
2个 C。
3个 D。
4个2.关于x的一元二次方程$(m-2)x^2+3x+m^2-4=0$有一个根是$ x=1$,则$m$的值为()。
A。
$m=2$ B。
$m=-2$ C。
$m=-2$或$2$ D。
$m\neq 2,-2$3.在同一坐标系中,正比例函数$y=x$与反比例函数$y=\frac{k}{x}$的图象大致是()。
A。
B。
C。
D。
4.已知反比例函数$y=\frac{k}{x}$的图象上有两点$A(x_1,y_1)$、$B(x_2,y_2)$,且$x_1<x_2$,则$y_1$与$y_2$的大小关系是()。
A。
$y_1y_2$ C。
$y_1=y_2$ D。
不能确定5.下列定理中,有逆定理存在的是()。
A。
对顶角相等B。
垂直平分线上的点到线段两端点的距离相等C。
全等三角形的面积相等D。
凡直角都相等6.如图,在等腰直角三角形$ABC$中,$\angleA=90^\circ$,$AB=AC$,$BD$平分$\angle ABC$,交$AC$于点$D$,$DE\perp BC$,若$BC=10$cm,则$\triangle DEC$的周长为()。
A。
$8$cm B。
$10$cm C。
$12$cm D。
$14$cm二、填空题:(每题3分,共36分)7.化简:$\frac{\sqrt{6}+\sqrt{2}}{\sqrt{6}-\sqrt{2}}=$。
8.分母有理化:$\frac{1}{\sqrt{3}+\sqrt{2}}=$。
9.方程$x(x-5)=6$的根是$\underline{\qquad\qquad}$。
10.某种品牌的笔记本电脑原价为5000元,如果连续两次降价的百分率都为10%,那么两次降价后的价格为$\underline{\qquad\qquad}$元。
2018-2019学年八年级下学期期末数学试卷一、选择题1.直线23y x =-的截距是( ) A .3-B .2-C .2D .32.如果关于x 的方程(3)2019a x -=有解那么实数a 的取值范围是( ) A .3a <B .3a =C .3a >D .3a ≠3.下列说法中正确的是( ) A .410x +=是二项方程 B .22x y y -=是二元二次方程C .132x x-=是分式方程 D 210-=是无理方程4.下列事件中,属于确定事件的是( )A .抛掷一枚质地均匀的骰子,正面向上的点数是6B .抛掷一枚质地均匀的骰子,正面向上的点数大于6C .抛一枚质地均匀的骰子,正面向上的点数小于6D .抛掷一枚质地均匀的骰子6次,“正面向上的点数是6”至少出现一次5.如果平行四边形ABCD 两条对角线的长度分别为8AC m =,12BD cm =,那么BC 边的长度可能是( ) A .2BC cm =B .6BC cm =C .10BC cm =D .20BC cm =6.已知四边形ABCD 中,90A B C ∠=∠=∠=︒,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( ) A .90D ∠=︒B .AB CD =C .AB BC =D .AC BD =二、填空题(本大题共12题)7.已知一次函数()32f x x =+,那么(2)f -= .8.已知函数37y x =-+,当2x >时,函数值y 的取值范围是 .9.如果将直线2y x =向上平移1个单位,那么平移后所得直线的表达式是 . 10.二项方程22540x +=在实数范围内的解是 .11.用换元法解方程22111x x x x --=-时,如果设21xy x =-,那么所得到的关于y 的整式方程为 .12.如果2x =是关于x 的方程21124kx x =+--的增根,那么实数k 的值为 .13.不透明的布袋里有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是 .14.如果一个多边形的每一个外角都等于30︒,那么这个多边形是 边形. 15.如果向量AD BC =u u u r u u u r,那么四边形ABCD 的形状可以是 (写出一种情况即可)16.写出一个是轴对称图形但不是中心对称图形的四边形: .17.已知正方形ABCD 的边长为1,如果将向量AD AC -u u u r u u u r 的运算结果记为向量m r,那么向量m r的长度为 .18.已知四边形ABCD 是矩形,点E 是边AD 的中点,以直线BE 为对称轴将ABE ∆翻折至FBE ∆,联结DF ,那么图中与AEB ∠相等的角的个数为 .三、解答题:(本大题共7题) 19.解方程:2x x += 20.解方程组22220x y x xy y -=⎧⎨--=⎩①②21.已知向量a r、b r (如图),请用向量加法的平行四边形法则作向量a b +r r (不写作法,画出图形)22.甲、乙两位同学同时从学校出发,骑自行车前往距离学校20千米的郊野公园.已知甲同学比乙同学平均每小时多骑行2千米,甲同学在路上因事耽搁了30分钟,结果两人同时到达公园.问:甲、乙两位同学平均每小时各骑行多少千米?23.已知ABC ∆,90A ∠<︒(如图),点D 、E 、F 分别在边AB 、BC 、AC 上,且四边形ADEF 是菱形.(1)请使用直尺与圆规,分别确定点D 、E 、F 的具体位置(不写画法,保留画图痕迹);(2)如果60A ∠=︒,4AD =,点M 在AB 边上,且满足EM ED =,求四边形AFEM 的面积;(3)当AB AC =时,求DEAC的值.24.为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图4表达的是小贾的爸爸行驶的路程y (米)与行驶时间x (分钟)的变化关系. (1)求线段BC 所表达的函数关系式;(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分行驶,当小贾与爸爸相距100米时,求小贾的行驶时间;(3)如果小贾的行驶速度是v 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出ν的取值范围.25.在梯形ABCD 中,//AD BC ,90A ∠=︒,45C ∠=︒.点E 在直线AD 上,联结BE ,过点E 作BE 的垂线,交直线CD 于点F . (1)如图,已知:BE EF =,求证:AB AD =; (2)已知:AB AD =①当点E 在线段AD 上,求证:BE EF =;②当点E 在射线DA 上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.参考答案一、选择题:(本大题共6题) 1.直线23y x =-的截距是( ) A .3-B .2-C .2D .3解:Q 在一次函数23y x =-中, 3b =-,∴一次函数23y x =-的截距3b =-.故选:A .2.如果关于x 的方程(3)2019a x -=有解那么实数a 的取值范围是( ) A .3a <B .3a =C .3a >D .3a ≠解:Q 关于x 的方程(3)2019a x -=有解, 30a ∴-≠,即3a ≠,故选:D .3.下列说法中正确的是( ) A .410x +=是二项方程 B .22x y y -=是二元二次方程C .132x x-=是分式方程 D 210-=是无理方程解:A .方程是一般式,且方程的左边只有2项,此方程是二项方程,此选项正确; B .22x y y -=是二元三次方程,此选项错误; C .132x x-=是一元一次方程,属于整式方程,此选项错误;D 210-=是一元二次方程,属于整式方程;故选:A .4.下列事件中,属于确定事件的是( )A .抛掷一枚质地均匀的骰子,正面向上的点数是6B .抛掷一枚质地均匀的骰子,正面向上的点数大于6C .抛一枚质地均匀的骰子,正面向上的点数小于6D .抛掷一枚质地均匀的骰子6次,“正面向上的点数是6”至少出现一次 解:A 、抛掷一枚质地均匀的骰子,正面向上的点数是6是随机事件;B 、抛掷一枚质地均匀的骰子,正面向上的点数大于6是不可能事件;C 、抛一枚质地均匀的骰子,正面向上的点数小于6是随机事件;D 、抛掷一枚质地均匀的骰子6次,“正面向上的点数是6”至少出现一次是随机事件; 故选:B .5.如果平行四边形ABCD 两条对角线的长度分别为8AC m =,12BD cm =,那么BC 边的长度可能是( ) A .2BC cm =B .6BC cm =C .10BC cm =D .20BC cm =解:设平行四边形ABCD 的对角线交于O 点, 4OA OC ∴==,6OB OD ==, 6464BC ∴-<<+210BC ∴<<, 6cm ∴符合,故选:B .6.已知四边形ABCD 中,90A B C ∠=∠=∠=︒,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( ) A .90D ∠=︒B .AB CD =C .AB BC =D .AC BD =解:由90A B C ∠=∠=∠=︒可判定四边形ABCD 为矩形,因此再添加条件:一组邻边相等,即可判定四边形ABCD 为正方形, 故选:C .二、填空题(本大题共12题,每题2分,港分24分) 7.已知一次函数()32f x x =+,那么(2)f -= 4- . 解:当2x =-时,(2)3(2)24f -=⨯-+=-. 故答案为:4-.8.已知函数37y x =-+,当2x >时,函数值y 的取值范围是 1y < . 解:Q 函数37y x =-+中,30k =-<, y ∴随着x 的增大而减小,当2x =时,3271y =-⨯+=, ∴当2x >时,1y <,故答案为:1y <.9.如果将直线2y x =向上平移1个单位,那么平移后所得直线的表达式是 21y x =+ . 解:原直线的2k =,0b =;向上平移2个单位长度,得到了新直线, 那么新直线的2k =,011b =+=. ∴新直线的解析式为21y x =+.故答案是:21y x =+.10.二项方程22540x +=在实数范围内的解是 无解 . 解:由22540x +=,得 227x =-, 20x >Q , ∴方程无解故答案为无解.11.用换元法解方程22111x x x x --=-时,如果设21xy x =-,那么所得到的关于y 的整式方程为 210y y +-= . 解:设21xy x =-,则原方程可化为:11y y -=,去分母,可得21y y -=, 即210y y +-=, 故答案为:210y y +-=. 12.如果2x =是关于x 的方程21124k x x =+--的增根,那么实数k 的值为 4或0 . 解:去分母得:224x k x +=+-, 把2x =代入得:4k =, 把2x =-代入得:0k =, 故答案为:4或0.13.不透明的布袋里有2个黄球、3个红球、5个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是10. 解:Q 在不透明的袋中装有2个黄球、3个红球、5个白球,它们除颜色外其它都相同, ∴从这不透明的袋里随机摸出一个球,所摸到的球恰好为红球的概率是:3323510=++.故答案为:310. 14.如果一个多边形的每一个外角都等于30︒,那么这个多边形是 十二 边形. 解:多边形的边数:3603012︒÷︒=, 则这个多边形的边数为12. 故答案为:十二.15.如果向量AD BC =u u u r u u u r,那么四边形ABCD 的形状可以是 平行四边形 (写出一种情况即可)解:Q 向量AD BC =u u u r u u u r, //AD BC ∴,且AD BC =,∴四边形ABCD 的形状可以是平行四边形.故答案是:平行四边形.16.写出一个是轴对称图形但不是中心对称图形的四边形: 等腰梯形(答案不唯一) . 解:是轴对称图形但不是中心对称图形的,例如:等腰梯形,等腰三角形,角,射线,正五边形等. 故答案为:等腰梯形(答案不唯一).17.已知正方形ABCD 的边长为1,如果将向量AD AC -u u u r u u u r 的运算结果记为向量m r,那么向量m r的长度为 1 .解:Q AD AC CD m -==u u u r u u u r u u u r r且||1CD =u u u r ,||1m ∴=r.故答案是:1.18.已知四边形ABCD 是矩形,点E 是边AD 的中点,以直线BE 为对称轴将ABE ∆翻折至FBE ∆,联结DF ,那么图中与AEB ∠相等的角的个数为 4 .解:由折叠知,BEF AEB ∠=∠,AE FE =, Q 点E 是AD 中点, AE DE ∴=, ED FE ∴=, FDE EFD ∴∠=∠,AEF EDF DFE AEB BEF ∠=∠+∠=∠=∠Q AEB EDF ∴∠=∠, //AD BC Q , AEB CBE ∴∠=∠,EDF EFD BEF AEB CBE ∴∠=∠=∠=∠=∠,故答案为:4三、解答题:(本大题共7题,满分58分) 192x x += 解:两边平方得,22x x +=, 移项得:220x x --=(2)(1)0x x -+=解得11x =-,22x =.检验,把1x =-代入原方程,左边≠右边,为增根舍去. 把2x =代入原方程,左边=右边,是原方程的解. 20.解方程组22220x y x xy y -=⎧⎨--=⎩①② 解:由②得()(2)0x y x y +-=,则0x y +=或20x y -=,所以方程组可变形为20x y x y -=⎧⎨+=⎩或220x y x y -=⎧⎨-=⎩,解得11x y =⎧⎨=-⎩或42x y =⎧⎨=⎩.21.已知向量a r、b r (如图),请用向量加法的平行四边形法则作向量a b +r r (不写作法,画出图形)解:如图AC u u u r即为所求.22.甲、乙两位同学同时从学校出发,骑自行车前往距离学校20千米的郊野公园.已知甲同学比乙同学平均每小时多骑行2千米,甲同学在路上因事耽搁了30分钟,结果两人同时到达公园.问:甲、乙两位同学平均每小时各骑行多少千米? 解:设乙平均每小时骑行x 千米,则甲平均每小时骑行(2)x +千米, 由题意得,2020122x x =++, 解得:110x =-,28x =,经检验:110x =-,28x =都是原方程的根,但110x =-,不符合题意,故舍去, 则甲平均每小时骑行8210+=千米.答:甲平均每小时骑行10千米,乙平均每小时骑行8千米.23.已知ABC ∆,90A ∠<︒(如图),点D 、E 、F 分别在边AB 、BC 、AC 上,且四边形ADEF 是菱形.(1)请使用直尺与圆规,分别确定点D 、E 、F 的具体位置(不写画法,保留画图痕迹);(2)如果60A ∠=︒,4AD =,点M 在AB 边上,且满足EM ED =,求四边形AFEM 的面积;(3)当AB AC =时,求DE AC的值.解:(1)D ,E ,F 的位置如图所示.(2)由题意,当60A ∠=︒,4AD =时,ADF ∆,EFD ∆,EMD ∆都是等边三角形,边长为4.2334123AFEM S ∴==四边形.(3)当AB AC =时,易知DE 是ABC ∆的中位线,12DE AC ∴=, ∴12DE AC =. 24.为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图4表达的是小贾的爸爸行驶的路程y (米)与行驶时间x (分钟)的变化关系.(1)求线段BC 所表达的函数关系式;(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分行驶,当小贾与爸爸相距100米时,求小贾的行驶时间;(3)如果小贾的行驶速度是v 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出ν的取值范围.解:(1)设线段BC 所表达的函数关系式为y kx b =+,根据题意得 15150022.53000k b k b +=⎧⎨+=⎩,解得2001500k b =⎧⎨=-⎩, ∴线段BC 所表达的函数关系式为2001500y x =-;(2)设小贾的行驶时间为x 分钟,根据题意得 150120100x x -=或120150(5)100x x --=或150(5)120100x x --=, 解得73x =或653x =或853x =(不合题意,舍去), 即当小贾与爸爸相距100米时,小贾的行驶时间为73分钟或653分钟;(3)当线段OD 过点B 时,小军的速度为150015100÷=(米/分钟); 当线段OD 过点C 时,小贾的速度为400300022.53÷=(米/分钟). 结合图形可知,当4001003v <<时,小贾在途中与爸爸恰好相遇两次(不包括家、图书馆两地).25.在梯形ABCD 中,//AD BC ,90A ∠=︒,45C ∠=︒.点E 在直线AD 上,联结BE ,过点E作BE的垂线,交直线CD于点F.(1)如图,已知:BE EF=;=,求证:AB AD(2)已知:AB AD=①当点E在线段AD上,求证:BE EF=;②当点E在射线DA上,①中的结论是否成立?如果成立,请写出证明过程;如果不成立,简述理由.【解答】证明:(1)如图1,过点F作FH AD⊥,交AD的延长线于点H,Q,AD BC//⊥,∴∠=∠=︒,且FH AD45C HDF∴∠=∠=︒,45HDF DFH∴=,DH HFQ,⊥BE EF∠+∠=︒,AEB ABEAEB HEF∴∠+∠=︒,且9090=,90ABE HEF∴∠=∠,且BE EF∠=∠=︒,A H∴∆≅∆ABE HEF AAS()∴=,AE HF=,AB EH∴=+=+=+=,EH ED DH ED HF ED AE AD∴=;AB AD(2)①如图2,在AB上截取AG AE∠=∠.=,连接EG,则AGE AEG90A ∠=︒Q ,180A AGE AEG ∠+∠+∠=︒, 45AGE ∴∠=︒.135BGE ∴∠=︒.//AD BC Q ,180C D ∴∠+∠=︒.又45C ∠=︒Q ,135D ∴∠=︒,BGE D ∴∠=∠.AB AD =Q ,AG AE =,BG DE ∴=.EF BE ⊥Q ,90BEF ∴∠=︒.又180A ABE AEB ∠+∠+∠=︒Q ,180AEB BEF DEF ∠+∠+∠=︒,90A ∠=︒,ABE DEF ∴∠=∠.在BGE ∆与EDF ∆中,BGE D BG DEABE DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()BGE EDF ASA ∴∆≅∆,BE EF ∴=;②如图3,延长BA 到G ,使AG AE =,∠=︒,EAGQ,90AE AG=AGE∴∠=︒,45Q,AD BC//∴∠=∠=︒,45C EDF∴∠=∠,EDF AGE⊥Q,EF BE∠+∠=︒,∴∠+∠=︒,且90BEA AEBFED BEA90∴∠=∠,FED EBA=,Q,AB ADAE AG=∠=∠,∴=,且EDF AGEDE BG∠=∠,FED EBA ∴∆≅∆()BGE EDF ASA∴=.BE EF。
2018-2019学年上海市八年级期末物理试卷一.选择题1.(3分)下列选项中最接近一个成年人体积的是()A.5×10﹣4立方米B.5×10﹣3立方米C.5×10﹣2立方米D.5×10﹣1立方米 2.(3分)冬天,室内取暖的暖气,很多都采用让流动的热水慢慢地流过散热器,其原因是()A.水比较便宜B.水的密度小C.水的比热容大 D.水的沸点高3.(3分)如图所示是四个实例中,在改变物体内能的方式上与其他三个实例不同的是()A.烧煮食物B.锯条发烫C.屁股“冒烟”D.搓手取暖4.(3分)如图所示,将两个底面平整,干净的铅柱紧压后,两个铅柱就会结合 在一起,即使在下面挂一个较重的物体也不会将它们拉开,这个实验表明()第1页(共28页)A.分子间存在斥力B.分子间有间隙C.分子间存在引力D.分子间既有斥力,又有引力5.(3 分)小王和小李分别是班里最轻和最重的两个,但他们却是一对好朋友。
某次他俩一起从楼底匀速走到三楼,关于他俩上楼时做功多少和功率的大小,以下判断正确的是()A.做功一样多,功率一样大B.做功一样多,小李的功率大C.小李做功多,小李功率大D.小李做功多,功率一样大6.(3分)下列过程中,由重力势能转化为动能的是()A.垫起的排球向上运动 B.跳高运动员过杆后下落C.拉满弦的弓把箭射出 D.出站的列车加速前进7.(3分)如图所示四个冲程图示中,属于机械能转化为内能的是()A.B.C.D.8.(3分)如图4所示四个利用简单机械提升重物的情景中,物体所受重力均为G,所使用简单机械的重力及摩擦力均不计。
为了使简单机械处于平衡状态,所需动力最小是()A.B. C .D.93A.水的重力与质量关系B.水的质量与体积关系C.水温与加热时间关系D.水的蒸发量与时间关系10.(3 分)如图所示三个完全相同的容器甲、乙、丙,在其中分别倒入水,则下列说法正确的是()A.甲杯中的水内能最大 B.乙杯中的水内能最大C.丙杯中的水内能最大 D.乙和丙杯中水的内能相等11.(3分)有A、B两块金属块体积分别是10立方厘米和20立方厘米,经测量则金属块它们的总质量是304克,若已知金属块A的密度是7.8克每立方厘米,克每立方厘米,则金属块B的密度是()A.19.3×103千克每立方米B.11.3×103千克每立方米C.8.9×103千克每立方米 D.2.7×103千克每立方米12.(3 分)用两个完全相同的电加热器同时给水和煤油分别加热,在加热过程中水和煤油的温度升高一样快,由此可以判定()(c水>c煤油、ñ水>ñ煤油)A.水的质量等于煤油的质量 B.水的体积大于煤油的体积C .水的质量大于煤油的质量D .水的体积小于煤油的体积二、填空题13.(3分)温度是表示物体的冷热程度的物理量。
上海市静安区2017-2018学年八年级(下)期末数学试卷一、选择题(本大题共6题,每题3分,满分18分)1.与是同类二次根式的是()A. B. C. D.【答案】B【解析】【分析】把各选项中的二次根式化为最简二次根式,然后根据同类二次根式的定义判断即可.【详解】A、与不是同类二次根式,故A错误;B、与是同类二次根式,故B正确;C、与不是同类二次根式,故C错误;D、与不是同类二次根式,故D错误;故选:B.【点睛】本题考查了同类二次根式的定义,熟练掌握同类二次根式的定义是解答本题的关键.化成最简二次根式后,如果被开方式相同,那么这几个二次根式叫做同类二次根式.2.下列函数中,一次函数的是()A. y=B. y=C. y=x﹣1D. y=2x2+4【答案】C【解析】【分析】根据一次函数的定义逐项判断即可.【详解】A、y=是反比例函数,不是一次函数;B、y=不是函数;C、y=x﹣1是一次函数;D、y=2x2+4是二次函数,不是一次函数;故选:C.【点睛】本题考查了一次函数的定义,一般地,形如y=kx+b,(k为常数,k≠0)的函数叫做一次函数3.下列命题中,假命题的是()A. 矩形的对角线相等B. 平行四边形的对角线互相平分C. 对角线互相垂直平分的四边形是菱形D. 对角线相等且互相垂直的四边形是正方形【答案】D【解析】【分析】根据平行四边形,矩形,菱形和正方形的对角线进行判断即可.【详解】A、矩形的对角线相等,是真命题;B、平行四边形的对角线互相平分,是真命题;C、对角线互相垂直平分的四边形是菱形,是真命题;D、对角线平分、相等且互相垂直的四边形是正方形,是假命题;故选:D.【点睛】本题考查了从对角线来判断特殊四边形的方法:对角线互相平分的四边形为平行四边形;对角线互相垂直平分的四边形为菱形;对角线互相平分且相等的四边形为矩形;对角线互相垂直平分且相等的四边形为正方形.也考查了真命题与假命题的概念.4.某校计划修建一条500米长的跑道,开工后每天比原计划多修15米,结果提前2天完成任务.如果设原计划每天修x米,那么根据题意可列出方程()A. =2B. =2C. =2D. =2【答案】A【解析】【分析】设原计划每天修x米,则实际每天修(x+15)米,根据时间=工作总量÷工作效率结合提前2天完成任务,即可得出关于x的分式方程,此题得解.【详解】设原计划每天修x米,则实际每天修(x+15)米.由题意,知原计划用的时间为天,实际用的时间为:天,故所列方程为:=2.故选:A.【点睛】本题考查了由实际问题抽象出分式方程,根据等量关系结合分式方程,找出未知数代表的意义是解题的关键.5.在五张完全相同的卡片上分别画上:等边三角形、平行四边形、等腰梯形、圆和正方形,在看不见图形的情况下随机抽出1张卡片,这张卡片上的图形是中心对称图形的概率是()A. B. C. D.【答案】C【解析】【分析】直接利用中心对称图形的定义结合概率公式得出答案.【详解】∵平行四边形、圆和正方形是中心对称图形,∴在看不见图形的情况下随机抽出1张卡片,这张卡片上的图形是中心对称图形的概率是:.故选:C.【点睛】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .6.下列说法正确的是()A. 若两个向量相等则起点相同,终点相同B. 零向量只有大小,没有方向C. 如果四边形ABCD是平行四边形,那么=D. 在平行四边形ABCD中,﹣=【答案】C【解析】【分析】根据平面向量的性质即可判断.【详解】A、错误.两个向量相等还可以平行的;B、错误.向量是有方向的;C、正确.平行四边形的对边平行且相等;D、错误.应该是,+=;故选:C.【点睛】本题考查平面向量、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.二.填空题(本大题共12题,每题3分,满分36分)【请将结果直接填入答题纸的相应位置上】7.化简=.【答案】【解析】试题分析:,故答案为:考点:分母有理化8.点A(1,3)_____(填“在”、或“不在”)直线y=﹣x+2上.【答案】不在.【解析】【分析】把A(1,3)代入y=﹣x+2验证即可.【详解】当x=1时,y=﹣x+2=1,∴点(1,3)不在直线y=﹣x+2上.故答案为:不在.【点睛】本题考查了一次函数图像上点的坐标特征,一次函数图像上点的坐标满足一次函数解析式.9.如果一次函数y=kx+2的函数值y随着x的值增大而减小,那么k的取值范围是_____.【答案】k<0.【解析】【分析】根据一次函数的性质解答即可.【详解】∵一次函数y=kx+2,函数值y随x的值增大而减小,∴k<0.故答案为:k<0.【点睛】本题考查了一次函数的图像与性质,对于一次函数y=kx+b(k为常数,k≠0),当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.10.如果关于x的方程bx2=2有实数解,那么b的取值范围是_____.【答案】b>0.【解析】【分析】先确定b≠0,则方程变形为x2=,根据平方根的定义得到>0时,方程有实数解,然后解关于b的不等式即可.【详解】根据题意得b≠0,x2=,当>0时,方程有实数解,所以b>0.故答案为:b>0.【点睛】本题考查了解一元二次方程−直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.11.方程=0的解是___.【答案】x=5.【解析】【分析】把两边都平方,化为整式方程求解,注意结果要检验.【详解】方程两边平方得:(x﹣3)(x﹣5)=0,解得:x1=3,x2=5,经检验,x2=5是方程的解,所以方程的解为:x=5.【点睛】本题考查了无理方程的解法,解含未知数的二次根式只有一个的无理方程时,一般步骤是:①移项,使方程左边只保留含有根号的二次根式,其余各项均移到方程的右边;②两边同时平方,得到一个整式方程;③解整式方程;④验根.12.一盒中只有黑、白两色的棋子(这些棋除颜色外无其他差别),设黑棋有x枚,白棋有y枚.如果从盒中随机取出一枚为黑棋的概率是,那么y=___.(请用含x的式子表示y)【答案】3x.【解析】【分析】根据盒中有x枚黑棋和y枚白棋,得出袋中共有(x+y)个棋,再根据概率公式列出关系式即可.【详解】∵从盒中随机取出一枚为黑棋的概率是,∴,整理,得:y=3x,故答案为:3x.【点睛】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .13.某厂去年1月份的产值为144万元,3月份下降到100万元,求这两个月平均每月产值降低的百分率.如果设平均每月产值降低的百分率是x,那么列出的方程是___.【答案】144(1﹣x)2=100.【解析】【分析】设平均每月产值降低的百分率是x,那么2月份的产值为144(1-x)万元,3月份的产值为144(1-x)2万元,然后根据3月份的产值为100万元即可列出方程.【详解】设平均每月产值降低的百分率是x,则2月份的产值为144(1﹣x)万元,3月份的产值为144(1﹣x)2万元,根据题意,得144(1﹣x)2=100.故答案为144(1﹣x)2=100.【点睛】本题考查由实际问题抽象出一元二次方程-求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.得到3月份的产值的等量关系是解决本题的关键.14.已知一个多边形的每个内角都是,则这个多边形的边数是_______.【答案】18【解析】【分析】首先计算出多边形的外角的度数,再根据外角和÷外角度数=边数可得答案.【详解】解:多边形每一个内角都等于多边形每一个外角都等于边数故答案为:【点睛】此题主要考查了多边形的外角与内角,关键是掌握多边形的外角与它相邻的内角互补,外角和为360°.15.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点B与点D重合,那么△DCF 的周长是___cm.【答案】14.【解析】【分析】根据翻转变换的性质得到BF=DF,根据三角形的周长公式计算即可.【详解】由翻转变换的性质可知,BF=DF,则△DCF的周长=DF+CF+CD=BF+CF+CD=BC+CD=14cm,故答案为:14.【点睛】本题考查的是翻转变换的性质,翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.16.如图,点G为正方形ABCD内一点,AB=AG,∠AGB=70°,联结DG,那么∠BGD=_____度.【答案】135.【解析】【分析】根据正方形的性质可得出AB=AD、∠BAD=90°,由AB=AG、∠AGB=70°利用等腰三角形的性质及三角形内角和定理可求出∠BAG的度数,由∠DAG=90°-∠BAG可求出∠DAG的度数,由等腰三角形的性质结合三角形内角和定理可求出∠AGD的度数,再由∠BGD=∠AGB+∠AGD可求出∠BGD的度数.【详解】∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°.∵AB=AG,∠AGB=70°,∴∠BAG =180°﹣70°﹣70°=40°,∴∠DAG =90°﹣∠BAG =50°,∴∠AGD =(180°﹣∠DAG )=65°,∴∠BGD =∠AGB +∠AGD =135°.故答案为:135.【点睛】本题考查了正方形的性质、等腰三角形的性质以及三角形内角和定理,根据等腰三角形的性质结合三角形内角和定理求出∠AGD 的度数是解题的关键.17.如图,四边形ABCD 是梯形,AD ∥BC ,AC =BD ,且AC ⊥BD ,如果梯形ABCD 的中位线长是5,那么这个梯形的高AH =___.【答案】5.【解析】【分析】过点D 作DF ∥AC 交BC 的延长线于F ,作DE ⊥BC 于E.可得四边形ACFD 是平行四边形,根据平行四边形的性质可得AD=CF ,再判定△BDF 是等腰直角三角形,根据等腰直角三角形的性质求出AH=BF 解答.【详解】如图,过点D 作DF ∥AC 交BC 的延长线于F ,作DE ⊥BC 于E.则四边形ACFD 是平行四边形,∴AD =CF ,∴AD +BC =BF ,∵梯形ABCD 的中位线长是5,∴BF=AD+BC=5×2=10.∵AC=BD,AC⊥BD,∴△BDF是等腰直角三角形,∴AH=DE=BF=5,故答案为:5.【点睛】本题考查了梯形的中位线,等腰直角三角形的判定与性质,平行四边形的判定与性质,梯形的问题关键在于准确作出辅助线.18.平面直角坐标系xOy中,点A(x1,y1)与B(x2,y2),如果满足x1+x2=0,y1﹣y2=0,其中x1≠x2,则称点A与点B互为反等点.已知:点C(3,8)、G(﹣5,8),联结线段CG,如果在线段CG上存在两点P,Q互为反等点,那么点P的横坐标x P的取值范围是__.【答案】﹣3≤x P≤3,且x p≠0.【解析】【分析】因为点P、Q是线段CG上的互反等点,推出点P在线段CC′上,由此可确定点P的横坐标x P的取值范围;【详解】如图,设C关于y轴的对称点C′(﹣3,8).由于点P与点Q互为反等点.又因为点P,Q是线段CG上的反等点,所以点P只能在线段CC′上,所点P的横坐标x P的取值范围为:﹣3≤x P≤3,且x p≠0.故答案为:﹣3≤x P≤3,且x p≠0.【点睛】本题考查坐标与图形的性质、点A与点B互为反等点的定义等知识,解题的关键是灵活运用所学知识解决问题,所以中考常创新题目.19.已知关于x的方程x2+(3﹣2k)x+k2+1=0的两个实数根分别是x1、x2,当|x1|+|x2|=7时,那么k的值是__.【答案】﹣2.【分析】先根据方程有两个实数根,确定△≥0,可得k≤,由x1•x2=k2+1>0,可知x1、x2,同号,分情况讨论即可.【详解】∵x2+(3﹣2k)x+k2+1=0的两个实数根分别是x1、x2,∴△=(3﹣2k)2﹣4×1×(k2+1)≥0,9﹣12k+4k2﹣4k2﹣4≥0,k≤,∵x1•x2=k2+1>0,∴x1、x2,同号,分两种情况:①当x1、x2同为正数时,x1+x2=7,即2k﹣3=7,k=5,∵k≤,∴k=5不符合题意,舍去,②当x1、x2同为负数时,x1+x2=﹣7,即2k﹣3=﹣7,k=﹣2,故答案为:﹣2.【点睛】本题考查了根与系数的关系和根的判别式.解此题时很多学生容易顺理成章的利用两根之积与和公式进行解答,解出k值,而忽略了限制性条件△≥0时k≤.三.解答题(本大题共8题,满分66分)【将下列各题的解答过程,做在答题纸上】20.解方程组:.【答案】,,,.【分析】由①得(x﹣y)(x﹣2y)=0,即x﹣y=0,x﹣2y=0,然后将原方程组化为或求解即可.【详解】,由①,得(x﹣y)(x﹣2y)=0,∴x﹣y=0,x﹣2y=0,所以原方程组可以变形为或,解方程组,得,;解方程组,得,,所以原方程组的解为:,,,.【点睛】本题考查了二元二次方程组的解法,解题思路类似与二元一次方程组,通过代入消元法转化为一元二次方程求解即可.21.解方程:【答案】x1=2,x2=﹣1.【解析】【分析】方程两边都乘以(x+3)(x﹣1),化为整式方程求解,然后检验即可.【详解】原方程化为,方程两边都乘以(x+3)(x﹣1)得:x﹣1﹣(x+3)(x﹣1)=﹣2x,x2﹣x﹣2=0,解得:x=2或﹣1,检验:当x=2时,(x+3)(x﹣1)≠0,所以x=2是原方程的解,当x=﹣1时,(x+3)(x﹣1)≠0,所以x=﹣1是原方程的解,所以原方程的解为:x1=2,x2=﹣1.【点睛】本题考查了分式方程的解法,其基本思路是把方程的两边都乘以各分母的最简公分母,化为整式方程求解,求出x的值后不要忘记检验.22.如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.(1)如果图中线段都可画成有向线段,那么在这些有向线段所表示的向量中,与向量相等的向量是;(2)设=,=,=.试用向量,或表示下列向量:=;=.(3)求作:.(请在原图上作图,不要求写作法,但要写出结论)【答案】(1);(2)+、+﹣;(3)如图所示见解析. .【解析】【分析】(1)由中位线定理得EF∥AC、EF=AC,HG∥AC、HG=AC,从而知EF=HG,且EF∥HG,根据相等向量的定义可得;(2)由可得;(3)由G为DC中点知,从而得=,据此根据三角形法则作图即可得.【详解】(1)∵E、F是AB、BC的中点,H、G是DA、DC的中点,∴EF∥AC、EF=AC,HG∥AC、HG=AC,∴EF=HG,且EF∥HG,∴,故答案为:;(2)由图知,则,故答案为:;(3)如图所示:.【点睛】本题考查平面向量的知识,解题的关键是掌握中位线定理、相等向量的定义及三角形法则.23.某大型物件快递公司送货员每月的工资由底薪加计件工资两部分组成,计件工资与送货件数成正比例.有甲乙两名送货员,如果送货量为x件时,甲的工资是y1(元),乙的工资是y2(元),如图所示,已知甲的每月底薪是800元,每送一件货物,甲所得的工资比乙高2元(1)根据图中信息,分别求出y1和y2关于x的函数解析式;(不必写定义域)(2)如果甲、乙两人平均每天送货量分别是12件和14件,求两人的月工资分别是多少元?(一个月为30天)【答案】(1)y1=20x+800;y2=18x+1200;(2)y1=8000元;y2=8760元.【解析】【分析】(1)设y1关于x的函数解析式为y1=kx+800,将(200,4800)代入,利用待定系数法即可求出y1=20x+800;根据每送一件货物,甲所得的工资比乙高2元,可设y2关于x的函数解析式为y2=18x+b,将(200,4800)代入,利用待定系数法即可求出y2=18x+1200;(2)根据甲、乙两人平均每天送货量分别是12件和14件,得出甲、乙两人一个月送货量分别是12×30=360件和14×30=420件.再把x=360代入y1=20x+800,x=420代入y2=18x+1200,计算即可求解.【详解】(1)设y1关于x的函数解析式为y1=kx+800,将(200,4800)代入,得4800=200k+800,解得k=20,即y1关于x的函数解析式为y1=20x+800;∵每送一件货物,甲所得的工资比乙高2元,而每送一件货物,甲所得的工资是20元,∴每送一件货物,乙所得的工资比乙高18元.设y2关于x的函数解析式为y2=18x+b,将(200,4800)代入,得4800=18×200+b,解得b=1200,即y2关于x的函数解析式为y2=18x+1200;(2)如果甲、乙两人平均每天送货量分别是12件和14件,那么甲、乙两人一个月送货量分别是12×30=360件和14×30=420件.把x=360代入y1=20x+800,得y1=20×360+800=8000(元);把x=420代入y2=18x+1200,得y2=18×420+1200=8760(元).【点睛】本题考查了一次函数的应用,利用待定系数法求直线的解析式,以及代数式求值,读懂题目信息,理解函数图象是解题的关键.24.如图,Rt△ABC中,∠ACB=90°,D是边BC上一点,点E、F分别是线段AB、AD中点,联结CE、CF、EF.(1)求证:△CEF≌△AEF;(2)联结DE,当BD=2CD时,求证:AD=2DE.【答案】(1)见解析;(2)见解析.【解析】分析】(1)在直角三角形ABC中,E为斜边AB的中点,利用斜边上的中线等于斜边的一半得到CE=AE,在直角三角形ACD中,F为斜边AD的中点,利用斜边上的中线等于斜边的一半得到AF=CF,再由EF=EF,利用SSS即可得证;(2)由EF为三角形ABD的中点,利用中位线定理得到EF与BD平行,EF等于BD的一半,再由BD=2DC,等量代换得到EF=CD,再由EF与CD平行,得到四边形CEFD为平行四边形,可得出DE=CF,再由CF=AF,等量代换得到DE=AF.【详解】证明:(1)∵∠ACB=90°,且E线段AB中点,∴CE=AB=AE,∵∠ACD=90°,F为线段AD中点,∴AF=CF=AD,在△CEF和△AEF中,,∴△CEF≌△AEF(SSS);(2)连接DE,∵点E、F分别是线段AB、AD中点,∴EF=BD,EF∥BC,∵BD=2CD,∴EF=CD.又∵EF∥BC,∴四边形CFEDD是平行四边形,∴DE=CF,∵CF=AF=FD,∴AD=2DE.【点睛】此题考查了全等三角形的判定与性质,中位线定理,直角三角形斜边上的中线等于斜边的一半,以及平行四边形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.25.如图,在直角坐标平面内,直线y=﹣x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC=OB.(1)求线段AB的长及点C的坐标;(2)设线段BC的中点为E,如果梯形AECD的顶点D在y轴上,CE是底边,求点D的坐标和梯形AECD 的面积.【答案】(1)A(﹣3,0),B(0,﹣4),C(2,0);(2)S梯形AECD=20.【解析】【分析】(1)令x=0求出点B的坐标,令y=0求出点A的坐标,根据勾股定理求出AB的长,然后根据OC=OB 即可求出点C的坐标;(2)首先证明梯形AECD是直角梯形,由△AOD∽△COB,求出OD的长,再由勾股定理求出BC、AD、AE的长即可解决问题;【详解】(1)令x=0,得到y=﹣4,∴B(0,﹣4),令y=0,得到x=﹣3,∴A(﹣3,0),∴AB==5,∵OC=OB,点C中x轴正半轴上,∴C(2,0)(2)∵AC=AB=5,EC=BE,∴AE⊥BC,∵CE是梯形AECD的底,∴AD∥CE,∴△AOD∽△COB,∴,∴,∴OD=6,∴D(6,0),∵BC=2,AD=3,AE=,∴S×AE=20.梯形AECD【点睛】本题考查一次函数与坐标轴的交点、相似三角形的判定与性质、勾股定理、梯形的性质等知识,解题的关键是熟练掌握基本知识,灵活运用所学知识解决问题,属于中考常考题型.26.如图,在矩形ABCD中,AB=1,对角线AC、BD相交于点O,过点O作EF⊥AC分别交射线AD与射线CB于点E和点F,联结CE、AF.(1)求证:四边形AFCE是菱形;(2)当点E、F分别在边AD和BC上时,如果设AD=x,菱形AFCE的面积是y,求y关于x的函数关系式,并写出x的取值范围;(3)如果△ODE是等腰三角形,求AD的长度.【答案】(1)见解析;(2);(3)AD的值为或.【解析】【分析】(1)由△DOE≌△BOF,推出EO=OF,∵OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可.(2)由cos∠DAC=,求出AE即可解决问题;(3)分两种情形分别讨论求解即可.【详解】(1)①证明:如图1中,∵四边形ABCD是矩形,∴AD∥BC,OB=OD,∴∠EDO=∠FBO,在△DOE和△BOF中,,∴△DOE≌△BOF,∴EO=OF,∵OB=OD,∴四边形EBFD是平行四边形,∵EF⊥BD,OB=OD,∴EB=ED,∴四边形EBFD是菱形.(2)由题意可知:,,∵,∴,∴,∵AE≤AD,∴,∴x2≥1,∵x>0,∴x≥1.即(x≥1).(3)①如图2中,当点E在线段AD上时,ED=EO,则Rt△CED≌Rt△CEO,∴CD=CO=AO=1,在Rt△ADC中,AD=.如图3中,当的E在线段AD的延长线上时,DE=DO,∵DE=DO=OC,EC=CE,∴Rt△ECD≌Rt△CEO,∴CD=EO,∵∠DAC=∠EAO,∠ADC=∠AOE=90°,∴△ADC≌△AOE,∴AE=AC,∵EO垂直平分线段AC,∴EA=EC,∴EA=EC=AC,∴△ACE是等边三角形,∴AD=CD•tan30°=,综上所述,满足条件的AD的值为或.【点睛】本题考查四边形综合题、矩形的性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.。