数字信号处理matlab实验4 离散系统的变换域分析

实验四 matlab 方法用于离散系统时域分析一、实验目的设计MATLAB 的M 文件，用来实现PID 调节器的功能，分析Kp 、Kd 、Ki 三个参数对系统性能的影响。

二、实验步骤开机执行程序，用鼠标双击图标进入MATLAB 命令窗口：Command Windows 新建M-file ，然后，输入设计好的程序。

调试，检查错误，然后运行。

观察系统对不同参数的相应曲线，分析其原因。

三、实验要求 实验之前，查阅有关资料，编写好相应的程序。

认真做好仿真记录,叙述Kp 、Kd 、Ki 三个参数对系统性能的影响。

五、实验原理 1、PID 原理简介将偏差的比例积分微分通过线性组合构成控制量，用这一控制量对被控对象进行控制，这样的控制器称之为PID 控制器。

比例积分微分控制发展历史悠久，是目前工业程序控制中，应用最为广泛的工业控制器之一。

PID 控制器对控制对象的系统模型要求不高，甚至在系统模型完全未知的情况下也能进行控制。

模拟PID 连续方程见式（1）：)(t U 电流控制量，)(t e 电流误差量])()(1)([)(0dt t de T d e T t e K t U dtip ++=⎰ττ （1）系统传输函数)(s G]11[)()()(s T s T K s E s U s G s s p ++==（2）以求和替代积分，向后差分替代微分，对连续形式PID 控制算法做离散等效，即ski s tT k e k e dt t de i e T d e )1()()(,)()(0--==∑⎰=ττ，可得理想PID 控制算法的数字型位置算式))1()(()()()(0--++=∑=k e k e K i e K k e K k U d ki i p（3）这里：s d p d i sp i p T T K K T T K K K *,*,==分别称之为PID 控制器的比例、积分、微分系数。

比例调节器的作用是对偏差作出瞬间的响应，偏差一旦产生，调节器立即产生控制作用使控制量向着偏差减小的方向变化，控制作用的强弱取决于比例系数Kp ，增加Kp 将加快系统的响应速度，有利于减少静差，但过大的比例系数会使系统有较大的超调，并可能产生振荡，使稳定性变坏。

一．
实验目的
1.
熟悉离散信号Z 变换的原理及性质。

2.熟悉常见信号的Z 变换。

3.了解正/反Z 变换的MATLAB 实现方法。

4.了解离散信号的Z 变换与其对应的理想抽样信号的傅氏变换和拉氏变换之间的关系。

5.了解利用MATLAB 实现离散系统的频率特性分析的方法。

二．实验内容
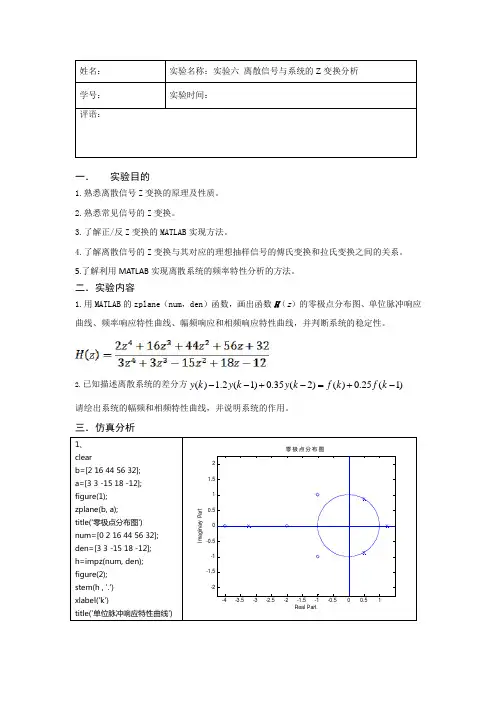
1.用MATLAB 的zplane （num ，den ）函数，画出函数H （z ）的零极点分布图、单位脉冲响应曲线、频率响应特性曲线、幅频响应和相频响应特性曲线，并判断系统的稳定性。

2.已知描述离散系统的差分方
() 1.2(1)0.35(2)()0.25(1)y k y k y k f k f k --+-=+-
请绘出系统的幅频和相频特性曲线，并说明系统的作用。

三．仿真分析
四．实验总结
1.进一步了解Z变换的原理及性质
2.进一步了解了信号的零极点分布与系统稳定性的关系。

matlab的离散信号的处理离散信号的处理是数字信号处理领域中的一个重要主题。

离散信号是指在时间上以离散的方式进行采样的信号，可以用数字序列来表示。

而离散信号的处理则是对这些数字序列进行各种操作和分析的过程。

在离散信号的处理中，最常见的操作之一是信号的采样。

采样是指在连续时间信号上以一定的时间间隔对信号进行取样。

采样后得到的离散信号可以用数字序列表示，其中每个采样点对应一个数字。

采样的频率决定了信号在时间上的分辨率，即每秒钟采样的次数。

较高的采样频率能够更准确地表示原始信号，但同时也会增加数据量和计算的复杂度。

离散信号的处理还包括信号的重构和插值。

重构是指从离散信号中恢复出连续时间信号的过程。

常见的重构方法包括线性插值、多项式插值和样条插值等。

这些方法能够通过对离散信号的插值来近似恢复出原始信号，从而进行后续的分析和处理。

在离散信号处理中，滤波也是一个重要的操作。

滤波是指通过选择合适的滤波器对信号进行处理，以去除不需要的频率成分或增强感兴趣的频率成分。

常见的滤波器包括低通滤波器、高通滤波器和带通滤波器等。

滤波器的设计和选择需要根据信号的特点和处理目标来确定，以达到最佳的效果。

除了上述操作外，离散信号的处理还可以包括时域分析和频域分析。

时域分析是指对信号在时间上的变化进行分析，常见的方法有时域图像的绘制、计算信号的均值和方差等。

频域分析则是通过将信号转换到频域来进行分析，常见的方法有傅里叶变换和离散傅里叶变换等。

频域分析可以帮助我们了解信号的频率成分和能量分布，从而更好地理解信号的特性。

在实际应用中，离散信号的处理可以应用于各种领域。

例如，在音频处理中，我们可以对音频信号进行采样、重构和滤波等操作，以实现声音的录制、转换和编辑。

在图像处理中，我们可以将图像转换为离散信号进行处理，例如进行图像增强、边缘检测和图像压缩等。

总结起来，离散信号的处理是数字信号处理领域中的重要内容，涵盖了信号的采样、重构、滤波和频域分析等操作。

2011届学士学位论文信号与系统中典型问题的MATLAB分析系别: 电子信息系专业: 电子信息科学与技术学号:姓名:指导教师:指导教师职称: 教授2011年4月30日信号与系统中典型问题的MATLAB分析摘要从信号与系统课程的特点出发，结合MATLAB软件优势，针对实例进行分析。

主要从连续信号、离散信号两方面应用MATLAB软件进行仿真和分析。

分别对连续信号和离散信号中线性时不变(LTI)系统信号分析，应用MATLAB软件进行仿真和分析。

对连续时间信号和离散时间信号的线性时间不变(LTI)系统的变换域，卷积和采样定理进行了模拟。

实例中运用了连续模块库、离散模块库等。

通过实例表明了MATLAB软件的便捷性，可以提高工作效率。

实践证明，采用MATLAB软件进行辅助分析可以我们对知识点的理解更深入更透彻。

关键词MATLAB仿真；时域分析；频域分析；卷积；序列卷和；冲激响应；阶跃响应；The Applied Research of Signal ProcessingBased on MATLABAbstract we give an overview of the examples from the characteristics of signal and system course, combining with MATLAB software advantages. The main idea is that MATLAB simulation and analysis software were applied in the continuous-time signals and discrete-time signals. In continuous-time signals and discrete-time signals the response signal of linear time invariant(LTI) system and its analysis of the transform domain and convolution and Sampling theorem were simulated. The examples used the continuous and discrete blocks library and communication toolbox, etc. Some examples show that processing signals can bring us great convenience and high efficiency. Practice has proved, using MATLAB software were aided analysis on knowledge points we can understand deeper and more thoroughly.Key-words MATLAB; the Time-domain Analysis；Frequency domain analysis；convolution ；Sequence convolution ；Impulse response ；Order step-response目录1引言 (1)2 MATLAB软件介绍 (2)3 MATLAB对连续时间信号的分析 (3)MATLAB仿真线性时不变(LTI)系统响应的信号表示 (3)MATLAB对连续信号变换域的分析 (4)连续时间信号的卷积计算及MATLAB的实现 (5)连续时间系统抽样定理的验证 (6)84 MATLAB对离散时间信号的分析 (10)离散系统的单位样值响应 (11)离散系统的变换域分析 (12)离散时间信号的卷积计算 (13)结论 (15)参考文献 (16)致谢 (17)附录一 (18)附录二 (19)附录三 (21)1 引言随着软件的发展，为仿真实验提供了另一思路，MATLAB软件具有强大的数值计算和矩阵处理功能。

实验一 常见离散信号的MATLAB 产生和图形显示一、 实验目的加深对常见离散信号的理解 二、实验原理1、单位抽样序列的产生,10,0{=≠=n n n ）（δ在MATLAB 中可以用zeros()函数实现 x=[1,zeros(1,N-1)]; 或x=zeros(1，N)； x(1)=1;2、单位阶跃序列的产生0,10,0{u ≥<=n n n ）（在MATLAB 中可以用ones()函数实现 x=one(1,N); 3、正弦序列的产生 在MATLAB 中实现方法如下： N=0:N-1X=A*sin(2*pi*f*n/fs+fai) 4、复正弦序列的产生jwn e A n x *)(=在MATLAB 中实现方法如下：n)*w *exp(j *A 1:0=-=x N n5、实指数序列的产生na A n x *)(= 在MATLAB 中实现方法如下：na A x N n .^*1:0=-=三、实验内容及步骤编制程序产生以下信号，并绘出其图形。

1）产生64点的单位抽样序列)(n δN=64x=[1,zeros(1,N-1)]stem(x)2）产生64点并移位20位的单位抽样序列)20(-n δN=64x=[0,zeros(1,N-1)] x(20)=1 stem(x)3）任意序列)5(7.0)4(9.2)3(6.5)2(8.1)1(4.3)(0.8)(-+-+-+-+-+=n n n n n n n f δδδδδδ b=[1];a=[8,3.4,1.8,5.6,2.9,0.7]; xh=[1,zeros(1,20)]; h=filter(b,a,xh) figure(1); n=0:20; stem(n,h,) legend('冲激')4）产生幅度A=3，频率f＝100，初始相位ϕ＝1.2，点数为32 点的正弦序列。

n=0:31;x=3*exp(j*314*n)figure(1)stem(n,x)5）产生幅度A=3，角频率ω＝314，点数为32 点的复正弦序列。

matlab离散信号时域分析实验报告Matlab离散信号时域分析实验报告引言：离散信号时域分析是数字信号处理中的重要内容，通过对信号在时域上的分析，可以了解信号的特征和性质。

本实验使用Matlab软件进行离散信号的时域分析，通过实验数据的采集和处理，探索信号的频率、幅度、相位等重要参数。

实验目的：1. 了解离散信号的基本概念和性质；2. 掌握Matlab软件在离散信号时域分析中的应用；3. 分析离散信号的频谱特性和时域波形。

实验步骤：1. 信号采集与导入首先，我们需要采集一段离散信号的数据，并将其导入Matlab中进行分析。

在实验中，我们选择了一个简单的正弦信号作为实验对象。

通过Matlab中的数据采集工具，我们可以方便地获取该信号的采样数据，并导入到Matlab中。

2. 时域波形绘制在Matlab中，我们可以使用plot函数绘制离散信号的时域波形。

通过对信号的采样数据进行绘制，我们可以直观地观察到信号的变化规律。

同时，我们还可以通过调整绘图参数，比如线型、颜色等，使得波形图更加美观。

3. 信号频谱分析离散信号的频谱分析是了解信号频率特性的重要手段。

在Matlab中，我们可以使用fft函数对信号进行频谱分析。

通过对信号的采样数据进行傅里叶变换，我们可以得到信号的频谱图。

频谱图可以清晰地展示信号的频率分布情况，对于分析信号的频率成分非常有帮助。

4. 信号幅度与相位分析除了频率特性，离散信号的幅度和相位也是需要关注的重要参数。

在Matlab中，我们可以使用abs函数计算信号的幅度，使用angle函数计算信号的相位。

通过对信号的采样数据进行计算，我们可以得到信号的幅度和相位信息。

这些信息对于了解信号的时域特性非常有帮助。

实验结果与分析：通过以上实验步骤，我们得到了离散信号的时域波形、频谱特性、幅度和相位信息。

通过观察实验结果，我们可以发现信号的频率成分、幅度变化以及相位差异等重要特征。

结论：通过本次实验，我们深入了解了离散信号的时域分析方法，并通过Matlab软件进行了实际操作。

班级： 学号： 姓名： 日期： 实验一：离散时间信号的分析一、实验目的利用DFT 卷积实现系统的时域分析二、实验原理在离散时间、连续频率的傅里叶变换中，由于卷积性质知道，对系统输出的计算可以通过求x[n]和h[n]的DTFT ，将得到的X(e jw )和H(e jw )相乘就可以得到Y(e jw )，进而再通过反变换得到y[n]。

这就避免了在时域进行繁琐的卷积求解。

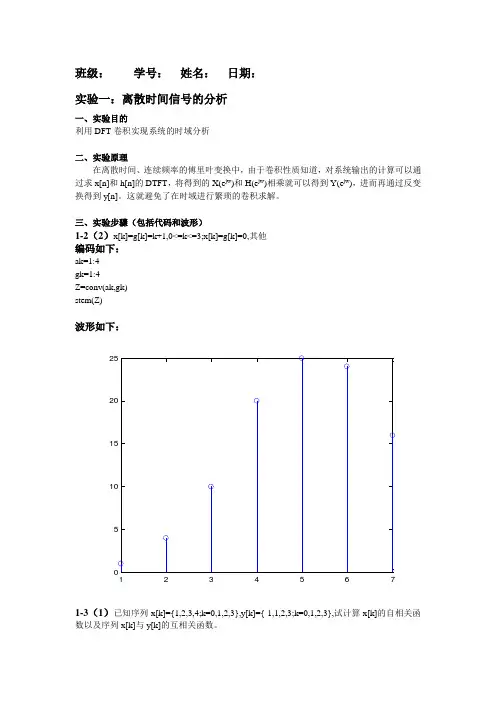
三、实验步骤（包括代码和波形）1-2（2）x[k]=g[k]=k+1,0<=k<=3;x[k]=g[k]=0,其他 编码如下：ak=1:4 gk=1:4Z=conv(ak,gk) stem(Z)波形如下：12345675101520251-3（1）已知序列x[k]={1,2,3,4;k=0,1,2,3},y[k]={-1,1,2,3;k=0,1,2,3},试计算x[k]的自相关函数以及序列x[k]与y[k]的互相关函数。

编码如下：x=[1,2,3,4];kx=0:3; y=[-1,1,-2,3];ky=0:3; xf=fliplr(x); s1=conv(x,xf); s2=conv(xf,y); yf=fliplr(y); s3=conv(yf,x);k1=kx(1)+ky(1):kx(end)+ky(end); kxf=-fliplr(kx);k2=kxf(1)+ky(1):kxf(end)+ky(end); kyf=-fliplr(ky);k3=kyf(1)+kx(1):kyf(end)+kx(end); subplot(2,2,1); stem(k1,s1);xlabel('k1');ylabel('s1'); subplot(2,2,2); stem(k2,s2);xlabel('k2');ylabel('s2'); subplot(2,2,3) stem(k3,s3);xlabel('k3');ylabel('s3');波形如下：0246102030k1s 1-4-2024-10-50510k2s 2-4-2024-10-50510k3s 3M-1已知g1[t]=cos(6*pi*t),g2=cos(14*pi*t),g3=cos(26*pi*t),以抽样频率f(max)=10HZ对上述三个信号进行抽样。

数字信号处理实验报告姓名：班级：09电信一班学号：2)]得下图二，图二图一3．将如下文件另存为：sigadd.m文件function [y,n] = sigadd(x1,n1,x2,n2)% 实现y(n) = x1(n)+x2(n)% -----------------------------% [y,n] = sigadd(x1,n1,x2,n2)% y = 在包含n1 和n2 的n点上求序列和,% x1 = 在n1上的第一序列% x2 = 在n2上的第二序列(n2可与n1不等)n = min(min(n1),min(n2)):max(max(n1),max(n2)); % y(n)的长度y1 = zeros(1,length(n)); y2 = y1; % 初始化y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; % 具有y的长度的x1y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; % 具有y的长度的x2y = y1+y2;在命令窗口输入：x1=[1,0.5,0.3,0.4];n1=-1:2;x2=[0.2,0.3,0.4,0.5,0.8,1];n2=-2:3; [y,n] = sigadd(x1,n1,x2,n2)得：y =n=-1:10;x=sin(0.4*pi*n);y=fliplr(x);n1=-fliplr(n);subplot(2,1,1),stem(n,x) subplot(2,1,2),stem(n1,y在命令窗口键入:n=-1:10; x=sin(0.4*pi*n);n (samples)实验结果：1.（1）在命令窗口输入：tic; [am,pha]=dft1(x)N=length(x);w=exp(-j*2*pi/N);for k=1:Nsum=0;for n=1:Nsum=sum+x(n)*w^((k-1)*(n-1));endam(k)=abs(sum);pha(k)=angle(sum);end;toc得到如下结果：am =Columns 1 through 11120.0000 41.0066 20.9050 14.3996 11.3137 9.6215 8.6591 8.1567 8.0000 8.1567 8.6591Columns 12 through 169.6215 11.3137 14.3996 20.9050 41.0066pha =Columns 1 through 110 1.7671 1.9635 2.1598 2.3562 2.5525 2.7489 2.9452 3.1416 -2.9452 -2.7489Columns 12 through 16-2.5525 -2.3562 -2.1598 -1.9635 -1.7671Elapsed time is 0.047000 seconds.（2）在命令窗口输入：tic;[am,pha]=dft2(x)N=length(x);n=[0:N-1];k=[0:N-1];w=exp(-j*2*pi/N);nk=n’*k;wnk=w.^(nk); Xk=x*wnk; am= abs(Xk); pha=angle(Xk); toc得到下图：figure(1)00.10.20.30.40.50.60.70.80.91signal x(n), 0 <= n <= 99（2）在命令窗口键入：n3=[0:1:99];y3=[x(1:1:10) zeros(1,90)]; ％添90个零。

实验4 离散系统的变换域分析实验目的：加深对离散系统的频率响应分析和零、极点分布的概念理解。

实验原理：离散系统的时域方程为∑∑==-=-Mk k Nk kk n x p k n y d)()(其变换域分析方法如下：频域 )()()(][][][][][ΩΩ=Ω⇔-=*=∑∞-∞=H X Y m n h m x n h n x n y m系统的频率响应为 Ω-Ω-Ω-Ω-++++++=ΩΩ=ΩjN N j jM M j e d e d d e p e p p D p H ......)()()(1010 Z 域 )()()(][][][][][z H z X z Y m n h m x n h n x n y m =⇔-=*=∑∞-∞=系统的转移函数为 N N MM zd z d d z p z p p z D z p z H ----++++++==......)()()(110110 分解因式 ∏-∏-=∑∑==-=-=-=-Ni i Mi i Ni ik Mi ik z z Kzd z p z H 11110)1()1()(λξ ，其中i ξ和i λ称为零、极点。

在MATLAB 中，可以用函数[z ，p ，K]=tf2zp （num ，den ）求得有理分式形式的系统转移函数的零、极点，用函数zplane （z ，p ）绘出零、极点分布图；也可以用函数zplane （num ，den ）直接绘出有理分式形式的系统转移函数的零、极点分布图。

使h=freqz(num,den,w)函数可求系统的频率响应，w 是频率的计算点，如w=0:pi/255:pi, h 是复数，abs(h)为幅度响应，angle(h)为相位响应。

另外，在MATLAB 中，可以用函数 [r ，p ，k]=residuez （num ，den ）完成部分分式展开计算；可以用函数sos=zp2sos （z ，p ，K ）完成将高阶系统分解为2阶系统的串联。

matlab 离散信号频谱分析实验报告实验目的：本实验旨在通过使用MATLAB软件对离散信号进行频谱分析，探究信号的频谱特性，并通过实验结果验证频谱分析的有效性和准确性。

实验原理：频谱分析是一种将信号从时域转换到频域的方法，通过分析信号的频谱特性可以了解信号的频率分布情况。

离散信号频谱分析主要基于离散傅里叶变换（DFT）和快速傅里叶变换（FFT）算法。

实验步骤：1. 生成离散信号：使用MATLAB中的函数生成一个离散信号，可以选择正弦信号、方波信号或其他类型的信号。

2. 绘制时域波形：将生成的离散信号在时域上进行绘制，观察信号的波形特征。

3. 进行频谱分析：使用MATLAB中的DFT或FFT函数对离散信号进行频谱分析，得到信号的频谱图像。

4. 绘制频谱图像：将频谱分析得到的结果进行绘制，观察信号在频域上的频率分布情况。

5. 分析频谱特性：根据频谱图像，分析信号的主要频率成分、频谱密度等特性。

实验结果与分析：通过实验我们选择了一个正弦信号作为实验对象，其频率为100Hz，幅值为1。

首先，我们绘制了该正弦信号的时域波形，观察到信号呈现出周期性的振荡特征。

接下来，我们使用MATLAB中的FFT函数对该离散信号进行频谱分析。

得到的频谱图像显示，信号的主要频率成分为100Hz，且幅值为1。

此外，频谱图像还显示了信号在其他频率上的幅值衰减情况，表明信号在频域上存在多个频率成分。

根据频谱图像，我们可以进一步分析信号的频谱特性。

首先，信号的主要频率成分为100Hz，这意味着信号的主要周期为0.01秒。

其次，频谱图像显示了信号在其他频率上的幅值衰减情况，说明信号在频域上存在多个频率成分，这可能与信号的采样率和信号源本身的特性有关。

实验结论：通过本次实验，我们成功地使用MATLAB对离散信号进行了频谱分析，并得到了信号的频谱图像。

实验结果表明，频谱分析是一种有效的信号分析方法，可以揭示信号的频率分布情况和频谱特性。

实验四 Z 变换【实验目的】 通过MATLAB 仿真离散时间系统，研究其时频域特性，加深对离散系统的冲激响应，频率响应分析和零极点分布概念和理解。

【实验原理】1.Z 变换原理（1）.Z 变换 在数字信号处理的分析方法中，除时域分析方法外，还有变换域分析方法。

后者通常指Z 变换和傅里叶变换法。

变换域分析的最大优点是将离散系统的差分方程转化为简单的代数方程，使其求解大大简化，也使得对系统的特性分析更为方便。

对于离散时间信号，设序列为x (n )，则其Z 变换定义为： ，其中z 为复变量，是一个以时部为横坐标，虚部为纵坐∑+∞-∞=-=n n z n x z X )()(标构成的平面上的变量。

Z 变换记作，X (z )存在的z 的集合称为收敛域])([ )(n x z X Z =（ROC ），一般为+-<<x x R z R 由于ROC 是由定义的，因此一般为环形区域。

根据ROC 的特点，可以判定序列是右边序z 列、左边序列、双边序列等。

Z 变换具有一些重要的特性，是傅里叶变换的推广，包括线性、时移特性、频移特性、尺度变换、共轭、翻褶、Z 域微分、序列相乘、序列卷积等一系列性质。

（2）.系统函数离散线性时不变（LTI ）系统的系统函数H (z )定义为：H (z ) = Z[h (n )] = (4.4)∑+∞-∞=-n n z n h )(若用差分方程表示系统，则有 )k -n (b )k -n (a M 0k k N0k x y k ∑∑===如果系统起始状态为零，直接对上式的两边Z 变换，并利用移位特性，有 ∑∑=-=-==N 0M 0)()()(k k k k k k z a z b Z X z Y z H 因此，系统函数H (z )的分子和分母的系数正好等于差分方程的系数。

归一化，即使得0a y (n )前的参数为1，此时可以对上式的分子、分母进行因式分解，可得∏∏=-=-=N k k M m z z z H 1111m )p -(1)c -(1K )(得到系统的增益函数K 、零点、极点。

matlab离散信号时域分析实验报告实验目的：本实验旨在通过使用Matlab对离散信号进行时域分析，探究离散信号的特性和变化规律，加深对信号处理理论的理解，提高实际应用能力。

实验仪器和材料：Matlab软件实验步骤：1. 生成离散信号：首先，我们使用Matlab生成一个离散信号，可以是正弦信号、方波信号等。

通过调整频率、幅度等参数，可以得到不同特性的信号。

2. 时域分析：接下来，我们对生成的离散信号进行时域分析，包括信号的幅度、相位、周期等特性进行分析，通过Matlab提供的函数和工具进行计算和可视化展示。

3. 变换分析：除了时域分析外，我们还可以对离散信号进行变换分析，如傅里叶变换、离散傅里叶变换等，通过观察频谱图和功率谱图等来分析信号的频率成分和能量分布情况。

4. 实验结果分析：最后，根据实验结果进行分析，总结离散信号的特性和变化规律，对信号处理理论进行深入理解。

实验结果：通过实验，我们得到了生成的离散信号的时域特性、频域特性等数据和图表，并对其进行了分析和总结。

我们发现不同频率、幅度的离散信号具有不同的时域特性和频域特性，这为我们理解信号处理理论提供了直观的实验数据和实例。

实验结论：通过本次实验，我们深入了解了Matlab对离散信号进行时域分析的方法和步骤，加深了对信号处理理论的理解，提高了实际应用能力。

同时，我们也发现了离散信号的特性和变化规律，为进一步的研究和应用提供了基础。

实验心得：本次实验让我对离散信号的时域分析有了更深入的理解，也提高了我在Matlab软件上的操作能力。

通过实验，我对信号处理理论有了更直观的认识，为今后的学习和研究打下了坚实的基础。

希望能够通过更多的实验和学习，不断提升自己在信号处理领域的能力和水平。

实验报告2012 年 04 月 06 日课程名称： 数字信号处理 实验名称： 离散信号及其MATLAB 实现 班级： 学号： 姓名：实验一 离散信号及其MATLAB 实验一、实验目的（1）熟悉MATLAB 的主要操作命令；（2）学会离散信号的表示方法及其基本运算； （3）掌握简单的绘图命令；（4）用Matlab 编程并学会创建函数。

二、实验内容（1）序列的加、减、乘、除和乘方运算。

输入A=[1 2 3 4 ]，B=[3 4 5 6]，起点n=0，求C=A+B ，D=A-B ，E=A.*B ，F=A./B ，G=A.^B ，并用stem 语句画出A ，B ，C ，D ，E ，F ，G 。

（2）用MATLAB 实现下列序列：① x(n)=n 8.0 0≤n ≤15 ② x(n)=n j e )32.0( 0≤n ≤15③ x(n)=3cos(0.125πn+0.2π)+2sin(0.25πn+0.1π) 0≤n ≤15(3)编写函数如stepshift （n0，n1，n2）实现u(n)的移动序列u(n-n0)，n1≤n ≤n2，给出该函数的图形。

设n1=0，n2=9，n0=2(4) x(n)=[1，-1，3，5]，起点n=0，产生并绘出下列序列的样本： x1(n)=2x(n+2)-x(n-1)-2x(n)三、实验程序及实验图形 实验（1） 1、 程序：n=[0:3];A=[1 2 3 4 ]; %定义序列A ，即一行四列的矩阵 B=[3 4 5 6]; %定义序列BC=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B; figure(1);subplot(2,2,1) %将图形界面分成2行2列，其中第一个显示下列图形 stem(n,A,'r*'); %绘制二维离散数据的火柴杆图，用红线和*号标出xlabel('n'); %x 轴标签为n ylabel('A'); %y 轴标签为A grid on; %绘制网格 subplot(2,2,2)stem(n,B);xlabel('n');ylabel('B');grid on; subplot(2,2,3)stem(n,C);xlabel('n');ylabel('C');grid on;title('序列的运算'); subplot(2,2,4);stem(n,D);xlabel('n');ylabel('D');grid on; figure(2); subplot(3,1,1)stem(n,E);xlabel('n');ylabel('E');grid on;title('序列的运算'); subplot(3,1,2)stem(n,F);xlabel('n');ylabel('F');grid on; subplot(3,1,3)stem(n,G);xlabel('n');ylabel('G');grid on;2、 运行结果1231234nA1230246nB1230510nC序列的运算123-2-1.5-1-0.50nD图1 A 、B 、C 、D 的波形00.511.522.532040nE序列的运算00.511.522.530.51nF0.511.522.530200040006000nG图2 E 、F 、G 的波形3、 实验结果分析：由图1和图2可知：序列的加、减、乘、除是在n 上的对应点的加、减、乘、除，.*、./、.^也是矩阵的对应点相乘、除、乘方，对离散序列进行运算可以看作是对两个行向量的运算。