11理论力学
- 格式:doc
- 大小:281.00 KB
- 文档页数:14


第十一章动量定理动量定理、动量矩定理和动能定理统称为动力学普遍定理.§11--1 动量与冲量1、动量的概念:产生的相互作用力⑴定义:质点的质量与速度的乘积称为质点的动量,-----记为mv。
质点的动量是矢量,它的方向与质点速度的方向一致。
kgms/单位)i p v 质点系的动量()i i i i c im r m r r m m ∑∑==∑质心公式:⑵、质点系内各质点动量的矢量和称为质点系的动量。
)idr p v dt ()i i dm r dt∑注意:质量m i是不变的如何进一步简化?参考重心、形心公式。
李禄昌()i i i i c im r m r r m m ∑∑==∑) p r r cm v =质点系的动量等于质心速度与其全部质量的乘积。
求质点系的动量问题转化为求刚体质心问题。
cωv C =0v Ccωcov C2.冲量的概念:tF IF I d d IF d 物体在力的作用下引起的运动变化,不仅与力的大小和方向有关,还与力作用时间的长短有关。
用力与作用时间的乘积来衡量力在这段时间内积累的作用。
冲量是矢量,方向与常力的方向一致。
冲量的单位是N.S 。
§11-2 动量定理—-确定动量与冲量的关系由牛顿第二定律:F v m )F v m d )称为质点动量定理的微分形式,即质点动量的增量v v ~ ⎰==-21d 12t t It F v m v m称为质点动量定理的积分形式,即在某一时间间隔⎰==-21d 12t t It F v m v m 2、质点系的动量定理(F (F外力:,内力:(F (F M FF F v tF F v i i d )(∑+)()(d d d e ie i It F p ∑=∑=)(d d e i F tp ∑=称为质点系动量定理的微分形式,即质点系动量的质点系动量对时间的导数等于作用于质点系的外力的矢量和(主矢)动力学与静力学联系。
)(112e ini Ip p =∑=-p p ~ 称为质点系动量定理的积分形式,即在某一时间)(d d e xx F tp ∑=)(d d e yy Ftp ∑=)(d d e z z F tp ∑=动量定理微分形式的投影式:动量定理积分形式的投影式:)(12e xx x Ip p ∑=-)(12e yy y Ip p ∑=-)(12e zz z Ip p ∑=-动量定理是矢量式,在应用时应取投影形式。


第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。
(×)2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。
(√)3. 质点系动量矩的变化与外力有关,与内力无关。
(√)4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。
(√)5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。
(×)6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。
(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)8. 如图所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+ 2213ml mr =+,式中m 为AB 杆的质量。
(×)9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式,而不需附加任何条件。
(×)10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。
(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。
5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。




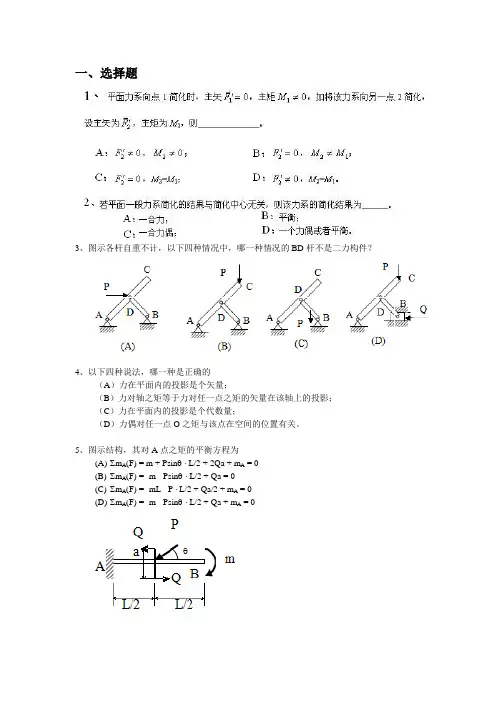
一、选择题3、图示各杆自重不计,以下四种情况中,哪一种情况的BD杆不是二力构件?4、以下四种说法,哪一种是正确的(A)力在平面内的投影是个矢量;(B)力对轴之矩等于力对任一点之矩的矢量在该轴上的投影;(C)力在平面内的投影是个代数量;(D)力偶对任一点O之矩与该点在空间的位置有关。
5、图示结构,其对A点之矩的平衡方程为(A)∑m A(F) = m + Psinθ⋅ L/2 + 2Qa + m A = 0(B)∑m A(F) = -m - Psinθ⋅ L/2 + Qa = 0(C)∑m A(F) = -mL - P ⋅ L/2 + Qa/2 + m A = 0(D)∑m A(F) = -m - Psinθ⋅ L/2 + Qa + m A = 06、作用在刚体上的力F对空间内一点O的矩是(A)一个通过O点的固定矢量;(B)一个代数量;(C)一个自由矢量;(D)一个滑动矢量。
7、已知物块重为P,放在地面上,物块与地面之间有摩擦,其摩擦角为ϕm=20︒,物块受图示Q力的作用,若Q=P,以下四种情况,哪一种说法是正确的。
8、点沿图示螺旋线自外向内运动,它走过的弧长与时间的一次方成正比,则该点(A)越跑越快;(B)越跑越慢;(C)加速度越来越大;(D)加速度越来越小。
9、点作曲线运动时,(A)若始终有v⊥a,则必有∣v∣ = 常量(B)若始终有v⊥a,则点必作匀速圆周运动(C)不可能存在某瞬时有v//a(D)若某瞬时v = 0,则其加速度a必等于零10、刚体作定轴转动时(A) 其上各点的轨迹必定为一圆;(B) 某瞬时其上任意两点的法向加速度大小与它们到转轴的垂直距离成反比;(C) 某瞬时其上任意两点的加速度方向互相平行;(D) 某瞬时在与转轴垂直的直线上的各点的加速度方向互相平行。
11、平移刚体上点的运动轨迹,(A) 必为直线;(B) 必为平面曲线;(C) 不可能是空间曲线;(D) 可能是空间曲线。
12、图示机构中,直角形杆OAB在图示位置的角速度为ω,其转向为顺时针向。

13.1 半径为R 的均质圆轮质量为m ,图a ,b 所示为圆轮绕固定轴O 转动,角速度为ω,图c 所示为圆轮在水平面上作纯滚动,质心速度为v 。
试分别计算它们的动能。
解:(a )圆轮绕固定轴O 转动,动能为 22223,21mR mR J J J T C O O =+==ω导得 243mR T = (b )圆轮绕固定轴O 转动,动能为2221,21mR J J T O O ==ω导得 241mR T = (c )圆轮在水平面上作纯滚动,由König 定理,动能为22221,,2121mR J R v J mv T C C ==+=ωω导得 243mR T =13.2 图示均质杆长l ,质量m ,绕点O 转动的角速度为ω,均质圆盘半径为R ,质量m 与杆相同,求下列三种情况下系统的动能:(a )圆盘固结于杆;(b )圆盘绕轴A 转动,相对于杆的角速度为ω-;(c )圆盘绕轴A 转动,相对于杆的角速度为ω。
解:(a )圆盘固结于杆,则圆盘的运动为绕点O 转动,角速度为ω,则系统动能为 222221222121,121,2121ml mR ml J J ml J J J T A +=+==+=ωω导得 22212132121ωm l R T ⎪⎭⎫ ⎝⎛+=(b )圆盘绕轴A 转动,相对于杆的角速度为ω-,则圆盘的绝对角速度等于零,则系统动能为l v ml J mv J T A A ωω==+=,121,212121221导得 222413ωml T = (c )圆盘绕轴A 转动,相对于杆的角速度为ω,则圆盘的绝对角速度等于2ω,则系统动能为()l v mR J ml J J mv J T A A ωωω===++=,21,121,2212121222122221导得 2222121321ωm R l T ⎪⎭⎫ ⎝⎛+= 13.3 输送器A 以10m/s 的速度沿轨道运动如图示,其上用轻杆吊一重450N 、半径为0.3m 的均质圆盘。
若圆盘以5rad/s 的角速度转动,试计算圆盘在此瞬时的动能。
解:均质圆盘作平面运动。
C (基点A ):i v v v )(A CA A C l v ω+=+=圆盘动能:m N 5.62762121)(212121222A 2C 2C ⋅=++=+=ωωωr g W l v g W J mv T13.4 均质杆CD 和EA 分别重50N 和80N ,铰接于点B 。
若杆EA 以2rad/s =ω绕A 转动,试计算图示位置两杆的动能。
解:B (基点D ):BD D B v v v +=m/s)(34.13B D ==v vm /s)(8.22B BD ==v v ,rad/s)(314CD =ωO 点为CD 杆的瞬心,)m/s (37.01CD C 1=ω=OC v则 )m N (44.5131212AE AE AE ⋅=ω=g W T )m N (50.79.012121212CD 2CD 2C CD CD 1⋅=ω+=g W v g W T13.5 图示机构中,曲柄OB 以r/min 0003=ω转动。
设m 6.03==r l ,杆AB 重2N ,求θ为任意位置时连杆AB 的动能,并计算 30=θ和 60时的数值。
解:设多余坐标ϕ,与θ存在以下关系θ=ϕcos sin r l 则有ωϕθ-=ϕ)cos /sin (r l 因 ϕ-θ=sin )2/(cos C l r x ,ϕ+θ=cos )2/(sin C l r y可得)sin()2/()(222C 2C 2C ϕ-θϕθ+ϕ+θ=+= rl l r y x v]cos /)sin(sin )cos /(sin 311[211212*********C AB ϕϕθθϕθωϕ--+=+=r g W l gW v g W Tm)N (91.9|30AB ⋅==θ Tm)N (92.5|60AB ⋅==θ T13.6 重量为W 的鼓轮沿水平面做纯滚动如图示,拉力F 与水平面成 30角。
轮子与水平面之间的静摩擦因数为s f 滚阻系数为δ,求轮心C 移动距离为x 的过程中力的功。
其中r R 2=。
解:受力分析:作用与鼓轮的外作用力系为重力、拉力、地面法向约束力、滑动摩擦力和滚阻力偶,如图所示。
因为0=C y ,所以 030sin N =+-F W F ()()30sin ,30sin ,30sin T N F W M F W f F F W F -=-=-=δ 拉力所做的功(将力向轮心简化,得到一力和一力偶): R x Frx F A +⋅= 30cos F滑动摩擦力所做的功: 0T T F T =+-=R x RF x F A滚阻力偶所做的功: ()R x F W R x MA M 30sin --=-=δ13.7 图示机构水平放置。
均质杆AB 重量为20kg ,长为2m ,其两端铰接两质量为5kg 、半径为300mm 的相同齿轮G 和H (可看作均质圆盘)。
若在齿轮H 上作用一力偶m N 5⋅=M ,求系统由静止开始运动20s 后齿轮H 的角速度。
解:因2/B l r v ω'=ω=故 ω=ω'3.0系统:A T T =-0θ=ω+ω+ω''M r m mr l m ])(212121[21212122222 对上式求导,注意到ω=θ ,α=ω,导出 2rad/s 564.2=α齿轮H 的角加速度α为常值,则角速度ω为rad/s 28.51=α=ωt13.8 一复摆绕点O 转动如图示,点O 离开其质心O '的距离为x 为何值时,摆从水平位置无初速地转到铅垂位置时的角速度为最大?并求此最大角速度。
解:复摆:A T T =-0mgx J x m =ω+ω'2O 221)(21 解出)/(2O 22'+=ωJ mx mgx令 0)/()(2/2O 22O 2=+-=∂ω∂''J mx mx J mg x求得 2O O 2''ρ==m J mx即O 'ρ=x 时ω有极值:O /'ρ=ωg因为 0)/()3(4/3O 2O 2222<+--=∂ω∂''J mx J mx gx m x 此ω为最大角速度。
13.9 等长、等重的三根均质杆用理想铰链连接,在铅垂平面内摆动。
求自图示位置无初速释放时杆AB 中点C 的加速度,以及运动到平衡位置时C 的速度。
设杆长m 1=l 。
解:系统:A T T =-0)cos (cos 2)(21312120222θ-θ=θ+θ⋅mgl l m ml对上式求导并令 45=θ,解出2C m/s 316.8sin 56-=θ-=θ=g l a将0=θ, 450=θ代入动能定理,求得 m/s 625.25/)22(6C -=--=θ=gl l v13.10 绕水平轴O 转动的滑轮上放一软链如图示。
稍有扰动时,软链即下滑而带动滑轮转动。
求软链脱离滑轮时的速度。
设软链重G ;滑轮重W ,半径为R ,可看作均质圆盘。
解:系统:A T T =-0)22()(212121222R R G R v R g W v g G π+π=+由上式解得 )2/()22(4W G G gR v +π+π=13.11 均质杆长l 2,在光滑水平面上从铅垂位置无初速地倒下如图示。
求其重心C 离开平面的高度为h 时的速度。
解:水平方向杆不受力作用,质心C 将铅垂下落,P 为杆速度瞬心,杆角速度为22C C //h l v PC v -==ω (1)杆AB :A T T =-0)()2(1212121222C h l mg l m mv -=ω+将式(1)代入,解得 )34/()(6)(22C h l h l g h l v -+-=13.12 将一均质半圆球放于光滑的水平和铅垂平面之间,并使其底面位于铅垂位置如图示。
今无初速地放开。
求半圆球转过 90,即当其底面位于水平位置时其质心C 的速度,并证明此后半圆球将继续侧转的最大角度)128/45arccos(=θ。
解:C (基点O ):n CO CO O C a a a a ++=τϕ+ϕ+=τcos sin n CO CO O Cx a a a a半球在转过 90过程中,0Cx >a ,由N1Cx F ma =可知01N >F ,即在此过程中半球绕O 作定轴转动:半球:A T T =-0,r mg mr 83522122=ω r g 8/15=ω,8/158383C gr r v =ω=90=ϕ(即 0=θ)后,半球作平面运动,由于水平方向无外力作用,质心水平速度保持不变。
半球:A T T =-0θ=cos 83212C r mg mv ,(0=ϕ为初始状态)解得)128/45arccos(=θ13.13 均质杆AB 长l ,重1W ,上端B 靠在光滑墙上,下端A 铰接于车轮轮心。
车轮重2W ,半径为r (可视作均质圆盘),在水平面上只能作纯滚动,滚动阻力不计。
设系统有图示位置(45=θ)开始运动,试用能量守恒定律计算此瞬时轮心A 的加速度。
解:AB 杆的速度瞬心为P ,则有θ==θcos //A A l v PA v ,θ= )2/(C l v (1)系统:const =+V T (取A 为重力势能零点)const cos 221)(2121211212112A 22A 222C 1221=θ++++θl W v g W r v r g W v g W l g W将式(1)代入上式,对时间求导得 0tg 21cos 3sin )23cos 3(112A 41A 221=θ-θθ-+θW l v g W a W W g将 45=θ,0A =v 代入上式,解出)94/(3211A W W g W a +=13.14 长l 、重W 的三根相同的均质杆用理想铰链连接如图示,在铅垂平面内运动。
一质量不计、刚度系数为k 的弹簧,一端与BC 杆的中点E 连接,另一端可沿光滑铅垂导槽滑动。
杆AB 和CD 与墙垂直时,弹簧不变形。
求系统在此瞬时有静止释放时杆AB 的角加速度。
解:系统为一自由度,设θ为广义坐标。
系统:A T T =-0 202022022)]cos 1([21)sin (sin 2])()[(21)(31212θθθθθθθ---=-+-⋅l k Wl l l g W l g W将上式对时间求导,导出 θθ--θ=θsin )cos 1(cos 2352kl Wl l g W将 0=θ代入上式,解得l g 5/6=θ13.15 一台阶圆柱大、小圆半径分别为1.3m 和0.6m ,质量为36kg ,对于转动轴的回转半径为1m 。