新同步课课精练 数学 高一年级(上)答案

C. 5D. 9A级：“四基”巩固训练一、选择题1. 已知集合S= {a, b, c}中的三个元素是厶ABC的三边长，那么△ ABC —定不是（）A .锐角三角形B.直角三角形C.钝角三角形D.等腰三角形答案D解析因为集合S= {a, b, c}中的元素是△ ABC的三边长，由集合元素的互异性可知a, b, c互不相等，所以△ ABC 一定不是等腰三角形.故选 D.2. 下列集合的表示方法正确的是（）A. 第二、四象限内的点集可表示为{（x, y）|xy W0, x€ R, y€ R}B. 不等式x- 1v4的解集为{x v5}C. {全体整数}D. 实数集可表示为R答案D解析A中应是xy<0; B中的本意是想用描述法表示，但不符合描述法的规范格式，缺少了竖线和竖线前面的代表元素x,应为{x|x<5} ; C中的“{ } ”与“全体”意思重复.故选D.3. 下列集合恰有两个元素的是（）2 2A. {x2-x= 0}B. {x|y=x2-x}C. {y|y2—y= 0}D. {y|y=x2-x}答案C解析A为一个方程集，只有一个元素；B为方程y= x2—x的定义域，有无数个元素；C为方程y2—y= 0的解，有0,1两个元素；D为函数y=x2—x的值域，有无数个元素.故选C.4. 已知集合A= {0,1,2}，则集合B = {x—y|x€ A,y€ A}中元素的个数是（）A. 1B. 3答案C解析根据已知条件，列表如下:根据集合中元素的互异性，由上表可知B= {0 , - 1,—2, 1,2}，因此集合B中共含有5个元素•故选C.5•若2?{xX—a>0}，贝U实数a的取值范围是（）A. a^2B. a>2C. a>2D. a= 2答案C解析因为2?{x|x—a>0}，所以2不满足不等式x—a>0，即满足不等式x—a<0,所以 2 —a<0,即a>2,故选 C.二、填空题6. ____________________________________________________________若A= { —2,2,3,4}, B = {x|x= t, t € A}，则用列举法表示B= __________ .答案{4,9,16}解析由题意，A= { —2,2,3,4}, B = {x|x = t2, t€ A}，依次计算出B中元素，用列举法表示可得B = {4,9,16}，故答案为{4,9,16}.7. 已知集合A= {x|ax2—3x—4二0, x€ R}，若A中至多有一个元素，则实数a的取值范围是_________ .答案 a = 0或a< —164 2解析当a= 0时，A= {x|x= —3}；当a^ 0时，关于x的方程ax —3x— 4 =0应有两个相等的实数根或无实数根，所以△= 9+ 16a< 0,即a< —箱.故所求9的a的取值范围是a = 0或a w—乔.8. __________________________________________ 已知集合A中的元素均为整数，对于k€ A,如果k—1?A且k+ 1?A,那么称k是A的一个“孤立元”.给定集合S= ｛123,4,5,6,7,8｝，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有____________________________________________ .答案6解析根据“孤立元”的定义，由S的3个元素构成的所有集合中，不含“孤立元”的集合为｛1,2,3｝，｛2,3,4｝，｛3,4,5｝，｛4,5,6｝，｛5,6,7｝，｛6,7,8｝，共有6 个.故答案为6.三、解答题9. 用适当的方法表示下列集合：(1) 绝对值不大于3的偶数的集合；(2) 被3除余1的正整数的集合；(3) 一次函数y= 2x—3图像上所有点的集合；x+y= 1，⑷方程组，' 的解集.y=—1解(1)｛—2,0,2｝.(2) ｛m|m= 3n+ 1，n€ N｝.(3) ｛(x, y)|y二2x—3｝.⑷｛(0,1)｝.10. 已知集合A= ｛a+ 3，(a+ 1)2，a2+ 2a + 2｝，若1€ A，求实数a 的值.解①若a+ 3= 1，则a= —2，此时A= ｛1,1,2｝，不符合集合中元素的互异性，舍去.②若(a+ 1)2= 1，贝U a = 0 或a= —2.当a= 0时，A= ｛3,1,2｝，满足题意；当a= —2时，由①知不符合条件，故舍去.③若 a + 2a + 2 = 1，则a= —1，此时A= ｛2,0,1｝，满足题意.综上所述，实数a的值为—1或0.B级：“四能”提升训练1 .已知集合 A= {xX = 3n + 1, n € Z }, B = {xX = 3n + 2, n € Z } , M = {x|x = 6n + 3, n € Z }.⑴若m € M ，则是否存在a € A , b € B ,使m = a + b 成立？(2)对于任意a € A , b € B ,是否一定存在 m € M ，使a + b = m ?证明你的结 论. 解 ⑴设 m = 6k + 3= 3k + 1 + 3k + 2(k € Z ), 令 a = 3k + 1, b = 3k + 2,贝U m = a + b.故若m € M ，贝U 存在a € A , b € B , 使 m = a + b 成立. (2)不一定.证明如下：设 a = 3k + 1, b = 3l + 2, k , l € Z ,贝U a + b = 3(k +1)+ 3. 当 k +1 = 2p(p € Z )时，a + b = 6p + 3€ M , 此时存在m € M ，使a + b = m 成立；当 k +1 = 2p + 1(p € Z )时，a + b = 6p + 6?M ，此时不存在 m € M ，使 a + b = m 成立.故对于任意a € A , b € B ,不一定存在 m € M ，使a + b = m. 2.设实数集S 是满足下面两个条件的集合：1①1?S;②若a € S ,贝U € S.1- a1(1) 求证：若 a € S ,贝U 1--€ S;a(2) 若 2€ S ,则S 中必含有其他的两个数，试求出这两个数； (3) 求证：集合S 中至少有三个不同的元素. 解 ⑴证明：••• 1?S,.・. 0?S ,即a M 0. 1 1由a € S,贝U € S 可得1 — € S , 1-a “ 11-1-a1故若a € S,贝U 1-匚€ S.a11-1-a1-a 1-a -11⑵由2€ S,知口 =- 1€ S;1 1由一1€ S,知=沙S,1 —(—1)21 1当扌€ S时，十二2€ S,1 — 21因此当2€ S时，S中必含有一1和㊁1 1(3)证明：由(1), 知a€ S,厂€ S,1—-€ S.I —a a1 1下证：a，三，1-a三者两两互不相等.1 2①若*仁，则a—沙1二°，无实数解,1 2②若a= 1 —a，则a2—a+ 1 = °,无实数解, a1 a；1 1 2③若二=1-1则a- a+仁°，无实数解,丄工1—11—a a'综上所述，集合S中至少有三个不同的元素.。

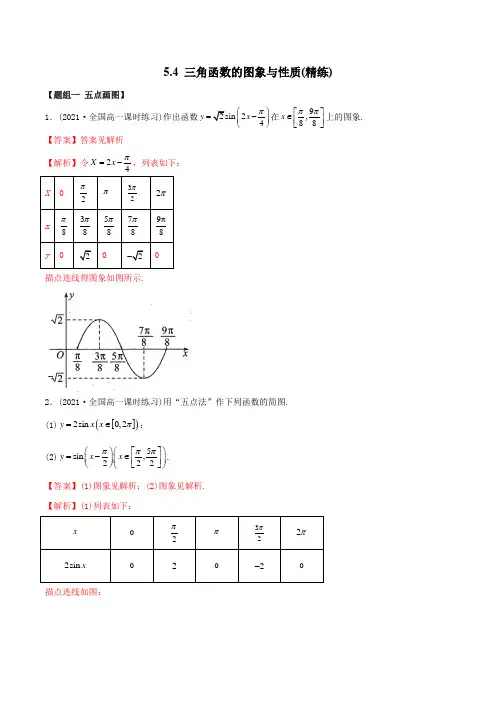
5.4 三角函数的图象与性质(精练)【题组一 五点画图】1．(2021·全国高一课时练习)作出函数24y x π⎛⎫=- ⎪⎝⎭在9,88x ππ⎡⎤∈⎢⎥⎣⎦上的图象.【答案】答案见解析 【解析】令2X x π=-，列表如下：描点连线得图象如图所示.2．(2021·全国高一课时练习)用“五点法”作下列函数的简图. (1)[]()2sin 0,2y x x π=∈；(2)5sin ,222y x x πππ⎛⎫⎛⎫⎡⎤=-∈ ⎪⎪⎢⎥⎝⎭⎣⎦⎝⎭.【答案】(1)图象见解析；(2)图象见解析. 【解析】(1)列表如下：描点连线如图：(2)列表如下：描点连线如图：3．(2021·全国)已知函数()2cos 1f x x =-.(1)完成下列表格，并用五点法在下面直角坐标系中画出()f x 在[]0,2π上的简图；(2)求不等式()1f x ≤的解集.【答案】(1)答案见解析；(2)572,266k k ππππ⎡⎤++⎢⎥⎣⎦(k Z ∈). 【解析】(1)由函数()2cos 1f x x =-，可得完成表格如下：可得()f x 在[]0,2π的大致图象如下：(2)由()1f x ≤，可得2cos 11x -≤，即cos x ≤，当[]0,2x π∈时，由cos x ≤，得57,66x ππ⎡⎤∈⎢⎥⎣⎦.又由函数cos y x =的最小正周期为2π，所以原不等式的解集为572,266k k ππππ⎡⎤++⎢⎥⎣⎦(k Z ∈). 【题组二 解三角不等式】1．(2021·全州县第二中学高一期中)使得sin cos x x >正确的一个区间是( ) A ．2ππ⎛⎫⎪⎝⎭，B ．342ππ⎛⎫ ⎪⎝⎭，C ．04π⎛⎫ ⎪⎝⎭，D ．64ππ⎛⎫ ⎪⎝⎭，【答案】A【解析】作出sin y x =与cos y x =的图象，如图：由图可知，若sin cos x x >，其中2ππ⎛⎫⎪⎝⎭，满足，故选：A2．(2021·上海市洋泾中学高一月考)满足2sin 13x π⎛⎫-= ⎪⎝⎭，[0,2)x π∈的角x 的集合___________.【答案】7,26ππ⎧⎫⎨⎬⎩⎭【解析】由2sin 13x π⎛⎫-= ⎪⎝⎭得，1sin 32x π⎛⎫-= ⎪⎝⎭，因为[0,2)x π∈，所以5333x πππ-≤-<.当5333x πππ-≤-<时， 若1sin 32x π⎛⎫-= ⎪⎝⎭，则3x π-可能的取值为6π，56π，相应的x 的取值为2π，76π.所以所求角x 的集合为7,26ππ⎧⎫⎨⎬⎩⎭.故答案为：7,26ππ⎧⎫⎨⎬⎩⎭.3．(2021·上海)函数sin 1cos xy x=+的定义域为______.【答案】{}2,x x k k ππ≠+∈Z【解析】要使函数有意义，则1cos 0x +≠， 即cos 1x ≠-，所以()2x k k ππ≠+∈Z . 故答案为：{}2,x x k k ππ≠+∈Z .4．(2021·陕西榆林十二中高一月考)若()0,x π∈，则满足2sin 2x 的x 的取值范围为______________； 【答案】30,,44πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭【解析】当()0,x π∈时，令2sin 2x，解得4x π=或34π，结合正弦函数的图象与性质，可得当0,x时，2sin 2x的解集为30,,44πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭. 故答案为：30,,44πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭5．(2021·全国高一课时练习)求函数的定义域：(1)tan 4y x π⎛⎫=+ ⎪⎝⎭；(2)y【答案】(1),4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭；(2),23x k x k k Z ππππ⎧⎫-<≤+∈⎨⎬⎩⎭.【解析】(1)由()42x k k Z πππ+≠+∈得：,4x k k Z ππ≠+∈，∴函数tan 4y x π⎛⎫=+ ⎪⎝⎭的定义域为,4x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭．(2)tan 0x ≥得：tan x ≤结合tan y x =的图象知：在,22ππ⎛⎫- ⎪⎝⎭上，满足tan x ≤x 应满足23x ππ≤-<，∴y =,23x k x k k Z ππππ⎧⎫-<≤+∈⎨⎬⎩⎭． 【题组三 周期】1．(2021·全国高一课时练习)下列函数是周期函数的有( ) ①sin y x = ②cos y x = ③2y xA ．①③B ．②③C ．①②D ．①②③【答案】C【解析】易得sin y x =和cos y x =是周期函数，2yx 不是周期函数.故选：C.2．(2021·镇远县文德民族中学校高一月考)函数()sin 26f x x π⎛⎫=- ⎪⎝⎭的最小正周期是( )A ．2πB ．πC ．2πD ．4π【答案】B【解析】由题意，函数()sin 26f x x π⎛⎫=- ⎪⎝⎭，根据正弦型函数的周期的计算方法，可得()f x 最小正周期为22T ππ==.故选：B. 3．(2021·全国高一课时练习)函数cos 3y x π⎛⎫=+ ⎪⎝⎭的最小正周期是( )A ．4πB ．2πC ．πD ．2π【答案】B【解析】因为cos 3y x π⎛⎫=+ ⎪⎝⎭，所以其最小正周期为221T ππ==,故选:B.4．(2021·北京丰台·高一期中)函数()cos 2f x x =的图象中，相邻两条对称轴之间的距离是( ) A ．2π B ．πC ．π2D ．π4【答案】C【解析】函数的最小正周期是22T ππ==，因此相邻两条对称轴之间的距离是22T π=． 故选：C ．5．(2021·北京通州区·)已知函数：①tan y x =，②sin y x =，③sin y x =，则其中最小正周期为π的是( ) A ．①② B ．①③C ．②③D ．①②③【答案】B【解析】①tan y x =最小正周期为π②sin y x =的图象，在y 轴右侧部分与sin y x =一样，又因为其为偶函数，图象关于y 轴对称，由图象可知它不是周期函数.③sin y x =的图象，可由sin y x =的图象，保持x 轴上半部分不变，x 轴下半部分图象向上翻折得到. 由图象可知，其最小正周期为π故选：B.6．(2021·蚌埠田家炳中学高一月考)(多选)下列函数中，最小正周期为π的是( ) A ．cos |2|y x =B ．|cos |y x =C ．cos 26y x π⎛⎫=+ ⎪⎝⎭D ．tan 24y x π⎛⎫=- ⎪⎝⎭【答案】ABC【解析】对于A ，cos |2|cos 2,y x x ==最小正周期为22T ππ==；对于B ，|cos |y x ==22T ππ==； 对于C ，cos 26y x π⎛⎫=+ ⎪⎝⎭，最小正周期为22T ππ==； 对于D ，tan 24y x π⎛⎫=- ⎪⎝⎭，最小正周期为2T π=，故选 ：ABC7．(2021·齐河县第一中学高一期中)(多选)下列函数周期为π的是( ) A ．sin y x = B ．cos y x =C ．tan y x =D ．2sin 24y x π⎛⎫=+ ⎪⎝⎭【答案】BCD【解析】sin y x =的最小正周期为2π；由cos y x =的图象是由y =cos x 的图象将x 轴上方的部分保持不变，下方的部分向上翻转而得到，由图象可知其周期为π；tan y x =的最小正周期为π；2sin 24y x π⎛⎫=+ ⎪⎝⎭的最小正周期为22ππ=.故选：BCD. 【题组四 奇偶性】1．(2021·池州市江南中学高一期末)下列函数中，最小正周期是π且是奇函数的是( ) A ．sin 2y x = B ．sin y x =C ．tan2xy = D ．cos 2y x =【答案】A【解析】A 选项，sin 2y x =的最小正周期是π，且是奇函数，A 正确. B 选项，sin y x =的最小正周期是2π，且是奇函数，B 错误.C 选项，tan2xy =的最小正周期为2π，且是奇函数，C 错误. D 选项，cos y x =的最小正周期是π，且是偶函数，D 错误. 故选：A2．(2021·陕西高一期末)下列函数为奇函数的是( ) A ．2cos y x x =+ B ．|sin |y x =C ．2sin y x x =D ．cos tan y x x =-【答案】C【解析】A.函数的定义域为R ，满足()()f x f x -=，所以函数是偶函数，故错误； B. 函数的定义域为R ，满足()()f x f x -=，所以函数是偶函数，故错误； C. 函数的定义域为R ，满足()()f x f x -=-，所以函数是奇函数，故正确；D. 函数的定义域为,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭，函数既不满足()()f x f x -=，也不满足()()f x f x -=-，所以函数既不是奇函数，也不是偶函数，故错误. 故选：C3．(2021·青海西宁·湟川中学高一开学考试)下列函数中，最小正周期为π，且为偶函数的是( )A ．tan 3y x π⎛⎫=+ ⎪⎝⎭B ．cos 22y x π⎛⎫=+ ⎪⎝⎭C ．sin 2y x =D ．sin y x =【答案】D【解析】A. tan 3y x π⎛⎫=+ ⎪⎝⎭的最小正周期为π，是非奇非偶函数，故错误；B. cos 2sin 22y x x π⎛⎫=+=- ⎪⎝⎭的最小正周期为π，是奇函数，故错误；C.如图所示：，sin 2y x =不周期函数，为偶函数，故错误；D. 如图所示：，sin y x =的最小正周期为π，是偶函数，故正确； 故选：D4．(2021·黑龙江绥化·)下列函数中，最小正周期为π，且为偶函数的有( ) A ．πtan 3y x ⎛⎫=- ⎪⎝⎭B ．πsin 22y x ⎛⎫=+ ⎪⎝⎭C ．sin 2y x =D ．sin y x =【答案】D【解析】πtan 3y x ⎛⎫=- ⎪⎝⎭的最小正周期为π，不是偶函数，A 不满足条件．cos 2πsin 22y x x ⎛⎫=+ ⎪=⎝⎭的最小正周期为2π，B 不满足条件．根据sin |2|y x =为偶函数，不是周期函数，C 不满足条件．根据()sin f x x ==π，且()()f x f x -=为偶函数，D 满足条件． 故选：D ．5．(2021·北京市昌平区实验学校高一期中)下列函数是奇函数的是( ) A ．()cos f x x x =+ B ．()2cos f x x x =+C ．()sin f x x x =+D ．()2sin f x x x =+【答案】C【解析】选项A. ()()11cos111cos1f f =+-=-+， 显然()()11f f ≠--，所以()f x 不是奇函数. 选项B. ()()()()22cos cos f x x x x x f x -=-+-=+=显然()()f x f x -≠-，所以()f x 为偶函数，不是奇函数. 选项C. ()()()()()sin sin f x x x x x f x -=-+-=-+=- 所以()f x 是奇函数.选项D. ()()11sin111sin1f f =+-=-， 显然()()11f f ≠--，所以()f x 不是奇函数. 故选：C6．(2021·上海)若函数()ππ2sin sin 44f x x m x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭是偶函数，则m =___________.【答案】2-【解析】因为函数为偶函数，则44f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭，所以ππππ2sin sin 2sin sin 44444444m m ππππ⎛⎫⎛⎫⎛⎫⎛⎫++-=-++-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，整理得200m +=-，解得2m =-，经检验，m 的值符合题意 故答案为: 2-. 【题组五 单调性】1．(2021·全国)函数()sin ,[,0]3f x x x ππ⎛⎫=-∈- ⎪⎝⎭的单调递增区间是( )A ．5,6ππ⎡⎤-⎢⎥⎣⎦B ．5,66ππ⎡⎤--⎢⎥⎣⎦ C ．,03π⎡⎤-⎢⎥⎣⎦ D ．,06π⎡⎤-⎢⎥⎣⎦【答案】D 【解析】由22,232k x k k Z πππππ-≤-≤+∈，解得522,66k x k k Z ππππ-≤≤+∈， 又0x π-≤≤，∴06x π-≤≤.所以函数()f x 的单调递增区间为,06π⎡⎤-⎢⎥⎣⎦.故选：D.2．(2021·全国)函数sin 24y x π⎛⎫=- ⎪⎝⎭的单调增区间是( )A ．3,()88k k k Z ππππ⎡⎤---+∈⎢⎥⎣⎦B ．32,2()88k k k Z ππππ⎡⎤---+∈⎢⎥⎣⎦C ．37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．372,2()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【答案】C【解析】因为sin 24y x π⎛⎫=- ⎪⎝⎭，所以sin 24y x π⎛⎫=-- ⎪⎝⎭，令3222,242k x k k Z πππππ+≤-≤+∈，解得37,88k x k k Z ππππ+≤≤+∈，故函数的单调递增区间为37,()88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦故选：C3．(2021·全国)下列函数中，周期为π，且在,42ππ⎡⎤⎢⎥⎣⎦上为减函数的是( )A ．y ＝sin (2)2x π+B ．y ＝cos (2)2x π+C ．y ＝sin ()2x π+D ．y ＝cos ()2x π+【答案】A【解析】对于选项A ，y ＝sin (2)2x π+＝cos 2x ，周期为π，当42ππx ≤≤时，22x ππ≤≤，所以cos 2y x =在[,]42ππ上是减函数，所以该选项正确；对于选项B ，y ＝cos 2sin 22x x π⎛⎫+=- ⎪⎝⎭，周期是π，在[,]42ππ上是增函数，所以该选项错误；对于选项C ，y ＝sin ()cos 2x x π+=，最小正周期是2π，所以该选项错误；对于选项D ，y ＝cos ()sin 2x x π+=-，最小正周期是2π，所以该选项错误.故选：A4．(2021·河南新乡县高中高一月考)函数()π2cos 3f x x ⎛⎫=- ⎪⎝⎭的单调递增区间是( )A ．π4π2π,2π(Z)33k k k ⎡⎤++∈⎢⎥⎣⎦B ．π2π2π,2π(Z)33k k k ⎡⎤++∈⎢⎥⎣⎦C ．2ππ2π,2π(Z)33k k k ⎡⎤-+∈⎢⎥⎣⎦D ．2π4π2π,2π(Z)33k k k ⎡⎤-+∈⎢⎥⎣⎦【答案】C【解析】()ππ2cos 2cos 33f x x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭，令()ππ+2π2πZ 3x k k k -≤≤-∈， 解得：()+2π2πZ 2ππ+33x k k k ≤-≤∈， 所以函数()π2cos 3f x x ⎛⎫=- ⎪⎝⎭的单调递增区间为2ππ2π,2π(Z)33k k k ⎡⎤-+∈⎢⎥⎣⎦即函数()π2cos 3f x x ⎛⎫=- ⎪⎝⎭的单调递增区间为2ππ2π,2π(Z)33k k k ⎡⎤-+∈⎢⎥⎣⎦，故选：C.5．(2021·安徽池州·高一期中)已知函数()()cos 06f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω的取值范围是( ) A ．(]0,1 B ．[]1,2 C ．71,2⎡⎤⎢⎥⎣⎦D ．72,2⎡⎤⎢⎥⎣⎦【答案】C【解析】72266226k k k x k x ππππππωππωω++-+⇒≤≤≤≤， 所以()()cos 06f x x πωω⎛⎫=-> ⎪⎝⎭的单调减区间为72266,k k ππππωω⎡⎤++⎢⎥⎢⎥⎢⎥⎣⎦，所以72266,,63k k ππππππωω⎡⎤++⎢⎥⎡⎤⊆⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，所以2667263k k πππωπππω⎧+⎪≤⎪⎪⎨⎪+⎪≥⎪⎩，解得121762k k ωω≥+⎧⎪⎨≤+⎪⎩，且k Z ∈，则712ω≤≤，则ω的取值范围是71,2⎡⎤⎢⎥⎣⎦，故选：C.6．(2021·湖北武汉·)若函数()2cos 2(0)3f x x πωω⎛⎫=-> ⎪⎝⎭在区间,62ππ⎛⎫⎪⎝⎭内単调递减.则ω的最大值为( ) A ．23B ．34C ．43D ．32【答案】C【解析】()2cos 22cos 2(0)33f x x x ππωωω⎛⎫⎛⎫=-=-> ⎪ ⎪⎝⎭⎝⎭当,62x ππ⎛⎫∈ ⎪⎝⎭且0>ω时，23333x πωπππωπω-<-<-，因为余弦函数cos y x =的单调递减区间为[]()2,2k k k Z πππ+∈，所以，[](),2,2333k k k Z πωπππωπππ⎛⎫--⊆+∈⎪⎝⎭， 所以，23323k k πωππππωππ⎧-≥⎪⎪⎨⎪-≤+⎪⎩，解得()46123k k k Z ω+≤≤+∈，由42613k k +≥+，可得112k ≤，k Z ∈且0>ω，0k ∴=，413ω≤≤. 因此，ω的最大值为43.故选：C7．(2021·安徽蚌埠·高一期末)已知函数()sin (0)f x x ωω=>在3,44ππ⎡⎤-⎢⎥⎣⎦上单调递增，则ω的取值范围是( ) A ．[)2,+∞ B ．(]0,2C ．2,3⎡⎫+∞⎪⎢⎣⎭D ．20,3⎛⎤⎥⎝⎦【答案】D 【解析】当22()22k x k k Z πππωπ-≤≤+∈时，因为0>ω，所以有11(2)(2)()22k x k k Z ππππωω-⋅≤≤+⋅∈，因此函数()sin (0)f x x ωω=>的递增区间为：2222[,]()k k k Z ππππωω-+∈，因为函数()sin (0)f x x ωω=>在3,44ππ⎡⎤-⎢⎥⎣⎦上单调递增，所以令0k =，且有32424ππωππω⎧⎪≤⎪⎪⎨⎪-⎪-≥⎪⎩，因为0>ω，所以解得：203ω<≤，故选：D8．(2021·北京市第六十六中学)函数()cos f x x =是( ) A ．奇函数，且在区间0,2π⎛⎫⎪⎝⎭上单调递增B ．奇函数，且在区间0,2π⎛⎫⎪⎝⎭上单调递减C ．偶函数，且在区间0,2π⎛⎫⎪⎝⎭上单调递增D ．偶函数，且在区间0,2π⎛⎫⎪⎝⎭上单调递减【答案】D【解析】由题意，函数()cos f x x =的定义域R ，且()()cos()cos f x x x f x -=-==， 所以函数()cos f x x =为偶函数，又由余弦函数的性质，可得()cos f x x =在区间0,2π⎛⎫⎪⎝⎭为递减函数.故选：D.9．(2021·全国)函数()2cos (0)4f x x πωω⎛⎫=+> ⎪⎝⎭在3,24ππ⎛⎫⎪⎝⎭上单调递减，则ω的最大值是( )A ．1B ．114C ．113D ．4【答案】C【解析】因为函数()2cos (0)4f x x πωω⎛⎫=+> ⎪⎝⎭在3,24ππ⎛⎫⎪⎝⎭上单调递减，所以314242T ππππω-=≤=，所以04ω<≤. 所以33,,,2424444x x πωππππππωω+∈⎛⎫⎛⎫∈++ ⎪ ⎪⎝⎭⎝⎭因为cos y x =的单调递减区间为[]2,2,k k k Z πππ+∈，所以2243244k k ππωπππωππ⎧+≥⎪⎪⎨⎪+≤+⎪⎩，解得1841,23k k k Z ω-+≤≤+∈，由于1841,23k k k Z -+≤+∈，故9,8k k Z ≤∈.所以当1k =时，得ω的最大区间：71123ω≤≤. 故ω的最大值是113. 故选：C.10(2021·兴仁市凤凰中学高一期末)函数tan(2)4y x π=-+的单调递减区间为_______________.【答案】3(,),2828k k k Z ππππ-+∈ 【解析】由题意可知tan(2)4y x π=--，则要求函数的单调递减区间只需求tan(2)4y x π=-的单调递增区间，由2,242k x k k Z πππππ-<-<+∈得3,2828k k x k Z ππππ-<<+∈，所以函数tan(2)4y x π=-+的单调递减区间为3(,),2828k k k Z ππππ-+∈. 故答案为：3(,),2828k k k Z ππππ-+∈. 【题组六 对称性】1．(2021·湖北十堰·)函数()43f x cos x ππ⎛⎫=- ⎪⎝⎭图象的一条对称轴可能是直线x =( )A ．53-B ．13- C ．3πD ．43π【答案】A 【解析】令(3)Z x k k πππ-=∈，解得()1Z 3k x k =+∈. 当2k =-时，53x =-.故选：A.2．(2021·北京市第六十六中学)如果函数()cos y x ϕ=+的一个零点是3π，那么ϕ可以是( ) A ．6π B ．6π-C ．3π D ．3π-【答案】A【解析】由题意，函数()cos y x ϕ=+的一个零点是3π，可得3cos()0πϕ+=，即,32k k Z ππϕπ+=+∈，解得,6k k Z πϕπ=+∈，当0k =时，可得6π=ϕ. 故选：A.3．(2021·河南(理))若函数()()sin f x x ϕ=+(()0,ϕπ∈)图象的一条对称轴为6x π=，则ϕ=( )A ．6π B ．3π C ．23π D ．56π 【答案】B 【解析】由题意知62k ππϕπ+=+(k ∈Z )，则3k πϕπ=+(k ∈Z )， 当0k =时，3πϕ=，符合题意，其它都不满足题意.故选：B.4．(2021·齐河县第一中学高一月考)tan(2)4y x π=+的对称中心为( )A ．,0),28k k Z ππ+∈( B ．(,0),28k k Z ππ-∈ C ．(,0),48k k Z ππ+∈ D ．(,0),48k k Z ππ-∈ 【答案】D【解析】由()tan f x x =的对称中心为(0),2k π， 令242k x ππ+=，可得48k x ππ=-()k ∈Z . 故选：D5．(2021·山西实验中学高一开学考试)(多选)下列关于函数n 3ta y x π+=⎛⎫ ⎪⎝⎭的说法错误的是( )A ．在区间5,66ππ⎛⎫- ⎪⎝⎭上单调递增 B ．最小正周期是πC ．图象关于点,04π⎛⎫⎪⎝⎭成中心对称 D ．图象关于直线6x π=成轴对称【答案】ACD【解析】A 项：令232k x k πππππ-<+<+，即()656k x k k Z ππππ<<+∈-，函数n 3ta y x π+=⎛⎫ ⎪⎝⎭的单调递增区间为()65,6k k k Z ππππ⎛⎫+ ⎪⎭-∈⎝，A 错误； B 项：最小正周期1T ππ==，B 正确；C 项：令32k x ππ+=，即()32k x k Z ππ=-+∈， 函数n 3ta y x π+=⎛⎫ ⎪⎝⎭关于点(),032k k Z ππ⎛⎫-+∈ ⎪⎝⎭成中心对称，C 错误； D 项：正切函数没有对称轴，则函数n 3ta y x π+=⎛⎫ ⎪⎝⎭也没有对称轴，D 错误，故选：ACD.6．(2021·浙江高一期末)(多选)下列关于函数tan 23y x π⎛⎫=-+ ⎪⎝⎭的说法正确的是( )A ．在区间,312ππ⎛⎫-- ⎪⎝⎭上单调递增 B ．最小正周期是2πC ．图象关于点5,012π⎛⎫⎪⎝⎭成中心对称 D ．图象关于直线12x π=-成轴对称【答案】BC【解析】tan 2tan(2)33y x x ππ⎛⎫=-+=-- ⎪⎝⎭，令2,232k x k k Z πππππ-+<-<+∈，得5,122122k k x k Z ππππ-+<<+∈，∴1k =-时，71212x ππ-<<-，所以tan 23y x π⎛⎫=-+ ⎪⎝⎭在,312ππ⎛⎫-- ⎪⎝⎭上单调递减，A 错误.由上知：最小正周期为2T π=，B 正确.当512x π=时有232x ππ-=，所以tan 23y x π⎛⎫=-+ ⎪⎝⎭关于点5,012π⎛⎫⎪⎝⎭成中心对称，C 正确.由正切函数的性质知：正切函数无对称轴，D 错误. 故选：BC7．(2021·陕西咸阳·高一期末)函数tan 26y x π⎛⎫=+ ⎪⎝⎭的对称中心为__________.【答案】,0,412k k Z ππ⎛⎫-∈ ⎪⎝⎭ 【解析】由正切函数性质，令262k x ππ+=，可得412k x ππ=-()k ∈Z . ∴函数tan 26y x π⎛⎫=+ ⎪⎝⎭的对称中心为,0,412k k Z ππ⎛⎫-∈⎪⎝⎭故答案为：,0,412k k Z ππ⎛⎫-∈ ⎪⎝⎭【题组七 值域】1．(2021·全国高一课时练习)若sin 23x m =+，且,66x ππ⎡⎤∈-⎢⎥⎣⎦，则m 的取值范围为( )A ．11,22⎡⎤-⎢⎥⎣⎦B ．51,42⎡⎤--⎢⎥⎣⎦C ．75,44⎡⎤--⎢⎥⎣⎦D ．71,42⎡⎤-⎢⎥⎣⎦【答案】C【解析】因为,66x ππ⎡⎤∈-⎢⎥⎣⎦，所以11sin 22x -≤≤，因为sin 23x m =+，所以112322m -≤+≤，解得7544m -≤≤-，故选：C2．(2021·陕西高一期末)已知函数()2cos 6f x x πω⎛⎫=+ ⎪⎝⎭在区间,34ππ⎛⎫- ⎪⎝⎭上的最小值小于零，则ω可取的最小正整数为( ) A ．1 B ．2C ．3D ．4【答案】D【解析】A ：1ω=，所以5,6612x ⎛⎫+∈- ⎪⎝⎭πππ，则()2cos 6f x x π⎛⎫=+ ⎪⎝⎭不存在最小值，不合题意，故A 错误；B ：2ω=，所以π22,623x ππ⎛⎫+∈- ⎪⎝⎭，则()2cos 26f x x π⎛⎫=+ ⎪⎝⎭不存在最小值，不合题意，故B 错误； C ：3ω=，所以5113,6612x ⎛⎫+∈- ⎪⎝⎭πππ，则()2cos 36f x x ⎛⎫=+ ⎪⎝⎭π不存在最小值，不合题意，故C 错误； D ：4ω=，所以774,666x ⎛⎫+∈- ⎪⎝⎭πππ，当46x +=ππ时， min ()20f x =-<，符合题意，故D 正确；故选：D.3．(2021·天水市第一中学高一期中)函数2tan 4tan 1y x x =+-的值域为____________ 【答案】[)5,-+∞【解析】因为2tan 4tan 1y x x =+- 令tan t x =，则t R ∈所以()()224125f t t t t =+-=+-，所以()[)5,f t ∈-+∞，故函数的值域为[)5,-+∞故答案为：[)5,-+∞4．(2021·上海杨浦·复旦附中高一期中)函数2()cos sin 1f x x x =++在7,46ππ⎛⎤⎥⎝⎦上的值域是___________.【答案】59,44⎡⎤⎢⎥⎣⎦【解析】()222cos sin 11sin sin 1sin sin 2f x x x x x x x =++=-++=-++令7sin ,,46t x x ππ⎛⎤=∈ ⎥⎝⎦，则1,12t ⎡⎤∈-⎢⎥⎣⎦，因为2()2f t t t =-++的对称轴方程为12t =，所以22minmax 115119()2,()2224224f t f t ⎛⎫⎛⎫=---+==-++= ⎪ ⎪⎝⎭⎝⎭所以59(),44f t ⎡⎤∈⎢⎥⎣⎦，所以59(),44f x ⎡⎤∈⎢⎥⎣⎦，所以函数2()cos sin 1f x x x =++在7,46ππ⎛⎤ ⎥⎝⎦上的值域是59,44⎡⎤⎢⎥⎣⎦，故答案为：59,44⎡⎤⎢⎥⎣⎦5．(2021·建平县实验中学)已知函数()2cos (0)6f x x πωω⎛⎫=+> ⎪⎝⎭，在[]0,π内的值域为⎡-⎣，则ω的取值范围为___________. 【答案】55,63⎡⎤⎢⎥⎣⎦【解析】函数()2cos (0)6f x x πωω⎛⎫=+> ⎪⎝⎭，当[]0,x π∈时，,666x πππωωπ⎡⎤+∈+⎢⎥⎣⎦，又()f x ⎡∈-⎣，1cos 6x πω⎛⎫∴-≤+ ⎪⎝⎭所以1166πππωπ+， 解得5563ω， ω∴的取值范围是55,63⎡⎤⎢⎥⎣⎦． 故答案为：55,63⎡⎤⎢⎥⎣⎦．。

（完整）新课程标准数学必修1第三章课后习题解答[唐金制]编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）新课程标准数学必修1第三章课后习题解答[唐金制]）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）新课程标准数学必修1第三章课后习题解答[唐金制]的全部内容。

新课程标准数学必修1第三章课后习题解答第三章函数的应用3．1函数与方程练习（P88）1。

(1）令f(x）=-x2+3x+5，作出函数f(x)的图象（图3—1—2—7（1)）,它与x轴有两个交点，所以方程—x2+3x+5=0有两个不相等的实数根.(2）2x(x-2）=—3可化为2x2-4x+3=0,令f（x)=2x2—4x+3，作出函数f（x)的图象(图3—1-2-7(2）)，它与x轴没有交点，所以方程2x(x-2)=-3无实数根.(3）x2=4x—4可化为x2-4x+4=0，令f（x)=x2—4x+4，作出函数f（x)的图象(图3-1—2—7（3)），它与x轴只有一个交点(相切),所以方程x2=4x—4有两个相等的实数根。

（4）5x2+2x=3x2+5可化为2x2+2x-5=0,令f(x)=2x2+2x—5,作出函数f(x）的图象（图3-1—2—7(4））,它与x轴有两个交点，所以方程5x2+2x=3x2+5有两个不相等的实数根。

图3-1—2—72.（1）作出函数图象（图3-1—2—8(1)),因为f(1）=1〉0,f(1.5）=-2.875<0,所以f(x)=—x3-3x+5在区间（1,1.5)上有一个零点。

又因为f（x)是(-∞,+∞）上的减函数，所以f(x)=-x3-3x+5在区间(1，1。

2017-2018学年高一数学必修1 全册同步课时作业目录1.1.1-1集合与函数概念1.1.1-2集合的含义与表示1.1.1-3集合的含义与表示1.1.2集合间的包含关系1.1.3-1集合的基本运算（第1课时）1.1.3-2集合的基本运算（第2课时）1.1习题课1.2.1函数及其表示1.2.2-1函数的表示法（第1课时）1.2.2-2函数的表示法（第2课时）1.2.2-3函数的表示法（第3课时）1.2习题课1.3.1-1单调性与最大（小）值（第1课时）1.3.1-2单调性与最大（小）值（第2课时）1.3.1-3单调性与最大（小）值（第3课时）1.3.1-4单调性与最大（小）值（第4课时）1.3.2-1函数的奇偶性（第1课时）1.3.2-2函数的奇偶性（第2课时）函数的值域专题研究第一章单元检测试卷A第一章单元检测试卷B 2.1.1-1基本初等函数（Ⅰ）2.1.1-2指数与指数幂的运算（第2课时）2.1.2-1指数函数及其性质（第1课时）2.1.2-2指数函数及其性质（第2课时）2.1.2-3对数与对数运算（第3课时）2.2.1-1对数与对数运算（第1课时）2.2.1-2对数与对数运算（第2课时）2.2.1-3对数与对数运算（第3课时）2.2.2-1对数函数及其性质（第1课时）2.2.2-2对数函数的图像与性质（第2课时）2.2.2-3对数函数的图像与性质2.3 幂函数图像变换专题研究第二章单元检测试卷A第二章单元检测试卷B3.1.1函数的应用3.1.2用二分法求方程的近似解3.2.1函数模型及其应用3.2.2函数模型的应用实例第三章单元检测试卷A第三章单元检测试卷B全册综合检测试题模块A全册综合检测试题模块B1.1.1-1集合与函数概念课时作业1.下列说法中正确的是()A.联合国所有常任理事国组成一个集合B.衡水中学年龄较小的学生组成一个集合C.{1，2，3}与{2，1，3}是不同的集合D.由1，0，5，1，2，5组成的集合有六个元素答案 A解析根据集合中元素的性质判断.2.若a 是R 中的元素，但不是Q 中的元素，则a 可以是( ) A.3.14 B.－2 C.78 D.7答案 D解析 由题意知a 应为无理数，故a 可以为7. 3.设集合M ＝{(1，2)}，则下列关系式成立的是( ) A.1∈M B.2∈M C.(1，2)∈M D.(2，1)∈M 答案 C4.若以方程x 2－5x ＋6＝0和方程x 2－x －2＝0的解为元素的集合为M ，则M 中元素的个数为( )A.1B.2C.3D.4 答案 C解析 M ＝{－1，2，3}.5.若2∈{1，x 2＋x}，则x 的值为( ) A.－2 B.1 C.1或－2 D.－1或2 答案 C解析 由题意知x 2＋x ＝2，即x 2＋x －2＝0.解得x ＝－2或x ＝1.6.已知集合M ＝{a ，b ，c}中的三个元素可构成某一三角形的三边长，那么此三角形一定不是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形 答案 D解析 因集合中的元素全不相同，故三角形的三边各不相同.所以△ABC 不可能是等腰三角形.7.设a ，b ∈R ，集合{1，a}＝{0，a ＋b}，则b －a ＝( ) A.1 B.－1 C.2 D.－2 答案 A解析 ∵{1，a}＝{0，a ＋b}，∴⎩⎪⎨⎪⎧a ＝0，a ＋b ＝1，∴⎩⎪⎨⎪⎧a ＝0，b ＝1.∴b －a ＝1，故选A. 8.下列关系中①－43∈R ；②3∉Q ；③|－20|∉N *；④|－2|∈Q ；⑤－5∉Z ；⑥0∈N .其正确的是________. 答案 ①②⑥ 9.下列说法中①集合N 与集合N *是同一个集合；②集合N 中的元素都是集合Z 中的元素；③集合Q 中的元素都是集合N 中的元素；④集合Q 中的元素都是集合R 中的元素. 其中正确的个数是________. 答案 2解析 由数集性质知①③错误，②④正确.10.集合{1，2}与集合{2，1}是否表示同一集合？________；集合{(1，2)}与集合{(2，1)}是否表示同一集合？______.(填“是”或“不是”) 答案 是，不是11.若{a ，0，1}＝{c ，1b ，－1}，则a ＝______，b ＝______，c ＝________.答案 －1 1 0解析 ∵－1∈{a ，0，1}，∴a ＝－1. 又0∈{c ，1b ，－1}且1b ≠0，∴c ＝0，从而可知1b＝1，∴b ＝1.12.已知集合A 中含有两个元素1和a 2，则a 的取值范围是________. 答案 a ∈R 且a ≠±1解析 由集合元素的互异性，可知a 2≠1，∴a ≠±1，即a ∈R 且a ≠±1. 13.对于集合A ＝{2，4，6}，若a ∈A ，则6－a ∈A ，那么a 的值是________. 答案 2或414.设A 表示集合{2，3，a 2＋2a －3}，B 表示集合{a ＋3，2}，若已知5∈A ，且5∉B ，求实数a 的值. 答案 －4解析 ∵5∈A ，且5∉B ，∴⎩⎪⎨⎪⎧a 2＋2a －3＝5，a ＋3≠5， 即⎩⎪⎨⎪⎧a ＝－4或a ＝2，a ≠2.∴a ＝－4. ►重点班·选做题15.若一数集的任一元素的倒数仍在该集合中，则称该数集为“可倒数集”. (1)判断集合A ＝{－1，1，2}是否为可倒数集； (2)试写出一个含3个元素的可倒数集.解析 (1)由于2的倒数为12不在集合A 中，故集合A 不是可倒数集.(2)若a ∈A ，则必有1a ∈A ，现已知集合A 中含有3个元素，故必有一个元素有a ＝1a ，即a＝±1，故可以取集合A ＝{1，2，12}或{－1，2，12}或{1，3，13}等.下面有五个命题：①集合N (自然数集)中最小的数是1；②{1，2，3}是不大于3的自然数组成的集合；③a ∈N ，b ∈N ，则a ＋b ≥2；④a ∈N ，b ∈N ，则a·b ∈N ；⑤集合{0}中没有元素. 其中正确命题的个数是( ) A.0 B.1 C.2 D.3答案 B解析 因为0是自然数，所以0∈N .由此可知①②③是错误的，⑤亦错，只有④正确.故选B.1.1.1-2集合的含义与表示含解析课时作业1.用列举法表示集合{x|x 2－2x ＋1＝0}为( ) A.{1，1} B.{1}C.{x ＝1}D.{x 2－2x ＋1＝0}答案 B2.集合{1，3，5，7，9}用描述法表示应是( ) A.{x|x 是不大于9的非负奇数} B.{x|x ≤9，x ∈N } C.{x|1≤x ≤9，x ∈N } D.{x|0≤x ≤9，x ∈Z }答案 A3.由大于－3且小于11的偶数组成的集合是( ) A.{x|－3<x<11，x ∈Q } B.{x|－3<x<11}C.{x|－3<x<11，x ＝2k ，x ∈Q }D.{x|－3<x<11，x ＝2k ，x ∈Z }答案 D4.集合{x ∈N *|x<5}的另一种表示法是( ) A.{0，1，2，3，4} B.{1，2，3，4} C.{0，1，2，3，4，5} D.{1，2，3，4，5}答案 B5.设集合M ＝{x|x ∈R 且x ≤23}，a ＝26，则( ) A.a ∉M B.a ∈MC.a ＝MD.{a|a ＝26}＝M答案 A解析 首先元素与集合关系只能用符号“∈”与“∉”表示.集合中元素意义不同的不能用“＝”连接，再有a ＝24>23，a 不是集合M 的元素，故a ∉M.另外{a|a ＝26}中只有一个元素26与集合M 中元素不相同.故D 错误.6.将集合⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫（x ，y ）⎪⎪⎪⎩⎪⎨⎪⎧x ＋y ＝5，2x －y ＝1表示成列举法，正确的是( ) A.{2，3} B.{(2，3)} C.{x ＝2，y ＝3} D.(2，3)答案 B7.下列集合中，不同于另外三个集合的是( ) A.{x|x ＝1} B.{x ＝1} C.{1}D.{y|(y －1)2＝0}答案 B解析A，C，D都是数集.8.下列集合表示同一集合的是()A.M＝{(3，2)}，N＝{(2，3)}B.M＝{(x，y)|x＋y＝1}，N＝{y|x＋y＝1}C.M＝{4，5}，N＝{5，4}D.M＝{1，2}，N＝{(1，2)}答案 C解析A中M是点集，N是点集，是两个不同的点；B中M是点集，N是数集；D中M是数集，N是点集，故选C.9.设集合A＝{1，2，3}，B＝{4，5}，M＝{x|x＝a＋b，a∈A，b∈B}，则M中元素的个数为()A.3B.4C.5D.6答案 B解析由集合中元素的互异性，可知集合M＝{5，6，7，8}，所以集合M中共有4个元素.10.坐标轴上的点的集合可表示为()A.{(x，y)|x＝0，y≠0或x≠0，y＝0}B.{(x，y)|x2＋y2＝0}C.{(x，y)|xy＝0}D.{(x，y)|x2＋y2≠0}答案 C解析坐标轴上的点的横、纵坐标至少有一个为0，故选C.11.将集合“奇数的全体”用描述法表示为①{x|x＝2n－1，n∈N*}; ②{x|x＝2n＋1，n∈Z}；③{x|x＝2n－1，n∈Z};④{x|x＝2n＋1，n∈R}；⑤{x|x＝2n＋5，n∈Z}.其中正确的是________.答案②③⑤12.已知命题：(1){偶数}＝{x|x＝2k，k∈Z}；(2){x||x|≤2，x∈Z}＝{－2，－1，0，1，2}；(3){(x，y)|x＋y＝3且x－y＝1}＝{1，2}.其中正确的是________.答案(1)(2)13.已知集合A＝{1，0，－1，3}，B＝{y|y＝|x|，x∈A}，则B＝________.答案{0，1，3}解析 ∵y ＝|x|，x ∈A ，∴y ＝1，0，3，∴B ＝{0，1，3}. 14.用∈或∉填空：(1)若A ＝{x|x 2＝x}，则－1________A ； (2)若B ＝{x|x 2＋x －6＝0}，则3________B ； (3)若C ＝{x ∈N |1≤x ≤10}，则8________C ； (4)若D ＝{x ∈Z |－2<x<3}，则1.5________D. 答案 (1)∉ (2)∉ (3)∈ (4)∉ ►重点班·选做题15.用另一种方法表示下列集合. (1){x||x|≤2，x ∈Z }；(2){能被3整除，且小于10的正数}； (3)坐标平面内在第四象限的点组成的集合. (4){(x ，y)|x ＋y ＝6，x ，y 均为正整数}； (5){－3，－1，1，3，5}. (6)被3除余2的正整数集合.答案 (1){－2，－1，0，1，2} (2){3，6，9}(3)⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫（x ，y ）⎪⎪⎪⎩⎪⎨⎪⎧x>0，y<0 (4){(1，5)，(2，4)，(3，3)，(4，2)，(5，1)} (5){x|x ＝2k －1，－1≤k ≤3，k ∈Z } (6){x|x ＝3n ＋2，n ∈N }16.已知集合{x|x 2＋ax ＋b ＝0}＝{2，3}，求a ，b 的值. 答案 －5 6解析 ∵{x|x 2＋ax ＋b ＝0}＝{2，3}， ∴方程x 2＋ax ＋b ＝0有两实根x 1＝2，x 2＝3. 由根与系数的关系得a ＝－(2＋3)＝－5，b ＝2×3＝6.1.下列集合是有限集的是( ) A.{x|x 是被3整除的数}B.{x ∈R |0＜x ＜2}C.{(x ，y)|2x ＋y ＝5，x ∈N ，y ∈N }D.{x|x 是面积为1的菱形}答案 C解析 C 中集合可化为：{(0，5)，(1，3)，(2，1)}.2.已知集合A ＝{x|x 2－2x ＋a>0}，且1∉A ，则实数a 的取值范围是( ) A.{a|a ≤1}B.{a|a ≥1}C.{a|a≥0}D.{a|a≤－1}答案 A解析因为1∉A，所以当x＝1时，1－2＋a≤0，所以a≤1，即a的取值范围是{a|a≤1}.1.1.1-3集合的含义与表示课时作业(三)1.设x ∈N ，且1x ∈N ，则x 的值可能是( )A.0B.1C.－1D.0或1答案 B解析 首先x ≠0，排除A ，D ；又x ∈N ，排除C ，故选B.2.下面四个关系式：π∈{x|x 是正实数}，0.3∈Q ，0∈{0}，0∈N ，其中正确的个数是( ) A.4 B.3 C.2 D.1 答案 A解析 本题考查元素与集合之间的关系，由数集的分类可知四个关系式均正确. 3.集合{x ∈N |－1<x<112}的另一种表示方法是( )A.{0，1，2，3，4}B.{1，2，3，4}C.{0，1，2，3，4，5}D.{1，2，3，4，5} 答案 C解析 ∵x ∈N ，且－1<x<112，∴集合中含有元素0，1，2，3，4，5，故选C.4.已知集合A ＝{x ∈N *|－5≤x ≤5}，则必有( ) A.－1∈A B.0∈A C.3∈A D.1∈A 答案 D解析 ∵x ∈N *，－5≤x ≤5，∴x ＝1，2，即A ＝{1，2}，∴1∈A. 5.集合M ＝{(x ，y)|xy<0，x ∈R ，y ∈R }是( ) A.第一象限内的点集 B.第三象限内的点集 C.第四象限内的点集 D.第二、四象限内的点集 答案 D解析 根据描述法表示集合的特点，可知集合表示的是横、纵坐标异号的点的集合，这些点在第二、四象限内.6.若a ，b ，c ，d 为集合A 的四个元素，则以a ，b ，c ，d 为边长构成的四边形可能是( ) A.矩形 B.平行四边形 C.菱形D.梯形答案 D解析 由于集合中的元素具有“互异性”，故a ，b ，c ，d 四个元素互不相同，即组成四边形的四条边互不相等.7.集合A ＝{x|x ∈N ，且42－x ∈Z }，用列举法可表示为A ＝________.答案 {0，1，3，4，6}解析 注意到42－x ∈Z ，因此，2－x ＝±2，±4，±1，解得x ＝－2，0，1，3，4，6，又∵x ∈N ，∴x ＝0，1，3，4，6.8.一边长为6，一边长为3的等腰三角形所组成的集合中有________个元素. 答案 1解析 这样的三角形只有1个，是两腰长为6，底边长为3的等腰三角形. 9.点P(1，3)和集合A ＝{(x ，y)|y ＝x ＋2}之间的关系是________. 答案 P ∈A解析 在y ＝x ＋2中，当x ＝1时，y ＝3，因此点P 是集合A 的元素，故P ∈A. 10.用列举法表示集合A ＝{(x ，y)|x ＋y ＝3，x ∈N ，y ∈N *}为________. 答案 {(0，3)，(1，2)，(2，1)}解析 集合A 是由方程x ＋y ＝3的部分整数解组成的集合，由条件可知，当x ＝0时，y ＝3；当x ＝1时，y ＝2；当x ＝2时，y ＝1.故A ＝{(0，3)，(1，2)，(2，1)}.11.若A ＝{－2，2，3，4}，B ＝{x|x ＝t 2，t ∈A}，用列举法表示集合B ＝________. 答案 {4，9，16}解析 由题意可知集合B 是由集合A 中元素的平方构成，故B ＝{4，9，16}.12.下列集合中：A ＝{x ＝2，y ＝1}，B ＝{2，1}，C ＝{(x ，y)|⎩⎪⎨⎪⎧x ＋y ＝3，x －y ＝1}，D ＝{(x ，y)|x ＝2且y ＝1}，与集合{(2，1)}相等的共有________个. 答案 2解析 因为集合{(2，1)}的元素表示的是有序实数对，由已知集合的代表元素知，元素为有序实数对的是C ，D ，而A 表示含有两个元素x ＝2，y ＝1的集合，B 表示含有2个元素的集合.13.设A 是满足x<6的所有自然数组成的集合，若a ∈A ，且3a ∈A ，求a 的值. 解析 ∵a ∈A 且3a ∈A ，∴a<6且3a<6，∴a<2. 又∵a 是自然数，∴a ＝0或1.14.已知集合A 含有两个元素a 和a 2，若1∈A ，求实数a 的值.解析 本题中已知集合A 中有两个元素且1∈A ，据集合中元素的特点需分a ＝1和a 2＝1两种情况，另外还要注意集合中元素的互异性.若1∈A ，则a ＝1或a 2＝1，即a ＝±1. 当a ＝1时，集合A 有重复元素，∴a ≠1；当a ＝－1时，集合A 含有两个元素1，－1，符合互异性. ∴a ＝－1. ►重点班·选做题15.已知集合A ＝{0，2，5，10}，集合B 中的元素x 满足x ＝ab ，a ∈A ，b ∈A 且a ≠b ，写出集合B.解析 当⎩⎪⎨⎪⎧a ＝0，b ≠0或⎩⎪⎨⎪⎧a ≠0，b ＝0时，x ＝0； 当⎩⎪⎨⎪⎧a ＝2，b ＝5或⎩⎪⎨⎪⎧a ＝5，b ＝2时，x ＝10； 当⎩⎪⎨⎪⎧a ＝2，b ＝10或⎩⎪⎨⎪⎧a ＝10，b ＝2时，x ＝20； 当⎩⎪⎨⎪⎧a ＝5，b ＝10或⎩⎪⎨⎪⎧a ＝10，b ＝5时，x ＝50. 所以B ＝{0，10，20，50}.1.已知A ＝{x|3－3x>0}，则有( ) A.3∈A B.1∈A C.0∈A D.－1∉A答案 C解析 因为A ＝{x|3－3x>0}＝{x|x<1}，所以0∈A.2.“今有三女，长女五日一归，中女四日一归，小女三日一归，问三女何时相会”.(选自《孙子算经》)，请将三女前三次相会的天数用集合表示出来.解析 三女相会的日数，即为5，4，3的公倍数，它们的最小公倍数为60，因此三女前三次相会的天数用集合表示为{60，120，180}.3.数集M 满足条件：若a ∈M ，则1＋a 1－a ∈M(a ≠±1且a ≠0)，已知3∈M ，试把由此确定的集合M 的元素全部求出来.解析 ∵a ＝3∈M ，∴1＋a 1－a ＝1＋31－3＝－2∈M ，∴1－21＋2＝－13∈M.∴1－131＋13＝12∈M ，∴1＋121－12＝3∈M.即M ＝⎩⎨⎧⎭⎬⎫3，－2，－13，12.4.设集合A ＝{x ，y}，B ＝{0，x 2}，若集合A ，B 相等，求实数x ，y 的值. 解析 因为A ，B 相等，则x ＝0或y ＝0.(1)当x ＝0时，x 2＝0，则B ＝{0，0}，不满足集合中元素的互异性，故舍去. (2)当y ＝0时，x ＝x 2，解得x ＝0或x ＝1.由(1)知x ＝0应舍去. 综上知：x ＝1，y ＝0.5.集合A ＝{x|⎩⎪⎨⎪⎧y ＝x ，y ＝x 2}可化简为________. 以下是两位同学的答案，你认为哪一个正确？试说明理由.学生甲：由⎩⎪⎨⎪⎧y ＝x ，y ＝x 2，得x ＝0或x ＝1，故A ＝{0，1}； 学生乙：问题转化为求直线y ＝x 与抛物线y ＝x 2的交点，得到A ＝{(0，0)，(1，1)}. 解析 同学甲正确，同学乙错误.由于集合A 的代表元素为x ，因此满足条件的元素只能为x ＝0，1；而不是实数对⎩⎪⎨⎪⎧x ＝0，y ＝0，⎩⎪⎨⎪⎧x ＝1，y ＝1.故同学甲正确.1.1.2集合间的包含关系课时作业(四)1.数0与集合∅的关系是()A.0∈∅B.0＝∅C.{0}＝∅D.0∉∅答案 D2.集合{1，2，3}的子集的个数是()A.7B.4C.6D.8答案 D3.下列集合中表示空集的是()A.{x∈R|x＋5＝5}B.{x∈R|x＋5>5}C.{x∈R|x2＝0}D.{x∈R|x2＋x＋1＝0}答案 D解析∵A，B，C中分别表示的集合为{0}，{x|x>0}，{0}，∴不是空集；又∵x2＋x＋1＝0无解，∴{x∈R|x2＋x＋1＝0}表示空集.4.已知集合P＝{1，2，3，4}，Q＝{y|y＝x＋1，x∈P}，那么集合M＝{3，4，5}与Q的关系是()A.M QB.M QC.Q MD.Q＝M答案 A5.下列六个关系式中正确的个数为()①{a，b}＝{b，a}；②{a，b}⊆{b，a}；③∅＝{∅}；④{0}＝∅；⑤∅ {0}；⑥0∈{0}.A.6B.5C.4D.3个及3个以下答案 C解析其中①②⑤⑥是正确的，对于③应为∅ {∅}或∅∈{∅}；对于④应为{0} ∅.6.若集合A＝{－1，2}，B＝{x|x2＋ax＋b＝0}，且A＝B，则有()A.a＝1，b＝－2B.a＝2，b＝2C.a＝－1，b＝－2D.a＝－1，b＝2答案 C解析由A＝B知－1与2是方程x2＋ax＋b＝0的两根，∴⎩⎪⎨⎪⎧－1＋2＝－a ，（－1）×2＝b ，∴⎩⎪⎨⎪⎧a ＝－1，b ＝－2. 7.集合P ＝{x|y ＝x 2}，Q ＝{y|y ＝x 2}，则下列关系中正确的是( ) A.P Q B.P ＝Q C.P ⊆Q D.P Q答案 D解析 P ，Q 均为数集，P ＝{x|y ＝x 2}＝R ，Q ＝{y|y ＝x 2}＝{y|y ≥0}，∴Q P ，故选D. 8.已知集合A {1，2，3}，且A 中至少含有一个奇数，则这样的集合A 的个数为( ) A.6 B.5 C.4 D.3答案 B解析 A ＝{1}，{3}，{1，2}，{1，3}，{2，3}共5个.9.若A ＝{(x ，y)|y ＝x}，B ＝{(x ，y)|yx ＝1}，则A ，B 关系为( )A.A BB.B AC.A ＝BD.A B答案 B10.已知集合A ＝{－1，3，m}，集合B ＝{3，4}，若B ⊆A ，则实数m ＝________. 答案 4解析 ∵B ⊆A ，A ＝{－1，3，m}，∴m ＝4.11.已知非空集合A 满足：①A ⊆{1，2，3，4}；②若x ∈A ，则5－x ∈A.符合上述要求的集合A 的个数是________. 答案 3解析 由“若x ∈A ，则5－x ∈A ”可知，1和4，2和3成对地出现在A 中，且A ≠∅.故集合A 的个数等于集合{1，2}的非空子集的个数，即3个.12.设集合A ＝{x ∈R |x 2＋x －1＝0}，B ＝{x ∈R |x 2－x ＋1＝0}，则集合A ，B 之间的关系是________. 答案 B A解析 ∵A ＝{－1－52，－1＋52}，B ＝∅，∴B A.13.已知M ＝{y|y ＝x 2－2x －1，x ∈R }，N ＝{x|－2≤x ≤4}，则集合M 与N 之间的关系是________. 答案 N M14.设A ＝{x ∈R |－1<x<3}，B ＝{x ∈R |x>a}，若A B ，求a 的取值范围. 答案 a ≤－1解析 数形结合，端点处单独验证.15.设集合A ＝{1，3，a}，B ＝{1，a 2－a ＋1}，B ⊆A ，求a 的值.解析 因为B ⊆A ，所以B 中元素1，a 2－a ＋1都是A 中的元素，故分两种情况. (1)a 2－a ＋1＝3，解得a ＝－1或2，经检验满足条件. (2)a 2－a ＋1＝a ，解得a ＝1，此时A 中元素重复，舍去. 综上所述，a ＝－1或a ＝2. ►重点班·选做题16.a ，b 是实数，集合A ＝{a ，ba ，1}，B ＝{a 2，a ＋b ，0}，若A ＝B ，求a 2 015＋b 2 016.答案 －1解析 ∵A ＝B ，∴b ＝0，A ＝{a ，0，1}，B ＝{a 2，a ，0}.∴a 2＝1，得a ＝±1.a ＝1时，A ＝{1，0，1}不满足互异性，舍去；a ＝－1时，满足题意.∴a 2015＋b 2 016＝－1.1.设a ，b ∈R ，集合{1，a ＋b ，a}＝{0，ba ，b}，则b －a 等于( )A.1B.－1C.2D.－2答案 C解析 ∵a ≠0，∴a ＋b ＝0，∴ba ＝－1.∴b ＝1，a ＝－1，∴b －a ＝2，故选C.2.设集合A ＝{x|－3≤x ≤2}，B ＝{x|2k －1≤x ≤k ＋1}且B ⊆A ，求实数k 的取值范围. 解析 ∵B ⊆A ，∴B ＝∅或B ≠∅.①B ＝∅时，有2k －1>k ＋1，解得k>2. ②B ≠∅时，有⎩⎪⎨⎪⎧2k －1≤k ＋1，2k －1≥－3，k ＋1≤2，解得－1≤k ≤1.综上，－1≤k ≤1或k>2.1.1.3-1集合的基本运算（第1课时）课时作业(五)1.(2014·广东)已知集合M ＝{－1，0，1}，N ＝{0，1，2}，则M ∪N ＝( ) A.{0，1} B.{－1，0，2} C.{－1，0，1，2} D.{－1，0，1}答案 C解析 M ∪N ＝{－1，0，1，2}.2.若集合A ＝{x|－2<x<1}，B ＝{x|0<x<2}，则集合A ∩B ＝( ) A.{x|－1<x<1} B.{x|－2<x<1} C.{x|－2<x<2} D.{x|0<x<1} 答案 D3.设A ＝{x|1≤x ≤3}，B ＝{x|x<0或x ≥2}，则A ∪B 等于( ) A.{x|x<0或x ≥1} B.{x|x<0或x ≥3} C.{x|x<0或x ≥2} D.{x|2≤x ≤3} 答案 A4.设集合A ＝{1，2}，则满足A ∪B ＝{1，2，3}的集合B 的个数是( ) A.1 B.3 C.4 D.8答案 C解析 ∵A ＝{1，2}，A ∪B ＝{1，2，3}，∴B ＝{3}或{1，3}或{2，3}或{1，2，3}，故选C.5.设集合M ＝{m ∈Z |－3<m<2}，N ＝{n ∈Z |－1≤n ≤3}，则M ∩N 等于( ) A.{0，1} B.{－1，0，1} C.{0，1，2} D.{－1，0，1，2} 答案 B解析 集合M ＝{－2，－1，0，1}，集合N ＝{－1，0，1，2，3}，M ∩N ＝{－1，0，1}. 6.若A ＝{x|x2∈Z }，B ＝{y|y ＋12∈Z }，则A ∪B 等于( )A.BB.AC.∅D.Z答案 D解析 A ＝{x|x ＝2n ，n ∈Z }为偶数集，B ＝{y|y ＝2n －1，n ∈Z }为奇数集，∴A ∪B ＝Z . 7.已知集合A ＝{－1，0，1}，B ＝{x|－1≤x<1}，则A ∩B ＝( )A.{0}B.{－1，0}C.{0，1}D.{－1，0，1}答案 B解析集合B含有整数－1，0，故A∩B＝{－1，0}.8.如果A＝{x|x＝2n＋1，n∈Z}，B＝{x|x＝k＋3，k∈Z}，那么A∩B＝()A.∅B.AC.BD.Z答案 B9.满足条件M∪{1}＝{1，2，3}的集合M的个数是________.答案 2解析M＝{1，2，3}或M＝{2，3}.10.下列四个推理：①a∈(A∪B)⇒a∈A；②a∈(A∩B)⇒a∈(A∪B)；③A⊆B⇒A∪B＝B；④A∪B＝A⇒A∩B＝B.其中正确的为________.答案②③④解析①是错误的，a∈(A∪B)时可推出a∈A或a∈B，不一定能推出a∈A.11.已知集合P，Q与全集U，下列命题：①P∩Q＝P，②P∪Q＝Q，③P∪Q＝U，其中与命题P⊆Q等价的命题有______个.答案 2解析①②都等价.12.已知A＝{x|x≤－1或x≥3}，B＝{x|a<x<4}，若A∪B＝R，则实数a的取值范围是________.答案a≤－113.若集合P满足P∩{4，6}＝{4}，P∩{8，10}＝{10}，且P⊆{4，6，8，10}，求集合P. 解析由条件知4∈P，6∉P，10∈P，8∉P，∴P＝{4，10}.14.已知集合A＝{x|x＋3≤0}，B＝{x|x－a<0}.(1)若A∪B＝B，求a的取值范围；(2)若A∩B＝B，求a的取值范围.解析(1)∵A∪B＝B，∴A⊆B，∴a＞－3.(2)∵A∩B＝B，∴B⊆A，∴a≤－3.►重点班·选做题15.已知A＝{x|2a<x≤a＋8}，B＝{x|x<－1或x>5}，若A∪B＝R，求a的取值范围.解析∵B＝{x|x<－1或x>5}，A∪B＝R，∴⎩⎪⎨⎪⎧2a<－1，a ＋8≥5，解得－3≤a<－12.1.若A ＝{x|x 2－5x ＋6＝0}，B ＝{x|x 2－6x ＋8＝0}，则A ∪B ＝________，A ∩B ＝________. 答案 A ＝{2，3}，B ＝{2，4}， ∴A ∪B ＝{2，3，4}，A ∩B ＝{2}.2.设S ＝{x|2x ＋1>0}，T ＝{x|3x －5<0}，则S ∩T ＝( ) A.∅ B.{x|x<－12}C.{x|x>53}D.{x|－12<x<53}答案 D解析 S ＝{x|x>－12}，T ＝{x|x<53}，在数轴上表示出S 和T ，可知选D.3.设集合A ＝{x|－5≤x<1}，B ＝{x|x ≤2}，则A ∩B 等于( ) A.{x|－5≤x<1} B.{x|－5≤x ≤2} C.{x|x<1} D.{x|x ≤2} 答案 A4.设集合A ＝{－1，1，3}，B ＝{a ＋2，a 2＋4}，A ∩B ＝{3}，则实数a ＝________. 答案 15.已知A ＝{|a ＋1|，3，5}，B ＝{2a ＋1，a 2＋2a ，a 2＋2a －1}，若A ∩B ＝{2，3}，则A ∪B ＝________.答案 {2，3，5，－5}解析 由|a ＋1|＝2，得a ＝1或－3，代入求出B ，注意B 中不能有5.6.已知M ＝{x|x ≤－1}，N ＝{x|x>a －2}，若M ∩N ≠∅，则a 的范围是________. 答案 a<1课时作业(六)1.1.3-2集合的基本运算（第2课时）1.已知U＝{1，3}，A＝{1，3}，则∁U A＝()A.{1，3}B.{1}C.{3}D.∅答案 D2.设全集U＝{x∈N*|x<6}，集合A＝{1，3}，B＝{3，5}，则∁U(A∪B)＝()A.{1，4}B.{1，5}C.{2，4}D.{2，5}答案 C3.设全集U＝{1，2，3，4，5}，集合A＝{1，2，3}，集合B＝{3，4，5}，则(∁U A)∪(∁U B)＝()A.{1，2，3，4，5}B.{3}C.{1，2，4，5}D.{1，5}答案 C解析∵∁U A＝{4，5}，∁U B＝{1，2}，故选C.4.若集合A＝{x|－1≤x≤2}，B＝{x|x<1}，则A∩(∁R B)＝()A.{x|x>1}B.{x|x≥1}C.{x|1<x≤2}D.{x|1≤x≤2}答案 D5.设P＝{x︱x<4}，Q＝{x︱x2<4}，则()A.P⊆QB.Q⊆PC.P⊆∁R QD.Q⊆∁R P答案 B6.已知全集U＝Z，集合A＝{x|x＝k3，k∈Z}，B＝{x|x＝k6，k∈Z}，则()A.∁U A ∁U BB.A BC.A＝BD.A与B中无公共元素答案 A解析∵A＝{x|x＝26k，k∈Z}，∴∁U A ∁U B，A B.7.设全集U＝{2，3，5}，A＝{2，|a－5|}，∁U A＝{5}，则a的值为()A.2B.8C.2或8D.－2或8答案 C解析∁U A＝{5}包含两层意义，①5∉A；②U中除5以外的元素都在A中.∴|a－5|＝3，解得a＝2或8.8.设全集U＝Z，A＝{x∈Z|x＜5}，B＝{x∈Z|x≤2}，则∁U A与∁U B的关系是()A.∁U A ∁U BB.∁U A ∁U BC.∁U A＝∁U BD.∁U A ∁U B答案 A解析∵∁U A＝{x∈Z|x≥5}，∁U B＝{x∈Z|x>2}.故选A.9.设A＝{x||x|＜2}，B＝{x|x＞a}，全集U＝R，若A⊆∁R B，则有()A.a＝0B.a≤2C.a≥2D.a＜2答案 C解析A＝{x|－2<x<2}，∁R B＝{x|x≤a}，在数轴上把A，B表示出来.10.已知全集U＝{1，2，3，4，5}，S U，T U，若S∩T＝{2}，(∁U S)∩T＝{4}，(∁U S)∩(∁U T)＝{1，5}，则有()A.3∈S∩TB.3∉S但3∈TC.3∈S∩(∁U T)D.3∈(∁U S)∩(∁U T)答案 C11.设全集U＝Z，M＝{x|x＝2k，k∈Z}，P＝{x|x＝2k＋1，k∈Z}，则下列关系式中正确的有________.①M⊆P；②∁U M＝∁U P；③∁U M＝P；④∁U P＝M.答案③④12.设全集U＝R，集合A＝{x|x≥0}，B＝{y|y≥1}，则∁U A与∁U B的包含关系是________. 答案∁U A ∁U B解析∵∁U A＝{x|x<0}，∁U B＝{y|y<1}，∴∁U A ∁U B.13.已知全集U，集合A＝{1，3，5，7，9}，∁U A＝{2，4，6，8}，∁U B＝{1，4，6，8，9}，求集合B.解析 借助韦恩图，如右图所示， ∴U ＝{1，2，3，4，5，6，7，8，9}. ∵∁U B ＝{1，4，6，8，9}， ∴B ＝{2，3，5，7}.14.设集合U ＝{1，2，3，4}，且A ＝{x ∈U|x 2－5x ＋m ＝0}，若∁U A ＝{2，3}，求m 的值. 解析 ∵∁U A ＝{2，3}，U ＝{1，2，3，4}， ∴A ＝{1，4}，即1，4是方程x 2－5x ＋m ＝0的两根. ∴m ＝1×4＝4.15.已知全集U ＝{2，0，3－a 2}，P ＝{2，a 2－a －2}且∁U P ＝{－1}，求实数a. 解析 ∵U ＝{2，0，3－a 2}，P ＝{2，a 2－a －2}，∁U P ＝{－1}，∴⎩⎪⎨⎪⎧3－a 2＝－1，a 2－a －2＝0，解得a ＝2.1.如果S ＝{1，2，3，4，5}，A ＝{1，3，4}，B ＝{2，4，5}，那么(∁S A)∩(∁S B)等于( ) A.∅ B.{1，3} C.{4} D.{2，5}答案 A解析 ∵∁S A ＝{2，5}，∁S B ＝{1，3}， ∴(∁S A)∩(∁S B)＝∅.2.设全集U ＝{1，2，3，4，5，6，7}，P ＝{1，2，3，4，5}，Q ＝{3，4，5，6，7}，则P ∩(∁U Q)等于()A.{1，2}B.{3，4，5}C.{1，2，6，7}D.{1，2，3，4，5}答案 A解析 ∵∁U Q ＝{1，2}，∴P ∩(∁U Q)＝{1，2}.3.设全集U ＝{1，2，3，4，5，6，7}，集合A ＝{1，3，5，7}，B ＝{3，5}，则正确的是( ) A.U ＝A ∪B B.U ＝(∁U A)∪B C.U ＝A ∪(∁U B) D.U ＝(∁U A)∪(∁U B)答案 C解析 ∵∁U B ＝{1，2，4，6，7}， ∴A ∪(∁U B)＝{1，2，3，4，5，6，7}＝U.4.已知A ＝{x|x<3}，B ＝{x|x<a}.若A ⊆B ，问∁R B ⊆∁R A 是否成立？ 答案 成立5.某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为________.答案126.如果S＝{x∈N|x<6}，A＝{1，2，3}，B＝{2，4，5}，那么(∁S A)∪(∁S B)＝________.答案{0，1，3，4，5}解析∵S＝{x∈N|x<6}＝{0，1，2，3，4，5}，∴∁S A＝{0，4，5}，∁S B＝{0，1，3}.∴(∁S A)∪(∁S B)＝{0，1，3，4，5}.课时作业(七)1.1习题课含解析(第一次作业)1.(2015·广东，理)若集合M＝{x|(x＋4)(x＋1)＝0}，N＝{x|(x－4)(x－1)＝0}，则M∩N＝() A.{1，4} B.{－1，－4}C.{0}D.∅答案 D2.设集合A＝{4，5，7，9}，B＝{3，4，7，8，9}，全集U＝A∪B，则集合∁U(A∩B)中的元素的个数为()A.3B.4C.5D.6答案 A3.集合M＝{x|x＝1＋a2，a∈N*}，P＝{x|x＝a2－4a＋5，a∈N*}，则下列关系中正确的是() A.M P B.P MC.M＝PD.M P且P M答案 A解析P＝{x|x＝1＋(a－2)2，a∈N*}，当a＝2时，x＝1而M中无元素1，P比M多一个元素.4.设U＝R，A＝{x|x>0}，B＝{x|x>1}，则A∩(∁U B)＝()A.{x|0≤x≤1}B.{x|0<x≤1}C.{x|x<0}D.{x|x>1}答案 B5.已知集合A＝{1，3，5，7，9}，B＝{0，3，6，9，12}，则A∩(∁N B)＝()A.{1，5，7}B.{3，5，7}C.{1，3，9}D.{1，2，3}答案 A6.已知方程x2－px＋15＝0与x2－5x＋q＝0的解集分别为S与M，且S∩M＝{3}，则p＋q 的值是()A.2B.7C.11D.14答案 D解析 由交集定义可知，3既是集合S 中的元素，也是集合M 中的元素.亦即是方程x 2－px ＋15＝0与x 2－5x ＋q ＝0的公共解，把3代入两方程，可知p ＝8，q ＝6，则p ＋q 的值为14.7.已知全集R ，集合A ＝{x|(x －1)(x ＋2)(x －2)＝0}，B ＝{y|y ≥0}，则A ∩(∁R B)为( ) A.{1，2，－2} B.{1，2} C.{－2} D.{－1，－2}答案 C解析 A ＝{1，2，－2}，而B 的补集是{y|y<0}，故两集合的交集是{－2}，选C. 8.集合P ＝{1，4，9，16，…}，若a ∈P ，b ∈P ，则a ⊕b ∈P ，则运算⊕可能是( ) A.除法 B.加法 C.乘法 D.减法答案 C解析 当⊕为除法时，14∉P ，∴排除A ；当⊕为加法时，1＋4＝5∉P ，∴排除B ；当⊕为乘法时，m 2·n 2＝(mn)2∈P ，故选C ； 当⊕为减法时，1－4∉P ，∴排除D.9.设全集U ＝Z ，集合P ＝{x|x ＝2n ，n ∈Z }，Q ＝{x|x ＝4m ，m ∈Z }，则U 等于( ) A.P ∪Q B.(∁U P)∪Q C.P ∪(∁U Q) D.(∁U P)∪(∁U Q)答案 C10.设S ，P 为两个非空集合，且S P ，P S ，令M ＝S ∩P ，给出下列4个集合：①S ；②P ；③∅；④S ∪P.其中与S ∪M 能够相等的集合的序号是( ) A.① B.①② C.②③ D.④答案 A11.设集合I ＝{1，2，3}，A 是I 的子集，若把满足M ∪A ＝I 的集合M 叫做集合A 的“配集”，则当A ＝{1，2}时，A 的配集的个数是( ) A.1 B.2 C.3 D.4答案 D解析 A 的配集有{3}，{1，3}，{2，3}，{1，2，3}共4个. 12.已知集合A ，B 与集合A@B 的对应关系如下表：________.答案 {2 012，2 013}13.已知A ＝{2，3}，B ＝{－4，2}，且A ∩M ≠∅，B ∩M ＝∅，则2________M ，3________M. 答案 ∉ ∈解析 ∵B ∩M ＝∅，∴－4∉M ，2∉M. 又A ∩M ≠∅且2∉M ，∴3∈M.14.若集合A ＝{1，3，x}，B ＝{1，x 2}，且A ∪B ＝{1，3，x}，则x ＝________. 答案 ±3或0解析 由A ∪B ＝{1，3，x}，B A ， ∴x 2∈A.∴x 2＝3或x 2＝x. ∴x ＝±3或x ＝0，x ＝1(舍).15.已知S ＝{a ，b}，A ⊆S ，则A 与∁S A 的所有有序组对共有________组. 答案 4解析 S 有4个子集，分别为∅，{a}，{b}，{a ，b}注意有序性.⎩⎪⎨⎪⎧A ＝{a}，∁S A ＝{b}和⎩⎪⎨⎪⎧A ＝{b}，∁S A ＝{a}是不同的.16.已知A ⊆M ＝{x|x 2－px ＋15＝0，x ∈R }，B ⊆N ＝{x|x 2－ax －b ＝0，x ∈R }，又A ∪B ＝{2，3，5}，A ∩B ＝{3}，求p ，a 和b 的值.解析 由A ∩B ＝{3}，知3∈M ，得p ＝8.由此得M ＝{3，5}，从而N ＝{3，2}，由此得a ＝5，b ＝－6.(第二次作业)1.(2014·北京，理)已知集合A＝{x|x2－2x＝0}，B＝{0，1，2}，则A∩B＝()A.{0}B.{0，1}C.{0，2}D.{0，1，2}答案 C解析解x2－2x＝0，得x＝0或x＝2，故A＝{0，2}，所以A∩B＝{0，2}，故选C.2.(高考真题·全国Ⅰ)已知集合M＝{0，1，2，3，4}，N＝{1，3，5}，P＝M∩N，则P的子集共有()A.2个B.4个C.6个D.8个答案 B解析由题意得P＝M∩N＝{1，3}，∴P的子集为∅，{1}，{3}，{1，3}，共4个，故选B.3.设集合A＝{x∈Z|0≤x≤5}，B＝{x|x＝k2，k∈A}，则集合A∩B＝()A.{0，1，2}B.{0，1，2，3}C.{0，1，3}D.B答案 A4.设M＝{1，2，m2－3m－1}，P＝{1，3}，且M∩P＝{1，3}，则m的值为()A.4B.－1C.－4或1D.－1或4答案 D5.已知集合M＝{x|y＝x2－1}，N＝{y|y＝x2－1}，那么M∩N等于()A.∅B.NC.MD.R答案 B解析∵M＝R，N＝{y|y≥－1}，∴M∩N＝N.6.若A∪B＝∅，则()A.A＝∅，B≠∅B.A≠∅，B＝∅C.A＝∅，B＝∅D.A≠∅，B≠∅答案 C7.设集合A＝{x|x∈Z且－15≤x≤－2}，B＝{x|x∈Z且|x|<5}，则A∪B中的元素个数是() A.10 B.11C.20D.21答案 C解析 ∵A ∪B ＝{x|x ∈Z 且－15≤x<5}＝{－15，－14，－13，…，1，2，3，4}，∴A ∪B 中共20个元素.8.已知全集U ＝{0，1，2}且∁U A ＝{2}，则集合A 的真子集的个数为( ) A.3 B.4 C.5 D.6答案 A解析 ∵A ＝{0，1}，∴真子集的个数为22－1＝3.9.如果U ＝{x|x 是小于9的正整数}，A ＝{1，2，3，4}，B ＝{3，4，5，6}，那么(∁U A)∩(∁U B)等于()A.{1，2}B.{3，4}C.{5，6}D.{7，8}答案 D解析 ∵∁U A ＝{5，6，7，8}，∁U B ＝{1，2，7，8}，∴(∁U A)∩(∁U B)＝{7，8}. 10.已知集合P ＝{x|－1≤x ≤1}，M ＝{－a ，a}，若P ∪M ＝P ，则a 的取值范围是( ) A.{a|－1≤a ≤1} B.{a|－1<a<1}C.{a|－1<a<1，且a ≠0}D.{a|－1≤a ≤1，且a ≠0}答案 D解析 由P ∪M ＝P ，得M ⊆P.所以⎩⎪⎨⎪⎧－1≤a ≤1，－1≤－a ≤1，即－1≤a ≤1.又由集合元素的互异性知－a ≠a ，即a ≠0， 所以a 的取值范围是{a|－1≤a ≤1，且a ≠0}.11.若A ，B ，C 为三个集合，且A ∪B ＝B ∩C ，则一定有( ) A.A ⊆C B.C ⊆A C.A ≠C D.A ＝∅答案 A12.已知集合A ＝{1，2，3}，B ＝{2，m ，4}，A ∩B ＝{2，3}，则m ＝________. 答案 313.集合A 含有10个元素，集合B 含有8个元素，集合A ∩B 含有3个元素，则集合A ∪B 有________个元素. 答案 15解析 由A ∩B 含有3个元素知，仅有3个元素相同，根据集合元素的互异性，集合的元素个数为10＋8－3＝15，或直接利用韦恩图得出结果.14.已知集合A＝{－1，2}，B＝{x|mx＋1>0}，若A∪B＝B，求实数m的取值范围.思路首先根据题意判断出A与B的关系，再对m分类讨论化简集合B，根据A，B的关系求出m的范围.解析∵A∪B＝B，∴A⊆B.①当m>0时，由mx＋1>0，得x>－1m，此时B＝{x|x>－1m}，由题意知－1m<－1，∴0<m<1.②当m＝0时，B＝R，此时A⊆B.③当m<0时，得B＝{x|x<－1m}，由题意知－1m>2，∴－12<m<0.综上：－12<m<1.点评在解有关集合交、并集运算时，常会遇到A∩B＝A，A∪B＝B等这类问题.解答时应充分利用交集、并集的有关性质，准确转化条件，有时也借助数轴分析处理，另外还要注意“空集”这一隐含条件.已知全集U＝{a，1，3，b，x2－2＝0}，集合A＝{a，b}，则∁U A＝________.答案{1，3，x2－2＝0}解析在全集U中除去A中的元素后所组成的集合即为∁U A，故∁U A＝{1，3，x2－2＝0}.1.(2015·新课标全国Ⅰ，文)已知集合A＝{x|x＝3n＋2，n∈N}，B＝{6，8，10，12，14}，则集合A∩B中元素的个数为()A.5B.4C.3D.2答案 D2.(2015·天津，理)已知全集U＝{1，2，3，4，5，6，7，8}，集合A＝{2，3，5，6}，集合B＝{1，3，4，6，7}，则集合A∩(∁U B)＝()A.{2，5}B.{3，6}C.{2，5，6}D.{2，3，5，6，8}答案 A3.(2016·天津)已知集合A＝{1，2，3，4}，B＝{y|y＝3x－2，x∈A}，则A∩B＝()A.{1}B.{4}C.{1，3}D.{1，4}答案 D解析由题意得，B＝{1，4，7，10}，所以A∩B＝{1，4}.4.(2014·辽宁)已知全集U＝R，A＝{x|x≤0}，B＝{x|x≥1}，则集合∁U(A∪B)＝()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}答案 D解析∵A∪B＝{x|x≤0或x≥1}，∴∁U(A∪B)＝{x|0<x<1}，故选D.5.(2013·山东，文)已知集合A，B均为全集U＝{1，2，3，4}的子集，且∁U(A∪B)＝{4}，B ＝{1，2}，则A∩(∁U B)＝()A.{3}B.{4}C.{3，4}D.∅答案 A解析由题意知A∪B＝{1，2，3}，又B＝{1，2}，所以A中必有元素3，没有元素4，∁U B ＝{3，4}，故A∩(∁U B)＝{3}.6.(2013·课标全国)已知集合A＝{1，2，3，4}，B＝{x|x＝n2，n∈A}，A∩B＝()A.{1，4}B.{2，3}C.{9，16}D.{1，2}答案 A7.(2013·山东)已知集合A＝{0，1，2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是() A.1 B.3C.5D.9答案 C解析逐个列举可得.x＝0，y＝0，1，2时，x－y＝0，－1，－2；x＝1，y＝0，1，2时，x －y＝1，0，－1；x＝2，y＝0，1，2时，x－y＝2，1，0.根据集合中元素的互异性可知集合B的元素为－2，－1，0，1，2.共5个.8.(2013·天津)已知集合A＝{x∈R||x|≤2}，B＝{x∈R|x≤1}，则A∩B＝()A.(－∞，2]B.[1，2]C.[－2，2]D.[－2，1]答案 D解析解不等式|x|≤2，得－2≤x≤2，所以A＝[－2，2]，所以A∩B＝[－2，1].9.(2012·福建)已知集合M＝{1，2，3，4}，N＝{－2，2}，下列结论成立的是()A.N⊆MB.M∪N＝MC.M∩N＝ND.M∩N＝{2}答案 D解析A项，M＝{1，2，3，4}，N＝{－2，2}，M与N显然无包含关系，故A错.B项同A项，故B项错.C项，M∩N＝{2}，故C错，D对.10.(2012·湖北)已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0<x<5，x∈N}，则满足条件A⊆C⊆B的集合C的个数为()A.1B.2C.3D.4答案 D解析A＝{1，2}，B＝{1，2，3，4}，A⊆C⊆B，则集合C的个数为24－2＝22＝4，即C＝{1，2}，{1，2，3}，{1，2，4}，{1，2，3，4}.故选D.11.(2012·山东)已知集合U＝{0，1，2，3，4}，集合A＝{1，2，3，4}，B＝{2，4}，则(∁U A)∪B 为()A.{1，2，4}B.{2，3，4}C.{0，2，4}D.{0，2，3，4}答案 C解析由题意知∁U A＝{0}，又B＝{2，4}，∴(∁U A)∪B＝{0，2，4}，故选C.12.(2014·重庆，理)设全集U＝{n∈N|1≤n≤10}，A＝{1，2，3，5，8}，B＝{1，3，5，7，∁U A∩B＝________.9}，则()答案{7，9}解析由题意，得U＝{1，2，3，4，5，6，7，8，9，10}，故∁U A＝{4，6，7，9，10}，(∁U A)∩B ＝{7，9}.1.(2014·大纲全国理改编)设集合M＝{x|x2－3x－4<0}，N＝{x|0≤x≤5}，则M∩(∁R N)＝() A.(0，4] B.[0，4)C.[－1，0)D.(－1，0)答案 D解析∵M＝{x|x2－3x－4<0}＝{x|－1<x<4}，N＝{x|0≤x≤5}，∴∁R N＝{x|x<0或x>5}.∴M∩(∁R N)＝{x|－1<x<0}.2.(2014·江西，文)设全集为R，集合A＝{x|x2－9<0}，B＝{x|－1<x≤5}，则A∩(∁R B)＝() A.(－3，0) B.(－3，－1)C.(－3，－1]D.(－3，3)答案 C解析由题意知，A＝{x|x2－9<0}＝{x|－3<x<3}，∵B＝{x|－1<x≤5}，∴∁R B＝{x|x≤－1或x>5}.∴A ∩(∁R B)＝{x|－3<x<3}∩{x|x ≤－1或x>5}＝{x|－3<x ≤－1}.3.(2010·北京)集合P ＝{x ∈Z |0≤x<3}，M ＝{x ∈R |x 2≤9}，则P ∩M ＝( ) A.{1，2} B.{0，1，2} C.{x|0≤x<3} D.{x|0≤x ≤3}答案 B4.(2016·浙江)已知集合P ＝{x ∈R |1≤x ≤3}，Q ＝{x ∈R |x 2≥4}，则P ∪(∁R Q)＝( ) A.[2，3] B.(－2，3]C.[1，2)D.(－∞，－2]∪[1，＋∞) 答案 B解析 由于Q ＝{x|x ≤－2或x ≥2}，∁R Q ＝{x|－2<x<2}，故得P ∪(∁R Q)＝{x|－2<x ≤3}.选B.5.(2014·四川，文)已知集合A ＝{x|(x ＋1)(x －2)≤0}，集合B 为整数集，则A ∩B ＝( ) A.{－1，0} B.{0，1}C.{－2，－1，0，1}D.{－1，0，1，2} 答案 D解析 由二次函数y ＝(x ＋1)(x －2)的图像可以得到不等式(x ＋1)(x －2)≤0的解集A ＝[－1，2]，属于A 的整数只有－1，0，1，2，所以A ∩B ＝{－1，0，1，2}，故选D.6.(2012·北京)已知集合A ＝{x ∈R |3x ＋2>0}，B ＝{x ∈R |(x ＋1)(x －3)>0}，则A ∩B ＝( ) A.(－∞，－1) B.(－1，－23)C.(－23，3)D.(3，＋∞)答案 D解析 A ＝{x|x>－23}，B ＝{x|x>3或x<－1}，则A ∩B ＝{x|x>3}，故选D.课时作业(八) 1.2.1函数及其表示含解析1.下列集合A 到集合B 的对应f 是函数的是( ) A.A ＝{－1，0，1}，B ＝{0，1}，f ：A 中的数平方 B.A ＝{0，1}，B ＝{－1，0，1}，f ：A 中的数开方 C.A ＝Z ，B ＝Q ，f ：A 中的数取倒数D.A ＝R ，B ＝{正实数}，f ：A 中的数取绝对值 答案 A2.设集合M ＝{x|0≤x ≤2}，N ＝{y|0≤y ≤2}，下图所示4个图形中能表示集合M 到集合N 的函数关系的个数是( )A.0B.1C.2D.3答案 B3.函数f(x)＝1＋x ＋x1－x的定义域( ) A.[－1，＋∞) B.(－∞，－1] C.R D.[－1，1)∪(1，＋∞)答案 D解析 由⎩⎪⎨⎪⎧1＋x ≥0，1－x ≠0，解得⎩⎪⎨⎪⎧x ≥－1，x ≠1.故定义域为[－1，1)∪(1，＋∞)，故选D. 4.设函数f(x)＝3x 2－1，则f(a)－f(－a)的值是( ) A.0 B.3a 2－1 C.6a 2－2 D.6a 2答案 A解析 f(a)－f(－a)＝3a 2－1－[3(－a)2－1]＝0.5.四个函数：①y＝x＋1；②y＝x3；③y＝x2－1；④y＝1x.其中定义域相同的函数有()A.①②和③B.①和②C.②和③D.②③和④答案 A6.函数f(x)＝11＋x2(x∈R)的值域是()A.[0，1]B.[0，1)C.(0，1]D.(0，1) 答案 C7.已知f(x)＝π(x∈R)，则f(π2)等于()A.π2B.πC.πD.不确定答案 B解析因为π2∈R，所以f(π2)＝π.8.函数y＝21－1－x的定义域为()A.(－∞，1)B.(－∞，0)∪(0，1]C.(－∞，0)∪(0，1)D.[1，＋∞)答案 B9.将下列集合用区间表示出来.(1){x|x≥1}＝________；(2){x|2≤x≤8}＝________；(3){y|y＝1x}＝________.答案(1)[1，＋∞)(2)[2，8] (3)(－∞，0)∪(0，＋∞)10.若f(x)＝5xx2＋1，且f(a)＝2，则a＝________.答案12或211.已知f(x)＝x2＋x－1，x∈{0，1，2，3}，则f(x)的值域为________.答案{－1，1，5，11}12.设函数f(n)＝k(n∈N*)，k是π的小数点后的第n位数字，π＝3.141 592 653 5…，则f(3)＝________.答案 113.若函数y ＝1x －2的定义域为A ，函数y ＝2x ＋6的值域是B ，则A ∩B ＝________. 答案 [0，2)∪(2，＋∞)解析 由题意知A ＝{x|x ≠2}，B ＝{y|y ≥0}，则A ∩B ＝[0，2)∪(2，＋∞). 14.已知函数f(x)＝x ＋3＋1x ＋2.(1)求函数的定义域； (2)求f(－3)，f(23)的值；(3)当a>0时，求f(a)，f(a －1)的值.解析 (1)使根式x ＋3有意义的实数x 的集合是{x|x ≥－3}，使分式1x ＋2有意义的实数x 的集合是{x|x ≠－2}，所以这个函数的定义域是{x|x ≥－3}∩{x|x ≠－2}＝{x|x ≥－3，且x ≠－2}. (2)f(－3)＝－3＋3＋1－3＋2＝－1； f(23)＝23＋3＋123＋2＝113＋38＝38＋333. (3)因为a>0，故f(a)，f(a －1)有意义. f(a)＝a ＋3＋1a ＋2；f(a －1)＝a －1＋3＋1（a －1）＋2＝a ＋2＋1a ＋1.15.已知f(x)＝13－x 的定义域为A ，g(x)＝1a －x的定义域是B. (1)若B A ，求a 的取值范围； (2)若A B ，求a 的取值范围. 解析 A ＝{x|x<3}，B ＝{x|x<a}.(1)若B A ，则a<3，∴a 的取值范围是{a|a<3}； (2)若A B ，则a>3，∴a 的取值范围是{a|a>3}.1.下列函数f(x)和g(x)中，表示同一函数的是( ) A.y ＝f(x)与y ＝f(x ＋1) B.y ＝f(x)，x ∈R 与y ＝f(t)，t ∈R C.f(x)＝x 2，g(x)＝x 3xD.f(x)＝2x ＋1与g(x)＝4x 2＋4x ＋1答案 B2.下列式子中不能表示函数y ＝f(x)的是( ) A.x ＝2yB.3x ＋2y ＝1C.x ＝2y 2＋1D.x ＝y答案 C3.已知函数f(x)＝2x －1，则f(x ＋1)等于( ) A.2x －1 B.x ＋1 C.2x ＋1 D.1答案 C4.若f(x)＝x 2－1x ，则f(x)的定义域为________.答案 {x|x ≤－1或x ≥1}5.下列每对函数是否表示相同函数？ (1)f(x)＝(x －1)0，g(x)＝1； (2)f(x)＝x ，g(x)＝x 2； (3)f(t)＝t 2t ，g(x)＝|x|x .答案 (1)不是 (2)不是 (3)是6.已知A ＝B ＝R ，x ∈A ，y ∈B 对任意x ∈A ，x →y ＝ax ＋b 是从A 到B 的函数，若输出值1和8分别对应的输入值为3和10，求输入值5对应的输出值.解析 由题意可得⎩⎪⎨⎪⎧3a ＋b ＝1，10a ＋b ＝8，解得⎩⎪⎨⎪⎧a ＝1，b ＝－2，所以对应关系f ：x →y ＝x －2，故输入值5对应的输出值为3.7.已知f(x)＝11＋x ，求[f(2)＋f(3)＋…＋f(2 016)]＋[f(12)＋f(13)＋…＋f(12 016)].答案 2 015解析 f(x)＋f(1x )＝11＋x＋11＋1x＝11＋x ＋x1＋x ＝1，则原式＝⎣⎡⎦⎤f （2）＋f （12）＋⎣⎡⎦⎤f （3）＋f （13）＋…＋⎣⎡⎦⎤f （2 016）＋f （12 016）＝2 015.8.已知函数g(x)＝x ＋2x －6，(1)点(3，14)在函数的图像上吗？ (2)当x ＝4时，求g(x)的值； (3)当g(x)＝2时，求x 的值.答案(1)不在(2)－3(3)14课时作业(九)1.2.2-1函数的表示法（第1课时）1.下列结论正确的是( )A.任意一个函数都可以用解析式表示B.函数y ＝x ，x ∈{1，2，3，4}的图像是一条直线C.表格可以表示y 是x 的函数D.图像可表示函数y ＝f(x)的图像答案 C2.某同学在一学期的5次大型考试中的数学成绩(总分120分)如下表所示：A.成绩y 不是考试次数x 的函数B.成绩y 是考试次数x 的函数C.考试次数x 是成绩y 的函数D.成绩y 不一定是考试次数x 的函数答案 B3.函数f(x)＝x ＋|x|x的图像是下图中的( )答案 C4.从甲城市到乙城市t min 的电话费由函数g(t)＝1.06×(0.75[t]＋1)给出，其中t>0，[t]为t 的整数部分，则从甲城市到乙城市5.5 min 的电话费为( ) A.5.04元 B.5.56元 C.5.84元 D.5.38元答案 A解析 g(5.5)＝1.06(0.75×5＋1)＝5.035≈5.04.。

（新课标）最新苏教版高中数学必修一§1.1 集合的含义及其表示（1）课后训练【感受理解】1．给出下列命题(其中N 为自然数集) ：①N 中最小的元素是1 ②若a ∈N 则-a ∉N ③ 若a ∈N,b ∈N ，则a+b 的最小值是2（4）x x 212=+的解可表示为}1,1{， 其中正确的命题个数为 . 2．用列举法表示下列集合.①小于12的质数构成的集合；②平方等于本身的数组成的集合；③由||||(,)a b a b R a b+∈所确定的实数的集合； ④抛物线221y x x =-+ (x 为小于5的自然数)上的点组成的集合.3. 若方程x 2-5x+6=0和方程x 2-x-2=0的解为元素的集合为M ，则M 中元素的个数为4．由2,2,4a a -组成一个集合A ，A 中含有3个元素，则a 的取值可以是【思考应用】5．由实数332,,,x x x x --所组成的集合里最多有 个元素.6. 由“,x xy ”组成的集合与由“0,||,x y ”组成的集合是同一个集合，则实数,x y 的值是否确定的？若确定，请求出来，若不确定，说明理由.7．定义集合运算：},),({B y A x y x xy z z B A ∈∈+==Θ，设集合}3,2{},1,0{==B A ，求集合B A Θ.8．关于x 的方程20(0)ax bx c a ++=≠，当,,a b c 分别满足什么条件时，解集为空集、含一个元素、含两个元素？9. 已知集合{,}A x x m m Z N Z ==+∈∈.(1)证明：任何整数都是A 的元素；(2)设12,,x x A ∈求证：12,x x A ⋅∈【拓展提高】9.设S 是满足下列两个条件的实数所构成的集合： ①1S ∉，②若a S ∈，则11S a ∈-， 请解答下列问题：（1）若2S ∈，则S 中必有另外两个数，求出这两个数；（2）求证：若a S ∈，则11S a-∈ （3）在集合S 中元素能否只有一个？请说明理由；（4）求证：集合S 中至少有三个不同的元素.§1.1集合的含义及其表示（2）课后训练1． 设a ，b ，c 均为非零实数，则x=||||||||a b c abc a b c abc+++的所有值为元素组成集合是________2． 集合}9,7,5,3,1{用描述法表示为 .3． 下列语句中，正确的是 .（填序号）（1）0与{0}表示同一个集合；（2）由1，2，3组成的集合可表示为{1，2，3}或{3，1，2}；（3）方程0)2()1(22=--x x 的所有解的集合可表示为{1，1，2，2} （4）集合}54{<<x x 可以用列举法表示.4．所有被3整除的数用集合表示为 .5．下列集合中表示同一集合的是` （填序号）（1）M={3，2}，N={2，3} （2）M={(3，2)}，N={（2，3）}（3）M={(,)1},{(,)1}x y x y N y x x y +==+= (4) M={1，2}，N={(1,2)}6.下列可以作为方程组⎩⎨⎧-=-=+13y x y x 的解集的是 （填序号） （1）{1,2},x y ==(2){1,2}(3){(1,2)} （4）{(,)12}(5){(,)12}x y x y x y x y ====且或（6）}0)2()1(),{(22=-+-y x y x7．用另一种方法表示下列集合.（1）{绝对值不大于2的整数} （2）{能被3整除，且小于10的正数}（3）}5,{Z x x x x x ∈<=且 （4）*},*,6),{(N y N x y x y x ∈∈=+（5）{5,3,1,1,3--}8．已知{}{}0|,0|22=+-==++=q px x x B q px x x A .当{}2=A 时，求集合B9．用描述法表示图中阴影部分（含边界）的点的坐标集合.10．对于*,N b a ∈,现规定：⎩⎨⎧⨯+=)()(*的奇偶性不同与的奇偶性相同与b a b a b a b a b a ，集合{(,)*36,,*}M a b a b a b N ==∈ （1） 用列举法表示b a ,奇偶性不同时的集合M.（2） 当b a ,奇偶性相同时的集合M 中共有多少个元素？【拓展提高】11 设元素为正整数的集合A 满足“若x A ∈,则10x A -∈”.（1）试写出只有一个元素的集合A ；（2）试写出只有两个元素的集合A ；（3）这样的集合A 至多有多少个元素？（4）满足条件的集合A 共有多少个？§1.2 子集·全集·补集（1）课后训练【感受理解】1． 设M 满足{1，2，3}⊆M ≠⊂{1，2，3，4，5，6}，则集合M 的个数为 2．下列各式中，正确的个数是 ①0={0}；②0∈{0}；③{1}∈{1，2，3}；④{1，2}⊆{1，2，3}；⑤{a ，b}⊆{a ，b}．3．设{|12}A x x =<< ，{|}B x x a =<，若A 是B 的真子集，则a 的取值范围是 .4．若集合A ={1，3，x}，B ={x 2，1}，且B ⊆A ，则满足条件的实数x 的个数为 . 5．设集合M ={(x,y)|x+y<0，xy>0}和N ={(x,y)|x<0，y<0}，那么M 与N 的关系为______________．6．集合A ={x|x=a 2-4a+5，a ∈R}，B ={y|y=4b 2+4b+3，b ∈R} 则集合A 与集合B 的关系是________．【思考应用】7.设x ，y ∈R ，B={(x,y)|y-3=x-2}，A={(x,y)|32y x --=1}，则集合A 与B 的关系是_______ ____． 8.已知集合{}{}|21,,|41,,A x x n n Z B x x n n Z ==+∈==±∈则,A B 的关系是 .9．设集合{}{}21,3,,1,,1,A a B a a a ==-+,A B =若则________=a .10．已知非空集合P 满足：(){}11,2,3,4;P ⊆()2,5a P a P ∈-∈若则，符合上述要求的集合P 有 个.11．已知A={2，4，x 2-5x+9}，B={3，x 2+ax+a}，C={x 2+(a+1)x-3，1}. 求（1）当A={2，3，4}时，求x 的值；（2）使2∈B ，BA ，求x a ,的值； （3）使B= C 的x a ,的值．【拓展提高】12．已知集合{}{},121|,52|-≤≤+=≤≤-=m x m x B x x A 满足,A B ⊆求实数m 的取值范围.(变式)已知集合{}{}|25,|121,A x x B x m x m =-<<=+<<-满足,A B ⊆求实数m 的取值范围.⊂ ≠§1.2 子集·全集·补集（2）课后训练【感受理解】1．设集合{}{},,3|,,4|22R b b y y B R a a x x A ∈+-==∈+-==则A ，B 间的关系为 . 2若U={x|x 是三角形}，P={x|x 是直角三角形}则U C P = . 3已知全集+=R U ，集合{}|015,,A x x x R =<-≤∈则_______.U C A = 4．已知全集}{非零整数=U ，集合}},42{U x x x A ∈>+=，则=A C U .5．设},61{},,5{N x x x B N x x x A ∈<<=∈≤=，则=B C A .【思考应用】6．设全集U={1，2，3，4，5}，M={1，4}，则U C M 的所有子集的个数是 .7．已知全集},21{*N n x x U n ∈==，集合}*,21{2N n x x A n ∈==，则=A C U .8．已知A A y ax y x A Z a ∉-∈≤-=∈)4,1(,)1,2(}3),{(,且，则满足条件a 的值为 .9．设U=R ，}1{},31{+≤≤=≥≤=m x m x B x x x P 或，记所有满足P C B U ⊆的m 组成的集合为M ，求M C U .10.（1）设全集{}{},1|,1|,+>=≤==a x x B x x A R U 且U C A B ⊆，求a 的范围.（2）已知全集{}{}{}22,3,23,2,,5,U U a a A b C A =+-==求实数b a 和的值.【拓展提高】10．已知全集}5{的自然数不大于=U ，集合}1,0{=A ，}1{<∈=x A x x B 且，}1{U x A x x C ∈∉-=且．（1）求U B ð，U C ð．（2）若}{A x x D ∈=，说明D B A ,,的关系.§1.3 交集·并集（1）课后训练【感受理解】1．设全集{1,2,3,4,5},{1,3,5},{2,4,5}U A B ===,则()()U U C A C B =I .2．设集合{|5,},{|1,}A x x x N B x x x N =≤∈=>∈，那么A B =I .3．若集合22{|21,},{|21,}P y y x x x N Q y y x x x N ==+-∈==-+-∈，则下列各式中正确的是 .(1);(2){0};(3){1};(4)P Q P Q P Q P Q N =∅==-=I I I I4．已知集合A={x|-5<x<5}，B={x|-7<x<a}，C={x|b<x<2}，且A ∩B=C ，则 a ，b 的值分别为 .【思考应用】5．设全集U={1，2，3，4}，A 与B 是U 的子集，若A ∩B ＝{1，3 }，则称(A,B)为一个“理想配集”.（若A ＝B ，规定(A,B)＝(B, A)；若A ≠B ，规定(A,B)与(B, A)是两个不同的“理想配集”）.那么符合此条件的“理想配集”的个数是 .6．记{}{},361T ,的三角形，至少有一内角为至少有一边为等腰三角形。

2021-2022年人教B版（2019）高一数学上册课时同步练第8课第1章章末综合检测【含答案】一、基础巩固1．下列各组对象不能构成集合的是( )A．拥有手机的人B．2019年高考数学难题C．所有有理数D．小于π的正整数【答案】B【解析】B选项中“难题”的标准不明确，不符合确定性，所以选B.2．命题“每一个四边形的四个顶点共圆”的否定是( )A．存在一个四边形，它的四个顶点不共圆B．存在一个四边形，它的四个顶点共圆C．所有四边形的四个顶点共圆D．所有四边形的四个顶点都不共圆【答案】A【解析】根据全称量词命题的否定是存在量词命题，得命题“每一个四边形的四个顶点共圆”的否定是“存在一个四边形，它的四个顶点不共圆”，故选A.3．已知集合P＝{x|x＜3}，Q＝{x|－1≤x≤4}，则P∪Q＝( )A．{x|－1≤x＜3} B．{x|－1≤x≤4}C．{x|x≤4} D．{x|x≥－1}【答案】C【解析】在数轴上表示两个集合，如图，易知P∪Q＝{x|x≤4}．4．已知全集U＝{1,2,3,4,5,6,7}，A＝{3,4,5}，B＝{1,3,6}，那么集合{2,7}是( )A．A∪B B．A∩BC．∁U(A∩B) D．∁U(A∪B)【答案】D【解析】∵A ∪B ＝{1,3,4,5,6}，∴∁U (A ∪B)＝{2,7}．5．设A ，B ，C 是三个集合，则“A∩B＝A∩C”是“B＝C”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B【解析】由A∩B＝A∩C，不一定有B ＝C ，反之，由B ＝C ，一定可得A∩B＝A∩C.所以“A∩B＝A∩C”是“B＝C”的必要不充分条件．故选B.6．设全集U ＝{0，1，2，3}，集合A ＝{x ∈U|x 2＋mx ＝0}，若∁U A ＝{1，2}，则实数m ＝________．【答案】－3【解析】由题意可知，A ＝{x ∈U|x 2＋mx ＝0}＝{0，3}，即0，3为方程x 2＋mx ＝0的两根，所以m ＝－3.7．“a<14”是“一元二次方程x 2－x ＋a ＝0有实数解”的________条件．【答案】充分不必要【解析】当一元二次方程x 2－x ＋a ＝0有实数解，则Δ≥0，即1－4a≥0，即a≤14，又“a<14”能推出“a≤14”，但“a≤14”不能推出“a<14”，即“a<14”是“一元二次方程x 2－x ＋a ＝0有实数解”的充分不必要条件．8．银川一中开展小组合作学习模式，高二某班某组王小一同学给组内王小二同学出题如下：若命题“∃x ∈R ，x 2＋2x ＋m≤0”是假命题，求m 的范围．王小二略加思索，反手给了王小一一道题：若命题“∀x ∈R ，x 2＋2x ＋m>0”是真命题，求m 的范围．你认为，两位同学题中m 的范围是否一致？________(填“是”“否”中的一个)【答案】是【解析】因为命题“∃x∈R，x2＋2x＋m≤0”的否定是“∀x∈R，x2＋2x＋m>0”，而命题“∃x ∈R，x2＋2x＋m≤0”是假命题，则其否定“∀x∈R，x2＋2x＋m>0”为真命题，所以两位同学题中的m的范围是一致的．9.设计如图所示的四个电路图，条件A：“开关S1闭合”；条件B：“灯泡L亮”，则A 是B的充要条件的图为________．【答案】乙【解析】对于图甲，开关S1闭合灯亮，反过来灯泡L亮，也可能是开关S2闭合，∴A是B的充分不必要条件．对于图乙，只有一个开关，灯如果要亮，开关S1必须闭合，∴A是B的充要条件．对于图丙，∵灯亮必须S1和S2同时闭合，∴A是B的必要不充分条件．对于图丁，灯一直亮，跟开关没有关系，∴A是B的既不充分也不必要条件．10．已知A＝{x|－1<x≤3}，B＝{x|m≤x<1＋3m}．(1)当m＝1时，求A∪B；(2)若B⊆∁R A，求实数m的取值范围.【答案】）（1）A∪B＝{x|－1<x<4}；（2）m>3或m≤－1 2【解析】(1)当m＝1时，B＝{x|1≤x<4}，A∪B＝{x|－1<x<4}．(2)∁R A＝{x|x≤－1或x>3}．当B＝∅，即m≥1＋3m时，得m≤－12，满足B⊆∁R A；当B≠∅时，要使B⊆∁R A成立，则⎩⎨⎧m<1＋3m ，1＋3m≤－1或⎩⎨⎧m<1＋3m ，m>3， 解得m>3.综上可知，实数m 的取值范围是m>3或m≤－12.二、拓展提升11.若非空集合A ，B ，C 满足A ∪B ＝C ，且B 不是A 的子集，则( ) A ．“x∈C”是“x∈A”的充分条件但不是必要条件 B ．“x∈C”是“x∈A”的必要条件但不是充分条件 C ．“x∈C”是“x∈A”的充要条件D ．“x∈C”既不是“x∈A”的充分条件也不是“x∈A”的必要条件 【答案】B【解析】由A ∪B ＝C 知，x ∈A ⇒x ∈C ，x ∈CD/⇒x ∈A.所以x ∈C 是x ∈A 的必要不充分条件．12．记实数x 1，x 2，…，x n 中的最大数为max{x 1，x 2，…，x n }，最小数为min{x 1，x 2，…，x n }．已知△ABC 的三边边长为a ，b ，c(a≤b≤c)，定义它的倾斜度为L ＝max a b ，bc ，c a ·min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ，则“L＝1”是“△ABC 为等边三角形”的( ) A ．必要而不充分条件 B ．充分而不必要条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【解析】当△ABC 是等边三角形时，a ＝b ＝c ， ∴L ＝max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ·min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝1×1＝1. ∴“L＝1”是“△ABC 为等边三角形”的必要条件． ∵a≤b≤c，∴max ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝ca.又∵L ＝1，∴min ⎩⎨⎧⎭⎬⎫a b ，b c ，c a ＝ac，即a b ＝a c 或b c ＝a c ，得b ＝c 或b ＝a ，可知△ABC 为等腰三角形，而不能推出△ABC 为等边三角形． ∴“L＝1”不是“△ABC 为等边三角形”的充分条件．13．设m ∈N *，一元二次方程x 2－4x ＋m ＝0有整数根的充要条件是m ＝________. 【答案】3或4 【解析】x ＝4±16－4m2＝2±4－m ，因为x 是整数，即2±4－m 为整数，所以4－m 为整数，且m≤4.又m ∈N *，取m ＝1,2,3,4.验证可得m ＝3,4符合题意，所以m ＝3,4时可以推出一元二次方程x 2－4x ＋m ＝0有整数根．14．设p ：12≤x≤1；q ：a≤x≤a＋1，若p 是q 的充分条件，则实数a 的取值范围是________．【答案】⎣⎢⎡⎦⎥⎤0，12【解析】因为q ：a≤x≤a＋1，p 是q 的充分条件，所以⎩⎨⎧a ≤12，a ＋1≥1，解得0≤a≤12.15．(本小题满分12分)下列命题中，判断条件p 是条件q 的什么条件；并说明理由． (1)p ：|x|＝|y|，q ：x ＝y ；(2)p ：△ABC 是直角三角形，q ：△ABC 是等腰三角形； (3)p ：四边形的对角线互相平分，q ：四边形是矩形．【答案】（1）必要不充分条件；（2）既不充分也不必要条件；（3）必要不充分条件 【解析】(1)因为|x|＝|y|⇒/x ＝y ，但x ＝y ⇒|x|＝|y|， 所以p 是q 的必要条件，但不是充分条件． (2)因为△ABC 是直角三角形⇒/△ABC 是等腰三角形， △ABC 是等腰三角形⇒/△ABC 是直角三角形， 所以p 既不是q 的充分条件，也不是q 的必要条件． (3)因为四边形的对角线互相平分⇒/四边形是矩形， 四边形是矩形⇒四边形的对角线互相平分，所以p是q的必要条件，但不是充分条件．16．已知a，b，c∈R，a≠0，判断“a－b＋c＝0”是“二次方程ax2＋bx＋c＝0有一根为－1”的什么条件？并说明理由．【答案】充要条件【解析】“a－b＋c＝0”是“二次方程ax2＋bx＋c＝0有一根为－1”的充要条件．理由如下：当a，b，c∈R，a≠0时，若“a－b＋c＝0”，则－1满足二次方程ax2＋bx＋c＝0，即“二次方程ax2＋bx＋c＝0有一根为－1”，故“a－b＋c＝0”是“二次方程ax2＋bx＋c＝0有一根为－1”的充分条件，若“二次方程ax2＋bx＋c＝0有一根为－1”，则“a－b＋c＝0”，故“a－b＋c＝0”是“二次方程ax2＋bx＋c＝0有一根为－1”的必要条件，综上所述，“a－b＋c＝0”是“二次方程ax2＋bx＋c＝0有一根为－1”的充要条件.。

2021-2022学年度人教版高一数学必修一各章节同步练习（含答案）1.1.1 集合的含义与表示课后作业· 练习案【基础过关】1．若集合A中只含一个元素1，则下列格式正确的是A.1=AB.0∈AC.1∉AD.1∈A2．集合{x∈N∗|x−2<3}的另一种表示形式是A.{0,1,2,3,4}B.{1,2,3,4}C.{0,1,2,3,4,5}D.{1,2,3,4,5} 3．下列说法正确的有①集合{x∈N|x3=x}，用列举法表示为{−1,0,l}；②实数集可以表示为{x|x为所有实数}或{R};③方程组{x+y=3,x−y=−1的解集为{x=1,y=2}.A.3个B.2个C.1个D.0个4．直角坐标系中，坐标轴上点的集合可表示为A.{(x,y)|x=0,y≠0,或x≠0,y=0}B. {(x,y)|x=0且y=0}C.{(x,y)|xy=0}D.{(x,y)|x,y不同时为0}5．若集合P含有两个元素1，2，集合Q含有两个元素1，a2，且P，Q相等，则a=____.6．已知集合A={(x,y)|y=2x+1}，B={(x,y)|y=x+3}，a∈A且a∈B，则a为 .7．设方程ax2+2x+1=0(a∈R)的根组成的集合为A，若A只含有一个元素，求a 的值.8．用适当的方法表示下列集合：(1)所有被3整除的整数；(2)满足方程x=|x|的所有x的值构成的集合B.【能力提升】集合P={x|x=2k,k∈Z}，M={x|x=2k+1,k∈Z}，a∈P,b∈M，设c= a+b，则c与集合M有什么关系？详细答案【基础过关】1．D【解析】元素与集合之间只存在“∈”与“∉”的关系，故1∈A正确.2．B【解析】由x－2＜3得x＜5，又x∈N∗，所以x＝1，2，3，4，即集合的另一种表示形式是{1，2，3，4}.3．D【解析】对于①，由于x∈N，而－1∉N，故①错误；对于②，由于“{ }”本身就具有“全部”、“所有”的意思，而且实数集不能表示为{R}，故②错误；对于③，方程组的解集是点集而非数集，故③错误.4．C【解析】坐标轴上的点分为x轴、y轴上的点，在x轴上的点纵坐标为0，在y轴上的点横坐标为0.5．±√2【解析】由于P，Q相等，故a2＝2，从而a＝±√2.6．(2，5)【解析】∵a∈A且a∈B，∴a是方程组{y＝2x＋1，y＝x＋3，的解，解方程组，得{x＝2，y＝5，∴a为(2，5).7．A中只含有一个元素，即方程ax2＋2x＋1＝0(a∈R)有且只有一个实根或两个相等的实根.(1)当a＝0时，方程的根为x＝－12；(2)当a≠0时，有△＝4－4a＝0，即a＝1，此时方程的根为x1＝x2＝－1.∴a的值为0或1.【备注】误区警示：初学者易自然认为ax2＋2x＋1＝0(a∈R)是一元二次方程，而漏掉对a的讨论，导致漏解.举一反三：若把“若A只含有一个元素”改为“若A含有两个元素”，则结论又如何？由题意知，a≠0，且△＝4－4a＞0，解得a＜1.所以a＜1且a≠0.8．(1){x|x＝3n，n∈Z}；(2)B＝{x｜x＝|x|，x∈R}.【能力提升】∵a∈P，b∈M，c＝a＋b，设a＝2k1，k1∈Z，b＝2k2＋1，k2∈Z，∴c＝2k1＋2k2＋1＝2(k1＋k2)＋1，又k1＋k2∈Z∴c∈M.1.1.2集合间的基本关系班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．设A={x|1<x<2}，B={x|x<a}，若A⊆B，则a的取值范围是A.a≤2 B.a≤1 C.a≥1 D.a≥22．设集合M={x|x=k2+14,k∈Z}，N={x|x=k4+12,k∈Z}，则A.M =NB.M⊆NC.M⫌ND. M⫋N3．已知集合A={1,−2,x2−1}，B={1,x2−3x,0}，若A=B，求实数x的值. 4．满足条件{1,2,3}⫋M⫋{1,2,3,4,5,6}的集合M的个数是A.8B.7C.6D.55．设集合M={(x,y)|x+y<0,xy>0}和P={(x,y)|x<0,y>0}，那么M与P的关系为 .6．含有三个实数的集合,既可表示成{a,ba,1},又可表示成{a2,a+b,0}，则a2015+b2016= .7．设集合A={(x,y)|y=2x−1}，B={(x,y)|y=x+3}，求A∩B.8．已知M={x | x2-2x-3=0},N={x | x2+ax+1=0,a∈R},且N⫋M,求a的取值范围.【能力提升】已知A={x||x−a|=4}，B={1,2,b}，是否存在实数a，使得对于任意实数b(b≠1,且b≠2)，都有A⊆B?若存在,求出对应的a的值；若不存在，说明理由.答案【基础过关】1．D【解析】∵A⊆B，∴a≥22．D【解析】本题考查集合间的基本关系. M={x|x=2k+14,k∈Z}, N={x|x=k+24,k∈Z}={x|x=m4,m∈Z}；而{x|x=2k+14,k∈Z}⫋{x|x=m4,m∈Z}；即M⫋N.选D.3．由A＝B，可得{x2－1＝0x2－3x＝－2，解得x＝1.4．C【解析】本题考查子集.由题意得M={1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,3,4,5},{1,2,3,4,6},{1,2,3,6,5}共6个.选C.5．M＝P【解析】∵xy＞0，∴x，y同号，又x＋y＜0，∴x＜0，y＜0，即集合M表示第三象限内的点.而集合P表示第三象限内的点，故M＝P.6．-1【解析】本题考查相等集合.由题意得{a,ba,1}={a2,a+b,0},所以ba=0,即b=0；此时{a,0,1}={a2,a,0}，所以a2=1，a=a，且a≠1，解得a=−1.所以a2015+ b2016=−1+0=−1.7．{y=2x−1y=x+3，解得{x=4y=7；所以A∩B={(4,7)}.【解析】本题考查集合的基本运算. 8．解：M={x | x2-2x-3=0}={3,-1};∵N ⫋M,当N=时，N ⫋M 成立,N={x | x 2+ax+1=0},∴a 2-4＜0, ∴-2＜a ＜2;当N≠时，∵N ⫋M, ∴3∈N 或 -1∈N;当3∈N 时，32-3a+1=0即a= -,N={3,},不满足N ⫋M;当-1∈N 时，(-1)2-a+1=0即a=2,N={-1},满足N ⫋M;∴a 的取值范围是-2<a ≤2.【解析】本题考查集合间的基本关系. 【能力提升】不存在.要使对任意的实数b 都有A ⊆B ，则1，2是A 中的元素，又∵A ＝{a －4，a ＋4}，∴{a －4＝1，a ＋4＝2或{a ＋4＝1，a －4＝2.这两个方程组均无解，故这样的实数a 不存在.1.1.3 集合的基本运算班级:__________姓名:__________设计人__________日期__________课后作业【基础过关】1．若A ⊆B ，A ⊆C ，B ={0，1，2，3，4}，C ={0，2，4，8}，则满足上述条件的集合A 的个数为 A.5B.6C.7D.82．已知全集U={1,2,3,4,5,6,7,8},A={3,4,5}, B={1,3,6},那么集合{2,7,8}是A.A ∪BB.A ∩BC.(∁U A )∩(∁U B )D.(∁U A )∪(∁U B )∅∅310313．若集合P={x∈N|-1<x<3},Q={x|x=2a,a∈P},则P∩Q=A.⌀B.{x|-2<x<6}C.{x|-1<x<3}D.{0,2}4．设全集U=R,集合M={x|x>1或x<-1},N={x|0<x<2},则N∩(∁U M)=A.{x|-2≤x<1}B.{x|0<x≤1}C.{x|-1≤x≤1}D.{x|x<1}5．某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为.6．集合A={(x,y)|x+y=0},B={(x,y)|x-y=2},则A∩B= .7．设集合A={x|0<x-m<3},B={x|x≤0,或x≥3},分别求满足下列条件的实数m.(1)A∩B=⌀;(2)A∪B=B.8．已知集合A={x|2≤x<7},B={x|3<x<10},C={x|x<a}.(1)求A∪B,(∁R A)∩B;(2)若A∩C≠⌀,求a的取值范围.【能力提升】已知集合A={x|x2-3x+2=0},B={x|x2-ax+a-1=0},C={x|x2-x+2m=0}.(1)若A∪B=A,求a的值;(2)若A∩C=C,求m的取值范围.详细答案【基础过关】1．D2．C【解析】借助Venn图易得{2,7,8}=∁U(A∪B),即为(∁U A)∩(∁U B).3．D【解析】由已知得P={0,1,2},Q={0,2,4},所以P ∩Q={0,2}. 4．B【解析】∁U M={x|-1≤x ≤1},结合数轴可得N ∩(∁U M )={x|0<x ≤1}. 5．12【解析】设两项运动都喜爱的人数为x ,依据题意画出Venn 图,得到方程15-x+x+10-x+8=30,解得x=3,∴喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12.6．{(1,-1)}【解析】A ∩B={(x ,y )|{x +y =0x −y =2}={(1,-1)}.7．因为A ={x |0<x -m <3},所以A ={x |m <x <m +3}. (1)当A ∩B =⌀时,需{m ≥0m +3≤3,故m =0.即满足A ∩B =⌀时,m 的值为0.(2)当A ∪B =B 时,A ⊆B ,需m ≥3,或m +3≤0,得m ≥3,或m ≤-3.即满足A ∪B =B 时,m 的取值范围为{m |m ≥3,或m ≤-3}.8．(1)因为A={x|2≤x<7},B={x|3<x<10},所以A ∪B={x|2≤x<10}. 因为A={x|2≤x<7},所以∁R A={x|x<2,或x≥7},则(∁R A)∩B={x|7≤x<10}. (2)因为A={x|2≤x<7},C={x|x<a},且A∩C≠⌀,所以a>2. 【能力提升】A={1,2}.(1)因为A ∪B=A ,所以B ⊆A ,故集合B 中至多有两个元素1,2.而方程x 2-ax+a-1=0的两根分别为1,a-1,注意到集合中元素的互异性,有 ①当a-1=2,即a=3时,B={1,2},满足题意; ②当a-1=1,即a=2时,B={1},满足题意. 综上可知,a=2或a=3. (2)因为A ∩C=C ,所以C ⊆A.①当C=⌀时,方程x 2-x+2m=0无实数解,因此其根的判别式Δ=1-8m <0,即 m >18.②当C={1}(或C={2})时,方程x 2-x+2m=0有两个相同的实数解x=1(或x=2),因此其根的判别式Δ=1-8m=0,解得m=18,代入方程x 2-x+2m=0,解得x=12,显然m=18不符合要求.③当C={1,2}时,方程x 2-x+2m=0有两个不相等的实数解x 1=1,x 2=2,因此x 1+x 2=1+2≠1,x 1x 2=2=2m ,显然不符合要求.综上,m >18.1.2.1 函数的概念班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．下列函数中,值域为(0,+∞)的是( )A.y=√xB.y=√xC.y=1xD.y=x 2+12．下列式子中不能表示函数y =f (x )的是 A.x =y 2+1B.y =2x 2+1C.x −2y =6D.x =√y3．函数y=√1−x2+√x2−1的定义域是( )A.(-1,1)B.(-∞,-1)∪(1,+∞)C.(0,1)D.{-1,1}4．若f(x)满足f(a∙b)=f(a)+f(b)，且f(2)=p，f(3)=q，则f(72)等于A.p+q B.3p+2q C.2p+3q D.p3+q25．若[a,3a−1]为一确定区间，则 a 的取值范围是 .6．函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0，0)，(1，2)，(3，1)，则f[f(3)]的值等于 .7．求下列函数的定义域.(1)y=√2x+1+√3−4x；(2)y=1|x+2|−1.8．已知f(x)=x1+x.(1)求f(2)+f(12)，f(3)+f(13)的值；(2)求f(2)+f(3)+f(4)+⋯+f(2013)+f(12)+f(13)+f(14)+⋯+f(12013)的值.【能力提升】已知函数f(x)对任意实数a,b,都有f(ab)=f(a)+f(b)成立.(1)求f(0),f(1)的值;(2)若f(2)=p,f(3)=q(p,q为常数),求f(36)的值.答案【基础过关】 1．B【解析】y=√x 的值域为[0,+∞),y=1x的值域为(-∞,0)∪(0,+∞),y=x 2+1的值域为[1,+∞).故选B. 2．A【解析】一个x 对应的y 值不唯一. 3．D【解析】要使函数式有意义,需满足{1−x 2≥0x 2−1≥0,解得x=±1,故选D.4．B【解析】f (72)＝f (8×9)＝f (8)＋f (9)＝3f (2)＋2f (3)＝3p ＋2q . 5．(12，＋∞)【解析】由题意3a －1＞a ，则a ＞12.【备注】误区警示：本题易忽略区间概念而得出3a －1≥a ，则a ≥12的错误.6．2【解析】由图可知f (3)＝1，∴f [f (3)]＝f (1)＝2.【备注】误区警示：本题在求解过程中会因不理解f [f (3)]的含义而出错. 7．(1)由已知得{2x ＋1≥0⇒x ≥－12，3－4x ≥0⇒x ≤34，∴函数的定义域为[−12，34].(2)由已知得：∵|x ＋2|－1≠0，∴|x ＋2|≠1， 得x ≠－3，x ≠－1.∴函数的定义域为(－∞，－3)∪(－3，－1)∪(―1，＋∞). 8．(1)f (2)＋f (12)＝21＋2＋121＋12＝23＋13＝1，f (3)＋f (13)＝31＋3＋131＋13＝34＋14＝1.(2)∵f(x)＋f (1x)＝x 1＋x＋1x1＋1x＝x 1＋x＋1x ＋1＝1，∴f (2)＋f (3)＋f (4)＋⋯＋f(2013)＋f (12)＋f (13)＋f (14)＋⋯＋f (12013)＝f (2)＋f (12)＋f (3)＋f (13)＋f (4)＋f (14)＋⋯＋f (2013)＋ f (12013)＝1＋1＋1＋⋯＋1(共2012个1相加) ＝2012. 【能力提升】(1)令a=b=0,得f(0)=f(0)+f(0),解得f(0)=0; 令a=1,b=0,得f(0)=f(1)+f(0),解得f(1)=0. (2)方法一 令a=b=2,得f(4)=f(2)+f(2)=2p, 令a=b=3,得f(9)=f(3)+f(3)=2q, 令a=4,b=9,得f(36)=f(4)+f(9)=2p+2q.方法二 因为36=22×32,所以f(36)=f(22×32)=f(22)+f(32)=f(2×2)+f(3×3)=f(2)+f(2)+f(3)+f(3)=2f(2)+2f(3)=2p+2q.【解析】题设只有一个函数方程,因此考虑特殊值0,1,通过解方程获解.1.2.2函数的表示法班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．已知y =f (x )是反比例函数，当x =2 时，y =1，则y =f (x ) 的函数关系式为 A.f (x )=1xB.f (x )=−1xC.f (x )=2xD.f (x )=−2x2．已知函数f (x )={2,x ∈[−1,1],x,x ∉[−1,1],若f [f (x )]=2,则x 的取值范围是A.∅B.[−1,1]C.(−∞,−1)∪(1.+∞)D.{2}∪[−1,1]3．已知函数f(x)={x +1,x ∈[−1,0]x 2+1,x ∈(0,1],则函数f(x)的图象是( )A. B. C. D.4．已知f (x )={3x +1,x ≥0,|x |,x <0,则f[f(−√2)]=A.2B.-2C.3√2+1D.−3√2+15．已知函数f (2x +1)=3x +2，且f (a )=4，则a = . 6．已知函数f (x )对于任意实数x 满足条件f (x+2)=1f(x),若f (1)=-5,则f[f (5)]= .7．已知a ，b 为常数，且a ≠0，f (x )=ax 2+bx ，f (x )=0，方程f (x )=x 有两个相等的实数根.求函数f (x )的解析式.8．如图，△OAB 是边长为2的正三角形，记△OAB 位于直线x =t (t >0) 左侧的图形的面积为f (t )，试求函数f (t ) 的解析式.【能力提升】下图是一个电子元件在处理数据时的流程图:(1)试确定y与x的函数关系式;(2)求f(-3), f(1)的值;(3)若f(x)=16,求x的值.答案【基础过关】1．C【解析】根据题意可设f(x)＝kx(k≠0)，∵当x＝2时，y＝1，∴1＝k2，∴k＝2.2．D【解析】若x∈[－1，1]，则有f(x)＝2∉[-1，1]，∴f(2)＝2；若x∉[－1，1]，则f(x)＝x∉[－1，1]，∴f[f(x)]＝x，此时若f[f(x)]＝2，则有x＝2.【备注】误区警示：本题易将x∉[－1，1]的情况漏掉而错选B.3．A【解析】当x=-1时,y=0,即图象过点(-1,0),D错;当x=0时,y=1,即图象过点(0,1),C错;当x=1时,y=2,即图象过点(1,2),B错.故选A.4．C【解析】∵f(－√2)＝|－√2|＝√2＞0，∴f[f(－√2)]＝f(√2)＝3√2＋1.【备注】无5．7 3【解析】f(2x＋1)＝3x＋2＝32(2x＋1)＋12，∴f(x)＝32x＋12，∴f(a)＝32a＋12＝4，解得a＝73 .6．-15【解析】由已知条件f (x+2)=1f(x)可得f (x+4)=1f(x+2)=f (x ),所以f (5)=f (1)=-5,所以f[f (5)]=f (-5)=f (-1)=1f(−1+2)=1f(1)=-15.7．∵f(x)＝ax 2＋bx ，且方程f (x )＝x 有两个相等的实数根，∴∆＝(b －1)2＝0，∴b ＝1，又∵f (2)＝0，∴4a ＋2＝0，∴a ＝－12，∴f(x)＝－12x 2＋x .8．OB 所在的直线方程为y ＝√3x .当t ∈(0，1]时，由x ＝t ，求得y ＝√3t ，所以f (t )＝√32t 2； 当t ∈(1，2]时，f (t )＝√3－√32(2−t)2；当t ∈(2，＋∞)时，f (t )＝√3，所以{√32t 2，t ∈(0，1]， √3－√32(2−t)2，t ∈(1，2]，√3，t ∈(2，＋∞).【能力提升】(1)由题意知y={(x +2)2,x ≥1x 2+2,x <1.(2)f (-3)=(-3)2+2=11, f (1)=(1+2)2=9.(3)若x ≥1,则(x+2)2=16,解得x=2或x=-6(舍去);若x<1,则x 2+2=16,解得x=√14(舍去)或x=-√14.综上可得,x=2或x=-√14.1.3.1单调性与最大（小）值班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．若函数f(x)在区间(a,b)上是增函数，在区间(c,d)上也是增函数，则函数f(x)在区间(a,b)∪(c,d)上A.必是增函数B.必是减函数C.先增后减D.无法确定单调性2．下列函数在(0，1)上是增函数的是A.y=1−2xB.y=−x2+2xC.y=5D.y=√x−13．函数f(x)={x+1,x≥0x−1,x<0,在R上是A.减函数B.增函数C.先减后增D.无单调性4．下面说法错误的是A.函数的单调区间一定是函数的定义域B.函数的多个单调增区间的并集不一定是其单调增区间C.具有奇偶性的函数的定义域关于原点对称D.关于原点对称的图象一定是奇函数的图象5．已知函数f(x)=x2−2(1−a)x+1 在区间(−∞,2]上为减函数,则a 的取值范围是_____________.6．设奇函数f(x)的定义域为[-5,5],且当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集是.7．.已知函数f(x)=axx−1,若2f(2)=f(3)+5.(l)求a 的值.(2)利用单调性定义证明函数f(x)在区间(1,+∞)的单调性.8．首届世界低碳经济大会在南昌召开，大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=12x2−200x+80000，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？【能力提升】函数f(x)的图象如图所示.(1)说出f(x)的单调区间,以及在每一个单调区间上它是增函数还是减函数;(2)依据图象说明函数的最值情况.答案【基础过关】1．D【解析】因为(a，b)，(c，d)不是两个连续的区间，所以无法确定其单调性.2．B【解析】选项A中y＝1－2x为减函数，C中y＝5为常数函数，D中y＝√x－1的定义域为[1，＋∞).3．B【解析】解答本题可先画出函数图象，由图象分析.函数f(x)的图象如图所示，由图结合单调性的定义可知，此函数在R上是增函数.4．A【解析】单调区间是定义域的子集，不一定是定义域，当多个单调区间并起来时，由单调性定义知，不再是单调区间.具有奇偶性的函数的定义域关于原点对称，是函数奇偶性判定的要求.奇函数的图象关于原点对称，反之，关于原点对称的图象一定是奇函数的图象.5．(－∞,1]6．(-2,0)∪(2,5]【解析】由图可知在区间(2,5]上f(x)<0,因为奇函数的图象关于原点对称,所以在(-2,0)上也有f(x)<0.7．(1)由2f(2)＝f(3)＋5,得2×2a2−1=3×a3−1+5,解得a＝2.(2)由(1)知f(x)＝2xx−1.任取x 1,x 2∈(1,＋∞)且x 1＜x 2,f (x 1)＜f (x 2)=2x 1x 1−1−2x 2x 2−1=2x 1(x 2−1)−2x 2(x 1−1)(x 1−1)(x 2−1)=2(x 2−x 1)(x1−1)(x 2−1),因为1＜x 1＜x 2,所以x 1－1＞0,x 2－1＞0,x 2－x 1＞0. 所以f (x 1)－f (x 2)＞0,即f (x 1)＞f (x 2). 所以f (x )在(1,＋∞)上是减函数.8．(1)由题意可知，二氧化碳的每吨平均处理成本为令t (x )＝y x=12x +80 000x－200，可以证明t (x )在(0，400)为减函数，在[400，＋∞)上是增函数，故每月处理量为400吨时，才能使每吨的平均处理成本最低，最低成本为200元.(2)设该单位每月获利为S ，则S ＝100x －y ＝100x －(12x 2－200x ＋80 000)＝−12x 2＋300x －80 000＝−12(x －300)2－35 000.因为400≤x ≤600，所以当x ＝400时，S 有最大值－40 000.故该单位不获利，需要国家每月至少补贴40 000元，才能不亏损. 【能力提升】(1)由题图可知:函数f(x)的单调增区间为[0,12];单调减区间为(-∞,0)和(12,+∞).(2)观察图象可知,函数没有最大值和最小值.1.3.2奇偶性班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．设f (x ) 在[-2，-1]上为减函数，最小值为3，且f (x ) 为偶函数，则f (x ) 在[1，2]上A.为减函数，最大值为3B.为减函数，最小值为-3C.为增函数，最大值为-3D.为增函数，最小值为32．已知函数y =f (x ) 是偶函数，其图象与x 轴有四个交点，则方程f (x )=0 的所有实根之和是 A.4B.2C.1D.03．函数y =f(x)是奇函数，图象上有一点为(a ，f(a))，则图象必过点A. (a ，f(−a))B. (−a ，f(a))C. (−a ，−f(a))D. (a ，1f(a)))4．设f (x )=ax 3+bx −5，其中a ，b 为常数，若f (−3)=7，则f (3)的值为 A.-7B.7C.17D.-175．已知定义在R 上的奇函数f (x )，当x >0 时，f (x )=x 2+|x |−1，那么x <0 时，f (x )= . 6．若函数f (x )=x+abx+1为区间[-1，1]上的奇函数，则a = ；b = .7．作出函数y =|x −2|(x +1)的图象，并根据函数的图象找出函数的单调区间. 8．已知函数f (x )=ax 3+bx 2+cx +d 是定义在R 上的偶函数，且当x ∈[1，2]时，该函数的值域为[−2，1]，求函数f (x )的解析式. 【能力提升】已知函数f (x )=-12x 2+x ,是否存在实数m ,n (m <n ),使得当x ∈[m ,n ]时,函数的值域恰为[2m ,2n ]?若存在,求出m ,n 的值;若不存在,说明理由.答案【基础过关】 1．D 2．D 3．C【解析】奇函数f (x )满足f (－x )＝－f (x)，故有f (－a )＝－f (a ).因为函数f (x )是奇函数，故点(a ，f (a ))关于原点的对称点(－a ，－f (a ))也在y ＝f (x )上，故选C. 4．D【解析】∵f(－3)＝a(－3)3−3b －5＝7， ∴27a ＋3b ＝－12， ∴f (3)＝27a ＋3b －5＝－17. 5．－x 2－|x |＋1 6．0 07．当x －2≥0，即x ≥2时，y ＝(x －2)(x ＋1)＝x 2－x －2＝(x −12)2−94；当x －2＜0，即x ＜2时，y ＝－(x －2)(x ＋1)＝－x 2＋x ＋2＝−(x −12)2＋94.所以y ＝{(x −12)2−94，x ≥2.−(x −12)2＋94，x <2.这是分段函数，每段函数图象可根据二次函数图象作出(如图)，其中(−∞，12]，[2，＋∞)是函数的单调增区间；(12，2)是函数的单调减区间.8．由f (x )为偶函数可知f (x )＝f (－x )，即ax 3＋bx 2＋cx ＋d ＝－ax 3＋bx 2－cx ＋d ，可得ax 3＋cx ＝0恒成立，所以a ＝c ＝0，故f(x)＝bx 2＋d .当b ＝0时，由题意知不合题意；当b ＞0，x ∈[1，2]时f (x )单调递增，又f (x )值域为[－2，1]，所以{f(1)＝－2，f (2)＝1⟹ {b ＋d ＝－2，4b ＋d ＝1⟹{b ＝1， d ＝−3；当b ＜0时，同理可得{f (1)＝1， f (2)＝−2⟹ {b ＋d ＝1， 4b ＋d ＝－2⟹{b ＝−1，d ＝2.所以f(x)＝x 2－3或f (x )＝−x 2＋2. 【能力提升】假设存在实数m ,n ,使得当x ∈[m ,n ]时,y ∈[2m ,2n ],则在[m ,n ]上函数的最大值为2n .而f (x )=-12x 2+x =-12(x-1)2+12在x ∈R 上的最大值为12,∴2n ≤12,∴n ≤14.而f (x )在(-∞,1)上是增函数,∴f (x )在[m ,n ]上是增函数,∴{f(m)=2mf(n)=2n,即{−12m 2+m =2m −12n 2+n =2n.结合m <n ≤14,解得m =-2,n =0.∴存在实数m =-2,n =0,使得当x ∈[-2,0]时,f (x )的值域为[-4,0].2.1.1指数与指数幂的运算班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．化简√−x 3x的结果为A.−√−xB.√xC.-√xD.√−x2．计算[(−√2)−2]−12的结果是A.√2B.−√2C.√22D.−√223．设13<(13)b <(13)a<1，则有A.a a <a b <b aB. a a <b a <a bC. a b <a a <b aD. a b <b a <a a4．下列说法中正确的个数是( )(1)49的四次方根为7; (2)√a n n=a(a≥0);(3)(a b)5=a 5b15; (4)√(−3)26=(-3)13.A.1B.2C.3D.45．若10m =2,10n=4,则102m−n 2=.6．已知x=12(2 0131n -2 013−1n ),n ∈N *,则(x+√1+x 2)n 的值为 .7．化简下列各式: (1)(√a 23·√a )÷√a 6;(2)(a 23b 12)·(-3a 12b13)÷(13a 16b56).8．求下列各式的值:(1)2532;(2)(254)−32;(3)√259+(2764)−13-π0.【能力提升】已知x 12+x−12=3,求下列各式的值:(1)x+x -1;(2)x 32+x −32+2x 2+x −2+3.答案【基础过关】 1．A【解析】要使式子有意义，需－x 3＞0，故x ＜0，所以原式＝－√－x . 2．A【解析】本题考查指数运算.注意先算中括号内的部分。

2022高一数学同步练习册参考答案大全高中，是高级中学的简称，全中国的中学分为初级中学与高级中学(普遍简称初中和高中)，两者同属于中等教育的范围。

下面是小编为大家整理的关于高一数学同步练习册参考答案大全，希望对您有所帮助!高一数学练习册答案1.1集合111集合的含义与表示1.D.2.A.3.C.4.{1,-1}.5.{x|x=3n+1,n∈N}.6.{2,0,-2}.7.A={(1,5),(2,4),(3,3),(4,2),(5,1)}.8.1.9.1,2,3,6.10.列举法表示为{(-1,1),(2,4)},描述法的表示方法不,如可表示为(x,y)|y=x+2,y=x2.11.-1,12,2.112集合间的基本关系1.D.2.A.3.D.4.,{-1},{1},{-1,1}.5..6.①③⑤.7.A=B.8.15,13.9.a≥4.10.A={,{1},{2},{1,2}},B∈A.11.a=b=1.113集合的基本运算(一)1.C.2.A.3.C.4.4.5.{x|-2≤x≤1}.6.4.7.{-3}.8.A∪B={x|x<3,或x≥5}.9.A∪B={-8,-7,-4,4,9}.10.1.11.{a|a=3,或-22113集合的基本运算(二)1.A.2.C.3.B.4.{x|x≥2,或x≤1}.5.2或8.6.x|x=n+12,n∈Z.7.{-2}.8.{x|x>6,或x≤2}.9.A={2,3,5,7},B={2,4,6,8}.10.A,B的可能情形有:A={1,2,3},B={3,4};A={1,2,4},B={3,4};A={1,2,3,4},B={3,4}.11.a=4,b=2.提示:∵A∩綂UB={2}，∴2∈A，∴4+2a-12=0a=4，∴A={x|x2+4x-12=0}={2,-6},∵A∩綂UB={2}，∴-6綂UB，∴-6∈B，将x=-6代入B,得b2-6b+8=0b=2,或b=4.①当b=2时,B={x|x2+2x-24=0}={-6,4},∴-6綂UB，而2∈綂UB，满足条件A∩綂UB={2}.②当b=4时,B={x|x2+4x-12=0}={-6,2},∴2綂UB，与条件A∩綂UB={2}矛盾.1.2函数及其表示121函数的概念(一)1.C.2.C.3.D.4.22.5.-2,32∪32,+∞.6.[1,+∞).7.(1)12,34.(2){x|x≠-1，且x≠-3}.8.-34.9.1.10.(1)略.(2)72.11.-12,234.121函数的概念(二)1.C.2.A.3.D.4.{x∈R|x≠0,且x≠-1}.5.[0，+∞).6.0.7.-15,-13,-12,13.8.(1)y|y≠25.(2)[-2,+∞).9.(0,1].10.A∩B=-2,12;A∪B=[-2,+∞).11.[-1,0).122函数的表示法(一)1.A.2.B.3.A.4.y=x100.5.y=x2-2x+2.6.1x.7.略.8.x1234y828589889.略.10.1.11.c=-3.122函数的表示法(二)1.C.2.D.3.B.4.1.5.3.6.6.7.略.8.f(x)=2x(-1≤x<0),-2x+2(0≤x≤1).9.f(x)=x2-x+1.提示:设f(x)=ax2+bx+c，由f(0)=1,得c=1，又f(x+1)-f(x)=2x，即a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x，展开得2ax+(a+b)=2x,所以2a=2,a+b=0,解得a=1，b=-1.10.y=1.2(02.4(203.6(404.8(601.3函数的基本性质131单调性与(小)值(一)1.C.2.D.3.C.4.[-2,0),[0,1),[1,2].5.-∞,32.6.k<12.7.略.8.单调递减区间为(-∞,1),单调递增区间为[1,+∞).9.略.10.a≥-1.11.设-10，∴(x1x2+1)(x2-x1)(x21-1)(x22-1)>0，∴函数y=f(x)在(-1，1)上为减函数.131单调性与(小)值(二)1.D.2.B.3.B.4.-5,5.5.25.6.y=316(a+3x)(a-x)(011.日均利润，则总利润就.设定价为x元，日均利润为y元.要获利每桶定价必须在12元以上，即x>12.且日均销售量应为440-(x-13)·40>0，即x<23,总利润y=(x-12)[440-(x-13)·40]-600(12132奇偶性1.D.2.D.3.C.4.0.5.0.6.答案不,如y=x2.7.(1)奇函数.(2)偶函数.(3)既不是奇函数，又不是偶函数.(4)既是奇函数，又是偶函数.8.f(x)=x(1+3x)(x≥0),x(1-3x)(x<0).9.略.10.当a=0时，f(x)是偶函数;当a≠0时，既不是奇函数，又不是偶函数.11.a=1，b=1，c=0.提示:由f(-x)=-f(x)，得c=0，∴f(x)=ax2+1bx,∴f(1)=a+1b=2a=2b-1.∴f(x)=(2b-1)x2+1bx.∵f(2)<3，∴4(2b-1)+12b<32b-32b<00单元练习1.C.2.D.3.D.4.D.5.D.6.B.7.B.8.C.9.A.10.D.11.{0,1,2}.12.-32.13.a=-1,b=3.14.[1,3)∪(3,5].15.f1217.T(h)=19-6h(0≤h≤11),-47(h>11).18.{x|0≤x≤1}.19.f(x)=x只有的实数解，即xax+b=x(_)只有实数解，当ax2+(b-1)x=0有相等的实数根x0，且ax0+b≠0时，解得f(x)=2_+2，当ax2+(b-1)x=0有不相等的实数根，且其中之一为方程(_)的增根时，解得f(x)=1.20.(1)x∈R,又f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x)，所以该函数是偶函数.(2)略.(3)单调递增区间是[-1,0],[1,+∞)，单调递减区间是(-∞,-1],[0,1].21.(1)f(4)=4×13=5.2,f(5.5)=5×1.3+0.5×3.9=8.45,f(6.5)=5×1. 3+1×3.9+0.5×65=13.65.(2)f(x)=1.3x(0≤x≤5),3.9x-13(56.5x-28.6(622.(1)值域为[22,+∞).(2)若函数y=f(x)在定义域上是减函数，则任取x1,x2∈(0,1]且x1f(x2)成立，即(x1-x2)2+ax1x2>0，只要a<-2x1x2即可，由于x1,x2∈(0,1]，故-2x1x2∈(-2,0)，a<-2，即a的取值范围是(-∞,-2).高一数学练习参考答案2.1指数函数211指数与指数幂的运算(一)1.B.2.A.3.B.4.y=2x(x∈N).5.(1)2.(2)5.6.8a7.7.原式=|x-2|-|x-3|=-1(x<2),2x-5(2≤x≤3),1(x>3).8.0.9.2011.10.原式=2yx-y=2.11.当n为偶数,且a≥0时,等式成立;当n为奇数时,对任意实数a,等式成立.211指数与指数幂的运算(二)1.B.2.B.3.A.4.94.5.164.6.55.7.(1)-∞,32.(2)x∈R|x≠0,且x≠-52.8.原式=52-1+116+18+110=14380.9.-9a.10.原式=(a-1+b-1)·a-1b-1a-1+b-1=1ab.11.原式=1-2-181+2-181+2-141+2-121-2-18=12-827.211指数与指数幂的运算(三)1.D.2.C.3.C.4.36.55.5.1-2a.6.225.7.2.8.由8a=23a=14=2-2,得a=-23,所以f(27)=27-23=19.9.47288,00885.10.提示：先由已知求出x-y=-(x-y)2=-(x+y)2-4xy=-63,所以原式=x-2xy+yx-y=-33.11.23.212指数函数及其性质(一)1.D.2.C.3.B.4.AB.5.(1,0).6.a>0.7.125.8.(1)图略.(2)图象关于y轴对称.9.(1)a=3,b=-3.(2)当x=2时,y有最小值0;当x=4时,y有值6.10.a=1.11.当a>1时，x2-2x+1>x2-3x+5，解得{x|x>4};当0212指数函数及其性质(二)1.A.2.A.3.D.4.(1)<.(2)<.(3)>.(4)>.5.{x|x≠0},{y|y>0，或y<-1}.6.x<0.7.56-0.12>1=π0>0.90.98.8.(1)a=0.5.(2)-4x4>x3>x1.10.(1)f(x)=1(x≥0),2x(x<0).(2)略.11.am+a-m>an+a-n.212指数函数及其性质(三)1.B.2.D.3.C.4.-1.5.向右平移12个单位.6.(-∞,0).7.由已知得0.3(1-0.5)x≤0.08,由于0.51.91=0.2667,所以x≥1.91,所以2h后才可驾驶.8.(1-a)a>(1-a)b>(1-b)b.9.815×(1+2%)3≈865(人).10.指数函数y=ax满足f(x)·f(y)=f(x+y);正比例函数y=kx(k≠0)满足f(x)+f(y)=f(x+y).11.34,57.2.2对数函数221对数与对数运算(一)1.C.2.D.3.C.4.0;0;0;0.5.(1)2.(2)-52.6.2.7.(1)-3.(2)-6.(3)64.(4)-2.8.(1)343.(2)-12.(3)16.(4)2.9.(1)x=z2y,所以x=(z2y)2=z4y(z>0,且z≠1).(2)由x+3>0,2-x<0，且2-x≠1,得-310.由条件得lga=0,lgb=-1，所以a=1,b=110,则a-b=910.11.左边分子、分母同乘以ex，去分母解得e2x=3,则x=12ln3.221对数与对数运算(二)1.C.2.A.3.A.4.03980.5.2lo_-logax-3logaz.6.4.7.原式=log2748×12÷142=log212=-12.8.由已知得(x-2y)2=xy，再由x>0,y>0,x>2y,可求得xy=4.9.略.10.4.11.由已知得(log2m)2-8log2m=0,解得m=1或16.221对数与对数运算(三)1.A.2.D.3.D.4.43.5.24.6.a+2b2a.7.提示：注意到1-log63=log62以及log618=1+log63,可得答案为1.8.由条件得3lg3lg3+2lg2=a,则去分母移项，可得(3-a)lg3=2alg2,所以lg2lg3=3-a2a.9.25.10.a=log34+log37=log328∈(3，4).11.1.222对数函数及其性质(一)1.D.2.C.3.C.4.144分钟.5.①②③.6.-1.7.-2≤x≤2.8.提示：注意对称关系.9.对loga(x+a)<1进行讨论:①当a>1时,0a,得x>0.10.C1：a=32，C2:a=3，C3:a=110，C4:a=25.11.由f(-1)=-2,得lgb=lga-1①,方程f(x)=2x即x2+lga·x+lgb=0有两个相等的实数根，可得lg2a-4lgb=0,将①式代入,得a=100,继而b=10.222对数函数及其性质(二)1.A.2.D.3.C.4.22,2.5.(-∞,1).6.log2047.logbab0得x>0.(2)x>lg3lg2.9.图略，y=log12(x+2)的图象可以由y=log12x的图象向左平移2个单位得到.10.根据图象,可得0222对数函数及其性质(三)1.C.2.D.3.B.4.0，12.5.11.6.1,53.7.(1)f35=2,f-35=-2.(2)奇函数，理由略.8.{-1，0，1，2，3，4，5，6}.9.(1)0.(2)如log2x.10.可以用求反函数的方法得到,与函数y=loga(x+1)关于直线y=x 对称的函数应该是y=ax-1,和y=logax+1关于直线y=x对称的函数应该是y=ax-1.11.(1)f(-2)+f(1)=0.(2)f(-2)+f-32+f12+f(1)=0.猜想:f(-x)+f(-1+x)=0,证明略.23幂函数1.D.2.C.3.C.4.①④.5.6.2518<0.5-12<0.16-14.6.(-∞,-1)∪23,32.7.p=1,f(x)=x2.8.图象略,由图象可得f(x)≤1的解集x∈[-1,1].9.图象略,关于y=x 对称.10.x∈0,3+52.11.定义域为(-∞,0)∪(0,∞),值域为(0，∞)，是偶函数，图象略.单元练习1.D.2.D.3.C.4.B.5.C.6.D.7.D.8.A.9.D.10.B.11.1.12.x>1.13.④.14.258.提示：先求出h=10.15.(1)-1.(2)1.16.x∈R，y=12x=1+lga1-lga>0,讨论分子、分母得-117.(1)a=2.(2)设g(x)=log12(10-2x)-12x,则g(x)在[3,4]上为增函数,g(x)>m对x∈[3,4]恒成立，m18.(1)函数y=x+ax(a>0),在(0,a]上是减函数,[a,+∞)上是增函数,证明略.(2)由(1)知函数y=x+cx(c>0)在[1,2]上是减函数,所以当x=1时,y 有值1+c;当x=2时,y有最小值2+c2.19.y=(ax+1)2-2≤14，当a>1时，函数在[-1，1]上为增函数，ymax=(a+1)2-2=14，此时a=3;当020.(1)F(x)=lg1-_+1+1x+2,定义域为(-1,1).(2)提示:假设在函数F(x)的图象上存在两个不同的点A,B，使直线AB恰好与y轴垂直,则设A(x1,y),B(x2,y)(x1≠x2),则f(x1)-f(x2)=0,而f(x1)-f(x2)=lg1-x1x1+1+1x1+2-lg1-x2x2+1-1x2+2=lg(1-x1)(x2+1)(x1+1)(1-x2)+x2-x1(x1+2)(x2+2)=①+②,可证①，②同正或同负或同为零,因此只有当x1=x2时,f(x1)-f(x2)=0,这与假设矛盾,所以这样的两点不存在.(或用定义证明此函数在定义域内单调递减)。

1.1集合的意义（第1课时）（作业）（夯实基础+能力提升）【夯实基础】一、单选题1．（2021·上海·格致中学高一期中）若集合{},,M a b c =中的元素是△ABC 的三边长，则△ABC 一定不是（ ） A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形 【答案】D【分析】根据集合元素的互异性即可判断.【详解】由题可知，集合{},,M a b c =中的元素是ABC 的三边长，则a b c ≠≠，所以ABC 一定不是等腰三角形．故选：D ．2．（2020·上海市奉贤区曙光中学高一阶段练习）下列语言叙述中，能表示集合的是（ ） A ．数轴上离原点距离很近的所有点；B ．太阳系内的所有行星C ．某高一年级全体视力差的学生；D ．与ABC 大小相仿的所有三角形【答案】B【分析】根据集合的确定性逐个判断即可【详解】对A ，数轴上离原点距离很近的所有点不满足确定性，故A 错误；对B ，太阳系内的所有行星满足集合的性质，故B 正确；对C ，某高一年级全体视力差的学生不满足确定性，故C 错误；对D ，与ABC 大小相仿的所有三角形不满足确定性，故D 错误故选：B【点睛】本题主要考查了集合的确定性，属于基础题二、填空题3．（2021·上海·上外附中高一期中）集合()(){}2140,A x x x ax x R =-++=∈中所有元素之和为3，则实数=a ________．【答案】2-【分析】由()()2140x x ax -++=得1231x x x a ++=-，即可求解参数．【详解】由()()2140x x ax -++=得10x -=或240x ax ++=所以11x =或23x x a +=-依题意得12313x x x a ++=-=，得2a =-故答案为：2-．4．（2019·上海市亭林中学高一期中）若{}{},27,8x y y +=，则整数x =____________.【答案】3【分析】根据集合相等的条件，列出方程组，即可求解.【详解】因为{}{},27,8x y y +=，由集合相等的条件，可得728x y y +=⎧⎨=⎩或827x y y +=⎧⎨=⎩， 解得3x =或92x =（舍）. 故答案为：35．（2019·上海市亭林中学高一期中）用符号“∈、∉、⊆、⊇”Q .【答案】∉【分析】根据元素与集合之间的关系得答案.Q故答案为：∉.6．（2021·上海市张堰中学高一期中）若{}242,a ∈，则实数=a ____________. 【答案】2±【分析】4是集合{}22,a 中的元素，所以只能是24a =，求出a 的值即可【详解】由题意得：24a =，解得：2a =±故答案为：2±7．（2021·上海市奉贤中学高一期中）若{}241,a ∈，则实数=a __________； 【答案】2±【分析】结合已知条件，利用元素与集合的关系即可求解.【详解】因为{}241,a ∈，所以24a =，解得2a =±. 故答案为：2±.8．（2021·上海·华东师范大学第三附属中学高一期中）已知集合{}2,0A a a =-，若a A ∈，则实数a 的值为___________.【答案】2【分析】根据集合元素的性质可求实数a 的值.【详解】因为a A ∈，故0a =或2a a a -=，若0a =，则20a a a -==，与元素的互异性矛盾，舍；若2a a a -=，则2a =或0a =（舍），而2a =时，符合元素的互异性，故实数a 的值为2，故答案为：2.9．（2021·上海市行知中学高一阶段练习）若{}242,,a a ∈，则实数=a _________.【答案】2-或4【分析】由{}242,,a a ∈，可得2a =±或4a =，分三种情况讨论即可求解.【详解】解：因为{}242,,a a ∈，所以24a =或4a =，即2a =±或4a =，当2a =时，{}{}22,,2,4,2a a =与集合中元素的互异性相矛盾，舍去； 当2a =-时，{}{}22,,2,4,2a a =-符合题意；当4a =时，{}{}22,,2,16,4a a =符合题意. 故答案为：2-或4.10．（2021·上海市桃浦中学高一阶段练习）下列对象能组成集合的是___________①桃浦中学一部分学生②倒数等于自身的实数③超过100页的书④世界知名艺术家⑤方程210x +=的全体解【答案】②③⑤.【分析】根据集合元素的三要素，确定性、互异性和无序性可判断.【详解】①桃浦中学一部分学生不符合确定性，不能构成集合；②倒数等于自身的实数有1-和1，可构成集合{}1,1-；③超过100页的书符合集合元素的特征，可以构成集合；④世界知名艺术家，“知名”没有确定性，不能构成集合；⑤方程210x +=无解，可构成空集.因此，能构成集合的为②③⑤.故答案为：②③⑤.11．（2021·上海市奉贤中学高一阶段练习）若a ∈R ，则构成集合{}1,1a -中的a 的取值范围是___________. 【答案】{}2a a ≠【分析】根据集合互异性，即可得答案.【详解】根据集合的互异性可得11a -≠，所以2a ≠，即a 的取值范围是{}2a a ≠ 故答案为：{}2a a ≠12．（2021·上海市新场中学高一阶段练习）下列各对象的全体，可以构成集合的是_________________（填序号）①高一数学课本中的难题；②高一年级中身高超过1.70米的同学．【答案】②【分析】根据集合中的元素满足确定性可得出结论.【详解】①中的对象不满足确定性，①中的对象不能构成集合；②中的对象满足确定性，②中的对象能构成集合.故答案为：②.13．（2021·上海大学附属南翔高级中学高一阶段练习）已知,a b ∈R ，若{}1,,0,,b a a b b a ⎧⎫+=⎨⎬⎩⎭，则b a -=____________；【答案】2【分析】由题意可得0a b +=，1b =，从而可求出a 的值，进而可得答案【详解】因为{}1,,0,,b a a b b a ⎧⎫+=⎨⎬⎩⎭，所以0,0a a b ≠+=，则1b a =-， 所以1,1b a ==-，所以1(1)2b a -=--=，故答案为：214．（2020·上海市第三女子中学高一期中）用适当的符号填空：0_____∅.【答案】∉【分析】结合空集、元素与集合的关系确定正确答案.【详解】空集没有任何元素，所以0∉∅.故答案为：∉15．（2021·上海·高一专题练习）下列各组中的两个集合相等的有____________（1）P ={x |x =2n ，n ∈Z }，Q ={x |x =2(n +1)，n ∈Z }（2）P ={x |x =2n -1，n ∈N +}，Q ={x |x =2n +1，n ∈N +}；（3）P ={x |x 2-x =0}，Q ={x |x =1(1)2n+-，n ∈Z }. （4）P ={x |y =x +1}，Q ={(x ，y )|y =x +1}【答案】（1）（3）【分析】根据集合的元素逐一分析，由此判断出正确结论.【详解】（1）中集合P ，Q 都表示所有偶数组成的集合，有P =Q ；（2）中P 是由1，3，5，…所有正奇数组成的集合，Q 是由3，5，7，…所有大于1的正奇数组成的集合，1∉Q ，所以P ≠Q .（3）中P ={0，1}，当n 为奇数时，x =1(1)2n +-=0，当n 为偶数时，x =1(1)2n+-=1，所以Q ={0，1}，P =Q . （4）中集合,P Q 的研究对象不相同，所以P ≠Q .故答案为：（1）（3）.【能力提升】一、单选题1．（2021·上海市奉贤中学高一阶段练习）设Q 所示有理数集，集合{},,0X x x a a b Q x ==+∈≠，在下列集合中：①{}2x x X ∈；②X ⎫∈⎬⎭；③1x X x ⎧⎫∈⎨⎬⎩⎭；④{}2x x X ∈；与X 相同的集合有（ ） A ．①② B ．②③ C ．①②④ D ．①②③【答案】D【分析】根据集合相等的含义，逐一分析①②③④，即可得答案【详解】对于①：集合{}2x x X ∈，则2(a p +=+解得2,2p a q b ==，即,22p q a b ==，是一一对于，所以与X 集合相同.对于②：集合X ⎫∈⎬⎭b =X 集合相同.对于③：集合1x Xx ⎧⎫∈⎨⎬⎩⎭2222a b a b a b ⎛=+- --⎝X 集合相同.对于④：1X -，但方程21x -无解，则2{|y y x =，}x X ∈与X 不相同．故选：D二、填空题2．（2020·上海·华东师范大学附属周浦中学高一阶段练习）若集合{}2440A x kx x =++=中只有一个元素，则实数k 的值为___________.【答案】0或1【分析】分0k =、0k ≠两种情况讨论，结合集合A 只有一个元素可得出关于k 的等式，综合可求得实数k 的值.【详解】当0k =时，{}{}4401A x x =+==-，合乎题意；当0k ≠时，则关于x 的二次方程2440kx x ++=只有一解，则16160Δk =-=，解得1k =.综上所述，0k =或1.故答案为：0或1.3．（2020·上海市奉贤中学高一阶段练习）若{}21,x x ∈，则x =___________. 【答案】1-【分析】根据集合元素的互异性得1x ≠且0x ≠，再结合题意得21x =，解方程即可得答案.【详解】解：根据集合元素的互异性可知2x x ≠，即1x ≠且0x ≠，因为{}21,x x ∈，所以21x =，解得1x =±（负舍） 所以1x =-故答案为：1-4．（2020·上海·高一单元测试）已知集合A ={}22,2a a a ++，若3A ∈，则实数a 的值是____________.【答案】32- 【分析】根据题意，可得23a +=或223+=a a ，然后根据结果进行验证即可．【详解】由题可知：集合{}22,2A a a a =++，3A ∈所以23a +=或223+=a a ，则1a =或32a =- 当1a =时，222a a a +=+，不符合集合元素的互异性， 当32a =-时，1,32⎧⎫=⎨⎬⎩⎭A ，符合题意所以32a =- 故答案为：32- 5．（2020·上海·南洋中学高一期中）已知集合A ={1,2,3}，B ={1,m }，若3-m A ∈，则实数m =______________【答案】0或2【分析】由已知集合A 的元素，分类讨论求参数m 值，再根据集合的性质确定m 的值.【详解】当31m -=时，得2m =；当32m -=时，得1m =；当33m -=时，得0m =；∵3-m A ∈，B ={1,m }，∴0m =或2m =.故答案为：0或26．（2021·上海市奉贤中学高一期中）用()C A 表示非空集合A 中元素的个数：定义()(),()()*()(),()()C A C B C A C B A B C B C A C B C A -≥⎧=⎨->⎩，若{1,2}A =，{}22()(2)0,B x x ax x ax x R =+++=∈，且*1A B =，设实数a 的所有可能取值构成集合S ，S =__________；【答案】{0,-【分析】根据新定义得出集合B 中元素个数，再由方程根的个数分析求解．【详解】由已知()2C A =，而*1A B =，则()1C B =或3，显然22()(2)0x ax x ax +++=的一个解是0x =，若()1C B =，则0a =，满足题意；若()3C B =，则0a ≠，方程已有两个根0x =和x a =-，220x ax ++=有两个相等的实根且不为0和a -，280a ∆=-=，a =±a =220x ax ++=的解为34x x ==a =-220x ax ++=的解为34x x =综上{0,S =-．故答案为：{0,-．7．（2021·上海市延安中学高一期中）设集合S 为实数集R 的非空子集，若对任意x S ∈，y S ∈，都有()x y S +∈，()x y S -∈，()xy S ∈，则称集合S 为“完美集合”.给出下列命题：①若S 为“完美集合”，则一定有0S ∈；②“完美集合”一定是无限集；③集合{},,A x x a a Z b Z ==∈∈为“完美集合”；④若S 为“完美集合”，则满足S T R ⊆⊆的任意集合T 也是“完美集合”.其中真命题是___________.（写出所有正确命题的序号）【答案】①③【分析】对于①③，可以利用完美集合的定义分析判断，对于②④可以举反例分析判断.【详解】因为x ，y 是集合中任意的元素，所以x 与y 可以是同一个元素，故0一定在完美集合中，故①正确；完美集合不一定是无限集，例如{0}，故②错误；集合{},,A x x a a Z b Z ==∈∈，在集合A 中任意取两个元素，x a y c =+=+，其中a ，b ，c ，d 为整数，则(x y a c b d +=+++(x y a c b d -=-+-5(xy ac bd ad bc =+++数倍的形式，故③正确；{0}S =，{0T =，1}，也满足④，但是集合T 不是一个完美集合，故④不正确.故答案为：①③8．（2021·上海·复旦附中青浦分校高一阶段练习）设集合{}0123,,,S A A A A =，在S 上定义运算⊕为：j i k A A A ⊕=，其中k 为i j +被4除的余数，i ，0j =，1，2，3，则满足关系式20()x x A A ⊕⊕=的x （x S ∈）的个数为________.【答案】2【解析】由已知中集合0{S A =，1A ，2A ，3}A ，在S 上定义运算⊕为：j i k A A A ⊕=，其中k 为i j +被4除的余数，i ，0j =，1，2，3，分别分析x 取0A ，1A ，2A ，3A 时，式子的值，并与0A 进行比照，即可得到答案．【详解】当0x A =时，20020220()()x x A A A A A A A A ⊕⊕=⊕⊕=⊕=≠当1x A =时，21122240()()x x A A A A A A A A ⊕⊕=⊕⊕=⊕==当2x A =时，22220220()()x x A A A A A A A A ⊕⊕=⊕⊕=⊕=≠当3x A =时，23322200()()x x A A A A A A A A ⊕⊕=⊕⊕=⊕==则满足关系式20()x x A A ⊕⊕=的()x x S ∈的个数为：2个．故答案为：2．【点睛】本题考查的知识点是集合中元素个数，其中利用穷举法对x 取值进行分类讨论是解答本题的关键.属于中档题.三、解答题9．（2021·上海·位育中学高一期中）已知集合A 为非空数集，定义：{}|,,S x x a b a b A ==+∈，{}|,,T x x a b a b A ==-∈.(1)若集合{}13A =，，求证：2S ∈，并直接写出集合T ；(2)若集合{}1234,,,A x x x x =，1234x x x x <<<，且T A =，求证：1423x x x x +=+；【答案】(1)证明见解析，{02}T =，；(2)证明见解析； 【分析】(1)根据题目的定义，直接计算集合S 、T 即可；(2)根据相等集合的概念即可得出结果；(1)根据题意，由集合}3{1A =，，计算集合{246}S =，，，{02}T =，，所以2S ∈； (2)由于1234{}A x x x x =，，，，1234x x x x <<<，且T A =，所以T 中也只包含4个元素，即213141{0}T x x x x x x =---，，，，剩下的元素满足2143x x x x -=-，即1423x x x x +=+；。

勢谓終杉推数学弊僧1第一秦谓后习懸解答第一章集合与函数概念1. 1集合练习(P5)1.(1)中国WA,美国gA,印度WA,英国0A.(2)TA={xl?=x}={0, 1}, ...-IgA. (3)VB={Mr2+.r-6=0}={-3, 2}, /.3^A.(4)VC={xeNll<x<10}={l, 2, 3, 4, 5, 6, 7, 8, 9, 10}, /.8ec, 9.1 EC.2.(1){X I?=9}或{_3, 3}; (2){2, 3, 5, 7};y = x + 3(3){(x, v)H }或{(1, 4)};(4){xWRI4x-5<3}或{xlr<2}.y = -2x + 6练习(P7)1.0, {a}, [b], {<?}, [a, b], {a, c}, {b, c}, {a, b, c}.2.(l)aW{a, b, c}.(2)\\r=0, x=0. Z. {A-L?=0}={0}.0e {0}.(3)V?+l=0, ：.x2=-l.又TXWR, 方程x~=-l无解.A{xeRk2+l=O}=0.A 0 = 0.⑷筆. (5)•.•?=!■, ...x=0 或x=l..・.{xl?=x}={0, 1}..•.{()}筆{0, 1}.(6)TF-3x+2=0, ：.X=1或x =2..：.{x\x--3x+2.=Q} = [l, 2}.Z.{2, 1}={1, 2}.3.(1)由于1是任何正整数的公约数，任何正整数都是自身的公约数，所以8 的公约数是1, 2, 4, 8,即B={1, 2, 4, 8}.?.A^B.(2)显然BqA,又•.•3GA,且3gB, .'.B呈A.(3)4与10的最小公倍数是20, 4与10的公倍数应是20的倍数，显然A=B.练习(P11)1.ADB={5, 8}, AUB={3, 5, 6, 7, 8}.2.V.Y2-4A--5=0,：.X=-1或x=5..・.A={xl?-4x-5=0}={-l, 5},同理，B={-1, 1}..\AUB={-1, 5}U{-1, 1}={-1, 1, 5}, AHB={-1, 5}0{-1, 1}={-1}.3.AAB={A-I X是等腰直角三角形}, AUB={xk是等腰三角形或直角三角形}.4.vCuB={2, 4, 6}, CuA={l, 3, 6, 7], /.An(CuB)={2, 4, 5}A{2, 4, 6}={2, 4},(CuA)n(CuB)={l, 3, 6, 7}A{2, 4, 6}={6}.习题1.1 A组(Pll)1.d) e ⑵丘⑶纟⑷丘⑸丘(6)e2.(1) G⑵纟(3)G3.(1){2, 3, 4, 5}; (2){-2, l};(3){0, 1, 2}.(3)V-3<2r-l<3, ：.-2<2x<4. ：.-l<x<2.又TxeZ, ...x=0, 1, 2. .•.B={xGZI-3<2r-l<3}={0, 1, 2}.44.(l){yly>-4}; (2){x時0}; (3){A-|A->-}.5.(1) V A={x\2x-3<3x}={x\x>-3}, B={xk>2}, .\-4gB, -3gA, {2}筆B, B筆A.(2)VA={X L X2-1=0}={-1, 1}, A 1 eA, {-1 厚A, 0呈A, {1, -1}=A. ⑶呈;呈.6.VB={xl3x-7>8-2x}={xlx>3},/. A U B={.Y I2<Y<4} U {X L Y>3}={X L Y>2},ADB={xl2Sx：<4} Pl {.Y k>3}={A-I3<A_<4}.7.依题意，可知A={1, 2, 3, 4, 5, 6, 7, 8},由U=AUB={xGNKfetV10所以 AC!B={1, 2, 3, 4, 5, 6, 7, 8}C1{1, 2, 3}={1, 2, 3}=B,Anc={l, 2, 3, 4, 5, 6, 7, 8}A{3, 4, 5, 6}={3, 4, 5, 6}=C. 又•.•BUC={1, 2, 3}U{3, 4, 5, 6}={1, 2, 3, 4, 5, 6}..•.An (BUC)={l, 2, 3, 4, 5, 6, 7, 8}CI{1, 2, 3, 4, 5, 6}={1, 2, 3, 4, 5, XVBnC={l, 2, 3}A{3, 4, 5, 6}={3},.•.AU(BnC)={l, 2, 3, 4, 5, 6, 7, 8}U {3}={1, 2, 3, 4, 5, 6, 7, 8}=A. &(l)AUB={xlr 是参加一百米跑的同学或参加二百米跑的同学}.⑵AnC={.rk 是既参加一百米跑又参加四百米跑的同学}.9. BnC={.rk 是正方形}, C 、B={xlx 是邻边不相等的平行卩L|边形}, CsA={.rk 是梯形}. 10. V A U B={xl3<x<7} u {xl2<x<10}={xl2<x<10}, /. C R (A U B)={xlx<2 或 x>10}. 又ADB={xl3Sx<7}ri {x\2<s< 10}={jrl3<r<7}, .°.*R(AriB)={xLx<3 或.r>7}.(C R A)ClB={xLr<3 或 ©7} Cl{xl2<r<10}={xl2<r<3 或 7<Y <10},AU(C R B)={A -|3<A -<7} U {X \X <2 或.Y>10} = {A'k<2 或 3<x<l 或 A >10}.习题1.2 A 组(P24)1. VA={1, 2}, AUB={1, 2}, .'.BeA, .\B=0, {1}, {2}, {1, 2}.2. 集合 D={(x, y)l2.r-y=l}n{(.r, y)l.r+4y=5}表示直线 2x-y=l 与直线.r+4y=5 的交点坐标;2x _ v ]由于D={(x, v)H}={(1, 1)},所以点(1, 1)在直线y=x 上，即D 筆C.x + 4y = 53. B={1, 4},当 a=3 时,A={3},则 AUB={1, 3, 4}, AAB=0; 当 af3 时，A={3, a},若 a=l,则 AUB={1, 3, 4}, AC!B={1}; 若 a=4,则 AUB={1, 3, 4}, APB={4};若 afl 且 a 护，贝lj AUB={1, a, 3, 4}, AC!B= 0. 综上所得， 当 a=3 时，AUB={1, 3, 4}, AflB=0; 当 a=l,则 AUB={1, 3, 4}, AC!B={1}; 当 a=4,则 AUB={1, 3, 4}, AHB={4}; 当 a 托且且 <#4 时，AUB={1, a, 3, 4}, AD B=0.4. 作出韦恩图，女fl 图1 -1-3-16所示，可知 B={0, 2, 4, 6, 8, 9, 10}.4 —兀n o⑷要使函数有意义，只需% < 4< '即xS4,且xfl. 兀H 1,1. 2函数及其表示练习(P19)171.(1)要使分式 ---- 有意义，需4x+7#0,即洋-一.4x + 7 47 7所以这个函数的定义域是(-8,——)U(——,+00)；4 4(2)要使根式有意义,需l-x>0,且x+3>0,即-3<x<l.所以这个函数的定义域是[-3, 1].2.(l)f(2)=28, f(-2)=-28, f(2)+f(-2)=0; (2)f(a)=3a'+2a, f(-a)=-3a3-2a, f(a)+f(-a)=0.3.(1)两个函数的对应法则相同，而表示导弹飞行高度与时间关系的函数y=500x-5x2是有实际背景的，这里©0;函数y=500x-5x2, xGR,这两个函数的定义域不同，故这两个函数不相等.⑵函数g(x)=x°= l(x#O)与函数f(x)= 1, x£R的对应法则相同，但定义域不同，所以不是相等的函数.已知函数解析式求函数值及不同变量的函数值的关系.练习(P23)1.设矩形一边长为xcm, 则另一边长为A/502 -x2 = A/2500-X2.由题意，得y=x『2500 —X? , xG（O, 50）.2.图(A)与事件⑵.图(B)与事件(3).图(D)与事件(1)吻合得最好图(O可叙述为:我出发后.为了赶时间.加速行驶.走了一段后，发现时间还早，于是放慢了速度.3.解析:由绝对值的知识，有f(x)=< '-x + 2, x <2./? &4•与A中元素60。

高中数学必修一同步训练及解析1．下列所给关系正确的个数是( ) ①π∈R ；②3∉Q ；③0∈N *；④|－4|∉N *. A ．1 B ．2 C ．3 D ．4解析：选B.①②正确，③④错误．2．下列各组集合，表示相等集合的是( ) ①M ＝{(3,2)}，N ＝{(2,3)}； ②M ＝{3,2}，N ＝{2,3}； ③M ＝{(1,2)}，N ＝{1,2}． A ．① B ．② C ．③D ．以上都不对解析：选B.①中M 中表示点(3,2)，N 中表示点(2,3)，②中由元素的无序性知是相等集合，③中M 表示一个元素：点(1,2)，N 中表示两个元素分别为1,2. 3．用描述法表示不等式x <－x －3的解集为________．答案：{x |x <－x －3}(或{x |x <－32})4．集合A ＝{x ∈N|2x 2－x －1＝0}用列举法表示为__________．解析：解方程2x 2－x －1＝0，得x ＝1或x ＝－12.又因为x ∈N ，则A ＝{1}．答案：{1}[A 级 基础达标]1．下面几个命题中正确命题的个数是( ) ①集合N *中最小的数是1； ②若－a ∉N *，则a ∈N *；③若a ∈N *，b ∈N *，则a ＋b 的最小值是2； ④x 2＋4＝4x 的解集是{2,2}． A ．0 B ．1 C ．2 D ．3解析：选C.N *是正整数集，最小的正整数是1，故①正确；当a ＝0时，－a ∉N *，但a ∉N *，故②错；若a ∈N *，则a 的最小值是1，又b ∈N *，b 的最小值也是1，当a 和b 都取最小值时，a ＋b 取最小值2，故③正确；由集合元素的互异性知④是错误的．故①③正确，故选C.2．设集合M ＝{x ∈R|x ≤33}，a ＝26，则( ) A ．a ∉M B ．a ∈M C ．{a }∈MD ．{a |a ＝26}∈M解析：选B.(26)2－(33)2＝24－27<0， 故26<3 3.所以a ∈M .3．若集合M ＝{a ，b ，c }，M 中的元素是△ABC 的三边长，则△ABC 一定不是( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰三角形解析：选D.根据元素的互异性可知，a ≠b ，a ≠c ，b ≠c .4．已知①5∈R ；②13∈Q ；③0＝{0}；④0∉N ；⑤π∈Q ；⑥－3∈Z.正确的个数为________．解析：③错误，0是元素，{0}是一个集合；④0∈N ；⑤π∉Q ，①②⑥正确． 答案：35．已知x 2∈{1,0，x }，则实数x ＝________.解析：∵x 2∈{1,0，x }，∴x 2＝1或x 2＝0或x 2＝x . ∴x ＝±1或x ＝0.但当x ＝0或x ＝1时，不满足元素的互异性． ∴x ＝－1. 答案：－16．设集合B ＝{x ∈N|62＋x∈N}．(1)试判断元素1和2与集合B 的关系； (2)用列举法表示集合B .解：(1)当x ＝1时，62＋1＝2∈N ；当x ＝2时，62＋2＝32∉N ，∴1∈B,2∉B .(2)令x ＝0,3,4代入62＋x∈N 检验，可得B ＝{0,1,4}．[B 级 能力提升]7．设集合A ＝{2,3,4}，B ＝{2,4,6}，若x ∈A 且x ∉B ，则x 等于( ) A ．2 B ．3 C ．4 D ．6解析：选B.∵x ∈{2,3,4}且x ∉{2,4,6}，∴x ＝3.8．定义集合运算：A *B ＝{z |z ＝xy ，x ∈A ，y ∈B }，设A ＝{1,2}，B ＝{0,2}，则集合A *B 的所有元素之和为( ) A ．0 B ．2 C ．3 D ．6解析：选D.∵z ＝xy ，x ∈A ，y ∈B ，∴z 的取值有：1×0＝0,1×2＝2,2×0＝0,2×2＝4， 故A *B ＝{0,2,4}，∴集合A *B 的所有元素之和为：0＋2＋4＝6.9．已知集合A ＝{x |2x ＋a >0}，且1∉A ，则实数a 的取值范围是________． 解析：∵1∉A ，∴2＋a ≤0，即a ≤－2. 答案：a ≤－2 10.用适当的方法表示下列集合： (1)所有被3整除的整数；(2)图中阴影部分点(含边界)的坐标的集合(不含虚线)； (3)满足方程x ＝|x |，x ∈Z 的所有x 的值构成的集合B . 解：(1){x |x ＝3n ，n ∈Z}；(2){(x ，y )|－1≤x ≤2，－12≤y ≤1，且xy ≥0}；(3)B ＝{x |x ＝|x |，x ∈Z}．11．已知集合A ＝{x |ax 2＋2x ＋1＝0}．(1)若A 中只有一个元素，求a 的取值范围； (2)若A 中至少有一个元素，求a 的取值范围． 解：(1)∵方程ax 2＋2x ＋1＝0只有一个解，若a ＝0，则x ＝－12；若a ≠0，则Δ＝0，解得a ＝1，此时x ＝－1. ∴a ＝0或a ＝1时，A 中只有一个元素． (2)①A 中只有一个元素时，a ＝0或a ＝1.②A 中有两个元素时，⎩⎪⎨⎪⎧a ≠0，Δ>0，解得a <1且a ≠0.综上，a ≤1.高中数学必修一同步训练及解析1．下列集合中是空集的是( ) A ．{x |x 2＋3＝3}B ．{(x ，y )|y ＝－x 2，x ，y ∈R}C ．{x |－x 2≥0}D ．{x |x 2－x ＋1＝0，x ∈R}解析：选D.∵方程x 2－x ＋1＝0的判别式Δ<0，∴方程无实根，故D 选项为空集，A 选项中只有一个元素0，B 选项中有无数个元素，即抛物线y ＝－x 2上的点，C 选项中只有一个元素0.2．已知集合A ＝{x |－1<x <2}，B ＝{x |0<x <1}，则( ) A ．A >B B ．A B C ．B A D ．A ⊆B解析：选C.利用数轴(图略)可看出x ∈B ⇒x ∈A ，但x ∈A ⇒x ∈B 不成立． 3．下列关系中正确的是________． ①∅∈{0}；②∅；③{0,1}⊆{(0,1)}；④{(a ，b )}＝{(b ，a )}． 解析：∅，∴①错误；空集是任何非空集合的真子集，②正确；{(0,1)}是含有一个元素的点集，③错误；{(a ，b )}与{(b ，a )}是两个不等的点集，④错误，故正确的是②. 答案：②4．图中反映的是四边形、梯形、平行四边形、菱形、正方形这五种几何图形之间的关系，则A 、B 、C 、D 、E 分别代表的图形的集合为__________________________．解析：由以上概念之间的包含关系可知：集合A ＝{四边形}，集合B ＝{梯形}，集合C ＝{平行四边形}，集合D ＝{菱形}，集合E ＝{正方形}．答案：A ＝{四边形}，B ＝{梯形}，C ＝{平行四边形}，D ＝{菱形}，E ＝{正方形}[A 级 基础达标]1．如果A ＝{x |x >－1}，那么( ) A ．0⊆A B ．{0}∈A C ．∅∈A D ．{0}⊆A解析：选D.A 、B 、C 的关系符号是错误的． 2．若{1,2}＝{x |x 2＋bx ＋c ＝0}，则( ) A ．b ＝－3，c ＝2 B ．b ＝3，c ＝－2 C ．b ＝－2，c ＝3 D ．b ＝2，c ＝－3解析：选A.由题意知1,2为方程x 2＋bx ＋c ＝0的两个根，所以⎩⎪⎨⎪⎧1＋2＝－b ，1×2＝c ，解得b ＝－3，c ＝2.3．符合条件{a P ⊆{a ，b ，c }的集合P 的个数是( ) A ．2 B ．3 C ．4 D ．5解析：选B.集合P 中一定含有元素a ，且不能只有a 一个元素，用列举法列出即可．4．设x ，y ∈R ，A ＝{(x ，y )|y ＝x }，B ＝{(x ，y )|yx＝1}，则A 、B 间的关系为________．解析：(0,0)∈A ，而(0,0)∉B ，故B A . 答案：B A5．已知集合A ＝{－1,3,2m －1}，集合B ＝{3，m 2}．若B ⊆A ，则实数m ＝________. 解析：由于B ⊆A ，则应有m 2＝2m －1，于是m ＝1. 答案：16．已知集合A ＝{(x ，y )|x ＋y ＝2，x ，y ∈N}，试写出A 的所有子集． 解：∵A ＝{(x ，y )|x ＋y ＝2，x ，y ∈N}， ∴A ＝{(0,2)，(1,1)，(2,0)}．∴A 的子集有：∅，{(0,2)}，{(1,1)}，{(2,0)}，{(0,2)，(1,1)}，{(0,2)，(2,0)}，{(1,1)，(2,0)}，{(0,2)，(1,1)，(2,0)}．[B 级 能力提升]7．集合M ＝{x |x 2＋2x －a ＝0，x ∈R}，且∅M ，则实数a 的取值范围是( ) A ．a ≤－1B ．a ≤1C ．a ≥－1D ．a ≥1解析：选C.∅M 等价于方程x 2＋2x －a ＝0有实根．即Δ＝4＋4a ≥0.解得a ≥－1. 8．设A ＝{x |1<x <2}，B ＝{x |x <a }，若A B ，则a 的取值范围是( ) A ．a ≥2 B ．a ≤1 C ．a ≥1 D ．a ≤2解析：选A.A ＝{x |1<x <2}，B ＝{x |x <a }，要使A B ，则应有a ≥2.9．设A ＝{x ∈R|x 2－5x ＋m ＝0}，B ＝{x ∈R|x －3＝0}，且B ⊆A ，则实数m ＝________，集合A ＝________.解析：B ＝{3}．∵B ⊆A ，∴3∈A ，即9－15＋m ＝0.∴m ＝6.解方程x 2－5x ＋6＝0，得x 1＝2，x 2＝3， ∴A ＝{2,3}． 答案：6 {2,3}10．设M ＝{x |x 2－2x －3＝0}，N ＝{x |ax －1＝0}，若N ⊆M ，求所有满足条件的a 的集合． 解：由N ⊆M ，M ＝{x |x 2－2x －3＝0}＝{－1,3}， 得N ＝∅或N ＝{－1}或N ＝{3}． 当N ＝∅时，ax －1＝0无解，∴a ＝0.当N ＝{－1}时，由1a ＝－1，得a ＝－1.当N ＝{3}时，由1a ＝3，得a ＝13.∴满足条件的a 的集合为{－1,0，13}．11．已知集合A ＝{x |1≤x ≤2}，B ＝{x |1≤x ≤a ，a ≥1}． (1)若A B ，求a 的取值范围； (2)若B ⊆A ，求a 的取值范围． 解：(1)若AB ，由图可知，a >2.(2)若B ⊆A ，由图可知，1≤a ≤2.高中数学必修一同步训练及解析1．已知集合A ＝{x |x >1}，B ＝{x |－1<x <2}，则A ∩B ＝( ) A ．{x |－1<x <2} B ．{x |x >－1}C ．{x |－1<x <1}D ．{x |1<x <2}解析：选D.如图所示．A ∩B ＝{x |x >1}∩{x |－1<x <2}＝{x |1<x <2}．2．已知集合M＝{1,2,3}，N＝{2,3,4}则()A．M⊆NB．N⊆MC．M∩N＝{2,3}D．M∪N＝{1,4}解析：选C.∵M＝{1,2,3}，N＝{2,3,4}．∴选项A、B显然不对．M∪N＝{1,2,3,4}，∴选项D错误．又M∩N＝{2,3}，故选C.3．设M＝{0,1,2,4,5,7}，N＝{1,4,6,8,9}，P＝{4,7,9}，则(M∩N)∪(M∩P)＝________.解析：M∩N＝{1,4}，M∩P＝{4,7}，所以(M∩N)∪(M∩P)＝{1,4,7}．答案：{1,4,7}4．已知集合A＝{x|x≥2}，B＝{x|x≥m}，且A∪B＝A，则实数m的取值范围是________．解析：A∪B＝A，即B⊆A，∴m≥2.答案：m≥2[A级基础达标]1．下列关系Q∩R＝R∩Q；Z∪N＝N；Q∪R＝R∪Q；Q∩N＝N中，正确的个数是() A．1B．2C．3D．4解析：选C.只有Z∪N＝N是错误的，应是Z∪N＝Z.2．已知集合P＝{x|x2≤1}，M＝{a}．若P∪M＝P，则a的取值范围是()A．(－∞，－1]B．[1，＋∞)C．[－1,1]D．(－∞，－1]∪[1，＋∞)解析：选C.由P＝{x|x2≤1}得P＝{x|－1≤x≤1}．由P∪M＝P得M⊆P.又M＝{a}，∴－1≤a≤1.3．已知集合M＝{x|－2≤x－1≤2}和N＝{x|x＝2k－1，k∈N＋}的关系的韦恩(Venn)图，如图所示，则阴影部分所示的集合的元素共有()A．3个B．2个C．1个D．无穷多个解析：选B.M＝{x|－1≤x≤3}，集合N是全体正奇数组成的集合，则阴影部分所示的集合为M∩N＝{1,3}，即阴影部分所示的集合共有2个元素．4．已知集合A＝{1,2,3}，B＝{2，m,4}，A∩B＝{2,3}，则m＝________.解析：∵A∩B＝{2,3}，∴3∈B，∴m＝3.答案：35．设集合A＝{x|－1<x<2}，B＝{x|x<a}，若A∩B≠∅，则a的取值范围是________．解析：利用数轴分析可知，a>－1.答案：a>－16．已知集合A ＝{x |⎩⎪⎨⎪⎧3－x >03x ＋6>0}，集合B ＝{m |3>2m －1}，求：A ∩B ，A ∪B .解：∵A ＝{x |⎩⎪⎨⎪⎧3－x >03x ＋6>0}＝{x |－2<x <3}，B ＝{m |3>2m －1}＝{m |m <2}．用数轴表示集合A ，B ，如图．∴A ∩B ＝{x |－2<x <2}，A ∪B ＝{x |x <3}．[B 级 能力提升]7．设A ＝{(x ，y )|(x ＋2)2＋(y ＋1)2＝0}，B ＝{－2，－1}，则必有( ) A ．A ⊇B B ．A ⊆B C ．A ＝B D ．A ∩B ＝∅解析：选D.A ＝{(x ，y )|(x ＋2)2＋(y ＋1)2＝0}＝{(－2，－1)}是点集，B ＝{－2，－1}是数集，所以A ∩B ＝∅.8．若集合A ＝{参加2012年奥运会的运动员}，集合B ＝{参加2012年奥运会的男运动员}，集合C ＝{参加2012年奥运会的女运动员}，则下列关系正确的是( ) A ．A ⊆B B ．B ⊆CC ．A ∩B ＝CD ．B ∪C ＝A解析：选D.参加2012年奥运会的运动员是参加2012年奥运会的男运动员和女运动员的总和，即A ＝B ∪C .9．满足条件{1,3}∪M ＝{1,3,5}的集合M 的个数是________． 解析：∵{1,3}∪M ＝{1,3,5}，∴M 中必须含有5， ∴M 可以是{5}，{5,1}，{5,3}，{1,3,5}，共4个． 答案：410．已知集合M ＝{x |2x －4＝0}，集合N ＝{x |x 2－3x ＋m ＝0}， (1)当m ＝2时，求M ∩N ，M ∪N ； (2)当M ∩N ＝M 时，求实数m 的值． 解：由题意得M ＝{2}．(1)当m ＝2时，N ＝{x |x 2－3x ＋2＝0}＝{1,2}， 则M ∩N ＝{2}，M ∪N ＝{1,2}． (2)∵M ∩N ＝M ，∴M ⊆N . ∵M ＝{2}，∴2∈N .∴2是关于x 的方程x 2－3x ＋m ＝0的解，即4－6＋m ＝0，解得m ＝2. 11．集合A ＝{x |－1≤x <3}，B ＝{x |2x －4≥x －2}． (1)求A ∩B ；(2)若集合C ＝{x |2x ＋a >0}，满足B ∪C ＝C ，求实数a 的取值范围． 解：(1)∵B ＝{x |x ≥2}， ∴A ∩B ＝{x |2≤x <3}．(2)C ＝{x |x >－a2}，B ∪C ＝C ⇒B ⊆C ，∴－a2<2，∴a >－4.高中数学必修一同步训练及解析1．若P＝{x|x<1}，Q＝{x|x>－1}，则()A．P⊆QB．Q⊆PC．∁R P⊆QD．Q⊆∁R P解析：选C.∵P＝{x|x<1}，∴∁R P＝{x|x≥1}，∴∁R P⊆Q.2．设集合A＝{4,5,7,9}，B＝{3,4,7,8,9}，全集U＝A∪B，则集合∁U(A∩B)中的元素共有() A．3个B．4个C．5个D．6个解析：选A.∵U＝A∪B＝{3,4,5,7,8,9}，A∩B＝{4,7,9}，∴∁U(A∩B)＝{3,5,8}．故选A.3．设集合U＝{1,2,3,4,5}，A＝{2,4}，B＝{3,4,5}，C＝{3,4}，则(A∪B)∩(∁U C)＝________. 解析：∵A∪B＝{2,3,4,5}，∁U C＝{1,2,5}，∴(A∪B)∩(∁U C)＝{2,3,4,5}∩{1,2,5}＝{2,5}．答案：{2,5}4．已知全集U＝{2,3，a2－a－1}，A＝{2,3}，若∁U A＝{1}，则实数a的值是________．解析：∵U＝{2,3，a2－a－1}，A＝{2,3}，∁U A＝{1}，∴a2－a－1＝1，即a2－a－2＝0，解得a＝－1或a＝2.答案：－1或2[A级基础达标]1．设集合U＝{1,2,3,4}，M＝{1,2,3}，N＝{2,3,4}，则∁U(M∩N)＝()A．{1,2}B．{2,3}C．{2,4}D．{1,4}解析：选D.∵M＝{1,2,3}，N＝{2,3,4}，∴M∩N＝{2,3}．又∵U＝{1,2,3,4}，∴∁U(M∩N)＝{1,4}．2．已知集合U＝{2,3,4,5,6,7}，M＝{3,4,5,7}，N＝{2,4,5,6}，则()A．M∩N＝{4,6}B．M∪N＝UC．(∁U N)∪M＝UD．(∁U M)∩N＝N解析：选B.由U＝{2,3,4,5,6,7}，M＝{3,4,5,7}，N＝{2,4,5,6}，得M∩N＝{4,5}，(∁U N)∪M ＝{3,4,5,7}，(∁U M)∩N＝{2,6}，M∪N＝{2,3,4,5,6,7}＝U.3．集合A＝{x|－1≤x≤2}，B＝{x|x＜1}，则A∩(∁R B)＝()A．{x|x＞1}B ．{x |x ≥1}C ．{x |1＜x ≤2}D ．{x |1≤x ≤2}解析：选D.∵B ＝{x |x ＜1}，∴∁R B ＝{x |x ≥1}， ∴A ∩∁R B ＝{x |1≤x ≤2}．4．已知全集U ＝{x |1≤x ≤5}，A ＝{x |1≤x ＜a }，若∁U A ＝{x |2≤x ≤5}，则a ＝________. 解析：∵A ∪∁U A ＝U ，∴A ＝{x |1≤x ＜2}．∴a ＝2. 答案：25．设集合A ＝{x |0≤x ≤4}，B ＝{y |y ＝x －3，－1≤x ≤3}，则∁R (A ∩B )＝________. 解析：∵A ＝{x |0≤x ≤4}， B ＝{y |－4≤y ≤0}， ∴A ∩B ＝{0}，∴∁R (A ∩B )＝{x |x ∈R ，且x ≠0}． 答案：{x |x ∈R ，且x ≠0}6．已知全集U ＝R ，A ＝{x |－4≤x ＜2}，B ＝{x |－1＜x ≤3}，P ＝{x |x ≤0或x ≥52}，求A ∩B ，(∁U B )∪P ，(A ∩B )∩(∁U P )．解：将集合A 、B 、P 表示在数轴上，如图．∵A ＝{x |－4≤x ＜2}，B ＝{x |－1＜x ≤3}， ∴A ∩B ＝{x |－1＜x ＜2}． ∵∁U B ＝{x |x ≤－1或x ＞3}，∴(∁U B )∪P ＝{x |x ≤0或x ≥52}，(A ∩B )∩(∁U P )＝{x |－1＜x ＜2}∩{x |0＜x ＜52}＝{x |0＜x ＜2}．[B 级 能力提升]7．已知集合U ＝R ，集合A ＝{x |x <－2或x >4}，B ＝{x |－3≤x ≤3}，则(∁U A )∩B ＝( ) A ．{x |－3≤x ≤4} B ．{x |－2≤x ≤3}C ．{x |－3≤x ≤－2或3≤x ≤4}D ．{x |－2≤x ≤4}解析：选B.∁U A ＝{x |－2≤x ≤4}．由图可知：(∁U A )∩B ＝{x |－2≤x ≤3}． 8.已知全集U ＝Z ，集合A ＝{x |x 2＝x }，B ＝{－1,0,1,2}，则图中的阴影部分所表示的集合等于( )A ．{－1,2}B ．{－1,0}C ．{0,1}D ．{1,2}解析：选A.依题意知A ＝{0,1}，(∁U A )∩B 表示全集U 中不在集合A 中，但在集合B 中的所有元素，故图中的阴影部分所表示的集合等于{－1,2}．9．设全集U ＝{0,1,2,3}，A ＝{x ∈U |x 2＋mx ＝0}，若∁U A ＝{1,2}，则实数m 的值为________．解析：如图，∵U ＝{0,1,2,3}， ∁U A ＝{1,2}， ∴A ＝{0,3}，∴方程x 2＋mx ＝0的两根为x 1＝0，x 2＝3， ∴0＋3＝－m ，即m ＝－3. 答案：－310．设全集U ＝{x |0<x <10，x ∈N *}，且A ∩B ＝{3}，A ∩(∁U B )＝{1,5,7}，(∁U A )∩(∁U B )＝{9}，求A ，B .解：如图所示，由图可得A ＝{1,3,5,7}，B ＝{2,3,4,6,8}．11．设集合A ＝{x |x ＋m ≥0}，B ＝{x |－2＜x ＜4}，全集U ＝R ，且(∁U A )∩B ＝∅，求实数m 的取值范围．解：由已知A ＝{x |x ≥－m }， ∴∁U A ＝{x |x ＜－m }，∵B ＝{x |－2＜x ＜4}，(∁U A )∩B ＝∅， ∴－m ≤－2，即m ≥2， ∴m 的取值范围是m ≥2.高中数学必修一同步训练及解析1．函数y ＝1x的定义域是( )A ．RB ．{0}C ．{x |x ∈R ，且x ≠0}D ．{x |x ≠1}解析：选C.要使1x 有意义，必有x ≠0，即y ＝1x的定义域为{x |x ∈R ，且x ≠0}．2．下列各组函数表示相等函数的是( )A ．f (x )＝⎩⎪⎨⎪⎧x ， x >0－x ， x <0与g (x )＝|x |B ．f (x )＝2x ＋1与g (x )＝2x 2＋xxC ．f (x )＝|x 2－1|与g (t )＝(t 2－1)2D ．f (x )＝x 2与g (x )＝x解析：选C.A ：f (x )的定义域是(－∞，0)∪(0，＋∞)，g (x )的定义域是R ，定义域不同． B ：f (x )的定义域是R ，g (x )的定义域是{x |x ≠0}，定义域不同．C ：f (x )＝|x 2－1|，g (t )＝|t 2－1|，虽然表示自变量的字母不同，但定义域与对应法则都相同．D ：f (x )＝|x |，g (x )＝x ，对应法则不相同．3．若[a,3a －1]为一确定区间，则a 的取值范围是________．解析：由题意3a －1＞a ，则a ＞12.答案：(12，＋∞)4．函数y ＝x 2－2x (－2≤x ≤4，x ∈Z)的值域为________．解析：∵－2≤x ≤4，x ∈Z ，∴x 取－2，－1,0,1,2,3,4.可知y 的取值为8,3,0，－1,0,3,8，∴值域为{－1,0,3,8}． 答案：{－1,0,3,8}[A 级 基础达标]1．下列对应关系中能构成实数集R 到集合{1，－1}的函数的有( ) ①②③A ．①B ．②C ．③D ．①③解析：选B.①中将自变量分为两类：一类是奇数，另一类是偶数．而实数集中除奇数、偶数之外，还有另外的数，如无理数，它们在集合{1，－1}中无对应元素；③中实数集除整数、分数之外，还有无理数，它们在集合{1，－1}中无对应元素；②符合题干要求．2．函数y ＝31－1－x的定义域是( )A ．(－∞，1)B ．(－∞，0)∪(0,1]C ．(－∞，0)∪(0,1)D ．[1，＋∞)解析：选B.由⎩⎨⎧1－x ≥0，1－1－x ≠0，解得⎩⎪⎨⎪⎧x ≤1，x ≠0.即得x ≤1且x ≠0，故选B.3．区间[5,8)表示的集合是( )A ．{x |x ≤5或x >8}B ．{x |5<x ≤8}C ．{x |5≤x <8}D ．{x |5≤x ≤8} 答案：C4．函数y ＝x 2x 2＋1(x ∈R)的值域是________．解析：y ＝x 2x 2＋1＝1－1x 2＋1，∴y 的值域为[0,1)． 答案：[0,1)5．设f (x )＝11－x，则f [f (x )]＝________.解析：f [f (x )]＝11－11－x ＝11－x －11－x＝x －1x .(x ≠0，且x ≠1)答案：x －1x(x ≠0，且x ≠1)6．求下列函数的定义域： (1)f (x )＝2x －1－3－x ＋1；(2)f (x )＝4－x 2x ＋1.解：(1)要使函数f (x )有意义，应有⎩⎪⎨⎪⎧2x －1≥0，3－x ≥0⇔⎩⎪⎨⎪⎧x ≥12，x ≤3⇔12≤x ≤3.∴f (x )的定义域是[12，3]．(2)函数f (x )的定义域是⎩⎨⎧⎭⎬⎫x |⎩⎪⎨⎪⎧ 4－x 2≥0x ＋1≠0⇔⎩⎨⎧⎭⎬⎫x |⎩⎪⎨⎪⎧－2≤x ≤2x ≠－1 ⇔{x |－2≤x ≤2，且x ≠－1}．∴f (x )的定义域是[－2，－1)∪(－1,2]．[B 级 能力提升]7．若函数f (x )＝ax 2－1，a 为一个正常数，且f [f (－1)]＝－1，那么a 的值是( ) A ．1 B ．0 C ．－1 D ．2解析：选A.f (－1)＝a －1，f [f (－1)]＝f (a －1) ＝a (a －1)2－1＝－1，所以a ＝1. 8．下列说法中正确的为( )A ．y ＝f (x )与y ＝f (t )表示同一个函数B ．y ＝f (x )与y ＝f (x ＋1)不可能是同一函数C ．f (x )＝1与f (x )＝x 0表示同一函数D ．定义域和值域都相同的两个函数是同一个函数解析：选A.两个函数是否是同一个函数与所取的字母无关，判断两个函数是否相同，主要看这两个函数的定义域和对应关系是否相同．9．已知函数f (x )对任意实数x 1，x 2，都有f (x 1x 2)＝f (x 1)＋f (x 2)成立，则f (0)＝________，f (1)＝________.解析：令x 1＝x 2＝0，有f (0×0)＝f (0)＋f (0)，解得f (0)＝0； 令x 1＝x 2＝1，有f (1×1)＝f (1)＋f (1)，解得f (1)＝0. 答案：0 010．求下列函数的值域． (1)y ＝x ＋1；(2)y ＝xx ＋1.解：(1)因为函数的定义域为{x |x ≥0}， ∴x ≥0，∴x ＋1≥1.所以函数y ＝x ＋1的值域为[1，＋∞)．(2)∵y ＝x x ＋1＝1－1x ＋1，且定义域为{x |x ≠－1}，∴1x ＋1≠0，即y ≠1. 所以函数y ＝xx ＋1的值域为{y |y ∈R ，且y ≠1}．11．已知函数f (x )＝x 2＋x －1， (1)求f (2)，f (a )；(2)若f (a )＝11，求a 的值； (3)求f (x )的值域．解：(1)f (2)＝22＋2－1＝5， f (a )＝a 2＋a －1.(2)∵f (a )＝a 2＋a －1，∴若f (a )＝11，则a 2＋a －1＝11， 即(a ＋4)(a －3)＝0. ∴a ＝－4或a ＝3.(3)∵f (x )＝x 2＋x －1＝(x ＋12)2－54≥－54，∴f (x )的值域为[－54，＋∞)．高中数学必修一同步训练及解析1．下列点中不在函数y ＝2x ＋1的图象上的是( )A ．(1,1)B ．(－2，－2)C ．(3，12)D ．(－1,0) 答案：D2．已知一次函数的图象过点(1,0)，和(0,1)，则此一次函数的解析式为( ) A ．f (x )＝－x B ．f (x )＝x －1 C ．f (x )＝x ＋1 D ．f (x )＝－x ＋1解析：选D.设一次函数的解析式为f (x )＝kx ＋b (k ≠0)，由已知得⎩⎪⎨⎪⎧ k ＋b ＝0，b ＝1，∴⎩⎪⎨⎪⎧k ＝－1，b ＝1.∴f (x )＝－x ＋1.3．已知f (x )＝2x ＋3，且f (m )＝6，则m 等于________．解析：2m ＋3＝6，m ＝32.答案：324．已知f (2x )＝x 2－x －1，则f (x )＝________.解析：令2x ＝t ，则x ＝t2，∴f (t )＝⎝⎛⎭⎫t 22－t 2－1，即f (x )＝x 24－x 2－1.答案：x 24－x 2－1[A 级 基础达标]1．已知f (x )是反比例函数，且f (－3)＝－1，则f (x )的解析式为( )A ．f (x )＝－3xB ．f (x )＝3xC ．f (x )＝3xD ．f (x )＝－3x 答案：B2．若f (1－2x )＝1－x 2x 2(x ≠0)，那么f (12)等于( )A ．1B ．3C ．15D ．30解析：选C.法一：令1－2x ＝t ，则x ＝1－t2(t ≠1)，∴f (t )＝4(t －1)2－1，∴f (12)＝16－1＝15.法二：令1－2x ＝12，得x ＝14，∴f (12)＝16－1＝15.3．一列货运火车从某站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一站停车，装完货以后，火车又匀加速行驶，一段时间后再次匀速行驶，下列图象可以近似地刻画出火车在这段时间内的速度变化情况的是( )解析：选B.根据题意，知火车从静止开始匀加速行驶，所以只有选项B 、C 符合题意，然后匀速行驶一段时间后又停止了一段时间，所以可以确定选B. 4．已知函数f (x )，g (x )分别由下表给出，x 1 2 3 g (x )321则f [g (1)]的值为________；当g [f (x )]＝2时，x ＝________. 解析：f [g (1)]＝f (3)＝1； g [f (x )]＝2，∴f (x )＝2， ∴x ＝1. 答案：1 15．若一个长方体的高为80 cm ，长比宽多10 cm ，则这个长方体的体积y (cm 3)与长方体的宽x (cm)之间的表达式是________．解析：由题意，知长方体的宽为x cm ，长为(10＋x ) cm ，则根据长方体的体积公式，得y ＝(10＋x )x ×80＝80x 2＋800x .所以y 与x 之间的表达式是y ＝80x 2＋800x (x >0)． 答案：y ＝80x 2＋800x (x >0)6．已知f (x )是一次函数，且满足3f (x ＋1)－2f (x －1)＝2x ＋17，求f (x )． 解：设f (x )＝ax ＋b (a ≠0)，则3f (x ＋1)－2f (x －1)＝3ax ＋3a ＋3b －2ax ＋2a －2b ＝ax ＋b ＋5a ＝2x ＋17，∴a ＝2，b ＝7，∴f (x )＝2x ＋7.[B 级 能力提升]7．已知f (x )是一次函数，2f (2)－3f (1)＝5,2f (0)－f (－1)＝1，则f (x )＝( ) A ．3x ＋2 B ．3x －2 C ．2x ＋3 D ．2x －3解析：选B.设f (x )＝kx ＋b (k ≠0)， ∵2f (2)－3f (1)＝5,2f (0)－f (－1)＝1， ∴⎩⎪⎨⎪⎧ k －b ＝5k ＋b ＝1，∴⎩⎪⎨⎪⎧k ＝3b ＝－2，∴f (x )＝3x －2. 8.已知函数f (x )的图象如图所示，则此函数的定义域、值域分别是( ) A ．(－3,3)；(－2,2) B ．[－3,3]；[－2,2] C ．[－2,2]；[－3,3] D ．(－2,2)；(－3,3)解析：选B.结合f (x )的图象知，定义域为[－3,3]，值域为[－2,2]． 9．已知f (x ＋1)＝x ＋2x ，则f (x )的解析式为________． 解析：∵f (x ＋1)＝x ＋2x ＝(x )2＋2x ＋1－1 ＝(x ＋1)2－1，∴f (x )＝x 2－1.由于x ＋1≥1，∴f (x )＝x 2－1(x ≥1)． 答案：f (x )＝x 2－1(x ≥1)10．2012年，第三十届夏季奥林匹克运动会在英国伦敦举行，其门票价格从20英磅到2000英磅不等，但最高门票：7月27日开幕式的贵宾票，价格高达2012英磅，折合人民币21352元，是2008年北京奥运会门票的四倍．为鼓励伦敦青少年到现场观看比赛，伦敦奥组委为伦敦市的14000名学生提供了一次免费门票机会，16岁以下青少年儿童的门票价格比最低价门票还要优惠些，有些比赛项目则无需持票观看，如马拉松、三项全能和公路自行车比赛均向观众免费开放．某同学打算购买x 张价格为20英磅的门票(x ∈{1,2,3,4,5}，需用y 英磅，试用函数的三种表示方法将y 表示成x 的函数． 解：解析法：y ＝20x ，x ∈{1,2,3,4,5}． 列表法：图象法：11．作出下列函数的图象： (1)y ＝x ＋2，|x |≤3；(2)y ＝x 2－2，x ∈Z 且|x |≤2.解：(1)因为|x |≤3，所以函数的图象为线段，而不是直线，如图(1)． (2)因为x ∈Z 且|x |≤2，所以函数的图象是五个孤立的点，如图(2)．高中数学必修一同步训练及解析1．已知集合A ＝{a ，b }，集合B ＝{0,1}，则下列对应不是A 到B 的映射的是( )解析：选C.A 、B 、D 均满足映射的定义，C 不满足A 中任一元素在B 中都有唯一元素与之对应，且A 中元素b 在B 中无元素与之对应．2．设函数f (x )＝⎩⎪⎨⎪⎧1－x 2，x ≤1，x 2＋x －2，x >1，则f [1f (2)]的值为( )A.1516B ．－2716C.89 D ．18解析：选A.∵f (2)＝22＋2－2＝4，∴f [1f (2)]＝f (14)＝1－(14)2＝1516.3．已知函数f (x )＝⎩⎪⎨⎪⎧x 2，x ≤00，x >0，则f (2)＋f (－2)＝________.答案：44．已知M ＝{正整数}，N ＝{正奇数}，映射f ：a →b ＝2a －1，(a ∈M ，b ∈N )，则在映射f 下M 中的元素11对应N 中的元素是________． 答案：21[A 级 基础达标]1．下列给出的式子是分段函数的是( )①f (x )＝⎩⎪⎨⎪⎧x 2＋1，1≤x ≤5，2x ，x ≤1.②f (x )＝⎩⎪⎨⎪⎧x ＋1，x ∈R ，x 2，x ≥2.③f (x )＝⎩⎪⎨⎪⎧2x ＋3，1≤x ≤5，x 2，x ≤1.④f (x )＝⎩⎪⎨⎪⎧x 2＋3，x <0，x －1，x ≥5.A ．①②B ．①④C ．②④D ．③④2.已知f (x )＝⎩⎪⎨⎪⎧x ＋2(x ≤－1)，x 2(－1＜x ＜2)，2x (x ≥2)，若f (x )＝3，则x 的值是( )A ．1B ．1或32C ．1，32或±3 D. 3解析：选D.该分段函数的三段各自的值域为(－∞，1]，[0,4)，[4，＋∞)，而3∈[0,4)， ∴f (x )＝x 2＝3，x ＝±3，而－1＜x ＜2，∴x ＝ 3.3．函数y ＝x ＋|x |x的图象为( )解析：选C.y ＝x ＋|x |x ＝⎩⎪⎨⎪⎧x ＋1 (x >0)x －1 (x <0)，再作函数图象．4.如图，函数f (x )的图象是折线段ABC ，其中点A ，B ，C 的坐标分别为(0,4)，(2,0)，(4,2)，则f (f (f (2)))＝________.解析：f (2)＝0，f (f (2))＝f (0)＝4，f (f (f (2)))＝f (4)＝2. 答案：25．已知f (x )＝⎩⎪⎨⎪⎧2x ，x <0x 2，x ≥0，若f (x )＝16，则x 的值为________．解析：当x <0时，2x ＝16，无解；当x ≥0时，x 2＝16，解得x ＝4. 答案：46．已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2，x ≤－1，2x ，－1<x <2，x 22，x ≥2.(1)求f (－74)；(2)求f (14)；(3)求f (4)；(4)若f (a )＝3，求a 的值．解：(1)f (－74)＝－74＋2＝14；(2)f (14)＝2×14＝12；(3)f (4)＝422＝8；(4)因为当x ≤－1时，x ＋2≤1，当x ≥2时，x 22≥2，当－1<x <2时，－2<2x <4.所以⎩⎪⎨⎪⎧－1<a <22a ＝3⇒a ＝32，或⎩⎪⎨⎪⎧a ≥2a 22＝3⇒a 2＝6⇒a ＝ 6.综上，若f (a )＝3，则a 的值为32或 6.[B 级 能力提升]7．若函数f (x )＝⎩⎪⎨⎪⎧2x ＋2 (－1<x <0)－12x (0≤x <2)，3 (x ≥2)则f (x )的值域是( )A ．(－1,2)B ．(－1,3]C ．(－1,2]D ．(－1,2)∪{3}解析：选D.对f (x )来说，当－1<x <0时，f (x )＝2x ＋2∈(0,2)；当0≤x <2时，f (x )＝－12x ∈(－1,0]；当x ≥2时，f (x )＝3.故函数y ＝f (x )的值域为(－1,2)∪{3}．故选D.8．映射f ：A →B ，A ＝{－3，－2，－1,1,2,3,4}，对于任意a ∈A ，在集合B 中和它对应的元素是|a |，则集合B 中的元素个数至少是( ) A ．4 B ．5 C ．6 D ．7解析：选A.对于A 中的元素±1，B 中有1与之对应；A 中的元素±2，B 中有一个元素2与之对应；A 中的元素±3，B 中有一个元素3与之对应；A 中的元素4，B 中有一个元素4与之对应，所以B 中的元素个数至少是4.9．设f ：A →B 是从集合A 到B 的映射，其中A ＝B ＝{(x ，y )|x ，y ∈R}，f ：(x ，y )→(x ＋y ，x －y )，那么A 中元素(1,3)所对应的B 中的元素为________，B 中元素(1,3)在A 中有________与之对应．解析：(1,3)→(1＋3,1－3)，即(4，－2)． 设A 中与(1,3)对应的元素为(x ，y )， 则⎩⎪⎨⎪⎧ x ＋y ＝1x －y ＝3，解得⎩⎪⎨⎪⎧x ＝2，y ＝－1. 答案：(4，－2) (2，－1)10．根据函数f (x )的图象如图所示，写出它的解析式．解：当0≤x ≤1时，f (x )＝2x ；当1<x <2时，f (x )＝2；当x ≥2时，f (x )＝3. 所以解析式为f (x )＝⎩⎪⎨⎪⎧2x ，0≤x ≤1，2，1<x <2，3，x ≥2.11．某市乘出租车计费规定：2公里以内5元，超过2公里不超过8公里的部分按每公里1.6元计费，超过8公里以后按每公里2.4元计费．若甲、乙两地相距10公里，则乘出租车从甲地到乙地共需要支付乘车费为多少元？ 解：设乘出租车走x 公里，车费为y 元， 由题意得y ＝⎩⎪⎨⎪⎧5，0<x ≤25＋1.6×(x －2)，2<x ≤8，14.6＋2.4×(x －8)，x >8即y ＝⎩⎪⎨⎪⎧5，0<x ≤21.8＋1.6x ，2<x ≤8，2.4x －4.6，x >8因为甲、乙两地相距10公里，即x ＝10>8，所以车费y ＝2.4×10－4.6＝19.4(元)． 所以乘出租车从甲地到乙地共需要支付乘车费为19.4元．高中数学必修一同步训练及解析1．函数y ＝－x 2的单调减区间是( ) A ．[0，＋∞) B ．(－∞，0] C ．(－∞，0) D ．(－∞，＋∞)解析：选A.根据y ＝－x 2的图象可得．2．下列函数中，在区间(0,1)上是增函数的是( ) A ．y ＝|x | B ．y ＝3－xC ．y ＝1xD ．y ＝－x 2＋4解析：选A.∵－1<0，所以一次函数y ＝－x ＋3在R 上递减；反比例函数y ＝1x在(0，＋∞)上递减；二次函数y ＝－x 2＋4在(0，＋∞)上递减．故选A.3．如图所示为函数y ＝f (x )，x ∈[－4,7]的图象，则函数f (x )的单调递增区间是________．答案：[－1.5,3]，[5,6]4．证明：函数y ＝xx ＋1在(－1，＋∞)上是增函数．证明：设x 1>x 2>－1，则y 1－y 2＝x 1x 1＋1－x 2x 2＋1＝x 1－x 2(x 1＋1)(x 2＋1)，∵x 1>x 2>－1，∴x 1－x 2>0，x 1＋1>0，x 2＋1>0，∴x 1－x 2(x 1＋1)(x 2＋1)>0.即y 1－y 2>0，y 1>y 2， ∴y ＝xx ＋1在(－1，＋∞)上是增函数．[A 级 基础达标]1．下列说法中正确的有( )①若x 1，x 2∈I ，当x 1<x 2时，f (x 1)<f (x 2)，则y ＝f (x )在I 上是增函数； ②函数y ＝x 2在R 上是增函数；③函数y ＝－1x在定义域上是增函数；④y ＝1x的单调递减区间是(－∞，0)∪(0，＋∞)．A ．0个B ．1个C ．2个D ．3个解析：选A.函数的单调性的定义是指定义在区间I 上任意两个值x 1，x 2，强调的是任意，从而①不对；②y ＝x 2在x ≥0时是增函数，x <0时是减函数，从而y ＝x 2在整个定义域上不具有单调性；③y ＝－1x 在整个定义域内不是单调递增函数．如－3<5，而f (－3)>f (5)；④y ＝1x的单调递减区间不是(－∞，0)∪(0，＋∞)，而是(－∞，0)和(0，＋∞)，注意写法． 2．函数y ＝x 2－3x ＋2的单调减区间是( ) A ．[0，＋∞) B ．[1，＋∞) C ．[1,2]D ．(－∞，32]解析：选D.由二次函数y ＝x 2－3x ＋2图象的对称轴为x ＝32且开口向上，所以单调减区间为(－∞，32]，故选D.3．函数y ＝f (x )在R 上为增函数，且f (2m )>f (－m ＋9)，则实数m 的取值范围是( ) A ．(－∞，－3) B ．(0，＋∞) C ．(3，＋∞)D ．(－∞，－3)∪(3，＋∞)解析：选C.因为函数y ＝f (x )在R 上为增函数，且f (2m )>f (－m ＋9)，所以2m >－m ＋9，即m >3，故选C.4．函数f (x )＝|x －3|的单调递增区间是________，单调递减区间是________． 解析：f (x )＝⎩⎪⎨⎪⎧x －3，x ≥3，－x ＋3，x <3.其图象如图所示，则f (x )的单调递增区间是[3，＋∞)，单调递减区间是(－∞，3]． 答案：[3，＋∞) (－∞，3]5．若函数f (x )＝ax ＋1x ＋2在区间(－2，＋∞)上单调递增，则a 的取值范围为________．解析：设任意的x 1，x 2∈(－2，＋∞)，且x 1<x 2，f (x 1)－f (x 2)＝ax 1＋1x 1＋2－ax 2＋1x 2＋2＝(x 1－x 2)(2a －1)(x 1＋2)(x 2＋2). ∵f (x )在(－2，＋∞)上单调递增， ∴f (x 1)－f (x 2)<0. ∴(x 1－x 2)(2a －1)(x 1＋2)(x 2＋2)<0， ∵x 1－x 2<0，x 1＋2>0，x 2＋2>0，∴2a －1>0，∴a >12.答案：(12，＋∞)6．作出函数y ＝x |x |＋1的图象并写出其单调区间． 解：由题可知y ＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，－x 2＋1，x <0，作出函数的图象如图所示，所以原函数的单调增区间为(－∞，＋∞)．[B 级 能力提升]7．对于函数y ＝f (x )，在给定区间上有两个数x 1，x 2，且x 1<x 2，使f (x 1)<f (x 2)成立，则y ＝f (x )( ) A ．一定是增函数 B ．一定是减函数 C ．可能是常数函数 D ．单调性不能确定解析：选D.由单调性定义可知，不能用特殊值代替一般值． 8．若函数f (x )在(－∞，＋∞)上为减函数，则( ) A ．f (a )>f (2a ) B ．f (a 2)<f (a )C ．f (a 2－1)<f (a )D ．f (a 2＋1)<f (a )解析：选D.∵a 2＋1－a ＝(a －12)2＋34>0，∴a 2＋1>a .∴f (a 2＋1)<f (a )．故选D.9．已知函数f (x )为区间[－1,1]上的增函数，则满足f (x )<f (12)的实数x 的取值范围为________．解析：由题设得⎩⎪⎨⎪⎧－1≤x ≤1，x <12，即－1≤x <12.答案：－1≤x <1210．作出函数f (x )＝|2x －1|的图象并写出其单调区间． 解：当x >12时，f (x )＝2x －1，当x ≤12时，f (x )＝－2x ＋1，所以f (x )＝⎩⎨⎧2x －1，x >12，－2x ＋1，x ≤12，画出函数的图象如图所示，所以原函数的单调增区间为[12，＋∞)，减区间为(－∞，12]．11．若f (x )＝x 2＋bx ＋c ，且f (1)＝0，f (3)＝0. (1)求b 与c 的值；(2)试证明函数f (x )在区间(2，＋∞)上是增函数．解：(1)∵f (1)＝0，f (3)＝0， ∴⎩⎪⎨⎪⎧1＋b ＋c ＝09＋3b ＋c ＝0，解得b ＝－4，c ＝3. (2)证明：∵f (x )＝x 2－4x ＋3， ∴设x 1，x 2∈(2，＋∞)且x 1＜x 2，f (x 1)－f (x 2)＝(x 21－4x 1＋3)－(x 22－4x 2＋3)＝(x 21－x 22)－4(x 1－x 2) ＝(x 1－x 2)(x 1＋x 2－4)，∵x 1－x 2＜0，x 1＞2，x 2＞2， ∴x 1＋x 2－4＞0. ∴f (x 1)－f (x 2)＜0， 即f (x 1)＜f (x 2)．∴函数f (x )在区间(2，＋∞)上为增函数．高中数学必修一同步训练及解析1．设函数f (x )＝2x －1(x <0)，则f (x )( ) A ．有最大值 B ．有最小值 C ．是增函数 D ．是减函数 解析：选C.画出函数f (x )＝2x －1(x <0)的图象，如右图中实线部分所示．由图象可知，函数f (x )＝2x －1(x <0)是增函数，无最大值及最小值．故选C.2．函数y ＝1x －1在[2,3]上的最小值为( )A ．2 B.12 C.13D ．－12解析：选B.函数y ＝1x －1在[2,3]上为减函数，∴y min ＝13－1＝12.3．函数f (x )＝1x 在[1，b ](b >1)上的最小值是14，则b ＝________.解析：∵f (x )在[1，b ]上是减函数，∴f (x )在[1，b ]上的最小值为f (b )＝1b ＝14，∴b ＝4. 答案：44．函数y ＝2x 2＋2，x ∈N *的最小值是________． 解析：∵x ∈N *，∴x 2≥1， ∴y ＝2x 2＋2≥4，即y ＝2x 2＋2在x ∈N *上的最小值为4，此时x ＝1. 答案：4[A 级 基础达标]1．函数f (x )＝x 2－4x ＋3，x ∈[1,4]，则f (x )的最大值为( ) A ．－1 B ．0 C ．3 D ．－2解析：选C.∵f (x )在[1,2]上是减函数，在[2,4]上是增函数，又f (1)＝0，f (4)＝3. ∴f (x )的最大值是3.2．函数f (x )＝⎩⎪⎨⎪⎧2x ＋6，x ∈[1，2]x ＋7，x ∈[－1，1]，则f (x )的最大值、最小值分别为( )A ．10、6B ．10、8C ．8、6D ．以上都不对解析：选A.f (x )在x ∈[－1,2]上为增函数，f (x )max ＝f (2)＝10，f (x )min ＝f (－1)＝6. 3．函数f (x )＝9－ax 2(a ＞0)在[0,3]上的最大值为( ) A ．9 B ．9(1－a ) C ．9－a D ．9－a 2解析：选A.x ∈[0,3]时f (x )为减函数，f (x )max ＝f (0)＝9. 4．函数f (x )＝x －2，x ∈{0,1,2,4}的最大值为________．解析：函数f (x )自变量的取值是几个孤立的数，用观察法即得它的最大值为f (4)＝2. 答案：25．函数f (x )＝x 2＋bx ＋1的最小值是0，则实数b ＝________. 解析：f (x )是二次函数，二次项系数1>0，则最小值为f (－b 2)＝b 24－b 22＋1＝0，解得b ＝±2. 答案：±26．已知函数f (x )＝⎩⎨⎧x 2 (－12≤x ≤1)1x(1＜x ≤2)，求f (x )的最大、最小值．解析：当－12≤x ≤1时，由f (x )＝x 2，得f (x )的最大值为f (1)＝1，最小值为f (0)＝0；当1＜x ≤2时，由f (x )＝1x，得f (2)≤f (x )＜f (1)，即12≤f (x )＜1. 综上f (x )max ＝1，f (x )min ＝0.[B 级 能力提升]7．已知函数f (x )＝－x 2＋4x ＋a ，x ∈[0,1]，若f (x )的最小值为－2，则f (x )的最大值为( )A ．－1B ．0C ．1D ．2解析：选C.因为f (x )＝－(x －2)2＋4＋a ，由x ∈[0,1]可知当x ＝0时，f (x )取得最小值，及－4＋4＋a ＝－2，所以a ＝－2，所以f (x )＝－(x －2)2＋2，当x ＝1时，f (x )取得最大值为－1＋2＝1.故选C.8．某公司在甲、乙两地同时销售一种品牌车，利润(单位：万元)分别为L 1＝－x 2＋21x 和L 2＝2x ，其中销售量单位：辆．若该公司在两地共销售15辆，则能获得的最大利润为( ) A ．90万元 B ．60万元 C ．120万元 D ．120.25万元解析：选C.设公司在甲地销售x 辆，则在乙地销售15－x 辆，公司获利为 L ＝－x 2＋21x ＋2(15－x ) ＝－x 2＋19x ＋30＝－(x －192)2＋30＋1924，∴当x ＝9或10时，L 最大为120万元．9．函数y ＝ax ＋1在区间[1,3]上的最大值为4，则a ＝______.解析：若a <0，则函数y ＝ax ＋1在区间[1,3]上是减函数，并且在区间的左端点处取得最大值，即a ＋1＝4，解得a ＝3，不满足a <0，舍去；若a >0，则函数y ＝ax ＋1在区间[1,3]上是增函数，当x ＝3时，y ＝4，∴3a ＋1＝4，∴a ＝1. 综上：a ＝1. 答案：110．已知函数f (x )＝1a －1x(a >0)．(1)证明f (x )在(0，＋∞)上单调递增；(2)若f (x )的定义域、值域都是[12，2]，求实数a 的值．解：(1)证明：设x 2>x 1>0，则f (x 2)－f (x 1)＝(1a －1x 2)－(1a －1x 1)＝1x 1－1x 2＝x 2－x 1x 1x 2. ∵x 2>x 1>0，∴x 2－x 1>0， ∴x 2－x 1x 1x 2>0，即f (x 2)>f (x 1)． ∴f (x )在(0，＋∞)上单调递增．(2)∵f (x )在(0，＋∞)上单调递增，且定义域和值域均为[12，2]，∴⎩⎨⎧f (12)＝1a －2＝12，f (2)＝1a －12＝2，∴a ＝25.11.如图所示，动物园要建造一面靠墙的两间一样大小的长方形动物笼舍，可供建造围墙的材料总长为30 m ，问每间笼舍的宽度x 为多少m 时，才能使得每间笼舍面积y 达到最大？每间最大面积为多少？ 解：设总长为b ， 由题意知b ＝30－3x ，可得y ＝12xb ，即y ＝12x (30－3x )＝－32(x －5)2＋37.5，x ∈(0,10)．当x ＝5时，y 取得最大值37.5，即每间笼舍的宽度为5 m 时，每间笼舍面积y 达到最大，最大面积为37.5 m 2.高中数学必修一同步训练及解析1．下列函数为偶函数的是( ) A ．f (x )＝|x |＋xB ．f (x )＝x 2＋1xC ．f (x )＝x 2＋xD ．f (x )＝|x |x2解析：选D.只有D 符合偶函数定义．2．f (x )＝x 3＋1x的图象关于( )A ．原点对称B ．y 轴对称C ．y ＝x 对称D ．y ＝－x 对称解析：选A.x ≠0，f (－x )＝(－x )3＋1－x＝－f (x )，f (x )为奇函数，关于原点对称．3．函数f (x )＝x 3＋ax ，f (1)＝3，则f (－1)＝________. 解析：显然f (x )是奇函数，∴f (－1)＝－f (1)＝－3. 答案：－34．若函数f (x )＝(x ＋1)(x －a )为偶函数，则a ＝________. 解析：f (x )＝x 2＋(1－a )x －a 为偶函数， ∴1－a ＝0，a ＝1. 答案：1[A 级 基础达标]1．下列命题中，真命题是( )A ．函数y ＝1x是奇函数，且在定义域内为减函数B ．函数y ＝x 3(x －1)0是奇函数，且在定义域内为增函数C ．函数y ＝x 2是偶函数，且在(－3,0)上为减函数D ．函数y ＝ax 2＋c (ac ≠0)是偶函数，且在(0,2)上为增函数解析：选C.选项A 中，y ＝1x在定义域内不具有单调性；B 中，函数的定义域不关于原点对称；D 中，当a ＜0时，y ＝ax 2＋c (ac ≠0)在(0,2)上为减函数，故选C. 2．下面四个结论：①偶函数的图象一定与y 轴相交； ②奇函数的图象一定通过原点； ③偶函数的图象关于y 轴对称；④既是奇函数又是偶函数的函数是f (x )＝0. 其中正确的个数为( ) A ．1 B ．2 C ．3 D ．4解析：选A.偶函数的图象关于y 轴对称，但不一定与y 轴相交，如y ＝1x2，故①错，③对；奇函数的图象不一定通过原点，如y ＝1x，故②错；既奇又偶的函数除了满足f (x )＝0，还要满足定义域关于原点对称，④错．故选A.3．已知函数f (x )＝ax 2＋bx ＋c (a ≠0)是偶函数，那么g (x )＝ax 3＋bx 2＋cx ( ) A ．是奇函数 B ．是偶函数C ．既是奇函数又是偶函数D ．是非奇非偶函数 解析：选A.g (x )＝x (ax 2＋bx ＋c )＝xf (x )，g (－x )＝－x ·f (－x )＝－x ·f (x )＝－g (x )，所以g (x )＝ax 3＋bx 2＋cx 是奇函数；因为g (x )－g (－x )＝2ax 3＋2cx 不恒等于0，所以g (－x )＝g (x )不恒成立．故g (x )不是偶函数．4．如图给出奇函数y ＝f (x )的局部图象，则f (－2)的值是________．解析：f (－2)＝－f (2)＝－32.答案：－325．已知函数f (x )＝ax 2＋bx ＋3a ＋b 为偶函数，其定义域为[a －1,2a ]，则a ＝________，b ＝________.解析：∵f (x )是定义域为[a －1,2a ]的偶函数，∴a －1＝－2a ，∴a ＝13.又f (－x )＝f (x )， 即13x 2－bx ＋1＋b ＝13x 2＋bx ＋1＋b . ∴b ＝0.答案：136．判断下列函数的奇偶性． (1)f (x )＝x －1＋1－x ； (2)f (x )＝|x |＋x 2；(3)f (x )＝⎩⎪⎨⎪⎧x －1 (x >0)0 (x ＝0).x ＋1 (x <0)解：(1)∵⎩⎪⎨⎪⎧x －1≥01－x ≥0.∴x ＝1.定义域为{1}，不关于原点对称，∴函数f (x )为非奇非偶函数．(2)f (x )＝|x |＋x 2＝2|x |， 定义域为(－∞，＋∞)，关于原点对称．且有f (－x )＝2|－x |＝2|x |＝f (x )， ∴f (x )为偶函数．(3)法一：显然定义域为(－∞，＋∞)，关于原点对称． 当x >0时，－x <0，则f (－x )＝1－x ＝－f (x )， 当x <0时，－x >0，则f (－x )＝－x －1＝－f (x )． 则f (－0)＝f (0)＝－f (0)＝0. ∴f (x )为奇函数．法二：作出函数f (x )的图象，可知f (x )的图象关于原点对称，所以f (x )为奇函数．[B 级 能力提升]7．若f (x )为偶函数，且当x ≥0时，f (x )≥2，则当x ≤0时( ) A ．f (x )≤2 B ．f (x )≥2C ．f (x )≤－2D ．f (x )∈R解析：选B.可画出f (x )的大致图象：易知当x ≤0时，有f (x )≥2.故选B.8．设偶函数f (x )的定义域为R ，当x ∈[0，＋∞)时f (x )是增函数，则f (－2)，f (π)，f (－3)的大小关系是( ) A ．f (π)>f (－3)>f (－2) B ．f (π)>f (－2)>f (－3) C ．f (π)<f (－3)<f (－2) D ．f (π)<f (－2)<f (－3)解析：选A.∵f (x )为偶函数，且当x ∈[0，＋∞)时，f (x )为增函数． 又∵f (－2)＝f (2)，f (－3)＝f (3)， 且2<3<π，∴f (2)<f (3)<f (π)，即f (－2)<f (－3)<f (π)．9．若偶函数f (x )在(－∞，0]上为增函数，则满足f (1)≤f (a )的实数a 的取值范围是________． 解析：由已知偶函数f (x )在(－∞，0]上为增函数， ∴f (x )在(0，＋∞)上是减函数，∴f (1)≤f (a )⇔⎩⎪⎨⎪⎧ a >0，1≥a 或⎩⎪⎨⎪⎧a ≤0－1≤a ⇔0<a ≤1，或－1≤a ≤0.。

高一上册数学课堂同步练习答案高一数学练习册答案1.下列幂函数为偶函数的是()A.y=某12B.y=3某C.y=某2D.y=某-1解析：选C.y=某2，定义域为R，f(-某)=f(某)=某2.2.若a<0，则0.5a,5a,5-a的大小关系是()A.5-a<5a<0.5aB.5a<0.5a<5-aC.0.5a<5-a<5aD.5a<5-a<0.5a解析：选B.5-a=(15)a，因为a<0时y=某a单调递减，且15<0.5<5，所以5a<0.5a<5-a.3.设α∈{-1,1，12，3}，则使函数y=某α的定义域为R，且为奇函数的所有α值为()A.1,3B.-1,1C.-1,3D.-1,1,3解析：选A.在函数y=某-1，y=某，y=某12，y=某3中，只有函数y=某和y=某3的定义域是R，且是奇函数，故α=1,3.4.已知n∈{-2，-1,0,1,2,3}，若(-12)n>(-13)n，则n=________.解析：∵-12<-13，且(-12)n>(-13)n，∴y=某n在(-∞，0)上为减函数.又n∈{-2，-1,0,1,2,3}，∴n=-1或n=2.答案：-1或21.函数y=(某+4)2的递减区间是()A.(-∞，-4)B.(-4，+∞)C.(4，+∞)D.(-∞，4)解析：选A.y=(某+4)2开口向上，关于某=-4对称，在(-∞，-4)递减.2.幂函数的图象过点(2，14)，则它的单调递增区间是()A.(0，+∞)B.[0，+∞)C.(-∞，0)D.(-∞，+∞)解析：选C.幂函数为y=某-2=1某2，偶函数图象如图.3.给出四个说法：①当n=0时，y=某n的图象是一个点;②幂函数的图象都经过点(0,0)，(1,1);③幂函数的图象不可能出现在第四象限;④幂函数y=某n在第一象限为减函数，则n<0.其中正确的说法个数是()C.3D.4解析：选B.显然①错误;②中如y=某-12的图象就不过点(0,0).根据幂函数的图象可知③、④正确，故选B.4.设α∈{-2，-1，-12，13，12，1,2,3}，则使f(某)=某α为奇函数且在(0，+∞)上单调递减的α的值的个数是()A.1B.2C.3D.4解析：选A.∵f(某)=某α为奇函数，∴α=-1，13，1,3.又∵f(某)在(0，+∞)上为减函数，∴α=-1.5.使(3-2某-某2)-34有意义的某的取值范围是()A.RB.某≠1且某≠3C.-3解析：选C.(3-2某-某2)-34=143-2某-某23，∴要使上式有意义，需3-2某-某2>0，解得-36.函数f(某)=(m2-m-1)某m2-2m-3是幂函数，且在某∈(0，+∞)上是减函数，则实数m=()A.2B.3解析：选A.m2-m-1=1，得m=-1或m=2，再把m=-1和m=2分别代入m2-2m-3<0，经检验得m=2.7.关于某的函数y=(某-1)α(其中α的取值范围可以是1,2,3，-1，12)的图象恒过点________.解析：当某-1=1，即某=2时，无论α取何值，均有1α=1，∴函数y=(某-1)α恒过点(2,1).答案：(2,1)8.已知2.4α>2.5α，则α的取值范围是________.解析：∵0<2.4<2.5，而2.4α>2.5α，∴y=某α在(0，+∞)为减函数.答案：α<09.把(23)-13，(35)12，(25)12，(76)0按从小到大的顺序排列____________________.解析：(76)0=1，(23)-13>(23)0=1，(35)12<1，(25)12<1，∵y=某12为增函数，∴(25)12<(35)12<(76)0<(23)-13.答案：(25)12<(35)12<(76)0<(23)-1310.求函数y=(某-1)-23的单调区间.解：y=(某-1)-23=1某-123=13某-12，定义域为某≠1.令t=某-1，则y=t-23，t≠0为偶函数.因为α=-23<0，所以y=t-23在(0，+∞)上单调递减，在(-∞，0)上单调递增.又t=某-1单调递增，故y=(某-1)-23在(1，+∞)上单调递减，在(-∞，1)上单调递增.11.已知(m+4)-12<(3-2m)-12，求m的取值范围.解：∵y=某-12的定义域为(0，+∞)，且为减函数.∴原不等式化为m+4>03-2m>0m+4>3-2m，解得-13∴m的取值范围是(-13，32).12.已知幂函数y=某m2+2m-3(m∈Z)在(0，+∞)上是减函数，求y的解析式，并讨论此函数的单调性和奇偶性.解：由幂函数的性质可知m2+2m-3<0⇒(m-1)(m+3)<0⇒-3又∵m∈Z，∴m=-2，-1,0.当m=0或m=-2时，y=某-3，定义域是(-∞，0)∪(0，+∞).∵-3<0，∴y=某-3在(-∞，0)和(0，+∞)上都是减函数，又∵f(-某)=(-某)-3=-某-3=-f(某)，∴y=某-3是奇函数.当m=-1时，y=某-4，定义域是(-∞，0)∪(0，+∞).∵f(-某)=(-某)-4=1-某4=1某4=某-4=f(某)，∴函数y=某-4是偶函数.∵-4<0，∴y=某-4在(0，+∞)上是减函数，又∵y=某-4是偶函数，∴y=某-4在(-∞，0)上是增函数.高一数学上册课堂练习题答案一、选择题1.某商店某种商品(以下提到的商品均指该商品)进货价为每件40元，当售价为50元时，一个月能卖出500件.通过市场调查发现，若每件商品的单价每提高1元，则商品一个月的销售量会减少10件.商店为使销售该商品的月利润，应将每件商品定价为()A.45元B.55元C.65元D.70元[答案] D[解析] 设每件商品定价为某元，则一个月的销量为500-(某-50)某10=1000-10某件，故月利润为y=(某-40)•(1000-10某)=-10(某-40)(某-100)，∵某>401000-10某>0，∴40∴当某=70时，y取值，故选D.2.某债券市场发行三种债券，A种面值为100元，一年到期本息和为103元;B种面值为50元，半年到期本息和为51.4元;C种面值为100元，但买入价为97元，一年到期本息和为100元.作为购买者，分析这三种债券的收益，从小到大排列为()A.B，A，CB.A，C，BC.A，B，CD.C，A，B[答案] B[解析] A种债券的收益是每100元收益3元;B种债券的利率为51.4-5050，所以100元一年到期的本息和为100(1+51.4-5050)≈105.68(元)，收益为5.68元;C种债券的利率为100-97100，100元一年到期的本息和为100(1+100-9797)≈103.09(元)，收益为3.09元.3.某厂原来月产量为a，一月份增产10%，二月份比一月份减产10%，设二月份产量为b，则()A.a=bB.a>bC.a[答案] B[解析] 一月份产量为a(1+10%)，二月份产量b=a(1+10%)(1-10%)=a(1-1%)，∴b4.甲、乙两人在一次赛跑中，路程S与时间t的函数关系如图所示，则下列说法正确的是()A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人的速度相同D.甲先到达终点[答案] D[解析] 从图可以看出，甲、乙两人同时出发(t=0)，跑相同多的路程(S0)，甲用时(t1)比乙用时(t2)较短，即甲比乙的速度快，甲先到达终点.5.如图所示，花坛水池中央有一喷泉，水管OA=1m，水从喷头A喷出后呈抛物线状，先向上至点落下，若点距水面2m，A离抛物线对称轴1m，则在水池半径的下列可选值中，最合算的是()A.3.5mB.3mC.2.5mD.2m[答案] C[解析] 建立如图坐标系，据题设y轴右侧的抛物线方程为y=a(某-1)2+2.∵抛物线过点A(0,1)∴将(0,1)点代入方程得a=-1，∴y=-(某-1)2+2.令y=0，得某=1+2，某=1-2(舍)，故落在水面上的最远点B到O点距离为(1+2)m，考虑合算，须达到要求条件下用料最少，∴选C.6.某市原来民用电价为0.52元/kw•h.换装分时电表后，峰时段(早上八点到晚上九点)的电价为0.55元/kw•h，谷时段(晚上九点到次日早上八点)的电价为0.35元/kw•h.对于一个平均每月用电量为200kw•h的家庭，要使节省的电费不少于原来电费的10%，则这个家庭每月在峰时段的平均用电量()A.至少为82kw•hB.至少为118kw•hC.至多为198kw•hD.至多为118kw•h[答案] D[解析] ①原来电费y1=0.52某200=104(元).②设峰时段用电为某kw•h，电费为y，则y=某某0.55+(200-某)某0.35=0.2某+70，由题意知0.2某+70≤(1-10%)y1，∴某≤118.答：这个家庭每月在峰时段的平均用电量至多为118kw•h.二、填空题7.英语老师准备存款5000元.银行的定期存款中存期为1年的年利率1.98%.试计算五年后本金和利息共有________元.[答案] 5514.99[解析] 根据题意，五年后的本息共5000(1+1.98%)5=5514.99(元).8.设物体在8∶00到16∶00之间的温度T是时间t的函数：T(t)=at2+bt+c(a≠0)，其中温度的单位是°C，时间的单位是小时，t=0表示12∶00，t取正值表示12∶00以后，若测得该物体在8∶00的温度为8°C，12∶00的温度为60°C,13∶00的温度为58°C，则T(t)=________.[答案] -3t2+t+60[解析] 将t=-4，T=8;t=0，T=60;t=1，T=58分别代入函数表达式中即可解出a=-3，b=1，c=60.三、解答题9.某物品的价格从1964年的100元增加到2004年的500元，假设该物品的价格年增长率是平均的，那么2022年该物品的价格是多少(精确到元)[解析] 从1964年开始，设经过某年后物价为y，物价增长率为a%，则y=100(1+a%)某，将某=40，y=500代入得500=100(1+a%)40，解得a=4.1，故物价增长模型为y=100(1+4.1%)某.到2022年，某=46，代入上式得y=100(1+4.1%)46≈635(元).10.有甲、乙两个水桶，开始时水桶甲中有a升水，水通过水桶甲的底部小孔流入水桶乙中，t分钟后剩余的水符合指数衰减曲线y=ae-nt，假设过5分钟时水桶甲和水桶乙的水相等，求再过多长时间水桶甲的水只有a8.[解析] 由题意得ae-5n=a-ae-5n，即e-5n=12，设再过t分钟桶甲中的水只有a8，得ae-n(t+5)=a8，所以(12)t+55=(e-5n)t+55=e-n(t+5)=18=(12)3，∴t+55=3，∴t=10.∴再过10分钟桶甲的水只有a8.11.某报纸上报道了两则广告，甲商厦实行有奖销售：特等奖10000元1名，一等奖1000元2名，二等奖100元10名，三等奖5元200名，乙商厦则实行九五折优惠销售.请你想一想;哪一种销售方式更吸引人哪一家商厦提供给消费者的实惠大.面对问题我们并不能一目了然.于是我们首先作了一个随机调查.把全组的16名学员作为调查对象，其中8人愿意去甲家，6人喜欢去乙家，还有两人则认为去两家都可以.调查结果表明：甲商厦的销售方式更吸引人，但事实是否如此呢请给予说明.[解析] 在实际问题中，甲商厦每组设奖销售的营业额和参加抽奖的人数都没有限制.所以这个问题应该有几种情形：(1)若甲商厦确定每组设奖.当参加人数较少时，少于1+2+10+200=213人，人们会认为获奖机率较大，则甲商厦的销售方式更吸引顾客.(2)若甲商厦的每组营业额较多时，他给顾客的优惠幅度就相应的小.因为甲商厦提供的优惠金额是固定的，共10000+2000+1000+1000=14000元.假设两商厦提供的优惠都是14000元，则可求乙商厦的营业额为14000÷5%=280000.所以由此可得：(1)当两商厦的营业额都为280000元时，两家商厦所提供的优惠同样多.(2)当两商厦的营业额都不足280000元时，乙商厦的优惠则小于14000元，所以这时甲商厦提供的优惠仍是14000元，优惠较大.(3)当两家的营业额都超过280000元时，乙商厦的优惠则大于14000元，而甲商厦的优惠仍保持14000元时，乙商厦所提供的优惠大.12.某种新栽树木5年成材，在此期间年生长率为20%，以后每年生长率为某%(某<20).树木成材后，既可以砍伐重新再栽，也可以继续让其生长，哪种方案更好[解析] 只需考虑10年的情形.设新树苗的木材量为Q，则连续生长10年后木材量为：Q(1+20%)5(1+某%)5,5年后再重栽的木材量为2Q(1+20%)5，画出函数y=(1+某%)5与y=2的图象，用二分法可求得方程(1+某%)5=2的近似根某=14.87，故当某<14.87%时就考虑重栽，否则让它继续生长._13.(湖南长沙同升湖实验学校高一期末)商场销售某一品牌的羊毛衫，购买人数n是羊毛衫标价某的一次函数，标价越高，购买人数越少.已知标价为每件300元时，购买人数为零.标价为每件225元时，购买人数为75人，若这种羊毛衫的成本价是100元/件，商场以高于成本价的相同价格(标价)出售，问：(1)商场要获取利润，羊毛衫的标价应定为每件多少元(2)通常情况下，获取利润只是一种“理想结果”，如果商场要获得利润的75%，那么羊毛衫的标价为每件多少元[解析] (1)设购买人数为n人，羊毛衫的标价为每件某元，利润为y元，则n=k某+b(k<0)，∴0=300k+b75=225k+b，∴k=-1b=300，∴n=-某+300.y=-(某-300)•(某-100)=-(某-200)2+10000，某∈(100,300]∴某=200时，yma某=10000即商场要获取利润，羊毛衫的标价应定为每件200元.(2)由题意得，-(某-300)•(某-100)=10000某75%∴某2-400某+30000=-7500，∴某2-400某+37500=0，∴(某-250)(某-150)=0∴某1=250，某2=150所以当商场以每件150元或250元出售时，可获得利润的75%.14.学校请了30名木工，要制作200把椅子和100张课桌.已知制作一张课桌与制作一把椅子的工时数之比为10∶7，问30名工人应当如何分组(一组制课桌，另一组制椅子)，能使完成全部任务最快[分析] 制作课桌和椅子中所花较多的时间即为完成任务的时间，只要它最小，即完成任务最快.[解析] 设某名工人制课桌，(30-某)名工人制椅子，一个工人在一个单位时间里可制7张课桌或10把椅子，∴制作100张课桌所需时间为函数P(某)=1007某，制作200把椅子所需时间为函数Q(某)=20010(30-某)，完成全部任务所需的时间f(某)为P(某)与Q(某)中的较大值.欲使完成任务最快，须使P(某)与Q(某)尽可能接近(或相等).令P(某)=Q(某)，即1007某=20010(30-某)，解得某=12.5，∵人数某∈N，考察某=12和13的情形有P(12)≈1.19，Q(12)≈1.111，P(13)≈1.099，Q(13)≈1.176，∴f(12)=1.19，f(13)=1.176，∵f(12)>f(13)，∴某=13时，f(某)取最小值，∴用13名工人制作课桌，17名工人制作椅子完成任务最快.[点评] 本题有几点需特别注意，人数某必须是自然数，故P(某)与Q(某)不相等，f(某)是P(某)与Q(某)中的较大者，完成任务最快的时间是f(某)的最小值.高一数学上册练习题答案第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的。

4.4 对数函数(精讲)考法一 对数函数的判断【例1】(1)(2021·全国高一课时练习)给出下列函数：①223log y x =；①3log (1)y x =-；①(1)log x y x +=；①log e y x =.其中是对数函数的有( ) A ．1个B ．2个C ．3个D ．4个(2)．(2021·全国高一课时练习)若函数2log 32a y x a a =+-+为对数函数，则a =( )A ．1B ．2C ．3D ．4【一隅三反】1．(2021·全国高一课时练习)下列函数表达式中，是对数函数的有( )①y ＝log x 2；①y ＝log a x (a ①R )；①y ＝log 8x ；①y ＝ln x ；①y ＝log x (x ＋2)；①y ＝log 2(x ＋1)． A ．1个 B ．2个 C ．3个 D ．4个2．(2021·全国高一课时练习)下列函数表达式中，是对数函数的有( )①log 2x y =；①()log a y x a =∈R ；①8log y x =；①ln y x =；①()log 2x y x =+；①42log y x =；①()2log 1y x =+. A ．1个 B ．2个 C ．3个 D ．4个3．(2021·全国高一课时练习)若函数()2()log 45a f x x a a =+--是对数函数，a =_________.考法二 对数函数的解析式或函数值【例2】(1)(2021·上海高一专题练习)对数函数的图像过点M (125，3)，则此对数函数的解析式为( ) A ．y ＝log 5xB ．y ＝15log xC ．y ＝13log xD ．y ＝log 3x (2)(2021·全国高一课前预习)设()log a f x x =(0a >且1a ≠)，若1(2)2f =，则12f ⎛⎫= ⎪⎝⎭( ). A ．2B ．2-C ．12-D ．12【一隅三反】1．(2021·全国高一课时练习)若某对数函数的图象过点()4,2，则该对数函数的解析式为( ) A ．2log y x =B ．42log y x =C ．2log y x =或42log y x =D ．不确定2．(2021·全国高一课时练习)若函数()()lo 1g a f x x =+(0,1)a a >≠的图像过点(7,3)，则a 的值为( )A B ．2C D ．12考法三 对数函数的定义域【例3】(1)(2021·奉新县第一中学高一月考)函数()ln 1x f x -=的定义域为( )A ．(]1,2B ．[]1,4C ．()1,4D ．[]2,4(2)．(2021·江苏)已知函数(2)x y f =的定义域是[]1,1-，则函数3(log )f x 的定义域是( ) A ．[]1,1-B ．1,33⎡⎤⎢⎥⎣⎦C ．[]1,3D ．(3)(2021·全国高一课前预习)若函数()lg 1y ax =+的定义域为(),1-∞，则a =( ) A ．1 B ．－1 C ．2 D ．无法确定【一隅三反】1．(2021·全国)函数()00.5log 21y x =-⎡⎤⎣⎦的定义域为( )A ．1,12⎛⎫ ⎪⎝⎭B ．1,2⎛⎫+∞ ⎪⎝⎭C ．()1,+∞D ．()1,11,2⎛⎫+∞ ⎪⎝⎭2．(2021·四川自贡·)函数3()log (21)xf x x =-的定义域是( ) A ．1,12⎛⎤ ⎥⎝⎦B ．1,12⎡⎤⎢⎥⎣⎦ C ．(1,)+∞ D ．1(,1)23．(2021·陕西宝鸡市·高一期末)若函数(1)f x +的定义域为[0 1]，，则(lg )f x 的定义域为( ) A ．[10 100]， B ．[1 2]， C ．[0 1]， D ．[0 lg2]，4(2021·全国高一课时练习)求下列函数的定义域(1)12y x=- (2)函数2()f x =(3)20()(54)lg(43)x f x x x =+-+考法四 对数函数的定点【例4】(2021·四川高一开学考试)函数()log 272=+-a y x (0a >，且1a ≠)的图象一定经过的点是( ) A ．7,22⎛⎫-- ⎪⎝⎭B ．()3,2--C ．()3,1--D ．()4,2--【一隅三反】1．(2021·镇远县文德民族中学校高一月考)函数()()log 310,1a y x a a =->≠的图象过定点( ) A ．2,13⎛⎫ ⎪⎝⎭B ．()1,0-C ．2,03⎛⎫ ⎪⎝⎭D ．()0,1-2．(2021·全国)函数()log 1a y x =-的图象必过的点是( ) A ．()1,0- B ．()1,0 C ．()0,0 D ．()2,03．(2021·湖北高一开学考试)已知函数log (3)2a y x =-+(0a >且1a ≠)的图象恒过定点P ，点P 在幂函数()y f x =的图象上，则lg (4)lg (25)f f +=( )A ．2-B ．2C ．1D ．1-考法五 对数函数的值域(最值)【例5】(1)(2021·浙江高一单元测试)已知184x ≤≤，则函数2()log f x x =的值域是 。

5.3 诱导公式(精练)【题组一 诱导公式化简】1．(2021·陕西咸阳市实验中学高一月考(理))(1)化简：πcos 2sin(π)cos(2π)5πsin 2αααα⎛⎫- ⎪⎝⎭⋅-⋅-⎛⎫+ ⎪⎝⎭(2)求值：5ππ11π5πsincos sin cos 6464⎛⎫-+ ⎪⎝⎭【答案】(1)2sin α-；． 【解析】(1)()()πcos 2sin πcos 2π5πsin 2αααα⎛⎫- ⎪⎝⎭⋅-⋅-⎛⎫+ ⎪⎝⎭ ()()πcos 2sin πcos 2ππsin 2αααα⎛⎫- ⎪⎝⎭=⋅--⋅-⎡⎤⎣⎦⎛⎫+ ⎪⎝⎭()2sin sin cos sin cos ααααα=⋅-⋅=-， (2)5ππ11π5πsincos sin cos 6464⎛⎫-+ ⎪⎝⎭ππππsin πcos sin 2πcos π6464⎛⎫⎛⎫⎛⎫⎛⎫=--+-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ππππsin cos sin cos 6464⎛⎫⎛⎫=+-⨯- ⎪ ⎪⎝⎭⎝⎭ππππ11sin cos sin cos 646422=+==2．(2021·银川三沙源上游学校高一期中(文))求下列各式的值． (1)tan 405sin 450cos750-+； (2)7sin tan 2cos 02ππ⎛⎫-++ ⎪⎝⎭. 【答案】(2)3. 【解析】(1)()()()tan 405sin 450cos750tan 45360sin 90360cos 302360-+=+-+++⨯tan 45sin 90cos30112=-+=-+=(2)77sin tan 2cos 0sin 4tan 02cos 0sin 02123222πππππ⎛⎫⎛⎫-++=-+++=++=+= ⎪ ⎪⎝⎭⎝⎭. 3．(2021·全国高一专题练习)化简：cos 210cos(420)tan 330tan 390sin 750cos900︒︒︒︒︒︒⋅-⋅⋅⋅.【解析】原式＝cos(18030)cos(36060)tan(36030)tan(36030)sin(72030)cos(720180)︒︒︒︒︒︒︒︒︒︒︒︒+⋅--⋅-+⋅+⋅+＝()cos30cos60tan 30tan 30sin 30cos180︒︒︒︒︒-⋅⋅-⋅⋅1((⨯⨯4．(2021·贺州市桂东高级中学高一月考)计算：(1)sin cos 44ππ⎛⎫-+ ⎪⎝⎭；(2)75sin cos tan 224πππ++. 【答案】(1)0；(2)0.【解析】(1)sin cos 44ππ⎛⎫-+ ⎪⎝⎭sincos44ππ=-+22=+0=(2)75sincos tan 224πππ++ sin 4cos 2tan 224πππππ⎛⎫⎛⎫=-+++ ⎪ ⎪⎝⎭⎝⎭sincostan224πππ=-++1010=5．(2021·全国高一课时练习)化简求值：(1)234cos coscos cos 5555ππππ+++； (2)24sin 2cos ()33n n n ππππ⎛⎫⎛⎫-⋅+∈ ⎪ ⎪⎝⎭⎝⎭Z ．【答案】(1)0；(2)答案见解析. 【解析】(1)23422coscoscos cos cos cos cos 5555555ππππππππ⎛⎫+++=++-+ ⎪⎝⎭22cos cos cos cos cos 055555ππππππ⎛⎫-=+--= ⎪⎝⎭．(2)①当n 为奇数时，原式24sin cos 33ππ⎛⎫⎛⎫=-⋅- ⎪⎪⎝⎭⎝⎭sin cos 33ππππ⎛⎫⎛⎫=-⋅+ ⎪ ⎪⎝⎭⎝⎭1sincos332ππ=-⋅== ②当n 为偶数时，原式24sin cos 33ππ=-⋅ sin cos 33ππππ⎛⎫⎛⎫=--⋅+ ⎪ ⎪⎝⎭⎝⎭sincos33ππ=⋅=【题组二 诱导公式与三角函数定义、同角运用】1．(2021·北京市第四十三中学)已知tan 2θ=，则sin cos()2cos sin()πθπθθπθ⎛⎫+-- ⎪⎝⎭=--( ) A ．2 B ．-2 C ．0D ．23【答案】B【解析】因为tan 2θ=， 所以sin cos()2cos sin()πθπθθπθ⎛⎫+-- ⎪⎝⎭--， 2cos cos sin θθθ=-，221tan θ==--，故选：B2．(2021·江西新余四中高一月考)已知3sin 5α=，则()()sin cos ππsin 2ααα--=⎛⎫- ⎪⎝⎭( ) A ．45-B ．45C ．35D ．35【答案】D【解析】()()()sin cos πsin cos 3sin πcos 5sin 2ααααααα---⋅-===⎛⎫- ⎪⎝⎭， 故选：D.3．(2021·淮北市树人高级中学高一期中)若3sin(π)5α+=，且α是第三象限角，则ππsin cos 22ππsin cos 22αααα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭( )A ．1B ．7C ．-7D ．-1【答案】B【解析】由()3sin πsin 5αα+=-=，则3sin 5α=-.又α是第三象限角，所以4cos 5α=-，所以ππ43sin cos cos sin 22557ππ43cos sin sin cos 2255αααααααα⎛⎫⎛⎫⎛⎫+-+-+- ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭===-⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选：B.4．(2021·河南新乡县高中高一月考)已知α为第二象限角，且115tan tan 4αα-=则πsin sin(π)2πsin sin(π)2αααα⎛⎫+-+ ⎪⎝⎭⎛⎫--- ⎪⎝⎭的值为______. 【答案】35【解析】由115tan tan 4αα-=，得24tan 15tan 40αα--=，得1tan 4α=-或tan 4α=. α为第二象限角，∴1tan 4α=-，π1sin sin(π)1cos sin 1tan 3241πcos sin 1tan 51sin sin(π)42αααααααααα⎛⎫+-+-⎪++⎝⎭∴====--⎛⎫+--- ⎪⎝⎭. 故答案为：35. 5．(2021·全国高一课时练习)已知角α的终边经过点P 43(,)55-.(1)求sin α的值；(2)求sin tan()2sin()cos(3)πααπαππα⎛⎫-- ⎪⎝⎭+-的值. 【答案】(1)35；(2)54. 【解析】(1)因为点P 43(,)55-，所以|OP |=1，sin α=35. (2)sin tan()cos tan sin 2sin()cos(3)sin (cos )sin cos ⎛⎫-- ⎪⨯⎝⎭==+---πααπααααππααααα1cos =α， 由三角函数定义知cos α=45，故所求式子的值为54．6．(2021·陕西咸阳·高一期末)已知()()()()()3sin cos tan 202127cos cos sin 2f παπαπααπααππα⎛⎫--- ⎪⎝⎭=⎛⎫+--+ ⎪⎝⎭(1)化简()f α；(2)若角α的终边经过点()2,3P -，求()f α. 【答案】(1)()1sin f αα=-；【解析】(1)3sin cos()tan(2021)2()7cos cos()sin()2f παπαπααπααππα⎛⎫--- ⎪⎝⎭=⎛⎫+--+ ⎪⎝⎭cos (cos )(tan )sin (cos )(sin )αααααα---=--sin cos cos 1cos sin cos sin sin αααααααα-==- (2)角α的终边经过点()2,3P -，sin α∴== ()1sin f αα∴=-= 7．(2021·河南(理))已知3cos 2sin 1sin 2cos 4αααα-=-+．(1)()()3cos cos sin 2235cos sin 3sin 22πππαααππαπαα⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭的值(2)求()22sin cos sin 122πππααα⎛⎫⎛⎫-+-⋅++ ⎪ ⎪⎝⎭⎝⎭的值．【答案】(1)12；(2)3．【解析】(1)由3cos 2sin 1sin 2cos 4αααα-=-+，解得tan 2α=．()()()()()()()()3cos cos sin cos sin cos 112235sin sin cos tan 2cos sin 3sin 22πππααααααππαααααπαα⎛⎫⎛⎫++- ⎪ ⎪-⋅--⎝⎭⎝⎭===-⋅⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭(2)由(1)得tan 2α=，所以()22sin cos sin 122πππααα⎛⎫⎛⎫-+-⋅++ ⎪ ⎪⎝⎭⎝⎭22sin sin cos 1ααα=+⋅+2222sin sin cos 1sin cos ααααα+⋅=++222tan tan 1tan 1ααα+=++ 82141+=++3= 8．(2021·全国高一专题练习)已知角α的终边经过点()3,6P m m -(0m ≠).(1)求()()sin cos sin 2cos 22απαπππαα++-⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭的值； (2)若α是第二象限角，求()23sin sin cos cos 22ππαπααα⎛⎫⎛⎫++--+ ⎪ ⎪⎝⎭⎝⎭的值.【答案】(1)13-；【解析】(1)0m ≠, cos 0α∴≠,即()()sin cos sin 2cos 22απαπππαα++-⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭ sin cos cos 2sin αααα--=+ tan 112tan αα--=+.又角α的终边经过点()3,6P m m -(0m ≠)， 6tan 23mmα-∴==-， 故()()()sin cos tan 121112tan 1223sin 2cos 22απαπαππααα++----===-++⨯-⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭；(2)α是第二象限角，0m ∴<，则sin α==cos α=== ()23sin sin cos cos 22ππαπααα⎛⎫⎛⎫∴++--+ ⎪ ⎪⎝⎭⎝⎭2cos sin cos sin αααα=++2⎛⎛=+⎝⎭⎝⎭. 9．(2021·全国)(1)已知sin()cos()tan(3)()3cos 2f πθπθπθθπθ-+-=⎛⎫- ⎪⎝⎭，求73f π⎛⎫- ⎪⎝⎭的值 (2)已知1sin cos 5αα+=-，2παπ<<，求sin(3)cos(2)sin()sin 2παπαπαα--++⎛⎫-++ ⎪⎝⎭的值．【答案】(2)17.【解析】(1)()()sin cos tan sin()cos()tan(3)()sin 3sin cos 2f θθθπθπθπθθθπθθ⋅-⋅--+-===--⎛⎫- ⎪⎝⎭所以77sin sin 2sin 3333f πππππ⎛⎫⎛⎫⎛⎫-=--=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)由1sin cos 5αα+=-，则112sin cos 25αα+=，所以242sin cos 25αα=-由2παπ<<，则sin 0,cos 0αα><设cos sin 0t αα=-<，则2244912cos sin 12525t αα=-=+= 由cos sin 0t αα=-<，所以7cos sin 5αα-=-1sin(3)cos(2)sin cos 157sin cos 7sin()sin 52παπαααπαααα---+++===-+⎛⎫--++ ⎪⎝⎭【题组三 角的拼凑】1．(2021·江西上饶·高一月考(理))若4sin 65x π⎛⎫+= ⎪⎝⎭，则cos 3x π⎛⎫-= ⎪⎝⎭___________.【答案】45【解析】依题意4cos cos sin 36265x x x ππππ⎛⎫⎛⎫⎛⎫-=+-=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故答案为：452．(2021·全国高一课时练习)已知1sin 62πα⎛⎫-= ⎪⎝⎭，那么2cos 3πα⎛⎫-= ⎪⎝⎭( )A B ．C ．12 D ．12-【答案】D【解析】因为1sin 62πα⎛⎫-= ⎪⎝⎭，所以21cos cos sin 32662ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=+-=--=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 故选：D3．(2021·全国高一课时练习)已知()1cos 753α︒+=，求()(cos 105sin 15)αα︒-+︒-的值． 【答案】0【解析】因为()()10575180αα︒-+︒+=︒，()()157590αα︒-++︒=︒， 所以()()cos 105cos 18075αα︒-=︒-︒+⎡⎤⎣⎦()1cos 753α=-︒+=-，()()sin 15sin 9075αα︒-=︒-+︒⎡⎤⎣⎦ ()1cos 753α=︒+=．所以()()11cos 105sin 15033αα︒-+︒-=-+=．。

3.3 幂函数(精练)【题组一 幂函数的概念】1．(2021·福建高一期末)若幂函数()f x 的图象过点()2,4，则()3f 的值为( ) A ．5 B ．6 C ．8 D ．9【答案】D【解析】设幂函数()f x x α=，因为幂函数()f x 的图象过点()2,4，所以24α=，解得2α=， 所以()2f x x =，所以()2339f ==，故选：D2．(2021·江苏省锡山高级中学高一期末)若幂函数()f x 经过点()3,33，且()8f a =，则a =( )A ．2B ．3C ．128D ．512【答案】A【解析】设()f x x α=，因为幂函数()f x 经过点()3,33，所以(3)(3)33f α==，解得3α=，所以()38f a a ==，解得2a =，故选：A3．(新教材苏教版必修第一册))若函数()21xf x a a =++是幂函数，则a =________． 【答案】0或1- 【解析】由函数()21xf x a a =++是幂函数，可得211a a ++=，解得0a =或1a =-， 故答案为：0或1-．4．(2021年湖南)若函数()222433mm y m m x+-=-+为幂函数，则实数m 的值为________；当此幂函数在()0,∞+单调递减，则实数m 的值为_________． 【答案】1或2 1【解析】由幂函数定义知：2331m m -+=，解得：1m =或2； 当1m =时，2241m m +-=-，此时幂函数在()0,∞+单调递减； 当2m =时，2244m m +-=，此时幂函数在()0,∞+单调递增；∴当幂函数在()0,∞+单调递减时，1m =.故答案为：1或2；1. 【题组二 幂函数的三要素】1．(2020·浙江高一课时练习)5个幂函数：①2y x ；②45y x =；③54y x =；④23y x =；⑤45y x -=.其中定义域为R 的是( ) A ．只有①② B ．只有②③ C ．只有②④ D ．只有④⑤【答案】C 【解析】①2yx 的定义域为(,0)(0,)-∞+∞，②45y x =的定义域为R ， ③54y x =的定义域为(0,)+∞， ④23y x =的定义域为R ，⑤45y x -=的定义域为(,0)(0,)-∞+∞， 故选：C .2．(步步高高一数学寒假作业：作业9幂函数)下列函数中，其定义域和值域不同的函数是( ) A ．13y x = B ．12y x -= C ．53y x = D ．23y x =【答案】D【解析】A 中，13y x =的定义域和值域均为R ；B 中，12y x-=的定义域为()0,∞+，值域为()0,∞+；C 中，53y x =的定义域和值域均为R ；D 中，23y x =的定义域为R ，值域为[)0,+∞，定义域和值域不相同 故选：D3．(2021·江苏省)(多选)已知{}1,1,2,3α∈-，则使函数y x α=的值域为R ，且为奇函数的α的值为( ) A ．－1 B ．1 C ．2 D ．3【答案】BD【解析】当1α=-时，11y x x-==，为奇函数，但值域为{}0y y ≠，不满足条件； 当1α=时，y x =为奇函数，值域为R ，满足条件； 当2α=时，2yx 为偶函数，值域为{}0y y ≥，不满足条件；当3α=时，3y x =为奇函数，值域为R ，满足条件. 故选BD.4．(2021·湖南高一期末)已知幂函数()y f x =的图象经过点()9,3，则()f x 的解析式是______． 【答案】()12f x x =【解析】幂函数()y f x =可设为()f x x α=，图象过点()9,3，则()993f α==，则12α=， 所以()12f x x =.故答案为：()12f x x =.5．(2021·浙江)已知幂函数 f (x ) = x α满足 f (3) = 33，则该幂函数的定义域为___________. 【答案】(0,)+∞ 【解析】因为f (3) =33，所以333α=，即1233α-=，解得12α=-，所以12()f x x -=，所以函数的定义域为(0,)+∞，故答案为：(0,)+∞6．(2021·上海市川沙中学高一期末)幂函数12y x =的定义域为________________. 【答案】[)0,+∞【解析】解：因为12y x x ==，所以0x ≥，所以函数的定义域为[)0,+∞ 故答案为：[)0,+∞ 【题组三 幂函数的性质】1(新教材人教版必修第一册))幂函数的图象过点(3， 3)，则它的单调递增区间是( ) A ．[-1，+∞) B ．[0，+∞) C ．(-∞，+∞) D ．(-∞，0)【答案】B【解析】设幂函数为f (x )=x α，因为幂函数的图象过点(3， 3)，所以f (3)=3α=3=123，解得α=12， 所以f (x )=12x ，所以幂函数的单调递增区间为[0，+∞).故选：B2．(2021·务川仡佬族苗族自治县汇佳中学高一期末)下列函数既是幂函数又是偶函数的是( ) A ．2()3f x x =B ．()f x x =C ．41()f x x =D ．3()-=f x x【答案】C【解析】幂函数的图象都经过点(1,1)，排除A ； ()f x x =与3()-=f x x 不是偶函数，排除B ，D.故选:C3．(2021·河北高一期末)已知幂函数()221()1m f x m m x +=+-在()0,∞+上单调递减，则实数m 的值为( )A ．2-B ．1-C ．1D ．2-或1【答案】A【解析】由于()f x 为幂函数，所以2112m m m +-=⇔=-或1m =；又函数()f x 在()0,∞+上单调递减，故当2m =-时符合条件，故选：A4．(2021·宁县第二中学高一期末)已知幂函数()223()22()n nf x n n xn -=+-∈Z 在(0,)+∞上是增函数，则n的值为( ) A ．1- B ．1 C ．3- D ．1和3-【答案】C【解析】因为函数是幂函数，所以2221+-=n n 解得：3n =-或1n =当3n =-时，()18=f x x 在()0,∞+上是增函数，符合题意. 当1n =时，()2f x x -=在()0,∞+上是减函数，不符合题意.故选：C5．(2021·四川高一期末)已知幂函数()()22222aaf x a a x+=--，满足()f x 在()0,x ∈+∞为减函数，则a 的值为( ) A ．3或1- B ．3 C ．1- D ．3-【答案】C【解析】由于幂函数()()22222aaf x a a x+=--在()0,x ∈+∞为减函数，所以，2222120a a a a ⎧--=⎨+<⎩，解得1a =-.故选：C.6．(2021·河南高一期末)已知幂函数()()()22231aa f x a a xa --=+-∈R 的图象在()0,∞+上单调递减，则实数a 的值是( )A ．1B ．2-C ．1或2-D ．512+ 【答案】A【解析】由幂函数定义得211a a +-=， 解得1a =或2a =-.当1a =时，()4f x x -=在()0,∞+上单调递减；当2a =-时，()5f x x =在()0,∞+上单调递增.故选：A7．(2021·山东高一期末)已知幂函数1234,,,a b c dy x y x y x y x ==== 在第一象限的图象如图所示，则( )A ．a b c d >>>B ．>>>b c d aC ．>>>d b c aD ．>>>c b d a【答案】B【解析】由图象可知，当2x =时，2222d a c b <<<，则a d c b <<< 故选：B8(2021·辽宁高一期末)幂函数23y x =的大致图像是( )A ．B ．C ．D ．【答案】B 【解析】203>，∴幂函数在第一象限内的图象为增函数，排除A ，C ，D ， 故选：B ．9．(2021·宁波中学高一期末)下列函数中，在其定义域内既是奇函数又是减函数的是( ) A ．()y x x R =-∈B ．3()y x x x R =--∈C ．1()()2xy x R =∈D ．1y x=-(x R ∈，且0)x ≠ 【答案】B【解析】对于A 选项，()()f x x x f x -=--=-=，为偶函数，故错误；对于B 选项，()()()()33f x x x x x f x -=----=+=-，为奇函数，且函数3,y x y x =-=-均为减函数，故3()y x x x R =--∈为减函数，故正确；对于C 选项，指数函数没有奇偶性，故错误；对于D 选项，函数为奇函数，在定义域上没有单调性，故错误. 故选：B10．(2021·河南高一期末)下列函数中，在(),1-∞-上是增函数的是( ) A ．3y x =- B ．24y x x =--C ．1x y x=+ D ．2y x =-【答案】C【解析】本题考查函数的单调性.A 项中，函数3y x =-在R 上单调递减，故A 错误；B 项中，二次函数24y x x =--的图像开口向下，对称轴方程为2x =-，故该函数在(],2-∞-上单调递增，在()2,-+∞上单调递减，故B 错误；C 项中，函数1111x y x x==-++，在(),1-∞-和()1,+∞上分别单调递增，故C 正确；D 项中，函数2y x =-在(],2-∞上单调递减，故D 错误. 故选：C11．(2021·江苏南通·高一期末)幂函数2232m m y x --=是偶函数，在()0,∞+上是减函数，则整数m 的值为( )A ．0B ．1C ．0或1D ．2【答案】A【解析】因为幂函数2232m m y x --=在()0,∞+上是减函数，所以22320m m --<，解得122m -<<，又m Z ∈，所以0m =或1m =， 当0m =时，221yxx 定义域为()(),00,-∞⋃+∞，且()2211x x =-，所以2y x 是偶函数，满足题意；当1m =时，331y x x-==定义域为()(),00,-∞⋃+∞，而()3311x x =--，所以3y x -=是奇函数，不满足题意，舍去； 综上，0m =. 故选：A12．(2021·辽宁高一期末)使幂函数y x α=为偶函数，且在(0,)+∞上是减函数的α值为( ) A ．1- B ．23-C ．12-D ．2【答案】B 【解析】A 选项，1y x=是奇函数，不符合题意. B 选项，321y x =为偶函数，且在(0,)+∞上是减函数，符合题意.C 选项，1y x=是非奇非偶函数，不符合题意.D 选项，2y x ，在()0,∞+上递增，不符合题意.故选：B13．(2021·山东高一期末)已知点(),8a 在幂函数()()1bf x a x =-的图象上，若()()130f m f m +-<，则实数m 的取值范围为_________．2⎝⎭【解析】因为()()1bf x a x =-为幂函数，所以11a -=，解得a =2所以()b f x x =，又(2,8)在()f x 上，代入解得3b =， 所以3()f x x =，为奇函数因为()()130f m f m +-<，所以()(13)(31)f m f m f m <--=-， 因为3()f x x =在R 上为单调增函数， 所以31m m <-，解得12m >， 故答案为：1,2⎛⎫+∞ ⎪⎝⎭14．(2021·湖南师大附中高一月考)已知幂函数2()(1)m f x m m x =--的图象关于y 轴对称，则m 的值为_________. 【答案】2【解析】由于()f x 是幂函数，所以211m m --=，解得2m =或1m =-.当2m =时，()2f x x =，图象关于y 轴对称，符合题意.当1m =-时，()11x xf x -==，图象关于原点对称，不符合题意. 所以m 的值为2. 故答案为：215．(2021·辽宁庄河高中高一开学考试)若幂函数()222=33mm y m xm ---+的图象不经过坐标轴，则实数m的值为___________. 【答案】1或2【解析】由题意得：2233120m m m m ⎧-+=⎨--≤⎩，解得：m=1或2，故答案为：1或2.16．(2021·全国高一期末)已知幂函数()()2133m f x m m x +=-+的图象关于原点对称，则满足()()132mma a +>-的实数a 的值构成的集合为________.3⎝⎭【解析】因为函数()()2133m f x m m x +=-+为幂函数，则2331m m -+=，得1m =或2m =.若1m =，则()2f x x =为偶函数，不合乎题意；若2m =，则()3f x x =为奇函数，合乎题意.所以，2m =.所以不等式可转化为()()22132a a +>-，即231480a a -+<，解得243a <<.故答案为：2,43⎛⎫⎪⎝⎭.17．(2020·湖北高一期中)已知幂函数()2m f x x +=过点()2,8，且2(1)(24)0f k f k ++-<，则实数k 的取值范围是_____． 【答案】()3,1-【解析】由题设可得23282m +==，故1m =，所以()3f x x =，所以()f x 为R 上的奇函数且为增函数，而2(1)(24)0f k f k ++-<等价于()2(1)(24)42f k f k f k +<--=-，所以2230k k +-<，故31k -<<. 故答案为：()3,1-.【题组四 幂函数的综合运用】1．(新教材苏教版必修第一册)已知幂函数()()2151m h x m m x +=-+为奇函数．(1)求实数m 的值；(2)求函数()()()11202g x h x h x x ⎛⎫⎡⎫=+-∈⎪ ⎪⎢⎣⎭⎝⎭，的值域．【答案】(1)0m =；(2)112⎛⎤⎥⎝⎦，． 【解析】(1)∵函数()()2151m h x m m x +=-+为幂函数，2511m m ∴-+=，解得0m =或5，当0m =时，()h x x =，()h x 为奇函数， 当5m =时，()6h x x =，()h x 为偶函数，函数()h x 为奇函数，0m ∴=；(2)由(1)可知，()h x x =，则()12g x x x =+-，102x ⎡⎫∈⎪⎢⎣⎭，，令12x t -=，则21122x t =-+，(]01t ∈，，则()22111(1)1222f t t t t =-++=--+，(]01t ∈，，函数()f t 为开口向下，对称轴为1t =的抛物线， ∴当0t =时，函数()102f =， 当1t =，函数()f t 取得最大值为1，∴()f t 的值域为112⎛⎤ ⎥⎝⎦，，故函数()g x 的值域为112⎛⎤⎥⎝⎦，．2．(2021·山西高一期末)已知函数()()2151m h x m m x +=-+为幂函数，且为奇函数.(1)求m 的值；(2)求函数()()12=+-g x h x x 在11,2x ⎡⎤∈-⎢⎥⎣⎦的值域.【答案】(1)0m =；(2)1,12⎡⎤⎢⎥⎣⎦【解析】(1)因为函数()()2151m h x m m x +=-+为幂函数，所以2511m m -+=，解得0m =或5m =. 即()h x x =或()6h x x =.又因为函数()h x 为奇函数，所以()h x x =，0m =. (2)()()1212g x h x x x x =+-=+-，设12t x =-，因为11,2x ⎡⎤∈-⎢⎥⎣⎦，所以0,3t ⎡⎤∈⎣⎦，212t x -=. 所以()22111122t y t t -=+=--+， 当1t =时，max 1y =，当0t =时，min 12y =，故值域为1,12⎡⎤⎢⎥⎣⎦. 3．(2021·赤峰二中高一期末(理))已知幂函数()2()1()kf x k k x k R =--∈，且在区间(0,)+∞内函数图象是上升的．(1)求实数k 的值；(2)若存在实数a ，b 使得函数f (x )在区间[a ，b ]上的值域为[a ，b ]，求实数a ，b 的值．【答案】(1)2；(2)a ＝0，b ＝1．【解析】(1)()2()1()k f x k k x k R =--∈为幂函数， ∴211k k --=，解得1k =-或2k =，又()f x 在区间(0,)+∞内的函数图象是上升的，0k ∴>，∴k ＝2；(2)∵存在实数a ，b 使得函数()f x 在区间,a b 上的值域为,a b ，且2()f x x =，∴()()f a a f b b =⎧⎨=⎩，即22a a b b ⎧=⎨=⎩， a b <，∴a ＝0，b ＝1．4．(2020·浙江高一课时练习)已知幂函数21322()()pp f x x p -++=∈N 在(0,)+∞上是增函数，且在定义域上是偶函数.(1)求p 的值，并写出相应的函数()f x 的解析式. (2)对于(1)中求得的函数()f x ，设函数()[()](21)()1g x qf f x q f x =-+-+，问是否存在实数(0)q q <，使得()g x 在区间(,4]-∞-上是减函数，且在区间(4,0)-上是增函数？若存在，请求出q ；若不存在，请说明理由.【答案】(1)当0p =或2p =时，32()f x x =；当1p =时，2()f x x =；(2)存在，130-. 【解析】(1)由于已知()f x 在(0,)+∞上是增函数，因而213022p p -++>，解得13p -<<. 又p ∈N ，因而0p =或1或2.当0p =或2p =时，32()f x x =，不是偶函数；当1p =时，2()f x x =，符合题意.(2)存在.理由如下： 由(1)知2()[()](21)()1()(21)()1g x qf f x q f x qf x q f x =-+-+=-+-+.由于2()0f x x =，因而当(,4]x ∈-∞-时，2()[16,)f x x =∈+∞，此时，函数()g x 单调递减，而函数()t f x =在(,4]-∞-上单调递减，则外层函数2(21)1y qt q t =-+-+在[16,)+∞上单调递增；当(4,0)∈-x 时，2()(0,16)f x x =∈，此时，函数()g x 单调递增，而函数()t f x =在(4,0)-上单调递减，则外层函数2(21)1y qt q t =-+-+在(0,16)上单调递减. 所以211620q q q -⎧-=⎪-⎨⎪->⎩，即130q =-. 所以存在130q =-满足题设条件. 5．(2021·上海市第二中学高一期末)已知幂函数223()mm y f x x --==(m ∈Z )在(0,)+∞是严格减函数，且为偶函数.(1)求()y f x =的解析式； (2)讨论函数5()(2)()y af x a x f x =+-⋅的奇偶性，并说明理由.【答案】(1)4()y f x x -==；(2)当2a =时，为偶函数；当0a =时，为奇函数；当2a ≠且0a ≠时，为非奇非偶函数.理由见解析.【解析】(1)因为幂函数223()m m y f x x --==(m Z ∈)在(0,)+∞是严格减函数，所以2230m m --<，即()()310m m -+< ，解得：13x ，因为m Z ∈，所以0,1,2m =，当0m =时，3()y f x x -==，此时()y f x =为奇函数，不符合题意；当1m =时，4()y f x x -==，此时()y f x =为偶函数，符合题意；当2m =时，3()y f x x -==，此时()y f x =为奇函数，不符合题意；所以4()y f x x -==，(2)4544(2)(2)y ax a x x ax a x ---=+-⋅=+-，令()4(2)F x ax a x -=+-当0a =时，()2F x x =-，()()()22F x x x F x -=-⨯-==-，此时是奇函数，当2a =时()4422F x x x -==，()()()444222F x x xx --=-==-，此时是偶函数， 当0a ≠且2a ≠时，()1(2)22F a a a =+-=-，()1(2)2F a a -=--=， ()()11F F ≠-，()()11F F -≠-，此时是非奇非偶函数函数.6．(2021·深圳市)已知幂函数()223mm y f x x --+==(其中22m -<<，m ∈Z )满足： ①在区间,0上为减函数；②对任意的x ∈R ，都有()()0f x f x --=.求幂函数()f x 的解析式，并求当[]0,4x ∈时，()f x 的值域.【答案】()4f x x =，值域为[]0,256【解析】22m -<<，m ∈Z ，1m ∴=-，0，1.对任意x ∈R ，都有()()0f x f x --=，即()()f x f x -=，f x 是偶函数.当1m =-时，()4f x x =，满足条件①②； 当1m =时，()0f x x =，不满足条件①；当0m =时，()3f x x =，条件①②都不满足，故同时满足条件①②的幂函数()f x 的解析式为()4f x x =，且在区间[]0,4上是增函数，∴当[]0,4x ∈时，函数()f x 的值域为[]0,256.。

1．已知f(x)＝x3－6x2＋9x－abc，a＜b＜c，且f(a)＝f(b)＝f(c)＝0.现给出如下结论：①f(0)f(1)＞0；②f(0)f(1)＜0；③f(0)f(3)＞0；④f(0)f(3)＜0.其中正确结论的序号是__________．2．函数f(x)＝13x3＋12ax2(a＞0)的递减区间是__________．3．函数ln()xf xx=的递增区间为__________．4．已知函数f(x)＋ln x，则f(2)，f(e)，f(3)三个数从小到大的顺序为__________．5．函数f(x)＝x－2sin x在(0，π)上的单调增区间为____．6．已知函数f(x)，g(x)满足g(x)≠0，()()xf xag x= (a＞0，且a≠1)，若f′(x)g(x)＞f(x)g′(x)，则a的取值范围是____．7．已知a∈R且函数f(x)＝13x3－ax＋3在区间(－2，－1)内是减函数，则a的取值范围是__________．8．函数f (x)的定义域为R，f(－1)＝2，对任意x∈R，f′(x)＞2，则f(x)＞2x＋4的解集为__________．9．设函数f(x)＝x3－3ax2＋3bx的图象与直线12x＋y－1＝0相切于点(1，－11)．(1)求a，b的值；(2)讨论函数f(x)的单调性．10．设函数f(x)＝x－1x－a ln x(a∈R)，讨论f(x)的单调性．参考答案1.答案：②③ 解析：设g (x )＝x 3－6x 2＋9x ＝0，则x 1＝0，x 2＝x 3＝3，其图象如下图：要使f (x )＝x 3－6x 2＋9x －abc 有3个零点，需将g (x )的图象向下平移，如图所示：又f ′(x )＝3x 2－12x ＋9＝0时，x 1＝1，x 2＝3，即得f (1)是极大值，f (3)是极小值. 故由图象可知f (0)·f (1)＜0，f (0)·f (3)＞0. 2.答案：(－a,0) 解析：f ′(x )＝x 2＋ax ＝x (x ＋a ). ∵a ＞0，∴当f ′(x )＜0时，得－a ＜x ＜0. ∴f (x )的递减区间是(－a,0).3.答案：(0，e) 解析：f (x )的定义域为(0，＋∞)，f ′(x )＝21ln xx-. 令f ′(x )＞0得1－ln x ＞0，解得0＜x ＜e. ∴f (x )的递增区间是(0，e).4.答案：f (2)＜f (e)＜f (3) 解析：f (x )的定义域为(0，＋∞).f ′(x )1x+＞0在(0，＋∞)上恒成立，∴f (x )在(0，＋∞)上单调递增， ∴f (2)＜f (e)＜f (3). 5.答案：π,π3⎛⎫⎪⎝⎭解析：f ′(x )＝1－2cos x ，令f ′(x )＞0得cos x ＜12.∵x ∈(0，π)，∴π3＜x ＜π， ∴f (x )的递增区间是π,π3⎛⎫⎪⎝⎭.6.答案：a ＞1 解析：∵2()()()()()0()()f x f x g x f x g x 'g x g x ⎛⎫-=> ⎪⎝⎭， ∴()()x f x a g x =为增函数，则a ＞1. 7.答案：[4，＋∞) 解析：f ′(x )＝x 2－a . ∵f (x )在(－2，－1)内是减函数，∴f ′(x )＝x 2－a ≤0在(－2，－1)上恒成立， 即a ≥x 2在(－2，－1)上恒成立.∵x ∈(－2，－1)，∴1＜x 2＜4.∴所求a 的范围是a ≥4.8.答案：(－1，＋∞) 解析：由题意，令φ(x )＝f (x )－2x －4， 则φ′(x )＝f ′(x )－2＞0，∴φ(x )在R 上是增函数. 又φ(－1)＝f (－1)－2×(－1)－4＝0， ∴当x ＞－1时，φ(x )＞φ(－1)＝0， 即f (x )－2x －4＞0，即f (x )＞2x ＋4. ∴解集为(－1，＋∞).9.答案：解：(1)求导得f ′(x )＝3x 2－6ax ＋3b .由于f (x )的图象与直线12x ＋y －1＝0相切于点(1，－11)，所以f (1)＝－11，f ′(1)＝－12，即13311,36312,a b a b -+=-⎧⎨-+=-⎩解得a ＝1，b ＝－3.(2)由a ＝1，b ＝－3得f ′(x )＝3x 2－6ax ＋3b ＝3(x 2－2x －3)＝3(x ＋1)(x －3).令f ′(x )＞0，解得x ＜－1或x ＞3； 又令f ′(x )＜0，解得－1＜x ＜3. 故当x ∈(－∞，－1)时，f (x )是增函数， 当x ∈(3，＋∞)时，f (x )也是增函数， 当x ∈(－1,3)时，f (x )是减函数10.答案：解：f (x )的定义域为(0，＋∞).22211()1a x ax f'x x x x -+=+-=.令g (x )＝x 2－ax ＋1，则对于方程x 2－ax ＋1＝0，Δ＝a 2－4. (1)当|a |≤2时，Δ≤0，f ′(x )≥0. 故f (x )在(0，＋∞)上单调递增.(2)当a ＜－2时，Δ＞0，g (x )＝0的两根都小于0，在(0，＋∞)上，f ′(x )＞0. 故f (x )在(0，＋∞)上单调递增.(3)当a ＞2时，Δ＞0，g (x )＝0的两根为1x =，2x =∴当0＜x ＜x 1时，f ′(x )＞0；当x 1＜x ＜x 2时，f ′(x )＜0；当x ＞x 2时，f ′(x )＞0.故f (x )分别在0,2a ⎛ ⎪⎝⎭，2a ⎛⎫++∞⎪ ⎪⎝⎭上单调递增，在22a a ⎛-+ ⎪⎝⎭上单调递减.。