07二次回归与RSREG

二次回归系数表得二次回归系数表是统计学中的一个重要概念，用于描述二次回归模型中各个变量的系数取值。

在进行回归分析时，我们经常会遇到非线性关系，此时就需要使用二次回归模型来描述变量之间的复杂关系。

二次回归模型可以表示为：Y = β0 + β1X + β2X^2 + ε，其中Y 表示因变量，X表示自变量，ε表示误差项。

β0、β1和β2分别表示截距项、一次项和二次项的系数。

二次回归系数表就是将这些系数的取值整理出来，用于解释模型中各个变量对因变量的影响程度。

在实际应用中，二次回归系数表可以帮助我们分析变量之间的关系，并进行预测和决策。

下面我们将从几个方面来介绍二次回归系数表的内容和应用。

二次回归系数表中的截距项β0表示当自变量X的取值为0时，因变量Y的取值。

它反映了在其他自变量不变的情况下，因变量的基准水平。

通过观察截距项的符号和大小，我们可以了解到在自变量为0时，因变量的大致取值范围。

一次项的系数β1表示自变量X的线性关系对因变量Y的影响。

一次项的系数可以告诉我们自变量的单位变化对因变量的影响程度。

如果β1的值为正，说明自变量的增加会导致因变量的增加；如果β1的值为负，说明自变量的增加会导致因变量的减少。

二次项的系数β2表示自变量X的平方项对因变量Y的影响。

二次项的系数可以反映自变量的非线性关系对因变量的影响。

如果β2的值为正，说明自变量的增加会加剧因变量的增加或减少；如果β2的值为负，说明自变量的增加会减轻因变量的增加或减少。

通过观察二次回归系数表中的系数取值，我们可以判断各个变量对因变量的影响程度和方向，并进行进一步的分析和预测。

在实际应用中，我们可以根据系数的大小和符号来判断自变量的重要性和影响程度，从而进行决策和优化。

需要注意的是，二次回归系数表中的系数取值只是样本估计值，其真实取值可能存在一定的误差。

因此，在进行数据分析和决策时，我们需要综合考虑各个因素，并进行合理的解释和判断。

二次回归系数表是回归分析中的重要工具，可以帮助我们理解变量之间的关系和进行预测和决策。

响应面法优化脂肪酶非水相催化合成生物柴油作者：郑毅王娅陈建平张艺来源：《海峡科学》2010年第02期[摘要]利用固定化脂肪酶非水相催化油酸与甲醇合成生物柴油。

在前期研究的基础上,采用响应面法优化影响催化体系的3个重要因素:酶添加量、有机溶剂量、底物摩尔比,获得最佳催化体系:在每g油酸加入0.568g的固定化脂肪酶及3.3mL的正己烷,油酸与甲醇摩尔比为1∶1.2。

对响应面分析结果进行验证试验,结果表明转化率达到95.56%,与响应面预测值95.99%的吻合程度较高。

[关键词]脂肪酶响应面法生物柴油﹡基金项目:福建省自然科学基金资助项目(2007J0217)。

﹡﹡通讯作者:郑毅,Email:eyizheng@生物柴油是生物质能的一种形式,其主要成分是脂肪酸甲酯或脂肪酸乙酯。

它是通过生物油脂中脂肪酸与短链醇(甲醇或乙醇)在一定的条件下反应得到的脂肪酸酯类物质。

生物柴油作为生物燃料,是一种可再生能源,受到全球科学家的广泛关注。

目前,工业上生物柴油的生产方法主要是化学合成法。

由于该法以强酸或强碱为催化剂,反应过程产生大量的污染物,对环境的负面影响极大。

利用脂肪酶进行生物柴油的催化合成,能较理想地避免化学合成法中产生的一系列负面效应,真正意义上实现了无污染、可再生的目的,打造了名副其实的“生物柴油”这一环保定义[1,2]。

本研究利用固定化脂肪酶催化油酸与甲醇合成生物柴油(油酸甲酯),采用响应面法对工艺条件进行优化,旨在以最优的反应体系实现最大限度的提高转化效率,为脂肪酶催化合成生物柴油提供实验依据。

1材料与方法1.1 材料1.1.1 固定化脂肪酶:采用硅藻土吸附法制得。

1.1.2 化学试剂:橄榄油(CP,中国医药集团上海化学试剂公司),聚乙烯醇PVA(聚合度1750±50),油酸(AR,汕头市西陇化工厂有限公司),甲醇(AR,天津市永大化学试剂开发中心),95%乙醇、正己烷均为AR。

1.1.3 主要仪器:恒温摇床(Beijing North TZ-Biotech Develop.Co.,SHK-99-Ⅱ)、电热恒温水浴锅(国华企业,THZ-82)、高速组织捣碎机(江苏省金坛市荣华仪器制造有限公司,JJ-2)。

经济统计学中的相关系数和回归模型经济统计学是研究经济现象和经济关系的一门学科，它通过收集、整理和分析大量的经济数据，来揭示经济规律和预测经济趋势。

在经济统计学中，相关系数和回归模型是两个重要的概念和工具。

相关系数是用来衡量两个变量之间相关程度的指标。

在经济统计学中，我们常常需要研究两个变量之间的关系，比如GDP和失业率、通货膨胀率和消费水平等。

相关系数可以告诉我们这两个变量之间是正相关还是负相关，以及相关程度的强弱。

常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。

皮尔逊相关系数是最常用的相关系数之一，它衡量的是两个变量之间的线性相关程度。

皮尔逊相关系数的取值范围是-1到1，当相关系数为1时，表示两个变量呈完全正相关；当相关系数为-1时，表示两个变量呈完全负相关；当相关系数为0时，表示两个变量之间没有线性相关关系。

通过计算皮尔逊相关系数，我们可以判断两个变量之间的相关性，并进一步分析其背后的经济关系。

斯皮尔曼相关系数是一种非参数的相关系数，它衡量的是两个变量之间的等级相关程度。

在某些情况下，变量之间的关系不是线性的，而是存在一种非线性的关系。

此时，斯皮尔曼相关系数可以更准确地反映两个变量之间的相关性。

与皮尔逊相关系数不同，斯皮尔曼相关系数的取值范围是-1到1，其含义与皮尔逊相关系数相同。

除了相关系数，回归模型也是经济统计学中常用的工具之一。

回归模型可以用来建立变量之间的数学关系，并通过拟合数据来预测未来的变量值。

在经济统计学中，回归模型可以用来研究一个变量对其他变量的影响，并进一步预测经济变量的走势。

线性回归模型是最常用的回归模型之一，它假设变量之间的关系是线性的。

线性回归模型可以通过最小二乘法来估计模型参数，并通过拟合数据来预测未来的变量值。

线性回归模型的优点是简单易懂、计算方便，但也有其局限性，比如无法处理非线性关系和存在异方差性的数据。

除了线性回归模型，还有许多其他类型的回归模型，比如多元回归模型、时间序列回归模型等。

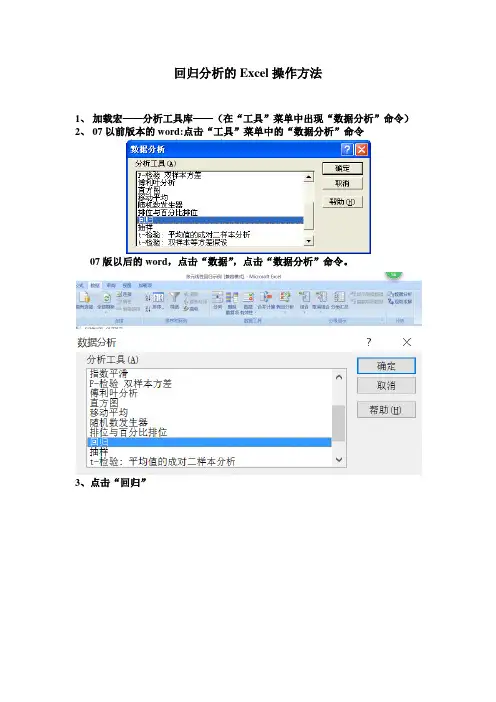
STATA一章回第归析分．在此处利用两个简单的回归分析案例让初学者学会使用STATA进行回归分析。

STATA版本：11.0案例1：某实验得到如下数据x 1 23455.56.27.7 y48.5对x y 进行回归分析。

第一步：输入数据（原始方法）1.在命令窗口输入input x y /有空格回车2.得到：3.再输入：1 42 5.53 6.24 7.75 8.5end4.输入list 得到5.输入reg y x 得到回归结果回归结果：x1.12?3.02?y2=0.98 T= (15.15) (12.32) R解释一下：SS是平方和，它所在列的三个数值分别为回归误差平方和（SSE）、残差平方和（SSR）及总体平方和（SST），即分别为Model、Residual和Total相对应的数值。

df（degree of freedom）为自由度。

MS为SS与df的比值，与SS对应，SS是平方和，MS是均方，是指单位自由度的平方和。

coef.表明系数的，因为该因素t检验的P值是0.001，所以表明有很强的正效应，认为所检验的变量对模型是有显著影响的。

_cons表示常数项6.作图可以通过Graphics——>twoway—twoway graphs——>plots——>Create案例2：加大一点难度1.格式文件CSV另存为excel首先将．2. 将csv文件导入STATA,选第一个>——>import——File3.输入list4.进行回归reg inc emp inv pow5.回归结果pow30.22?inv4.35?emp18.18?395741.7??inc。

stata 二次项解释
在Stata中，二次项是指两个变量之间的交互项，是使用多元线性回归模型时经常用到的一种变量转换方式。

在多元线性回归模型中，如果一个自变量与因变量之间的关系不是简单的线性关系，那么就需要使用更复杂的模型来解释它们之间的关系。

这时，我们就可以引入二次项，将自变量之间的关系转换为一种非线性的形式。

例如，在一个回归模型中，有两个自变量X和Y，它们之间的关系可能不仅仅是线性的，还可能是一种二次函数的形式。

这时，我们可以使用二次项来描述它们之间的关系，即添加一个X^2项和一个Y^2项到回归模型中，以此来模拟一个二次函数的形式。

在解释二次项时，我们需要注意一些问题。

首先，二次项并不是一种独立的变量，而是两个自变量之间的交互项，因此它的解释必须依赖于它所代表的自变量的取值范围。

其次，由于二次项是一种非线性的形式，它的解释可能更加复杂和困难。

因此，我们需要仔细地分析数据，准确理解二次项的含义和效应。

- 1 -。

sas rsreg用法SAS RSREG用法指的是使用SAS软件中的RSREG过程进行回归分析。

RSREG（Robust Standard Errors）过程提供了一种弥补普通最小二乘法（OLS）回归中标准误差的不稳定性的方法。

通过使用鲁棒标准误差，RSREG可以在存在异方差性和模型中存在异常值时提供更合理和可靠的回归结果。

在本文中，我们将详细介绍SAS RSREG的用法，以及如何一步一步回答相关问题。

一、安装SAS软件并准备数据首先，您需要确保已成功安装SAS软件，接下来为了演示，我们将使用一份假设的数据集来说明SAS RSREG的用法。

您可以使用任何数据集来进行操作。

二、导入数据和设置工作目录在SAS软件中，您需要将数据导入到工作环境中，并设置合适的工作目录。

通过以下代码段来完成这些操作：LIBNAME mydata 'C:\MyData'; /* 设置工作目录*/DATA mydata.mydataset; /* 设置数据集名称*/INFILE 'C:\Data\mydata.csv' DLM=','; /* 导入数据*/INPUT var1 var2 var3; /* 指定数据的变量*/RUN;在这个例子中，我们假设数据集保存在C盘的Data文件夹中，且文件名为mydata.csv。

我们将数据导入到名为mydataset的数据集中，并设置工作目录为C盘的MyData文件夹。

三、运行RSREG过程一旦数据导入并设置好工作目录，我们可以开始运行RSREG过程来进行回归分析。

以下是一段基本的SAS代码，用于运行RSREG：PROC RSREG DATA=mydata.mydataset;MODEL y = x1 x2 x3 / ROBUST;OUTPUT OUT=mydata.output PREDICTED=ypred RESIDUALS=residuals;RUN;在这段代码中，我们使用PROC RSREG语句来告诉SAS我们要运行的是RSREG过程。

SAS数据分析笔记1.SASINSIGHT启动：方法1：Solution→Analysis→InteractiveDateAnalysis方法2：在命令栏内输入insight方法3：程序编辑窗口输入以下代码，然后单击Submit按钮；Procinsight；Run；1.1一维数据分析用sasinsight做直方图、盒形图、马赛克图。

直方图：Analysis→Histogram/BarChart盒形图：Analysis→Boxplot马赛克图：Analysis→Boxplot/Mosaicplot（Y）1.2二维数据分析散点图：Analysis→Scatteryplot(YX）曲线图：Analysis→Lineplot（YX）1.3三维数据分析旋转图：Analysis→RotationgPlot曲面图：Analysis→RotationgPlot设置FitSurface等高线图：Analysis→Countorplot1.4分布分析包括：直方图、盒形图、各阶矩、分位数表，直方图拟合密度曲线，对特定分布进行检验。

1.4.1Analysis→Distribution（Y）第一部分为盒形图，第二部分为直方图，第三部分为各阶矩，第四部分为分位数表。

1.4.2添加密度估计A：参数估计：给出各种已知分布（正态，指数等），只需要对其中参数进行估计；Curves→ParametricDensityB：核估计：对密度函数没有做假设，曲线性状完全依赖于数据；Curves→KernelDensity1.4.3分布检验Curves→CDFconfidencebandCurves→TestforDistribution1.5曲线拟合Analysis→Fit（YX）:分析两个变量之间的关系1.6多变量回归Analysis→Fit（YX）1.7方差分析Analysis→Fit（YX）1.8相关系数计算Analysis→Multivariate1.9主成分分析Analysis→Multivariate2.SASANAL YST启动：方法1：Solution→Analysis→Analyst方法2：在命令栏内输入analyst2.1分类计算统计量：Data→Summarizebygroup2.2随机抽样：Data→RandomSample2.3生成报表：Report→Tables2.4变量计算：Date→Transform2.5绘制统计图2.5.1条形图：Graph→BarChart→Horizontal2.5.2饼图：Graph→PieChart2.5.3直方图：Graph→Histogram2.5.4概率图：Graph→Probalityplot2.5.5散点图：Graph→Scatterplot2.6统计分析与计算2.6.1计算描述性统计量Statistics→Descriptive→SummartStatistics只计算简单统计量Statistics→Descriptive→Distribution可计算一个变量的分布信息Statistics→Descriptive→Correlations可计算变量之间的相关关系Statistics→Descriptive→Frequencycounts可计算频数2.6.2列联表分析Statistics→TableAnalysis2.7假设检验2.7.1单样本均值Z检验：检验单样本均值与某个给定的数值之间的关系Statistics→Hypothesistests→One-SampleZ-testforamean2.7.2单样本均值t检验：适用于不了解变量的方差情形推断该样本来自的总体均数μ与已知的某一总体均属μ0是否相等Statistics→Hypothesistests→One-Samplet-testforamean2.7.3单样本比例检验：检验取离散值的变量取某个值的比例Statistics→Hypothesistests→One-Sampletestforaproportion2.7.4单样本方差检验：检验样本方差是否等于给定的值。

数据分析中常见的七种回归分析以及R语言实现（三）数据分析中常见的七种回归分析以及R语言实现（四）---多项式回归数据分析中常见的七种回归分析以及R语言实现（三）---岭回归因某种原因未写到博客里，想要学习的请点击查看。

在我们平时做回归的时候，大部分都是假定自变量和因变量是线性，但有时候自变量和因变量可能是非线性的，这时候我们就可能需要多项式回归了，多项式回归就是自变量和因变量是非线性所做的一个回归模型，其表达式：Y=A0 A1X1 A2X2^2 ANXN^2 u公式存手打，不是很好看，其特定就是右边的等式只有一个自变量，但却以不同的次幂出现，这时候在令Xn^n=XnJ,将模型转换成相应的多元线性回归模型Y=A0 A1X1J A2X2J A3X3J.... u等，从而可以使用最小二乘法进行参数估计；R语言代码，这里我使用R语言自带的身高体重的数据作为示例，也好久没做一个完整的分析了，这次稍微分析全一些，可以参考《R 语言实战》回归篇确定问题首先我们要想知道升高和体重是否有什么关联，如果有关联那又是怎么样的关联呢？数据说明这里我们使用R语言自带的women数据集，这个不需要安装说明包，R语言自己就自带了，存在两个字段，体重和身高height 身高weight 体重数据探索和可视化首先我们先使用head()函数看看数据的前六行，因为这样我们可以大致确定数据集的字段名称和数据内容；然后在使用summary()得到数据集的总概括head(women)体重的数值大约是是身高的一半，这是我们的猜测；summary(women)体重的最小值是58，最大值是72，均值为65；这时候我们在使用看一下身高随体重的分布，因为数据集就两个列；可以直接使用Plot函数plot(women)可以看得出体重和身高大致呈现线性关系，略有非线性的因素；这时候我们在回归建模前先看看两个变量的相关系数，这时候我们使用cor函数得到他们的皮尔森相关系数矩阵cor(women)身高体重相关系数高达0.995，说明高度相关；接下来我们使用lm函数建模fit <- lm(weight~height,data=women)summary(fit)截距项和体重都和身高高度显著，模型残差1.525，调整后的可决系数是0.9903；模型算是接近完美了，不过由于我们前面看到数据有些轻微的非线性分布，我们能否改进这个模型呢？多项式回归这里我们使用多项式回归去拟合数据，给它增加一个二次项，也就是height^2,这里不能增加过多的幂次项，因为有可能导致过拟合，I(height^2)，I函数具体用法可以查查；fit2 <- lm(weight~height I(height^2),data=women)summary(fit2)从上结果上三个项都高度显著，模型貌似更优了，模型残差0.384，调整后的可决系数0.999；数据分析培训这里就说那么多。

第七章回归分析本章介绍用于回归分析的常用SAS过程，包括一般回归分析过程REG、建立二次响应曲面回归模型过程RSREG、逐步回归分析过程STEPWISE、非线性回归分析过程NLIN等。

§7.1 一般回归分析过程 REG7.1.1 概述REG过程是一个通用回归过程，用最小二乘法估计线性回归模型。

此过程可以有多个模型(MODEL)语句，输入数据可以是原始样本数据，也可以是相关阵，可打印模型中的参数估计值、预测值、残差及置信区间等，并可作线性假设检验。

7.1.2 过程说明可用下列语句调用REG过程：PROC REG 选项;LABEL：MODEL 因变量表=回归变量表/选项;OUTPUT OUT=数据集关键字=名称表;BY 变量表;（1）PROC REG 选项;常用的选项有：DATA=数据集指定要分析的数据集，缺省时为最新建立的数据集。

ALL 要求各种输出项。

SIMPLE 为每个变量打印简单统计量。

NOPRINT 抑制正常的打印输出。

CORR 打印模型中所有变量的相关阵。

USSCP 为所用变量打印平方和及叉积阵。

（2）LABEL :MODEL 因变量=回归变量/选项;LABEL是模型标号，可省略。

如果使用多个模型，则可给予模型标号名称，便于区别。

常用的选项有：NOPRINT 抑制回归分析结果的打印输出。

NOINT 抑制模型中常数项的出现，缺省时模型中包括常数项。

I 打印X'X的逆矩阵。

XPX 打印X'X阵。

ALL 要求各项输出。

P 打印观测值号、实测值、预测值及残差。

R 要求残差分析。

包括预测值及残差的标准误，学生化残差及COOK'S统计量D。

CLM 打印每个观测值的因变量期望值的95%可信上下限，给出参数估计的变异范围，而不是预测区间。

CLI 要求为每一个观测值打印95%可信度的上下限。

DW 要求计算DURBIN-WASTON统计量，可检验误差是否有一阶自相关。

第七章 回归分析１７４ PARTIAL 要求打印每个回归变量的偏回归影响图。

一、用REG过程进行回归分析SAS/STAT中提供了几个回归分析过程，包括REG（回归）、RSREG（二次响应面回归）、ORTHOREG（病态数据回归）、NLIN（非线性回归）、TRANSREG（变换回归）、CALIS（线性结构方程和路径分析）、GLM（一般线性模型）、GENMOD（广义线性模型），等等。

我们这里只介绍REG过程，其它过程的使用请参考《SAS 系统――SAS/STAT软件使用手册》。

REG过程的基本用法为：PROC REG DATA=输入数据集选项;VAR 可参与建模的变量列表;MODEL 因变量＝自变量表 / 选项;PRINT 输出结果;PLOT 诊断图形;RUN;REG过程是交互式过程，在使用了RUN语句提交了若干个过程步语句后可以继续写其它的REG 过程步语句，提交运行，直到提交QUIT语句或开始其它过程步或数据步才终止。

例如，我们对SASUSER.CLASS中的WEIGHT用HEIGHT和AGE建模，可以用如下的简单REG 过程调用：proc reg data=sasuser.class;var weight height age;model weight=height age;run;就可以在输出窗口产生如下结果，注意程序窗口的标题行显示“PROC REG Running”表示REG 过程还在运行，并没有终止。

See outputAGE的作用不显著，所以我们只要再提交如下语句：model weight=height;run;就可以得到第二个模型结果：See output事实上，REG提供了自动选择最优自变量子集的选项。

在MODEL语句中加上“SELECTION= 选择方法”的选项就可以自动挑选自变量，选择方法有NONE（全用，这是缺省）、FORWARD （逐步引入法）、BACKWARD（逐步剔除法）、STEPWISE（逐步筛选法）、MAXR（最大增量法）、MINR（最小增量法）、RSQUARE（选择法）、ADJRSQ（修正选择法）、CP（Mallows的统计量法）。

第２７卷第２期２００８年４月华中农业大学学报’ＪｏｕｍａｌｏｆＨｕａｚｈｏｎｇＡｇｒｉｃｕｌｔｕｒａｌＵｎｉＶｅｒｓｉｔｙＶ０１．２７Ｎｏ．２Ａｐｒ．２００８，３２１～３２５可逆性魔芋葡甘聚糖凝胶的制备工艺★孙建清杨莉莉熊善柏一杨依姗刘鑫（华中农业大学食品科学技术学院／湖北省水产品加工工程技术研究中心，武汉４３∞７０）摘要采用响应面分析法对可逆性魔芋葡甘聚糖凝胶的制备条件进行了优化，观察了不同碱试剂及其浓度对可逆性魔芋葡甘聚糖凝胶特性的影响。

结果表明；在碳酸钠、磷酸钠、氢氧化钙和磷酸氢二钠４种碱试剂中，采用磷酸氢二钠可在中性或弱碱性条件下制备可逆性魔芋葡甘聚糖凝胶；魔芋葡甘聚糖浓度、磷酸氢二钠浓度和加热时间对可逆性魔芋葡甘聚糖凝胶特性有显著影响；可逆性魔芋葡甘聚糖凝胶最佳的制备条件为魔芋葡甘聚糖浓度２．８２％、磷酸氢二钠浓度１．ｏｏ％、９５℃下加热３．ｏｏｈ。

关键词魔芋葡甘聚糖；可逆性凝胶；响应面分析法中图法分类号ＴＳ２０１．１文献标识码Ａ文章编号１０００—２４２１（２００８）０２一０３２卜０５魔芋葡甘聚糖是魔芋块茎中所含的一种水溶性中性多糖，由Ｄ葡萄糖和口甘露糖通过口一１，４糖苷键聚合而成，且每隔１７～１９个糖残基上连接有１个乙酰基。

葡甘聚糖具有吸水、增稠、胶凝和成膜等性能，对高血脂、糖尿病、肥胖症、便秘等具有良好的预防和治疗作用，被广泛应用于食品、化工、医药等领域［１－３］。

魔芋葡甘聚糖在碱性溶液中加热可形成有弹性的凝胶体［４］，因而传统的魔芋豆腐、魔芋粉丝等魔芋凝胶食品是在碱性条件下加热成型后再经漂洗加工而成的，存在成份单一、营养差及难着味等缺陷。

１９８３年原和雄开发出在ｏ～１０℃呈液态或糊状而在常温或６０℃以上则变为固态的可逆性葡甘聚糖凝胶睁６ｌ，并以此为基础开发出蛋白质魔芋制品、糊状巧克力、多种口味的布丁等多种新型魔芋凝胶食品［７｜，而我国在这方面的研究仅有ｌ篇专利报告［８］。

笔者以魔芋葡甘聚糖为原料，观察了胶凝剂种类和浓度对可逆魔芋凝胶特性影响，旨在优化可逆性魔芋凝胶的制备工艺，制备弱碱性可逆性魔芋凝胶，为开发新型魔芋凝胶食品提供科学依据。

回归分析-简单线性回归、多元线性回归比较：方差分析是处理试验数据的一类统计方法。

这类统计方法的特点是所考察的指标（因变量）Y 是测量得到的数值变量（连续变量），而影响指标的因子（自变量）水平是试验者安排的几个不同值（称这种因子为分类变量或离散变量）。

试验的目的是找出影响指标的主要因子及水平。

在实际问题中，还经常遇到这样一些数据，它们不是有意安排的试验得到的数据，而是对生产过程测量记录下来的数据。

对它们进行分析，目的是想找出对我们所关心的指标（因变量）Y 有影响为因素（也称自变量或回归变量）m x x x ,......,,21，并建立用m x x x ,......,,21预报Y 的经验公式。

对于现实世界，不仅要知其然，而且要知其所以然。

顾客对商品和服务的反映对于商家是至关重要的，但是仅仅有满意顾客的比例是不够的，商家希望了解什么是影响顾客观点的因素，以及这些因素是如何起作用的。

类似地，医疗卫生部门不能仅仅知道某流行病的发病率，而且想知道什么变量影响发病率，如何影响发病率的。

发现变量之间的统计关系，并且用此规律来帮助我们进行决策才是统计实践的最终目的。

一般来说，统计可以根据目前所拥有的信息（数据）来建立人们所关心的变量和其他有关变量的关系。

这种关系一般称为模型（model ）。

假如用Y 表示感兴趣的变量，用X 表示其他可能与Y 有关的变量（x 也可能是若干变量组成的向量）。

则所需要的是建立一个函数关系Y=f(X)。

这里Y 称为因变量或响应变量（dependent variable, response variable ），而X 称为自变量，也称为解释变量或协变量（independent variable ，explanatory variable, covariate)。

建立这种关系的过程就叫做回归（regression ）。

一旦建立了回归模型，除了对各种变量的关系有了进一步的定量理解之外，还可以利用该模型(函数或关系式)通过自变量对因变量做预测（prediction ）。

⽤REG过程进⾏回归分析⼀、⽤REG过程进⾏回归分析SAS/STAT中提供了⼏个回归分析过程，包括REG（回归）、RSREG（⼆次响应⾯回归）、ORTHOREG（病态数据回归）、NLIN（⾮线性回归）、TRANSREG（变换回归）、CALIS（线性结构⽅程和路径分析）、GLM（⼀般线性模型）、GENMOD（⼴义线性模型），等等。

我们这⾥只介绍REG过程，其它过程的使⽤请参考《SAS 系统――SAS/STAT软件使⽤⼿册》。

REG过程的基本⽤法为：PROC REG DATA=输⼊数据集选项;VAR 可参与建模的变量列表;MODEL 因变量＝⾃变量表 / 选项;PRINT 输出结果;PLOT 诊断图形;RUN;REG过程是交互式过程，在使⽤了RUN语句提交了若⼲个过程步语句后可以继续写其它的REG 过程步语句，提交运⾏，直到提交QUIT语句或开始其它过程步或数据步才终⽌。

例如，我们对SASUSER.CLASS中的WEIGHT⽤HEIGHT和AGE建模，可以⽤如下的简单REG 过程调⽤：proc reg data=sasuser.class;var weight height age;model weight=height age;run;就可以在输出窗⼝产⽣如下结果，注意程序窗⼝的标题⾏显⽰“PROC REG Running”表⽰REG 过程还在运⾏，并没有终⽌。

See outputAGE的作⽤不显著，所以我们只要再提交如下语句：model weight=height;run;就可以得到第⼆个模型结果：See output事实上，REG提供了⾃动选择最优⾃变量⼦集的选项。

在MODEL语句中加上“SELECTION= 选择⽅法”的选项就可以⾃动挑选⾃变量，选择⽅法有NONE（全⽤，这是缺省）、FORWARD （逐步引⼊法）、BACKWARD（逐步剔除法）、STEPWISE（逐步筛选法）、MAXR（最⼤增量法）、MINR（最⼩增量法）、RSQUARE（选择法）、ADJRSQ（修正选择法）、CP（Mallows的统计量法）。