直角坐标系与球面坐标系转换

坐标计算方法在地理信息系统（GIS）和地理定位领域，坐标计算是一项重要的技术，它涉及到地图上点的位置和距离的计算。

在本文中，我们将介绍几种常用的坐标计算方法，包括直角坐标系下的点距离计算、经纬度坐标系下的距离计算以及坐标转换方法。

1. 直角坐标系下的点距离计算。

直角坐标系是平面坐标系的一种，可以用x和y坐标值来表示平面上的点。

在直角坐标系下，两点之间的距离可以用勾股定理来计算，即d = √((x2-x1)² + (y2-y1)²)。

其中，(x1, y1)和(x2, y2)分别是两点的坐标值，d表示两点之间的距离。

举个例子，如果点A的坐标是(3, 4)，点B的坐标是(7, 1)，那么点A和点B之间的距离可以用上述公式计算得出。

2. 经纬度坐标系下的距离计算。

经纬度坐标系是用来表示地球表面上点的位置的坐标系。

在地图上，经度用来表示东西方向的位置，纬度用来表示南北方向的位置。

在经纬度坐标系下，两点之间的距离可以用球面三角形的余弦定理来计算，即cos(d) = sin(φ1)sin(φ2) +cos(φ1)cos(φ2)cos(Δλ)，其中d表示两点之间的距离，φ1和φ2分别是两点的纬度，Δλ表示两点的经度差。

举个例子，如果点A的经纬度是(40.7128°N, 74.0060°W)，点B的经纬度是(34.0522°N, 118.2437°W)，那么点A和点B之间的距离可以用上述公式计算得出。

3. 坐标转换方法。

在实际应用中，我们经常需要将不同坐标系下的坐标进行转换。

例如，将经纬度坐标转换为直角坐标，或者将直角坐标转换为经纬度坐标。

这时，我们可以利用一些数学公式和算法来进行坐标转换。

对于经纬度坐标转换为直角坐标，可以利用球面坐标系下的公式进行计算；而对于直角坐标转换为经纬度坐标，可以利用逆向的球面坐标系下的公式进行计算。

总结。

在地理信息系统和地理定位领域，坐标计算是一项基础而重要的技术。

1 天球坐标系、地球坐标系和卫星测量中常用的坐标系的建立方法.天球直角坐标系天球坐标系天球球面坐标系坐标系地球直角坐标系地球坐标系地球大地坐标系常用的天球坐标系：天球赤道坐标系、天球地平坐标系和天文坐标系。

在天球坐标系中，天体的空间位置可用天球空间直角坐标系或天球球面坐标系两种方式来描述.1 天球空间直角坐标系的定义地球质心O为坐标原点，Z轴指向天球北极，X轴指向春分点，Y轴垂直于XOZ 平面，与X轴和Z轴构成右手坐标系。

则在此坐标系下,空间点的位置由坐标（X，Y，Z)来描述.春分点：当太阳在地球的黄道上由天球南半球进入北半球，黄道与赤道的交点）2 天球球面坐标系的定义地球质心O为坐标原点，春分点轴与天轴（天轴：地球自转的轴）所在平面为天球经度(赤经）测量基准-—基准子午面，赤道为天球纬度测量基准而建立球面坐标.空间点的位置在天球坐标系下的表述为（r,α，δ)。

天球空间直角坐标系与天球球面坐标系的关系可用图2—1表示：岁差和章动的影响岁差:地球实际上不是一个理想的球体，地球自转轴方向不再保持不变，这使春分点在黄道上产生缓慢的西移，这种现象在天文学中称为岁差。

章动：在日月引力等因素的影响下,瞬时北天极将绕瞬时平北天极旋转，大致呈椭圆,这种现象称为章动。

极移：地球自转轴相对地球体的位置并不是固定的，因而，地极点在地球表面上的位置，是随时间而变化的,这种现象称为极移。

地球的自转轴不仅受日、月引力作用而使其在空间变化，而且还受地球内部质量不均匀影响在地球内部运动。

前者导致岁差和章动，后者导致极移。

协议天球坐标系:为了建立一个与惯性坐标系统相接近的坐标系，人们通常选择某一时刻,作为标准历元，并将此刻地球的瞬时自转轴（指向北极）和地心至瞬时春分点的方向，经过瞬时的岁差和章动改正后，分别作为X轴和Z轴的指向，由此建立的坐标系称为协议天球坐标系.3 地球坐标系地球直角坐标系和地球大地坐标系的转换其中:过椭球面上一点的法线，可作无限个法截面，其中一个与该点子午面相垂直的法截面同椭球面相截形成的闭合的圈称为卯酉圈。

球极坐标系-回复球极坐标系的概念和应用是数学和物理学中的重要内容之一。

本文将从球坐标系的定义入手，逐步解释球坐标系的转换公式、坐标系之间的关系，以及其在物理学中的应用。

首先，我们先来了解球坐标系的定义。

球坐标系是一种广泛应用于三维空间中的坐标系，它可以用来描述空间中的点的位置。

球坐标系由三个参数表示，分别是“半径r”、“极角θ”和“方位角φ”。

其中，“半径r”表示点到坐标原点的距离，也可以理解为点所在的球面的半径；“极角θ”表示点与z轴的夹角，范围为0到π；“方位角φ”表示点在xy平面上的投影与x轴的夹角，范围为0到2π。

通过这三个参数，可以唯一确定三维空间中的点的位置。

接下来，我们将讨论球坐标系和直角坐标系之间的转换关系。

在直角坐标系中，一个点的位置可以用其在x轴上的投影x、在y轴上的投影y和在z轴上的投影z表示。

而在球坐标系中，一个点的位置可以用r、θ和φ表示。

那么，如何将一个点的直角坐标转换为球坐标呢？我们可以利用三角函数的性质来求解。

首先，根据平面几何的知识，可以得到点的半径r与点在x、y和z轴上的投影之间的关系：r = √(x^2 + y^2 + z^2)其次，我们可以通过勾股定理来求解点的极角θ：θ= arccos(z / r)最后，可以通过求解点在xy平面上的投影与x轴的夹角来得到点的方位角φ：φ= arctan(y / x)通过以上公式，我们可以将任意一点的直角坐标转换为球坐标。

接下来，我们将讨论球坐标系在物理学中的应用。

球坐标系在物理学中非常常见且广泛应用，尤其在描述天体力学、电场分布和量子力学等方面。

举个例子，我们可以用球坐标系来描述地球上某一点的地理位置。

其中，半径r可以表示该点距离地球的中心的距离，极角θ可以表示该点距离地球北极的夹角，方位角φ可以表示该点在地理经度上的位置。

又比如，球坐标系在描述电场分布时可以更加简洁明了，由于球坐标系中电荷对应的电势存在一个1/r的关系，这样可以方便地分析电场的强度分布。

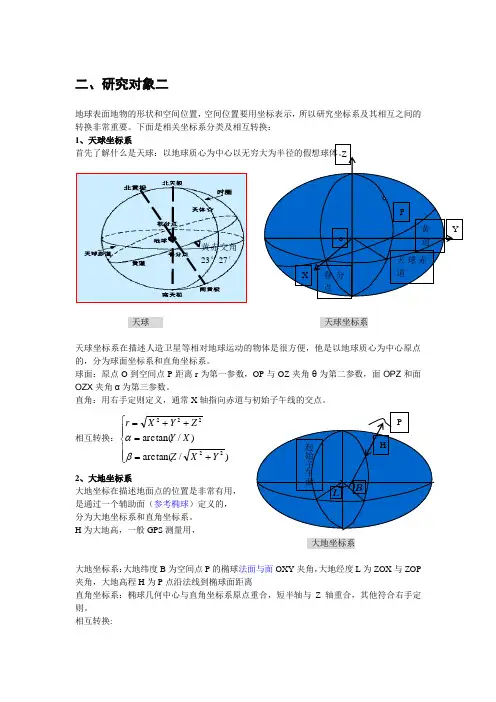
二、研究对象二地球表面地物的形状和空间位置，空间位置要用坐标表示，所以研究坐标系及其相互之间的转换非常重要。

下面是相关坐标系分类及相互转换： 1、天球坐标系首先了解什么是天球：以地球质心为中心以无穷大为半径的假想球体。

天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便，他是以地球质心为中心原点的，分为球面坐标系和直角坐标系。

球面：原点O 到空间点P 距离r 为第一参数，OP 与OZ 夹角θ为第二参数，面OPZ 和面OZX 夹角α为第三参数。

直角：用右手定则定义，通常X 轴指向赤道与初始子午线的交点。

相互转换：⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用， 是通过一个辅助面（参考椭球）定义的， 分为大地坐标系和直角坐标系。

H 为大地高，一般GPS 测量用，大地坐标系大地坐标系：大地纬度B 为空间点P 的椭球法面与面OXY 夹角，大地经度L 为ZOX 与ZOP 夹角，大地高程H 为P 点沿法线到椭球面距离直角坐标系：椭球几何中心与直角坐标系原点重合，短半轴与Z 轴重合，其他符合右手定则。

相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径，其中3、惯性坐标系（CIS ）与协议天球坐标系① 惯性坐标系（CIS ）:在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系：以某一约定时刻t0作为参考历元，把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴，以对应的春分点为X 轴的指向点，以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。

大地坐标转空间直角坐标方法大地坐标（经纬度）是地球表面上用于描述位置的一种坐标系统，常用的表示方式是用经度和纬度来表示一个位置。

而空间直角坐标是一种三维坐标系统，它由东西、南北和垂直地面三个方向组成。

大地坐标转换为空间直角坐标的方法分为两步：首先将大地坐标转换为大地平面坐标系坐标，然后再将大地平面坐标转换为空间直角坐标。

第一步，将大地坐标转换为大地平面坐标系坐标，常用的方法有三角形式法和高斯投影法。

1.三角形式法：三角形式法是根据大地三角形的性质，通过计算大地纬度和经度的变化量，将大地坐标转换为大地平面坐标。

具体步骤如下：（1）选取一个参考点，确定该点的大地坐标和大地平面坐标。

（2）计算待转换点的纬度和经度的变化量，即ΔB和ΔL。

（3）根据大地坐标的定义，计算待转换点的大地平面坐标，即X和Y。

2.高斯投影法：高斯投影法是一种常用的大地平面坐标投影方法，它是根据高斯球面正轴投影的原理，通过计算大地纬度和经度的变化量，将大地坐标转换为大地平面坐标。

具体步骤如下：（1）确定投影中央经线，选择一个参考点，确定该点的大地坐标和大地平面坐标。

（2）计算待转换点的纬度和经度的变化量，即ΔB和ΔL。

（3）根据高斯投影的计算公式，计算待转换点的大地平面坐标，即X和Y。

第二步，将大地平面坐标转换为空间直角坐标，常用的方法有高斯变换法和椭球投影法。

1.高斯变换法：高斯变换法是将大地平面坐标通过高斯投影法计算得到的坐标转换为空间直角坐标。

具体步骤如下：（1）选择一个参考点，确定参考点的大地平面坐标和空间直角坐标。

（2）计算待转换点的大地平面坐标与参考点的大地平面坐标之差，即ΔX和ΔY。

（3）根据高斯变换的计算公式，计算待转换点的空间直角坐标，即X、Y和Z。

2.椭球投影法：椭球投影法是将大地平面坐标通过椭球投影的原理，将大地平面坐标转换为空间直角坐标。

具体步骤如下：（1）选择一个参考点，确定参考点的大地平面坐标和空间直角坐标。

第一章大地坐标第一节大地坐标系统科技名词定义中文名称：大地坐标系英文名称：geodetic coordinate system定义：以参考椭球中心为原点、起始子午面和赤道面为基准面的地球坐标系。

应用学科：测绘学（一级学科）；大地测量学（二级学科）大地坐标系（geodetic coordinate system）是大地测量中以参考椭球面为基准面建立起来的坐标系。

地面点的位置用大地经度、大地纬度和大地高度表示。

大地坐标系的确立包括选择一个椭球、对椭球进行定位和确定大地起算数据。

一个形状、大小和定位、定向都已确定的地球椭球叫参考椭球。

参考椭球一旦确定，则标志着大地坐标系已经建立。

大地坐标系亦称为地理坐标系。

大地坐标系是用来表述地球上点的位置的一种地区坐标系统。

它采用一个十分近似于地球自然形状的参考椭球作为描述和推算地面点位置和相互关系的基准面。

一个大地坐标系统必须明确定义其三个坐标轴的方向和其中心的位置。

通常人们用旋转椭球的短轴与某一规定的起始子午面分别平行干地球某时刻的平均自转轴和相应的真起始子午面来确定坐标轴的方向。

若使参考椭球中心与地球平均质心重合，则定义和建立了地心大地坐标系。

它是航天与远程武器和空间科学中各种定位测控测轨的依据。

若椭球表面与一个或几个国家的局部大地水准面吻合最好，则建立了一个国家或区域的局部大地坐标系。

大地坐标系中点的位置是以其大地坐标表示的，大地坐标均以椭球面的法线来定义。

其中，过某点的椭球面法线与椭球赤道面的交角为大地纬度；包含该法线和大地子午面与起始大地子午面的二面角为该点的大地经度；沿法线至椭球面的距离为该点的大地高。

大地纬度、大地经度和大地高分别用大写英文字母B、L、H表示。

大地坐标系是以地球椭球赤道面和大地起始子午面为起算面并依地球椭球面为参考面而建立的地球椭球面坐标系。

它是大地测量的基本坐标系，其大地经度L、大地纬度B和大地高H为此坐标系的3个坐标分量。

它包括地心大地坐标系和参心大地坐标系。

❝§3-1 球面坐标系、坐标变换的意义与一般公式❝§3-2 决定新极Q 的地理坐标φ0，λ0❝§3-3 地理坐标φ，λ换算为球面极坐标α，Z❝球面余弦公式Ac b c b a cos sin sin cos cos cos ⋅⋅+⋅=Cc B b A a sin sin sin sin sin sin ==Bc a c a b cos sin sin cos cos cos ⋅⋅+⋅=Cb a b ac cos sin sin cos cos cos ⋅⋅+⋅=❝球面正弦公式sinacos B =cos b sin c －sin b cos c cos A❝球面边正弦与邻角余弦之积公式球面三角形的基本公式边的余弦公式定理：球面三角形任意边的余弦等于其它两边余弦的乘积加上这两边的正弦及其夹角余弦的连乘积。

Ac b c b a cos sin sin cos cos cos +=正弦公式定理：球面三角形各边的正弦和对角的正弦成正比。

Cc B b A a sin sin sin sin sin sin ==一、球面坐标系、坐标变换为在球面上确定点位可是需要采用不同的坐标系。

制图实践中常使用的有地理坐标系（φ、λ），球面坐标系（a, z）和球面直角坐标系（x,y）。

目前以上三种坐标系在测绘技术上应用最为广泛。

三者之间可以进行简单的相互换算。

如下图，其中K 为球面上一点地理坐标为，球面极坐标为。

P 是地理坐标系极点，Q 是球面极坐标系新极点。

二、坐标变换的一般公式()λϕ，()00λϕ，()z ，α由地理坐标系到球面极坐标系之间的变换：()000cos cos cos sin sin cos λλϕϕϕϕ-+=z 在球面三角形PQA ，由边的余弦公式有：()()ϕϕ--=︒︒90cos 90cos cos 0z ()()()00cos 90sin 90sin λλϕϕ---+︒︒即式中φ0、λ0是球面坐标原点Q的地理坐标()000cos sin cos cos sin cos sin λλϕϕϕϕ--=a z )sin(cos sin sin 0λλϕ-=a z 由第一正余弦公式有()()ϕϕ--=︒︒90cos 90sin cos sin 0a z ()()()00cos 90sin 90cos λλϕϕ----︒︒即由正弦公式有()a z sin 90sin )sin(sin 0ϕλλ-=-︒由此得到：()000cos cos cos sin sin cos λλϕϕϕϕ-+=z ()()0000cos sin cos cos sin sin cos λλϕϕϕϕλλϕ---=tga由球面极坐标到地理坐标之间的变换：a z z cos sin cos cos sin sin 00ϕϕϕ+=在球面三角形PKQ ，由余弦公式有：()()zcos 90cos 90cos 0ϕϕ-=-︒︒()αϕcos sin 90sin 0z -+︒即式中φ0、λ0是球面坐标原点Q的地理坐标()αϕϕλλϕcos sin sin cos cos cos cos 000z z -=-)sin(cos sin sin 0λλϕ-=a z 由第一正余弦公式有()()()z cos 90sin cos 90sin 00ϕλλϕ-=--︒︒()αϕcos sin 90cos 0z --︒即由正弦公式有()a z sin 90sin )sin(sin 0ϕλλ-=-︒由此得到：αϕϕϕcos sin cos cos sin sin 00z z +=()zz tg sin cos sin cos cos sin cos 000αϕϕαϕλλ-=-由地理坐标到球面直角坐标间的变换：如图POP 1为中央经线，其经度为，新极点Q 位于赤道上，其经度为球面上点A 地理坐标为，，过A 点作垂直圈QAB 与中央经线交于B ，令BO＝x,，BA ＝y 则A 的球面直角坐标为（x ，y）0λ︒+900λϕλ在球面直角三角形PBA 有()()()0cos 9090ctg ctg x λλφ︒︒-=--()()0sin 90sin sin λλϕ--=︒y 于是得到由地理坐标到球面直角坐标的变换公式为()0sec λλϕ-=tg tgx ()0sin cos sin λλϕ-=y在球面直角三角形PBA 有()()yx cos 90cos 90cos -=-︒︒ϕ()()090sin λλ-=-︒tgyctg x 于是得到yx cos sin sin =ϕ()xtgy tg sec 0=-λλ在一般情况下，大多数地图投影都采用地理坐标表示球面位置建立平面直角坐标与的关系。

不同经纬度转换坐标方法一、经纬度转换为直角坐标系坐标经纬度是地球表面上一个点的位置坐标，而直角坐标系是平面上的坐标系。

为了将经纬度转换为直角坐标系的坐标，可以使用投影算法来实现。

1. 地心经纬度坐标系转换为地心直角坐标系地心经纬度坐标系是以地球中心为原点建立的坐标系，将地球表面上的点投影到地球球面上。

将地心经纬度坐标系转换为地心直角坐标系，可以使用球面转直角坐标变换公式来实现。

2. 大地坐标系转换为地心直角坐标系大地坐标系是以地球表面上某一点为原点建立的坐标系，将地球表面上的点投影到地球球面上。

将大地坐标系转换为地心直角坐标系，可以使用大地坐标系转换为地心经纬度坐标系的公式，再将地心经纬度坐标系转换为地心直角坐标系。

二、直角坐标系转换为经纬度将直角坐标系的坐标转换为经纬度，可以使用反投影算法来实现。

1. 地心直角坐标系转换为地心经纬度坐标系地心直角坐标系是以地球中心为原点建立的坐标系，将地球表面上的点投影到地球球面上。

将地心直角坐标系转换为地心经纬度坐标系，可以使用直角坐标转球面坐标变换公式来实现。

2. 地心直角坐标系转换为大地坐标系地心直角坐标系转换为大地坐标系的方法与地心经纬度坐标系转换为大地坐标系类似，只是在转换过程中需要考虑椭球参数。

三、经纬度转换为平面坐标系坐标在地图制图和测量等应用中，经常需要将经纬度坐标转换为平面坐标系的坐标。

常用的转换方法有以下几种：1. 经纬度转换为UTM坐标UTM坐标是一种平面坐标系，适用于大范围的地图测绘。

将经纬度转换为UTM坐标，可以使用UTM投影算法来实现。

2. 经纬度转换为高斯-克吕格坐标高斯-克吕格坐标是一种平面坐标系，适用于小范围的地图测绘。

将经纬度转换为高斯-克吕格坐标，可以使用高斯投影算法来实现。

四、平面坐标系坐标转换为经纬度将平面坐标系的坐标转换为经纬度，可以使用反投影算法来实现。

1. UTM坐标转换为经纬度将UTM坐标转换为经纬度，可以使用UTM反投影算法来实现。

测量常用的坐标系有哪些各有何特点坐标系是用来描述和定位空间中物体位置的一种方式。

在测量领域，常用的坐标系有直角坐标系、极坐标系和球坐标系。

每种坐标系都有其独特的特点和适用场景。

直角坐标系直角坐标系是最常见和最简单的坐标系。

它由两个相互垂直的轴组成，通常表示为X轴和Y轴。

在直角坐标系中，每个点的位置由其在X轴和Y轴上的坐标表示。

X轴和Y轴的交点称为原点，用(0,0)表示。

特点： 1. 简单直观：直角坐标系以直线和直角为基础，易于理解和使用。

2.坐标计算方便：通过简单的几何关系，可以通过坐标计算两个点之间的距离和角度。

3. 适用于平面测量：直角坐标系主要用于平面测量，如地图绘制、建筑布局等。

4. 不适用于曲面测量：直角坐标系无法准确描述曲面上的点的位置，因此在某些测量场景下不适用。

极坐标系极坐标系使用角度和距离来描述点的位置。

它以一个固定点为极点，以一条规定方向为极轴。

极坐标系中，点的位置由极径（距离）和极角（与极轴的夹角）来表示。

特点： 1. 独特的表示方式：相比直角坐标系，极坐标系通过角度和距离的组合来表示点的位置，具有其独特的表达方式。

2. 适用于圆形测量：极坐标系在测量圆形或呈放射状分布的物体时很有优势，如计算轮胎的直径、孔洞的位置等。

3.不适用于直线测量：极坐标系不适用于描述直线上的点的位置，精准度较低。

4.笛卡尔坐标的转换：极坐标系可以与直角坐标系进行转换，相互之间可以转化表达点的位置。

球坐标系球坐标系是一种用于描述三维空间中点的位置的坐标系。

它由两个角度和一个距离组成。

球坐标系的极点位于球心，其中一个角度是与一个确认的轴之间的角度，其他则是与这个确定的轴之间的角度。

特点： 1. 适用于球面测量：球坐标系特别适用于描述球面上物体的位置，如天体测量、机器人定位等。

2. 三维空间表达能力强：球坐标系不仅可以表示平面上的点，还可以表示三维空间中的点的位置。

3. 计算复杂度较高：由于球坐标系需要通过角度和距离来表示点的位置，所以计算复杂度较高，不够直观简单。

ecef转为平面直角坐标系
在平面直角坐标系中，一个点的坐标表示为(x, y)，其中x表示点在x轴上的位置，y表示点在y轴上的位置。

而ecef坐标系是一个地球坐标系，它使用地球的中心点作为原点，x轴指向经度为0度的点，y轴指向经度为90度的点，z轴指向地球的北极点。

要将一个点的ecef坐标转换为平面直角坐标系，可以按照以下步骤进行计算：
1. 计算球面坐标系中点的经度(λ)和纬度(φ)。

可以使用以下公式来计算：
λ = atan2(y, x)
φ = atan2(z, sqrt(x^2 + y^2))
2. 将球面坐标系中的经度和纬度转换为弧度。

3. 使用球面坐标系中的经度和纬度以及地球半径(R)来计算点在地球上的位置坐标：
X = R * cos(φ) * cos(λ)
Y = R * cos(φ) * sin(λ)
Z = R * sin(φ)
4. 将点在地球上的位置坐标投影到平面直角坐标系中。

这可以通过将点的纬度和经度视为x和y坐标来实现。

综上所述，可以按照上述步骤将ecef坐标转换为平面直角坐标系。

utm坐标与wgs转化公式UTM坐标和WGS84坐标是两种常用的地理坐标系，UTM坐标是一种平面直角坐标系，而WGS坐标是一种球面坐标系。

由于两者的坐标系不同，需要进行坐标转化才能相互转换。

以下是UTM坐标和WGS84坐标转化的公式：1.UTM坐标转WGS84坐标公式$$begin{aligned}phi &= arctanleft[frac{tan(mathrm{Northing}/(mathrm{K_0} times mathrm{R}))}{mathrm{cos}(mathrm{Easting}/(mathrm{K_0} times mathrm{R}))}right]lambda &= frac{mathrm{Easting}}{mathrm{K_0} times mathrm{R}} - frac{180^{circ}}{pi} + frac{mathrm{Zone} times 6 - 183^{circ}}{57.29577951}N &= mathrm{K_0} timesfrac{mathrm{SemiMajorAxis}}{sqrt{1-mathrm{e}^2 sin^2 phi}} M &= frac{mathrm{SemiMajorAxis}}{(1-mathrm{e}^2/4 -3mathrm{e}^4/64 - 5mathrm{e}^6/256)times(1-mathrm{e}^2 sin^2 phi)^{3/2}}y &= frac{mathrm{Northing}}{mathrm{K_0}} - frac{(1 +2mathrm{t}^2 + mathrm{t}^4)M}{6} sin phi cos phi^3 + frac{(5 - 2mathrm{t}^2 + 28mathrm{t}^4 - 3mathrm{t}^6)M}{120} sinphi^5 cos phi^5x &= frac{mathrm{Easting}}{mathrm{K_0}} +frac{M}{mathrm{cos} phi} - frac{(1 + 2mathrm{t}^2 +mathrm{t}^4)M}{24} cos phi^3 + frac{(5 - 2mathrm{t}^2 +28mathrm{t}^4 - 3mathrm{t}^6)M}{720} cos phi^5h &= mathrm{Height} - mathrm{OrthometricHeight}end{aligned}$$其中，$phi$为纬度，$lambda$为经度，$N$为卯酉圈曲率半径，$M$为子午线弧长，$y$为真实坐标系下的纵坐标，$x$为真实坐标系下的横坐标，$h$为高度偏差。

球坐标系的表示方法球坐标系是一种三维坐标系，由一个原点和三个坐标轴构成。

它通常用于描述球面上的点的位置。

球坐标系中的点由两个角度和一个半径来确定。

这两个角度分别是极角和方位角，而半径表示点到原点的距离。

极角是指点与正轴之间的夹角，范围通常为0到π。

方位角是指点在极平面上与正x轴之间的夹角，范围通常为0到2π。

半径表示点到原点的距离，可以是正的、零或负的。

在球坐标系中，原点通常被称为极点，与它的连线对应于极轴。

正z轴垂直于极平面，并指向正z方向。

正x轴在极平面上，并指向正x方向。

正y轴是垂直于极平面的轴，并指向正y方向。

为了表示球坐标系中的点，通常使用以下符号：- (r,θ,φ):其中r是半径，θ是极角，φ是方位角。

在球坐标系中，我们可以使用不同的单位来度量极角和方位角。

一种常用的单位是弧度。

弧度是一个角所对应的弧长与其所在圆的半径之比。

以弧度为单位，极角的范围是从0到π，方位角的范围是从0到2π。

另一种常用的单位是角度。

角度是用度数来度量的，其中一个圆的弧长等于360度。

在角度制下，极角的范围是0到180度，方位角的范围是0到360度。

为了在球坐标系和直角坐标系之间进行转换，可以使用以下公式：- x = r × sin(θ) × cos(φ)- y = r × sin(θ) × sin(φ)- z = r × cos(θ)这些公式将球坐标系中的点转换为直角坐标系中的点。

通过这些公式，我们可以在两个坐标系之间互相转换。

球坐标系在各种领域中都有广泛的应用，例如天文学中描述星体的位置、物理学中描述粒子的位置和运动、计算机图形学中描述三维场景的位置等等。

了解球坐标系的表示方法可以帮助我们更好地理解和应用这些领域中的相关知识。

用球坐标表示
球坐标是一种三维空间的坐标系，它由一个半径和两个角度组成。

球坐标系常用于描述球面上的点，也常用于天文学、物理学和工程学中。

在球坐标系中，一个点的位置可以用三个数表示：半径 r、极角θ和方位角φ。

其中，半径 r 表示点到坐标原点的距离，极角θ是点在 x-y 平面上的投影与 x 轴之间的夹角，方位角φ则是从 x 轴开始逆时针旋转到点的连线与 x-y 平面的交线的夹角。

球坐标系和直角坐标系之间可以通过一些公式进行转换。

例如，给定直角坐标系中的一个点 (x, y, z)，可以用以下公式将其转换为球坐标系中的点 (r, θ, φ)：
r = sqrt(x^2 + y^2 + z^2)
θ = acos(z / r)
φ = atan2(y, x)
反过来，给定球坐标系中的一个点 (r, θ, φ)，可以用以下公式将其转换为直角坐标系中的点 (x, y, z)：
x = r * sin(θ) * cos(φ)
y = r * sin(θ) * sin(φ)
z = r * cos(θ)
使用球坐标系可以方便地描述球面上的点，例如地球上的经纬度就是一种球坐标系。

此外，在物理学中，球坐标系也经常用于描述原子的位置和运动状态。

球坐标与直角坐标的转换公式
球坐标与直角坐标是两种不同的坐标系，它们之间的转换需要用到一些公式。

下面是球坐标与直角坐标的转换公式：
1. 球坐标系中的点P(x,y,z)到直角坐标系中的点P'(x',y',z')的转换公式：
x' = r*sinθ*cosφ
y' = r*sinθ*sinφ
z' = r*cosθ
其中，r是点P到坐标原点的距离，θ是点P与z轴的夹角，φ是点P在x-y平面上的投影与x轴的夹角。

2. 直角坐标系中的点P'(x',y',z')到球坐标系中的点P(x,y,z)的转换公式：
r = sqrt(x'^2 + y'^2 + z'^2)
θ= arccos(z'/r)
φ= arctan(y'/x')
其中，sqrt表示平方根，arccos表示反余弦函数，arctan表示反正切函数。

以上就是球坐标与直角坐标的转换公式，它们在三维计算机图形学、物理学、天文学等领域都有广泛的应用。

球面坐标偏导数球面坐标系是一种常用的坐标系，适用于描述球体上的点的位置。

在球面坐标系中，点的位置由纬度、经度和半径三个参数确定。

在研究球面坐标系时，我们经常需要计算某个点在不同方向上的变化率，即偏导数。

本文将介绍球面坐标系中的偏导数及其应用。

1. 球面坐标系的简介球面坐标系是一种由纬度、经度和半径确定的坐标系。

其中，纬度表示点在垂直于球体表面的方向上的位置，取值范围为-90°到90°；经度表示点在水平方向上的位置，取值范围为0°到360°；半径表示点到球心的距离。

2. 球面坐标系的转换在球面坐标系中，点的位置可以通过以下公式与直角坐标系中的位置相互转换：x = r * sin(φ) * cos(θ)y = r * sin(φ) * sin(θ)z = r * cos(φ)其中，x、y、z为直角坐标系中的位置，r为半径，φ为纬度，θ为经度。

3. 球面坐标系中的偏导数在球面坐标系中，我们常常需要计算某个点在不同方向上的变化率，即偏导数。

对于球面坐标系中的函数，我们可以通过以下公式计算其偏导数：∂f/∂r = (∂f/∂x) * (∂x/∂r) + (∂f/∂y) * (∂y/∂r) + (∂f/∂z) * (∂z/∂r)∂f/∂φ = (∂f/∂x) * (∂x/∂φ) + (∂f/∂y) * (∂y/∂φ) + (∂f/∂z) * (∂z/∂φ)∂f/∂θ = (∂f/∂x) * (∂x/∂θ) + (∂f/∂y) * (∂y/∂θ) + (∂f/∂z) * (∂z/∂θ)其中，∂f/∂r、∂f/∂φ、∂f/∂θ分别表示函数f对半径、纬度、经度的偏导数。

4. 偏导数的物理意义偏导数描述了函数在不同方向上的变化率。

在球面坐标系中，偏导数可以用于描述球体上某点的切线方向上的变化率。

例如，在地理学中，我们可以利用纬度和经度的偏导数计算某点的切线方向上的地理方向，从而确定该点的位置。