七年级三线八角_练习题

专题03三线八角★知识归纳●同位角、内错角、同旁内角的概念1. “三线八角”模型如图，直线AB、CD与直线EF相交(或者说两条直线AB、CD被第三条直线EF所截)，构成八个角，简称为“三线八角”，如图1.图1要点梳理：⑴两条直线AB,CD与同一条直线EF相交．⑵“三线八角”中的每个角是由截线与一条被截线相交而成．2. 同位角、内错角、同旁内角的定义在“三线八角”中，如上图1，（1）同位角：像∠1与∠5，这两个角分别在直线AB、CD的同一方，并且都在直线EF的同侧，具有这种位置关系的一对角叫做同位角.（2）内错角：像∠3与∠5，这两个角都在直线AB、CD之间，并且在直线EF的两侧，像这样的一对角叫做内错角. （3）同旁内角：像∠3和∠6都在直线AB、CD之间，并且在直线EF的同一旁，像这样的一对角叫做同旁内角.要点梳理：(1)“三线八角”是指上面四个角中的一个角与下面四个角中的一个角之间的关系，显然是没有公共顶点的两个角.(2)“三线八角”中共有4对同位角，2对内错角，2对同旁内角．●同位角、内错角、同旁内角位置特征及形状特征要点梳理：巧妙识别三线八角的两种方法：(1)巧记口诀来识别：一看三线，二找截线，三查位置来分辨.(2)借助方位来识别根据这三种角的位置关系，我们可以在图形中标出方位，判断时依方位来识别，如图2．★实操夯实一．选择题（共15小题）1．下列图形中，∠1和∠2不是同位角的是（）A．B．C．D．【解答】解：A、∠1和∠2是同位角，故此选项不合题意；B、∠1和∠2是同位角，故此选项不合题意；C、∠1和∠2不是同位角，故此选项符合题意；D、∠1和∠2是同位角，故此选项不合题意；故选：C．2．下列所示的四个图形中，∠1和∠2是同位角的是（）A．②③B．①②③C．③④D．①②④【解答】解：图①②④中，∠1和∠2是同位角，故选：D．3．如图，下列说法错误的是（）A．∠A与∠C是同旁内角B．∠1与∠3是同位角C．∠2与∠3是内错角D．∠3与∠B是同旁内角【解答】解：A、∠A与∠C是同旁内角，故A正确；B、∠1与∠3是同旁内角，故B错误；C、∠2与∠3是内错角，故C正确；D、∠3与∠B是同旁内角，故D正确；故选：B．4．给出下列说法：（1）两条直线被第三条直线所截，同位角相等；（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；（3）相等的两个角是对顶角；（4）从直线外一点到这条直线的垂线段，叫做这点到直线的距离．其中正确的有（）A．0个B．1个C．2个D．3个【解答】解：（1）同位角只是一种位置关系，只有两条直线平行时，同位角相等，错误；（2）强调了在平面内，正确；（3）不符合对顶角的定义，错误；（4）直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度．故选：B．5．已知∠1和∠2是同旁内角，∠1＝40°，∠2等于（）A．160°B．140°C．40°D．无法确定【解答】解：同旁内角只是一种位置关系，两直线平行时同旁内角互补，不平行时无法确定同旁内角的大小关系，故选D．6．在下列四个图中，∠1与∠2是同位角的图是（）A．①②B．①③C．②③D．③④【解答】解：①∠1和∠2是同位角；②∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角；③∠1和∠2是同位角；④∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角．故选：B．7．如图，直线a、b被直线c所截，互为同旁内角是（）A．∠4和∠6B．∠2和∠7C．∠4和∠5D．∠4和∠6【解答】解：∵直线a、b被直线c所截，∴互为同旁内角是∠4和∠5．故选：C．8．如图，∠1与∠2是同位角，若∠1＝63°，则∠2的大小是（）A．27°B．63°C．27°或63°D．不能确定【解答】解：因为被截的两条直线是相交还是平行无法确定，所以∠2与∠1的关系也无法确定，故∠2大小不能确定．故选：D．9．如图，直线AD，BE被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是（）A．∠4，∠2B．∠2，∠6C．∠5，∠4D．∠2，∠4【解答】解：∠1的同位角是∠2，∠5的内错角是∠6，故选：B．10．下列说法正确的是（）A．小于平角的角是直角B．相等的角是对顶角C．同位角相等D．互为邻补角的两角和等于180°【解答】解：A、小于平角的角是直角，也有可能是锐角，故本选项错误；B、如等腰三角形的两底角相等但不是对顶角，故本选项错误；C、两直线平行，同位角相等，故本选项错误；D、互为邻补角的两角和等于180°，故本选项正确．故选：D．11．如图，图中∠1与∠2是同位角的是（）A．（2）（3）B．（2）（3）（4）C．（1）（2）（4）D．（3）（4）【解答】解：（1）（2）（4）中，∠1与∠2是同位角；图（3）中，∠1与∠2不是同位角，因为这两个角的边所在的直线没有一条公共边．故选：C．12．如图，∠ADE和∠CED是（）A．同位角B．内错角C．同旁内角D．互为补角【解答】解：由图知，∠ADE和∠CED是直线AB和AC被DE所截形成的，在截线两侧，且在两被截线之间，故是内错角．故选：B．13．如图，直线a，b被直线c所截，则下列说法中错误的是（）A．∠1与∠3是对顶角B．∠1与∠2是邻补角C．∠3与∠4是内错角D．∠2与∠4是同位角【解答】解：A、∠1与∠3是对顶角，说法正确；B、∠2与∠3是邻补角，说法正确；C、∠3与∠4是同旁内角，故原说法错误；D、∠2与∠4是同位角，说法正确；故选：C．14．如图所示，下列说法中错误的是（）A．∠A和∠2是同旁内角B．∠A和∠3是同位角C．∠A和∠B是同旁内角D．∠C和∠1是内错角【解答】解：A、∠A和∠2不是同旁内角，原说法错误，故此选项符合题意；B、∠A和∠3是同位角，原说法正确，故此选项不符合题意；C、∠A和∠B是同旁内角，原说法正确，故此选项不符合题意；D、∠C和∠1是内错角，原说法正确，故此选项不符合题意；故选：A．15．如图，平行直线AB、CD与相交直线EF、GH相交，图中的同旁内角共有（）A．4对B．8对C．12对D．16对【解答】解：直线AB、CD被EF所截有2对同旁内角；直线AB、CD被GH所截有2对同旁内角；直线CD、EF被GH所截有2对同旁内角；直线CD、GH被EF所截有2对同旁内角；直线GH、EF被CD所截有2对同旁内角；直线AB、EF被GH所截有2对同旁内角；直线AB、GH被EF所截有2对同旁内角；直线EF、GH被AB所截有2对同旁内角．共有16对同旁内角．故选：D．二．填空题（共3小题）16．如图，射线DE、DC被直线AB所截得的用数字表示的角中，∠4与∠1是同位角．【解答】解：∠4与∠1是同位角，故答案为：∠1．17．如图，∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B 或∠A．【解答】解：∠A与∠BDG是直线AC、DE被直线AB所截形成的同位角，∠A与∠BFG是直线AC、DE被直线AB所截形成的同位角；∠1与∠CGF是直线AC、AB被直线DE所截形成的内错角；∠A与∠2是直线AB、BC被直线AC所截形成的同旁内角，∠2与∠B是直线AC、AB被直线BC所截形成的同旁内角，∠2与∠CGF是直线BC、DE被直线AC所截形成的同位角；故∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B或∠A．18．如图，∠1与∠B是同旁内角，它们是由直线AC和CB被直线AB所截而形成．【解答】解：∠1与∠B是直线AC、BC被AB所截而成的同旁内角，故答案为：同旁内；AC、BC、AB．。

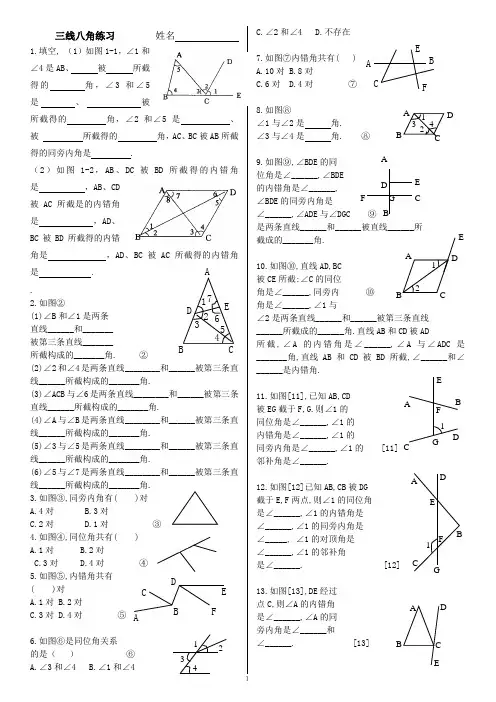
１三线八角练习 姓名1.填空, （1）如图1-1，∠1和∠4是AB 、 被 所截得的 角，∠3和∠5是 、 被所截得的 角，∠2和∠5是 、被 所截得的 角，AC 、BC 被AB 所截得的同旁内角是 .（2）如图1-2，AB 、DC 被BD 所截得的内错角是 ，AB 、CD 被AC 所截是的内错角是 ，AD 、BC 被BD 所截得的内错角是 ，AD 、BC 被AC 所截得的内错角是 . . 2.如图② (1)∠B 和∠1是两条 直线______和_______ 被第三条直线_______ 所截构成的_______角. ② (2)∠2和∠4是两条直线________和______被第三条直线______所截构成的_______角. (3)∠ACB 与∠6是两条直线________和______被第三条直线______所截构成的_______角. (4)∠A 与∠B 是两条直线________和______被第三条直线______所截构成的_______角. (5)∠3与∠5是两条直线________和______被第三条直线______所截构成的_______角. (6)∠5与∠7是两条直线________和______被第三条直线______所截构成的_______角. 3.如图③,同旁内角有( )对 A.4对 B.3对 C.2对 D.1对 ③ 4.如图④,同位角共有( ) A.1对 B.2对 C.3对 D.4对 ④ 5.如图⑤,内错角共有 ( )对 A.1对 B.2对 C.3对 D.4对 ⑤ 6.如图⑥是同位角关系 的是（ ） ⑥ A.∠3和∠4 B.∠1和∠4 C.∠2和∠4 D.不存在 7.如图⑦内错角共有( ) A.10对 B.8对C.6对D.4对 ⑦8.如图⑧ ∠1与∠2是 角. ∠3与∠4是 角. ⑧ 9.如图⑨,∠BDE 的同位角是∠______,∠BDE的内错角是∠______,∠BDE 的同旁内角是 ∠______,∠ADE 与∠DGC ⑨ 是两条直线______和______被直线______所截成的_______角.10.如图⑩,直线AD,BC被CE 所截:∠C 的同位角是∠______,同旁内 ⑩ 角是∠______,∠1与 ∠2是两条直线______和______被第三条直线______所截成的______角.直线AB 和CD 被AD所截,∠A 的内错角是∠______,∠A 与∠ADC 是_______角,直线AB 和CD 被BD 所截,∠______和∠______是内错角.11.如图[11],已知AB,CD被EG 截于F,G.则∠1的 同位角是∠______,∠1的 内错角是∠______,∠1的 同旁内角是∠______,∠1的 [11] 邻补角是∠______. 12.如图[12]已知AB,CB 被DG 截于E,F 两点,则∠1的同位角 是∠______,∠1的内错角是 ∠______,∠1的同旁内角是∠_____, ∠1的对顶角是 ∠______,∠1的邻补角 是∠______. [12] 13.如图[13],DE 经过 点C,则∠A 的内错角 是∠______,∠A 的同 旁内角是∠______和 ∠______. [13] B C AD E 1 2 3 7 6 5 4 D A B C E F 1 2 3 4 A B C E F A B CD 1 2 3 4A BC D E F G A B C DE 1 2 A B CDE FG 1 A B D E FCG1A B C D E14.如图[14]三条直线L1,L2,L3两两相交,则图中共有_______对对顶角,______对邻补角,____对同位角,___对同旁内角,____对内错角. [14]15.如图[15],∠1的同旁内角是∠_____和∠_____,∠2的内错角是∠______,∠3与∠B是___________. [15]16.如图[16]∠1与∠4是______角, ∠1与∠3是______角,∠2与∠D是_______角,∠3与∠D是_______角,∠4与∠D是_______角,∠4与∠B是_______角. [16]17.如图[17]直线AB和CD被EC所截,则∠1与∠2是______角,∠1与∠3是______角,∠1与∠C是______角,∠2与∠C是______角,∠4与∠C是______角. [17]18.如图[18]同位角，内错角，同旁内角的对数分别是________,________,___________.19.如图[19]∠1的同位角是∠______,∠2的同旁内角是∠_____,∠1的内错角是∠______.[18] [19]20.如图[20]在∠1,∠2,∠3,∠4,∠5, ∠6中同位角有______对.同旁内角有______对. [20]21.如图：∠1=︒53，∠2=︒127，∠3=︒53，试说明直线AB与CD，BC与DE的位置关系。

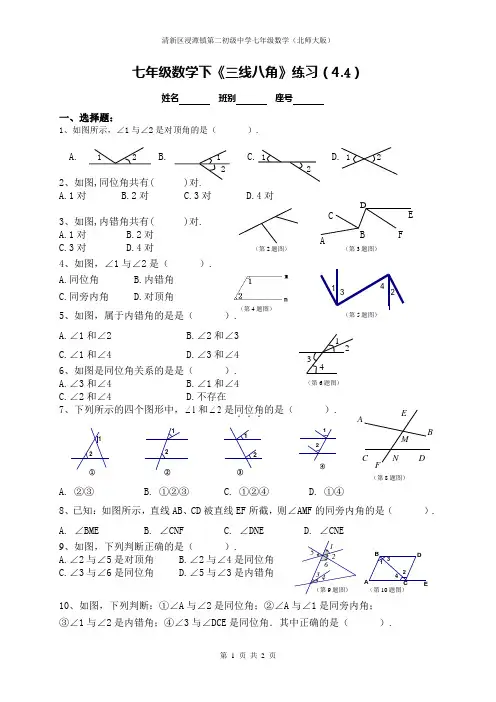
①2121②12③12④七年级数学下《三线八角》练习（4.4）姓名 班别 座号一、选择题：1、如图所示，∠1与∠2是对顶角的是（ ）.A. 1 2B. 1C. 1D. 1 2222、如图,同位角共有( )对.A.1对B.2对C.3对D.4对3、如图,内错角共有( )对. A.1对 B.2对C.3对D.4对 4、如图，∠1与∠2是（ ）. A.同位角 B.内错角 C.同旁内角 D.对顶角5、如图，属于内错角的是是（ ）.A.∠1和∠2B.∠2和∠3C.∠1和∠4D.∠3和∠46、如图是同位角关系的是是（ ）.A.∠3和∠4B.∠1和∠4C.∠2和∠4D.不存在 7、下列所示的四个图形中，1∠和2∠是同位角．．．的是（ ）.A. ②③B. ①②③C. ①②④D. ①④8、已知：如图所示，直线AB 、CD 被直线EF 所截，则∠AMF 的同旁内角的是（ ）. A. ∠BME B. ∠CNF C. ∠DNE D. ∠CNE 9、如图，下列判断正确的是（ ）.A.∠2与∠5是对顶角B.∠2与∠4是同位角C.∠3与∠6是同位角D.∠5与∠3是内错角10、如图，下列判断：①∠A 与∠2是同位角；②∠A 与∠1是同旁内角； ③∠1与∠2是内错角；④∠3与∠DCE 是同位角．其中正确的是（ ）.（第8题图）NMFE DCB A234 （第6题图） 1（第2题图） DABC E F（第3题图）（第4题图）2134图6（第5题图）654321（第9题图）EDC BA 4321（第10题图）A.①、②、③B.①、②、④C.②、③、④D.①、②、③、④ 二、填空题：11、如图∠1与∠2是 角，∠3与∠4是 角.12、①12∠∠与是 角；它们是由直线 和直线 ，被直线 所截得的； ②14∠∠与是 角；它们是由直线 和直线 ，被直线 所截得的；③3∠与5∠是 角；它们是由直线 和直线 ，被直线 所截得的.13、如图，∠1与∠B 是 和 被 所截构成的 角；∠2与∠B 是直线_ 和_ 被直线_ 所截构成的 角．14、如图，∠1、∠2、∠3中，______和_____是同位角，______和_____是同旁内角．15、如图，（1）∠1与∠4直线_____与直线____被直线______所截形成的__________． （2）∠2与∠3是直线_____与直线____被直线______所截形成的_________．16、(1) ∠1与∠B 是直线 、 被直线 所截得 角； （2）∠1与∠2是直线 、 被直线 所截得 角； （3）∠B 与∠4是直线 、 被直线 所截得 角； （4）∠B 与∠3是直线 、 被直线 所截得 角．17、（1）如图，直线AD 、BC 被直线AC 所截，找出图中由AD 、BC 被直线AC 所截而成的内错角是 和 .（2）∠3和∠4是直线 和 被 所截，构成 角. （3）∠BAD 与∠CDA 是直线 和 被 所截，构成 角. （4）∠DCE 与∠ABC 是直线 和 被 所截，构成 的 角.A BCD 123 4 （第11题图）ba n m 23 145（第12题图）（第13题图）（第14题图）4321DCBA （第15题图）（第16题图）4321DCBA （第17题图）。

七年级数学下册垂线三线八角练习题◆回顾归纳1．两条直线互相垂直，•其中的一条直线叫做另一条直线的_______，•交点叫做________．2．过一点有且只有_______与已知直线_______．3．连结直线外一点与直线上各点的所有线段中，________最短．4．直线外一点到这条直线的________的长度，叫做点到直线的距离．5．如图1直线AB，CD与EF相交，构成_______个角，其中∠1与∠5是_______，∠3与∠5是______，∠4与∠5是_______．图1 图2 图3 图4◆课堂测控知识点一垂线垂线段1．如图2所示，CD⊥AB，则点D是_____，∠ADC=∠CDB=________．2．如图3所示，l1⊥l2，垂足为_____，∠1与∠2是一组_____的邻补角，∠1 与______是一对_______的对顶角．3．（经典题）如图4所示，l1⊥l2，图中与直线L1垂直的直线是（）A．直线a B．直线L2 C．直线a，b D．直线a，b，c4．如图5所示，若∠ACB=90°，BC=8cm，•AC=•6cm，•则B•点到AC•边的距离为________．图5 图6 图7 图85．如图6所示，直线L外一点P到L的距离是________的长度．知识点二同位角内错角同旁内角6．如图7所示，图中的同位角有______对．7．如图8所示，下列说法不正确的是（）A．∠1与∠B是同位角 B．∠1与∠4是内错角C．∠3与∠B是同旁内角 D．∠C与∠A不是同旁内角8．如图9所示，∠1与∠2是哪两条直线被另一条直线所截，构成的是什么角的关系？∠3与∠D呢？图9◆课后测控1．如图10所示，直线AB，CD交于点O，OE⊥AB且∠DOE=40°，则∠COE=_____．图10 图11 图122．如图11所示，AO⊥OB于点O，∠AOB：∠BOC=3：2，则∠AOC=_______．3．如图12所示，AB与CD交于点O，OE⊥CD，OF⊥AB， ∠BOD= 25 °，•则∠AOE=____，∠DOF=_____．4．（教材变式题）如图所示，图（1）中∠1<∠2，图（2）中∠1=∠2．试用刻度量一量比较两图中PC，PD的大小．5．如图所示，分别过P画AB的垂线．6．（原创题）如图，OA⊥OC，OB⊥OD，且∠AOD=3∠BOC，求∠BOC的度数．◆拓展创新7．（经典题）我国“十一五”规划其中一重要目标是，建设社会主义新农村，国家对农村公路建设投资近1000亿人民币．西部的某落后山村准备在河流M上架上一座桥梁，如图所示，桥建在何处才能使A，B两个村庄的之间修建路面最短？答案:回顾归纳1．垂线，垂足 2．一条直线，垂直 3．垂线段4．垂线段 5．八，同位角，内错角，同旁内角课堂测控1．垂足，90° 2．O，相等，∠3，90°3．D（点拨：∵L1∥L2，a⊥L1，b⊥L1，c⊥L1）4．8cm（点拨：点到直线距离定义）5．PC的长（点拨：PE>PD>PC，PA>PB>PC）6．2（点拨：∠ADE与∠B，∠ADC与∠B）7．D（点拨：∠C与∠A是直线AB，BC被AC所截的同旁内角）8．AB，CD被AC所截，∠1与∠2是内错角关系；AC与CD被AD所截，∠3与∠D是同旁内角关系．课后测控1．140°（点拨：∠DOB=∠AOC=90°-40°=50°）2．150°（点拨：∠AOB=90°，3x=90°，x=30°，∠BOC=60°）3．65°，115°（点拨：∠AOC=∠BOD=25°，∠AOE=90°-∠AOC=90°-25°=65°）• 4．图（1）量得PC<PD，图（2）量得PC=PD．5．如图．6．∵∠BOD=90°，∠AOC=90°，∠BOD+∠AOC=180°∴∠AOD=180°-∠BOC，又∵∠AOD=3∠BOC∴3∠BOC=180°-∠BOC，∴∠BOC=45°解题技巧：本题扣住∠AOD=2×90°-∠BOC 这一关键式子．7．如图所示．（1）将A 向下平移河宽长度得A′； （2）连A′B 交河岸于M ；（3）过M 作MN⊥a，交河岸b 于N ，MN 即为架桥处； （4）连AN ，则AN+MN+BM 最短．七年级数学下册期末模拟题一 选择题(每小题3分,共12题,共计36分)1.下列计算正确的是（ ） A.9 =±3 B.|﹣3|=﹣3 C.9 =3D.﹣32=92.如果c 为有理数，且c≠0，下列不等式中正确的是（ ） A.3c ＞2c B.cc 23 C.3+c ＞2+c D.﹣3c ＜﹣2c3.下列说法不正确的是（ ）A.过任意一点可作已知直线的一条平行线B.同一平面内两条不相交的直线是平行线C.在同一平面内，过直线外一点只能画一条直线与已知直线垂直D.平行于同一直线的两直线平行4.若点P （﹣a ，4﹣a ）是第二象限的点，则a 的取值范围是（ ）A.a ＜4B.a ＞4C.a ＜0D.0＜a ＜45.对于图中标记的各角，下列条件能够推理得到a ∥b 的是（ ） A.∠1=∠2 B.∠2=∠4 C.∠3=∠4D.∠1+∠4=180°6.如图，直线a ∥b ，直线c 与a 、b 相交，∠1=70°，则∠2的大小是（ ） A.20° B.50° C.70°D.110°7.某次考试中，某班级的数学成绩统计图如下．下列说法错误的是（ ）A.得分在70～80分之间的人数最多B.该班的总人数为40C.得分在90～100分之间的人数最少D.及格（≥60分）人数是268.若方程mx+ny=6的两个解是⎩⎨⎧==11y x ，⎩⎨⎧-==12y x ，则m ，n 的值为（ ） A.4，2 B.2，4 C.﹣4，﹣2 D.﹣2，﹣49.如果不等式组⎩⎨⎧<->-mx x x )1(312的解集是x ＜2，那么m 的取值范围是（ ）A.m=2B.m ＞2C.m ＜2D.m≥210.若（3x ﹣y+5）2+|2x ﹣y+3|=0，则x+y 的值为（ ） A.2B.﹣3C.﹣1D.311.为了改善住房条件，小亮的父母考察了某小区的A 、B 两套楼房，A 套楼房在第3层楼，B 套楼房在第5层楼，B 套楼房的面积比A 套楼房的面积大24平方米，两套楼房的房价相同，第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积，小亮设A 套楼房的面积为x 平方米，B 套楼房的面积为y 平方米，根据以上信息列出了下列方程组．其中正确的是（ ） A.B.C.D.12.某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其它费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高（ ）A.40%B.33.4%C.33.3%D.30%二 填空题(每小题3分,共6题,共计18分)13.小于17的所有正整数和是 ．14..如图所示，若AB ∥DC ，∠1=39°，∠C 和∠D 互余，则∠D= ，∠B= ．15.若关于x 、y 的二元一次方程组⎩⎨⎧=-=+k y x ky x 95的解也是二元一次方程2x+3y=6的解，则k﹣21的算术平方根为 ． 16.将点A 先向下平移3个单位，再向右平移2个单位后得B （﹣2，5），则A 点关于y 轴的对称点坐标为 ．17.若关于x 的不等式组⎩⎨⎧->->-22132x x a x 的解集中只有4个整数解,则a 取值范围是18.如图,在平面直角坐标系中,已知点A(1,1)，B(﹣1,1)，C(﹣1,﹣2)，D(1,﹣2)，把一根长为2017个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在A 处，并按A→B→C→D→A…的规律紧绕在四边形ABCD 的边上,则细线的另一端所在位置的点的坐标是 ．三 计算综合题(共7题,共计66分)19.(本小题8分)解下列方程组或不等式组:（1）⎪⎩⎪⎨⎧=-=-132353y x y x (2)⎩⎨⎧-≥-->-3219235x x x ．20.(本小题8分)某校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后，随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分． 根据以上信息解决下列问题：（1）在统计表中，m=，n=，并补全直方图；（2）扇形统计图中“C组”所对应的圆心角的度数是度；（3）若该校共有964名学生，如果听写正确的个数少于24个定为不合格，请你估算这所学校本次比赛听写不合格的学生人数．21.(本小题10分)在平面直角坐标系中，三角形ABC的三个顶点的位置如图所示，点A′的坐标是（﹣2，2），现将三角形ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．（1）请画出平移后的三角形A′B′C′（不写画法），并写出点B′、C′的坐标；（2）求三角形ABC的面积．22.(本小题10分)已知：如图，B、E分别是AC、DF上一点，∠1=∠2，∠C=∠D．求证：∠A=∠F．23.(本小题8分)商店为了对某种商品促销，将定价为3元的商品，以下列方式优惠销售：若购买不超过5件，按原价付款；若一次性购买5件以上，超过部分打八折．如果用27元钱，最多可以购买该商品多少件？24.(本小题10分)已知2台大收割机和5台小收割机同时工作2h共收割小麦3.6hm2，3台大收割机和2台小收割机同时工作5h共收割小麦8hm2．求1台大收割机和1台小收割机每小时各收割小麦多少公顷（hm2）？（1）分析：如果设1台大收割机每小时各收割小麦x hm2，和1台小收割机每小时各收割小麦y hm2，则2台大收割机和5台小收割机同时工作1h共收割小麦hm2，3台大收割机和2台小收割机同时工作1h共收割小麦hm2（均用含x，y的代数式表示）；（2）根据以上分析，结合题意，请你列出方程组，求出1台大收割机和1台小收割机每小时各收割小苗多少公顷（hm2）？25(本小题10分)某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动，收费标准如下：人数m 0＜m≤100100＜m≤200m＞200 收费标准（元/人）90 85 75 甲、乙两所学校计划组织本校学生自愿参加此项活动．已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．经核算，若两校分别组团共需花费20 800元，若两校联合组团只需花费18 000元．（1）两所学校报名参加旅游的学生人数之和超过200人吗？为什么？（2）两所学校报名参加旅游的学生各有多少人？。

三线八角练习题一、选择题1. 在下列图形中，能构成三线八角关系的是：A. 平行线B. 相交线C. 垂直线D. 重合线2. 下列关于三线八角的说法，正确的是：A. 三线八角中的角都是锐角B. 三线八角中的角都是直角C. 三线八角中的角都是钝角D. 三线八角中的角可以是锐角、直角或钝角3. 在三线八角中，同位角的性质是：A. 相等B. 互补C. 和为180度D. 无法确定二、填空题1. 在三线八角中，若一条直线与两条平行线相交，则形成的同位角是______，内错角是______。

2. 若两条平行线之间的距离为5cm，则这两条平行线上的任意一对同位角之间的距离为______。

3. 在三线八角中，若两条直线平行，则它们的同旁内角是______。

三、判断题1. 三线八角中的同位角一定相等。

（）2. 三线八角中的内错角一定互补。

（）3. 两条平行线上的任意一对同旁内角之和为180度。

（）四、作图题1. 请画出两条平行线，并在其中一条平行线上任取一点，过该点作另一条平行线的垂线，标出三线八角。

2. 请画出两条相交线，并在其中一条相交线上任取一点，过该点作另一条相交线的平行线，标出三线八角。

五、解答题1. 已知直线AB与直线CD平行，直线EF与直线CD相交，形成三线八角。

若∠1=120°，求∠2、∠3和∠4的度数。

2. 在三角形ABC中，AB=AC，点D为BC上的一点，且BD=DC。

若∠BAC=40°，求∠BDC的度数。

3. 已知直线l1与直线l2平行，直线l3与直线l2相交，形成三线八角。

若∠1=∠2，求证：直线l1与直线l3平行。

六、应用题1. 在一个平面直角坐标系中，直线y = 2x + 1与x轴相交于点A，与直线y = x + 3相交于点B。

求证：点A、B与原点O形成的三角形OAB是一个等腰直角三角形。

2. 在一块长方形菜地中，菜地的长边与两块平行的小路相交，形成三线八角。

已知小路之间的距离为10米，长边上的一个角为60°，求菜地长边的长度。

5.1.2垂线三线八角♦回顾归纳1. _____________________________________________________ 两条直线互相垂直，？其中的一条直线叫做另一条直线的 _________________________________ , ?交点叫做 _________ .2. ____________________ 过一点有且只有 ___ 与已知直线 . 3•连结直线外一点与直线上各点的所有线段中， _____________ 最短.4. ____________________________ 直线外一点到这条直线的 的长度，叫做点到直线的距离.5. _____________________________________ 如图1直线AB, CD 与EF 相交，构成 个角，其中/I 与/5是 _______________________________ ,/3与♦课堂测控3.（经典题）如图4所示，11丄12，图中与直线L 1垂直的直线是（ ）,/4与/5是知识点一垂线垂线段1.如图2所示, CDLAB 则点D 是 ,/ ADC / CDB=2.如图3所示,h 丄",垂足为,/1与/2是一组的邻补角,是一对的对顶角.A8C图4A .直线aB .直线L2C .直线a, bD .直线a,b, c(1)♦课后测控1.2.如图 11 所示，AQLOB 于点 O,/ AOB / BOC=33.如图12所示，AB 与CD 交于点O?则/ AOE=___/ DOF= ____4.（教材变式题）如图所示，图（1）中/ 1</ 2,图（2）中/仁/ 2 .试用刻度量一量比较 两图中PC PD 的大小.5 .如图6所示，直线L 外一点P 到L 的距离是 __________ 的长度.知识点二 同位角 内错角 同旁内角6.如图7所示，图中的同位角有 __________ 对. 7 .如图8所示，下列说法不正确的是（ ）A ./I 与/B 是同位角B . Z1与/4是内错角C . /3与/B 是同旁内角D . /C 与/A 不是同旁内角 &如图9所示，/I 与/2是哪两条直线被另一条直线所截，构成的是什么角的关系？ /3与/D 呢？图92,则/ AOC=5•如图所示，分别过P画AB的垂线.6.（原创题）如图，OALOC OBLOD且/ AOD=Z BOC求/ BOC 的度数.♦拓展创新7.（经典题）我国“十一五”规划其中一重要目标是，建设社会主义新农村，国家对农村公路建设投资近1000亿人民币.西部的某落后山村准备在河流M上架上一座桥梁，如图所示，桥建在何处才能使A, B两个村庄的之间修建路面最短？B7答案: 回顾归纳1 •垂线，垂足2 •一条直线，垂直3 •垂线段4 •垂线段5 •八，同位角，内错角，同旁内角课堂测控1 .垂足，90°2 • 0,相等，/ 3, 90°3• D （点拨：T L i 〃L2, a丄L i, b丄l_i, c丄L i）4• 8cm （点拨：点到直线距离定义）5• PC的长（点拨：PE>PD>PC PA>PB>PC6• 2 （点拨：/ ADE 与/ B,/ ADC与/ B）7• D （点拨：/C与/A是直线AB, BC被AC所截的同旁内角）8• AB CD被AC所截，/1与/2是内错角关系；AC与CD被AD所截，/3与/D是同旁内角关系.课后测控1• 140° （点拨：/ DOB/ AOC=90 -40° =50°）2• 150° （点拨：/ AOB=90 , 3x=90°, x=30°,/ BOC=60 ）3• 65°, 115°（点拨：/ AOC/ BOD=25 , / AOE=90 - / AOC=90 -25° =65°）?4•图（1）量得PC<PD图（2）量得PC=PD5 •如图••••/ BOD=90 , / AOC=90 , / BOD/ AOC=180•••/ AOD=180 - / BOC 又T/ AOD=/ BOC••• 3/BOC=180 - / BOC：/ BOC=45解题技巧：本题扣住/ AOD=Z90°- / BOC这一关键式子.7 •如图所示.(1 )将A向下平移河宽长度得A';(2)连A'B交河岸于M(3)过M作MN L a,交河岸b于N, MN即为架桥处;(4)连AN 贝U AN+MN+B最短.。

一、选择题（每题3分，共15分）1. 在下列图形中，哪个图形是三线八角图形？A. 正方形B. 等边三角形C. 长方形D. 等腰梯形2. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形是：A. 正方形B. 等腰梯形C. 等腰直角三角形D. 长方形3. 在一个三线八角图形中，如果三个角分别是60°、60°、120°，那么这个图形是：A. 正方形B. 等腰梯形C. 等边三角形D. 长方形4. 下列关于三线八角图形的说法正确的是：A. 三线八角图形一定是等腰梯形B. 三线八角图形的三个角都是直角C. 三线八角图形一定是等腰梯形或正方形D. 三线八角图形的三个角都是锐角5. 一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的面积与一个等边三角形的面积之比是：A. 1:1B. 1:2C. 2:1D. 3:1二、填空题（每题5分，共25分）6. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形的面积是正方形面积的______。

7. 如果一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的边长是等边三角形边长的______。

8. 一个三线八角图形的三个角分别是45°、45°、90°，那么这个图形的周长是正方形周长的______。

9. 一个三线八角图形的三个角分别是60°、60°、120°，那么这个图形的面积是等边三角形面积的______。

10. 一个三线八角图形的三个角分别是30°、60°、90°，那么这个图形的周长是等边三角形周长的______。

三、解答题（每题10分，共20分）11. （1）画出一个三线八角图形，并标出三个角的大小。

七年级三线八角_练习题◆回顾归纳1．两条直线互相垂直，•其中的一条直线叫做另一条直线的_______，•交点叫做________．2．过一点有且只有_______与已知直线_______．3．连结直线外一点与直线上各点的所有线段中，________最短．4．直线外一点到这条直线的________的长度，叫做点到直线的距离．5．如直线AB，CD与EF相交，构成_______个角，其中∠1与∠5是_______，∠3与∠5是______，∠4与∠5是_______．◆课堂测控知识点一垂线垂线段1．CD⊥AB，则点D是_____，∠ADC=∠CDB=________．2．，l1⊥l2，垂足为_____，∠1与∠2是一组_____的邻补角，∠1•与______是一对_______的对顶角．3．（经典题），l1⊥l2，与直线L1垂直的直线是（）A．直线aB．直线L2C．直线a，bD．直线a，b，c4．，若∠ACB=90°，BC=8cm，•AC=•6cm，•则B•点到AC•边的距离为________．5．直线L外一点P到L的距离是________的长度．知识点二同位角内错角同旁内角6．的同位角有______对．7．下列说法不正确的是（）A．∠1与∠B是同位角B．∠1与∠4是内错角C．∠3与∠B是同旁内角D．∠C与∠A不是同旁内角8．∠1与∠2是哪两条直线被另一条直线所截，构成的是什么角的关系？∠3与∠D呢？◆课后测控1．直线AB，CD交于点O，OE⊥AB且∠DOE=40°，则∠COE=_____．2．AO⊥OB于点O，∠AOB：∠BOC=3：2，则∠AOC=_______．3．AB与CD交于点O，OE⊥CD，OF⊥AB，•∠BOD=•25•°，•则∠AOE=____，∠DOF=_____．4．（教材变式题）中∠1<∠2，中∠1=∠2．试用刻度量一量比较两PC，PD的'大小．5．分别过P画AB的垂线．6．（OA⊥OC，OB⊥OD，且∠AOD=3∠BOC，求∠BOC的度数．◆拓展创新7．（经典题）我国“十一五”规划其中一重要目标是，建设社会主义新农村，国家对农村公路建设投资近1000亿人民币．西部的某落后山村准备在河流M上架上一座桥梁，桥建在何处才能使A，B 两个村庄的之间修建路面最短？。

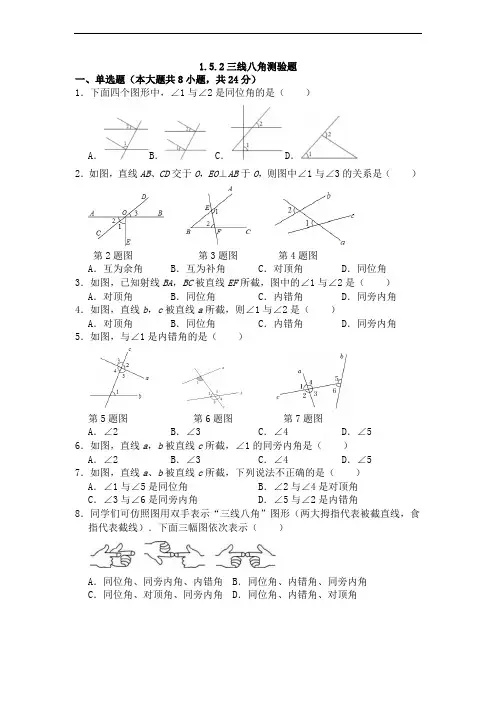
1.5.2三线八角测验题一、单选题（本大题共8小题，共24分）1．下面四个图形中，∠1与∠2是同位角的是（）A．B．C．D．2．如图，直线AB、CD交于O，EO⊥AB于O，则图中∠1与∠3的关系是（）第2题图第3题图第4题图A．互为余角B．互为补角C．对顶角D．同位角3．如图，已知射线BA，BC被直线EF所截，图中的∠1与∠2是（）A．对顶角B．同位角C．内错角D．同旁内角4．如图，直线b，c被直线a所截，则∠1与∠2是（）A．对顶角B．同位角C．内错角D．同旁内角5．如图，与∠1是内错角的是（）第5题图第6题图第7题图A．∠2 B．∠3 C．∠4 D．∠56．如图，直线a，b被直线c所截，∠1的同旁内角是（）A．∠2 B．∠3 C．∠4 D．∠57．如图，直线a、b被直线c所截，下列说法不正确的是（）A．∠1与∠5是同位角B．∠2与∠4是对顶角C．∠3与∠6是同旁内角D．∠5与∠2是内错角8．同学们可仿照图用双手表示“三线八角”图形（两大拇指代表被截直线，食指代表截线）．下面三幅图依次表示（）A．同位角、同旁内角、内错角B．同位角、内错角、同旁内角C．同位角、对顶角、同旁内角D．同位角、内错角、对顶角二、填空题（本小题共2题，每题3分，共6分）9．如图，直线a，b被c所截，则∠1与∠2是（填内错角，同位角或同旁内角）．第9题图第10题图10．如图，点D是BC上一点，∠C＝65°，则图中与∠C构成同旁内角的角有个，这些角的度数和为．三、解答题（本小题共9个大题，共70分）11．（6分）如图，直线EF交AB于G，交CD于M．（1）图中有多少对对顶角；（2）图中有多少对邻补角；（3）图中有多少对同位角；（4）图中有多少对同旁内角；（5）写出图中的内错角．12．（6分）如图所示，已知∠1＝115°，∠2＝65°，∠3＝100°．（1）图中所有角中（包含没有标数字的角），共有几对内错角？（2）求∠4的大小．13．（6分）分别指出下列图中的同位角、内错角、同旁内角．14．（6分）如图，已知∠A＝65°，∠1＝∠C．（1）在图中画出∠A的对顶角；（2）直接写出∠1的同位角；（3）直接写出∠C的同旁内角；（4）求∠B的度数．（要求写出推理过程及理由）15．（6分）如图，直线a、b被直线l所截，已知∠1＝40°，试求∠2的同位角及同旁内角的度数．16．（6分）如图，吴老师在黑板上画了一个图形，请你在这个图形中分别找出∠A的所有的同位角、内错角和同旁内角．17．（10分）如图，用数字标出的八个角中，同位角、内错角、同旁内角分别有哪些？请把它们一一写出来．18．（10分）如图所示．（1）指出与∠5为同位角的有哪些角，分别是哪两直线被哪一条直线所截形成的；（2）指出与∠2是同旁内角的有哪些角，分别是哪两直线被哪一条直线所截形成的？19．（10分）如图，按要求解答下列问题．（1）写出∠A的同位角和同旁内角；（2）写出∠4的内错角和同旁内角．。

介父从州今凶分市天水学校三线八角练习题1．：如图中，∠1与∠4是直线_____、______被直线_____所截得到_______; ∠2与∠3是直线_____、______被直线_____所截得到_______;2、上图中，∠1与∠4是直线_____、______被直线_____所截得到_______; ∠2与∠3是直线_____、______被直线_____所截得到_______;3、AC、BC被AB所截的同位角是___________、内错角是___________、同旁内角是___________________．4、图中，∠1与∠2是直线_____、______被直线_____所截得到_______; ∠1与∠4是直线_____、______被直线_____所截得到_______;∠1与∠3是直线_____、______被直线_____所截得到_______;5、如图1，∠1与∠2是直线_____、______被直线_____所截得到_______;如图2，∠1与∠4是直线_____、______被直线_____所截得到_______;如图3，∠1与∠3是直线_____、______被直线_____所截得到_______;6、如图，∠1与∠2是直线_____、______被直线_____所截得到_______;∠3与∠4是直线_____、______被直线_____所截得到_______;7、如图，∠1与∠2是直线_____、______被直线_____所截得到_______;∠3与∠4是直线_____、______被直线_____所截得到_______;8、如图，∠1与∠2是直线_____、______被直线_____所截得到_______;∠1与∠3是直线_____、______被直线_____所截得到_______;∠1与∠5是直线_____、______被直线_____所截得到_______;∠6与∠4是直线_____、______被直线_____所截得到_______;9、如图，∠1与∠2是直线_____、______被直线_____所截得到_______;∠3与∠4是直线_____、______被直线_____所截得到_______;∠1与∠4是直线_____、______被直线_____所截得到_______;∠3与∠2是直线_____、______被直线_____所截得到_______;10、如图∠BAD与∠CDA是直线____和____所截，构成的同旁内角；∠1和∠2是直线____和____被____所截构成的内错角；∠3和∠4是____和____被____所截构成的内错角；∠DCA与∠ABC是直线____和____被____所截，构成的同旁内角。

５．１．３㊀同位角㊁内错角㊁同旁内角㊀１．能解释同位角㊁内错角㊁同旁内角等概念的意义．２．会在图形中正确识别同位角㊁内错角㊁同旁内角．㊀开心预习梳理,轻松搞定基础.１．两条直线被第三条直线所截,可得到同位角㊁内错角和同旁内角．如图,图中共有４对同位角,它们分别是㊀㊀㊀㊀与㊀㊀㊀㊀㊁㊀㊀㊀㊀与㊀㊀㊀㊀㊁㊀㊀㊀㊀与㊀㊀㊀㊀㊁㊀㊀㊀㊀与㊀㊀㊀㊀;图中共有两对内错角,它们是㊀㊀㊀㊀与㊀㊀㊀㊀㊁㊀㊀㊀㊀与㊀㊀㊀㊀;图中共有两对同旁内角,它们是㊀㊀㊀㊀与㊀㊀㊀㊀㊁㊀㊀㊀㊀与㊀㊀㊀㊀．(第１题)㊀㊀㊀㊀(第２题)２．如图,ø１与ø２是直线㊀㊀㊀㊀㊁㊀㊀㊀㊀被直线㊀㊀㊀㊀所截得的㊀㊀㊀㊀角;ø２与ø３是直线㊀㊀㊀㊀㊁㊀㊀㊀㊀被直线㊀㊀㊀㊀所截得的㊀㊀㊀㊀角;ø１与ø４是直线㊀㊀㊀㊀㊁㊀㊀㊀㊀被直线㊀㊀㊀㊀所截得的㊀㊀㊀㊀角;ø３与ø４是直线㊀㊀㊀㊀㊁㊀㊀㊀㊀被直线㊀㊀㊀㊀所截得的㊀㊀㊀㊀角．㊀重难疑点,一网打尽.３．如图,ø１与ø２不是同位角的是(㊀㊀)．４．在如图所示的５个角中,ø１和ø３是㊀㊀㊀㊀角,ø１和ø４是㊀㊀㊀㊀角,ø２和ø５是㊀㊀㊀㊀角,ø１和ø５是㊀㊀㊀㊀角,ø３和ø４是㊀㊀㊀㊀角．(第４题)㊀㊀㊀㊀(第５题)５．如图,ø１的同位角为㊀㊀㊀㊀,ø３的内错角为㊀㊀㊀㊀,øC的同位角为㊀㊀㊀㊀,øA的同旁内角为㊀㊀㊀㊀㊀㊀㊀．同一平面内,两条直线不是相交就是平行．６．如图,ø１和ø２,ø３和ø４分别是哪两条直线被哪一条直线所截形成的?它们各是什么角?(第６题)㊀源于教材,宽于教材,举一反三显身手.７．如图,同位角有m 对,内错角有n 对,同旁内角有p 对,则m ＋n ＋p 的值是(㊀㊀)．A．８B ．１６C ．３２D．６４(第７题)㊀㊀㊀(第８题)㊀㊀㊀(第９题)８．如图,在ø１,ø２,ø３,ø４,ø５中,同位角的对数㊁内错角的对数㊁同旁内角的对数,正确的是(㊀㊀)．A．１,１,４B ．１,２,４C ．２,１,４D．１,１,５９．如图,内错角的对数是(㊀㊀)．A．２B ．４C ．６D．８１０．探究题:(１)如图(１),两条水平的直线被一条竖直的直线所截,同位角有㊀㊀㊀㊀对,内错角有㊀㊀㊀㊀对,同旁内角有㊀㊀㊀㊀对;(２)如图(２),三条水平的直线被一条竖直的直线所截,同位角有㊀㊀㊀㊀对,内错角有㊀㊀㊀㊀对,同旁内角有㊀㊀㊀㊀对;(３)如图(３),两条水平的直线被两条竖直的直线所截,同位角有㊀㊀㊀㊀对,内错角有㊀㊀㊀㊀对,同旁内角有㊀㊀㊀㊀对;(４)根据以上探究的规律写出:①四条水平的直线被一条竖直的直线所截,同位角有㊀㊀㊀㊀对,内错角有㊀㊀㊀㊀对,同旁内角有㊀㊀㊀㊀对;②三条水平的直线被两条竖直的直线所截,同位角有㊀㊀㊀㊀对,内错角有㊀㊀㊀㊀对,同旁内角有㊀㊀㊀㊀对．(第１０题)５．１．３㊀同位角㊁内错角㊁同旁内角１．ø１㊀ø３㊀ø５㊀ø７㊀ø２㊀ø４㊀ø６㊀ø８ø３㊀ø６㊀ø４㊀ø５㊀ø３㊀ø５㊀ø４㊀ø６２．略㊀３．C４．对顶㊀内错㊀同旁内㊀邻补㊀同位５．øA E G㊁øB㊀ø２㊀ø２㊀ø１㊁ø２㊁øC㊁øB ６．图(１):ø１和ø２是直线A B㊁C D被直线B D所截的内错角;ø３和ø４是直线A D㊁B C被直线B D所截的内错角．图(２):ø１和ø２是直线A B㊁C D被直线B C所截的同位角;ø３和ø４是直线A B㊁B C被直线A C所截的同旁内角．７．C㊀８．A㊀９．C１０．(１)４㊀２㊀２㊀(２)１２㊀６㊀６㊀(３)１６㊀８㊀８(４)①２４㊀１２㊀１２㊀②３６㊀１８㊀１８。

相交线B．有公共极点，且又相等的角为对顶角1．判断题（对的打“√” ，错的打“×” ）C．角的两边互为反向延伸线且有公共极点的两个角为对顶角（1）没有公共边的两个角是对顶角. （）D．有公共极点的两个角为对顶角.（2）有公共极点的两个角是对顶角. （）（ 2）以下说法正确的选项是（）（3）两条直线订交所成的四个角中，不相邻的两个角是对顶角.（）A．不是对顶角就不相等B．相等的角为对顶角（4）有公共极点且有一条公共边的两个角互为邻补角. （）C．不相等的角不是对顶角D．上陈述法都不对（5）对顶角的补角相等 . （）（ 3）以下各图中∠ 1 和∠ 2 为对顶角的是（）2．填空（ 1）对顶角的重要性质是.（2）一条直线与端点在这条直线上的一条射线构成的两个角是.（3）两个角互为邻补角，它们的均分线所成的角是度.（ 4）假如两个角的均分线订交成90°的角，那么这两个角是（）A．对顶角B．互补的两个角C．互为邻补角D．以上答案都不对5．已知直线AB、 CD订交于点 O，∠ AOC+∠ BOD=230°，求∠ BOC的度数 .（4）如图 2— 11，直线 AB、 CD、 EF 订交于点 O，则∠ AOC的对顶角6．如图 2— 14，已知直线 AB、 CD、 EF订交于点 O，∠ 1：∠ 2：∠ 3=2：3：4，求∠ 4的度数 .是，∠ AOD 的对顶角是，∠ BOC 的邻补角是和，∠ BOE的邻补角是和.3．如图 2— 12 直线 AB、CD、 EF 订交于点O，且∠ 1=∠ 2，试说明 OE是∠AOC的均分线 .4．选择题（ 1）以下说法正确的选项是（）A．有公共极点，且方向相反的两个角为对顶角17．如图 2— 15，已知直线 AB 、CD 订交于点 O ，OE 均分∠ BOD ，且∠ BOD=10°，求∠ AOC 的度数 .【素质优化训练】1．如图 2— 16，点 O 是直线 AB 上的一点， OC 、OD 是两条射线且分别在 AB 的双侧，∠ AOC=∠ BOD （ 1）求∠ COD 的度数；（ 2）∠ AOC 与∠ BOD 是对顶角吗？为何？一、判断（每题 1 分，共 10 分）1. 极点同样而且相等的两个角是对顶角.( )2. 订交直线构成的四个角中如有一个角是直角 , 就称这两条直线相互垂直.( )3. 直线外一点到这条直线的垂线段叫做这点到这条直线的距离 .( )4. 如图 1, ∠2和∠8 是对顶角 .( )5.如图 1,∠2和∠4 是同位角 .()859 16.如图 1,∠1和∠3是同位角 .()27. 如图 1, ∠ 9 和∠ 10 是同旁内角 , ∠1 和∠ 7 也是同旁内角.( )10 7 8. 如图 1, ∠2和∠10 是内错角 .( )6 439.O 是直线 AB 上一点 ,D 分别在 AB 的双侧 , 且∠ DOB=∠AOC,(1)则 C,O,D?三点在同一条直线上.( )M P 10. 如图 2, 此中共有 4 对同位角 ,4 对内错角 ,4 对同旁内 角 .()ADBC二、填空（每空1 分，共 29 分）NQ(2)11. 如图 3, 直线 L 截直线 a,b 所得的同位角有 ______对 , 它们ab是 ______;?内错角有 ___对 , 它们是 _____ _;6 54 1 同旁内角有 ______ 对 ,? 它们是 _____ _;? 对顶角l 783 2_____?对 ,? 它们是 _____ _.(3) PAM 512.如图 4,∠1的同位角是 ________, ∠ 1 的内错角是 463________, ∠ 1?的同旁内角是 _______.2BN1OQE (4)D13. 如图 5, 直线 AB,CD 订交于 O,OE 均分∠ AOD,FO ⊥OD 于 O,∠41=40°, 则∠ 2=?___ __,∠ 4=______.AB2O 114. 如图 6,AB ⊥CD 于 O,EF 为过点 O 的直线 ,MN 均分∠ AOC,F若∠ EON=100?° ,? 那么C∠ EOB=_____ , ∠ BOM=_____ .(5)15. 如图 7,AB 是向来线 ,OM 为∠ AOC 的角均分线 ,ON 为∠ BOC 的角均分线 ,则 OM,ON 的地点关系是 _______.16. 直线外一点与直线上各点连接的线段中, 以 _________为最短 .17. 从直线外一点到这条直线的 ____ ____ 叫做这点到直线的距离 .2CEMCABCNDBOMFNBAO AO D(6)(7)(8)18. 经过直线外或直线上一点 , 有且只有 ______直线与已知直线垂直 .19. 如图 8, 要证 BO ⊥ OD,请完美证明过程 , 并在括号内填上相应依照 : ∵ AO⊥ CO,∴∠ AOC=__________(___________). 又∵∠ COD=40° ( 已知 ), ∴∠ AOD=_______.?∵∠ BOC=∠ AOD=50° ( 已知 ), ∴∠ BOD=_______,∴ _______⊥ _______(__________).20. 如图 9, 直线 AB,CD 被 EF 所截 , ∠ 1=∠ 2, 要证∠ 2+∠ 4=180° , 请完美证明过程 ,? 并在括号内填上相应依照 . ∵直线 AB 与 EF 订交 , ∴∠ 1=∠3=(__________), 又∵∠ 1+?∠ 4=180° (___________), ∠ 1=∠ 2( 已知 ),∴∠ 2=∠ 3, ∠ 2+∠ 4=180° (____________________) 三、选择（每题 3 分，共 30 分）.21. 以下语句正确的选项是 ()A. 相等的角为对顶角B. 不相等的角必定不是对顶角C. 不是对顶角的角都不相等D. 有公共极点且和为 180°的两个角为邻补角22. 两条订交直线与此外一条直线在同一平面内 , 它们的交点个数是()A.1B.2C.3或 2 D.1或 2或323. 如图 10,PO ⊥ OR,OQ ⊥ PR,能表示点到直线 ( 或线段 ) 的距离的线段有 ( )A.1 条B.2 条C.3 条D.5 条PADCQOBO R(10)(11)A DBFCE(12)24. 如图 ,OA ⊥ OB,OC ⊥ OD,则()A. ∠ AOC=∠ AODB. ∠ AOD=∠ DOBC. ∠ AOC=∠ BODD. 以上结论都不对25. 以下说法正确的选项是 ()A. 在同一平面内 , 过已知直线外一点作这条直线的垂线有且只有一条B. 连接直线外一点和直线上任一点 , 使这条线段垂直于已知直线C. 作出点 P 到直线的距离D. 连接直线外一点和直线上任一点的线段长是点到直线的距离26. 如图 12, 与∠ C 是同旁内角的有 (). A.2B.3C.4D.527. 以下说法正确的选项是 ( ).3A. 两条直线订交成四个角 , 假如有三个角相等 , 那么这两条直线垂直 .B. 两条直线订交成四个角 , 假如有两个角相等 , 那么这两条直线垂直 .C. 两条直线订交成四个角, 假如有一对对顶角互余, 那么这两条直线垂直 .D. 两条直线订交成四个角 , 假如有两个角互补 , 那么这两条直线垂直 .28. 假如∠ 1 与∠ 2 互为补角 , 且∠ 1>∠ 2, 那么∠ 2 的余角是 () A.1( ∠1+∠2) B.1∠1 C.1( ∠1- ∠2) D.1∠ 2222229. 已知 OA ⊥ OC,∠ AOB:∠ AOC=2:3, 则∠ BOC 的度数是 ( )A.30 °B.150 °C.30 °或 150°D. 以上答案都不对以下图 中共有 30. 右图共有几对对顶角（）A.18 对B.16 对C.20对D.22 对AD四、作图题（ 4+3=7 分） 31、如图 , 按要求作出 :(1)AE ⊥ BC 于 E; (2)AF ⊥ CD 于 F;(3) 连接 BD,作 AG ⊥ BD 于 G.（1）（ 2）五、解答题 . （每题 6 分，共 24 分）33. 如 图 , 已 知 ∠ ABC=90° , ∠ 1= ∠ 2, ∠ DCA=∠ CAB, 求 证 :(1)CD ⊥ CB;(2)CD? 均分∠ ACE.ADB 21EC34. 如图 ,OE,OF 分别是∠ AOC 与∠BOC 的均分线 , 且 OE ⊥ OF,求证 :A,O,B? 三点在同向来线上 .C32、以下左图， 一辆汽车在直线形的公路ABBC上 由EFA 向B 行驶， M 、 N 分别是位于公路 AB 双侧的乡村，（ 1）此刻公路 AB 上修 建一个商场C ，使获得 M 、 N 两乡村距离最短，请在图中画出点C（ 2）设汽车行驶到点 P 地点时离乡村 M 近来；行驶到点 Q 地点时，距离乡村N 近来，请在图中公路 AB 上分别画出 P 、 Q 两点的地点。

三线八角1.如图所示,直线a,b被直线c所截,∠1与∠2是( )A. 同位角B. 内错角C. 同旁内角D. 邻补角2.如图,属于内错角的是（）A. ∠1和∠2B. ∠2和∠3C. ∠1和∠4D. ∠3和∠43.下列图形中，与不是同位角的是（）A. B. C. D.4.如图,下列说法错误的是( )A. ∠A与∠EDC是同位角B. ∠A与∠ABF是内错角C. ∠A与∠ADC是同旁内角D. ∠A与∠C是同旁内角5.如图,按各组角的位置判断错误的是( )A. ∠1与∠A是同旁内角B. ∠3与∠4是内错角C. ∠5与∠6是同旁内角D. ∠2与∠5是同位角6.观察图，并完成下面的填空：(1)∠1与______是同位角；(2)∠2与______是内错角；(3)∠5与______是同旁内角。

7.如图：∠6的同位角是______，∠1的内错角是______.8.如图填空。

(1)若ED，BC被AB所截，则∠1与______是同位角。

(2)若ED，BC被AF所截，则∠3与______是内错角。

(3)∠1与∠3是AB和AF被______所截构成的______角。

(4)∠2与∠4是______和______被BC所截构成的______角。

9.如图，直线AB，CD与直线EF分别交于点O，P.(1)写出∠1的同位角，∠2的同旁内角和内错角；(2)假设图形里面同位角的对数为a，同旁内角的对数为b，内错角的对数为c，则a+b+c=___；(3)如果要知道图中8个角的度数，条件中至少应给出几个角的度数?10.如图，下列说法错误的是（）A. ∠A与∠B是同旁内角B. ∠3与∠1是同旁内角C. ∠2与∠3是内错角D. ∠1与∠2是同位角11.如图，下列判断正确的是（）A. 4对同位角，4对内错角，4对同旁内角B. 4对同位角，4对内错角，2对同旁内角C. 6对同位角，4对内错角，4对同旁内角D. 6对同位角，4对内错角，2对同旁内角12.如图，有下列说法：①能与∠EDF构成内错角的角有2个；②能与∠BFD构成同位角的角有2个；③若∠EDF+∠DFB=180∘，则∠DEA=∠B；④能与∠C构成同旁内角的角有4个。

三线八角练习题一、选择题1. 在平面几何中，两条直线相交，形成的角叫做：A. 邻角B. 对顶角C. 同位角D. 内错角2. 如果两条直线被第三条直线所截，那么同位角的特点是：A. 相等B. 不等C. 互补D. 互余3. 对顶角的性质是：A. 相等B. 不等C. 互补D. 互余4. 三线八角中，内错角的特点是：A. 相等B. 不等C. 互补D. 互余5. 当两条平行线被第三条直线所截时，同旁内角的特点是：A. 相等B. 不等C. 互补D. 互余二、填空题6. 当两条直线相交时，形成的角中，不相邻的两个角叫做________。

7. 如果两条直线相交，它们的对顶角具有________的性质。

8. 当两条平行线被第三条直线所截时，同位角具有________的特点。

9. 在三线八角中，内错角是指两条直线被第三条直线所截时，位于截线同侧的两个角，它们具有________的特点。

10. 同旁内角是指两条平行线被第三条直线所截时，位于截线同侧的两个角，它们具有________的特点。

三、判断题11. 两条平行线被第三条直线所截，同旁内角互补。

（）12. 两条直线相交，形成的角中，相邻的两个角叫做邻角。

（）13. 对顶角一定相等。

（）14. 同位角一定相等。

（）15. 内错角一定相等。

（）四、简答题16. 请解释什么是三线八角，并说明它们在几何中的重要性。

17. 描述两条平行线被第三条直线所截时，各对角之间的关系。

18. 举例说明对顶角和内错角在实际问题中的应用。

五、计算题19. 如图所示，直线AB和CD相交于点O，已知∠AOC=40°，求∠AOD 的度数。

20. 若两条平行线被第三条直线所截，且同位角的度数为60°，求内错角的度数。

六、证明题21. 证明：如果两条直线平行，那么它们被第三条直线所截时，同旁内角互补。

22. 证明：两条直线相交，形成的对顶角一定相等。

七、应用题23. 在一个平面直角坐标系中，点A(-3,4)，点B(-3,-2)，点C(1,-2)在同一直线上，点D(1,4)，求证∠BAC和∠BDC是对顶角。

人教版七年级数学下册《识别三线八角》专项练习题-附含答案【模型讲解】如图已知直线a b被直线c d所截直线a c d相交于点O按要求完成下列各小题．(1)在图中的∠1～∠9这9个角中同位角共有多少对？请你全部写出来；(2)∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？【分析】根据同位角、内错角和同旁内角的特征（同位角形如“F” 内错角形如“Z” 同旁内角形如“U”）判断即可.【详解】解：(1)如题图所示：同位角共有5对：分别是∠1和∠5 ∠2和∠3 ∠3和∠7 ∠4和∠6 ∠4和∠9；(2)由三线八角的判断方法∠4和∠5是由c b d三线组成并且构成“U”形图案所以∠4和∠5是同旁内角同理可得：∠6和∠8也是同旁内角故∠6和∠8之间的位置关系与∠4和∠5的相同．【模型演练】1．如图同位角共有（）对．A．6B．5C．8D．7【答案】A【分析】根据同位角的概念解答即可．【详解】解：同位角有6对∠4与∠7 ∠3与∠8 ∠1与∠7 ∠5与∠6 ∠2与∠9 ∠1与∠3故选：A．【点睛】此题考查同位角关键是根据同位角解答．2．如图下列判断中正确的个数是（）（1）∠A 与∠1是同位角；（2）∠A 和∠B 是同旁内角；（3）∠4和∠1是内错角；（4）∠3和∠1是同位角．A ．1个B ．2个C ．3个D ．4个 【答案】C【分析】准确识别同位角、内错角、同旁内角的关键 是弄清哪两条直线被哪一条线所截．也就是说 在辨别这些角之前 要弄清哪一条直线是截线 哪两条直线是被截线．【详解】解：（1）∠A 与∠1是同位角 正确 符合题意；（2）∠A 与∠B 是同旁内角．正确 符合题意；（3）∠4与∠1是内错角 正确 符合题意；（4）∠1与∠3不是同位角 错误 不符合题意．故选：C ．【点睛】此题主要考查了三线八角 在复杂的图形中识别同位角、内错角、同旁内角时 应当沿着角的边将图形补全 或者把多余的线暂时略去 找到三线八角的基本图形 进而确定这两个角的位置关系．3．如图 B ∠的内错角是（ ）A ．1∠B ．2∠C ．3∠D ．4∠【答案】A【分析】根据内错角的定义判断即可；【详解】解：A 、B ∠的内错角是1∠ 故此选项符合题意；B 、B ∠与2∠是同旁内角 故此选项不合题意；C 、B ∠与3∠是同位角 故此选项不合题意；D 、B ∠与4∠不是内错角 故此选项不合题意；答案：A．【点睛】本题主要考查了内错角的判定准确分析判断是解题的关键．4．下列所示的四个图形中∠1和∠2是同位角的是（）A．②③B．①②③C．①②④D．①④【答案】C【分析】根据同位角的定义逐一判断即得答案．【详解】图①中的∠1与∠2是同位角图②中的∠1与∠2是同位角图③中的∠1与∠2不是同位角图④中的∠1与∠2是同位角所以在如图所示的四个图形中图①②④中的∠1和∠2是同位角．故选：C．【点睛】本题考查了同位角的定义属于基础概念题型熟知概念是关键．5．如图所示下列说法不正确的是（）A．∠1和∠2是同旁内角B．∠1和∠3是对顶角C．∠3和∠4是同位角D．∠1和∠4是内错角【答案】A【分析】根据对顶角、邻补角、同位角、内错角定义判断即可．【详解】A. ∠1和∠2是邻补角故此选项错误；B. ∠1和∠3是对顶角此选项正确；C. ∠3和∠4是同位角此选项正确；D. ∠1和∠4是内错角 此选项正确；故选A.【点睛】此题考查对顶角 邻补角 同位角 内错角 同旁内角 解题关键在于掌握各性质定义.6．如图 有下列说法：其中结论正确的是（ ）①若//DE AB 则180DEF EFB ∠+∠=︒；②能与EDC ∠构成内错角的角的个数有1个③能与DEC ∠构成同位角的角的个数有2个；④能与B ∠构成同旁内角的角的个数有4个A ．①B ．①④C ．①②④D ．①③④ 【答案】B【分析】根据平行线的性质、同位角、内错角、同旁内角的定义解答即可．【详解】解：①若DE ∠AB 则∠DEF +∠EFB =180° 故①正确；②能与∠EDC 构成内错角的角的个数有2个 只有∠DEF 和∠DEA 故②错误；③能与∠DEC 构成同位角的角的个数有1个 只有∠A 故③错误；④能与∠B 构成同旁内角的角的个数有4个 分别为∠BDE 、∠BFE 、∠A 、∠C 故④正确． 故选B ．【点睛】本题主要考查了同位角、内错角、同旁内角及平行线的性质 正确理解同位角、内错角、同旁内角的定义是解答本题的关键．7．如图 直线AD BE 被直线BF 和AC 所截 则∠1的同位角和∠5的内错角分别是（ ）A．∠4 ∠2B．∠2 ∠6C．∠5 ∠4D．∠2 ∠4【答案】B【分析】同位角：两条直线a b被第三条直线c所截（或说a b相交c）在截线c的同旁被截两直线a b的同一侧的角我们把这样的两个角称为同位角；内错角：两条直线被第三条直线所截两个角分别在截线的两侧且夹在两条被截直线之间具有这样位置关系的一对角叫做内错角．根据此定义即可得出答案．【详解】解：∠直线AD BE被直线BF和AC所截∠∠1与∠2是同位角∠5与∠6是内错角故选：B．【点睛】本题考查的知识点是同位角和内错角的概念解题的关键是熟记内错角和同位角的定义．8．已知图（1）—（4）：在上述四个图中∠1与∠2是同位角的有（）.A．（1）（2）（3）（4）B．（1）（2）（3）C．（1）（3）D．（1）【答案】C【分析】根据同位角的定义；两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线（截线）的同旁则这样一对角叫做同位角进行判断即可．【详解】图①③中∠1与∠2是同位角；故选C．【点睛】此题主要考查了同位角关键是掌握同位角的边构成“F“形．9．如图直线AD、BC被直线AC所截则∠1和∠2是().A．内错角B．同位角C．同旁内角D．对顶角【答案】A【分析】根据三线八角的概念以及内错角的定义作答即可．【详解】如图所示∠1和∠2两个角都在两被截直线(直线b和直线a)异侧并且在第三条直线c（截线）的两旁故∠1和∠2是直线b、a被c所截而成的内错角．故选A．【点睛】本题考查了同位角、内错角、同旁内角的定义．在截线的同旁找同位角和同旁内角在截线的两旁找内错角．要结合图形熟记同位角、内错角、同旁内角的位置特点比较它们的区别与联系．两条直线被第三条直线所截所形成的八个角中有四对同位角两对内错角两对同旁内角．10．如图下列判断正确的是（）A．∠2与∠5是对顶角B．∠2与∠4是同位角C．∠3与∠6是同位角D．∠5与∠3是内错角【答案】A【分析】根据对顶角、同位角、同旁内角、内错角的定义分别进行分析即可．【详解】解：A、∠2与∠5是对顶角故此选项正确；B、∠2与∠4是不是同位角故此选项错误；C、∠3与∠6是同旁内角故此选项错误；D、∠5与∠3不是内错角故此选项错误；故选A．【点睛】本题考查同位角、内错角、同旁内角；对顶角、邻补角．第II卷（非选择题）请点击修改第II卷的文字说明二、填空题11．（1）如图：①所示两条水平的直线被一条倾斜的直线所截同位角有____________对内错角有__________对同旁内角有___________对；（2）如图②所示三条水平的直线被一条倾斜的直线所截同位角有_____________对内错角有__________对同旁内角有_____________对；（3）根据以上探究的结果n（n为大于1的整数）条水平直线被一条倾斜的直线所截同位角有___________对内错角有___________对同旁内角有___________对（用含n的式子表示）．根据以上探究的结果n（n为大于1的整数）条水平直线被一条竖直直线所截同位角有2n(n-1)对内错角有n(n-1)对同旁内角有n(n-1)对故答案为：2n(n-1) n(n-1) n(n-1)．【点睛】本题考查了同位角、内错角、同旁内角解答此类题确定三线八角是关键可直接从截线入手．对平面几何中概念的理解一定要紧扣概念中的关键词语要做到对它们正确理解对不同的几何语言的表达要注意理解它们所包含的意义．12．如图∠1和∠3是直线______ 和______ 被直线______ 所截而成的______ 角；图中与∠2是同旁内角的角有______ 个．【答案】AB AC DE内错3【分析】根据内错角和同旁内角的定义得出即可．【详解】解：∠1和∠3是直线AB和AC被直线DE所截而成的内错角；图中与∠2是同旁内角的角有∠6、∠5、∠7 共3个.故答案为AB；AC；DE；内错；3．【点睛】此题考查同位角、内错角、同旁内角等知识点能根据图形找出各对角是解题的关键.根据内错角和同旁内角的定义得出即可.13．如图AB、DC被BD所截得的内错角是___________ AB、CD被AC所截是的内错角是_________ AD、BC被BD所截得的内错角是_________ AD、BC被AC所截得的内错角是_____________.【答案】∠1和∠5 ∠4和∠8 ∠6和∠2 ∠3和∠7【分析】根据内错角（两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的两旁则这样一对角叫做内错角）的定义即可得.【详解】解：AB、DC被BD所截得的内错角是∠1和∠5 AB、CD被AC所截是的内错角是∠4和∠8 AD、BC被BD所截得的内错角是∠6和∠2 AD、BC被AC所截得的内错角是∠3和∠7.故答案为：∠1和∠5 ∠4和∠8 ∠6和∠2 ∠3和∠7.14．如图直线l截直线a b所得的同位角有__对它们是___；内错角有___对它们是___；同旁内角有___对 它们是___；对顶角___对 它们是___．【答案】 4 6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠ 2 4∠与8∠ 3∠与5∠ 2 4∠与5∠ 3∠与8∠ 4 1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠【分析】根据对顶角的定义 内错角的定义 同旁内角的定义 同位角的定义解答即可．【详解】直线l 截直线a b 所得的同位角有4对 分别是6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠；内错角有2对 它们是4∠与8∠ 3∠与5∠；同旁内角有2对 它们是4∠与5∠ 3∠与8∠；对顶角有4对 它们是1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠．故答案为：4；6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠；2；4∠与8∠ 3∠与5∠；2；4∠与5∠ 3∠与8∠；4；1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠【点睛】此题考查两直线相交所成的角 对顶角的定义 内错角的定义 同旁内角的定义 同位角的定义 熟记各定义是解题的关键．15．如图 射线DE 、DC 被直线AB 所截得的用数字表示的角中 ∠4与 ___ 是同位角 ∠4与 ___ 是内错角 ∠4与 ___ 是同旁内角．【答案】 ∠1 ∠2 ∠5、∠3【分析】根据同位角 内错角和同旁内角的定义解答即可.【详解】解：如图 射线DE 、DC 被直线AB 所截得的用数字表示的角中 ∠4与∠1是同位角 ∠4与∠2是内错角 ∠4与∠5、∠3是同旁内角．故答案为∠1 ∠2 ∠5、∠3．【点睛】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键 可直接从截线入手．对平面几何中概念的理解一定要紧扣概念中的关键词语要做到对它们正确理解对不同的几何语言的表达要注意理解它们所包含的意义．16．如图标有角号的7个角中共有_____对内错角___对同位角____对同旁内角．【答案】 4 2 4.【分析】根据内错角同位角及同旁内角的定义即可求得此题．【详解】解：如图共有4对内错角：分别是∠1和∠4 ∠2和∠5 ∠6和∠1 ∠5和∠7；2对同位角：分别是∠7和∠1 ∠5和∠6；4对同旁内角：分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2．故答案为(1). 4 (2). 2 (3). 4.【点睛】本题考查内错角同位角同旁内角的定义解题关键是熟练掌握定义．三、解答题17．如图∠1、∠2、∠3、∠4、∠5中哪些是同位角？哪些是内错角？哪些是同旁内角？【答案】同位角有∠1和∠5；∠4和∠3；内错角有∠2和∠3；∠1和∠4；同旁内角有∠3和∠5；∠4和∠5；∠4和∠2．【分析】同位角：两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线（截线）的同旁则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的两旁则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的同旁则这样一对角叫做同旁内角．依此即可得出答案．【详解】解：∠∠1和∠5在截线AC同侧在被截直线BE CE同方向所成的角；∠4和∠3 在截线CE的上方被截直线DB、EB的左侧∠同位角有∠1和∠5；∠4和∠3 共2对；∠∠2和∠3在截线BD两侧被截直线AC与CE内部；∠1和∠4在截线BE两侧被截直线AC与CE 内部∠内错角有∠2和∠3；∠1和∠4 共2对；∠∠3和∠5在截线CD同侧被截直线CB与DB内部；∠4和∠5在截线CE同侧被截直线CB与EB 的内部；∠4和∠2在截线BE同侧被截直线DB与DE的内部∠同旁内角有∠3和∠5；∠4和∠5；∠4和∠2 共3对.【点睛】本题考查了同位角、内错角、同旁内角三线八角中的某两个角是不是同位角、内错角或同旁内角完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时应从角的两边入手具有上述关系的角必有两边在同一直线上此直线即为截线而另外不在同一直线上的两边它们所在的直线即为被截的线．同位角的边构成“F“形内错角的边构成“Z“形同旁内角的边构成“U”形．18．如图已知AC与EH交于点B BF与AC交于点D．问图中同位角和对顶角各有几对？并具体写出各对同位角和对顶角．【答案】同位角有7对具体见解析；对顶角有4对具体见解析【分析】根据同位角和对顶角的定义解答．【详解】同位角有7对 分别为：A ∠与HBC ∠ A ∠与FBC ∠ A ∠与GDB ∠ FBC ∠与FDG ∠ FBH ∠与FDG ∠ ABD ∠与ADF ∠ EBD ∠与ADF ∠；对顶角有4对 分别为：EBC ∠与ABH ∠ ABE ∠与HBC ∠ ADB ∠与FDG ∠ ADF ∠与GDB ∠． 【点睛】此题考查同位角和对顶角的定义 熟记定义是解题的关键．19．如图所示．①∠AED 和∠ABC 可看成是直线__________、__________被直线__________所截得的__________角； ②∠EDB 和∠DBC 可看成是直线__________、__________被直线__________所截得的__________角； ③∠EDC 和∠C 可看成是直线__________、__________被直线__________所截得的__________角．【答案】ED ；BC ；AB ；同位；ED ；BC ；BD ；内错；ED ；BC ；AC ；同旁内【详解】解：（1）∠AED 和∠ABC 可看成是直线ED 、BC 被直线AB 所截得的同位角；（2）∠EDB 和∠DBC 可看成是直线ED 、BC 被直线BD 所截得的内错角；（3）∠EDC 和∠C 可看成是直线ED 、BC 被直线AC 所截得的同旁内角．故答案为ED BC AB 同位；ED BC BD 内错；ED BC AC 同旁内．点睛：本题考查了同位角、内错角、同旁内角．两条直线被第三条直线所截形成的角中 若两个角都在两直线的同侧 并且在第三条直线（截线）的同旁 则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中 若两个角都在两直线的之间 并且在第三条直线（截线）的两旁 则这样一对角叫做内错角；两条直线被第三条直线所截形成的角中 若两个角都在两直线的之间 并且在第三条直线（截线）的同旁 则这样一对角叫做同旁内角．20．如图：（1）写出图中EDM ∠的同位角： ；（2）如果AB ∠CD 那么图中与FHC ∠相等的角有 个（FHC ∠除外）；（3）当EDM ∠=∠ 时 AB ∠CD 理由： ；（4）如果A ∠与ABD ∠互补 那么E ∠与F ∠有什么关系？说明理由．【答案】（1）EHM ∠ ACM ∠；（2）3；（3）ABD 内错角相等 两直线平行；（4）E F ∠=∠ 理由见解析．【分析】（1）根据同位角的定义即可求解； （2）先根据AB ∥CD 得到=FHC FGA ∠∠ 再根据对顶角相等得到∠FHC =∠DHE =∠FGA =∠EGB 即可求解；（3）根据内错角相等 两直线平行；确定EDM ∠的内错角即可求解；（4）根据A ∠与ABD ∠互补 得到AF ∥DE 即可得到E F ∠=∠．【详解】解：（1）因为直线EF 和ED 被直线CM 所截所以EDM ∠的同位角是EHM ∠因为直线AC 和ED 被直线CM 所截所以EDM ∠的同位角是ACM ∠故答案为：EHM ∠ ACM ∠；（2）∠AB ∥CD∠=FHC FGA ∠∠∠∠FHC 和∠DHE 互为对顶角 ∠FGA 和∠EGB 互为对顶角∠∠FHC =∠DHE =∠FGA =∠EGB故答案为：3；（3）当EDM ∠=∠ABD 时 AB ∥CD 理由：内错角相等 两直线平行；故答案为：ABD 内错角相等 两直线平行；（4）E F ∠=∠ 理由如下：因为A ∠与ABD ∠互补 （已知）所以AF ∥DE （同旁内角互补 两直线平行）所以E F ∠=∠．（两直线平行 内错角相等）【点睛】本题考查了平行线的性质与判定 对顶角相等等知识 熟知相关知识点并能结合图形灵活应用是解题关键．21．如图找出标注角中的同位角、内错角和同旁内角．【答案】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8 ∠1与∠7．【分析】根据同位角：两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线(截线)的同旁则这样一对角叫做同位角；内错角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线(截线)的两旁则这样一对角叫做内错角；同旁内角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线(截线)的同旁则这样一对角叫做同旁内角结合图形进行分析即可．【详解】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8 ∠1与∠7．【点睛】本题主要考查了三线八角解题关键是掌握同位角的边构成“F”形内错角的边构成“Z”形同旁内角的边构成“U”形．22．如图BE是AB的延长线指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE．【答案】见解析【详解】试题分析：（1）（2）同旁内角 “同旁”指在第三条直线的同侧；“内”指在被截两条直线之间．（3）内错角 “内”指在被截两条直线之间；“错”即交错 在第三条直线的两侧．（一个角在第三直线左侧 另一角在第三直线右侧）试题解析：（1）∠A 和∠D 是由直线AE 、CD 被直线AD 所截形成的 它们是同旁内角；（2）∠A 和∠CBA 是由直线AD 、BC 被直线AE 所截形成的 它们是同旁内角；（3）∠C 和∠CBE 是由直线CD 、AE 被直线BC 所截形成的 它们是内错角．23．已知：如图是一个跳棋棋盘 其游戏规则是一个棋子从某一个起始角开始 经过若干步跳动以后 到达终点角跳动时 每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置1∠跳到终点位置3∠有两种不同路径 路径1：193∠−−−−→∠−−−→∠同旁内角内错角；路径2：1126103∠−−−→∠−−−→∠−−−→∠−−−−→∠内错角内错角同位角同旁内角.试一试：（1）写出从起始位置1∠跳到终点位置8∠的一种路径；（2）从起始位置1∠依次按同位角、内错角、同旁内角的顺序跳 能否跳到终点位置8∠？ 【答案】（1）1128∠→∠→∠内错角同旁内角（答案不唯一）；（2）能跳到终点位置8∠.其路径为1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一） 【分析】（1）根据同旁内角、内错角和同位角的定义进行选择路径即可；（2）先判断能够到达终点位置 在根据定义给出具体路径即可.【详解】（1）可以是这样的路径：1128∠→∠→∠内错角同旁内角.（答案不唯一）（2）从起始位置1∠依次按同位角内错角同旁内角的顺序跳 能跳到终点位置8∠.其路径为 1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一）. 【点睛】本题考查的是同位角、内错角和同旁内角的定义 熟知这些角的特征是解题的关键.。

7.2.1 对顶角和三线八角基础训练1.如图所示,∠1与∠2是对顶角的是( )2.如图所示,与∠1是同位角的是( )A.∠2B.∠3C.∠4D.∠53.图中是对顶角量角器,用它测量角的原理是_________.4.如图所示,∠1和∠3是直线_________,_________被直线_________所截构成的内错角,∠2和∠4是直线AC,BC被直线AB所截构成的_________角.5.如图,直线AB,CD,EF相交于点O.(1)请你分别找出∠AOC,∠AOE,∠COE的对顶角;(2)如果∠AOC=40°,那么∠BOD,∠BOC的度数分别是多少?培优提升1.如图所示,直线a、b被直线c所截,∠1与∠2是( )A.同位角B.内错角C.同旁内角D.邻补角2.下列说法正确的是( )A.如果两个角相等,那么这两个角是对顶角B.有公共顶点并且相等的两个角是对顶角C.如果两个角不相等,那么这两个角一定不是对顶角D.以上说法都不对3.如图,下列说法错误的是( )A.∠A与∠C是同旁内角B.∠1与∠3是同位角C.∠2与∠3是内错角D.∠3与∠B是同旁内角4.如图,三条直线AB,CD,EF相交于点O,则∠AOE+∠DOB+∠COF等于( )A.150°B.180°C.210°D.120°5.如图,与∠B互为同旁内角的角分别是__________.6.如图,已知a,b,c三条直线两两相交,∠1=2∠3,∠1+∠3=150°,则∠1+∠2+∠3=__________.7.如图,找出图中∠1的同位角、内错角、同旁内角.8.如图,已知直线AB,CD,MN相交于点O,∠1=22°,∠2=46°,求∠3的度数.9.如图,直线AB,CD相交于点O,由点O引射线OG,OE,OF,使OC平分∠EOG,∠AOG=∠EOF.如果∠BOD=62°,求∠FOC的度数.10.如图,当光线从空气中射入水中时,光线的传播方向会发生改变,在物理学中这种现象叫做光的折射,若∠1=43°,∠2=27°,则光的传播方向改变了多少度?参考答案【基础训练】1.【答案】B2.【答案】D3.【答案】对顶角相等4.【答案】AD;BC;AC;同旁内5.解:(1)∠AOC,∠AOE,∠COE的对顶角分别是∠BOD,∠BOF,∠DOF.(2)根据对顶角相等可知∠BOD=∠AOC=40°.根据邻补角的定义可知∠BOC+∠AOC=180°,所以∠BOC=180°-∠AOC=180°-40°=140°.【培优提升】1.【答案】A2.【答案】C解：对顶角相等,但相等的角不一定是对顶角.3.【答案】B解：∠1与∠3是同旁内角,不是同位角.4.【答案】B解：由对顶角的性质得∠AOC=∠DOB,所以∠AOE+∠DOB+∠COF=∠AOE+∠AOC+∠CO F=180°. 5.【答案】∠BAC,∠BAE,∠C解：BC和AC被AB所截,∠B与∠BAC是同旁内角;BC和DE被AB所截,∠B与∠BAE是同旁内角,AB和AC被BC所截,∠B与∠C是同旁内角,故与∠B互为同旁内角的角共有3个.6.【答案】240°解：因为∠1=2∠3,∠1+∠3=150°,∠2=∠3(对顶角相等),所以∠1+∠2+∠3=2∠3+∠3+∠3=4∠3,2∠3+∠3=150°(等量代换).所以∠3=60°.所以∠1+∠2+∠3=4∠3=240°.7.解:∠1的同位角是∠3和∠6.∠1的内错角是∠4和∠7.∠1的同旁内角是∠2和∠5.分析：能构成同位角、内错角、同旁内角的基本图形是两条直线被第三条直线所截.8.解:由题图可知∠DON=∠2=46°(对顶角相等).因为∠3+∠DON+∠1=180°(平角的定义),所以∠3=180°-∠DON-∠1=112°.分析：由题图可知∠DON与∠1和∠3构成一个平角,利用这一关系即可求解.9.解:因为OC平分∠EOG,所以∠1=∠2.因为∠AOG=∠FOE,所以∠FOE+∠1=∠AOG+∠2,即∠FOC=∠AOC.又因为∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD,所以∠FOC=∠BOD=62°.分析：解题的关键是抓住题目中一明一暗的两条角平分线,一明是指OC平分∠EOG,一暗是指能推出OC平分∠AOF,然后结合∠AOC与∠BOD是对顶角即可求解.10.解:由题意可知,∠DFB=∠1(对顶角相等).又因为∠1=43°(已知),所以∠DFB=43°(等量代换).所以∠DFB-∠2=43°-27°=16°,即光的传播方向改变了16°.。

三线八角和平行线定义【例题讲解】1、如图所示 ,∠ 1 和∠ 2 是对顶角的图形有()12112221A.1 个B.2 个C.3 个D.4 个2、图，直线 a,b 相交， 1 45 ，求2, 3, 4 的度数。

【轻松试一试】已知，如图，AOC 35 , COF 80 ，求：AOD和DOF 的度数【例题讲解】1、如图，直线AB、CD、 EF 相交于点O，AOE 的对顶角是，COF的邻补角是若AOC：AOE =2：3，EOD 130 ，则BOC =【轻松试一试】如图，直线AB、 CD相交于点 O，COE FOB 90 , AOC 30 则EOF余角、补角的应用（互为邻补角的两个角平分线_________ ）【例题讲解】AC为一直线， O是 AC上一点，且∠AOB=120°， OE、 OF分别平分∠ AOB、∠ BOC。

E BFA CO（1）求∠ EOF的大小（2）当 OB绕 O点旋转 OE、OF仍为∠ AOB和∠ BOC的角平分线，问 OE、 OF有怎样的位置关系？【轻松试一试】（邻补角在折叠问题中的应用）将一张长方形纸片按如图的方式折叠，BC、BD为折痕，试判断∠CBD的度数是多少？二、垂线及其性质（重点）（一）垂线的定义：当两条直线相交的四个角中，有一个角是直角时，就说这两条直线是互相垂直的，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

如图，直线 AB 、 CD 互相垂直，记作AB CD ，垂足为O。

1、如遇到线段与线段、线段与射线、射线与射线、线段或射线与直线垂直，特指它们所在的直线互相垂直。

C2、掌握如下的推理过程：（如上图）已知），AB CD (AOCCOBBOD AOD 90 (垂直定义）.A OB 反之，AOC 90 (已知）D AB CD (垂直定义）（二）垂线的画法性质 1过一点有且只有一条直线与已知直线垂直。

性质 2连接直线外一点与直线上各点的所有线段中，垂线段最短。