数独第一课(1)

第一课数独、九宫格数独、九宫格、三宫格
为了不让大家被这些概念搞混了头脑，还是简单说一下各名称的起源吧。

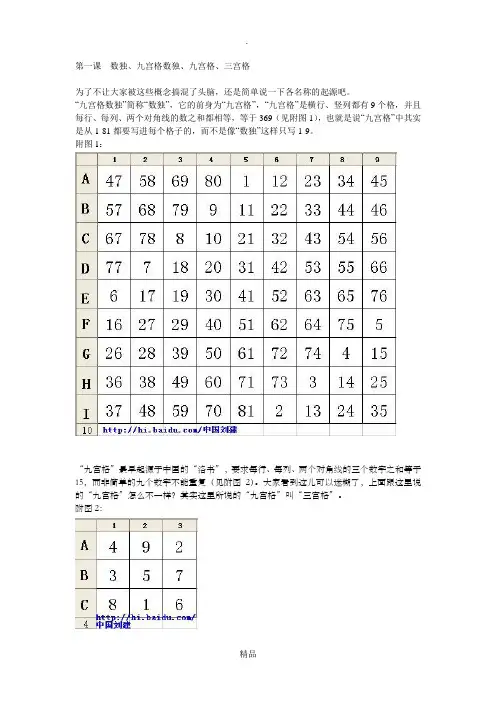
“九宫格数独”简称“数独”，它的前身为“九宫格”，“九宫格”是横行、竖列都有9个格，并且每行、每列、两个对角线的数之和都相等，等于369（见附图1），也就是说“九宫格”中其实是从1-81都要写进每个格子的，而不是像“数独”这样只写1-9。

附图1：
“九宫格”最早起源于中国的“洛书”，要求每行、每列、两个对角线的三个数字之和等于15，而非简单的九个数字不能重复（见附图2）。

大家看到这儿可以迷糊了，上面跟这里说的“九宫格”怎么不一样？其实这里所说的“九宫格”叫“三宫格”。

附图2：
上面所说的三宫格，中间一小格称为“中宫”，上面三格称为“上三宫”，下面三格称为“下三宫”，左右两格分别称为“左宫”和“右宫”（见附图3）。

附图3：
大家看到了，不管是“九宫格”还是“三宫格”，数字的填写方法是固定的。

而“数独”则不同，共有6,670,903,752,021,072,936,960（约有6.67×10的21次方）种组合，如果不计算重复（如数字交换、对称等）的，那么有5,472,730,538个组合。

如有侵权请联系告知删除，感谢你们的配合！。

风靡全球的数独游戏教学内容：数独的由来及基本解法教学目标：1、了解数独的历史发展过程2、让学生掌握基本的解数独的方法3、通过数独数学史的介绍，让学生感受数学文化的独特魅力。

教学重点；让学生掌握基本的解数独的方法教学过程：一、介绍数独的历史由来。

“数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。

概括来说，它就是一种填数字游戏。

但这一概念最初并非来自日本，而是源自拉丁方块，它是十八世纪的瑞士数学家欧拉发明的。

出生于1707年的欧拉被誉为有史以来最伟大的数学家之一。

欧拉从小就是一个数学天才，大学时他在神学院里攻读古希伯来文，但却连续13次获得巴黎科学院的科学竞赛的大奖。

1783年，欧拉发明了一个“拉丁方块”，他将其称为“一种新式魔方”，这就是数独游戏的雏形。

不过，当时欧拉的发明并没有受到人们的重视。

直到20世纪70年代，美国杂志才以“数字拼图”的名称将它重新推出。

1984年日本益智杂志Nikoli的员工金元信彦偶然看到了美国杂志上的这一游戏，认为可以用来吸引日本读者，于是将其加以改良，并增加了难度，还为它取了新名字称做“数独”，结果推出后一炮而红，让出版商狂赚了一把。

至今为止，该出版社已经推出了21本关于数独的书籍，有一些上市后很快就出现了脱销。

数独后来的迅速走红，主要归功于一位名叫韦恩·古尔德的退休法官。

古尔德现在居住在爱尔兰，1997年，无意中发现这个游戏，并编写了一个计算机程序来自动生成完整的数独方阵。

2004年年底，伦敦《时报》在古尔德的建议下开辟了数独专栏，《每日电讯报》紧随其后，在2005年1月登出了数独。

后来，世界各国数十家日报相继开辟专栏来介绍数独，有的甚至把它摆在头版大事炒作，招揽读者。

专门介绍这种娱乐的杂志和一本又一本的书籍如雨后春笋般涌现，相关的比赛，网站和博客等等，也接二连三地冒出来。

此外，出版商还授权软件商开发了上百个数独游戏软件。

供人们在网上购买。

标准数独目录第一篇一、什么是数独二、元素构成第六篇直观法解题一、宫摒除数对二、列摒除数对三、宫摒除对隐藏行列摒余解四、行列摒除对隐藏宫摒余解五、数对的聚焦六、一些例子另一、多重数对解题第一篇一、什么是数独？数独（Sudoku）又叫做九宫格数独，是一种源自于18世纪末的瑞士，后在美国发展，并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格中填入1-9的数字，且使数字1-9在每一行、每一列和每一宫中都只出现一次。

这种游戏全面考验做题者的观察能力和推理能力，虽然玩法简单，但是数字的排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

二、元素构成宫格（Cell）：又称单元格、格位，是数独中最小的单元，标准数独中共有81格；行（Row）：横向9个单元格的集合，标准数独共有9行，可用R1、R2、R3......R8、R9来表示，也可用A、B、C......H、I来表示；列（Column）：纵向9个单元格的集合，标准数独共有9列，可用C1、C2、C3......C8、C9来表示，也可用1、2、3......8、9来表示；宫（Box）：三行与三列相交之处共有九单元，每个单元称为宫，可用第一宫、第二宫、第三宫......第八宫、第九宫来表示。

单元（Unit）：行、列、宫都称为单元。

三、数独规则标准数独的规则为：数独每行、每列及每宫填入的数字必须为1-9，且不能重复。

数独谜题按规则填写数字，最终必须只能有一个结果，也就是唯一解（Unique Solution），如果存在无解或两个及以上的解，则不被承认是数独谜题。

先举个例子看看：上图中给定了一些已知数字（黑色），你能把空格中的数字填写完整么？答案：蓝色数字为自己填写的数字。

是不是很简单呢！四、解题方法数独解题方法分为两种：直观法和候选数法。

直观法又称纸笔模式，就是不做任何记号，直接从数独的盘势观察线索，推论答案的方法。

数独教案第一章标准数独一、常见元素：盘而、格、行、列、宫、格的坐标、区二、规则：把数字1—9填入空格内，使每行、每列和每宫内的数字均不重复。

第二章宫内排除法利用排除原理，对每一个宫进行观察，选用某个相同的数字对同一个宫进行排除，最终得到该宫内只有一格可以填入该数字。

例题6 3 25 1 73 8 6 5 44 8 52 5 8 19 1 53 6 7 1 29 3 69 6 5第三章行列排除法利用排除原理，对一行或一列进行观察，选用某个相同的数字对同一行或同一列进行排除，最终得到该行或该列内只有一格可以填入该数字。

1 2 3 4 5 6 7 8 9A1 2 3 4 5 6 7 8 9例题第四章区块排除法利用排除原理，在某宫中形成一个区块（并排的2格或3格内比含有某个数字），再利用区块作为条件继续排除。

43 971 62 385 3 56 781 6 5 492 57 2 4 89 93 212 3 4 5 6 7 8 96 —61 2∣ 5∣6 A A O V OI第五章数对占位法数对（数组）的概念是同行、同列或同宫中，某两格（三格）内只能包含两个（三个）数字，而暂时还不能确定这两个（三个）数的具体位置，这时我们可以把这两个（三个）数字看做一个整体，占住那两格（三格），使其他数字不能填入这两格（三格），再用区块排除法填其他数字。

1、宫内隐形数对（数组）2、行列内隐形数对（数组）3. 显性数对（数组）例题第六章唯一余数法唯一余数法简称唯余法，是利用同行、同列或同宫内数字不能重复的原理，使某一格内最终只剩下一个数字可填的方法。

具体情况是出现了8个不同的数字，且都对同一格影响，导致该格内不能再填这8个数，只能填入未出现的第9个数字。

1、行列唯余2、行或列与宫结合的唯余3＞行.列、宫结合的唯一余数法例题数独的解法和思路总的来说只划分为排除法和唯余法,而数对站位法等思路只是一种辅助构成可以运用排除或唯余的间接方法。