实验设计与数据处理第八章例题及课后习题答案

13125916机电硕1308班周晓易1.某工厂进行技术改造，以减少工业酒精中甲醇含量的波动。

原工艺生产的工业酒精中甲醇含量的总体方差为0.35.技术改造后，进行抽样检验，样品数为25个，结果样品甲醇含量的样本方差为0.15。

问技术改造后工业酒精中甲醇含量的波动性是否更小？（α=0.05）答：检验技术改造后工业酒精中甲醇含量的波动性是否更小，要使用χ2单侧（左侧）检验。

已知σ2=0.35，n=25，s2=0.15。

当α=0.05时，χ20.95（24）=CHIINV（0.95，24）=13.848，而χ2=24*0.15/0.35=10.286，χ20.95（24）>χ2，说明技术改革后产品中甲醇含量的波动较之前有显著减少。

2. A与B两人用同一种分析方法测定金属钠中铁的含量，测试结果分别为：A：8.0,8.0,10.0,10.0,6.0，6.0,4.0,6.0,6.0,8.0B:7.5,7.5,4.5,4.0,5.5,8.0,7.5,7.5,5.5,8.0试问A、B二人测定的铁的精密度是否有显著性差异？（α=0.05）解答如图：这里F＞1，为右侧检验，这时F 单尾临界值＞1，对于右侧检验，如果F＜F 单尾临界，或者P(F<=f) 单尾＞α，就可以认为第一组数据较第二组数据的方差没有显著增大，否则就认为第一组的数据较第二组的数据的方差有显著增大。

在本例中，由于P＞0.05，所以A、B 二人测定的铁的精密度无显著性差异。

3. 用新旧工艺冶炼某种金属材料，分别从两种产品中抽样，测定试样中的杂质含量，结果如下：旧工艺：2.69, 2.28, 2.57, 2.30, 2.23, 2.42, 2.61, 2.64, 2.72, 3.02, 2.45, 2.95, 2.51新工艺：2.26, 2.25, 2.06, 2.35, 2.43, 2.19, 2.06, 2.32, 2.34试问新工艺是否更稳定，并检验两种工艺之间是否存在系统误差？（α=0.05）解答：由于s21<s22，故新工艺比旧工艺更稳定；又因为F＜1，所以为左侧检验。

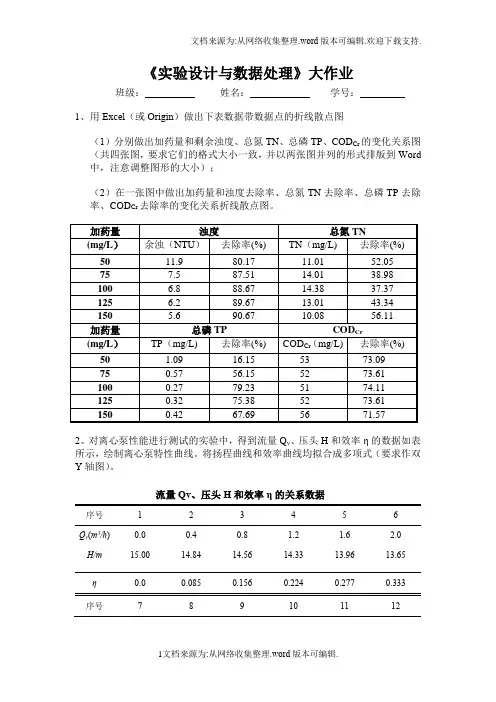
《实验设计与数据处理》大作业班级：姓名：学号：1、用Excel（或Origin）做出下表数据带数据点的折线散点图（1）分别做出加药量和剩余浊度、总氮TN、总磷TP、COD Cr的变化关系图（共四张图，要求它们的格式大小一致，并以两张图并列的形式排版到Word 中，注意调整图形的大小）；（2）在一张图中做出加药量和浊度去除率、总氮TN去除率、总磷TP去除率、COD Cr去除率的变化关系折线散点图。

2、对离心泵性能进行测试的实验中，得到流量Q v、压头H和效率η的数据如表所示，绘制离心泵特性曲线。

将扬程曲线和效率曲线均拟合成多项式（要求作双Y轴图）。

流量Qv、压头H和效率η的关系数据序号123456Q v(m3/h) H/m0.015.000.414.840.814.561.214.331.613.962.013.65η0.00.0850.1560.2240.2770.333序号789101112Q v(m3/h) H/mη2.413.280.3852.812.810.4163.212.450.4463.611.980.4684.011.300.4694.410.530.4313、用分光光度法测定水中染料活性艳红（X-3B）浓度，测得的工作曲线和样品溶液的数据如下表:（1）列出一元线性回归方程，求出相关系数，并绘制出工作曲线图。

（2）求出未知液（样品）的活性艳红（X-3B）浓度。

4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定，得到如下一组数据：试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。

提示：⑴作实验点的散点图，分析c~x之间可能的函数关系，如对数函数y=a+blgx、双曲函数(1/y)=a+(b/x)或幂函数y=dx b等；⑵对各函数关系分别建立数学模型逐步讨论，即分别将非线性关系转化成线性模型进行回归分析，分析相关系数：如果R≦0.553，则建立的回归方程无意义，否则选取标准差SD最小（或R最大）的一种模型作为某伴生金属c与含量距离x之间经验公式。

试验设计与数据处理》第三章：统计推断3- 13解：取假设HO : u1-u2w 0和假设H1: u1-u2 > 0用sas 分析结果如下:Sample StatisticsGroupNMeanStd. Dev.Std. Errorx8 0.231875 0.0146 0.0051 y100.20970.00970.0031Hypothesis TestNull hypothesis:Mean 1 - Mean 2 = 0Alternative:Mean 1 - Mean 2 A= 0If Varianees Aret statistie DfPr > tEqual3.878 16 0.0013 Not Equal3.70411.670.0032由此可见p 值远小于0.05,可认为拒绝原假设，即认为2个作家所写的小品文中 由 3 个字母组成的词的比例均值差异显著。

3-14解：用sas 分析如下: Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1 Alternative:Varia nee 1 / Varia nee 2 A = 1- Degrees of Freedom -FNumer. Denom.Pr > F第四章:方差分析和协方差分析4- 1 解:Sas 分析结果如下：Dependent Variable: ySum ofSouree DF Squares Mean Square F Value Pr > F Model 41480.823000370.20575040.88<.00012.27 7 由p 值为0.2501 > 0.05 （显著性水平） 9 0.2501，所以接受原假设， 两方差无显著差异Source DF Type I SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n627.000000004.500000000.830.5684Source DF Type III SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n 627.000000004.500000000.830.5684由结果可知， 在不同浓度下得率有显著差异， 在不同温度下得率差异不明显， 交 互作用的效应不显著。

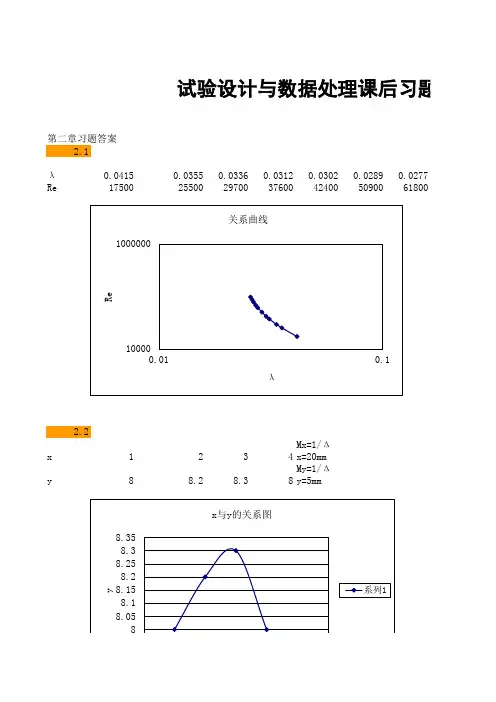
水平号12345678序号AB112478224857336336448715551284663663775142887521y5.86.34.95.444.533.6SUMMARY OUTPU回归统计Multiple R 0.99970596265R Square 0.99941201175Adjusted R Sq 0.99917681646标准误差0.03240370349190230180220170210137.5138138138.5139139.5140底水量（x 1）/g 2202302404.0,4.5,3.0,3.6。

已知试验指标与两因素之间成二元线性关系，试用回归分析法139.5140吸氨时间（x 2）/min 136.5137吸氨时间（x 2）/min 选用均匀表U 8*(85)安排实验，8个试验结果（吸氨量/g）依次为：5.8,6.3,4.9,5.4,出较好工艺条件，并预测该条件下相应的吸氨量。

138.5139170180190200210137240第七章 均匀设计1、在啤酒生产的某项工艺实验中，选取了底水量（A）和吸氨时间（B）两个因素都取了8个水平，进行试验设计，因素水平如下。

试验指标为吸氨量，越大越好。

137.5回归方程模型为y =a+b 1x 1+b 2x 2136.5200底水量（x 1）/g观测值8方差分析dfSS MS F Significance F 回归分析28.9235 4.461754249.285714288.38342726421残差50.005250000000.00105总计78.92875Coefficients 标准误差t Stat P-value Lower 95%Intercept 96.52583333331.4768020536165.36138888561.5871169308092.7295928008底水量（x1）/-0.69666666660.010********-66.7626010421.42755955001-0.7234906467吸氨时间（x2）0.021*********.0005217491941.84641500741.470141026900.020********RESIDUAL OUTP 观测值预测 y 残差15.797500000000.0024999999926.32250000000-0.022******** 4.88250.017499999994 5.4075-0.00750000005 3.967500000000.032499999996 4.49250.007500000007 3.0525-0.052500000083.577500000000.022********观测值预测 y15.7975000000026.322500000003 4.88254 5.40755 3.967500000006 4.49257 3.052583.57750000000R=0.99 和Significance F=8.38342726421806E-09<0.01,说明该回归方程非常显y=96.5-0.70X 1+0.02X 2个因素，越好。

《试验设计与数据处理》专业：机械工程班级：机械11级专硕学号：S110805035 姓名：赵龙第三章：统计推断3-13 解：取假设H0：u1-u2≤0和假设H1：u1-u2＞0用sas分析结果如下：Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05，可认为拒绝原假设，即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。

3-14 解：用sas分析如下：Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501＞0.05（显著性水平），所以接受原假设，两方差无显著差异第四章：方差分析和协方差分析4-1 解：Sas分析结果如下：Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知，p值小于0.001，故可认为在水平a=0.05下，这些百分比的均值有显著差异。

试验设计与数据处理学院班级学号学生姓名指导老师第一章4、 相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为：±。

5、1）、压力表的精度为级，量程为，则 max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2）、1mm 的汞柱代表的大气压为，所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3）、1mm 水柱代表的大气压为gh ρ，其中29.8/g m s = 则：3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值算数平均值 几何平均值 调和平均值 标准差s 标准差σ 样本方差S 2 总体方差σ2算术平均误差△极差R7、S2＝，S2＝ F ＝S2/ S2＝= 而F （）=，= 所以F （）< F <两个人测量值没有显着性差异，即两个人的测量方法的精密度没有显着性差异。

|||69.947|7.747 6.06ppd x =-=>分析人员A分析人员B8样本方差18样本方差210Fa值104F值668470566888.旧工艺新工艺%%%%%%%%%%%%%%%%%%%%%%t-检验: 双样本异方差假设变量1变量2平均方差观测值139假设平均差0df8t Stat-38.P(T<=t) 单尾0t 单尾临界P(T<=t) 双尾0t 双尾临界F-检验双样本方差分析变量 1变量 2平均 方差 观测值 13 9 df 128FP(F<=f) 单尾 0 F 单尾临界9. 检验新方法是否可行，即检验新方法是否有系统误差，这里采用秩和检验。

求出各数据的秩，如下表所示：1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 17此时对于 α =，查临界值表得：T1=66，T2=102。

实验设计与数据处理(第二版部分答案)试验设计与数据处理学院班级学号学生姓名指导老师第一章4、相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为：18.2±0.0182mg 。

5、1）、压力表的精度为1.5级，量程为0.2MPa ，则 max 0.2 1.5%0.003330.3758R x MPa KPax E x ∆=⨯==∆=== 2）、1mm 的汞柱代表的大气压为0.133KPa ， 所以max 20.1330.1331.6625108R x KPax E x -∆=∆===⨯ 3）、1mm 水柱代表的大气压为gh ρ，其中29.8/g m s = 则：3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ20.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²＝3.733，S ₂²＝2.303F ＝S ₁²/ S ₂²＝3.733/2.303=1.62123而F 0.975 （9.9）=0.248386，F 0.025(9.9)=4.025994 所以F 0.975 （9.9）< F <F 0.025(9.9)两个人测量值没有显著性差异，即两个人的测量方法的精密度没有显著性差异。

分析人员A分析人员B8 7.5 样本方差1 3.733333 8 7.5 样本方差2 2.302778 10 4.5 Fa 值 0.248386 4.025994104F 值1.62123|||69.947|7.747 6.06p pd x =-=>6 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 df 12 8 F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349. 检验新方法是否可行，即检验新方法是否有系统误差，这里采用秩和检验。

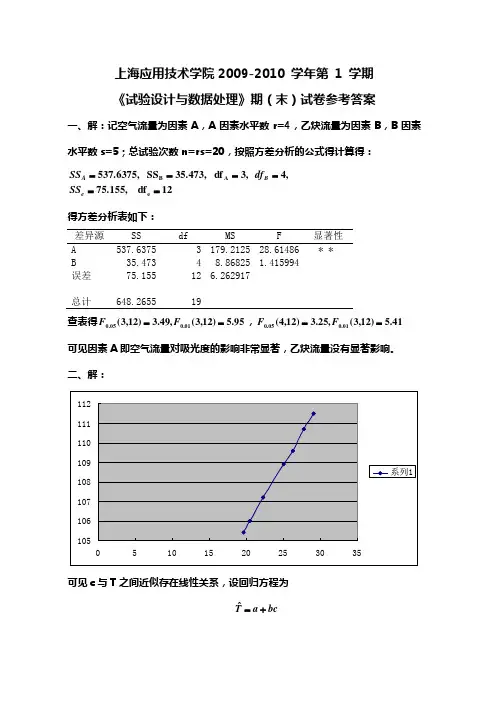
上海应用技术学院2009-2010 学年第 1 学期 《试验设计与数据处理》期（末）试卷参考答案一、解：记空气流量为因素A ，A 因素水平数r=4，乙炔流量为因素B ，B 因素水平数s=5；总试验次数n=rs=20，按照方差分析的公式得计算得：12df 75.155,,4 ,3df 35.473,SS 537.6375,e A B ======e B A SS df SS得方差分析表如下： 差异源 SS df MS F 显著性A 537.6375 3 179.2125 28.61486 * *B 35.473 4 8.86825 1.415994误差 75.155 12 6.262917 总计 648.2655 19查表得95.5)12,3(,49.3)12,3(01.005.0==F F ，41.5)12,3(,25.3)12,4(01.005.0==F F 可见因素A 即空气流量对吸光度的影响非常显著，乙炔流量没有显著影响。

二、解：可见c 与T 之间近似存在线性关系，设回归方程为bc a T+=ˆ 代入回归计算公式可得：a=92.911，b=0.6381，相关系数R ×R=0.9995说明所建立的回归方程与试验数据拟合得很好。

三、解：采用分数法，试验区间为[3,8]，以1为单位可等分为5份，设桶数为x 时试验指标值为f(x),则：第一次试验点在3/5即6桶处，得试验指标值f(6); 第二次试验点在2/5即5桶处，得试验指标值f(5),比较两次试验结果f(6)>f(5),舍掉区间[3,5]；第三次试验点在区间[5,8]的2/3即7桶处，得试验指标f(7),比较试验指标得f(6)>f(7)，试验结束，最优结果为6桶。

四、解：（1）这是一个4因素2水平的试验，但还有一个交互作用，为5因素2水平，可将因素A，B，C，D分别放在正交表的第1，2，4，7列，交互作用A×（2）按照直观分析法得计算结果如下：因素主次 C A×B B A D（3）根据上一步排出的因素主次，可知交互作用A×B比因素B，A对试验指标的影响更大，所以确定A、B的水平应按A、B各水平搭配的好坏来确定。

单因素方差分析：用同种原料织成的布，用不同的染整工艺处理后进行缩水率试验，试用方差分析考察不同工艺对缩水率是否有显著影响。

这里采用不同的染整工艺，每种工艺处试验结理四块布，记A为染整工艺这一因子。

它的五个水平记为,,,,A A A A A12345果如下：2111n m ij i j C x n m ==⎛⎫= ⎪⨯⎝⎭∑∑=1093.72052111nm ij i j R x m ==⎛⎫= ⎪⎝⎭∑∑=1149.2575211n miji j W x ===∑∑=1183.63 则组内偏差平方和：e SS W R =-=34.3725 组间偏差平方和：t SS R C =-=55.537 总偏差平方和：T SS W C =-=89.9095双因素无重复试验设计方差分析：为了考察材质和淬火温度对某种钢材淬火后的弯曲变形的影响，对四种不同材质分别用五种不同的淬火温度进行试验，测得其淬火后试件的延伸率数据如下：试对表中数据作方差分析来回答：不同材质对延伸率有显著影响吗，不同温度对延伸率有显著影响吗？解：a=4，b=5T SS 2211abiji j T x ab ===-=∑∑38.352A SS 22011a i i T T b ab==-=∑0.32B SS 22011b j j T T a ab ==-=∑36.397e T A B SS SS SS SS =--=1.635双因素有重复试验设计方差分析：试确定三种不同的材料和三种不同的使用环境对蓄电池输出电压的影响，为此，对每种水平组合重复测输出电压4次，测得数据()100V ⨯列入下表，试分析各因)111a b rijk i j k T x ====∑∑∑=3771220011a A i i T SS T br abr ==-∑=114881939-14220441=118161236⨯⨯ 220011b B j j T SS T ar abr ==-∑=115211689-14220441=392951236⨯⨯ 2222000*********a b a b A Bij i j i j i j T SS T T T r br ar abr⨯=====--+∑∑∑∑ =11111829261-4881939-5211689+14220441=111924121236⨯⨯⨯⨯ 220111111abra b e ijkij i j k i j SS x T r ======-∑∑∑∑∑=1475281-1829261=179664⨯三因素试验设计方差分析：某农作物的B 族维生素含量与3个因子有关。

1.在^xcel中用AVERAGE函数计算平均值，用STEDV函数计算标准偏差，得到结果如表1所示。

表1该污水厂进、出水水质标准偏差及平均值COD SS 氨氮进水出水进水出水进水出水标准偏差102.70497 5.6417987 40.44311 2.2590321 7.7226061 1.1480863 平均值368.39 42.05 243.39 16.65 33.77 1.85图1该污水厂进、出水水质示意图2.在excel中作图如下:（1）加药量（mg/L）加药量（mg/L）图6加药量与浊度去除率、总磷去除率、总氮去除率、COD 去除率的关系图3. (1)图2总磷随加药质的变化关系图 图3余浊随加药质的变化关系图5075 100125150加药量(mg/L)5075100125150加药量(mg/L)图4总氮随加药■的变化关系图 图5 COD 随加药■的变化关系图(8)瓣泰2 0164 2108 6 4 (T/SUONH50 49 485756554 3 2 155 5 5 (q/SUIQooo o Oo o o o O图7进水量Q 与SVI 关系图10.015.020.025.030.035.0水温(笆)图8水温与SVI 关系图0.0010.00 20.00 30.00 40.00 50.00 60.00 70.00SV30 (%)图9 SV30与SVI 关系图0.00 20.0025.00 45.00 2(10(1HUM Hloo O oo O O.O.O. 8 6 430.0035.00 40.00 进水流量Q (万m3/d)50.00II)2((T /SUI0.002.004.006.00 8.0010.0012.00MLSS (g/L)图10 MLSS 与SVI 关系图(2) 用excel 中correl 函数求出相关系数r,再根据0V|rl<l,存在一定线性关系：①0 VlrlVO.3,微弱相关；②0.3VIHV0.5,低度相关;③0.5<lrl<0.8,显著相关；④0.8 <lrlVl,高度相关。

试验设计与数据处理课后习题机械工程6120805019 李东辉第三章3-7分别使用金球和铂球测定引力常数（单位：）1. 用金球测定观察值为 6.683，6.681, 6.676, 6.678, 6.679, 6.6722. 用铂球测定观察值为 6.661, 6.661，6.667, 6.667, 6.664设测定值总体为N（u，）试就1,2两种情况求u的置信度为0.9的置信区间，并求的置信度为0.9的置信区间。

用sas分析结果如下：第一组：第二组:3-13下表分别给出两个文学家马克吐温的8篇小品文以及斯诺特格拉斯的10篇小品文中由3个字母组成的词的比例：马克吐温：0.225 0.262 0.217 0.240 0.230 0.229 0.235 0.217斯诺特格拉斯：0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.220 0.201设两组数据分别来自正态总体，且两个总体方差相等，两个样本相互独立，问两个作家所写的小品文中包含由3个字母组成的词的比例是否有显著差异（a=0.05）取假设H0：u1-u2≤0和假设H1：u1-u2＞0用sas分析结果如下：Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05，可认为拒绝原假设，即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。

第八章 正交试验结果的极差分析极差分析法具有计算简便、直观形象、简单易懂等优点，是正交试验结果分析最常用的方法。

第一节 单指标正交试验结果的极差分析极差分析法包括计算和判断两个步骤，其内容如图8-1所示。

极差分析法1、计算2、判断① K jm ，K jm② R j图8-1极差分析法示意图在图8-1中，K jm 是第j 列因素m 水平所对应的试验指标的和，jm K 是k jm 的平均值。

由jm K 的大小可以判断j 因素的优水平，和各因素的最优组合。

R j 是第j 列因素的极差。

R j ＝max(j1K ,j2K ,…,jm K )－min(j1K ,j2K ,…,jm K )R j 反映了第j 列因素的水平变动时，试验指标的变动幅度。

R j 越大，说明该因素对试验指标的影响越大。

根据极差R j 的大小，可以判断因素的主次。

极差分析法的计算与判断可直接在试验结果分析表上进行，下面以例7-2来说明（见表8-1）。

（一）确定因素的优水平和最优水平组合首先分析A 因素各水平对试验指标的影响。

A 因素1水平所对应的试验指标之和为K A1＝y 1＋y 2＋y 3＝0＋17＋24＝41，其平均值A1K ＝31 K A1＝13.7；同理，A 因素2水平所对应的试验指标之和为K A2＝y 4＋y 5＋y 6＝12＋47＋28＝87，其平均值A2K ＝31 K A2＝29；A 因素3水平所对应的试验指标之和为K A3＝y 7＋y 8＋y 9＝1＋18＋42＝61，其平均值A3K ＝31K A3＝20.3。

从表8-1还可以看出，在考察A 因素所进行的三组试验(A 1、A 2、A 3)中，B 、C 、D 因素的各水平都只出现了一次，且由于B 、C 、D 之间无交互作用，因此对A 1、A 2、A 3来说，三组试验的试验条件是完全一样的。

A1K 、A2K 、A3K 的大小反映了A 1、A 2、A 3对试验指标的影响的大小。