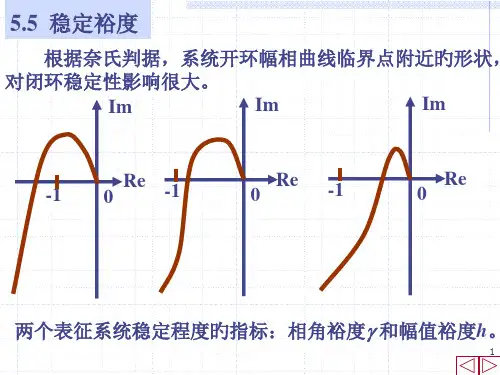
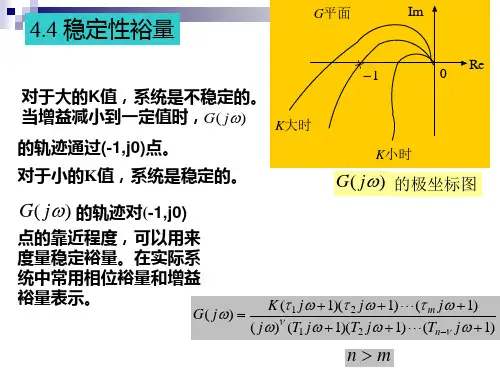
王划一-自动控制原理-5-3稳定裕度

格式：ppt
大小：562.00 KB
文档页数：38

下载文档原格式

王划一-自动控制原理-5-3稳定裕度

= arctan3.16 2arctan0.316
= 37.4
当(g) = 180时
180 = arctang 180 2arctan0.1g
求得
arctang =2arctan0.1g g = 8.94
20 lg h
20 lg A(g )
20
lg
k g g2 12
9.03dB
因为 > 0，所以闭环系统是稳定旳。
0
0 20 40 60 80
能够看出，调整时间与相角裕度和幅值穿越频率都有关系。假如两个二阶系统旳相同，则它们旳超调量也相同，这时比较大旳系统，调整时间较短。
17
例5-19 一单位反馈控制系统，其开环传递函数
G(s)
7
s(0.087s 1)
试用相角裕度估算过渡过程指标p% 与ts。
解：系统开环伯德图如图示
33
四、奈奎斯特稳定判据
内容应用
5.5 稳定裕度
根据奈氏判据，系统开环幅相曲线临界点附近旳形状，
对闭环稳定性影响很大。
Im
Im
Im
-1
Re 0
-1
Re 0
-1
Re 0
两个表征系统稳定程度旳指标：相角裕度和幅值裕度h。
1
（1）幅值裕度h ：令相角为180时相应旳频率为g （相角穿越频率），频率为g 时相应旳幅值A(g)旳倒数，
定义为幅值裕度h ，即 h 1 A(g )
10 11.5
0
1
20
40dB/dec
()/()
0
90
180
19
2) 高阶系统
近似旳关系式
p
0.16 0.4( 1

自动控制原理之稳定性裕量分析.ppt

G(
j)
(
K (1 j 1)( 2 j 1)( m j j) (T1 j 1)(T2 j 1)(Tn
1)
j 1)
nm
一、相位裕度、相角裕度(Phase Margin)
设系统的增益交界频率(Gain cross-over frequency)为 c A( jc ) G( jc )H( jc ) 1 定义相角裕度为 G( jc )H ( jc ) (180) 180 G( jc )H ( jc )
写出系统的开环传递函数判别系统的稳定性如果系统是稳定的则求看对数幅频特性1031021011040202040608020dbdec20dbdec40dbdec40dbdec00101radsdblg20lg20lg20lg20lg2010010arctgarctgarctg系统稳定573标准二阶系统中阶跃瞬态响应与频率响应之间的关系ss2n图38标准形式的二阶系统方块图在图38所示的标准二阶系统中单位阶跃响应中的最大超调量可以精确地与频率响应中的谐振峰值联系在一起
dB
dB
c
0
Log
0
Log c
90 180 270
Log
Positive Phase Margin
Stable System
90 180 270
Log
Negative Phase Margin
Unstable System
二、增益裕度、幅值裕度(Gain Margin)Kg
设系统的相位交界频率(Phase cross-over frequency) x
相角裕度的含义是
对于闭环稳定系统，如果开环相频特性再滞后度，则系统将变为临界稳定。
当 0 时，相位裕量为正值；

(自动控制原理)稳定裕度

2 干扰和噪声
外部干扰和噪声会降低系统的稳定裕度。
3 参数变化
系统参数的变化会对稳定裕度产生影响。
提高稳定裕度的方法和技巧
1
参数调整
通过调整系统参数来增加稳定器类型和参数来提高稳定裕度。
3
滤波器应用
通过滤波器来减少干扰和噪声对系统稳定裕度的影响。
结论和总结
稳定裕度是评估系统稳定性的重要指标，它能够确保系统在面对干扰和参数变化时保持稳定。了解稳定裕度的定义、计算方法和影响因素，以及提高稳定裕度的方法和技巧，对于优化系统设计和提高系统可靠性至关重要。
(自动控制原理)稳定裕度
稳定裕度是评估系统稳定性的重要指标。它衡量系统在面对干扰时的能力，是确保系统可靠运行的关键。
定义稳定裕度
稳定裕度可以定义为系统离稳定界限的距离。它衡量了系统在存在不确定因素或参数变化时仍然保持稳定的能力。
稳定裕度的公式和计算方法
稳定裕度公式
常见的稳定裕度公式是：稳定裕度 = 1 / (1 + G(s))
计算方法
计算稳定裕度时，需要确定系统的传递函数，并对其进行频率响应分析。
1. 确定幅值裕度和相位裕度的要求。 2. 绘制系统的频率响应曲线。 3. 根据要求的裕度计算稳定裕度。
稳定裕度的意义和重要性
1 系统可靠性
稳定裕度能够确保系统在面对干扰或参数变化时保持稳定性。
2 容错能力
稳定裕度增加系统的容错能力，即使出现不确定情况也能维持系统的稳定。
3 稳定边界
通过评估稳定裕度，可以确定系统的稳定边界，并提前采取措施来避免系统不稳定。
常见的稳定裕度指标
相位裕度幅值裕度增益裕度
系统响应相位与稳定边界相差的角度值。系统响应幅值与稳定边界之间的比例关系。系统传递函数增益与单位增益相差的值。

自控控制原理习题王建辉第5章答案

第五章频率法5-1用时域与频域法分析设计和设计系统的主要区别是什么？ 5-2用时域法分析和设计系统的主要优点是什么？ 5-3奈氏稳定判据的本质是什么？5-4何谓幅值裕度与相位裕度，并举例说明之。

5-5试述二阶系统闭环频率特性与时域中阶跃相应之间的关系。

5-6试定性叙述伯德图各段与时域指标之间的对应关系。

5-7已知单位反馈系统的开环传递函数为 W K (s)=110+s当系统的给定信号为（1）)30sin()(01+=t t x r(2) )452cos(2)(02-=t t x r(3))452cos(2)30sin()(03--+=t t t x r求系统的稳态输出。

解：5-7（1）系统的闭环传递函数为1110)(1)()(+=+=s s W s W s W K K B因为)30sin()(0+=t t x r )30(0)(+=t j r ej X ω 02.511arctan29054.012110)(j j B eej W --=+=ωωω)2.530(09054.0)()()(-+==t j B r c ej W j X j X ωωω所以)8.24sin(9054.0)(0+=t t x c 解：5-7（2）系统的闭环传递函数为1110)(1)()(+=+=s s W s W s W K K B因为)452cos(2)(0-=t t x r 化为正弦表达形式则)452sin(2)(0+=t t x r )452(02)(+=t j r ej X ω 3.1011arctan28944.012110)(j j B eej W --=+=ωωω)3.10452(07888.1)()()(-+==t j B r c ej W j X j X ωωω所以)7.342sin(7888.1)(0+=t t x c解：5-7（3）根据叠加原理，系统的输出为5-7（1）-5-7（2）)7.342sin(7888.1)8.24sin(9054.0)(0+-+=t t t x c5-8绘出下列各传递对应的幅相频率特性。

《自动控制原理》第5章控制系统的频域分析：稳定裕度

0.4
0.2
0
0
5
10
15
20
25
30
35
40
Time (sec)
一、根据开环对数频率特性分析系统性能（三频段）
1、低频段分析系统的？
低频斜率系统型别
0dB/dec
0
-20dB/dec
Ⅰ
-40dB/dec
Ⅱ
阶跃输入稳态误差
1 K 1
0 0
19
低频段分析系统的稳态性能
斜率决定系统的型，ess 低频段高度决定开环增益K
1 h
A( x )
-1
幅值裕度h 1
A(x )
9
L(ω) 最小相位系统
Φ(ω)
90
-20dB/dec
h
h 20lg( A(x )) L(x )dB
不稳定
ω
h>0:系统是稳定的。
ω
180
270
10
例1：已知系统开环传递函数为：
G(s)
s2 (s
200 2)(s
1)
求幅值裕度和相角裕度。
时域：动态过程的开始部分。
28
二、根据闭环对数频率特性分析系统性能自学部分
29
本章学习重点
理解频率特性的定义熟练掌握串联开环系统的频率特性极坐标图和 Bode图的绘制熟练掌握Nyquist 稳定判据掌握根据开环对数频率特性分析闭环系统的动态性能和稳态性能。
30
时域：动态过程的中间部分。
高阶系统：经验公式
0.16 0.4( 1 1) 35 90 sin
ts
(4
~
9)
1
c
阅读：218页例5-16

《自动控制原理》胡寿松 5-3 频域稳定判据频域稳定判据

①辅助函数F(s) 建立了系统的开环极点和闭
环极点与F(s)的零极点之间的直接联系；
②辅助函数F(s)建立了闭合曲线ГF和ГGH 之间
的几何转换关系。若已知开环传递函数G(s)H(s)的条件下，就可求出辅助函数F(s)。这些特点为幅角原理的
应用创造了条件。
（3）s平面闭合曲线Г的构造
系统的闭环稳定性取决于系统闭环传递函数
因此，辅助函数F(s)的分子分母同阶，即其零
点数与极点数相等,即为n。于是，辅助函数进一步
可表示为：
G( s) M 1 ( s) N 2 ( s) M 1 ( s) N 2 ( s) M ( s) ( s) G( s) H ( s) 1 G( s) H ( s) N1 ( s) N 2 ( s) M 1 ( s) M 2 ( s) N ( s) M ( s) N ( s)
定程度（相对稳定性），还可以用于分析系统的
动态性能以及指出改善系统性能指标的途径。
因此，奈奎斯特稳定判据是一种重要而实用
的稳定性判据，工程上应用十分广泛。
1
奈氏判据的数学基础
数学基础：复变函数中的幅角原理。
（1）幅角原理
F (s) 1 G(s) H (s) 为s的有理分式，分子分母同阶。
s平面任选一点s=σ+jω，通过F(s) 映射，在F(s)平
lim
1
0
A(0 ) | G ( j 0 ) H ( j 0 ) |

e
j [ ( 90 )]
G1 ( j 0) e
jG1 ( j 0 )
e
j [ ( 90 ) G1 ( j 0 )]
(0 ) G ( j 0 ) H ( j 0 ) (90 ) G1 ( j 0)

《自动控制原理》胡寿松 5-3 频域稳定判据频域稳定判据

定程度（相对稳定性），还可以用于分析系统的
动态性能以及指出改善系统性能指标的途径。
因此，奈奎斯特稳定判据是一种重要而实用
的稳定性判据，工程上应用十分广泛。
1
奈氏判据的数学基础
数学基础：复变函数中的幅角原理。
（1）幅角原理
F (s) 1 G(s) H (s) 为s的有理分式，分子分母同阶。
s平面任选一点s=σ+jω，通过F(s) 映射，在F(s)平

s s
(s z )ds (s z )ds 0
2 2
12
s
s 21
同理，对于未被闭合曲线Γ包
围的其它零、极点zi, pj，均有：
( s zi ) ( s p j ) 0
于是在右图中有:
F ( s) ( s z1 ) ( s z2 ) ( s zn ) ( s p1 ) ( s p2 ) ( s pn ) 2 (2 ) (2 )(1 1) 0
N (s) M ( s) F ( s) 1 G(s) H ( s) N (s)
K

(s z )
i i 1 i
n
(s p )
i 1
n
式中，z1,z2 ,…,zn和p1,p2,…,pn分别为辅助函数
F(s)的零点和极点。
辅助函数F(s)具有以下特点：
①F(s)的零点、极点的个数相同，均为n个; ②F(s)的零点zi为闭环极点，极点pi为开环极点; ③F(s)与开环传递函数G(s)H(s)之间只差常量1。
F ( s) 1 G( s) H ( s)
K ( s zi )
i 1

自动控制原理5第五节稳定裕度

Kg
1
A( g )
j AgΒιβλιοθήκη G(s平面在对数坐标图上，采用Lg表示Kg的分贝值
Lg 20 lg K g 20 lg A( g )
-1 g
c
→∞ 0
c
Lg称为对数幅值稳定裕度或增益稳定裕度，
由于Lg应用较多，通常直接被称为幅值稳
定裕度。
→0
定义：幅值穿越频率时的相频特性与－180°之差为相角稳定裕度。即
手工绘制波德图步骤：
1、确定转折频率：10、40，
在(1,20log200)点画斜率为-20dB/dec的斜线至=10；
2、在=10~40之间画斜率为-40dB/dec的斜线；
3、 =40后画斜率为-60dB/dec的斜线。
19
ωc' g c
1 5 0 210
上图蓝线为原始波德图。(c ) 209 180 ,c 38 ，显然闭环系统是不稳定的。为了使相位稳定裕度达到30度，可将幅频曲线向下平移。即将开环放
-210
c＝1.583 2=23.3°
-240
-270
0.1
1
12
－40dB/dec
c＝5.12 1=-16°
g＝3.16
10
－60dB/dec
100
一般而言，当L()在c处的斜率处于－20dB/dec段时，系统是稳定的；当L()在c处的斜率处于－40dB/dec段时，系统可能稳定也可能不稳定，即使稳定，相位裕量也是较小的；当L()在c处的斜率处于－60dB/dec段时，系统是一般是不稳
(c ) (180 ) 180 (c )
6
j
L()
G(s平面
Ag
-1 g

自动控制原理53稳定裕度

（1）幅值裕度h ：令相角为180时对应的频率为g （相角穿越频率），频率为g 时对应的幅值A(g)的倒数，定义为幅值裕度h ，即 1 h A( g ) 或 20lgh = 20lg A(g)
（2）相角裕度：令幅频特性过零分贝时的频率为c （幅值穿越频率），则定义相角裕度为
K (T1 s 1) G( s ) 2 s (T2 s 1)
= 180 + arctancT1 180 arctancT2
(3) 1、2保持不变， h =2/1 中频段宽度
h
与中频段的斜率有关，而且还与中频段宽度有关：中频段宽度
10
() Mr 70 p% 8 60 100 7 50 80 6 40 60 5 30 40 4 p 20 20 3 Mr 10 0 2 0 1 0 0.2 0.4 0.6 0.8 1.0
24
② Mr 、 b 与ts 的关系
M ( b )
2 n
( ) 4(n b )
2 n 2 2 b
2
0.707
b n 1 2 2 2 4 2 4 4
ts 3
n
b t s
3

1 2 2 2 4 2 4 4
25
2. 高阶系统
M p 0.16 0.4( M r 1)
ts k1
c
k1 2 1.5( M r 1) 2.5( M r 1)
C(s)
由A(c) =1，计算开环截止频率c有 2 n 1 c n 1 4 4 2 2 c c2 ( 2n )2
14
则相角裕度为
() p%
100 80 60 40 20 0

自动控制原理王划一3

n —无阻尼自振频率。 —阻尼比，
2
传递函数及方框图
n C(s) R(s) s 2 2 n s n 2
R(s)
n 2 s 2 2 n s n
2
C(s)
等效的开环传函及方框图
n2 G(S) s(s 2 n ) n -1
c(t ) L [ s 2 n s n
s0
s0
T T2
1 2T 2 2 (Ts 1) 3
s0
1 T T2 T3 C (s) 3 2 s Ts 1 s s t t 1 2 1 T c( t ) t Tt T 2 T 2 e T t 2 Tt T 2 (1 e ) 2 2

1 2
d

1 2
)
n 1 2
d
arctg

（2）峰值时间 t p
c(t) 1 - e - n t (cos d t dc(t) 由 dt 0, 有 (cos d t p

1
2
s i n d t )
t t p
- n e e
r(t)
Rt
t
r(t)
三．抛物线函数（匀加速函数）
Rt 2 t 0 r (t ) t 0 0 1 R=1/2时，称为单位抛物线函数。R ( S ) S3
0
t
四．脉冲函数
0 r (t ) A h t 0 及t h
r(t) 1/h
th
h
t
当h 时，则称为单位脉冲函数。 r(t) t0 (t) 0 t 0
1.定义上升时间 t r : 单位阶跃响应第一次达到其稳态值所需时间

《自动控制原理》胡寿松第05#6章频域稳定裕度.ppt

?
0.69
?b
上升时间：
tr
?
2 .202 T
?
2.202
?b
调节时间：
ts
?
3T
?
3
?b
说明 ? b和延迟
时间、上升时间、调节时间也成反比。
（2）二阶系统带宽 ? b
设二阶系统的闭环传递函数为
? (s) ?
s2
?
?
2 n
2??
n
s
?
?
2 n
故有 | ? ( j0) |? 1。
系统的幅频特性： |? ( j? ) |?
贝时，对应的频率 ? b称为带宽频率，即带宽频率 ? b为满足下列方程的解：
20 lg ? ( j? b ) ? 20 lg ? ( j0) ? 3
对于Ⅰ型和Ⅰ型以上系统，由于 ? ( j0) ? 1 故有：
20 lg ? ( j? b ) ? ? 3(dB )
显然，当 ? >? b时，有 20 lg ? ( j? ) ? 20 lg ? ( j0) ? 3
③物理意义：稳定系统在截止频率 ωc处若相角再迟后一个γ角度，则系统处于临界状态；若相角迟后大于γ ，系统将变成不稳定。
j
-1 ωx
1
γ ωc
0
∠G(jω c)Ｈ(jω c) G(jω)Ｈ(jωc)
上述两图中， γ均为正值
（2）幅值裕度
①在开环幅相频率特性曲线中定义
幅值裕度是指在(-1,j0)点处的幅值1与开环幅相
d? (1? 2? 2 )2 ? 1
即A与ζ成反比关系，根据假设，又 A与? b成正比关系，故可得， ? b与阻尼比 ζ成反比关系。

自控简要答案王划一杨西侠著

《自动控制原理》（第2版）习题答案第2章2-1 （1）t e t e tt23sin 3123cos 122--+- （2）6 + 3t（3）)334(322+++---t t e e t t（4）t t ωωωsin 1132-2-2 （1）2351853t t e e --+- （2）t e 2-（3）t e a b t ae n t nn n t n n ωωζωωζωζωsin cos --++ （4）t a Aa t a A e b a A at ωωωωωωωsin cos 222222++++⎪⎭⎫ ⎝⎛++- 2-3 （a ）)()()(2110f f ms f s X s X i ++= （b ）212110)()()(k k s k k f fs k s X s X i ++= 2-4 （a ）)()()(t u t kx t xm =+ （b ）)()()(2121t u t x k k k k t xm =++ 2-5 （a ）)()()()()(2212121t u R dtt du C R R t u R R dt t du C R R r r c c +=++ （b ）)()()()()()(22121221t u R t u R R dt t du C R R L dt t u d LC R r c c c =++++ 2-6 252312)14(100)()(2+++=s s s s R s C 2523125231210)()(22++++⋅=s s s s s R s E 2-7 t t e e t c 2241)(--+-=2-8 )1)(2(23)(+++=s s s s G t t e e t h ---=24)(2-9 （a ）1)(1)()(32213+++⋅-=s R R C s CR R R s U s U r c （b ）13221)()()(R R R s R CR s U s U r c ++-= 2-10 （a ）))((1)()(432121G G G G G G s R s C -+++= （b ）)(1)1()()(21221H H G G G s R s C -++= （c ）331311321332123113211)()(H G H G H G G G G H G G H G G H G G G G s R s C ++++++= 2-11 （a ）32211)()(G G G G s R s C ++= （b ）HG H H G s R s C 111)1()()(+--= （c ）121223121)()()(H G G H G G G G s R s C +++= 2-12 （a ）))((1)1()()(23111232123111134321H G H G H H G G G H G H G H G G G G G G s R s C --++++++= ))((1)1(1)()(2311123212311123423H G H G H H G G G H G H G H H G G H G s R s E --++++-+⋅= （b ）21212121312)()(G G G G G G G G s R s C ++-++-= 21212131)1(1)()(G G G G G G s R s E ++-+⋅= 2-13 （a ）12121211)()(H G G G G G G s R s C ++= 121211211)1(1)()(H G G G G H G G s R s E +++⋅= 12121231211)1(1)()(H G G G G G G H G G s D s C ++++⋅-= 12121231211)1(1)()(H G G G G G G H G G s D s E ++-+⋅= （b ）434242143421)()(G G G G G G G G G G G s R s C ++++= 434242111)()(G G G G G G G s R s E ++-= 434241)()(G G G G G s D s C ++= 434241)()(G G G G G s D s E ++-=2-14 （a ）))((1)(23113343321231134321H G H G H G G H G G G H G H G G G G G G s G -+++-++= （b ）3541432326543211)(H G G H G G H G G G G G G G G s G +-+=（c ） 15.1（d ）))((1)1()(ch af ehgf ch gb af gb ed abcd s G +----++=第3章 3-1 60070600)(2++=s s s G ζ = 1.43 ωn = 24.5 3-2 ζ = 0.6 ωn = 2 σ % = 9.48% t p = 1.96 t r = 1.38 t s = 2.53-3 ζ = 0.5 ωn = 1σ % = 16.3% t p = 2.42 t r = 3.63 t s = 63-4 （1）12211)(KT s T s T s ⋅++=φ （2）)5)(2()3(15)(+++=s s s s φ （3）25.06.04016.0)3.0(40)(22++=++=s s s s φ 3-5 （1）ζ = 0.1 ωn = 5)26.8497.4sin(005.11)(5.0︒+-=-t e t c tσ % = 72.9% t s = 6ζ = 0.1 ωn = 10)26.8494.9sin(005.11)(︒+-=-t e t c tσ % = 72.9% t s = 3ζ = 0.1 ωn = 1)26.84994.0sin(005.11)(1.0︒+-=-t e t c tσ % = 72.9% t s = 30（2）ζ = 0.5 ωn = 5)6033.4sin(155.11)(5.2︒+-=-t e t c tσ % = 16.3% t s = 1.23-6 （1）图1 ζ = 0.1 ωn = 1 σ % = 72.9% t s = 30图2 ζ = 0.5 ωn = 1图2 ζ = 0.0745 ωn = 0.7453-7 （1）K h = 0.216（2）10)101()1(10)(21++++=s K s s K s h h φ 10)101(10)(22+++=s K s s h φ （3）474.01015.0 16.310====ζωnσ % = 18.4% t p = 1.128 t s = 2（4）原系统 ζ = 0.158 ωn = 3.16 σ % = 60.5% t p = 1.006 t s = 6加入比例微分和速度反馈后，阻尼比增大，使系统超调量减小，响应速度加快。

自动控制原理稳定裕度

从这两方面考虑，则要求系统不仅是稳定的，还应具有一定的安全系数。也就是不仅需要关心系统是否稳定，还应关心系统稳定的程度，这就是所谓的相对稳定性。相对稳定性也称为稳定裕度。
对于最小相位系统，根据奈奎斯特稳定判据知，如果极坐标图不包围 (1，j0) 点，系统是稳定的；如果包围 (1，j0) 点，系统就是不稳定的。因此，可以利用极坐标图与 (1点，的j0) 接近程度来衡量系统的相对稳定性。
和两种稳定裕度来衡量系的稳定程度。
一般来说：幅值裕量：要求大于6dB，一般选10～20dB 相角裕量：要求大于30°，一般选γ＝40°～ 60°
Friday, October 23, 2020
15
三、从波特图上确定增益裕量和相角裕量
根据上节所述的 G( j)H ( j)幅相频率特性图之间的关系，可知在波特图上确定增益裕量的步骤：
当极坐标图通过 (1, j0)点时，幅值裕度为 0dB 。它表明系统已经处于不稳定的边缘，开环增益不能再增加了。当极坐标图在任何非零的有限频率内与负实轴不相交时，由奈奎斯特稳定判据表明系统必然不包围 (1, j0)点，则幅值裕度的分贝值为无穷大，从理论上讲，这意味着在出现不稳定之前，开环增益可达到无穷大。
Friday, October 23, 2020
8
显然，最小相位系统的极坐标图与 (1, j0)点的接近程度可以分别用极坐标图穿过负实轴的位置和极坐标图幅值为1时的相角来表示。
定义极坐标图穿过负实轴（此时 () 180）时对应的
频率 g 为相角穿越频率；定义幅值 A() 1时对应的频率 c为幅值穿越频率。
G(s)
as 1 s2
试确定相角裕度为45°时参数a的值。
G(
j)

河南理工大学自动控制原理第5章第3讲 Nyquist稳定性判据及稳定裕度2012

φ(s) = G(s) = M (s)
1+ G(s)H (s) M (s) + N(s)
设辅助函数：F (s) = 1+ G(s)H (s) = N (s) + M (s) N (s)
☻F(s)的极点是系统的开环极点，一般是已知的；
☻F(s)的零点是系统的闭环极点。
8
辅助方程：F(s) = 1+ G(s)H(s) = N(s) + M (s) N(s)
圆s
=
R⋅e jθ
,R
→ ∞,θ
=
π
2
~
−π
2
Ⅲ部分负虚轴ω = −∞ → 0−
Ⅳ部分为半径为无穷小的右半圆
s
= r ⋅ejβ ,r
→ 0, β
= −π
2
~
π
2
下面讨论对于这种奈魁斯特路径的映射Gk ( jω ) ：
1、第Ⅰ和第Ⅲ部分：常规的奈氏图Gk ( jω)，关于实轴对称；
ω = ∞+
Ⅰ
ω = 0+
[解]：显然这是I型系统。先根据奈
氏路径画出完整的映射曲线。
ω =Байду номын сангаас0−
从图上看出：映射曲线顺时针包围(-1,j0)一圈，逆时针包围(-1,j0) 一圈，所以R=1-1=0，而P = 0 ，故 Z = P − R = 0 ，闭环系统是稳定的。
ω = +∞ −1 ω = −∞
ω = 0+
21
[例5]某最小相位系统的开环频率特性如下图所示，试用奈氏判据判断闭环系统稳定性。
杨金显
yangjinxian@.c n
河南理工大学电气工程与自动化学院1

自动控制原理53稳定裕度共38页文档

自动控制原理53稳定裕度
11、战争满足了，或曾经满足过人的好斗的本能，但它同时还满足了人对掠夺，破坏以及残酷的纪律和专制力的欲望。 ——查·埃利奥特 12、不应把纪律仅仅看成教育的手段。纪律是教育过程的结果，首先是学生集体表现在一切生活领域—— 生产、日常生活、学校、文化等领域中努力的结果。— —马卡连柯(名言网)
13、遵守纪律的风气的培养，只有领导者本身在这方面以身作则才能收到成效。—— 马卡连柯 14、劳动者的组织性、纪律性、坚毅精神以及同全世界劳动者的团结一致，是取得最后胜利的保证。—— 列宁摘自名言网
15、机会是不守纪律的。——雨果
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
பைடு நூலகம்
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
38

自动控制_05e稳定裕度

A(c )
2
c 1 c 2
1, 解得：c 1.25
截止频率处的相角为：
(c ) 90 arctgc arctg0.2c 155.38
相角裕度为： 180 (c ) 180 155.38 24.6
幅值裕度：先求穿越频率ωx 在穿越频率ωx处的相角为：
例5-12 设控制系统如下图 R( s) k C (s) 所示，当K=10和K=100时， s ( s 1)(s 5) 试求系统的相角裕度和幅值裕度。解：相角裕度和幅值裕度可以从Bode图中求得。当k=10时，开环系统Bode如左所示。这时系统的 8dB 相角裕度和幅值裕度大约是21度和8dB。因此系统在不稳定之前， 21 增益可以增加 8dB.
相角裕度和幅值裕度的计算：
相角裕度：先求截止频率ωc
0.2k 2 A( ) (当k 10时) 2 2 | s | | s 1 | | 0.2s 1 | 1 1 0.04
A(c ) 1 ，所以 2 (1 2 )(1 0.04 2 ) 4 在截止频率处，解此方程较困难，由于 c 较小，所以可采用近似解法。
10。所以原 ) 180 30 150 ，从图中看出： c (c ) 20lg A(10) 22dB 始幅频曲线向下移动 Lh 20lg A(c
设新的开环放大系数为K1，原始的开环放大系数为K=200 则有 22 20log K 20log K1 。解得： K1 15
(x ) 90 arctgx arctg0.2x 180

即：arctgx arctg0.2x 90

x 0.2x 1, 解得：x 2.24 由三角函数关系得：

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ts 3
12 10 8 6 4 2 0 0
ts c
n
1 4 4 2 2
c t s
3

6 tan

20 40 60 80
可以看出，调节时间与相角裕度和幅值穿越频率都有关系。如果两个二阶系统的相同，则它们的超调量也相同，这时比较大的系统，调节时间较短。
17
例5-19 一单位反馈控制系统，其开环传递函数 7 G( s) s(0.087 s 1) 试用相角裕度估算过渡过程指标p% 与ts。解：系统开环伯德图如图示由图可得， c =7， = 58.7 根据 = 58.7 ，可得 = 0.592，则
5
3.16( s 1) G( s) 2 s (0.1s 1) 2
() = arctan 180 2arctan0.1
= arctan3.16 2arctan0.316 = 37.4 当(g) = 180时 180 = arctang 180 2arctan0.1g arctang =2arctan0.1g 求得 g = 8.94 k g 20 lg h 20 lg A( g ) 20 lg 2 2 9.03dB g 1
（3）具有尽可能大的0分贝频率，以提高闭环系统的快速性。（4）为了提高系统抗干扰能力，开环对数幅频特性高频段应有较大的负斜率。
23
3.7.2 用闭环频率特性分析系统的动态性能 1. 二阶系统
2 n 其闭环传函为 ( s ) 2 2 s 2n s n 其闭环频率特性为 2 n ( j ) 2 2 ( n ) j 2n
5.6 闭环频率特性
一. 开环和闭环频率特性的关系对于单位反馈控制系统，闭环频率特性与开环频率特性的关系为
Gk ( j ) ( j ) 1 Gk ( j )
P 1
Gk ( j ) Gk ( j ) 1 Gk ( j ) 1 Gk ( j ) M ( ) ( )
p % = 9.95% ts = 0.52(s)
直接求解系统，得 = 0.64 ts = 0.522(s) 两者基本上是一致的。
p% = 7.3%
18
L()/dB
20 0 20dB/dec 1 10 11.5
7 G( s) s(0.087 s 1)

40dB/dec
20
0 90 180
0.2 g 0.02 g 1 0.2 g 0.02 g tan 90
1 g 15.8 0.2 0.02
8
最小相位系统中频段的斜率与相对应：中频段的斜率为20dB/dec时， > 0。中频段的斜率为40dB/dec时，可正可负，如果为正，其值比较小。中频段的斜率为60dB/dec时，一定为负。 > 0，系统一定是稳定的。
9
例5-18
L()/dB 20 0
K (T1 s 1) G( s ) 2 s (T2 s 1)
40dB/dec
T1 > T2
20dB/dec =1/T 2 2
1 =1/T1

40dB/dec
()
0
90 180

10
= 180 + ()
= arctan(c /1 ) arctan(c /2 ) (1) c 、2保持不变， 1 (2) c 、1保持不变， 2
2 n 2 2 b
2
0.707
b n 1 2 2 2 4 2 4 4
ts 3
n
b t s
3

1 2 2 2 4 2 4 4
26
2. 高阶系统
M p 0.16 0.4( M r 1)
ts k1
c
k1 2 1.5( M r 1) 2.5( M r 1)
K (T1 s 1) G( s ) 2 s (T2 s 1)
= 180 + arctancT1 180 arctancT2
(3) 1、2保持不变， h =2/1 中频段宽度
h
与中频段的斜率有关，而且还与中频段宽度有关：中频段宽度
11
2
27
5. 7 . 3 开环频域指标与闭环频域指标的关系 1. 与Mr 的关系一般， Mr出现在c 附近，就是说用c 代替小，可近似认为 1
B

G(jc)
0
r 来计算Mr ，并且较 1+G(jc)
AB=∣1+G(jc)∣
于是有
c
A
G( jc ) G( jc ) G( jc ) 1 Mr 1 G( jc ) AB G( jc ) sin sin
()/()

19
2) 高阶系统近似的关系式
1 p 0.16 0.4( 1) sin k1 ts
c
1 1 k1 2 1.5( 1) 2.5( 1)2 sin sin
上式表明，高阶系统的随着的增大而减小，调节时间
随着的增大也减小，且随增大而减小。

1 2
p e
100%
70 60 50 40 30 p 20 10 0 0 0.2 0.4 0.6 0.8 1.0
由图明显看出，越大， p%越小；越小， p% 越大。为使二阶系统不致于振荡太厉害以及调节时间太长，一般希望 16 30 70
② 、c与ts 之间的关系在时域分析中，知
C(s)
由A(c) =1，计算开环截止频率c有 2 n 1 c n 1 4 4 2 2 c c2 ( 2n )2
15
则相角裕度为
() p%
100 80 60 40 20 0
= 180 + (c)
=180 90 arctan(c/2n ) 2 arctan 2 2 1 4 4 在时域分析中，知
① Mr与p%的关系
M ( )

2 n
2 ( n 2 )2 4(n )2
d M ( ) 0 r d
r n 1 2 2
24
Mr
1 2 1 2
当 > 0.707时，不存在谐振峰值，幅频特殊性单调衰减；当 < 0.707时，Mr 越小，系统阻尼性能越好越大， p%越小。
0
A
Gk(j)
0A Gk ( j ) M ( ) 1 Gk ( j ) PA
( ) 0 A PA
12
Mm
M0
0.707M0
二.闭环频率特性（1）零频幅值特性M0 ： = 0时的闭环幅频特性值。
r
b

（2）谐振峰值Mr ：幅频特性极大值与零频幅值之比 Mr = Mm/M0。（3）谐振频率r ：出现谐振峰值时的频率。
= 180+ (c)
因为 > 0，所以闭环系统是稳定的。
6
例5-17
20 0
L()/dB 20dB/dec 10 1 5
K G( s) s(1 0.02 s )(1 0.2 s )
50 40dB/dec

()
0 90 180 270
60dB/dec
1
28
2. c 与b 的关系
5.5 稳定裕度
根据奈氏判据，系统开环幅相曲线临界点附近的形状，对闭环稳定性影响很大。 Im Im Im
-1
Re -1 0
0
Re
-1
0
Re
两个表征系统稳定程度的指标：相角裕度和幅值裕度h。
1
（1）幅值裕度h ：令相角为180时对应的频率为g （相角穿越频率），频率为g 时对应的幅值A(g)的倒数，定义为幅值裕度h ，即 1 h A( g ) 或 20lgh = 20lg A(g)
() Mr 70 p% 8 60 100 7 50 80 6 40 60 5 30 40 4 p 20 20 3 Mr 10 0 2 0 1 0 0.2 0.4 0.6 0.8 1.0
25
② Mr 、 b 与ts 的关系
M ( b )
2 n
( ) 4(n b )
5
10
140.7
50

219.3
7
K G( s) s(1 0.02 s )(1 0.2 s )
() = 90 arctan0.2 arctan0.02 = 180+ (c) = 90 arctan0.2c arctan0.02c c arctan0.2g arctan0.02g = 90
3
L()/dB
c
g
h(dB)

()/(°)
0

180
4
例5-16 已知单位负反馈的最小相位系统，其开环对数幅频特性如图示，试求开环传递函数；计算系统的稳定裕度。 L()/dB 40dB/dec 20dB/dec
1
3.16
10

60dB/dec
k ( s 1) 解：系统的开环传递函数为 G ( s ) 2 s (0.1s 1) 2 k c = 3.16 A( c ) 2 c 2 1 k=频特性过零分贝时的频率为c （幅值穿越频率），则定义相角裕度为
= 180 + (c)
2
A(g)
Im h 具有如下含义：如果系统是稳定的，那么系统的 Re 开环增益增大到原来的h 倍时，则系统就处于临界稳定了。
-1
c
0
具有如下含义：如果

王划一-自动控制原理-5-3稳定裕度

合集下载