2019-2020学年高中数学 2.5.1等比数列前n项和的求解练习 新人教A版必修5

新人教A 版必修5一、选择题1．等比数列{a n }中，已知前4项之和为1，前8项和为17，则此等比数列的公比q 为( )A ．2B ．－2C ．2或－2D ．2或－12．公比为2的等比数列{a n }的各项都是正数，且a 3a 11＝16，那么log 2a 10＝( ) A ．4 B ．5 C ．6 D ．73．设{a n }是由正数组成的等比数列，S n 为其前n 项和，已知a 2a 4＝1，S 3＝7，则S 5＝( )A.152B.314C.334D.1724．若等比数列{a n }对于一切自然数n 都有a n ＋1＝1－23S n ，其中S n 是此数列的前n项和，又a 1＝1，则其公比q 为( ) A ．1 B ．－23 C.13D ．－135．设数列{a n }的通项a n ＝(－1)n －1·n ，前n 项和为S n ，则S xx ＝( ) A ．－xx B ．－1005 C ．xxD ．10056．设S n为等比数列{a n}的前n项和，8a2＋a5＝0，则S5S2＝( )A．11 B．5 C．－8 D．－11二、填空题7．数列{a n}的前n项和S n＝log0.1(1＋n)，则a10＋a11＋…＋a99＝________. 8．设等比数列{a n}的前n项和为S n，若a1＝1，S6＝4S3，则a4＝________.三、解答题9．在等比数列{a n}中，a1＋a n＝66，a2·a n－1＝128，且前n项和S n＝126，求n 及公比q.10．已知{a n}是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列．(1)求数列{a n}的通项；(2)求数列{2a n}的前n项和S n.2-5-1同步检测1 C2 B3 B4 C5 B6 D7 －1 8 39 [解析] ∵a1a n＝a2a n－1＝128，又a1＋a n＝66，∴a1、a n是方程x2－66x＋128＝0的两根，解方程得x1＝2，x2＝64，∴a1＝2，a n＝64或a1＝64，a n＝2，显然q≠1.若a1＝2，a n＝64，由a1－a n q1－q＝126得2－64q＝126－126q，∴q＝2，由a n＝a1q n－1得2n－1＝32，∴n＝6.若a1＝64，a n＝2，同理可求得q＝12，n＝6.综上所述，n的值为6，公比q＝2或1 2 .10 [解析] (1)由题设知公差d≠0，由a1＝1，a1，a3，a9成等比数列得1＋2d1＝1＋8d1＋2d，解得d＝1，或d＝0(舍去)，故{a n}的通项a n＝1＋(n－1)×1＝n.(2)由(1)知2a n＝2n，由等比数列前n项和公式得S n ＝2＋22＋23＋…＋2n＝21－2n1－2＝2n＋1－2.24600 6018 怘@E28618 6FCA 濊36040 8CC8 賈c28003 6D63 浣 21028 5224 判q) 32468 7ED4 绔37379 9203 鈃24431 5F6F 彯。

第1课时等比数列前n项和的求解A级基础巩固一、选择题1．设｛a n｝是公比为正数的等比数列，若a1＝1，a5＝16，则数列{a n｝前7项的和为（）A．63 B．64 C．127 D．128解析：设数列｛a n}的公比为q（q＞0），则有a5＝a1q4＝16，所以q＝2，数列的前7项和为S7＝错误!＝错误!＝127。

答案：C2．设在等比数列｛a n｝中，公比q＝2，前n项和为S n,则错误!的值为( )A。

错误! B.错误! C.错误! D.错误!解析：根据等比数列的公式,得错误!＝错误!＝错误!＝错误!＝错误!.答案：A3．一座七层的塔，每层所点的灯的盏数都等于上面一层的2倍，一共点381盏灯，则底层所点灯的盏数是( )A．190 B．191 C．192 D．193解析：设最下面一层灯的盏数为a1，则公比q＝12，n＝7,由错误!＝381,解得a1＝192。

答案：C4．已知数列｛a n}满足3a n＋1＋a n＝0，a2＝－错误!，则｛a n｝的前10项和等于（) A．－6(1－3－10) B。

错误!(1－3－10）C．3（1－3－10) D．3(1＋3－10)解析：因为3a n＋1＋a n＝0，a2＝－43≠0，所以a n≠0，所以错误!＝－错误!，所以数列｛a n}是以－13为公比的等比数列．因为a2＝－错误!，所以a1＝4，所以S10＝错误!＝3（1－3－10)．答案：C5．已知S n是等比数列｛a n}的前n项和，若存在m∈N*，满足S2mS m＝9，a2ma m＝错误!，则数列{a n｝的公比为（)A．－2 B．2 C．－3 D．3解析：设数列｛a n}的公比为q,若q＝1，则错误!＝2,与题中条件矛盾,故q≠1.因为错误!＝错误!＝q m＋1＝9,所以q m＝8。

所以错误!＝错误!＝q m＝8＝错误!，所以m＝3，所以q3＝8，所以q＝2。

答案：B二、填空题6．在等比数列｛a n}中，公比q＝2,前99项的和S99＝30，则a3＋a6＋a9＋…＋a99＝________．解析：因为S99＝30，即a1（299－1)＝30,数列a3，a6,a9，…，a99也成等比数列且公比为8，所以a3＋a6＋a9＋…a99＝错误!＝错误!＝错误!×30＝错误!。

温馨提示：此套题为Word 版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

课后巩固作业（十四）(30分钟 50分)一、选择题(每小题4分，共16分)1.等比数列2，4，8，16，…的前n 项和S n 等于（ ） （A ）2n+1-1 （B ）2n -2 （C ）2n （D ）2n+1-22.等比数列{a n }的前3项和等于首项的3倍，则该等比数列的公比为（ ）（A ）-2 （B ）1 （C ）-2或1 （D ）2或-13.等比数列{a n }的首项为1，公比为q （q ≠1），前n 项和为S n ，则11a +21a +31a +…+n1a 等于（ ） （A ）n 1S （B ）n 1n Sq- （C ）S n （D ）n 1n 1q S -4.已知等比数列{a n }中,公比q =12,且a 1+a 3+a 5+…+a 99=60,则a 1+a 2+a 3+…+a 100=（ ）(A)100 (B)90 (C)120 (D)30 二、填空题(每小题4分，共8分)5.若等比数列{a n }的首项为1，公比为q ，则它的前n 项和S n 可以用n ，q 表示成S n =_____.6.（2011·北京高考）在等比数列{a n }中，若11a 2=，a 4=-4，则公比q=_____；|a 1|+|a 2|+…+|a n |=______． 三、解答题(每小题8分，共16分)7.已知等比数列{a n }的前n 项和为S n ，若S 4=1，S 8=4,求a 13+a 14+a 15+a 16的值.8.若等比数列前n 项，前2n 项，前3n 项的和分别为S n ,S 2n ,S 3n ,求证：()22n 2n n 2n 3n S S S S S +=+.【挑战能力】（10分）设数列{a n }的前n 项和为S n ,若S 1=1，S 2=2，且S n+1-3S n +2S n-1=0(n ≥2且*n N ∈),试判断数列{a n }是不是等比数列?答案解析1.【解析】选D.由已知条件可得此等比数列的首项a 1=2，公比4q 22==，故前n 项和n n 1n 212S 2212+⨯-==--（）. 2.【解析】选C.由已知可得S 3=3a 1，即a 1+a 1q+a 1q 2=3a 1,又a 1≠0，∴q 2+q-2=0，解得q=1或q=-2.3.【解题提示】构成的新数列11a ，21a ，31a ，…，n a 1是首项为1，公比为1q的等比数列.【解析】选B.∵n nn 11q 1q S 1q 1q⨯--==--（）, ∴nn 123n1111111q T 1a a a a 1q⨯-=+++⋯+=-（） =n n n 1n 1S 1q 11q q q---=-·. 4.【解析】选B.由题意,S 奇=60,∴S 偶=q ·S 奇12=×60=30,∴S 100=S 奇+S 偶=60+30= 90.5.【解析】当q=1时，此数列是各项为1的常数列，故S n =n.当q ≠1时，则n n 1q S 1q-=-.故n n n q 1S 1q q 11q =⎧⎪=-⎨ ≠⎪-⎩（）， （）..答案：n n q 11q q 11q =⎧⎪-⎨ ≠⎪-⎩（） （）6.【解析】∵341a q 42==-，∴q=-2， ∴()n 1n 1a 22-=⨯-，∴|a n |=2n-2，∴|a 1|+|a 2|+…+|a n |()n n 1112122122--==--.答案：-2 2n-1-21[]7.【解题提示】利用等比数列前n 项和的性质，若数列{a n }为等比数列，S n 为其前n 项和，则S n ,S 2n -S n ,S 3n -S 2n ，…仍构成等比数列，其公比为q n （q ≠-1）.【解析】∵数列{a n }为等比数列，∴S 4,S 8-S 4,S 12-S 8,S 16-S 12也构成等比数列，故（S 8-S 4）2=S 4(S 12-S 8),即（4-1）2=1×（S 12-4），解得S 12=13.同理可解得S 16=40，∴a 13+a 14+a 15+a 16=S 16-S 12=40-13=27. 8.【证明】方法一：根据等比数列的性质，有 S 2n =S n +q n S n =S n (1+q n ), S 3n =S n +q n S n +q 2n S n ,所以222n 2n n S S S +=+［S n (1+q n )］2=2n S (2+2q n +q2n ), S n (S 2n +S 3n )=2n S (2+2q n +q2n ). 所以22n 2n S S +=S n (S 2n +S 3n ).方法二：依题意可得S n ,S 2n -S n ,S 3n -S 2n 仍成等比数列，所以（S 2n -S n )2=S n (S 3n -S 2n ),整理得22n 2n S S +=S n (S 2n +S 3n ).【方法技巧】巧用等比数列的前n 项和的性质.(1)“片段和”性质：等比数列{a n }中，公比为q(q ≠-1),前m 项和为S m (S m ≠0),则S m ,S 2m -S m ,S 3m -S 2m ,…,S km -S (k-1)m ,…构成公比为q m 的等比数列，即等比数列的前m 项和与以后依次m 项的和构成等比数列. (2)“相关和”性质：n n n m n m S S q S q +=+⇔=n m nmS S S +- (q 为公比).【挑战能力】【解析】∵S n+1-3S n +2S n-1=0（n ≥2，*n N ∈）, ∴（S n+1-S n ）-2(S n -S n-1)=0, ∴a n+1-2a n =0，即*n 1na 2(n 2,n N )a +=≥∈. ∴a 2,a 3,a 4,…,a n ,…构成公比为2的等比数列. 又a 1=S 1=1,a 2=S 2-S 1=1,∴21a 12a =≠. ∴数列{a n }不是等比数列.。

2021年高中数学 2.5.1等比数列前n 项和的求解练习 新人教A 版必修5►基础梳理1．(1)等比数列的前n 项和公式：当q≠1时，________或________，当q ＝1时，__________．(2)已知数列{a n }是等比数列，a 1＝3，公比q ＝2，则其前6项和S 6＝______． (3)已知数列{a n }是等比数列，a 1＝3，公比q ＝1，则其前6项和S 6＝______．2．(1)等比中项关系：对于数列{a n }(a n ≠0)，若a n a n ＋2＝a 2n ＋1 (n∈N *)，则数列{a n }是________．等比数列的第二项起每一项都是它相邻前一项与相邻后一项的________．(2)已知数列{a n }是等比数列，其通项公式为：a n ＝2·3n －1(n ∈N *)，则a n a n ＋2＝________，a 2n ＋1＝________，所以________________．3．(1)若数列{a n }是等比数列，S n 是其前n 项的和，k ∈N *，那么S k ，S 2k －S k ，S 3k －S 2k 成________(S k ≠0)．(2)已知数列{a n }是等比数列，其通项公式为：a n ＝2n －1(n ∈N *)，则S 2＝______，S 4－S 2＝______，S 6－S 4＝______，故S 2，S 4－S 2，S 6－S 4成______数列．4．(1)若数列{a n }的前n 项和S n ＝p (1－q n)，且p ≠0，q ≠0，q ≠1，则数列{a n }是 __________．(2)数列{a n }的前n 项和S n ＝2(1－3n)，则数列{a n }的通项公式是__________，故数列{a n }是________．基础梳理1．(1)S n ＝a 1（1－q n）1－q S n ＝a 1－a n q1－qS n ＝na 1(2)189 (3)182．(1)等比数列 等比中项(2)4·32n 4·32n a n a n ＋2＝a 2n ＋1 3．(1)等比数列 (2)3 12 48 等比 4．(1)等比数列(2)a n ＝－4·3n －1(n∈N *) 等比数列►自测自评1．设{a n }是公比为正数的等比数列，若a 1＝1，a 5＝16，则数列{a n }前7项的和为( ) A ．63 B ．64 C ．127 D ．1282．数列{2n －1}的前99项和为( )A ．2100－1B ．1－2100C ．299－1D ．1－2993．等比数列1，a ，a 2，a 3，…a n的前n 项和为( )A ．1＋a （1－a n －1）1－a B.1－a n1－aC.a n ＋1－1a －1D ．以上都错4．设f (n )＝2＋24＋27＋…＋23n ＋10(n ∈N *)，则f (n )＝________． 自测自评1．解析：设数列{a n }的公比为q (q ＞0)，则有a 5＝a 1q 4＝16，∴q ＝2，数列的前7项和为S 7＝a 1（1－q 7）1－q ＝1－271－2＝127.答案：C2．解析：a 1＝1，q ＝2，∴S 99＝1×（1－299）1－2＝299－1.答案：C 3．D4．解析：数列2，24，…，23n ＋10是首项为a 1＝2，公比q ＝23＝8，项数为n ＋4的等比数列，∴f (n )＝2（1－8n ＋4）1－8＝27(8n ＋4－1)．答案：27(8n ＋4－1)►基础达标1．等比数列{a n }的通项公式是a n ＝⎝ ⎛⎭⎪⎫12n，则前3项和S 3的值为( ) A .38B .58C .78D .981．解析：S 3＝a 1＋a 2＋a 3＝12＋14＋18＝78.故选C.答案：C2．1和4的等差中项和等比中项分别是( ) A ．5，2 B ．5，－2 C .52，4 D .52，±22．解析：1和4的等差中项为1＋42＝52，等比中项为±1×4＝±2.故选D.答案：D3．(xx·大纲全国卷)已知数列{a n }满足3a n ＋1＋a n ＝0，a 2＝－43，则{a n }的前10项和等于( )A . －6(1－3－10)B .19(1－3－10) C ．3(1－3－10) D ．3(1＋3－10)3．解析：先根据等比数列的定义判断数列{a n }是等比数列，得到首项与公比，再代入等比数列前n 项和公式计算．由3a n ＋1＋a n ＝0，得a n ＋1a n ＝－13，故数列{a n }是公比q ＝－13的等比数列．又a 2＝－43，可得a 1＝4，所以S 10＝4⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫－13101－⎝ ⎛⎭⎪⎫－13＝3(1－3－10)．答案：C4．(xx·新课标全国卷Ⅱ)等比数列{a n }的前n 项和为S n ，已知S 3＝a 2＋10a 1，a 5＝9，则a 1＝( )A .13B ．－13C .19D ．－194．解析：先设出公比q ，然后根据已知条件列出方程组，求出a 1. 设公比为q ，∵S 3＝a 2＋10a 1，a 5＝9，∴⎩⎪⎨⎪⎧a 1＋a 2＋a 3＝a 2＋10a 1，a 1q 4＝9，∴⎩⎪⎨⎪⎧a 1q 2＝9a 1，a 1q 4＝9， 解得a 1＝19，故选C.答案：C5．数列1，1＋2，1＋2＋22，…，1＋2＋22＋…＋2n －1的前n 项和等于( ) A ．2n ＋1－n B ．2n ＋1－n －2 C ．2n －n D ．2n5．解析：设此数列为{a n }，则a n ＝1＋2＋22＋…＋2n －1＝2n －1，∴前n 项和S n ＝2n ＋1－n －2.故选B.答案：B ►巩固提高6．等比数列{a n }中，已知对任意正整数n ，a 1＋a 2＋a 3＋…＋a n ＝2n －1，则a 21＋a 22＋a 23＋…＋a 2n 等于( )A ．(2n －1)2B .13(2n －1) C ．4n －1 D .13(4n －1)6．解析：令n ＝1得a 1＝1；当n ≥2时，由a 1＋a 2＋…＋a n ＝2n－1，得a 1＋a 2＋…＋a n －1＝2n －1－1， 两式相减得a n ＝2n －2n －1＝2n －1.∴a n ＝2n －1，a 2n ＝4n －1.∴a 21＋a 22＋…＋a 2n ＝1－4n1－4＝13(4n－1)．故选D.答案：D7．数列1，x ，x 2，x 3，…，x n －1，…的前n 项和是( )A .1－x n1－x B .1－x n －11－xC .1－x n ＋11－xD ．以上均不正确7．解析：1＋x ＋x 2＋…＋x n －1＝⎩⎪⎨⎪⎧n ，x ＝1，1－x n 1－x，x ≠1.故选D.答案：D8．(xx·北京西城区期末)已知{a n }是公比为2的等比数列，若a 3－a 1＝6，则a 1＝________；1a 21＋1a 22＋…＋1a 2n＝________．8．2 13⎝⎛⎭⎪⎫1－14n9．已知数列{a n }：a 1，a 2，a 3，…，a 4，构造一个新数列a 1，a 2－a 1，a 3－a 2，…，a n －a n －1，此数列是首项为1，公比为13的等比数列．(1)求数列{a n }的通项；(2)求数列{a n }的前n 项和S n .9．分析：(1)观察新数列的各项发现其前n 项和为a n ，将问题转化为等比数列的前n 项和．(2)根据(1)中求出的通项公式求出S n .解析：(1)当n ≥2时，a n ＝a 1＋(a 2－a 1)＋(a 3－a 2)＋…＋(a n －a n －1)＝1＋13＋132＋…＋13n －1＝1－⎝ ⎛⎭⎪⎫13n1－13＝32⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫13n .当n ＝1时，a 1＝1，也适合． ∴a n ＝32⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫13n (n ∈N *)．(2)S n ＝a 1＋a 2＋a 3＋…＋a n＝32⎝ ⎛⎭⎪⎫1－13＋32⎝ ⎛⎭⎪⎫1－132＋32⎝ ⎛⎭⎪⎫1－133＋…＋32⎝ ⎛⎭⎪⎫1－13n＝32⎣⎢⎡⎦⎥⎤n －⎝ ⎛⎭⎪⎫13＋132＋133＋ (13)＝32⎣⎢⎡⎦⎥⎤n －13⎝ ⎛⎭⎪⎫1－13n1－13＝34(2n －1)＋14⎝ ⎛⎭⎪⎫13n －1.10．已知等差数列{a n }及等比数列{b n }，其中b 1＝1，公比q<0，且数列{a n ＋b n }的前三项分别为2、1、4.(1)求a n 及q ；(2)求数列{a n ＋b n }的前n 项和P n .10．解析：(1)设{a n }的首项为a 1，公差为d ，∵a 1＋b 1＝2，a 2＋b 2＝1，a 3＋b 3＝4，∴a 1＋1＝2，a 1＋d ＋q ＝1，a 1＋2d ＋q 2＝4.解得：a 1＝1，q ＝－1或3，∵q <0，∴q ＝－1，d ＝1.∴a n ＝a 1＋(n －1)d ＝1＋(n －1)＝n (n ∈N *)． (2)记数列{a n }及{b n }的前n 项和分别为S n 、T n ，则S n ＝na 1＋n （n －1）2d ＝12n (n ＋1)，T n ＝b 1（1－q n ）1－q ＝1－（－1）n 1－（－1）＝1－（－1）n2.当n 为偶数时，T n ＝0；当n 为奇数时，T n ＝1，故当n 为偶数时，P n ＝S n ＝12n (n ＋1)＝12n2＋12n ； 当n 为奇数时，P n ＝S n ＋1＝12n (n ＋1)＋1＝12n 2＋12n ＋1.1．在等比数列中，有五个元素：a 1，q ，n ，a n ，S n ，其中a 1与q 是两个基本的量，数列中其他各项可以用a 1与q 表示，由通项公式、前n 项和公式及已知条件列出方程及方程组是解决这一类问题的基本方法．2．等比数列求和时小心分公比q ＝1与q≠1讨论．3．研究数列时很多时候需要从通项上入手，从第n 项是什么着手，这种方法对于解决问题很有好处．U24275 5ED3 廓=30526 773E 眾22212 56C4 囄22489 57D9 埙Vn40265 9D49 鵉a 26954 694A 楊31866 7C7A 籺39818 9B8A 鮊37586 92D2 鋒。

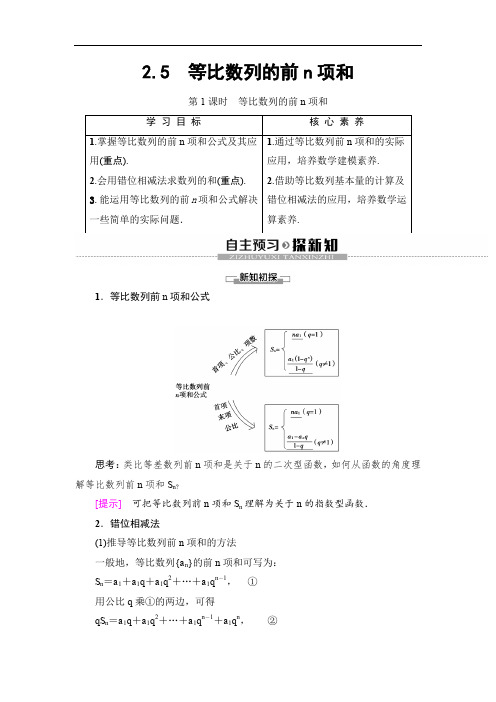
2.5 等比数列的前n 项和第1课时 等比数列的前n 项和1．等比数列前n 项和公式思考：类比等差数列前n 项和是关于n 的二次型函数，如何从函数的角度理解等比数列前n 项和S n ?[提示] 可把等比数列前n 项和S n 理解为关于n 的指数型函数． 2．错位相减法(1)推导等比数列前n 项和的方法一般地，等比数列{a n }的前n 项和可写为： S n ＝a 1＋a 1q ＋a 1q 2＋…＋a 1q n －1， ① 用公比q 乘①的两边，可得 qS n ＝a 1q ＋a 1q 2＋…＋a 1q n －1＋a 1q n ，②由①－②，得(1－q )S n ＝a 1－a 1q n ， 整理得S n ＝a 1（1－q n ）1－q(q ≠1)．(2)我们把上述方法叫错位相减法，一般适用于数列{a n ·b n }前n 项和的求解，其中{a n }为等差数列，{b n }为等比数列，且q ≠1.思考：等比数列的前n 项和公式的推导还有其他的方法吗？[提示] 根据等比数列的定义，有：a 2a 1＝a 3a 2＝a 4a 3＝…＝a n a n －1＝q ，再由合比定理，则得a 2＋a 3＋a 4＋…＋a na 1＋a 2＋a 3＋…＋a n －1＝q ，即S n －a 1S n －a n＝q ，进而可求S n .1．等比数列1，x ，x 2，x 3，…(x ≠0)的前n 项和S n 为( ) A ．1－x n 1－xB ．1－x n －11－xC ．⎩⎨⎧1－x n1－x （x ≠1），n （x ＝1）D ．⎩⎨⎧1－x n －11－x （x ≠1），n （x ＝1）C [当x ＝1时，数列为常数列，又a 1＝1，所以S n ＝n . 当x ≠1时，q ＝x ，S n ＝a 1（1－x n ）1－x ＝1－x n1－x.]2．等比数列{a n }中，a 1＝1，q ＝2，则S 5＝________． 31 [S 5＝a 1（1－q 5）1－q ＝1－251－2＝31.]3．数列12，24，38，416，…的前10项的和S 10＝________． 509256[S 10＝12＋24＋38＋…＋929＋10210， 则12S 10＝14＋28＋…＋9210＋10211.两式相减得，12S 10＝12＋14＋18＋…＋1210－10211＝12⎣⎢⎢⎡⎦⎥⎥⎤1－⎝ ⎛⎭⎪⎫12101－12－10211，所以S 10＝509256.]4．某厂去年产值为a ，计划在5年内每年比上一年的产值增长10%，从今年起5年内，该厂的总产值为________．11(1.15－1)a [去年产值为a ，从今年起5年内各年的产值分别为1.1a ，1.12a ，1.13a ，1.14a ，1.15a .所以1.1a ＋1.12a ＋1.13a ＋1.14a ＋1.15a ＝a ·1.1－1.161－1.1＝11(1.15－1)a.]n (1)S 2＝30，S 3＝155，求S n ； (2)a 1＋a 3＝10，a 4＋a 6＝54，求S 5；(3)a 1＋a n ＝66，a 2a n －1＝128，S n ＝126，求q . [解] (1)由题意知 ⎩⎨⎧a 1（1＋q ）＝30，a 1（1＋q ＋q 2）＝155， 解得⎩⎨⎧a 1＝5，q ＝5或⎩⎪⎨⎪⎧a 1＝180，q ＝－56.从而S n ＝14×5n ＋1－54或S n ＝1 080×⎣⎢⎢⎡⎦⎥⎥⎤1－⎝ ⎛⎭⎪⎫－56n 11. (2)法一：由题意知⎩⎪⎨⎪⎧a 1＋a 1q 2＝10，a 1q 3＋a 1q 5＝54，解得⎩⎪⎨⎪⎧a 1＝8，q ＝12，从而S 5＝a 1（1－q 5）1－q ＝312. 法二：由(a 1＋a 3)q 3＝a 4＋a 6， 得q 3＝18，从而q ＝12. 又a 1＋a 3＝a 1(1＋q 2)＝10，所以a 1＝8，从而S 5＝a 1（1－q 5）1－q ＝312.(3)因为a 2a n －1＝a 1a n ＝128，所以a 1，a n 是方程x 2－66x ＋128＝0的两根． 从而⎩⎨⎧a 1＝2，a n ＝64或⎩⎨⎧a n ＝2，a 1＝64.又S n ＝a 1－a n q 1－q＝126，所以q 为2或12.1．在等比数列 {a n }的五个量a 1，q ，a n ，n ，S n 中，已知其中的三个量，通过列方程组，就能求出另外两个量，这是方程思想与整体思想在数列中的具体应用．2．在解决与前n 项和有关的问题时，首先要对公比q ＝1或q ≠1进行判断，若两种情况都有可能，则要分类讨论．1．在等比数列{a n }中．(1)若a 1＝2，a n ＝162，S n ＝112，求n 和q ； (2)已知S 4＝1，S 8＝17，求a n .[解] (1)由S n ＝a 1－a n q 1－q 得112＝2－162q1－q ，∴q ＝－2，又由a n ＝a 1q n －1得162＝2(－2)n －1，∴n ＝5.(2)若q ＝1，则S 8＝2S 4，不合题意，∴q ≠1， ∴S 4＝a 1（1－q 4）1－q＝1，S 8＝a 1（1－q 8）1－q＝17，两式相除得1－q 81－q 4＝17＝1＋q 4，∴q ＝2或q ＝－2，∴a 1＝115或a 1＝－15，∴a n ＝115·2n －1或－15·(－2)n －1.从借贷后第二个月开始等额还贷，分6个月付清，试问每月应支付多少元？(1.016≈1.061，1.015≈1.051)思路探究：解决等额还贷问题关键要明白以下两点：(1)所谓复利计息，即把上期的本利和作为下一期本金，在计算时每一期本金的数额是不同的，复利的计算公式为S ＝P (1＋r )n ，其中P 代表本金，n 代表存期，r 代表利率，S 代表本利和．(2)从还贷之月起，每月还贷金额是构成等比数列还是等差数列，首项是什么，公比或公差是多少．[解] 法一：设每个月还贷a 元，第1个月后欠款为a 0元，以后第n 个月还贷a 元后，还剩下欠款a n 元(1≤n ≤6)，则a 0＝10 000，a 1＝1.01a 0－a ， a 2＝1.01a 1－a ＝1.012a 0－(1＋1.01)a ， …a 6＝1.01a 5－a ＝…＝1.016a 0－[1＋1.01＋…＋1.015]a . 由题意，可知a 6＝0，即1.016a 0－[1＋1.01＋…＋1.015]a ＝0， a ＝1.016×1021.016－1.∵1.016≈1.061，∴a ＝1.061×1021.061－1≈1 739.故每月应支付1 739元．法二：一方面，借款10 000元，将此借款以相同的条件存储6个月，则它的本利和为S 1＝104(1＋0.01)6＝104×(1.01)6(元)．另一方面，设每个月还贷a 元，分6个月还清，到贷款还清时，其本利和为 S 2＝a (1＋0.01)5＋a (1＋0.01)4＋…＋a＝a [（1＋0.01）6－1]1.01－1＝a [1.016－1]×102(元)．由S 1＝S 2，得a ＝1.016×1021.016－1.以下解法同法一，得a ≈1 739，故每月应支付1 739元．解数列应用题的具体方法步骤(1)认真审题，准确理解题意，达到如下要求：①明确问题属于哪类应用问题，即明确是等差数列问题还是等比数列问题，还是含有递推关系的数列问题？是求a n ，还是求S n ？特别要注意准确弄清项数是多少．②弄清题目中主要的已知事项．(2)抓住数量关系，联想数学知识和数学方法，恰当引入参数变量，将文字语言翻译成数学语言，将数量关系用数学式子表达．(3)将实际问题抽象为数学问题，将已知与所求联系起来，列出满足题意的数学关系式．2．一个热气球在第一分钟上升了25 m 的高度，在以后的每一分钟里，它上升的高度都是它在前一分钟里上升高度的80%. 这个热气球上升的高度能超过125 m 吗？[解] 用a n 表示热气球在第n 分钟上升的高度， 由题意，得a n ＋1＝45a n ，因此，数列{a n }是首项a 1＝25，公比q ＝45的等比数列．热气球在前n 分钟内上升的总高度为S n ＝a 1＋a 2＋…＋a n ＝a 1（1－q n ）1－q ＝25×⎣⎢⎢⎡⎦⎥⎥⎤1－⎝ ⎛⎭⎪⎫45n 1－45＝125×[1－(45)n]<125. 故这个热气球上升的高度不可能超过125 m.1．对于S 64＝1＋2＋4＋8＋…＋262＋263，用2乘以等式的两边可得2S 64＝2＋4＋8＋…＋262＋263＋264，对这两个式子作怎样的运算能解出S 64?[提示] 比较两式易知，两式相减能消去同类项，解出S 64，即S 64＝1－2641－2＝264－1.2．由项数相等的等差数列{n }与等比数列{2n }相应项的积构成新的数列{n ·2n }是等比数列吗？是等差数列吗？该数列的前n 项和S n 的表达式是什么？[提示] 由等差数列及等比数列的定义可知数列{n ·2n }既不是等差数列，也不是等比数列．该数列的前n 项和S n 的表达式为S n ＝1·21＋2·22＋3·23＋…＋n ·2n .3．在等式 S n ＝1·21＋2·22＋3·23＋…＋n ·2n 两边同乘以数列{2n }的公比后，该等式的变形形式是什么？认真观察两式的结构特征，你能将求S n 的问题转化为等比数列的前n 项和问题吗？[提示] 在等式S n ＝1·21＋2·22＋3·23＋…＋n ·2n ，① 两边同乘以{2n }的公比可变形为2S n ＝1·22＋2·23＋3·24＋…＋(n －1)·2n ＋n ·2n ＋1，② ②－①得：S n ＝－1·21－22－23－24－…－2n ＋n ·2n ＋1 ＝－(21＋22＋23＋…＋2n )＋n ·2n ＋1.此时可把求S n 的问题转化为求等比数列{2n }的前n 项和问题．我们把这种求由一个等差数列{an }和一个等比数列{b n }相应项的积构成的数列{a n b n }前n 项和的方法叫错位相减法．【例3】 已知等比数列{a n }满足：a 1＝12，a 1，a 2，a 3－18成等差数列，公比q ∈(0，1)，(1)求数列{a n }的通项公式；(2)设b n ＝na n ，求数列{b n }的前n 项和S n .思路探究：(1)根据a 1，a 2，a 3－18成等差数列求得公比q ，写出通项公式； (2)由b n ＝na n 可知利用错位相减法求和． [解] (1)设等比数列{a n }的公比为q ，a 1＝12，因为a 1，a 2，a 3－18成等差数列，所以2a 2＝a 1＋a 3－18， 即得4q 2－8q ＋3＝0， 解得q ＝12或q ＝32，又因为q ∈(0，1)，所以q ＝12， 所以a n ＝12·⎝ ⎛⎭⎪⎫12n －1＝12n .(2)根据题意得b n ＝na n ＝n2n ， S n ＝12＋222＋323＋…＋n 2n ， ① 12S n ＝122＋223＋324＋…＋n 2n ＋1， ②作差得12S n ＝12＋122＋123＋…＋12n －n 2n ＋1，S n ＝2－(n ＋2)⎝ ⎛⎭⎪⎫12n.1．本题中设c n ＝na n，求数列{c n }的前n 项和S n ′.[解] 由题意知c n ＝n ·2n ，所以S n ′＝1×21＋2×22＋3×23＋…＋(n －2)×2n －2＋(n －1)×2n －1＋n ·2n ， 2S n ′＝1×22＋2×23＋3×24＋…＋(n －2)×2n －1＋(n －1)×2n ＋n ·2n ＋1， 两式相减得：－S n ′＝1×21＋22＋23＋24＋…＋2n －1＋2n －n ·2n ＋1＝2（1－2n ）1－2－n ·2n ＋1＝(1－n )·2n ＋1－2，所以S n ′＝(n －1)·2n ＋1＋2.2．本题中设d n ＝(2n －1)a n ，求数列{d n }的前n 项和T n . [解] 由题意可得：T n ＝1×12＋3×122＋…＋(2n －1)×12n ，12T n ＝1×122＋3×123＋…＋(2n －3)×12n ＋(2n －1)×12n ＋1， 两式相减得12T n ＝1×12＋2×122＋…＋2×12n －(2n －1)×12n ＋1＝12＋12×1－12n －11－12－(2n －1)×12n ＋1＝32－12n －1－2n －12n ＋1，所以T n ＝3－42n －2n －12n ＝3－2n ＋32n.错位相减法的适用题目及注意事项(1)适用范围：它主要适用于{a n }是等差数列，{b n }是等比数列，求数列{a n b n }的前n 项和．(2)注意事项：①利用“错位相减法”时，在写出S n 与qS n 的表达式时，应注意使两式错对齐，以便于作差，正确写出(1－q )S n 的表达式．②利用此法时要注意讨论公比q 是否等于1的情况．1．在等比数列的通项公式和前n 项和公式中，共涉及五个量：a 1，a n ，n ，q ，S n ，其中首项a 1和公比q 为基本量，且“知三求二”．2．前n 项和公式的应用中，注意前n 项和公式要分类讨论，即当q ≠1和q ＝1时是不同的公式形式，不可忽略q ＝1的情况．3．一般地，如果数列{a n }是等差数列，{b n }是等比数列且公比为q ，求数列{a n ·b n }的前n 项和时，可采用错位相减法求和.1．判断正误(1)求等比数列{a n }的前n 项和时可直接套用公式S n ＝a 1（1－q n ）1－q 来求．( )(2)若首项为a 的数列既是等差数列又是等比数列，则其前n 项和为S n ＝na .( )(3)若某数列的前n 项和公式为S n ＝－aq n ＋a (a ≠0，q ≠0且q ≠1，n ∈N *)，则此数列一定是等比数列．( )[答案] (1)× (2)√ (3)√[提示] (1)错误．在求等比数列前n 项和时，首先应看公比q 是否为1，若q ≠1，可直接套用，否则应讨论求和．(2)正确．若数列既是等差数列，又是等比数列，则是非零常数列，所以前n 项和为S n ＝na .(3)正确．根据等比数列前n 项和公式S n ＝a 1（1－q n ）1－q (q ≠0且q ≠1)变形为S n ＝a 11－q －a 11－q q n (q ≠0且q ≠1)，若令a ＝a 11－q，则和式可变形为S n ＝a －aq n .2．已知等比数列{a n }的首项a 1＝3，公比q ＝2，则S 5等于( ) A ．93 B ．－93 C ．45 D ．－45 A [S 5＝a 1（1－q 5）1－q ＝3（1－25）1－2＝93.]3．在公比为整数的等比数列{a n }中，如果a 1＋a 4＝18，a 2＋a 3＝12，则这个数列的前8项之和S 8＝________．510 [a 1＋a 4＝a 1(1＋q 3)＝18，a 2＋a 3＝a 1(q ＋q 2)＝12，两式联立解得q ＝2或12，而q 为整数，所以q ＝2，a 1＝2，代入公式求得S 8＝2（1－28）1－2＝510.]4．求和：12＋34＋58＋716＋…＋2n －12n .[解] 设S n ＝12＋34＋58＋716＋…＋2n －12n＝12＋322＋523＋724＋…＋2n －32n －1＋2n －12n ，① 则12S n ＝122＋323＋524＋…＋2n －32n ＋2n －12n ＋1.② ①－②，得12S n ＝12＋222＋223＋224＋…＋22n －2n －12n ＋1 ＝12＋12＋122＋…＋12n －1－2n －12n ＋1 ＝12＋12－12n －1×121－12－2n －12n ＋1＝32－12n －1－2n －12n ＋1＝32－2n ＋32n ＋1，∴S n ＝3－2n ＋32n .。

2019-2020学年高中数学 2.5等比数列的前n 项和（第1课时)课后练习（含解析) 新人教A 版必修5【巩固演练】1.等比数列{a n }中，公比q=-2，S 5=44，则a 1的值为( )(A)4 (B)-4 (C)2 (D)-22.设{a n }是公比为正数的等比数列，若a 1=1，a 5=16，则数列{a n }的前6项的和为( )(A)63 (B)64 (C)127 (D)1283设{a n }是等比数列，其前n 项和为S n ，且S 3=3a 3，求此数列的公比q.4.设S n 为等比数列{a n }的前n 项和，8a 2+a 5=0，则52S S ( )(A)-11 (B)-8 b (C)5 (D)115.在等比数列{a n }中，若a 1=12，a 4=-4，则公比q=______；|a 1|+|a 2|+…+|a n |=_______. 【挑战能力】6.已知等比数列{a n }中，若前10项的和是10，前20项的和是30，则前30项的和是______.7.数列123424816，，，，…的前10项的和为( ) (A)507256(B)507128 (C)509128 (D)509256人教A 必修5第二章 2.5等比数列前n 项和第一课时课后练习答案1【解析】选A. 515a (1q )S 441q -==-，故51a [1(2)]441(2)--=--，解得a 1=4. 2.【解析】选A.a 1=1，a 5=16，则q=2，6616a (1q )12S 1q 12--==--63.= 3. 【解析】当{a n }为常数列时，q=1；当q ≠1时，S 3=3a 3，所以3211a (1q )3a q 1q-=-，解得1q 2=-， 综上知，q=1或1q 2=-， 4.【解析】选A.设等比数列的首项为a 1，公比为q.由已知q=1不成立，因此q ≠1.又因为8a 2+a 5=0，所以8a 1q+a 1q 4=0，所以q 3+8=0，所以q=-2， 所以551221S a (1q )1q S 1q a (1q )--=⋅--5521q 1(2)11.1q 14---===--- 5.【解析】∵a 4=12q 3=-4，∴q=-2， ∴a n =12×(-2)n-1，∴|a n |=2n-2， ∴|a 1|+|a 2|+…+|a n |=()n n 1112122122--=--.答案：-2 n 1122-- 6．【解析】因为数列{a n }是等比数列，所以有S 10,S 20-S 10,S 30-S 20成等比数列， ∴(S 20-S 10)2=S 10(S 30-S 20)，即(30-10)2=10×(S 30-30)，得S 30-30=40，解得S 30=70.7.【解析】选D.∵a n =nn 2， ∴S 10=234101*********,22222+⨯+⨯+⨯+⋯+⨯ 12S 10=234511111112341022222+⨯+⨯+⨯+⋯+⨯， 两式相减得，1 2S10=23451011 111111110 2222222+++++⋯+-⨯=101111[1()]13509 22101, 12512512 12--⨯=-=-∴S10=509 256.。

2.5 等比数列前n 项和特色训练(一)一、等比数列前n 项和的计算例1 在等比数列{a n }中，S 3＝72，S 6＝632，求a n .分析 要求a n ，需求首项a 1，公比q ，由条件可列出关于a 1和q 的两个方程，解方程组即可．解：►变式训练1 在等比数列{a n }中，a 1＋a n ＝66，a 3a n －2＝128，S n ＝126，求n 和q .解：二、利用等比数列前n 项和的性质解题例2 在等比数列{a n }中，已知S n ＝48，S 2n ＝60，求S 3n . 分析 可用等比数列前n 项和公式求解，也可用等比数列的性质S n ，S 2n －S n ，S 3n －S 2n 成等比数列求解．解：►变式训练2 等比数列的前n 项和为S n ，若S 10＝10，S 20＝30，S 60＝630，求S 70的值．解：三、错位相减法的应用例3 求和：S n ＝x ＋2x 2＋3x 3＋…＋nx n(x ≠0)． 分析 分x ＝1和x ≠1两种情况． 解：►变式训练3 求数列1,3a,5a 2,7a 3，…，(2n －1)a n －1的前n 项和．解2.5 等比数列前n 项和特色训练(二)一、等比数列前n 项和的证明问题例1 设{a n }是由正数组成的等比数列，S n 是其前n 项和，证明：log 0.5S n ＋log 0.5S n ＋22>log 0.5S n ＋1.证明：►变式训练1 已知等比数列前n 项，前2n 项，前3n 项的和分别为S n ，S 2n ，S 3n ，求证：S 2n ＋S 22n ＝S n (S 2n ＋S 3n )．证明二、等比数列前n 项和的实际应用例2 为保护我国的稀土资源，国家限定某矿区的出口总量不能超过80吨，该矿区计划从2010年开始出口，当年出口a 吨，以后每年出口量均比上一年减少10%.(1)以2010年为第一年，设第n 年出口量为a n 吨，试求a n 的表达式；(2)因稀土资源不能再生，国家计划10年后终止该矿区的出口，问2010年最多出口多少吨？(保留一位小数)参考数据：0.910≈0.35. 解：►变式训练2一个热气球在第一分钟上升了25 m 的高度，在以后的每一分钟里，它上升的高度都是它在前一分钟里上升高度的80%.这个热气球上升的高度能超过125 m 吗？解三、等差数列、等比数列的综合问题例3 设{a n }是等差数列，b n ＝⎝ ⎛⎭⎪⎫12a n ，已知：b 1＋b 2＋b 3＝218，b 1b 2b 3＝18，求等差数列的通项a n .解►变式训练3 在等比数列{a n }中，a n >0 (n ∈N *)，公比q ∈(0,1)，且a 1a 5＋2a 3a 5＋a 2a 8＝25，又a 3与a 5的等比中项为2.(1)求数列{a n }的通项公式；(2)设b n ＝log 2 a n ，数列{b n }的前n 项和为S n ，当S 11＋S 22＋…＋S nn最大时，求n 的值． 2.5 等比数列前n 项和特色训练(一)参考答案例1解 由已知S 6≠2S 3，则q ≠1，又S 3＝72，S 6＝632，即⎩⎪⎨⎪⎧a 1(1－q 3)1－q ＝72， ①a 1(1－q 6)1－q ＝632. ②②÷①得1＋q 3＝9，∴q ＝2.可求得a 1＝12，因此a n ＝a 1q n －1＝2n －2.►变式训练1解 ∵a 3·a n －2＝a 1·a n ，∴a 1a n ＝128，解方程组⎩⎪⎨⎪⎧a 1a n ＝128，a 1＋a n ＝66，得①⎩⎪⎨⎪⎧a 1＝64，a n ＝2，或②⎩⎪⎨⎪⎧a 1＝2，a n ＝64.将①代入S n ＝a 1－a n q1－q，可得q ＝12，由a n ＝a 1q n －1可解得n ＝6.将②代入S n ＝a 1－a n q1－q，可得q ＝2，由a n ＝a 1qn －1可解得n ＝6.故n ＝6，q ＝12或2.例2解 方法一 因为S 2n ≠2S n ，所以q ≠1，由已知得⎩⎪⎨⎪⎧a 1(1－q n )1－q ＝48a 1(1－q 2n)1－q＝60①②②÷①得1＋q n＝54，即q n＝14.③将③代入①得a 11－q ＝64，所以S 3n ＝a 1(1－q 3n )1－q ＝64×⎝⎛⎭⎪⎫1－143＝63.方法二 因为{a n }为等比数列，所以S n ，S 2n －S n ，S 3n －S 2n 也成等比数列，所以(S 2n －S n )2＝S n (S 3n －S 2n )，所以S 3n ＝(S 2n －S n )2S n＋S 2n ＝(60－48)248＋60＝63.►变式训练2 等比数列的前n 项和为S n ，若S 10＝10，S 20＝30，S 60＝630，求S 70的值．解 设b 1＝S 10，b 2＝S 20－S 10，…，则b 7＝S 70－S 60.因为S 10，S 20－S 10，S 30－S 20，…，S 70－S 60成等比数列，所以b 1，b 2，…，b 7成等比数列，首项为b 1＝10，公比为q ＝b 2b 1＝2010＝2. 求得b 7＝10·26＝640.由S 70－S 60＝640，得S 70＝1 270. 例3解 (1)当x ＝1时，S n ＝1＋2＋3＋…＋n ＝n (n ＋1)2.(2)当x ≠1时，S n ＝x ＋2x 2＋3x 3＋…＋nx n ，xS n ＝x 2＋2x 3＋3x4＋…＋(n －1)x n ＋nx n ＋1，∴(1－x )S n ＝x ＋x 2＋x 3＋…＋x n －nx n ＋1＝x (1－x n)1－x－nx n ＋1.∴S n ＝x (1－x n )(1－x )2－nx n ＋11－x. 综上可得S n＝⎩⎪⎨⎪⎧n (n ＋1)2 (x ＝1)x (1－x n)(1－x )2－nxn ＋11－x (x ≠1且x ≠0).►变式训练3 解 (1)当a ＝0时，S n ＝1.(2)当a ＝1时，数列变为1,3,5,7，…，(2n －1)，则S n ＝n [1＋(2n －1)]2＝n 2.(3)当a ≠1且a ≠0时，有S n ＝1＋3a ＋5a 2＋7a 3＋…＋(2n －1)a n－1①aS n ＝a ＋3a 2＋5a 3＋7a 4＋…＋(2n －1)a n ②①－②得S n －aS n ＝1＋2a ＋2a 2＋2a 3＋…＋2a n －1－(2n －1)a n，(1－a )S n ＝1－(2n －1)a n ＋2(a ＋a 2＋a 3＋a 4＋…＋a n －1)＝1－(2n －1)a n ＋2·a (1－a n －1)1－a ＝1－(2n －1)a n＋2(a －a n)1－a，又1－a ≠0，∴S n ＝1－(2n －1)a n 1－a ＋2(a －a n)(1－a )2.综上，S n＝⎩⎪⎨⎪⎧1 (a ＝0)n 2(a ＝1)1－(2n －1)a n1－a ＋2(a －a n)(1－a )2(a ≠0且a ≠1).§2.5 等比数列前n 项和特色训练(二)参考答案例1 证明 设{a n }的公比为q ，由题设知a 1>0，q >0，当q ＝1时，S n ＝na 1，从而S n ·S n ＋2－S 2n ＋1＝na 1·(n ＋2)a 1－(n ＋1)2a 21＝－a 21<0.当q ≠1时，S n ＝a 1(1－q n )1－q，从而S n ·S n ＋2－S 2n ＋1＝a 21(1－q n )(1－q n ＋2)(1－q )2－a 21(1－q n ＋1)2(1－q )2＝－a 21q n <0.综上知，S n ·S n ＋2<S 2n ＋1，∴log 0.5(S n ·S n ＋2)>log 0.5S 2n ＋1. 即log 0.5S n ＋log 0.5S n ＋22>log 0.5S n ＋1.►变式训练1证明 方法一 设此等比数列的公比为q ，首项为a 1，当q ＝1时，则S n ＝na 1，S 2n ＝2na 1，S 3n ＝3na 1，S 2n ＋S 22n ＝n 2a 21＋4n 2a 21＝5n 2a 21，S n (S 2n ＋S 3n )＝na 1(2na 1＋3na 1)＝5n 2a 21，∴S 2n ＋S 22n ＝S n (S 2n ＋S 3n )．当q ≠1时，则S n ＝a 11－q (1－q n)，S 2n ＝a 11－q (1－q 2n)，S 3n ＝a 11－q(1－q 3n)，∴S 2n ＋S22n＝⎝⎛⎭⎪⎫a 11－q 2·[(1－q n )2＋(1－q 2n )2]＝⎝ ⎛⎭⎪⎫a 11－q 2·(1－q n )2·(2＋2q n ＋q 2n )．又S n (S 2n ＋S 3n )＝⎝⎛⎭⎪⎫a 11－q 2·(1－q n )2·(2＋2q n ＋q 2n)， ∴S 2n ＋S 22n ＝S n (S 2n ＋S 3n )．方法二 根据等比数列性质，有S 2n ＝S n ＋q n S n ＝S n (1＋q n)，S 3n ＝S n ＋q n S n ＋q 2n S n ，∴S 2n ＋S 22n ＝S 2n ＋[S n (1＋q n )]2＝S 2n (2＋2q n＋q 2n)，S n (S 2n ＋S 3n )＝S 2n (2＋2q n ＋q 2n )．∴S 2n ＋S 22n ＝S n (S 2n ＋S 3n )．例2解 (1)由题意知每年的出口量构成等比数列，且首项a 1＝a ，公比q ＝1－10%＝0.9，∴a n ＝a ·0.9n －1(n ≥1)．(2)10年的出口总量S 10＝a (1－0.910)1－0.9＝10a (1－0.910)．∵S 10≤80，∴10a (1－0.910)≤80，即a ≤81－0.910，∴a ≤12.3.故2010年最多出口12.3吨．►变式训练2解 用an 表示热气球在第n 分钟上升的高度，由题意，得a n ＋1＝45a n ，因此，数列{a n }是首项a 1＝25，公比q ＝45的等比数列．热气球在前n 分钟内上升的总高度为：S n ＝a 1＋a 2＋…＋a n ＝a 1(1－q n )1－q ＝25×⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫45n 1－45＝125×⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫45n <125.故这个热气球上升的高度不可能超过125 m.例3 解 设等差数列{a n }的公差为d ，则b n ＋1b n ＝⎝ ⎛⎭⎪⎫12a n ＋1⎝ ⎛⎭⎪⎫12a n ＝⎝ ⎛⎭⎪⎫12a n ＋1－a n ＝⎝ ⎛⎭⎪⎫12d.∴数列{b n }是等比数列，公比q ＝⎝ ⎛⎭⎪⎫12d .∴b 1b 2b 3＝b 32＝18，∴b 2＝12. ∴⎩⎪⎨⎪⎧b 1＋b 3＝178b 1·b 3＝14，解得⎩⎪⎨⎪⎧b 1＝18b 3＝2或⎩⎪⎨⎪⎧b 1＝2b 3＝18.当⎩⎪⎨⎪⎧b 1＝18b 3＝2时，q 2＝16，∴q ＝4(q ＝－4<0舍去)此时，b n ＝b 1q n －1＝⎝ ⎛⎭⎪⎫18·4n －1＝22n －5.由b n ＝⎝ ⎛⎭⎪⎫125－2n ＝⎝ ⎛⎭⎪⎫12a n ，∴a n＝5－2n .当⎩⎪⎨⎪⎧b 1＝2b 3＝18时，q 2＝116，∴q ＝14⎝ ⎛⎭⎪⎫q ＝－14<0舍去此时，b n ＝b 1qn －1＝2·⎝ ⎛⎭⎪⎫14n －1＝⎝ ⎛⎭⎪⎫122n －3＝⎝ ⎛⎭⎪⎫12a n ，∴a n ＝2n －3.综上所述，a n ＝5－2n 或a n ＝2n －3.►变式训练3 解 (1)∵a 1a 5＋2a 3a 5＋a 2a 8＝25，∴a 23＋2a 3a 5＋a 25＝25，又a n >0，∴a 3＋a 5＝5.又a 3与a 5的等比中项为2，∴a 3a 5＝4，而q ∈(0,1)，∴a 3>a 5，∴a 3＝4，a 5＝1.∴q ＝12，a 1＝16，∴a n＝16×⎝ ⎛⎭⎪⎫12n －1＝25－n.(2)b n ＝log 2 a n ＝5－n ，∴b n ＋1－b n ＝－1，∴{b n }是以b 1＝4为首项，－1为公差的等差数列，∴S n ＝n (9－n )2，∴S n n ＝9－n2， ∴当n ≤8时，S n n >0；当n ＝9时，S n n ＝0；当n >9时，S nn <0.∴当n ＝8或9时，S 11＋S 22＋S 33＋…＋S nn最大．。

2.5.1 等比数列的前n 项和（1）一、选择题1.等比数列{}n a 的前n 项和为n S ，已知9,105123=+=a a a S ，则=1a （ ）A 、31B 、31-C 、91D 、91- 2.设等比数列{}n a 的前n 项和为n S ，若1322a a a =，且4a 与72a 的等差中项为45，则=5S （ ）A 、29B 、31C 、33D 、353.等比数列{}n a 的前n 项和为n S ，且0>n a ，已知7,1342==S a a ，则=5S （ ） A 、215 B 、431 C 、433 D 、217 4.在等比数列{}n a （n ∈N*）中，若11a =，418a =，则该数列的前10项和为（ ） A ．4122- B 、9122- C 、10122- D 、11122- 二、填空题5.首项为1，公比为2的等比数列的前4项和4S = .6.等比数列{}n a 的前n 项和为n S ，已知1S ，22S ，33S 成等差数列，则{}n a 的公比为 .7.等比数列{}n a 的前n 项和为n S ，若3230S S +=，则公比q =_______.8.等比数列{}n a 的前n 项和为n S ，公比不为1,若11a =,且对任意的n N ∈,都有2120n n n a a a +++-=,则5S =_________________.7.已知{}n a 是首项为1的等比数列，n S 是{}n a 的前n 项和，且369S S =,则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为 _______三、简答题9.等比数列{}n a 的前n 项和为n S ,337,4S a ==,求n a .10.等比数列{}的前n 项和为，已知,,成等差数列.（1）求{}的公比q ；（2）若－＝3，求nS .11.等比数列{}n a 的公比,1<q 前n 项和为n S ，已知,5,2243S S a ==求数列{}n a 的通项公式.12.在等比数列{}n a 中,12118,32,n n a a a a -+=⋅=前n 项和30n S =，求n 和公比q .13.已知是等差数列，且成等比数列. （Ⅰ）求数列的通项公式;（Ⅱ）求数列{}2n a 的前n 项和.n a n s 1S 3S 2S n a 1a 3a {}n a 11a =139,,a a a {}n a n S2.5 等比数列的前n 项和（1）1-4：CBBC 5、15 6、137、2- 8、11 1122,212271()2239(),3359:n n n n n n n n q a S q a S --===-⎡⎤--⎢⎥⎣⎦=-=⋅-=当时，当时， 10、181(1);(2)1()232n n q S ⎡⎤=-=--⎢⎥⎣⎦11-21(2)21(2)n n n n n q a q a +-=-=-=-=-11:当时，当时，（） 12、14,22n q ==或113:(1)01;1(2)12;22n n n n n n n d a d a na S n a n S +========-当时，当时，当时，当时，。

2019-2020年高中数学第二章数列2.3.2等比数列的前N 项和同步训练新人教B 版必修5分钟训练(预习类训练,可用于课前)1.在等比数列{a n }中，S n =65，n=4，q=，则a 1=_____________.解析：S n =321])32(1[1)1(411--=--a q q a n=65，即：a 1=27. 答案：272.等比数列{a n }中，a 1=3,q=2，则S 6=_____________.解析：S 6==189.答案：1893.求和：x+x 2+x 3+…+x n =_____________.解析：当n=1时，S n =n;当n=0时，S n =0，当x≠1,0时，S n =，当x=0时也满足.故x+x 2+…x n =⎪⎩⎪⎨⎧≠--=)1(,1)1()1(,x x x x n n n 答案：n(x=1)或4.等比数列｛a n ｝的各项都是正数，若a 1=81,a 5=16,则它的前5项和是_____________.解析：设等比数列｛a n ｝的公比为q ，a 1=81,a 5=16，得q=±,又等比数列的各项都是正数，则其公比q=，所以S 5==211，即S 5=211.或利用S 5==211.答案：21110分钟训练(强化类训练，可用于课中)1.计算：1+3+3+…+的值是( )A. B.C. D.解析：此数列是以1为首项，为公比的等比数列，而=1×()n-1=()9,∴n=10，∴S 10=.故选D.答案：D2.在等比数列{a n }中,a 1=2,前n 项和为S n ,若数列{a n +1}也是等比数列,则S n 等于( )A.2n+1-2B.3nC.2nD.3n -1解析：因数列{a n }为等比数列，则a n =2q n-1，因数列{a n +1}也是等比数列，则(a n+1+1)2=(a n +1)(a n+2+1) a n+12+2a n+1=a n a n+2+a n +a n+2a n +a n+2=2a n+1a n (1+q 2-2q)=0 q=1.即a n =2，所以S n =2n.答案：C3.某人为了观看xx 年奥运会，从xx 年起，每年5月10日到银行存入a 元定期储蓄，若年利率为p 且保持不变，并约定每年到期存款均自动转为新的一年定期，到xx 年将所有的存款及利息全部取回，则可取回的钱的总数（元）为( )A.a(1+p)7B.a(1+p)8C.［(1+p)7-(1+p)］D.［(1+p)8-(1+p)］解析：xx 年存入的a 元到xx 年所得的本息和为a(1+p)7，xx 年存入的a 元到xx 年所得的本息和为a(1+p)6，依此类推，则xx 年存入的a 元到xx 年的本息和为a(1+p)，每年所得的本息和构成一个以a(1+p)为首项，1+p 为公比的等比数列，则到xx 年取回的总额为a(1+p)+a(1+p)2+…+a(1+p)7=p a p p p a =+-+-+)1(1])1(1)[1(7［(1+p)8-(1+p)］. 答案：D4.数列{a n }中，a n+1=，已知该数列既是等差数列又是等比数列，则该数列的前20项和S 20=_______________.解析：设数列中的每一项为a ，代入到已知等式中，得：a=，求出a=5,a=0（舍去）.S 20=20×5=100. 答案：1005.求等比数列1，2，4，…从第5项到第10项的和.解：由a 1=1,a 2=2得q=2,∴S 4=21)21(1,1521)21(110104--⨯==--⨯S =1 023.从第5项到第10项的和为S 10-S 4=1 008.6.在等比数列{a n }中S 3=4,S 6=36，求a n .解：∵,∴q≠1,∴S 3=qq a S q q a --==--1)1(,41)1(61631=36, 两式相除得1+q 3=9,∴q=2.将q=2代入S 3=4，得a 1=，∴a n =×2n-1=×2n+1.30分钟训练(巩固类训练，可用于课后)1.一条信息，若一人得知后用一天时间将信息传给2人，这2人每人又用一天时间传给未知此信息的另外2人，如此继续下去，要传遍100万人口的城市，所需时间大约是( )A.3个月B.1个月C.10天D.20天解析：本题即为求等比数列1,2,22,23,…,2n-1，…的前n 项和为100万时n 为多少的问题. 于是=106，∴2n =106+1，两边取对数得：nlg2=lg106,n=≈20.答案：D2.等比数列{a n }中，已知a 1=1，且共有偶数项，若其奇数项之和为85，偶数项之和为170，则公比q=__________,项数共有____________项.解析： 设项数为2k(k ∈N *)，则(a 1+a 3+a 5+…+a 2k-1)·q=a 2+a 4+a 6+…+a 2k.∴q==2.又∵a 1=1,∴S n =2n -1.又∵S n =170+85=255,∴n=8.即共有8项.答案：2 83.设等比数列{a n }的公比为q ，前n 项和为S n ，若S n+1、S n 、S n+2成等差数列，则q 的值为____________.解析：S n =,2S n =S n+1+S n+2，则有2·=qq a q q a n n --+--++1)1(1)1(2111，∴q 2+q-2=0,∴q=-2.答案：-24.有一座七层塔，每层所点灯的盏数都是上面一层的2倍，一共点381盏灯，则底层所点灯的盏数为____________.解析：要求底层点灯的盏数，所以设底层为a 1盏，作为数列的首项.共381盏灯，列出前n项和.即：S 7=211)211(71--a =381a 1=192. 答案：1925.已知数列{a n }是等比数列，且a 1+a n =66，a 2a n-1=128，且前n 项和S n =126，求n 及公比q. 解：∵a 1a n =a 2a n-1=128,a 1+a n =66,∴a 1、a n 可看作方程x 2-66x+128=0的两根，解得x 1=2,x 2=64.∴a 1=2,a n =64或a 1=64,a n =2.若a 1=2,a n =64,显然q≠1，由=126,得2-64q=126-126q,∴q=2.由a n =a 1q n-1，得2n-1=32,∴n=6.若a 1=64,a n =2，同理可求得q=,n=6.综上述可知，n 的值为6，公比q 为2或.6.已知数列{a n }的通项公式为a n =n·a n (a ＞0且a≠1)，求S n .解：S n =a+2a 2+3a 3+…+n·a n ①①×a 得：aS n =a 2+2a 3+…+(n-1)a n +na n+1 ②①-②得：(1-a)S n =a+a 2+a 3+…+a n -n·a n+1=.∴S n =.7.设等比数列{a n }的前n 项和为S n ，已知S 4=1,S 8=17,求{a n }的通项公式.解：设{a n }的公比为q ，由S 4=1,S 8=17知q≠1,所以得=1. ①=17, ②由①②式整理得=17,解得q 4=16.所以q=2或q=-2.将q=2代入①式得a 1=，所以a=.将q=-2代入①式得a 1=，所以a n =.8.某工厂去年的产值是100万元，计划今后3年内一年比一年产值增长10%，从今年起的第三年，这个工厂的年产值是多少万元？这三年的总产值是多少万元？（精确到万元，1.13≈1.33）解：设去年的产值为a 1万元，今年的产值以及以后各年的产值依次为a 2万元，a 3万元……由于a n+1=a n (1+0.1)，故数列{a n }是等比数列，则第三年该厂的年产值为a 4=a 1q 3=100×1.13≈133（万元）.这三年的总产值为S 4-a 1=1.11)1.11(1001)1(4141--=---a q q a -100≈364（万元）. 9.数列{a n }的前n 项和为S n ，且a 1=1,a n+1=S n ，n=1,2,3, …,求:（1）a 2，a 3，a 4的值及数列{a n }的通项公式；（2）a 2+a 4+a 6+…+a 2n 的值.解：（1）由a 1=1，a n+1=S n ，n=1，2，3，…，得a 2=S 1=a 1=，a 3=S 2=(a 1+a 2)=，a 4=S 3=(a 1+a 2+a 3)=，由a n+1-a n =(S n -S n-1)= a n （n≥2），得a n+1=a n （n≥2）.又a 2=，所以a n =()n-2(n≥2)，∴数列{a n }的通项公式为a n =⎪⎩⎪⎨⎧≥=-.2,)34(31,1,12n n n （2）由（Ⅰ）可知a 2,a 4, …，a 2n 是首项为，公比为()2，项数为n 的等比数列，∴a 2+a 4+a 6+…+a 2n =·]1)34[(73)34(1)34(1222-=--n n. 10.某市xx 年底有住房面积1 200万平方米，计划从xx 年起，每年拆除20万平方米的旧住房.假定该市每年新建住房面积是上年年底住房面积的5%.（1）分别求xx 年底和xx 年底的住房面积；（2）求2024年底的住房面积.（计算结果以万平方米为单位，且精确到0.01）解：（1）xx 年底的住房面积为：1 200（1+5%）-20=1 240（万平方米），xx 年底的住房面积为：1 200（1+5%）2-20（1+5%）-20=1 282（万平方米），∴xx 年底的住房面积为1 240万平方米，xx 年底的住房面积为1 282万平方米.（2）2024年底的住房面积为：1 200（1+5%）20-20（1+5%）19-20（1+5%）18-…-20（1+5%）-20=1 200（1+5%）20-20×≈2 522.64（万平方米）∴2024年底的住房面积约为2 522.64万平方米..。