1.4.2_角平分线(2)PPT课件

格式：ppt
大小：1.04 MB
文档页数：19

下载文档原格式

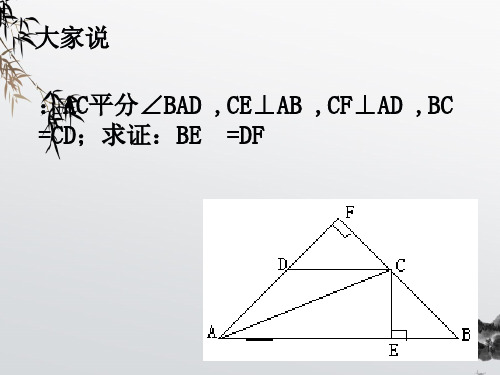
《角平分线》PPT课件 (公开课获奖)2022年北师大版 (3)

2、如以以以下图 ,从点O出发有
三条射线 ,那么图中有个
角 ,它们分别是
．
C B
OA
D O AC B
(3)哈尔滨在北京的北偏东大约多少度 ?
例填空
1 4
___ ____
11700 ___ ___
3018
____
________
201536 ___________
想一想:
线 ,DE⊥AB ,垂足为E . 〔〔21〕〕求：证CD：A=B4c=mA,C求A+CC的D长；
稳固练习：
1、到三角形三边距离相等的点是三角形〔〕的交点 .
A、三条角平分线 B、三条中线
C、三条高线
D、三边中垂线
2、△ABC中 ,AC = BC ,∠C = 90° ,
AD平分∠CAB ,DE⊥AB ,CD = 2 ,
大家说
：AC平分∠BAD ,CE⊥AB ,CF⊥AD ,BC =CD；求证：BE =DF
1.4.2 角平分线
• 学习目标：
• 1、通过尺规作图 ,发现并推证三角形三条角平分线交于一点 ,且此点到三角形三边距离相等 .
• 2、能够综合运用角平分线定理及逆定理解决有关的计算与证明 .
练一练：且如CE图=,BBFE.⊥求A证C：于点ED,C在F⊥∠BAABC于的F平, 分线上
A
D OE
B
C
1、如图1, D、E分别是AB、AC上的点.
是
∠ ABC与∠ DBC是不是同一个角?
是
∠BAC与∠ DAE是不是同一个角不是?
∠BAC与∠ ACB是不是同一个角?
2、如图2 ,图A 中共共有有10个多角少个角E ?D请分别表

北师大版八年级数学下册同步精品1.4.2 角平分线(2)(课件)

C
过内心作三角形三边的垂线段都相等.
探究新知
拿出任意剪的一个三角形纸片，通过折叠找出每个角的
角平分线，观察这三条角平分线，你是否发现同样的结论？
A
A
A
B
C
B
C
B
C
猜想：三角形三个角的平分线相交于一点, 并且这一点到三条边的距离相等
怎么证明结论呢？
探究新知
已知：如图 1-25，在 △ABC 中，角平分线 BM 与角平分线 CN 相交于点 P，过点 P 分别作 AB，BC，AC 的垂线，垂足分别是 D，E，F. 求证：∠ A 的平分线经过点 P，
∵
∠C=
90
°
，∴
∠B=
1 2
×90 °=45 ° .
∴ ∠BDE = 90 °- 45 °= 45 ° .
∴ BE=DE（等角对等边）.
在等腰直角三角形 BDE 中，
BD = 2DE2 = 4 2 cm（勾股定理）. ∴ AC = BC = CD + BD =（4 + 4 2 ）cm.
探究新知
例：如图，在△ABC 中，AC=BC，∠C=90 ° ，AD是△ABC的角平分线，DE⊥AB，垂足为 E. （2）求证：AB=AC+CD. （2）证明：由（1）的求解过程易知， Rt△ACD≌Rt△AED（HL）. ∴ AC = AE（全等三角形的对应边相等）. ∵ BE = DE = CD， ∴ AB = AE + BE = AC + CD.
直角和钝角的三条角平分线也具有同样的性质
探究新知
归纳总结
三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.
A
M D NP F

八年级数学下册1.4.2角平分线课件新版北师大版

度数，可以求此角的度数。
3
应用三解决实际问题
可以运用角平分线及其性质来解决直角三角形、等腰三角形等问题。
角平分线的练习
练习一画出角的平分线
练习用尺规等工具作出各种角的平分线。
练习二用角平分线定理求角度
练习应用角平分线定理来求出角的度数。
练习三解决实际问题
练习将角平分线应用于解决不同的实际问题。
总结
1 角平分线的重要性
角平分线是许多的几何问题的基础课件的学习，你是否已经对角平分线有了更好的理解？
3 知识点回顾
通过课件中的练习，你是否已经掌握了角平分线的基本定义、性质、作用、应用及求解方法？
可用尺规作图法作出一条角的平分线。
角平分线的作用
寻找角平分线
可以用尺规作图法求角平分线。
确定长度
若一个角的一条平分线已知其长度，则可以求出与此平分线相应两边的长度。
证明定理
可以用角平分线定理来证明一些定理。
角平分线的应用
1
应用一求角平分线
通过尺规作图等方法求角平分线。
应用二求角度大小
2
已知一个角的一条平分线与相应两边的
角平分线课件：北师大版八年级数学下册1.4.2
本课件将深入讲解角平分线的定义、性质、作用、应用和练习，助你更好地掌握这一知识点。
角平分线的定义
什么是角平分线
角平分线是指可以将一个角平分成两个相等的角的线段。
角平分线的性质
作图
1.角平分线可以互相平分。
2.如果一个角的两条平分线相交，则它们所截的弧上的点都在相同的直线上。

《角平分线》三角形的证明PPT(第2课时)

探究点二
问题：如图，在△ABC中．AC=BC，∠C=90°，AD是△ABC的角平分线， DE⊥AB，垂足为E． (2)求证：AB=AC+CD．解：证明：由(1)的求解过程易知 Rt△ACD≌Rt△AED( HL ) ∴AC=AE ∵BE=DE=CD ∴AB=AE+BE=AC+CD.
强化训练
1.直线l₁、l₂、l₃表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有几处？
定的期限内固沙造林2400公顷，实际每月固沙造林的面积比原计划多30公顷，结果提前4个月
完成原计划任务. 原计划每月固沙造林多少公顷？
如果设原计划每月固沙造林x公顷，
2400
2400
那么原计划完成一期工程需要______x____个月，实际完成一期工程用了__x__+_3_0__个月.
活动探究
问题2：(1)2010年上海世博会吸引了成千上万的参现者．某一时段内的统计结果显示，前a天日均参观人数35万，后b天日均参观人数45万，这(a+b)天日均参观人数为多少万人？
前置学习
3.
下列
a π
，
1 ，1x x 1 5
y
，
a2 a
b2 b
， 3x2 ，0中，是分式的有__x1_1___a_a2 _ bb_2_；
是整式的有__aπ___15_x__y ____3x_2 ____0______.
活动探究
探究点一
问题1：面对日益严重的土地沙化问题，某县决定分期分批固沙造林. 一期工程计划在一
本题基本思路：两条直线相交只有一个交点.要想证明三条直线相交于一点，只要能证明两条直线的交点在第三条直线上即可.

1_4_2角平分线(二)

白银市三中导学案学科：数学年级：八主备人：曾万军教研组长：教务处：上课时间：2014 年3 月12日学生姓名：课题 1.4.2角平分线（二）课时2课型二、合作交流1. 证明三角形三条角平分线的性质定理：三角形的三条角平分线相交于一点，并且这个点到三条边的距离相等. 已知：求证：证明：三边垂直平分线三条角平分线三角形锐角三角形交于三角形内一点交于三角形内一点钝角三角形交于三角形外一点直角三角形交于斜边的中点交点性质到三角形三个顶点的距离相等到三角形三边的距离相等“距离”的区别两点之间的距离点到直线的距离学习目标 1.证明与角的平分线的性质定理和判定定理相关的结论． 2.角平分线的性质定理和判定定理的灵活使用． 3.提升综合使用数学知识和方法解决问题的水平．重难点教学重点1.三角形三个内角的平分线的性质．2.综合使用角平分线的判定和性质定理，解决几何中的问题．教学难点角平分线的性质定理和判定定理的综合应用．一、自主预习1、如图：E 是∠AOB 的平分线上一点，EC ⊥OA ，ED ⊥OB ，垂足为C ，D 。

求证：（1）OC=OD ，（2）DF=CF 。

OFEDCBA三、展示拓展[例3]如图，在△ABC 中．AC=BC ，∠C=90°，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为E ．(1)已知CD=4 cm ，求AC 的长； (2)求证：AB=AC+CD ．四、检测反馈1、如图，在△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于F ，若BF=AC ，则∠ABC 的度数是 .2、在△ABC 中，AB=AC ，∠A=50°，AB 的垂直平分线DE 交AC 于点D ，垂足为E ，则∠DBC 的度数是 .3、如图，已知点C 是∠AOB 的平分线上一点，点P 、P′分别在边OA 、OB 上. 假如要得到OP=O P′，需要添加以下条件中的某一个即可，请你写出所有可能的结果的序号为____________：①∠OCP=∠OC P′ ②∠OPC=∠OP′C ； ③PC=P′C ； ④PP′⊥OC4、如图：在△ABC 中，∠B ，∠C 相邻的外角的平分线交于点D 。

八年级数学三角形三条内角的平分线

A．110° B．120° C．130° D．140°
解析：由已知，O到三角形三边的距离
相等，所以O是内心，即三条角平分线
的交点，AO，BO，CO都是角平分线，
所以有∠CBO＝∠ABO＝ 1∠ABC，∠BCO＝∠ACO＝ 1∠ACB，
2
2
∠ABC＋∠ACB＝180°－40°＝140°，
∠OBC＋∠OCB＝70°，
D
B
拓展思维
5.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
l1
l3
l2
P2
l1
P1
P3
P4
l3
l2
课堂小结
三角形内角平分线的性质
性质：三角形的三条角平分线交于一点，并且这一点到三条边的距离相等．
学校P的位置,P在何处？
A
B
C
讲授新课
一三角形的内角平分线活动1 分别画出下列三角形三个内角的平分线，你发现了什么？
发现：三角形的三条角平分线相交于一点.
活动2 分别过交点作三角形三边的垂线，用刻度尺量一量，每组垂线段，你发现了什么？
你能证明这个结论吗？
发现：过交点作三角形三边的垂线段相等.
的角平分线，DE⊥AB于E，F在AC上,BD=DF.
求证：CF=EB.
证明：∵AD平分∠CAB,
A
DE⊥AB，∠C＝90°（已知）,
∴ CD＝DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
CD=ED（已证）,
DF=DB （已知）,
F
E
∴ Rt△CDF≌Rt△EDB (HL).

湘教版八年级下册数学课件第2课时角平分线的性质定理的逆定理

CA，垂足分别为D，E，F.
∵BM是△ABC的角平分线，
点P在BM上，
B
∴PD=PE.同理PE=PF.
A
ND
F
P
M
C E
∴PD=PE=PF.
即点P到三边AB，BC，CA的距离相等.
想一想：点P在∠A的平分线上吗？这说明三角形
的三条内角平分线有什么关系？
A
点P在∠A的平分线上.
D
N
F
P
M
B
C
E
结论：三角形的三条内角平分线交于一点，并
到角的两边的距离相等的点在角的平分线上.
讲授新课
一角平分线的性质定理的逆定理
问题：交换角的平分线的性质中的条件和结论，你能
得到什么命题，这个新命题正确吗？
角平分线的性质：
A
角的平分线上的点到角的两边的距离相等. D
几何语言：
C
∵ OC平分∠AOB，
O
且PD⊥OA， PE⊥OB
P
E
B
∴ PD= PE 猜想:
方法总结
由已知，O 到三角形三边的距离相等，得O是三条内角平分线的交点，再利用三角形内角和定理即可求出∠BOC的度数．
归纳总结角的平分线的性质角的平分线的判定
图形
C P
C P
已知条件
结论
OP平分∠AOB PD⊥OA于D PE⊥OB于E
PD=PE
PD=PE PD⊥OA于D PE⊥OB于E
结论
三角形的内角平分线相交于内部一点
活动2 分别过交点作三角形三边的垂线，用刻度尺量一量，每组垂线段，你发现了什么？
你能证明这个结论吗？发现：过交点作三角形三边的垂线段相等

《角的平分线的性质》示范公开课教学PPT课件【部编新人教版八年级数学上册】

三角形的三条角平分线交于一点.
创设情境探究新知应用新知巩固新知课堂小结布置作业
典型例题
例2：如图，要在S区建一个集贸市场，使它到公路、铁路的距离相等，并且离公路与铁路的交叉处500m.这个集贸市场应建于何处（在图上标出它的位置，比例尺为1：20000）?
A
C
D
B
M
S
N
AB：500=1： 20 000 AB=2.5cm
情景导入
（2）下图是一个平分角的仪器，其中AB=AD，BC=DC.将点A放在角的定点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是这个角的平分线.你能说明它的道理吗?
分析
在△ACD和△ACB中
AD=AB，DC=BC AC=AC
△ACD≌△ACB
∠DAC=∠BAC
AC平分∠BAD
创设情境探究新知应用新知巩固新知课堂小结布置作业
思考
做一做：你能用三角形全等证明这个结论吗?
已知：如图，OC是∠AOB的平分线，P是OC上任意一点，做 PD⊥OA，PE⊥OB，垂足分别是D，E.求证：PD=PE.
分析：要证明PD=PE，只要证明它们所在的△OPD≌△OPE，而△OPD≌△OPE的条件由已知容易得到它满足公理（AAS）.故结论可证.
创设情境探究新知应用新知巩固新知课堂小结布置作业
情景导入（1）画一画：在纸上任意画一个角，用剪刀剪下，用折纸的方法，如何确定角的平分线?
（1）在准备好的角上标好字母A，O，B；
（2）把∠ AOB对折，使得这个角得两边重合；
A
（3）折痕就是∠AOB的角平分线.
O
B
创设情境探究新知应用新知巩固新知课堂小结布置作业

角平分线(1-2)

§1．4．1角平分线（一）教学目标（一）知识目标1．角平分线的性质定理的证明。

2．角平分线的判定定理的证明。

3．用尺规作已知角的角平分线。

（二）能力目标1．进一步发展学生的推理证明意识和推理能力，培养学生将文字语言转化为符号语言，图形语言的能力。

2．体验解决问题策略的数学思想方法，提高实践能力。

教学重点1．角平分线的性质和判定定理的证明。

2．用尺规作已知角的角平分线并说明理由。

教学难点1．正确地表述角平分线性质定理的逆命题。

2．正确地将文字语言转化成符号语言和图形语言，对几何命题加以证明。

教学过程1、创设问题情境：〖思考与探索〗有一种蜘蛛网的主网线是它相邻的主网线构成的角平分线(如图)，如果蜘蛛在∠AOB 平分线OC上一点P处,为尽快爬到OA或OB上控制猎物,它应该选择什么路线,两条路线长度关系怎样?（蜘蛛实例的思考与探索，实际上既复习了点到直线的距离这一概念，又发现了角平分线上的点到角两边的距离相等这一性质定理。

）2、新课引入问题：（1）还记得角平分线的概念吗？（2）还记得角平分线上的点有什么性质吗？你是怎样得到的？（3）你是怎样理解结论的？（4）以前我们用折纸的方法得到了一个结论，我们能进行严格意义的证明吗？师：（板演:画出一个角平分线；然后在平分线上任取一点，作出这一点到角两边的距离。

）问：你能否将蜘蛛实例的结论转化为一个命题，写出以知与求证进行证明？已知：OC 是∠AOB 的平分线，点P 在OC 上，PD ⊥OA ，PE ⊥OB ，垂足分别是D 、E.求证：PD=PE.（注：将文字语言转化成符号语言和图形语言由师生共同完成）证明∵AC 平分∠AOB ，∴∠AOC=∠BOC=21∠AOB 。

又∵∠AOC=∠BOC=RT ∠,OC=OC ∴△AOC ≌△BOC （HL ）∴CD=CE(全等三角形的对应边相等)(请学生回答蜘蛛控制猎物的方法、两条路线长度关系) 定理：在角平分线上的点到角的两边的距离相等。

角的平分线性质说课课件

A
B D C
∵ 如图， DC⊥AC，DB⊥AB （已知）
∴
BD = CD ，( 在角的平分线上的点到角 )
的两边的距离相等。
A B C
（×）
D
不必再证全等
∵ AD平分∠BAC, DC⊥AC，DB⊥AB （已知）
∴
在角的平分线上的点到角的） DB = DC ，（
√
两边的距离相等。
B
A D
C
A
如图：在△ABC中， ∠C=90° AD是∠BAC的平分线， F DE⊥AB于E，F在AC上，BD=DF；求证：CF=EB
１．以Ｏ为圆心，适当长为半径作弧，交ＯＡ于Ｍ，交ＯＢＮ于．２．分别以Ｍ，Ｎ为圆心．大于 1/2 ＭＮ的长为半径作弧．两弧在∠ＡＯＢ的内部交于Ｃ．３．作射线ＯＣ．
Ｍ
Ｃ
Ｂ
Ｎ
Ｏ
射线ＯＣ即为所求．
OC是∠AOB的平分线，点P是射线OC上的任意一点，
1. 操作测量：取点 P 的三个不同的位置，分别过点 P 作 PD⊥OA，PE ⊥OB,点D、E为垂足，测量PD、PE的长.将三次数据填入下表：
活动3：
运用角平分线的性质解决实际问题。
活动4：
小结:
你本节课学到了哪些知识?
布置作业:
(1)P22第2、3题； (2)作三角形ABC的三条角平分线，你会发现什么?
小结
拓展
定理角的平分线上的点到角的两边的距离相等. ∵OC是∠AOB的平分线,P是OC 上任意一点,PD⊥OA,PE⊥OB, 垂足分别是D,E(已知) ∴PD=PE(角的平分线上的点到角的两边的距离相等). 用尺规作角的平分线.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

的傍心.这样点有三个.
【全品作业】第19页A组：1--9题。
1.必做题：【全品作业】第19页：
B组：10--14题； 2 .选做题：【全品作业】第20页：
C组：15题；
下课了!
结束寄语
• 严格性之于数学家,犹如道德之于人. • 证明的规范性在于：条理清晰，因果相应,言必有据. 这是初学证明者谨记和遵循的原则.
角平分线,DE⊥AB,垂足为E.
E
(1)如果CD=4cm,求AC的长;
(2)求证:AB=AC+CD.C NhomakorabeaD
B
老师期望:你能正确地解答并规范地写出其过程.
自我检测 1 2.三条公路两两相交，现计划修建一个油库。（1）如果要求油库到两条公路AB,AC的距离都相等，那么如果选择油库P的位置？（2）如果要求油库到这三条公路的距离都相等，那么又如何选择油库的位置Q? 请你画图做出油库的位置P和Q,要求保留作图痕迹。
点拨：要证明三条直线相交于一点，只要证明其中两条直线的交点在第三条直线上即可。
命题:三角形三个角的平分线相交于一点.
已知：如图，△ABC的角平分线．
BM、CN相交于点P，求证：P点在∠BAC的角平分线上．证明：过P点作PD⊥AB，PF⊥AC， PE⊥BC，其中D、E、F是垂足 ∴PD=PE 同理：PE=PF．∴PD=PE=PF． B A M F E C
N
D P
∵BM是△ABC的角平分线,点P在BM上
∴点P在∠BAC的平分线上
∴△ABC的三条角平分线相交于点P．且到三边的距离相等。
定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.
如图,在△ABC中, ∵BM,CN,AH分别是△ABC的 A
ND
B
P E
M F
C
三条角平分线,且PD⊥AB,
PE⊥BC,PF⊥AC(已知),
∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等). 老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.
自我检测 1 如图,在△ABC中,已知
挑战自我
A
AC=BC,∠C=900,AD是△ABC的
（一）知识回顾
角平分线上的点到这个角的两边距离相等.
A
∵OC是∠AOB的平分线,P是OC上任意, PD⊥OA,PE⊥OB,垂足分别是D,E(已知 O ) ∴PD=PE(角平分线上的点到这个角的两边距离相等).
1 2
D
P
E B
C
（一）知识回顾
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
A
B
C
自我检测二
习题1.9
1.已知:如图,∠C=900, ∠B=300,AD是Rt△ABC的角平分线. 求证:BD=2CD.
A
B
D
C
自我检测三
2.已知:如图,△ABC的外角∠CBD和∠BCE的角平分线相交于点F. 求证:点F在∠DAE的平分线上.
A
B D F
C
E
自我检测四
3.如图，已知∠MAN=1200,AC平分∠MAN，B,D分别在 AM和AN上。（1）如图（1），当∠CDA=∠CBA=900 时，求证：AB+AD=AC;(2)如图（2）中，当 ∠DCB+∠MAN=1800 时，(1)中的结论还成了吗？请说明理由。
小结
拓展
D 1 2
A P C
定理角平分线上的点到这个角的两边距离相等. 逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上. O
E
B
定理:三角形的三条角平分线相交于一点,
并且这一点到三边的距离相等(这个交点叫做三角形的内心). 三角形一个内角和与它不相邻的两个外角的平分线交于一点, 这个的点叫做三角形
1.4.2 角平分线性质的应用学习目标： 1.会证明并掌握三角形的三条角平分线的性质； 2.进一步提高推理证明意识和能力。
剪一个三角形纸片，通过折叠找出每个角的角平分线，观察这三条角平分线，你是否发现同样的结论？与同伴交流．
结论:三角形三个角的平分线相交于一点.
怎样证明这个结论呢?
A D
∵PD⊥OA,PE⊥OB,垂足分别是D,E(
1
已知), 且PD=PE, ∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的
O
2
P
E B
C
点,在这个角的平分线上).
（一）知识回顾
作三角形的三个内角的角平分线，你发现了什么？发现：三角形的三个内角的角平分线交于一点．这一点到三角形三边的距离相等．
N D A
图（1）
C
N D
C
B
M
A
图（2）
B
M
自我检测五
5.已知:如图,P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB, 垂足分别C,D. 求证: (1)OC=OD; (2)OP是CD的垂直平分线.
A
C O D P
B
老师期望:做完题目后,一定要“悟”到点东西, 纳入到自己的认知结构中去.