动点最值问题

初一动点最值的题目有多种，这里给出部分典型例题。

1.数轴上点A，B所表示的数为-1和3，则A，B两点间的距离是 _______；若
点P也是数轴上的点，P到点A，B的距离之和为5，则点P表示的数是 _______．2.已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点，其对应
的数为x。

(1) 若点P到点A、点B的距离相等，求点P对应的数；
(2) 数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请
求出x的值；若不存在，说明理由；
(3) 现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同
时向右运动，点P以6个单位长度/秒的速度同时从O点向左运动。

当点A 与点B之间的距离为3个单位长度时，求点P所对应的数是多少？
请注意，这些问题可能需要一些数学基础知识来解决，例如数轴的概念、距离的计算等。

在解题时，要仔细阅读题目，理解问题的要求，并灵活运用所学知识进行求解。

动点最值题精讲动点最值问题是数学中一个非常重要的问题，它表示了在动态变化中，某个参数随时间而变化时可能取到的最大或最小值。

在这个过程中，我们需要找到这个参数随时间变化的规律，并且计算出这个参数的最大最小值，这需要我们掌握动点最值问题的方法和技巧。

在本文中，我们将更深入地探讨这个问题，并提供几个常见的例子和解决方案。

1. 动点最值问题的基本原理动点最值问题在数学中的表现形式是，一个点 P 在过程中不断变化，变化规律可以表示为：X=f(t), Y=g(t)。

其中 X，Y 分别表示点 P 的横坐标和纵坐标，t 表示时间。

我们需要确定 t 的范围，然后求出 X 和 Y 的最小值和最大值。

解决这个问题的基本方法是通过求导数，在函数的关键点处判断函数的值。

由于我们要求的是最大最小值，所以我们需要找到 f(t) 和 g(t) 的导数。

求导可能比较复杂，但是十分必要。

我们将在下文中讨论如何求解动点最值问题的各个方面。

2. 解决动点最值问题的技巧我们将解决动点最值问题分为以下几个步骤。

第一步，使用物理学的方法。

从物理学（运动学）的角度分析问题，求出变化过程中的速度和加速度等参数。

这种方法适用于解决一个物体在直线或平面上运动的问题。

我们可以将问题抽象为一个物理学问题，然后使用速度和加速度的公式来解决问题。

第二步，使用数学方法。

这是更为常见的方法，也是本文的核心部分。

在这种情况下，我们需要找到一个函数来表示参数的变化过程，然后对该函数求导，找到关键点，最终确定最大最小值。

第三步，使用计算机方法。

现代计算机很擅长解决动点最值问题，因为它们能够计算复杂的函数和大量的数据。

我们可以使用计算机做出模拟，然后找到最大或最小点。

这种方法往往需要程序员或科学家具备一定的计算机技能。

第四步，使用统计学方法。

在某些情况下，使用统计学方法可能更好。

例如，当我们面对大量数据时，我们可以用统计方法来确定数据变化的趋势。

在这种情况下，我们可能使用回归方法或其他统计学方法来找到变化过程的规律，最终决定最大最小值。

动点最值问题的常用解法动点最值问题是数学中一个很有趣的问题，它往往涉及到最大值或最小值的求解，难度并不小。

针对这种问题，数学家们提出了各种不同的解法，本文将介绍其中一些常用的方法。

一、拉格朗日乘数法拉格朗日乘数法是一种利用约束条件求函数的最值的方法。

其基本思路是利用不等式的等式条件，将约束条件和目标函数融合，建立拉格朗日函数，最后对其求导，解出最优解。

这种方法的优点是精度高，适用条件广。

但是，由于需要解方程组，所以计算量比较大。

举个例子，要求函数 $f(x,y)$ 在方程 $g(x,y) = 0$ 的限制下的最大值，我们可以建立拉格朗日函数：$$L(x,y,\lambda) = f(x,y)+\lambda g(x,y)$$其中 $\lambda$ 为拉格朗日乘数。

对拉格朗日函数分别对$x,y,\lambda$求偏导数，并使它们等于0，得到以下方程组：$$\begin{cases}\nabla f(x,y) + \lambda \nabla g(x,y) = 0\\g(x,y) = 0\end{cases}$$解出这个方程组，就可以得到函数 $f(x,y)$ 在 $g(x,y)=0$ 限制下的最优解了。

二、图像解法图像解法是一种简单直观的方法，适合于几何意义比较明显的问题。

它的基本思路是将问题转化为图像，然后利用图像来求解最值问题。

例如，要求函数 $f(x,y)$ 在直线 $y=kx$ 上的最大值，我们可以将其转化为函数 $g(x) = f(x,kx)$ 的最大值问题。

接下来，我们可以利用图像解法，通过观察函数$g(x)$ 在 $[a,b]$ 区间的图像，来确定它的最大值点。

显然，最大值点的横坐标为$x_0$，纵坐标为 $f(x_0,kx_0)$，即可得到函数 $f(x,y)$ 在 $y=kx$ 上的最大值。

三、证明解法证明解法也是一种常用的方法，它的基本思路是通过分析问题的性质，得到问题的最值解，并给出相应的证明过程。

动点问题（最值）1.如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．（1）当t为何值时，∠AMN=∠ANM？（2）当t为何值时，△AMN的面积最大？并求出这个最大值．2.如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜103）秒．解答如下问题：（1）当t为何值时，PQ∥BO？（2）设△AQP的面积为S，①求S与t之间的函数关系式，并求出S的最大值；②若我们规定：点P、Q的坐标分别为（x1，y1），（x2，y2），则新坐标（x2﹣x1，y2﹣y1）称为“向量PQ”的坐标．当S取最大值时，求“向量PQ”的坐标．3.如图，在O A B C中，点A在x轴上，∠A O C=60o，O C=4c m．O A=8c m．动点P从点O出发，以1cm／s的速度沿线段OA→AB运动；动点Q同时．．从点O出发，以acm／s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．(1)填空：点C的坐标是(______，______)，对角线OB的长度是_______cm；(2)当a=1时，设△OPQ的面积为S，求S与t的函数关系式，并直接写出当t为何值时，S的值最大?* (3)当点P在OA边上，点Q在CB边上时，线段PQ与对角线OB交于点M.若以O、M、P 为顶点的三角形与△OAB相似，求a与t的函数关系式，并直接写出t的取值范围．4.如图，⊙C 的内接△AOB 中，AB=AO=4,tan∠AOB=43,抛物线2y ax bx =+经过点A(4，0)与点（-2，6）（1）求抛物线的函数解析式． （2）直线m 与⊙C 相切于点A 交y 轴于点D ，动点P 在线段OB 上，从点O 出发向点B 运动;同时动点Q 在线段DA 上，从点D 出发向点A 运动，点P 的速度为每秒1个单位长，点Q 的速度为每秒2个单位长，当PQ⊥AD 时,求运动时间t 的值（3）点R 在抛物线位于x 轴下方部分的图象上，当△ROB 面积最大时，求点R 的坐标.。

GFD AEA C BD FBACDB动点问题最值最值问题有四种情形：定点到动点的最值，动点在圆上或直线上，就是点到圆的最近距离，和点到直线的最近距离；三角形两边之和大于第三边的问题，当两边成一直线最大；几条线段之和构成一条线段最小；还有就是对称点最小问题。

一、定点到动点所在圆的最大或最小值，动点在一个定圆上运动，其实质是圆外一点到圆的最大或最小距离，就是定点与圆心所在直线与圆的交点的两个距离。

方法：证明动点在圆上或者去找不变的特殊三角形，证明两个三角形相似，求出某些边的值。

1．如图，△ABC 、△EFG 均是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长的最小值是（ ） A ．32-B ．13+C ．2D ．13-提示：点M 在以AC 为直径的圆上2．（2015•咸宁）如图，已知正方形ABCD 的边长为2，E 是边BC 上的动点，BF ⊥AE 交CD 于点F ，垂足为G ，连结CG ．下列说法：①AG ＞GE ；②AE =BF ；③点G 运动的路径长为π；④CG 的最小值为﹣1．其中正确的说法是 ②③ ．（把你认为正确的说法的序号都填上）提示：G 在以AB 为直径的圆上：正确答案是：②④3、如图，正方形ABCD 的边长为4cm,正方形AEFG 的边长为1cm ，如果正方形AEFG 绕点A旋转，那么C 、F 两点之间的最小距离为 4、如图，在边长为2的菱形ABCD 中，∠A=60°,M 是AD 边的中点，N 是AB 边上一动点，将△AMN 沿MN 所在直线翻折得到△A ′MN ，连接A ′C ，则A ′C 长度的最小值是 5、如图，等腰直角△ACB ，AC=BC=5，等腰直角△CDP ，且PB=2，将△CDP 绕C 点旋转.（1）求证：AD=PB（2）若∠CPB=135°，求BD ；（3）∠PBC= 时，BD 有最大值，并画图说明； ∠PBC= 时，BD 有最小值，并画图说明.分析：在△ABD 中有：BD ≤AB+AD ，当BD=AB+AD 时BD 最大，此时AB 与AD 在一条直线上，且AD 在BA 的延长线上，又△ACB 是等腰直角三角形，∠CAB=45°，由（1）知∠PBC=∠CAD=180°-45°=135° BD ≥AB-AD ，当BD=AB-AD 时BD 最小，此时，AB 与AD 在一条直线上，且AD 此时∠CAD=45°，所以∠PBC=∠CAD=45°6、如图，△ABC 和△ADE 都是等腰直角三角形，∠ACB=∠ADE=90°,∠BAE=135°,AD=1，2，F 为BE 中点.（1）求CF 的长（2）将△ADE 绕A 旋转一周，求点F 运动的路径长； （3）△ADE 绕点A 旋转一周，求线段CF 的范围.CO ABPE ABC DFD A BC EHGF DAEH G FDA Exy MCM 1M 2A PO B A提示：本题根据中点构造三角形相似，△BOF ∽△BAE,且122OF AE == 7、如图，AB=4，O 为AB 中点，⊙O 的半径为1，点P 是⊙O 上一动点，以点P 为直角顶点的等腰△PBC （点P ，B ，C 按逆时针方向排列）则线段AC 的取值范围 2≤AP ≤32 提示：发现定等腰直角△AOC 与等腰直角△OBE ，从而得到相似。

初中动点最值问题题型1. 什么是动点最值问题？初中数学中的动点最值问题是指给定一个动点在某个区域内移动的情况，我们需要找出在这个过程中，某个量的最大值或最小值。

这个问题涉及到数学中的函数、图像和变量的运动等概念。

2. 动点最值问题的解决思路要解决动点最值问题，我们需要经过以下几个步骤：步骤一：明确问题首先，我们需要明确问题，确定要求解的量是什么。

常见的量包括距离、时间、面积等。

步骤二：建立模型接下来，我们需要建立一个数学模型来描述动点的运动情况。

这通常涉及到函数和变量的运用。

可以根据具体情况选择直角坐标系或极坐标系来建立模型。

步骤三：求解最值通过对模型进行分析和计算，可以得到函数表达式。

然后使用数学方法求解该函数的最大值或最小值。

常见的求解方法有导数法、平方差法等。

步骤四：验证答案得到答案后，我们需要验证它是否符合实际情况。

可以通过数学推导、图像观察等方式进行验证。

3. 动点最值问题的例子下面以一个具体的例子来说明动点最值问题的解决思路：例子：一个人在河边沿着一条弯曲的小路行走，他从A点出发，经过B、C、D三个点，最后到达E点。

小路的形状如下图所示：我们需要求解以下两个问题：1.从A点到E点的最短距离是多少？2.从A点到E点经过的路径是什么？步骤一：明确问题1.最短距离2.路径步骤二：建立模型我们可以将小路看作一个连续函数，使用直角坐标系来建立模型。

假设小路的函数表达式为y = f(x)。

步骤三：求解最值1.最短距离：我们需要求解函数f(x)在区间[AB]、[BC]、[CD]和[DE]上的最小值。

2.路径：根据求解出来的最小值，可以确定经过哪些点构成了最短路径。

步骤四：验证答案1.最短距离：通过计算和比较，可以验证最小值是否正确。

2.路径：通过观察图像和计算距离，可以验证路径是否正确。

4. 总结初中动点最值问题是数学中常见的一类问题，需要运用函数、图像和变量的概念来建立模型，并通过数学方法求解最大值或最小值。

有限制条件的动点最值问题(一)有限制条件的动点最值问题1. 问题定义动点最值问题是指在一定的限制条件下，寻找函数在某个区间内的最大值或最小值。

有限制条件的动点最值问题则是在问题定义中增加了特定的限制条件，进一步限制了解的范围。

2. 相关问题线性约束下的动点最值问题在问题解决过程中，需要考虑线性约束条件给解的空间带来的限制。

例如，给定一个函数 f(x) 在区间 [a, b] 上连续, 在区间的两个端点上的函数值已知，求函数在该区间上的最大值或最小值。

非线性约束下的动点最值问题如果约束条件是非线性的，即给定的限制条件与 x 的关系不满足线性关系，代表了更加复杂的约束条件。

解决这类问题通常需要运用较为复杂的数学方法，如拉格朗日乘子法等。

多约束条件下的动点最值问题多约束条件下的动点最值问题通常指同时满足多个限制条件下的最优值。

这类问题的解决需要将多个约束条件转化为一个综合条件，从而求出最优解。

动点最大/最小值问题的实际应用动点最值问题在实际生活中有广泛的应用。

例如，在生产过程中确定某种材料的最佳用量，以达到最大效益；在投资过程中找到最佳的投资组合，以最大化收益等。

3. 解决方法解决有限制条件的动点最值问题通常需要采用数学方法进行求解，具体方法根据问题的特点选择。

其中，常见的解决方法包括但不限于：- 求导法：对给定的函数进行求导，寻找函数的极值点，从而得到最大/最小值。

- 极值判定法：通过判定函数在区间内各个端点处的值以及在极值点处的值来确定最值。

- 条件转化法：将给定的约束条件进行转化，使其成为易于计算的形式，再寻求最值。

4. 总结有限制条件的动点最值问题是求解函数在给定约束条件下的最大值或最小值。

针对不同的约束条件，采用不同的数学方法可以解决这类问题。

在实际应用中，有限制条件的动点最值问题能够辅助我们做出更优的决策，提高效益。

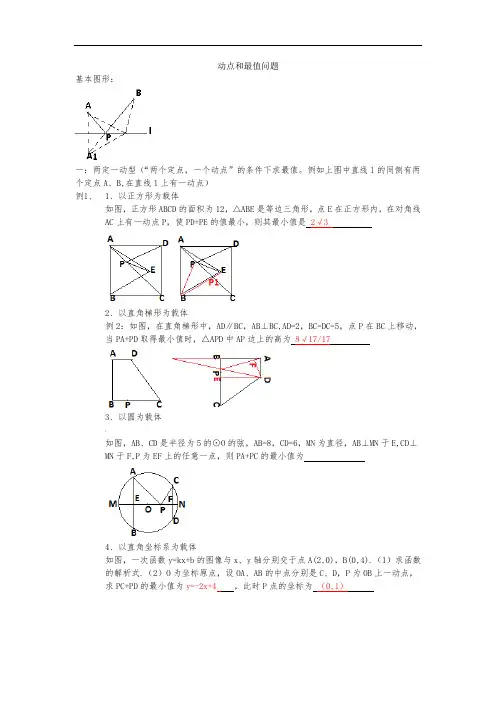
动点和最值问题基本图形：一：两定一动型（“两个定点，一个动点”的条件下求最值。

例如上图中直线l的同侧有两个定点A、B,在直线l上有一动点）例1、1、以正方形为载体如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形内，在对角线AC上有一动点P，使PD+PE的值最小，则其最小值是2√32、以直角梯形为载体例2：如图，在直角梯形中，AD∥BC，AB⊥BC,AD=2，BC=DC=5，点P在BC上移动，当PA+PD取得最小值时，△APD中AP边上的高为8√17/173、以圆为载体:如图，AB、CD是半径为5的⊙O的弦，AB=8，CD=6，MN为直径，AB⊥MN于E,CD⊥MN于F,P为EF上的任意一点，则PA+PC的最小值为4、以直角坐标系为载体如图，一次函数y=kx+b的图像与x、y轴分别交于点A(2,0)，B(0,4).（1）求函数的解析式.（2）O为坐标原点，设OA、AB的中点分别是C、D，P为OB上一动点，求PC+PD的最小值为y=-2x+4 ，此时P点的坐标为（0,1）5、以抛物线为载体已知y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A、B两点，与y轴交于点C，其中A（-3,0），C（0，-2），若在x=-1上存在点P，使得△PBC的周长最小，则P 的坐标为（-1，-4/3）二、一定两动型（“一个定点”+“两个动点”）1、以三角形为载体如图，在阅角△ABC中，AB=4√2，∠BAC=45°，∠BAC的平分线交BC于点D,M、N 分别是AD、AB上的动点，则BM+MN的最小值是|2、以正方形、圆、角为载体正方形ABCD的边长为2，E为AB的中点，P是AC上的一动点.连接BD，则PB+PE 的最小值是√5如图，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB, ∠AOC=60°，P是OB上的一动点，则PA+PC的最小值是2√3如图，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR周长的最小值是10√2 .三、两定两动型（两个定点+两个动点）.恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷（A ）和世界级自然保护区星斗山（B ）位于笔直的沪渝高速公路X 同侧，AB=50km,A 、B 到直线X 的距离分别为10km 和40km,要在沪渝高速公路旁修建一服务区P,向A 、B 两景区运送游客.小民设计了两种方案，图10（1）是方案一的示意图(AP 与直线X 垂直，垂足为P),P 到A 、B 的距离之和S 1=PA+PB ； 图10（2）是方案二的示意图(点A 关于直线X 的对称点是A'，连接BA'交直线X 于点P),P 到A 、B 的距离之和S 2=PA+PB.(1).求S 1 、S 2 ,并比较它们的大小.、(2).请你说明S 2=PA+PB 的值为最小.(3).拟建的恩施到张家界高速公路Y与沪渝高速公路垂直，建立如图所示的直角坐标系，B 到直线Y 的距离为30km,请你在X旁和Y 旁各修建一服务区P 、Q,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.解:⑴图10（1）中过B 作BC ⊥AP,垂足为C,则PC=40,又AP=10,[∴AC=30 ． 1分在Rt △ABC 中，AB=50 AC=30 ∴BC=40∴ BP=24022=+BC CPS 1=10240+ 2分⑵图10（2）中，过B 作BC ⊥AA ′垂足为C ，则A ′C=50，又BC=40∴BA'=4110504022=+图11（1） X A BY B'由轴对称知：PA=PA'∴S 2=BA'=4110 3分∴1S ﹥2S 4分(2)如 图10（2），在公路上任找一点M,连接MA,MB,MA'，由轴对称知MA=MA' :∴MB+MA=MB+MA'﹥A'B∴S 2=BA'为最小 7分（3）过A 作关于X 轴的对称点A', 过B 作关于Y 轴的对称点B'，连接A'B',交X 轴于点P, 交Y 轴于点Q,则P,Q 即为所求 ８分 过A'、 B'分别作X 轴、Y 轴的平行线交于点G, A'B'=5505010022=+ ∴所求四边形的周长为55050+ 10分。

初中数学动点最值问题动点最值问题，听起来有点复杂，但其实就像是在追逐一个小精灵，想要抓住它最美的瞬间。

想象一下，你在操场上，看到一个小球在地上滚动，突然停下来了，这个瞬间就是它的“最值”。

你心里想，这个小球到底能滚多远，能停在哪个地方？这就是我们今天要聊的事情，动点和最值，听着是不是有点小激动呢？好啦，首先我们要明白动点是什么。

动点，就像是一个在平面上随意移动的小家伙，想去哪就去哪。

可能它是个调皮的孩子，也可能是一只自由的小鸟，飞来飞去。

无论它怎么动，我们的任务就是观察它，并且找出它在某个范围内能达到的最远或最近的地方。

比如说，我们把它限制在一个圈里，那它能飞得多远呢？能停在哪里呢？这些问题可真让人好奇。

最值问题就来了。

最值，就像是大海里的珍珠，可能是最亮的、最美的，甚至是最难找到的。

我们要做的就是在众多选择中，找到那个“最”的东西。

想象你在找最美的花，或者是最甜的水果，都是这个道理。

数学里也有这样的挑战，动点在某个条件下，它的坐标要达到一个最高或最低点。

就像你想找一个能够给你最大快乐的游乐设施，或者最美的风景，都是为了追寻那一刻的“最值”。

而这其中，几何图形就像是我们的舞台。

我们把动点的路径画出来，就像是在纸上画了一幅美丽的画。

它在直线上移动，有时候它在曲线中徘徊。

你会发现，只要我们把动点的路径画出来，它就会让我们的思路更加清晰。

就像是绘画，越详细，越好理解。

找到动点的最值，也就像是画出那幅画的关键部分，让整幅画变得生动起来。

再说说具体的方法。

我们可以用一些简单的数学工具，比如导数。

听起来复杂？其实就是找出动点的变化率。

如果你把动点的运动过程写成一个方程，导数就像是这方程的“教练”，告诉你在某一点它的变化有多快，甚至是最慢。

就像运动员在比赛中要知道自己的速度一样，动点也需要这个“教练”来指导它，找到最佳的表现。

动点不只是停留在数学课本里，它还跟我们的生活息息相关。

比如说，你在跑步的时候，想要找到最省力的方式，或者在玩游戏时想要找到最快的过关路线，这些都跟动点的最值问题有着千丝万缕的联系。

动点问题——线段最值动点问题中，经常要求线段的最值。

首先要弄清动点的运动轨迹，从哪里到哪里，是直线还是曲线，有没有特殊位置；然后根据图形特征找解决问题途径。

一般来说，能找到图中求最值的位置，就按特殊位置的特征求最值；若找不到图中最值的特殊位置，最好建立函数，用函数思想解决最值问题。

一、找到特殊位置，求线段最值（或动点路程）1、(2019泰安)如图，矩形ABCD 中，AB =4,AD =2,E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是。

分析：取DE ,DC 中点分别为M ,N .点F 从E 运动到点C ，则点P 从点M 运动到点N .根据“垂线段最短”，当BP 垂直于MN 时，PB 最小。

作BH ⊥MN 垂足为H .当点P 与点H 重合时，PB 最小。

PB =BH∠CEB =∠EBH =045 122PB DE =+ 12222=⨯+ 22=说明：从起点到终点，先找出点P 的运动轨迹，再分析最值。

2、(2019宿迁)如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE =1,F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边三角形EFG ，连接CG ,则CG 的最小值为 分析：点F 在起点B 处时，作等边'EBB ∆,连接'B G ，得射线''B F ,点G 在其上运动。

∵ 'BE B E =,'''BEB B EF FEG B EF ∠+∠=∠+∠,EF EG =∴△EBF ≌△'EB G∴∠'GB E =∠FBE =090. 当点'B 在EF 上时，CG ⊥'B G ，CG 最小。

（根据“垂线段最短”） 35122CG =+= 3、（2019桂林）如图，在矩形ABCD 中，AB =3，AD =3，点P 是AD 边上的一个动点，连接BP ，作点A 关于直线BP 的对称点1A ，连接1A C ,设1A C 的中点为Q ，当点P 从点A 出发，沿边AD 运动到点D 时停止运动，点Q 的运动路径长为。