精品 八年级数学下册 正方形练习题

18.2.3 正方形正方形的性质与判定第1课时正方形的性质01基础题知识点1正方形的定义1．在四边形ABCD中，若AD∥BC，AD＝BC，AB＝BC，∠B＝90°，则四边形ABCD 的形状是(D)A．平行四边形B．矩形C．菱形D．正方形2．如图，Rt△ABC中，∠ACB＝90°，D、E、F分别是AB、AC、BC的中点，连接DE、DF、CD，如果AC＝BC，那么四边形DECF是正方形．知识点2正方形的性质3．正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于(B)A．30°B．45°C．60°D．75°4．正方形是轴对称图形，它的对称轴共有(D)A．1条B．2条C．3条D．4条5．正方形具有而矩形不一定具有的性质是(B)A．四个角都相等B．四边都相等C．对角线相等D．对角线互相平分6．(凉山中考)如图，菱形ABCD中，∠B＝60°，AB＝4，则以AC为边的正方形ACEF的周长为(C)A．14 B．15C．16 D．177．(吉林中考)如图，四边形ABCD，AEFG都是正方形，点E，G分别在AB，AD上，连接FC，过点E作EH∥FC交BC于点H.若AB＝4，AE＝1，则BH的长为(C)A．1 B．2 C．3 D．3 28．(来宾中考)正方形的一条对角线长为4，则这个正方形的面积是(A)A．8 B．4 2C．8 2 D．169．如图，四边形ABCD是正方形，延长AB到E，使AE＝AC，则∠BCE的度数是22.5°.10．(泸州中考)如图，正方形ABCD中，E，F分别为BC，CD上的点，且AE⊥BF，垂足为点G.求证：AE＝BF.证明：∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠C＝90°.∵AE⊥BF，∴∠ABG＋∠BAE＝90°.又∵∠ABG＋∠CBF＝90°，∴∠BAE＝∠CBF.∴△ABE≌△BCF(ASA)．∴AE＝BF.02中档题11．如图，将正方形OABC放在平面直角坐标系xOy中，O是原点，若点A的坐标为(1，3)，则点C的坐标为(C)A．(3，1) B．(－1，3)C．(－3，1) D．(－3，－1)12．(龙岩中考)如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连接BD并延长交EG于点T，交FG于点P，则GT＝(B)A. 2 B．2 2 C．2 D．113．如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S1、S2，则S1＋S2的值为(B)A．16 B．17 C．18 D．1914．(济源校级期中)如图，已知正方形ABCD 的边长为16，M 在DC 上，且DM ＝4，N 是AC 上的一动点，则DN ＋MN 的最小值是20．15．(广安中考)如图，在正方形ABCD 中，P 是对角线AC 上的一点，连接BP ，DP ，延长BC 到E ，使PB ＝PE.求证：∠PDC ＝∠PEC.证明：∵四边形ABCD 是正方形，∴BC ＝CD ，∠BCP ＝∠DCP. 在△BCP 和△DCP 中，⎩⎪⎨⎪⎧BC ＝DC ，∠BCP ＝∠DCP PC ＝PC ，， ∴△BCP ≌△DCP(SAS)． ∴∠PDC ＝∠PBC. ∵PB ＝PE ， ∴∠PBC ＝∠PEC. ∴∠PDC ＝∠PEC.16．(周口校级一模)如图，G ，E 分别是正方形ABCD 的边AB ，BC 上的点，且AG ＝CE ，AE ⊥EF ，AE ＝EF ，求∠FCD 的度数．解：∵AE ⊥EF ，∴∠AEF ＝90°.∴∠AEB ＋∠FEC ＝180°－∠AEF ＝180°－90°＝90°. ∵四边形ABCD 是正方形， ∴∠B ＝90°，AB ＝BC.∴∠AEB ＋∠BAE ＝180°－∠B ＝180°－90°＝90°. ∴∠BAE ＝∠FEC.在△AGE 和△ECF 中，⎩⎨⎧AG ＝EC ，∠GAE ＝∠CEF ，AE ＝EF ，∴△AGE ≌△ECF(SAS)． ∴∠AGE ＝∠ECF.∵AB ＝BC ，AG ＝CE ，∴BG ＝BE.∴∠BGE ＝45°.∴∠AGE ＝180°－∠BGE ＝180°－45°＝135°. ∴∠ECF ＝135°.∴∠FCD ＝∠ECF －∠ECD ＝135°－90°＝45°.03 综合题17．已知正方形ABCD 的边长为a ，两条对角线AC 、BD 相交于点O ，P 是射线AB 上任意一点，过P 点分别作直线AC 、BD 的垂线PE 、PF ，垂足为E 、F.(1)如图1，当P 点在线段AB 上时，PE ＋PF 的值是否为定值？如果是，请求出它的值；如果不是，请加以说明；(2)如图2，当P 点在线段AB 的延长线上时，求PE －PF 的值． 解：(1)是定值．∵四边形ABCD 为正方形，∴AC ⊥BD. ∵PF ⊥BD ，∴PF ∥AC.同理：PE ∥BD.∴四边形PFOE 为矩形．∴PE ＝OF. 又∵∠PBF ＝45°，∴PF ＝BF. ∴PE ＋PF ＝OF ＋FB ＝OB ＝22a. (2)∵四边形ABCD 为正方形，∴AC ⊥BD. ∵PF ⊥BD ，∴PF ∥AC.同理：PE ∥BD.∴四边形PFOE 为矩形．∴PE ＝OF. 又∵∠PBF ＝∠ABO ＝45°，∴PF ＝BF. ∴PE －PF ＝OF －BF ＝OB ＝22a.第2课时 正方形的判定01基础题知识点正方形的判定1．下列说法不正确的是(C)A．对角线互相垂直的矩形是正方形B．对角线相等的菱形是正方形C．有一个角是直角的平行四边形是正方形D．一组邻边相等的矩形是正方形2．已知四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是(D)A．∠D＝90°B．AB＝CDC．AD＝BC D．BC＝CD3．如图，将矩形纸片折叠，使A点落在BC上的F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是(A)A．邻边相等的矩形是正方形B．对角线相等的菱形是正方形C．两个全等的直角三角形构成正方形D．轴对称图形是正方形4．(日照中考)小明在学习了正方形之后，给同桌小文出了道题．从下列四个条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD中选两个作为补充条件，使▱ABCD成为正方形(如图)．现有下列四种选法，你认为其中错误的是(B)A．①②B．②③C．①③D．②④5．矩形各内角的平分线围成一个(B)A．平行四边形B．正方形C．矩形D．菱形6．(龙东中考)如图，菱形ABCD中，对角线AC、BD相交于点O，不添加任何辅助线，请添加一个条件AC＝BD(或∠ABC＝90°等)，使四边形ABCD是正方形(填一个即可)．7．如图，把一个矩形纸片对折两次，然后剪下一个角．为了得到一个正方形，剪刀与折痕所成的角的度数应为45°.8．(扬州中考改编)如图，已知Rt△ABC中，∠ABC＝90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线AE平移至△FEG，DE，FG相交于点H.连接CG，求证：四边形CBEG是正方形．证明：根据旋转和平移可得∠GEF＝90°，∠CBE＝90°，CG∥BE，CB＝BE.∴∠BCG＋∠CBE＝180°.∴∠BCG＝90°.∴四边形CBEG是矩形．∵CB＝BE，∴矩形CBEG是正方形．9．如图，在平面直角坐标系中，四边形ABCD的顶点坐标分别是A(－2，0)、B(0，－2)、C(2，0)、D(0，2)，求证：四边形ABCD是正方形．证明：由四边形ABCD的顶点坐标分别是A(－2，0)、B(0，－2)、C(2，0)、D(0，2)，可知OA＝OB＝OC＝OD＝2，∴四边形ABCD为矩形．∵AC⊥BD，∴四边形ABCD是正方形．02中档题10．如图，在矩形ABCD中，AD＝2AB，E、F分别是AD、BC的中点，连接AF与BE、CE与DF，分别交于点M、N，则四边形EMFN是(A)A．正方形B．菱形C．矩形D．无法确定11．(威海中考)如图，在△ABC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE＝BF.添加一个条件，仍不能证明四边形BECF为正方形的是(D) A．BC＝AC B．CF⊥BFC．BD＝DF D．AC＝BF12．(南京中考)如图，在四边形ABCD中，AB＝BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD.垂足分别为M，N.(1)求证：∠ADB＝∠CDB；(2)若∠ADC＝90°，求证：四边形MPND是正方形．证明：(1)∵BD平分∠ABC，∴∠ABD＝∠CBD.又∵BA＝BC，BD＝BD，∴△ABD≌△CBD(SAS)．∴∠ADB＝∠CDB.(2)∵PM⊥AD，PN⊥CD，∴∠PMD＝∠PND＝90°.又∵∠ADC＝90°，∴四边形MPND是矩形．∵∠ADB＝∠CDB，PM⊥AD，PN⊥CD，∴PM＝PN.∴四边形MPND是正方形．03综合题13．(青岛中考)已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E.(1)求证：△AOD≌△EOC；(2)连接AC，DE，当∠B＝∠AEB＝45°时，四边形ACED是正方形？请说明理由．解：(1)证明：∵四边形ABCD是平行四边形，∴AD∥BC.∴∠ADO＝∠ECO，∠DAO＝∠CEO.又∵OD＝OC，∴△AOD≌△EOC(AAS)．(2)理由：∵△AOD≌△EOC，∴OA＝OE.又∵OC＝OD，∴四边形ACED是平行四边形．∵∠B＝∠AEB＝45°，∴AB＝AE，∠BAE＝90°.∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD.∴∠COE＝∠BAE＝90°.∴▱ACED是菱形．∵AB＝AE，AB＝CD，∴AE＝CD.∴菱形ACED是正方形．。

人教版八年级数学(下)正方形练习题1. 简答题1. 什么是正方形？2. 正方形有哪些性质？3. 如何计算正方形的周长和面积？2. 填空题1. 一个正方形的边长为8cm，它的周长是\_\_\_cm。

2. 一个正方形的边长为12m，它的面积是\_\_\_平方米。

3. 一个正方形的周长是36cm，那么它的边长是\_\_\_cm。

4. 一个正方形的面积是100平方米，它的边长是\_\_\_m。

3. 计算题1. 一个正方形的周长是40cm，它的边长是\_\_\_cm，面积是\_\_\_平方厘米。

2. 一个正方形的面积是144平方米，它的边长是\_\_\_m，周长是\_\_\_m。

4. 解答题小明画了一个正方形，周长是56cm。

请你帮他计算一下这个正方形的边长和面积。

5. 应用题小红家的花园是一个正方形，边长为10m。

她要在花园的四周修建一个围墙，围墙的高度为1.5m，围墙的底部距离花园边沿0.5m。

请你帮她计算一下需要多少米的围墙材料。

以上是关于人教版八年级数学(下)正方形练题的内容。

---Note: The above document contains practice questions on squares for 8th-grade mathematics (part 2) of People's Education Press. Itincludes multiple-choice questions, fill in the blanks, calculation questions, and application questions.。

初二下册数学正方形练习题正方形是一种特殊的四边形，其中四条边长度相等且四个内角均为直角。

在初二下册数学中，我们学习了有关正方形的基本概念、性质和应用。

本文将通过解答一些正方形练习题的方式，帮助同学们巩固对正方形的理解。

题1：已知正方形ABCD的边长为6cm，求其面积和周长。

解：正方形的边长相等，所以AB = BC = CD = AD = 6cm。

正方形的面积可以通过边长的平方来计算，即6cm * 6cm = 36cm²。

周长可以通过边长乘以4来计算，即6cm * 4 = 24cm。

所以正方形ABCD的面积为36cm²，周长为24cm。

题2：正方形EFGH的面积是64cm²，求其边长和周长。

解：设正方形EFGH的边长为x cm。

根据正方形面积的计算公式，我们可以得到方程x * x = 64。

解这个方程可得x² = 64，开根号得到x = 8。

所以正方形EFGH的边长为8cm。

周长可以通过边长乘以4来计算，即8cm * 4 = 32cm。

所以正方形EFGH的边长为8cm，周长为32cm。

题3：正方形IJKL和正方形MNOP是相似的，正方形IJKL的边长为10cm，求正方形MNOP的边长、面积和周长。

解：由于正方形IJKL和正方形MNOP是相似的，它们的对应边长的比值相等。

设正方形MNOP的边长为y cm，根据相似性质可以得到方程10/y = y/10。

通过交叉相乘可得y² = 100，开根号得到y = 10。

所以正方形MNOP的边长为10cm。

正方形的面积和周长可以使用边长的平方和边长乘以4的方法计算。

正方形IJKL的面积为10cm * 10cm = 100cm²，周长为10cm * 4 = 40cm。

所以正方形MNOP的面积为100cm²，周长为40cm。

通过解答这些练习题，我们复习了正方形的基本概念和性质，并且学会了如何计算正方形的面积和周长。

最新（⼈教版）⼋年级数学下册《正⽅形》测试卷及答案正⽅形⼀、选择题(每⼩题4分,共12分)1.如图是⼀张矩形纸⽚ABCD,AD=10cm,若将纸⽚沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )A.4cmB.6cmC.8cmD.10cm2.(2013·凉⼭州中考)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边的正⽅形ACEF的周长为( )A.14B.15C.16D.173.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的⾯积为8,则BE=( )A.2B.3C.2D.2⼆、填空题(每⼩题4分,共12分)4.如图正⽅形ABCD与正三⾓形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的⼤⼩可以是.5.如图,已知正⽅形ABCD的边长为1,连接AC,BD,相交于点O,CE平分∠ACD交BD于点E,则DE= .6.(2013·绵阳中考)对正⽅形ABCD进⾏分割,如图1,其中E,F分别是BC,CD的中点,M,N,G分别是OB,OD,EF的中点,沿分化线可以剪出⼀副“七巧板”,⽤这些部件可以拼出很多图案,图2就是⽤其中6块拼出的“飞机”.若△GOM的⾯积为1,则“飞机”的⾯积为.三、解答题(共26分)7.(8分)(2013·黔东南州中考)如图,在正⽅形ABCD中,点M是对⾓线BD上的⼀点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点 F.求证:AM=EF.8.(8分)如图,△ABC是等腰直⾓三⾓形,∠A=90°,点P,Q分别是AB,AC上的⼀动点,且满⾜BP=AQ,D是BC的中点.(1)求证:△PDQ是等腰直⾓三⾓形.(2)当点P运动到什么位置时,四边形APDQ是正⽅形,并说明理由.【拓展延伸】9.(10分)在正⽅形ABCD中,点P是CD边上⼀动点,连接PA,分别过点B,D作BE ⊥PA,DF⊥PA,垂⾜分别为E,F,如图①.(1)请探究BE,DF,EF这三条线段的长度具有怎样的数量关系?若点P在DC的延长线上,如图②,那么这三条线段的长度之间⼜具有怎样的数量关系?若点P在CD的延长线上呢,如图③,请分别直接写出结论.(2)就(1)中的三个结论选择⼀个加以证明.答案解析1.【解析】选A.∵四边形CEFD是正⽅形,AD=BC=10cm,BE=6cm,∴CE=EF=CD=10-6=4(cm).2.【解析】选C.∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三⾓形,∴AC=AB=4,∴正⽅形ACEF的周长是AC+CE+EF+FA=4×4=16.3.【解析】选C.过B点作BF⊥CD,与DC的延长线交于点F,则有△BCF≌△BAE,∴BE=BF,四边形BEDF是正⽅形,∴S四边形ABCD=S正⽅形BEDF=8,∴BE==2.4.【解析】由SSS知△ABE≌△ADF,∴∠BAE=∠DAF,当△AEF在正⽅形内部时,∠BAE=15°,当△AEF在正⽅形外部时,如图∠BAE+∠DAF=330°,∴∠BAE=165°.答案:15°或165°5.【解析】过E作EF⊥DC于点F.∵四边形ABCD是正⽅形,∴AC⊥BD.∵CE平分∠ACD交BD于点E,∴EO=EF.∵正⽅形ABCD的边长为1,∴AC=,∴CO=AC=.∴CF=CO=,∴EF=DF=DC-CF=1-,∴DE==-1.答案:-16.【解析】连接AC,四边形ABCD是正⽅形,AC⊥BD,E,F分别是BC,CD的中点,EF ∥BD,AC⊥EF,CF=CE,△EFC是等腰直⾓三⾓形,直线AC是△EFC底边上的⾼所在直线,根据等腰三⾓形“三线合⼀”,AC必过EF的中点G,点A,O,G和C在同⼀条直线上,OC=OB=OD,OC⊥OB,FG是△DCO的中位线,OG=CG=OC,M,N分别是OB,OD的中点,OM=BM=OB,ON=DN=OD,OG=OM=BM=ON=DN=BD,等腰直⾓三⾓形GOM的⾯积为1,OM·OG=OM2=1,OM=,BD=4OM=4,2AD2=BD2=32,AD=4,图2中飞机⾯积等于图1中多边形ABEFD的⾯积,飞机⾯积=正⽅形ABCD的⾯积-三⾓形CEF的⾯积=16-2=14.答案:147.【证明】如图,过点M作MP⊥AB于点P,过点M作MQ⊥AD于点Q.∵四边形ABCD是正⽅形,∴四边形MFDQ和四边形PBEM是正⽅形,四边形APMQ是矩形,∴AP=QM=DF=MF,PM=PB=ME,∵在△APM和△FME中,∴△APM≌△FME(SAS),∴AM=EF.8.【解析】(1)连接AD.∵△ABC是等腰直⾓三⾓形,D是BC的中点,∴AD⊥BC,AD=BD=DC,∠DAQ=∠B,⼜∵BP=AQ,∴△BPD≌△AQD,∴PD=QD,∠BDP=∠ADQ,∵∠BDP+∠ADP=90°,∴∠ADP+∠ADQ=∠PDQ=90°,∴△PDQ为等腰直⾓三⾓形.(2)当P点运动到AB的中点时,四边形APDQ是正⽅形;理由如下:由(1)知△ABD为等腰直⾓三⾓形,当P为AB的中点时,DP⊥AB,即∠APD=90°,⼜∵∠BAC=90°,∠PDQ=90°,∴四边形APDQ为矩形,⼜∵DP=AP=AB,∴四边形APDQ为正⽅形.9.【解析】(1)在图①中,BE,DF,EF这三条线段长度具有这样的数量关系:BE-DF=EF;在图②中,BE,DF,EF这三条线段长度具有这样的数量关系:DF-BE=EF;在图③中,BE,DF,EF这三条线段长度具有这样的数量关系:DF+BE=EF.(2)答案不唯⼀.对图①中结论证明如下:∵BE⊥PA,DF⊥PA,∴∠BEA=∠AFD=90°,∵四边形ABCD是正⽅形,∴AB=AD,∠BAD=90°,∴∠BAE+∠DAF=∠ADF+∠DAF=90°,∴∠BAE=∠ADF,∴△BAE≌△ADF,∴BE=AF,AE=DF,∵AF-AE=EF,∴BE-DF=EF.。

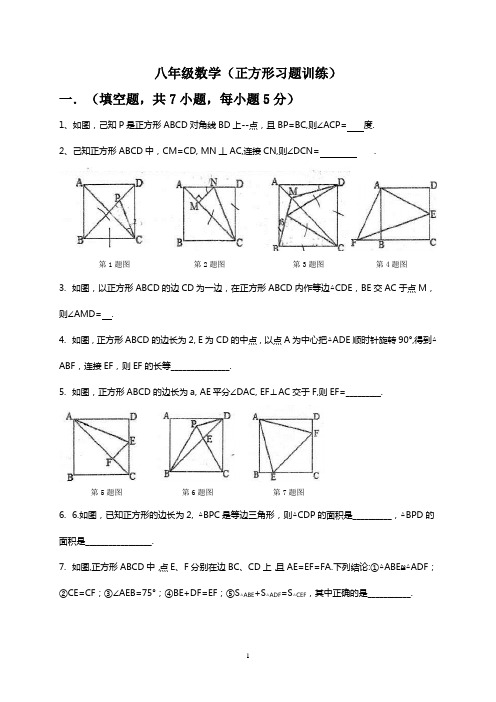
八年级数学（正方形习题训练）一．（填空题，共7小题，每小题5分）1、如图，己知P是正方形ABCD对角线BD上--点，且BP=BC,则∠ACP= 度.2、己知正方形ABCD中，CM=CD, MN丄AC,连接CN,则∠DCN= .第1题图第2题图第3题图第4题图3.如图，以正方形ABCD的边CD为一边，在正方形ABCD内作等边△CDE，BE交AC于点M，则∠AMD= .4.如图，正方形ABCD的边长为2, E为CD的中点，以点A为中心把△ADE顺时针旋转90°,得到△ABF，连接EF，则EF的长等_______________.5.如图，正方形ABCD的边长为a, AE平分∠DAC, EF⊥AC交于F,则EF=_________.第5题图第6题图第7题图6.6.如图，已知正方形的边长为2, △BPC是等边三角形，则△CDP的面积是__________，△BPD的面积是_________________.7.如图,正方形ABCD中，点E、F分别在边BC、CD上，且AE=EF=FA.下列结论:①△ABE≌△ADF；②CE=CF；③∠AEB=75°；④BE+DF=EF；⑤S△ABE+S△ADF=S△CEF，其中正确的是___________.二.（解答题，共4小题，共65分）1.（15分）如图，点B、C分别在两条直线y=2x和y=kx上.,点A、D是x轴上两点，已知四边形ABCD是正方形，则求k的值2.（15分）如图，正方形ABCD中，E是BD上一-点，AE的延长线交CD于F,交BC的延长线于G, M 是FG的中点.（1）求证：①∠1 = ∠2；②EC丄MC.（2）试问当∠1等于多少度时，△ECG为等腰三角形？请说明理由.3.（15分）如图所示，正方形ABCD中，在AD的延长线上取点E、F,使DE=AD, DF=BD,连接BF 分别交CD、CE于H、G。

求证：△GHD是等腰三角形.4.（20分）点E 是正方形ABCD 外一点，点F 在DE 上，且AF=AE=2, ∠EAF=90°, FB=3. （1）求证：△AFD≌△AEB；（2）求∠DEB的度数.（3）求正方形ABCD的面积答案及解析一．（填空题，共7小题）1.22.5°2.22.5°3.120°4.102-5.()a13-6.17.二.（解答题，共4小题）1.2.3.4.。

18.2.3《正方形》精选练习一、选择题1.下列命题中，正确的是（）.A.有一组邻边相等的四边形是菱形B.对角线互相平分且垂直的四边形是矩形C.两组邻角相等的四边形是平行四边形D.对角线互相垂直且相等的平行四边形是正方形2.下列命题是真命题的是（）A.四边都相等的四边形是矩形B.菱形的对角线相等C.对角线互相垂直的平行四边形是正方形D.对角线相等的平行四边形是矩形3.如图,在正方形ABCD外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC为 ( )A.45°B.55°C.60° .75°4.下列命题是真命题的是（）A.菱形的对角线互相平分B.一组对边平行，一组对边相等的四边形是平行四边形C.对角线互相垂直且相等的四边形是正方形D.对角线相等的四边形是矩形5.下列命题中，真命题是（）A.有两边相等的平行四边形是菱形B.对角线垂直的四边形是菱形C.四个角相等的菱形是正方形D.两条对角线相等的四边形是矩形6.下列命题是真命题的是( )A.对角线互相平分的四边形是平行四边形B.对角线相等的四边形是矩形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是正方形7.如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE长为（）A.2﹣2B.﹣1C.﹣1D.2﹣8.如图所示，在正方形ABCD的内部，作等边三角形BCE，则∠AEB的度数为( )A.60°B.65°C.70°D.75°9.如图，在平面直角坐标系xOy中，点A、C、F在坐标轴上，E是OA的中点，四边形AOCB是矩形，四边形BDEF是正方形，若点C的坐标为(3,0)，则点D的坐标为( )A.(1,2.5)B.(1,1+)C.(1,3)D.(-1,1+)10.如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD上，∠EFD=60°.若将四边形EBCF 沿EF折叠，点B恰好落在AD边上，则BE的长度为（）A.1B.C.D.211.如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为( )A.6B.8C.10D.1212.如图，在正方形ABCD中，点P是AB上一动点(不与A，B重合)，对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N.下列结论：①△APE≌△AME；②PM＋PN=BD；③PE2＋PF2=PO2.其中正确的有( )A.0个B.1个C.2个D.3个二、填空题13.对角线长为2的正方形的周长为___________，面积为__________。

19.3 正方形1.菱形、矩形、正方形都具有的性质是( C )(A)对角线相等(B)对角线互相垂直(C)对角线互相平分(D)对角线平分一组对角2.下列命题错误的是( C )(A)对角线互相平分的四边形是平行四边形(B)对角线相等的平行四边形是矩形(C)一条对角线平分一组对角的四边形是菱形(D)对角线互相垂直的矩形是正方形3.已知四边形ABCD中,∠A=∠B=∠C=∠D,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( D )(A)∠D=90° (B)AB=CD(C)AD=BC (D)BC=CD4.如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( B )(A)2 (B)(C) (D)15.能使平行四边形ABCD为正方形的条件是AC=BD且AC⊥BD(答案不唯一) (填上一个条件即可).6.如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是AC=BD或(AB⊥BC)(答案不唯一) .7.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,则△AFC的面积为2 .8.(2018武汉)以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是30°或150°.9.已知:如图,四边形ABCD是正方形,分别过点A,C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB,DN分别交l2于Q,P点.求证:四边形PQMN是正方形.证明:因为PN⊥l1,QM⊥l1,所以PN∥QM,∠PNM=90°.因为PQ∥NM,所以四边形PQMN是矩形.因为四边形ABCD是正方形,所以∠BAD=∠ADC=90°,AB=AD=DC.所以∠1+∠2=90°.又∠3+∠2=90°,所以∠1=∠3.所以△ABM≌△DAN.所以AM=DN.同理AN=DP.所以AM+AN=DN+DP,即MN=PN.所以四边形PQMN是正方形.10.已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.(1)求证:四边形ABCD是菱形;(2)如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形.证明:(1)在△ADE与△CDE中,所以△ADE≌△CDE(S.S.S.),所以∠ADE=∠CDE,因为AD∥BC,所以∠ADE=∠CBD,所以∠CDE=∠CBD,所以BC=CD,因为AD=CD,所以BC=AD,所以四边形ABCD为平行四边形,因为AD=CD,所以四边形ABCD是菱形.(2)因为BE=BC,所以∠BCE=∠BEC,因为∠CBE∶∠BCE=2∶3,所以∠CBE=180°×=45°,因为四边形ABCD是菱形,所以∠ABE=45°,所以∠ABC=90°,所以四边形ABCD是正方形.11.(开放探究题)已知,如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM 的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并说明理由.(1)证明:因为AD,AN分别是∠BAC的内角、外角平分线,所以∠BAD=∠CAD,∠CAE=∠MAE.因为∠BAD+∠CAD+∠CAE+∠MAE=180°.所以2∠CAD+2∠CAE=180°.所以∠CAD+∠CAE=90°,即∠DAE=90°,因为AD⊥BC,CE⊥AN,所以∠ADC=∠AEC=∠DAE=90°,所以四边形ADCE是矩形.(2)解:当△ABC是以∠BAC为直角的等腰直角三角形时,四边形ADCE是正方形.理由如下:因为△ABC是以∠BAC为直角的等腰直角三角形,AD⊥BC,所以∠CAD=∠BAD=45°.∠ACD=45°.所以∠CAD=∠ACD=45°.所以AD=CD.因为四边形ADCE是矩形,所以四边形ADCE是正方形.12.(拓展探究题)如图,四边形ABCD,DEFG都是正方形,连结AE,CG.(1)求证:AE=CG;(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.(1)证明:因为AD=CD,DE=DG,∠ADC=∠GDE=90°,又∠CDG=90°+∠ADG=∠ADE,所以△ADE≌△CDG.所以AE=CG.(2)解:猜想:AE⊥CG.证明:如图,设AE与CG交点为M,AD与CG交点为N.由(1)得△ADE≌△CDG,所以∠DAE=∠DCG.又因为∠ANM=∠CND,所以∠CND+∠DCN=90°,即∠ANM+∠DAE=90°,所以∠AMN=∠ADC=90°.所以AE⊥CG.。

八年级数学下册正方形能力提高题1.判别题：(1)四边相等的四边形是正方形。

（） (2)四个内角相等的四边形是正方形。

（）(3)邻边相等的平行四边形是正方形。

（） (4)有一个角为直角的平行四边形是正方形。

（） (5)对角线相等的平行四边形是正方形。

（） (6)正方形既是菱形又是矩形。

（）2.正方形一边上任一点到这个正方形两条对角线的距离之和等于对角线的（）A.31B.21C.41D.2倍3.边长为a的正方形的面积与对角线为b的正方形的面积相等,则a、b的大小关系是（）A.a>bB.a=bC.a<bD.a≥b4.如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有（）A.1个B.2个C.3个D.4个第4题图第5题图第6题图5.在平面直角坐标系中,称横、纵坐标均为整数的点为整点,如下图所示的正方形内（包括边界）整点的个数是（）A.13B.21C.17D.256.如图,正方形ABCD的对角线AC与BD相交于O点,在BD上截取BE=BC,连接CE,点P是CE上任意一点，PM⊥BD于M,PN⊥BC于N,若正方形ABCD的边长为1，则PM+PN=（）A.1B.2C.22D.217.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF= 度．CA DPEF第7题图第8题图第9题图第10题图8.如图,在正方形ABCD中,AB=8,AE=2,EF=25点E在AB上,点F在AD上,则CF=9.如图,ABCD是正方形,是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,若正方形面积为64，那么△AEM的面积是_________10.如图,在正方形ABCD中,P是AD上任一点,PE⊥AC,PF⊥BD,点E、F分别是垂足,BD+AC=212,则PE+PF=______11.如图,以正方形ABCD的对角线BD为边作正三角形BDE,过E作EF⊥AD,交DA的延长线于F,则∠AEF= ；若正三角形BDE的周长是122，正方形面积为_______第11题图第12题图第13题图12.如图,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有2015个这样大小的正方形这样摆放,则阴影面积的总和是cm2．13.如图,边长为2a的正方形ABCD和边长为2b的正方形BEFG排放在一起，O1和O2分别是两个正方形的中心,则阴影部分的面积为，线段O1O2的长为．14.如图,在正方形ABCD中,E是DB延长线上的一点,且∠ECB=150.求证:EC=BD.15.如图,在正方形ABCD中,M为BC上任一点,N是CD的中点,且AM=DC+CM.求证:AN平分∠DAM.16.如图,在正方形ABCD中,对角线AC与BD相交于点O,AF平分∠BAC,交BD于点F.求证:AB-OF=OA.17.如图,在正方形ABCD中，E是BC边上一点，过点E作AE的垂线分别交CD、AB的延长线于点F、G.求证：BE=BG+CF.18.如图,在正方形ABCD中,△PAQ是正三角形,设AB=10,求PB的长.。

八年级数学《正方形》练习题【同步达纲练习】一、填空1.正方形既是相等的矩形，又是有一个角是的菱形.2.正方形和菱形比较，除具有的性质外，它们具有的共同性质还有：四条边都，对角线 .3.对角线的四边形是正方形.4.正方形和矩形比较，除具有的性质外，它们还具有的共同性质还有：四个角都，对角线.5.如果一个正方形的边长恰好等于边长为m的正方形对角线的长，那么这两个正方形周长和为，面积的和为 .6.如图4.6-12，正方形ABCD中，E、F分别是CD、DA上的点，并且EF＝AF+CE，∠BEF ＝∠BEC，那么∠EBF＝度.7.如图4.6-13，正方形ABCD中，E是CF上的点，四边形BEFD是菱形，那么∠BEF＝度.图4.6-12 图4.6-138.如图4.6-14，E是正方形ABCD边BC延长线上的一点，若EC＝AC，AE交CD于F，那么∠AFC＝度.图4.6-14 图4.6-159.如图4.6-15，将边长为12的正方形纸片ABCD的顶点A折叠至DC边上一点E，若DE为5，则折痕PQ的长为 .10.P是正方形ABCD内一点，△PAB为正三角形，若正方形的面积为1，则△PAB的面积为 .二、选择题1.下列命题是真命题的是( )A.一组对边平行且另一组对边相等的四边形是平行四边形B.对角线相等的四边形是矩形C.一组对边平行且有一组对角相等的四边形是平行四边形D.对角线互相垂直且相等的四边形是正方形2.正方形具有而矩形不一定具有性质是( )A.对角线互相平分B.对角线相等C.对角线互相平分且相等D.对角线互相垂直3.下列命题中，错误的是( )A.对角线相等且互相垂直的四边形是菱形B.两组对边分别相等的四边是平行四边形C.有一个角是直角的平行四边形是矩形D.四个角相等的菱形是正方形4.如图，正方形ABCD中，CE＝MN，∠MCE＝35°，那么∠ANM是( )A.45°B.55°C.65°D.75°5.下列命题正确的是( )A.一组对边平行，另一组对边相等的四边形是平行四边形B.以一条对角线所在直线为对称轴的平行四边形是菱形C.顺次连结矩形四条边中点所得的四边形仍是矩形6.下列命题中，假命题是( )A.矩形的对角线相等B.菱形的对角线互相垂直C.正方形的对角线相等且互相垂直D.梯形的对角线互相平分7.在正方形ABCD的对角线AC上取一点E，使AE＝AB，作EF⊥AC交BC于F，则下列关系式成立的是( )A.BF＝ECB.BF≠ECC.BF＜ECD.BF＞EC8.以正方形ABCD的边AB向外作等边三角形ABE，BD、CE交于F，则∠AFD的度数为( )A.50°B.60°C.67.5°D.75°9.在正方形ABCD中，E、F、G、H分别是AB、BC、CD、DA的三等分点，则四边形EFGH 是( )A.正方形B.菱形C.矩形D.平行四边形10.给出下列结论：(1)正方形具有平行四边形的一切性质，(2)正方形具有矩形的一切性质，(3)正方形具有菱形的一切性质，(4)正方形共有两条对称轴，(5)正方形共有四条对称轴，其中正确的结论有( )A.2B.3个C.4个D.5个三、解答题1.在正方形ABCD的边BC的延长线上取一点E，使CE＝AC，连结AE交CD于F，求∠AFD 的度数?2.如图所示，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L、M、D在AK 的同旁，连结BK和DM，求证：BK＝DM.3.如图，已知正方形ABCD，在BC上取一点E，延长AB至F，使BF＝BE，AE的延长线交CF于G，求证AG⊥CF.4.如图，E为正方形ABCD的边AB延长线上一点，DE交AC于F，交BC于G，H为GE的中点.求证：BF⊥BH.5.如图，E 、F 分别在正方形ABCD 的边BC 、CD 上，且∠EAF ＝45°，求证：EF ＝BE+DF.【素质优化训练】如图，M 为正方形ABCD 的AB 边上的中点，MN ⊥DM ，BN 平分∠CBG. 求证：DM ＝MN【生活实际运用】如图，正方形ABCD 的对角线相交于点O.点O 是正方形A ′B ′C ′O 的一个顶点.如果两个正方形的边长相等，那么正方形A ′B ′C ′O 绕点O 无论怎样转动，两个正方形重叠部分的面积，总等于一个正方形面积的41，想一想这是为什么.【知识探究学习】如图，已知E 是正方形ABCD 的边BC 上的中点，F 是CD 上一点，AE 平分∠BAF ，求证：AF ＝BC+CF.参考答案一、1.邻边相等直角 2.平行四边形相等互相垂直且平分每一组对角 3.相互平分相等互相垂直 4.平行四边形是直角互相垂直 5.4(2+1)m 3m2 6.45°37.150° 8.112.5° 9.13 10.4二、1.C 2.D 3.A 4.B 5.B 6.D 7.A 8.C 9.A 10.C三、1.67.5° 2.提示：证△MAD≌△KAB(SAS) 3.提示：证△ABE≌△CBF，再证∠AGC ＝∠ABE＝90° 4.先证△BCF≌△DCF，得：∠CDF＝∠CBF，进而证∠GBF＝∠HBG，得：∠FBG+∠GBH＝∠GBH+∠HBE＝90°，得BF⊥BH 5.提示：延长CB到G，使BG＝FD，证△ABG ≌△ADF，得：∠BAG＝∠DAF，再证△AEF≌△AEG，得EF＝EG＝EB+BG＝EB+DF【素质优化训练】提示：取AD的中点E，连EM.【生活实际运用】略.【知识探究学习】提示：延长FC交AE的延长线于H.。