初三总复习圆

圆一、本章知识结构图二、本章知识点（一）圆的基本性质1.半圆与弧，直径与弦①半圆是弧，但弧不一定是半圆，等弧只能出现在同圆或等圆中，弧所对的圆心角等，弧长相等，这样的弧才是等弧.②直径是弦（图中最长的弦），但弦并非为直径.2.圆是轴对称图形，任何一条直径所在的直线都是它的对称轴.垂径定理及推论①推论中注意非直径的弦这个条件，其实一条直线满足下述五个条件的两个，就能推出其他三个.（i）过圆心；（i i）垂直弦；（i i i）平分弦；（iv）平分弦所对的劣弧；（v）平分弦所对的优劣.②过圆内一点最短弦的问题.③圆中两条平行所夹的弧相等.④垂直平分半径的弦的问题.如图CD为⊙O直径，AB为⊙O的弦，AB垂直平分OC.则△AOC、△BOC均为正三角形.⑤赵州桥问题，弦长a，弦心距d，半径r，弓形高之间的关系.3.圆的旋转的不变性弧、弦、圆心角之间的相等关系：在同圆或等圆中，两个圆心角，两条弧，两条弦中有一组量相等，它们所对应的其余各组量也相等.①一条弦对唯一圆心角，但对两条弧.②同圆或等圆中，弦等，弦心距等；弦长弦心距短. 4.圆周角、圆心角的关系定理及推论. ①圆周角的概念.②在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.③在同圆或等圆中，如果两个圆周角相等，则它们所对的弧相等. ④半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.EODCBAOBA CEDFOABPOA B CDM OCDABAOBC 12C 3CADB⑤圆周角、圆内角、圆外角的关系. ⑥圆内接四边形对角互补，逆命题亦真.⑦一组对边平行的圆内接四边形是矩形或等腰梯形. ⑧图中A 、B 、C 、D 共圆.⑨如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形.⑩矩形四个顶点共圆，菱形四边的中点共圆. （二）点、直线、圆和圆的位置关系. 1.点与圆的位置关系.①圆、圆内部、圆外部的集合观点的定义.②点与圆的位置关系与d 、r 数量关系的联系OP=d ，⊙O 的半径为r.③三点作圆问题.④三角形的外接圆；一个圆有无数个内接三角形，但一个三角形只有唯一一个外接圆；三角形的外心是三边垂直平分线的交点，它到三角形三个顶点距离相等；锐角三角形的外心在三角形内，直角三角形的外心是有斜边的中点，钝角三角形的外心在三角形之外.⑤反证法.2.直线与圆的位置关系.①判定方法：公共点的个数；d 、r 的关系判定.②切线的判定：（i ）d=r ；（ii ）经过半径的外端并且垂直于这条半径的直线是圆的切线.③切线的性质：（i ）d=r ；（ii ）切线垂直于过切点的半径；（iii ）过切点垂直于切线的直线必过圆心；（iv ）过圆心垂直于切线的直线必过切点；（v ）直线与圆只有一个公共点.④判定切线时，若已知直线过圆上的点，连半径证垂直；OCBADACDBABCDOAlOBAC若没有给出直线过圆上的某点，作垂线段，证垂线段等于半径；切线问题常用的辅助线是将切点与圆心相连，构造垂直.⑤两条切线问题.（i ）l 1、l 2分别切⊙O 于A 、B ，且l 1// l 2，则AB 为⊙O 的直径.反之，若AB 为⊙O 的直径，则 l 1// l 2.（ii ）PA ·PB 切⊙O 于A 、B ，则PA ＝PB ；PO 平分∠APB ；BC//PO ；∠CAB ＝12∠APB ；⌒AE = ⌒BE ；BD 平分∠OBC ；∠ADB ＋∠APB ＝∠AEB ；E 为△PAB 的内心.⑥三条切线问题（i ）三角形有唯一内切圆，圆心是三角形内角平分线的交点，叫三角形的内心，内心到三角形三边的距离相等，一个圆有无数个外切三角形.（ii ）如图：△ABC 内切圆的半径r ，△ABC 的周长为l ，则△ABC 的面积12ABC S rl ∆=.（iii ）若D 、E 、F 为切点，则AE ＝AF ＝12（AB＋AC －BC ），BF ＝BD ＝12（AB ＋BC －AC ），CD ＝CE ＝12（AC＋BC －AB ）（iv ）如图：Rt △ABC 中，∠C ＝90°，AB 、BC 、CA 的长分别为c 、a 、b.则r=12（a+b-c ）或r=ab a b c++（v ）PA 、PB 切⊙O 于A 、B ，C 为弧AB 上任一点，过C 的圆的切线交PA 于E ，交PB 于F ，则△PFE 的周长等于PA ＋PB ，∠FOE ＝90°－12∠P.（vi ）AB 、BC 、CD 分别切⊙O 于E 、F 、G 且AB//CD.则BC=BE+CG ； ∠BOC=90°；以BC 为直径的圆与EG 相切.⑥四条切线问题（i ）四边形ABCD 为⊙O 的外切四边形，则AB ＋CD=AD+BC.（三）正多边形和圆①将一个圆n 等分，依次连接每个分点得到的多边形是圆的内接正n 边形；过每个分点作圆的切线，OBC AFE DOC BAEAC BFEOPGE OAB CDFDABCFEDCBAABCDEOnOAB以相邻的切线的交点为顶点的多边形是圆的外切正n 边形.②正n 边形的n 条半径将正n 边形分成n 个全等的等腰三角形；半径、边心距将正n 边形分成2n 个全等的直角三角形.③各边相等的圆内接多边形是正多边形，但各角相等的圆内接多边形不一定是正多边形（如长方形）；各角相等的圆外切多边形是正多边形，但各边相等的圆外切多边形不一定是正多边（如一般菱形）.④正n 边形是轴对称图形，有n 条对称轴，偶数边正多边形是中心对称图形.（四）弧长和扇形面积 1.弧长、扇形面积2,180360n R n R l S ππ==扇形 12S lR =扇形其中l 为扇形的弧长，R 为半径.2.圆锥的侧面展开图.圆锥的侧面展开图是扇形.扇形的弧长是底面圆的周长，扇形面积是圆锥的侧面积. 四、典型问题1、如图，AB 是⊙O 的直径，点C 是BA 延长线上一点，CD 切⊙O 于D 点，弦DE//CB ，Q 是AB 上一动点，CA ＝1，CD 是⊙O 半径的3倍.（1）求⊙O 的半径R ；（2）在Q 从A 向B 运动的过程中，图中阴影部分的面积是否发生变化？若发生变化，请你指出变化范围；若不发生变化，请你求出其面积.BEF CA2、如图，O A ⊥BC ，∠AOB ＝50°，试确定∠ADC 的大小.3、如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于D ，求BC 、AD 、BD 的长.4、如图，在△ABC 中，∠A ＝50°，⊙O 截△ABC 的三边所得的弦长相等，则∠BOC等于.DBOAC。

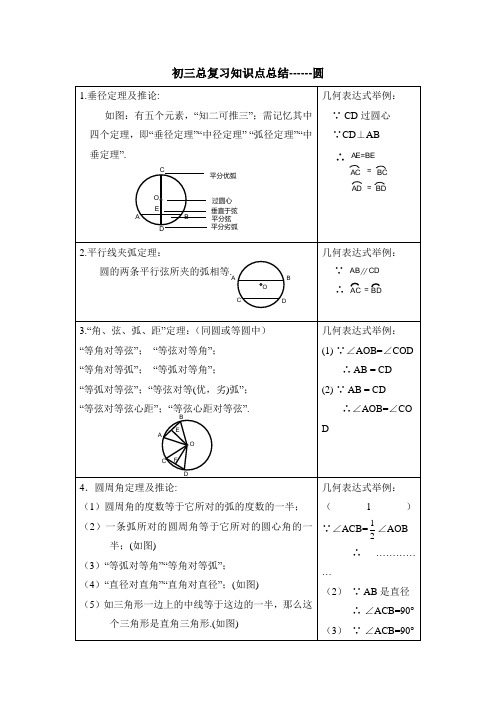
初三总复习知识点总结------圆（1）（2）（3）（4）∴ AB是直径（4）∵ CD=AD=BD∴ΔABC是RtΔ5．圆内接四边形性质定理:圆内接四边形的对角互补，并且任何一个外角都等于它的内对角. 几何表达式举例：∵ABCD是圆内接四边形∴∠CDE =∠ABC ∠C+∠A =180°6．切线的判定与性质定理:如图：有三个元素，“知二可推一”；需记忆其中四个定理.（1）经过半径的外端并且垂直于这条半径的直线是圆的切线；（2）圆的切线垂直于经过切点的半径；※（3）经过圆心且垂直于切线的直线必经过切点；※（4）经过切点且垂直于切线的直线必经过圆心. 几何表达式举例：（1）∵OC是半径∵OC⊥AB∴AB是切线（2）∵OC是半径∵AB是切线∴OC⊥AB （3）……………7．切线长定理:从圆外一点引圆的两条切线，它们的切线长相等；圆心和这一点的连线平分两条切线的夹角. 几何表达式举例：∵ PA、PB是切线∴ PA=PB∵PO过圆心PABO线∴PA·PB=PC·PD11．关于两圆的性质定理:（1）相交两圆的连心线垂直平分两圆的公共弦； （2）如果两圆相切，那么切点一定在连心线上.（1） （2）几何表达式举例： （1） ∵O 1，O 2是圆心∴O 1O 2垂直平分AB（2） ∵⊙1 、⊙2相切∴O 1 、A 、O 2三点一线12．正多边形的有关计算:（1）中心角αn ，半径R N ， 边心距r n ，边长a n ，内角βn ， 边数n ； （2）有关计算在RtΔAOC 中进行.公式举例：(1) αn =n360︒； (2) n 1802n ︒=α几何B 级概念：（要求理解、会讲、会用，主要用于填空和选择题） 一 基本概念：圆的几何定义和集合定义、 弦、 弦心距、 弧、 等弧、 弓形、弓形高 三角形的外接圆、三角形的外心、三角形的内切圆、 三角形的内心、 圆心角、圆周角、 弦切角、 圆的切线、 圆的割线、 两圆的内公切线、 两圆的外公切线、 两圆的内（外）、 公切线长、 正多边形、 正多边形的中心、 正多边形的半径、 正多边形的边心距、 正多边形的中心角. 二 定理：1． 不在一直线上的三个点确定一个圆.AB O1O2AO1O2αn βnABCDEOa r n nnR2．任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆. 3．正n边形的半径和边心距把正n边形分为2n个全等的直角三角形.三公式：1.有关的计算：（1）圆的周长C=2πR；（2）弧长L=；（3）圆的面积S=πR2.（4）扇形面积S扇形=LR21360Rn2=π；（5）弓形面积S弓形=扇形面积S AOB±ΔAOB的面积.（如图）2.圆柱与圆锥的侧面展开图：（1）圆柱的侧面积：S圆柱侧=2πrh；(r:底面半径；h:圆柱高)（2）圆锥的侧面积：S圆锥侧=. （L=2πr，R是圆锥母线长；r是底面半径）四常识：1．圆是轴对称和中心对称图形.2．圆心角的度数等于它所对弧的度数.3．三角形的外心⇔两边中垂线的交点⇔三角形的外接圆的圆心；三角形的内心⇔两内角平分线的交点⇔三角形的内切圆的圆心. 4．直线与圆的位置关系：（其中d表示圆心到直线的距离；其中r表示圆的半径）直线与圆相交⇔ d＜r ；直线与圆相切⇔ d=r ；直线与圆相离⇔ d ＞r.5．圆与圆的位置关系：（其中d表示圆心到圆心的距离，其中R、r表示两个圆的半径且R≥r）两圆外离⇔d＞R+r；两圆外切⇔d=R+r；两圆相交⇔R-r ＜d＜R+r；两圆内切⇔d=R-r；两圆内含⇔d＜R-r.6．证直线与圆相切，常利用：“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线.7．关于圆的常见辅助线：。

初三(初三)数学复习知识点圆初三数学知识点圆★重点★①圆的重要性质;②直线与圆、圆与圆的位置关系;③与圆有关的角的定理;④与圆有关的比例线段定理。

☆内容提要☆一、圆的差不多性质1.圆的定义(两种)2.有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

3.“三点定圆”定理4.垂径定理及其推论5.“等对等”定理及其推论5. 与圆有关的角：⑴圆心角定义(等对等定理)⑵圆周角定义(圆周角定理，与圆心角的关系)⑶弦切角定义(弦切角定理)二、直线和圆的位置关系1.三种位置及判定与性质：2.切线的性质(重点)3.切线的判定定理(重点)。

圆的切线的判定有⑴…⑵…4.切线长定理三、圆换圆的位置关系1.五种位置关系及判定与性质：(重点：相切)2.相切(交)两圆连心线的性质定理3.两圆的公切线：⑴定义⑵性质四、与圆有关的比例线段1.相交弦定理2.切割线定理五、与和正多边形1.圆的内接、外切多边形(三角形、四边形)2.三角形的外接圆、内切圆及性质3.圆的外切四边形、内接四边形的性质4.正多边形及运算中心角：内角的一半：(右图)(解Rt△OAM可求出相关元素, 、等)六、一组运算公式1.圆周长公式2.圆面积公式3.扇形面积公式4.弧长公式5.弓形面积的运算方法6.圆柱、圆锥的侧面展开图及相关运算七、点的轨迹六条差不多轨迹八、有关作图1.作三角形的外接圆、内切圆2.平分已知弧3.作已知两线段的比例中项4.等分圆周：4、8;6、3等分九、差不多图形十、重要辅助线1.作半径那个工作可让学生分组负责收集整理,登在小黑板上,每周一换。

要求学生抽空抄录同时阅读成诵。

其目的在于扩大学生的知识面,引导学生关注社会,热爱生活,因此内容要尽量广泛一些,能够分为人一辈子、价值、理想、学习、成长、责任、友谊、爱心、探究、环保等多方面。

如此下去,除假期外,一年便能够积存40多则材料。

假如学生的脑海里有了众多的鲜活生动的材料,写起文章来还用乱翻参考书吗?2.见弦往往作弦心距3.见直径往往作直径上的圆周角事实上,任何一门学科都离不开死记硬背,关键是经历有技巧,“死记”之后会“活用”。

中考圆知识点总结复习圆是初中数学中重要的一章，所以复习圆的知识点是中考复习的重点之一、下面是关于圆的相关知识点的总结复习。

1.圆的定义与要素圆是指平面上到一点距离等于固定的一点的所有点的集合。

在一个圆中，距离固定点（圆心）的距离叫做半径，而连接圆心与圆上任意一点的线段叫做半径。

圆上的任意一段弧称为弦，弦的中点称为弦的中点。

2.圆的性质(1)圆上的任意一条弦都小于等于圆的直径。

(2)如果两条弦等长，则它们所对应的弧相等。

(3)圆上的两个相邻的弧所对应的圆心角相等。

(4)圆上任意两条弦所对应的圆心角一定小于等于180°，当且仅当两条弦所对应的圆心角相等时，这两条弦等长。

(5)在同一个圆或等圆上，圆心角相等的弧相等，弦长相等的圆心角相等。

3.圆的证明(1)两个平行弦所对应的圆心角相等。

证明方法：连接两个圆心与平行弦的中点，用平行线性质证明两个等腰三角形的两个底角相等。

(2)相等弧的圆心角相等。

证明方法：用反证法，假设相等的弧对应的圆心角不相等，然后利用圆周角的性质推导出矛盾。

(3)等腰三角形的底角对应的圆心角相等。

证明方法：连接两个顶点与圆心，利用等腰三角形的性质证明两个三角形的两个底角相等。

(4)正三角形的顶角对应的圆心角为120°。

4.圆周角和弧度制(1)圆周角：一个圆周角等于360°，半圆角等于180°，直角等于90°。

(2)弧度制：角度制中一个圆周角等于360°，而弧度制中一个圆周角等于2π（即360°=2π）。

5.弧长和扇形面积(1)弧长：一个圆的弧长等于它的圆周角所对应的弧x半径。

弧长公式：弧长=圆周角/360°x2πr(2)扇形面积：一个圆的扇形面积等于它的圆周角所对应的扇形面积。

扇形面积公式：扇形面积=圆周角/360°xπr²6.圆的切线和切点(1)切线：圆上的一条切线与圆的切点只有一个。

九年级初三圆知识点大汇总考点一、圆的相关概念1、圆的定义在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

2、圆的几何表示以点O为圆心的圆记作“⊙O”，读作“圆O”考点二、弦、弧等与圆有关的定义（1）弦连接圆上任意两点的线段叫做弦。

（如图中的AB）（2）直径经过圆心的弦叫做直径。

（如途中的CD）直径等于半径的2倍。

（3）半圆圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

（4）弧、优弧、劣弧圆上任意两点间的部分叫做圆弧，简称弧。

弧用符号“⌒”表示，以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。

大于半圆的弧叫做优弧（多用三个字母表示）；小于半圆的弧叫做劣弧（多用两个字母表示）考点三、垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

垂径定理及其推论可概括为：过圆心垂直于弦直径平分弦知二推三平分弦所对的优弧平分弦所对的劣弧考点四、圆的对称性1、圆的轴对称性，圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。

2、圆的中心对称性，圆是以圆心为对称中心的中心对称图形。

考点五、弧、弦、弦心距、圆心角之间的关系定理1、圆心角，顶点在圆心的角叫做圆心角。

2、弦心距，从圆心到弦的距离叫做弦心距。

3、弧、弦、弦心距、圆心角之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦想等，所对的弦的弦心距相等。

推论：在同圆或等圆中，如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

考点六、圆周角定理及其推论1、圆周角，顶点在圆上，并且两边都和圆相交的角叫做圆周角。

初三圆的知识点总结图一、圆的基本定义1. 圆的定义- 圆心- 半径- 直径- 圆周2. 圆的表示方法- 用圆心坐标和半径表示- 用方程式表示二、圆的性质1. 圆的对称性- 轴对称- 中心对称2. 圆的内接图形- 弦- 直径- 切线3. 圆的外切图形- 外切正多边形- 外切圆三、圆的计算公式1. 圆的周长计算公式- 周长与直径的关系- 周长与半径的关系2. 圆的面积计算公式- 面积与半径的关系 - 环形面积的计算四、圆的应用1. 圆在几何中的应用- 圆与直线的关系- 圆与圆的关系2. 圆在实际生活中的应用 - 建筑设计- 机械制造- 日常生活中的圆五、圆的相关定理1. 垂径定理- 定理内容- 定理的应用2. 圆周角定理- 定理内容- 定理的应用3. 圆的切线定理- 切线与半径的关系 - 切线与弦的关系六、圆的作图方法1. 用圆规画圆- 步骤说明- 注意事项2. 圆的五等分- 方法介绍- 应用实例七、圆的方程1. 标准圆方程- 方程形式- 参数解释2. 一般圆方程- 方程形式- 参数解释八、圆与坐标系1. 圆的坐标方程- 圆心和半径的坐标表示- 圆与坐标轴的关系2. 圆与直线的交点- 解析方法- 交点求解九、圆的进阶知识1. 圆锥曲线- 椭圆- 双曲线- 抛物线2. 非欧几何中的圆- 球面几何- 双曲几何请根据上述框架在Word文档中创建内容，并添加适当的图表、公式和示例以增强文档的可读性和实用性。

您可以根据实际需要调整各个部分的内容和顺序。

记得在编辑时使用清晰、专业的语言，并确保文档的格式规范、逻辑清晰。

总复习圆综合复习【考纲要求】1.圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明定会有下降趋势，不会有太复杂的大题出现；2.今后的中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．【知识网络】【考点梳理】考点一、圆的有关概念1. 圆的定义如图所示，有两种定义方式：①在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆．固定的端点O叫做圆心，以O为圆心的圆记作⊙O，线段OA叫做半径；②圆是到定点的距离等于定长的点的集合．要点进阶：圆心确定圆的位置，半径确定圆的大小． 2.与圆有关的概念①弦：连接圆上任意两点的线段叫做弦；如上图所示线段AB ，BC ，AC 都是弦． ②直径：经过圆心的弦叫做直径，如AC 是⊙O 的直径，直径是圆中最长的弦．③弧：圆上任意两点间的部分叫做圆弧，简称弧，如曲线BC 、BAC 都是⊙O 中的弧，分别记作BC ，BAC ．④半圆：圆中任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆，如AC 是半圆． ⑤劣弧：像BC 这样小于半圆周的圆弧叫做劣弧． ⑥优弧：像BAC 这样大于半圆周的圆弧叫做优弧． ⑦同心圆：圆心相同，半径不相等的圆叫做同心圆． ⑧弓形：由弦及其所对的弧组成的图形叫做弓形． ⑨等圆：能够重合的两个圆叫做等圆．⑩等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．⑪圆心角：顶点在圆心的角叫做圆心角，如上图中∠AOB ，∠BOC 是圆心角．⑫圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角，如上图中∠BAC 、∠ACB 都是圆周角． 要点进阶：圆周角等于它所对的弧所对的圆心角的一半.圆外角度数等于它所夹弧的度数的差的一半. 圆内角度数等于它所夹弧的度数的和的一半.考点二、圆的有关性质 1.圆的对称性圆是轴对称图形，经过圆心的直线都是它的对称轴，有无数条．圆是中心对称图形，圆心是对称中心，又是旋转对称图形，即旋转任意角度和自身重合． 2.垂径定理①垂直于弦的直径平分这条弦，且平分弦所对的两条弧．②平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．如图所示．要点进阶：在图中(1)直径CD ，(2)CD ⊥AB ，(3)AM ＝MB ，(4)C C A B =，(5)AD BD =．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三． 注意：(1)(3)作条件时，应限制AB 不能为直径．3.弧、弦、圆心角之间的关系①在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；②在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．4.圆周角定理及推论①圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．②圆周角定理的推论：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．要点进阶：圆周角性质的前提是在同圆或等圆中．考点三、与圆有关的位置关系1.点与圆的位置关系如图所示．d表示点到圆心的距离，r为圆的半径．点和圆的位置关系如下表：点与圆的位置关系d与r的大小关系点在圆内d＜r点在圆上d＝r点在圆外d＞r要点进阶：(1)圆的确定：①过一点的圆有无数个，如图所示．②过两点A、B的圆有无数个，如图所示．③经过在同一直线上的三点不能作圆．④不在同一直线上的三点确定一个圆．如图所示．(2)三角形的外接圆经过三角形三个顶点可以画一个圆，并且只能画一个．经过三角形三个顶点的圆叫做三角形的外接圆．三角形外接圆的圆心叫做这个三角形的外心．这个三角形叫做这个圆的内接三角形．三角形的外心就是三角形三条边的垂直平分线交点．它到三角形各顶点的距离相等，都等于三角形外接圆的半径．如图所示．2.直线与圆的位置关系①设r为圆的半径，d为圆心到直线的距离，直线与圆的位置关系如下表．②圆的切线．切线的定义：和圆有唯一公共点的直线叫做圆的切线．这个公共点叫切点．切线的判定定理：经过半径的外端．且垂直于这条半径的直线是圆的切线．友情提示：直线l是⊙O的切线，必须符合两个条件：①直线l经过⊙O上的一点A；②OA⊥l．切线的性质定理：圆的切线垂直于经过切点的半径．切线长定义：我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分这两条切线的夹角．③三角形的内切圆：与三角形各边都相切的圆叫三角形的内切圆，三角形内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形，三角形的内心就是三角形三个内角平分线的交点．要点进阶：找三角形内心时，只需要画出两内角平分线的交点．三角形外心、内心有关知识比较3.圆与圆的位置关系在同一平面内两圆作相对运动，可以得到下面5种位置关系，其中R、r为两圆半径(R≥r)．d为圆心距．要点进阶：①相切包括内切和外切，相离包括外离和内舍．其中相切和相交是重点．②同心圆是内含的特殊情况．③圆与圆的位置关系可以从两个圆的相对运动来理解．④“r1－r2”时，要特别注意，r1＞r2．考点四、正多边形和圆1.正多边形的有关概念正多边形的外接圆(或内切圆)的圆心叫正多边形的中心．外接圆的半径叫正多边形的半径，内切圆的半径叫正多边形的边心距，正多边形各边所对的外接圆的圆心角都相等，这个角叫正多边形的中心角，正多边形的每一个中心角都等于360n°．要点进阶：通过中心角的度数将圆等分，进而画出内接正多边形，正六边形边长等于半径．2.正多边形的性质任何一个正多边形都有一个外接圆和一个内切圆，这两圆是同心圆．正多边形都是轴对称图形，偶数条边的正多边形也是中心对称图形，同边数的两个正多边形相似，其周长之比等于它们的边长(半径或边心距)之比．3.正多边形的有关计算定理：正n 边形的半径和边心距把正n 边形分成2n 个全等的直角三角形．正n 边形的边长a 、边心距r 、周长P 和面积S 的计算归结为直角三角形的计算．360n a n =°，1802sin n a R n =°，180cos n r R n=°， 2222n n a R r ⎛⎫=+ ⎪⎝⎭，n n P n a =，1122n nnn n S a r n P r ==．考点五、圆中的计算问题 1.弧长公式：180n Rl π=，其中l 为n °的圆心角所对弧的长，R 为圆的半径． 2.扇形面积公式：2360n R S π=扇，其中12S lR =扇．圆心角所对的扇形的面积，另外12S lR =扇．3.圆锥的侧面积和全面积：圆锥的侧面展开图是扇形，这个扇形的半径等于圆锥的母线长，弧长等于圆锥底面圆的周长． 圆锥的全面积是它的侧面积与它的底面积的和． 要点进阶：（1）在计算圆锥的侧面积时要注意各元素之间的对应关系，千万不要错把圆锥底面圆半径当成扇形半径．（2）求阴影面积的几种常用方法(1)公式法；(2)割补法；(3)拼凑法；(4)等积变形法；(5)构造方程法．考点六、四点共圆 1.四点共圆的定义四点共圆的定义：如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”.2.证明四点共圆一些基本方法：1.从被证共圆的四点中先选出三点作一圆，然后证另一点也在这个圆上，若能证明这一点，即可肯定这四点共圆．或利用圆的定义，证各点均与某一定点等距.2.如果各点都在某两点所在直线同侧，且各点对这两点的张角相等，则这些点共圆． （若能证明其两张角为直角，即可肯定这四个点共圆，且斜边上两点连线为该圆直径.）3.把被证共圆的四点连成四边形，若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时，即可肯定这四点共圆．4.把被证共圆的四点两两连成相交的两条线段，若能证明它们各自被交点分成的两线段之积相等，即可肯定这四点共圆；或把被证共圆的四点两两连结并延长相交的两线段，若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积，即可肯定这四点也共圆． 即利用相交弦、切割线、割线定理的逆定理证四点共圆.考点七、与圆有关的比例线段（补充知识）1.相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等.2.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项.3.割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等.圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统一归纳为圆幂定理）定理图形已知结论证法相交弦定理⊙O中，AB、CD为弦，交于P.PA·PB＝PC·PD. 连结AC、BD，证：△APC∽△DPB.相交弦定理的推论⊙O中，AB为直径，CD⊥AB于P.PC2＝PA·PB. 用相交弦定理.切割线定理⊙O中，PT切⊙O于T，割线PB交⊙O于APT2＝PA·PB连结TA、TB，证：△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线，交⊙O于A、CPA·PB＝PC·PD过P作PT切⊙O于T，用两次切割线定理【典型例题】类型一、圆的有关概念及性质例1． BC为O的弦，∠BOC=130°，△ABC为O的内接三角形，求∠A的度数.【变式】如图，∠AOB＝100°，点C 在⊙O 上，且点C 不与A 、B 重合，则∠ACB 的度数为（ ）A ．50B ．80或50C ．130D ．50 或130类型二、与圆有关的位置关系例2．如图，已知正方形的边长是4cm ，求它的内切圆与外接圆组成的圆环的面积．（答案保留π）例3．如图，已知⊙O 的半径为6cm ，射线PM 经过点O ，10cm OP ，射线PN 与⊙O 相切于点Q ．A,B 两点同时从点P 出发，点A 以5cm/s 的速度沿射线PM 方向运动，点B 以4cm/s 的速度沿射线PN 方向运动．设运动时间为t s ． （1）求PQ 的长；（2）当t 为何值时，直线AB 与⊙O 相切？A BO【变式】已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）连接AD并延长交BE于点F，若OB=9，2sin3ABC∠=，求BF的长．类型三、与圆有关的计算例4．如图，有一个圆O和两个正六边形T1，T2． T1的6个顶点都在圆周上，T2的6条边都和圆O相切（我们称T1，T2分别为圆O的内接正六边形和外切正六边形）．（1）设T1，T2的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；（2）求正六边形T1，T2的面积比S1：S2的值．【变式】有一个亭子，它的地基是半径为8m的正六边形，求地基的周长和面积．（结果保留根号）类型四、与圆有关的综合应用例5．如图，AB是⊙O的直径，C为⊙O上一点，∠BAC的平分线交⊙O于点D，过点D作EF∥BC，交AB、AC的延长线于点E、F．（1）求证：EF为⊙O的切线；（2）若sin∠ABC=，CF=1，求⊙O的半径及EF的长．【变式】已知：如图，△ABC中，∠BAC=90°，点D在BC边上，且BD=BA，过点B画AD的垂线交AC于点O，以O为圆心，AO为半径画圆．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为8，tan∠C=，求线段AB的长，sin∠ADB的值．例6．（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为弧BC上一动点，求证：PA=PB+PC；（2）如图2，四边形ABCD是⊙O的内接正方形，点P为弧BC上一动点，求证：；（3）如图3，六边形ABCDEF是⊙O的内接正六边形，点P为弧BC上一动点，请探究PA、PB、PC 三者之间有何数量关系，并给予证明．【变式】（1）如图①，M、N分别是⊙O的内接正△ABC的边AB、BC上的点且BM=CN，连接OM、ON，求∠MON的度数；（2）图②、③、…④中，M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、…正n边形ABCDEFG…的边AB、BC上的点，且BM=CN，连接OM、ON，则图②中∠MON的度数是，图③中∠MON的度数是；…由此可猜测在n边形图中∠MON的度数是；（3）若3≤n≤8，各自有一个正多边形，则从中任取2个图形，恰好都是中心对称图形的概率是 .一、选择题1．已知半径分别是3和5的两个圆没有公共点，那么这两个圆的圆心距d的取值范围是（）A．d＞8 B．d＞2 C．0≤d＜2 D．d＞8或d＜22．如图，等腰梯形ABCD内接于半圆D，且AB＝1，BC＝2，则OA＝( )A．132+B．2 C．323+D．152+3．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝4 cm，以点C为圆心，以2 cm的长为半径作圆，则⊙C与AB的位置关系是( )A．相离 B．相切 C．相交 D．相切或相交第2题第3题第5题4．已知圆O1、圆O2的半径不相等，圆O1的半径长为3，若圆O2上的点A满足AO1＝3，则圆O1与圆O2的位置关系是( )A．相交或相切 B．相切或相离 C．相交或内含 D．相切或内含5．如图所示，在圆O内有折线OABC，其中OA＝8，AB＝2，∠A＝∠B＝60°，则BC的长为( )A．19 B．16 C．18 D．206．如图，MN是半径为0.5的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN 上一动点，则PA+PB的最小值为( )A．22B．2 C．1 D．27．如图，分别以A，B为圆心，线段AB的长为半径的两个圆相交于C，D两点，则∠CAD的度数为_______．8．如图，现有圆心角为90°的一个扇形纸片，该扇形的半径是50cm．小红同学为了在圣诞节联欢晚会上表演节目，她打算剪去部分扇形纸片后，利用剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠)，那么被剪去的扇形纸片的圆心角应该是________度．第7题第8题第9题9．如图，AB⊥BC，AB＝BC＝2 cm，OA与OC关于点O中心对称，则AB、BC、CO、OA所围成的面积是________cm2．10．如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点，若两圆的半径分别为3 cm和5 cm，则AB的长为________cm．11．将半径为4 cm的半圆围成一个圆锥，在圆锥内接一个圆柱(如图所示)，当圆柱的侧面的面积最大时，圆柱的底面半径是________cm．第10题第11题12．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+∠A；②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；③设OD=m，AE+AF=n，则S△AEF=mn；④EF是△ABC的中位线．其中正确的结论是．13．如图，已知点E在△ABC的边AB上，∠C=90°，∠BAC的平分线交BC于点D，且D在以AE为直径的⊙O上．（1）证明：BC是⊙O的切线；（2）若DC=4，AC=6，求圆心O到AD的距离；（3）若，求的值．14．如图，在Rt△ABC中，∠ABC＝90°，斜边AC的垂直平分线交BC于点D，交AC于点E，连接BE．(1)若BE是△DEC外接圆的切线，求∠C的大小；(2)当AB＝1，BC＝2时，求△DEC外接圆的半径．15．如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连接AF交BC于E，∠ABC的平分线BD交AF于D，连接BF．(1)证明：AF平分∠BAC；(2)证明：BF＝FD；(3)若EF＝4，DE＝3，求AD的长．16. 如图，已知：AC是⊙O的直径，PA⊥AC，连接OP，弦CB∥OP，直线PB交直线AC于D，BD＝2PA．(1)证明：直线PB是⊙O的切线；(2)探究线段PO与线段BC之间的数量关系，并加以证明；(3)求sin∠OPA的值．。

一、圆的定义和性质1.圆的定义：平面上到定点的距离等于定长的点的集合。

2.圆的要素：圆心、半径、圆周。

3.圆的性质：（1）半径相等的两个圆是同心圆；（2）同圆中，圆心角等于圆周角的1/2；（3）同弧上的两条弦所对的圆心角相等；（4）圆心角相等的弧相等；（5）相等弧所对的弦相等；（6）正多边形的内角和是定值，因此内接于一个圆的正多边形的各个内角相等；（7）直径是弦中最长的。

二、弧与圆周角1.弧的定义：圆上两点间的弧是以这两点为端点的两条互不相交的圆弧中，长的那一段。

2.弧的性质：（1）圆周角所对的弧是唯一确定的；（2）全周角所对的弧是定长的。

3.圆周角的定义：以圆心为端点的两条互不相交的射线所夹的角。

4.圆周角的度量：可以用角的度数来衡量。

三、切线与弦1.切线的定义：切线是与圆只有一个公共点的直线。

2.切线与半径的关系：切线与半径的关系是切线⊥半径。

3.弦的定义：两点之间的线段叫做弦。

4.弦的性质：（1）圆内的弦比它们所对的圆心角小，而且与一个圆心角的两个弧所对的弧一样；（2）相等的弦所对的圆心角相等。

四、相交弦定理1.弦上的点：如果一个点在弦上，则这个点到两个端点的距离相等。

2.相交弦定理：如果两个弦相交于圆内的一个点，则这两个弦上的两个点一定分别在另一个弦上的两侧。

五、余弦定理1.面积的性质：圆内、圆外的面积相等，夹在一个圆内的圆周弧的面积也相等。

2.余弦定理：在一个圆上，任意两条弧所对的圆心角的余弦值相等。

六、正多边形的面积公式1.正六边形的面积：正六边形的面积=3×（边长）²×√3÷22.正八边形的面积：正八边形的面积=2×（边长）²×√23.正十二边形的面积：正十二边形的面积=3×（边长）²×√34. 正十六边形的面积：正十六边形的面积=4×（边长）²×tan(22.5°)。