统计实验作业
- 格式:doc
- 大小:353.00 KB
- 文档页数:8

统计学实验题根据图形说明大学生每月生活开支1、消费方式:在消费方式上面,大多数人的态度为能省则省,但是也有大部分人毫不在乎,想花就花。
事先做好消费计划的好习惯拥有的人不多。
2、生活费来源:大学生由于没有完全独立,所以绝大多数学生的生活费来源还是以父母给予为主。
但是,勤工助学,奖学金等自力更生的学生也有一小部分。
3、生活费主要花销:大学生主要在校园里生活,所以还是以伙食消费为主。
这是比较健康的合理的消费方式,同时,大学生在学习上面的花销很少,说明学生或许不太重视学业。
4、买东西钱不够时的选择:买东西钱不够,大多数学生选择向父母要钱,这说明学生任然缺乏独立自主的意识,而且向同学借钱的消费观念需要改进。
5、消费倾向:消费时,绝大部分学生选择经济实惠的东西,这跟大学生有限的生活费有关。
6、消费时考虑的因素:大学生对商品要求不高,主要考虑商品的价格。
7、大学生买东西看重的方面:大学生买东西更喜欢外形美观和质量好的商品。
8、学生外出打工的原因:学生校外打工的主要原因还是补贴日用和渴望独立,可见大学生已经具有独立意识,脱离父母的佑护。
9、周围同学消费情况:大多数学生消费比较实际,说明学生活比较朴素,没有盲目消费。
通过以上的统计分析,我们基本得出以下结论:第一、对于生活费均值的分析结果:1.通过对本校大二学生生活费的总体计量,发现学生的月生活费平均数为764,生活费500元~800元所占频数最高。
;2.单因素分析的结果表明,性别对生活费均值没有显著影响。
第二、对于生活费来源的分析结果:1.描述统计的结果显示,生活费的主要来源都集中在父母供给中,其他来源依次是:勤工俭学、助学贷款及其他。
2.男女生而言,男生的生活费主要来源中来自父母的比女生稍低,而勤工俭学的比女生稍多,助学贷款比例相差不大。
3.本科生还是传统的以靠父母读书为主。
第三、对于生活费主要支出的分析结果:1.就抽样总体而言,生活费的主要支出集中在伙食费上,其他支出依次是:衣着、娱乐休闲、学习用品、日化用品。

统计实习实验报告一、实习背景及目的随着我国经济社会的快速发展,数据统计与分析在各个领域发挥着越来越重要的作用。
为了提高自己在实际工作中运用统计学知识解决问题的能力,我参加了为期两周的统计实习。
本次实习主要通过操作统计软件,对给定的数据进行整理、分析及预测,从而掌握统计学的基本原理和方法,培养自己的数据挖掘和分析能力。
二、实习内容与过程1. 数据整理首先,我们需要对实习所给的数据进行整理。
数据来源于某公司的销售数据,包括产品名称、销售数量、销售价格、销售时间等字段。
通过Excel等软件,我们将数据进行清洗、去重、排序等操作,使得数据更加规范和便于分析。
2. 描述性统计分析接下来,我们对数据进行描述性统计分析。
通过计算各字段的均值、标准差、最大值、最小值等统计量,了解数据的分布特征和基本概况。
此外,我们还利用图表(如直方图、饼图等)对数据进行可视化展示,以便更直观地了解数据。
3. 关联分析为了找出数据中各字段之间的关联关系,我们采用Pearson相关系数对销售数量、销售价格等字段进行相关性分析。
通过计算得到的相关系数,我们可以判断各字段之间的线性关系强弱。
此外,我们还利用卡方检验对数据进行独立性检验,以判断销售数量和销售时间等字段是否独立。
4. 预测分析基于上述统计分析结果,我们进一步对销售数量进行预测。
采用时间序列分析方法,以销售时间为自变量,销售数量为因变量,建立线性回归模型。
通过模型拟合和参数优化,我们得到了较为满意的预测结果,从而为企业提供了有力的决策依据。
5. 实习总结与反思在本次实习过程中,我们不仅复习了统计学的基本理论知识,还学会了如何运用统计软件(如Excel、SPSS等)进行数据处理和分析。
通过实习,我们深刻认识到了统计学在实际工作中的重要意义,同时也培养了自己的数据挖掘和分析能力。
在今后的学习和工作中,我们将继续努力提高自己的统计学素养,为解决实际问题提供有力的支持。
三、实习成果1. 完成了数据整理和清洗工作,得到了规范的数据表格。

统计学作业
将抗生素注入人体会产生抗生素与血浆蛋白质结合现象,以致减少了药性,下表列出5种常用的抗生素注入牛的体内时,抗生素与血浆蛋白质结合的百分比
抗生素青霉素四环素链霉素红霉素氯霉素
1 29.6 27.3 5.8 21.6 29.2
2 24.
3 32.6 6.2 17.
4 32.8
3 28.5 30.8 11.0 18.3 25.0
4 32.0 34.8 8.3 19.0 24.2
试在显著性水平a=0.05下检验这些百分比的均值有无显著性差异。
解:以u1,u2,u3,u4,u5依次表示青霉素,四环素,链霉素,红霉素,氯霉素与血浆蛋白质结合的百分比均值,本题需假设检验
Ho:u1=u2=u3=u4=u5,
H1:u1,u2,u3,u4,u5不全相等。
折线散点图:
SUMMARY
组观测数求和平均方差
青霉素 4 114.4 28.6 10.35333
四环素 4 125.5 31.375 10.05583
链霉素 4 31.3 7.825 5.6825
红霉素 4 76.3 19.075 3.2625
氯霉素 4 111.2 27.8 15.92
方差分析
差异源SS df MS F P-value F crit 组间1480.823 4 370.2058 40.88488 6.73978E-08 3.055568 组内135.8225 15 9.054833
总计1616.646 19
Fa(4,15)=3.06 <F=40.88488 所以接受H0,认为这些均值无显著性差异。
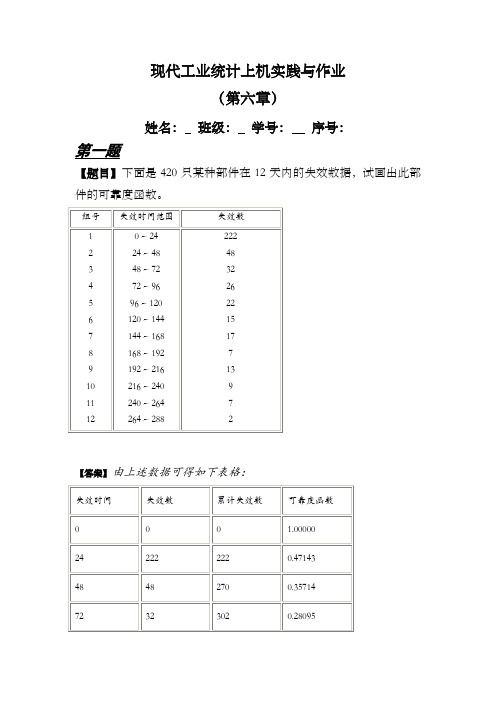
现代工业统计上机实践与作业(第六章)姓名:班级:学号:序号:第一题【题目】下面是420只某种部件在12天内的失效数据,试画出此部件的可靠度函数。
组号失效时间范围失效数1 2 3 4 5 6 7 8 91011120 ~ 2424 ~ 4848 ~ 7272 ~ 9696 ~ 120120 ~ 144144 ~ 168168 ~ 192192 ~ 216216 ~ 240240 ~ 264264 ~ 288222483226221517713972【答案】由上述数据可得如下表格:失效时间失效数累计失效数可靠度函数0 0 0 1.0000024 222 222 0.4714348 48 270 0.3571472 32 302 0.2809596 26 328 0.21905 120 22 350 0.16667 144 15 365 0.13095 168 17 382 0.09048 192 7 389 0.07381 216 13 402 0.04286 240 9 411 0.02143 264 7 418 0.00476 28824200.00000300250200150100501.00.80.60.40.20.0失效时间可靠度函数某部件的可靠度函数第二题【题目】对1575台电视机迸行高温老化试验,每隔4小时测试一次,直到36小时后共失效85台,具体数据统计如下:测试时间t i4 8 12 16 20 24 28 32 36 i t 内失效数39188924221试估计t=0,4,8,12,16,20,24,28,32的失效率各是多少,并画出失效率曲线 【答案】失效时间 失效个数 累计失效数 失效率 0 0 0 0.0000000 4 39 39 0.0063477 8 18 57 0.0029644 12 8 65 0.0013245 16 9 74 0.0014990 20 2 76 0.0003336 24 4 80 0.0006689 28 2 82 0.0003349 32 2 84 0.0003353 361850.0001678403020100.0070.0060.0050.0040.0030.0020.0010.000失效时间失效率电视机失效率曲线第三题【题目】由5个相互独立的单元组成的一个串联系统,每个单元在t=l000小时的可靠度皆为0.970,试问在相同的规定时间内此系统的可靠度是多少?假如用类似的10个单元组成一个串联系统,其系统可靠度又是多少?【答案】假如5个:可靠度=0.97*0.97*0.97*0.97*0.97=0.858734假如10个:可靠度(1000)= 0.97*0.97*0.97*0.97*0.97*0.97*0.97*0.97*0.97*0.97=0.737424第四题【题目】由串联和并联混合组成的系统称为混联系统,试计算下图6.7.1所示的混联系统的可靠度,其中每个单元的可靠度已在图6.7.1上标明,它们都是在同一规定时间的可靠度。

1、一家大型商业银行在多种地区设有分行,其业务重要是进行基础设施建设、国家重点项目建设、固定资产投资等项目旳贷款。
近年来,该银行旳贷款额平稳增长,但不良贷款额也有较大比例旳增长,这给银行业务旳发展带来较大压力。
为弄清晰不良贷款形成旳因素,管理者但愿运用银行业务旳有关数据做些定量分析,以便找出控制不良贷款旳措施。
该银行所属旳25家分行旳有关业务数据是“例11.6.x ls”。
(1)试绘制散点图,并分析不良贷款与贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳关系;2计算不良贷款、贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳有关系数(2)求不良贷款对贷款余额旳估计方程;从表系数可以看出常量、应收贷款、项目个数、固定资产投资额,都接受原假设,只有贷款余额回绝原假设,因此只有贷款余额对不良贷款起作用。
系数a模型 非原则化系数原则系数 t S ig. B 原则 误差试用版1(常量) -1.022.782-1.306 .206 各项贷款余额 (亿元).040.010.8913.837.001本年合计应收贷款 (亿元) .148.079.2601.879.075贷款项目个数 (个).015.083.034.175.863本年固定资产投资额 (亿元)-.029.015-.325-1.937.067a. 因变量: 不良贷款 (亿元)从共线性可以看出,第五个特性值对贷款余额解释87%,相应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。
因此不是太共线。
、线性方程为Y=0.01X Y为不良贷款,X为贷款余额。
4 检查不良贷款与贷款余额之间线性关系旳明显性(α=0.05);回归系数旳明显性(α=0.05);通过对上表分析得出:贷款余额线性关系通过明显性检查,回归系数2.练习《记录学》教材P330练习题11.1、11.6、11.7、11.8、11.15,相应旳数据文献为“习题11.1.xls”、“习题11.6.xls”、“习题11.7.xls”、“习题11.8.xls”、“习题11.15.xls”。

统计学实验内容一、频数统计1.A公司在招聘时采用了综合能力测试(满分为100分),由于应聘的人数较多,现随机抽取了157名应聘者的测试成绩,其测试分数的数据如book1所示。
(1)根据上面的资料,进行分组,并确定组数和组距。
根据资料判断,进行分组,分为六组,组距为10。
(2)编制频率分布表上限成绩频数频率19 10~20 16 0.10191129 20~30 27 0.17197539 30~40 56 0.35668849 40~50 39 0.24840858 50~60 14 0.08917268 60~70 5 0.031847合计157接收频率累积 %19 16 10.19%29 27 27.39%39 56 63.06%49 39 87.90%59 14 96.82%69 5 100.00%其他0 100.00%(3)画出直方图。
2. 为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果见book2。
(1) 指出表中的数据属于什么类型?定序型(2) 制作一张频数分布表;服务质量等级频数频率1 A 14 0.142 B 21 0.213 C 32 0.324 D 18 0.185 E 15 0.15合计100(3)绘制一张条形图,反映服务质量的分布。
等量质计数项:服务质量等级服务质量等级汇总A 14B 21C 32D 18E 15总计100二、参数估计1.已知灯管使用寿命服从正态分布,其标准差为50小时。
现从一批产品中抽取25个作为样本,测得其平均使用寿命为1600小时,要求在95%的概率保证下估计该批产品平均使用寿命的置信区间。
(运用CONFIDENCE函数)标准差50置信度0.95样本容量25平均值1600极限误差19.59964置信区间1580.4 1619.6抽样平均误差 19.59964,置信区间即(1580.4003~1619.59964)2.在一篇关于“通货紧缩”的文章中,作者考察了各种各样投资的收益情况。
描述统计量(Statistics)选项中做:四分位数,五个百分位数(自行确定),均值,中位数,众数,标准差,方差,均值的标准误s.e.mean,偏度系数,峰度系数;⑶做直方图histogram并配正态曲线;⑷结合直方图和数值分析结果,对该变量值分布的形态做简要描述:是否服从或近似服从正态分布?是否偏斜及方向如何?其分布近似服从正态分布,而且呈现右偏。
三个频数表:⑴按变量值升序排列;⑵按变量值value降序排列;⑶按变量值频数count升序排列)描述统计,并计算Z分数。
复制粘贴输出结果和Z分数计算结果(最小值和最大值)。
判断数据集当中是否有异常值(说明依据的是切比雪夫定理还是经验法则,同时说明理由)。
依据经验法则,没有异常值理由:依据经验法则,z分数在区间[-3,3]之间为正常值,由z分数描述统计知,其最大值为2.43558,最小值为-1.55130。
所以z分数均在[-3,3]之间为正常值,不存在异常值。
实验三统计量选项中选择全部项目,并做均值的99%置信区间。
解释描述统计的结果;⑵做盒形图和茎叶图,并根据输出结果说明是否存在异常值和极端值。
受教育年数的均值为12.88,其99%的置信区间为[12.69,13.08]。
5%的截尾均值为12.91;中位数是12.00;方差是8.904;标准差是2.984;最小值最大值分别为0和20;全距为20;四分位距是3;偏态为-0.168 峰度为0.71。
由盒形图可知存在5个异常值O,2个极端值*。
观测分布和期望分布;cells ⑵做卡方检验;statistics⑶做列联系数和V系数。
回答下列问题:第一,从列联表中能否看出两变量是否相互独立(即没有关系),依据是什么从列联表中可以看出幸福感与性别之间有关系,依据是观测值与期望值并不相等第二,如果变量间有关系,试说明关系的强度关系较弱,因为列联系数和V系数均为0.072<0.3,且趋近于0。
第三,解释检验结果,说明是否要拒绝原假设。
第1篇一、实验目的本次实验旨在通过实际操作,加深对统计学基本概念和方法的理解,提高运用统计方法分析数据的能力。
通过本次实训,学生应掌握以下内容:1. 熟悉统计软件的基本操作;2. 掌握描述性统计、推断性统计的基本方法;3. 能够运用统计方法对实际问题进行分析;4. 提高数据收集、整理和分析的能力。
二、实验内容1. 数据收集:通过查阅相关资料,收集一组实际数据,例如某地区居民消费水平、学生成绩等。
2. 数据整理:对收集到的数据进行整理,包括数据的清洗、缺失值的处理等。
3. 描述性统计:运用统计软件对数据进行描述性统计,包括计算均值、标准差、方差、中位数、众数等。
4. 推断性统计:运用统计软件对数据进行推断性统计,包括t检验、方差分析、回归分析等。
5. 结果分析:根据统计结果,对实际问题进行分析,并提出相应的建议。
三、实验步骤1. 数据收集:从网络、书籍或实地调查等方式收集一组实际数据。
2. 数据整理:将收集到的数据录入统计软件,并进行数据清洗和缺失值处理。
3. 描述性统计:(1)打开统计软件,选择数据文件;(2)运用统计软件的描述性统计功能,计算均值、标准差、方差、中位数、众数等;(3)观察统计结果,分析数据的分布情况。
4. 推断性统计:(1)根据实际问题,选择合适的统计方法;(2)运用统计软件进行推断性统计;(3)观察统计结果,分析数据之间的关系。
5. 结果分析:(1)根据统计结果,对实际问题进行分析;(2)结合实际情况,提出相应的建议。
四、实验结果与分析1. 描述性统计结果:根据实验数据,计算得到以下统计量:均值:X̄ = 100标准差:s = 15方差:σ² = 225中位数:Me = 95众数:Mo = 105分析:从描述性统计结果可以看出,该组数据的平均值为100,标准差为15,方差为225,中位数为95,众数为105。
这表明数据分布较为集中,且波动较大。
2. 推断性统计结果:(1)t检验:假设检验H₀:μ = 100,H₁:μ ≠ 100。
应⽤统计学上机⼯商管理学院《应⽤统计学》实验作业班级学号姓名上课教师2017年11⽉实验⼆建⽴数据⽂件1.建⽴⼀个数据⽂件记录试录⼊以下数据,并按要求进⾏变量定义。
数据:要求:将录⼊结果截图粘贴在作业题⽬答案处(变量视图和数据视图)。
(1)变量名同表格名,以“()”内的内容作为变量标签。
对性别(Sex)设值标签“男=0;⼥=1”。
(2)正确设定变量类型。
其中学号设为数值型;⽇期型统⼀⽤“mm/dd/yyyy“型号;⽣活费⽤货币型。
(3)变量值宽统⼀为10,⾝⾼与体重、⽣活费的⼩数位2,其余为0。
答案:1准备⼯作。
打开SPAA2选择变量视图,依次录⼊学号,姓名,性别等。
2.对⼤学⽣创业问题设计⼀份调查问卷。
要求格式正确,题⽬类型包括开放题、封闭题(单选、多选都有)、半封闭题三种类型,题⽬个数10-15个。
答案:3.⽤第2题得到的调查问卷进⾏模拟调查(10份),并将得到的结果录⼊到SPSS中,(1)将录⼊结果保存为xxx.sav⽂件,并将录⼊结果截图粘贴在作业题⽬答案处(变量视图和数据视图)。
答案:实验三数据的整理1. 某地区农科所为了研究该地区种植的两个⼩麦品种“中麦9号”、“豫展1号”产量的差异,从该地区的两个村庄各选5块⽥地,分别种植两个品种⼩麦,使⽤相同的⽥间管理,收获后,测得各个地块⽣产的⼩麦的千粒重(g)数据资料如表3-1所⽰。
表3-1 某地区⼩麦种植要求:量,并建⽴数据⽂件,完成分类汇总⼯作。
步骤:1.准备⼯作。
打开3-1⽂件,通过⽂件--打开,将⽂件放⼊打开窗⼝。
2.选择数据---分类汇总。
3.打开分类汇总窗⼝,将⼩麦品种放⼊分组变量对话框中,将千粒重放⼊变量摘要对话框中。
4.选择函数选项,在函数对话框中选择均值选项5.选择继续--确定,得出结果。
以此⽅式得出村对⼩麦千粒重的分类汇总。
2.某地20家企业的情况如表3-2所⽰。
表3-2 企业年产值与年⼯资总额要求:根据上述资料建⽴数据⽂件,并完成下列统计整理⼯作,并回答有关问题:(1)调⽤排序命令对企业按部门、年产值的主次顺序进⾏排序。
统计学大作业调查实验报告《统计学调查实验报告》一、引言统计学是应用数学的一门重要学科,其通过收集、分类、整理、分析和解释数据,为决策提供有效的依据。
为了深入理解统计学的应用,我们进行了一项调查实验,并撰写本报告,以总结实验过程和结果。
本报告的目的是通过实际调查实验的结果,来阐述统计学在实践中的重要性。
二、实验方法我们选择了一个高校的学生群体作为调查对象。
通过发放调查问卷,我们收集了与学生相关的各种数据,包括年龄、性别、学习成绩、兴趣爱好等。
为了控制变量,我们要求被调查者按照实验设计自愿参与,并确保调查过程的随机性和代表性。
三、数据分析在数据收集完成后,我们使用了统计学方法对数据进行了分析。
首先,我们计算了平均值、标准差和频数分布等基本统计量,并得出了数据的基本统计特征。
然后,我们使用图表展示了不同变量之间的关系,例如年龄与性别、学习成绩与兴趣爱好等。
此外,我们还进行了假设检验、方差分析和回归分析等进一步的统计分析。
四、实验结果通过数据分析,我们得出了一些有意义的结果。
首先,我们发现男女学生在兴趣爱好上存在差异:男生更倾向于体育和游戏,而女生更倾向于文学和音乐。
其次,我们发现年龄对学习成绩的影响不显著,但是性别对学习成绩有明显的差异,女生的平均分高于男生。
此外,我们还发现学习成绩与父母的教育程度和家庭背景密切相关。
这些结果对于学校教育和家庭教育有着重要的启示。
五、讨论与结论本次调查实验结果表明统计学在实践中的重要性。
通过收集和分析大量的数据,我们能够找出数据中隐藏的规律和关系。
这对于做出准确的决策非常重要,无论是在教育、医疗还是商业等领域。
同时,本实验还暴露了一些问题,例如个别数据的异常值和样本容量的局限性,这些都需要在未来的调查实验中加以改进。
综上所述,统计学调查实验是一项有益的实践活动。
通过实际操作和数据分析,我们深入了解了统计学的应用和局限性。
在今后的学习和工作中,我们将更加重视统计学的知识和方法,以提高自己的决策能力和分析能力。
《统计学》实验
学院
专业
年级
学号
姓名
统计学实验
实验一用Excel搜集数据
实验目的:掌握用EXCEL进行抽样
实验资料:如某班50名学生统计学成绩如下:
56、80、66、49、85、65、97、71、70、52、
59、72、83、75、67、73、72、70、88、69、
79、61、64、86、74、73、61、90、68、57、
68、63、92、39、77、90、73、72、85、83、
78、83、65、75、67、85、98、72、77、68
实验要求:利用Excel从中抽样选取15人成绩,写出步骤。
实验步骤:
实验二用Excel整理数据
实验目的:用Excel进行统计分组
实验资料:任意收集你所在班级课程考试成绩,对其按60以下、60~70、70~80、80~90、90以上分为5个组。
实验要求:使用Excel直方图分析工具产生直方图,写出步骤。
实验步骤:
实验三用EXCEL相关分析
实验目的:用EXCEL进行相关分析
实验资料:试收集本班10位学生身高和体重的统计资料。
(注:每位同学搜集到的资料应该不同)。
实验要求:利用excel求出身高和体重的相关系数(单号利用函数计算相关系数,双号用相关系数宏计算相关系数),写出实验步骤。
实验步骤:
备注:1每位同学考试前把电子版交到学习委员手中,否则影响该门功课最终成绩,每人要建立以自己名字命名的文件夹,如:“张三统计学实验作业;
2学习委员要把该班的全部同学电子版收起后,要建立要该班命名的文件夹,如:“经
管091统计学实验作业”,发到邮箱houxihong126@,如果有误,则统计学考试结束后,亲自交到代课老师手里;每个班至少3人要打印,希望主动,否则班长,团支、学委必须打印。
3.完成作业后把
4.实验步骤参考删掉
4.实验步骤参考:
实验一用Excel搜集数据
实验步骤参考:
假定有100名消费者,即100个总体单位,每个总体单位给一个编号,共有从1到100个编号,从中选取15人进行工资收入调查。
输入工作表后如图13-1所示:
图:13-1总体各单位编号表
输入各总体单位的编号后,可按以下步骤操作:
第一步:单击工具菜单,选择数据分析选项(若无数据分析选项,可在工具菜单下选择加载宏,在弹出的对话框中选择分析工具库,便可出现数据分析选项),打开数据分析对话框,从中选择抽样。
如图13-2所示:
图13-2数据分析对话框
第二步:单击抽样选项,弹出抽样对话框。
如图13-3
图13-3 抽样对话框
第三步:在输入区域框中输入总体单位编号所在的单元格区域,在本例是$A$1:$J$10,系统将从A列开始抽取样本,然后按顺序抽取B列至J列。
如果输入区域的第一行或第一列为标志项(横行标题或纵列标题),可单击标志复选框。
第四步:在抽样方法项下,有周期和随机两种抽样模式:
“周期”模式即所谓的等距抽样,采用这种抽样方法,需将总体单位数除以要抽取的样本单位数,求得取样的周期间隔。
如我们要在100个总体单位中抽取12个,则在“间隔”框中输入8。
“随机模式”适用于纯随机抽样、分类抽样、整群抽样和阶段抽样。
采用纯随机抽样,只需在“样本数”框中输入要抽取的样本单位数即可;若采用分类抽样,必须先将总体单位按某一标志分类编号,然后在每一类中随机抽取若干单位,这种抽样方法实际是分组法与随机抽样的结合;整群抽样也要先将总体单位分类编号,然后按随机原则抽取若干类作为样本,对抽中的类的所有单位全部进行调查。
可以看出,此例的编号输入方法,只适用于等距抽样和纯随机抽样。
第四步:指定输出区域,在这里我们输入$A$14,单击确定后,即可得到抽样结果,如图13-4
图13-4等距抽样结果
实验二用Excel整理数据
实验步骤参考:
【例13-2】50名工人的月产量资料如图13-5所示:
图13-5工人月产量资料
然后按以下步骤操作。
第一步:在工具菜单中单击数据分析选项,从其对话框的分析工具列表中选择直方图,打开直方图对话框。
如图13-6所示:
图13-6直方图对话框
第二步:在输入区域输入$A$1:$J$5,在接收区域输入$A$9:$A$15。
接收区域指的是分组标志所在的区域,假定我们把分组标志输入到A9:A15单元格,注意这里只能输入每一组的上限值,即130,160,190,220,250,280,310。
第三步:选择输出选项,可选择输入区域、新工作表组或新工作薄。
我们在这里选择输入区域,可以直接选择一个区域,也可以直接输入一个单元格(代表输出区域的左上角),这里我们推荐只输入一个单元格(本例为A7),因为我们往往事先并不知道具体的输出区域有多大。
第四步:选择图表输出,可以得到直方图;选择累计百分率,系统将在直方图上添加累积频率折线;选择柏拉图,可得到按降序排列的直方图。
第五步:按确定按钮,可得输出结果如图13-7:
图13-7频数分布和直方图
应当注意,上图实际上是一个条形图,而不是直方图,若要把它变成直方图,可按如下操作:
用鼠标左键单击任一直条,然后右键单击,在弹出的快捷菜单中选取数据系列格式,弹出数据系列格式对话框,如图13-8所示:
图13-8数据系列格式对话框
在对话框中选择选项标签,把间距宽度改为0,按确定后即可得到直方图,如图13-9所示:
实验三 用EXCEL 相关分析
实验步骤参考:
首先把有关数据输入EXCEL 的单元格中,如图13-24
图13-24 EXCEL 数据集
用EXCEL 进行相关分析有两种方法,一是利用相关系数函数,另一种是利用相关分析宏。
1.利用函数计算相关系数
在EXCEL 中,提供了两个计算两个变量之间相关系数的方法,CORREL 函数和PERSON 函数,这两个函数是等价的,这里我们介绍用CORREL 函数计算相关系数:
第一步:单击任一个空白单元格,单击插入菜单,选择函数选项,打开粘贴函数对话框,在函数分类中选择统计,在函数名中选择CORREL ,单击确定后,出现CORREL 对话框。
第二步:在array1中输入B2:B11,在array2中输入C2:C11,即可在对话框下方显示出计算结果为0.896。
如图13-25所示:
图13-25CORREL对话框及输入结果
2.用相关系数宏计算相关系数
第一步:单击工具菜单,选择数据分析选项,在数据分析选项中选择相关系数,弹出相关系数对话框,如图13-26所示:
图13-26相关系数对话框
第二步:在输入区域输入$B$1:$C$1,分组方式选择逐列,选择标志位于第一行,在输出区域中输入$E$1,单击确定,得输出结果如图13-27
图13-27相关分析输出结果
在上面的输出结果中,身高和体重的自相关系数均为1,身高和体重的相关系数为0.896,和用函数计算的结果完全相同。