当前位置：文档之家 › 实验报告二-SAS的描述统计功能

实验报告二-SAS的描述统计功能

  • 格式：doc
  • 大小：4.96 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

SAS软件实验二单描述统计分析

SAS软件实验二单描述统计分析
验中 p= 0.4754>0.05 知不拒绝原假设，认为差量 diff 服从正态分布； 进而由 t 检验中 p= 0.189365>0.05 知接受原假设，认为差量均值显著为 0， 这说明: 两种不同饲料喂养的情况下，幼鼠体内钙留存量不具有显著性差异。
思考练习
data shiyan2; input x1 x2; diff=x1-x2; cards; 33 23.3 35.8 28.8 31.4 42.6 25.8 31.6 29 22.4 30.2 ; proc univariate data=shiyan2 normal ; var diff; run; 21.7 19.4 26.8 32 23.1 25.3 23.7 21.8 17.6
饲料 1 33.1 饲料 2 36.7 实验要求：
（1） 用 SAS 的 Viewtable 窗口将表中数据建立 SAS 数据集； （2） 用 Univeriate 过程分别检验两种不同饲料喂养的情况下， 幼鼠体内钙留存量的正态 性； （3） 用 Means 过程检验两种不同饲料喂养的情况下，幼鼠体内钙留存量是否具有显著 性差异。 （显著性水平 =0.05）
结果分析：
由 Shapiro-Wilk 检验中 p= 0.8944>0.05 知不拒绝原假设，认为差量 diff 服从正态分布； 进而由 t 检验中 p= 0.0004<0.05 知拒绝原假设，认为差量均值显著不为 0， 这说明: 服药前后该新药对 Baci 含量有显著影响。
五，实验结果分析或总结
通过这次实验，我学会了用 SAS 统计分析软件进行简单描述统计分析；学会了做正态性检 验。
思考练习
从 10 例腹泻病患者服用某种新药前和后 1 天的粪便中测得大肠杆菌（Baci）的数据如下， 试分析服药前后该新药对 Baci 含量有无显著影响。 病人编号 1 2 3 4 5 6

SAS学习系列11.-对数据做简单的描述统计

SAS学习系列11.-对数据做简单的描述统计

11. 对数据做简单的描述统计（一）使用proc means描述数据用proc means过程步，可以对数据做简单的描述统计，包括：非缺省值个数、均值、标准差、最大值、最小值等。

基本语法：PROC MEANS data = 数据集<可选项>;V AR 变量列表;CLASS 分组变量;<BY 变量;><WEIGHT 变量;> （加权平均的权数）<FREQ 变量;> （相应观测出现的频数）说明：（1）可选项“MAXDEC = n”用来指定输出结果的小数位数；（2）默认是对数据集的所有数值变量的非缺省值做描述统计，若想包含缺省值，加上可选项“MISSING”；（3）V AR语句指定要做描述统计的变量；CLASS语句指定按分组变量对数据进行分组分别做描述统计；BY语句同CLASS语句（需要事先按BY变量排好序）；（4）默认输出非缺省值个数、均值、标准差、最大值、最小值；也可以自己指定需要输出的描述统计量：MAX ——最大值；MIN——最小值；MEAN——均值；MEDIAN——中位数；MODE——众数；N——非缺省值个数；NMISS——缺省值个数；RANGE——极差；STDDEV——标准差；SUM——累和；例1 鲜花销售的数据（C:\MyRawData\Flowers.dat），变量包括顾客ID，销售日期，petunias，snapdragons，marigolds三种花的销量：读取数据，计算新变量销售月份month，并使用proc sort按照月份排序，并使用proc means的by语句来按照月份描述数据。

代码：data sales;infile'c:\MyRawData\Flowers.dat';input CustID $ @9SaleDate MMDDYY10.Petunia SnapDragon Marigold;Month = MONTH(SaleDate);proc sort data = sales;by Month;/* Calculate means by Month for flower sales; */proc means data = sales MAXDEC = 0;by Month;var Petunia SnapDragon Marigold;title'Summary of Flower Sales by Month';run;运行结果：（二）使用统计量有时候需要将统计量存入新数据集，以便进一步做数据分析，或者与原数据集合并。

实验三 SAS描述统计分析

实验三 SAS描述统计分析

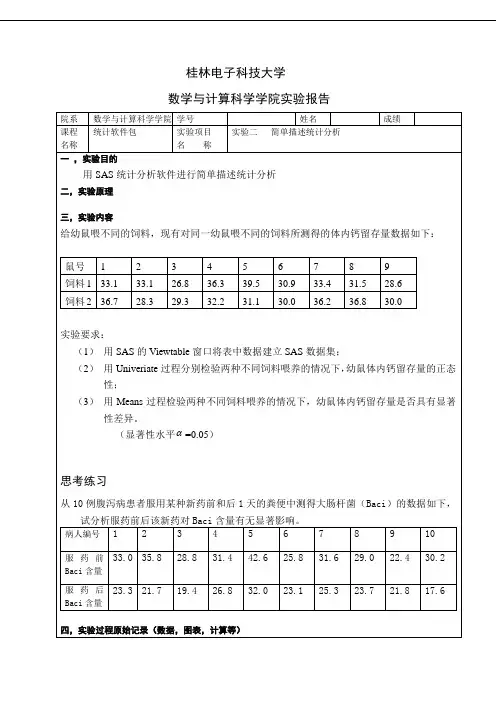
实验三SAS描述统计分析对数据进行频数统计、计算特征统计量和将数据图形化的过程称为描述统计。

其目的是为了揭示数据的集中趋势、分散程度和数据分布形态，展示极端数据，最后做出说明现象本质的初步结论。

用图形对数据进行描述性统计分析具有直观、鲜明、形象、便捷等特点，在表达统计数据时可以给人留下深刻的印象。

统计图形的种类很多，利用SAS可以方便的绘制常用的统计图形。

3.1 实验目的掌握使用SAS对数据作描述性统计分析的方法。

掌握SAS/GRAPH所提供的常用图形功能，能用SAS的统计图形对数据进行描述性统计分析。

3.2 实验内容一、用INSIGHT计算统计量、绘制统计图形二、用“分析家”计算统计量、绘制统计图形三、编程实现描述性统计（MEANS、UNIVARIATE、FREQ过程）、编程绘制统计图（GPLOT 和GCHART过程）3.3 实验指导一、用INSIGHT计算统计量【实验3-1】按性别分别计算SASHELP.CLASS中身高的均值、标准差、中位数和其它四分位数，简单分析学生身高的状况。

1. 在INSIGHT中打开数据集在菜单中选择“Solution（解决方案）”→“Analysis（分析）”→“Interactive Data Analysis （交互式数据分析）”，打开“SAS/INSIGHT Open”对话框，在对话框中选择数据集：SASHELP.CLASS，单击“Open（打开）”按钮，即可在INSIGHT中打开数据窗口，如图3-1左所示。

2. 用Distribution菜单项计算统计量(1) 选择菜单“Analyze（分析）”→“Distribution (Y)（分布）”，打开“Distribution (Y)”对话框。

在数据集CLASS的变量列表中，选择height，然后单击“Y”按钮，height被选为分析变量，选择sex，然后单击“Group”按钮，sex被选为分组变量，如图3-1右所示。

SAS与统计分析实验报告

SAS与统计分析实验报告

SAS与统计分析实验报告⼀、实习⽬的：1、了解SAS系统的基本知识及操作⽅法。

2、学会运⽤SAS系统进⾏数据的处理与分析。

⼆、实习⼯具：SAS软件三、实习内容：1、T测验①单组样本均数的T测验例：已知某⼩麦品种的平均株⾼为65cm,施肥后，随机抽取10株⼩麦进⾏测量，得到10株⼩麦株⾼分别为64 cm、66 cm、63 cm、68 cm、70 cm、65 cm、67 cm、68 cm、66 cm、69 cm.试验施肥后平均株⾼与已知的平均株⾼65 cm间的差异显著性。

●假如株⾼变量名为G，SAS程序如下：data whq1;input G@@;cards;64 66 63 68 70 65 67 68 66 69;run;proc ttest data=whq1 ci=none h0=65alpha=0.05;var G;run;●程序说明：过程选项h0=65 指定零假设 ho:u=65,检验抽样总体的均值是否为65，alpha=0.05⽤来指定结果中各统计量可信区间的置信⽔平。

语句var G指定要检验的变量。

●程序运⾏结果：The TTEST ProcedureStatisticsLower CL Upper CLVariable N Mean Mean Mean Std Dev Std Err Minimum Maximum G 10 65.011 66.6 68.189 2.2211 0.7024 63 70T-TestsVariable DF t Value Pr > |t|G 9 2.28 0.0487●结果说明：结果中⾸先给出了输⼊数据集中分析变量的有关统计量，其中包括均数及其可信区间、标准差及其可信区间。

然后给出均数的标准误、观测值最⼤值和最⼩值。

最后，给出单组样本均数⽐较的T检验结果。

本例中t=2.28，对应的P值为0.0487。

根据分析结果可作出结论：施肥后平均株⾼与已知的平均株⾼65 cm有显著差异。

SAS的描述统计功能

SAS的描述统计功能

2.2.2 用“分析家”计算统计量
❖1. 启动“分析家”
▪ 选择主菜单“Solutions（解决方 案）”→“Analysis（分析）”→“Analyst （分析家）”，打开“分析家”窗口。
▪ 选择主菜单“File（文件）”→“Open By SAS Name”，打开“Select A Member”对话 框，选择数据集Mylib.sryzc。
2.3 统计图形
❖2.3.1 定量变量的图形表示 ❖2.3.2 分类变量的图形表示
2.3.1 定量变量的图形表示
❖1. 直方图
▪ 对于数值型变量，常用直方图（histogram） 来展示变量取值的分布。将变量取值的范围分 成若干区间，在等间隔区间的情况，每个区间 的长度称为组距。考察数据落入每一区间的频 数与频率，在每个区间上画一个矩形，它的宽 度是组距，它的高度可以是频数、频率或密度 （频率／组距），在高度是密度的情况，每一 矩形的面积恰是数据落入区间的频率，这种直 方图可以估计总体的概率密度。
❖2. 校正平方和（Corrected sum of squares）
n
CSS (xi x)2
i1
2.1.5 其它统计量
❖3. 未校正平方和（Uncorrected sum of squares）
n
USS xi2
i1
❖4. k阶原点矩
Ak
1 n
n i1
xik,k1,2,...
• 其中A1即为均值 x 。
家庭总支出 2060 2236 1455 1040 2366 1966 2400 1250 1350 1794 2550 1380 1200 2305 1316
2.2.1 用INSIGHT计算统计量
❖2. 在INSIGHT中打开数据集

SAS软件及部分常用功能简介

SAS软件及部分常用功能简介
颜色和字体选择
使用适当的颜色和字体，使图表更加美观和 专业。
动态数据可视化
交互式图表
允许用户通过点击或拖动来交互地查看数据。
时间序列动画
展示随时间变化的数据趋势。
动态更新
随着数据的改变，图表能够自动更新。
数据筛选
允许用户根据特定条件筛选数据，并实时反 映在图表上。
05
编程与自定义功能
SAS编程语言基础
SAS软件及部分常用功能简介
• SAS软件概述 • 数据导入与处理 • 统计分析功能 • 数据可视化功能 • 编程与自定义功能

01
SAS软件概述
SAS软件简介
SAS（Statistical Analysis System）软件是由美国北卡罗来纳大学于1966年开发的统计分析软件，最初 主要用于农业领域的数据分析。经过多年的发展，SAS已成为全球领先的数据分析和统计分析解决方案提 供商。
SAS软件采用模块化设计，用户可以根据需要选择不同的模块进行数据处理、统计分析、数据挖掘、 预测建模等。
SAS软件的特点与优势
强大的数据处理能力
SAS提供了丰富的数据导入、导出和转换工具，支持多种 数据格式和数据库系统，能够高效地处理大规模数据集。
灵活的数据挖掘功能
SAS的数据挖掘工具能够帮助用户发现隐藏在数据中的模 式和关联，支持多种数据挖掘算法，如决策树、神经网络 、聚类等。
饼图
用于表示各部分在整体中所占的比 例。
03
02
折线图
用于展示时间序列数据或连续变量 的变化趋势。
散点图
用于展示两个变量之间的关系。
04
图表制作与美化
选择数据
确保数据准确无误，是制作图表的基础。

sas分析报告

sas分析报告

sas分析报告：分析报告sas sas结果分析如何用sas显著性分析sas结果读取篇一：sas统计分析报告《统计软件》报告聚类分析和方差分析在统计学成绩分析中的应用班级：精算0801班姓名：张倪学号：2008111500 报告2011年11月指导老师：郝际贵成绩：目录一、背景及数据来源.................................................... 1 二、描述性统计分析.................................................... 2 三、聚类分析................................................................ 4 四、方差分析................................................................ 6 五、结果分析与结论. (8)聚类分析和方差分析在统计学成绩分析中的应用一、背景及数据来源SAS 系统全称为Statistics Analysis System，最早由北卡罗来纳大学的两位生物统计学研究生编制，并于1976年成立了SAS软件研究所，正式推出了SAS软件。

SAS是用于决策支持的大型集成信息系统，但该软件系统最早的功能限于统计分析，至今，统计分析功能也仍是它的重要组成部分和核心功能。

SAS 系统是一个组合软件系统，它由多个功能模块组合而成，其基本部分是BASE SAS模块。

BASE SAS模块是SAS系统的核心，承担着主要的数据管理任务，并管理用户使用环境，进行用户语言的处理，调用其他SAS模块和产品。

也就是说，SAS系统的运行，首先必须启动BASE SAS模块，它除了本身所具有数据管理、程序设计及描述统计计算功能以外，还是SAS系统的中央调度室。

它除可单独存在外，也可与其他产品或模块共同构成一个完整的系统。

实验报告二-SAS的描述统计功能

实验报告二-SAS的描述统计功能

实验报告实验项目名称SAS的描述统计功能所属课程名称统计分析及SAS实现实验类型验证性实验实验日期2016-10-20班级数学与应用数学学号姓名成绩⑴利用INSIGHT模块画出直方图：图2.1 INSIGHT模块绘制频数直方图⑵利用“分析家”绘制频数直方图：图2.2“分析家”绘制频数直方图⑶编程绘制频数直方图：proc gchart data=lmf.p21;vbar grade;run;图2.3 编程绘制频数直方图②求出上述数据的平均值、中位数、四分之一分位点及四分之三分位点：⑴利用INSIGHT模块求平均值、中位数、四分之一分位点及四分之三分位点：图2.4 利用INSIGHT模块求统计量表2.1 利用INSIGHT模块求矩统计量：矩统计量（moment）表2.2 利用INSIGHT模块求分位数：分位数（quantiles）由表2.1、表2.2得出，均值（mean）为77.7167，中位数（med）为81.0000，四分之一分位点（Q1）为72.0000，四分之三分位点（Q3）为86.0000。

⑵利用“分析家”求平均值、中位数、四分之一分位点及四分之三分位点：Ⅰ. 利用Summary Statistics菜单计算描述性统计量：图2.5 Summary Statistics菜单计算描述性统计量Ⅱ. 利用Distributions菜单计算描述性统计量：表2.3 利用“分析家”模块求矩统计量：矩统计量（moment）表2.4 “分析家”求基本统计测度：基本统计测度（Basic Statistical Measure）表2.5 “分析家”求分位数：分位数（quantiles）由表2.3、表2.4、表2.5得出，均值（mean）为77.71667，中位数（med）为81.00000，四分之一分位点（Q1）为72.0，四分之三分位点（Q3）为86.0。

⑶利用编程求平均值、中位数、四分之一分位点及四分之三分位点：proc means data=lmf.p21 mean median Q1Q3;var grade;run;表2.6 编程求数据的平均值、中位数、四分之一分位点及四分之三分位点：由表2.6得出，均值（mean）为77.7166667，中位数（med）为81.0000000，四分之一分位点（Q1）为72.0000000，四分之三分位点（Q3）为86.0000000。

【卫生统计学】02 SAS统计分析概述

【卫生统计学】02 SAS统计分析概述

• 程序：
• data male; • set prg2_01; • if sex=‘m’ then output;
相当于
If sex=‘female’ then delete;
有时，then output
• run;
可省略。
Set ：调用work里的当 前临时数据集
程序：
Data male female; Set prg2_01; If sex=‘m’ then output male;
❖“Help” 可随时提供帮助咨询
14
7、菜单下方的工具栏
New（清除log窗口和output窗口的内容,建 立新文件），
Open（打开文件）， Save（储存文件）， Print（打印）， View（预览）， Cut（裁剪），
Copy（复制）， Paste（粘贴）， Undo（恢复）， Explorer（游览窗口）, Submit（运行）， Clear all (删除editor窗口内容), Help（提供帮助）
(2)分析方法丰富。 SAS汇集了大量的统计方法，从简单描述统计量 的计算到多因素分析，从时间序列分析到质量控制 等。仅SAS/STAT就包括了8类方法28个分析过程。
7
(3)对数据的连续处理。 SAS能同时处理多个输入文件，能从几个数据 集中组合变量值、观测值，建立子集，连接、合 并和修改数据。SAS可存储一个合法的结果或中间 结果，以便以后使用。
▪
(2)为相应数据域定义变量名；
▪
(3)确定变量的读入模式。
▪
Input语句格式：
▪
input 变量名 [变量类型]；
▪Cards语句的功能：标志数据块的开始；
▪
格式为：

实验报告二sas的描述统计功能

实验报告二sas的描述统计功能

实验报告实验项目名称SAS的描述统计功能所属课程名称统计分析及SAS实现实验类型验证性实验实验日期2016-10-20班级数学与应用数学学号姓名成绩⑴利用INSIGHT模块画出直方图：图2.1 INSIGHT模块绘制频数直方图⑵利用“分析家”绘制频数直方图：图2.2“分析家”绘制频数直方图⑶编程绘制频数直方图：proc gchart data=lmf.p21;vbar grade;run;图2.3 编程绘制频数直方图②求出上述数据的平均值、中位数、四分之一分位点及四分之三分位点：⑴利用INSIGHT模块求平均值、中位数、四分之一分位点及四分之三分位点：图2.4 利用INSIGHT模块求统计量表2.1 利用INSIGHT模块求矩统计量：矩统计量（moment）表2.2 利用INSIGHT模块求分位数：分位数（quantiles）由表2.1、表2.2得出，均值（mean）为77.7167，中位数（med）为81.0000，四分之一分位点（Q1）为72.0000，四分之三分位点（Q3）为86.0000。

⑵利用“分析家”求平均值、中位数、四分之一分位点及四分之三分位点：Ⅰ. 利用Summary Statistics菜单计算描述性统计量：图2.5 Summary Statistics菜单计算描述性统计量Ⅱ. 利用Distributions菜单计算描述性统计量：表2.3 利用“分析家”模块求矩统计量：矩统计量（moment）表2.4 “分析家”求基本统计测度：基本统计测度（Basic Statistical Measure）表2.5 “分析家”求分位数：分位数（quantiles）由表2.3、表2.4、表2.5得出，均值（mean）为77.71667，中位数（med）为81.00000，四分之一分位点（Q1）为72.0，四分之三分位点（Q3）为86.0。

⑶利用编程求平均值、中位数、四分之一分位点及四分之三分位点：proc means data=lmf.p21 mean median Q1Q3;var grade;run;表2.6 编程求数据的平均值、中位数、四分之一分位点及四分之三分位点：由表2.6得出，均值（mean）为77.7166667，中位数（med）为81.0000000，四分之一分位点（Q1）为72.0000000，四分之三分位点（Q3）为86.0000000。

医学统计学：SAS实验-统计描述

医学统计学：SAS实验-统计描述
关联度； • 对于n维表， PROC FREQ可以进行分层分析，计
算第一层和交叉层的统计量。 • FREQ过程也可以将结果输出到SAS数据集中。
FREQ过程由下列语句控制：
Proc freq [选择项]；
Tables 请求式┅[/选择项]；
Weight 变量；
By
变量表；
Output [选择项]；
FREQ过程——可以生成单向和多向的频数表和 交叉表。
MEANS过程——用来对数据集中的数值变量计 算简单的描述统计量( N、Mean、Std Dev、 Minimum、Maximum)。
• SUMMARY过程——用来计算单个变量的基本统计 量，它和MEANS过程的不同之处在于该过程不在 OUTPUT窗口输出结果，除非加上命令PRINT，而 MEANS过程总是在OUTPUT窗口输出。
173.6 175.3 178.4 181.5 170.5 176.4 170.8 171.8 180.7 170.7
173.8 164.4 170.0 175.0 177.7 171.4 162.9 179.0 174.9 178.3
174.5 174.3 170.4 173.2 174.5 173.7 173.4 173.9 172.9 177.9
171.2 177.1 170.7 173.6 167.2 170.7 174.7 171.8 167.3 174.8
168.5 178.7 177.3 165.9 174.0 170.2 169.5 172.1 178.2 170.9
171.3 176.1 169.7 177.9 171.1 179.3 183.5 168.5 175.5 175.9
**语句的简单说明**
• Tables语句

SAS中的描述性统计过程

SAS中的描述性统计过程

SAS中的描述性统计过程(2012-08-01 18:07:01)转载▼标签：分类：数据分析挖掘杂谈SAS中的描述性统计过程描述性统计指标的计算可以用四个不同的过程来实现，它们分别是means过程、summary过程、univariate过程以及tabulate过程。

它们在功能范围和具体的操作方法上存在一定的差别，下面我们大概了解一下它们的异同点。

相同点：他们均可计算出均数、标准差、方差、标准误、总和、加权值的总和、最大值、最小值、全距、校正的和未校正的离差平方和、变异系数、样本分布位置的t检验统计量、遗漏数据和有效数据个数等，均可应用by语句将样本分割为若干个更小的样本，以便分别进行分析。

不同点：（1）means过程、summary过程、univariate过程可以计算样本的偏度（skewness）和峰度（kurtosis），而tabulate过程不计算这些统计量；（2）univariate过程可以计算出样本的众数（mode），其它三个过程不计算众数；（3）summary过程执行后不会自动给出分析的结果，须引用output语句和print过程来显示分析结果，而其它三个过程则会自动显示分析的结果；（4）univariate过程具有统计制图的功能，其它三个过程则没有；（5）tabulate过程不产生输出资料文件（存储各种输出数据的文件），其它三个均产生输出资料文件。

统计制图的过程均可以实现对样本分布特征的图形表示，一般情况下可以使用的有chart过程、plot过程、gchart过程和gplot过程。

大家有没有发现前两个和后两个只有一个字母‘g’（代表graph）的差别，其实它们之间（只差一个字母g的过程之间）的统计描述功能是相同的，区别仅在于绘制出的图形的复杂和美观程度。

chart过程和plot过程绘制的图形类似于我们用文本字符堆积起来的图形，只能概括地反映出资料分布的大体形状，实际上这两个过程绘制的图形并不能称之为图形，因为他根本就没有涉及一般意义上图形的任何一种元素（如颜色、分辨率等）。

第2章SAS的描述统计功能2010317-文档资料

第2章SAS的描述统计功能2010317-文档资料
程的开始； TABLES语句用于创建有关变量所构成的各种表
格并进行相应的假设检验和计算。
31
例如，统计数据集Sasuser.Exam2_1中变量R_Id和 Income频数的代码如下：
proc freq data = sasuser.Exam2_1;
tables R_Id Income; run;
2.1 描述性统计的基本概念 2.2 在SAS中计算统计量 2.3 统计图形
3
第二章 SAS的描述统计功能
2.1 描述性统计的基本概念 一、统计学的基本概念 二、表示数据位置的统计量 三、表示数据分散程度的统计量 四、表示数据分布形状的统计量 五、其它统计量
4
描述性统计：
26
单击“Statistics”按钮，打开“Summary Statistics： Statistics”对话框。
27
28
3. 通过Distributions菜单计算描述性统计量 选择主菜单“Statistics（统计）”
→“Descriptive（描述性统计）” →“Distributions（分布）”， 打开“ Distributions”对话框，选择变量列表中的 Income，单击“Analysis”按钮，选定分析变量。
首先将数据从小到大排序为：x(1)，...，x(n)，
然后计算：
中位数


x
(
n 1 2
)
1
2
(
x
(
n
)
2

x
(
n
1)
)
2
n为奇数 n为偶数
9
第二章 2.1 描述性统计的基本概念
3. 众数（Mode） 观测值中出现最多的数称为众数。

sas实践总结与体会

sas实践总结与体会

sas实践总结与体会在当今数字化的时代，数据的分析和处理变得愈发重要。

SAS 作为一款功能强大的数据分析软件，为我们提供了丰富的工具和方法来应对各种数据相关的任务。

通过一段时间的 SAS 实践，我积累了不少宝贵的经验，也有了许多深刻的体会。

首先，SAS 的学习曲线并非平坦。

初接触时，面对其众多的功能模块和复杂的语法规则，确实感到有些不知所措。

但随着不断的学习和实践，逐渐发现只要掌握了一些核心的概念和常用的命令，就能逐渐上手并完成一些基本的数据分析任务。

在实际的项目中，数据的导入和清理是第一步，也是至关重要的一步。

有时候，我们拿到的数据可能存在缺失值、异常值或者格式不一致等问题。

SAS 提供了一系列强大的工具，如 PROC IMPORT、PROC SQL 等，帮助我们将数据顺利地导入到系统中，并进行初步的筛选和整理。

在这个过程中，需要耐心和细心，确保数据的质量和准确性。

例如，有一次在处理一个包含大量销售数据的文件时，发现其中部分产品的价格出现了负数，经过仔细检查，原来是数据录入时的错误。

通过使用 SAS 的条件判断和数据替换功能，成功地纠正了这些错误，为后续的分析打下了坚实的基础。

数据探索和可视化也是 SAS 实践中的重要环节。

通过使用 PROC SGPLOT 等过程，我们可以直观地了解数据的分布、趋势和关系。

比如，绘制柱状图来比较不同地区的销售业绩，或者绘制折线图观察产品销量随时间的变化。

这些可视化的结果能够帮助我们快速发现数据中的规律和异常，从而提出有针对性的分析思路。

在进行数据分析时，SAS 的统计分析功能发挥了巨大的作用。

无论是描述性统计分析，还是假设检验、回归分析等，SAS 都提供了相应的过程和方法。

例如，在研究消费者年龄与购买行为之间的关系时，使用了线性回归分析，通过 SAS 输出的结果，不仅能够得到回归方程的系数和显著性水平，还能对模型的拟合优度进行评估。

这让我们能够准确地判断变量之间的关系，并做出合理的预测和决策。

sas统计分析报告

sas统计分析报告

《统计软件》报告聚类分析和方差分析在统计学成绩分析中的应用班级：精算0801班学号：报告时间：2011年11月成绩：目录一、背景及数据来源 (1)二、描述性统计分析 (2)三、聚类分析 (4)四、方差分析 (6)五、结果分析与结论 (8)聚类分析和方差分析在统计学成绩分析中的应用一、背景及数据来源SAS 系统全称为Statistics Analysis System，最早由北卡罗来纳大学的两位生物统计学研究生编制，并于1976年成立了SAS软件研究所，正式推出了SAS 软件。

SAS是用于决策支持的大型集成信息系统，但该软件系统最早的功能限于统计分析，至今，统计分析功能也仍是它的重要组成部分和核心功能。

SAS 系统是一个组合软件系统，它由多个功能模块组合而成，其基本部分是BASE SAS模块。

BASE SAS模块是SAS系统的核心，承担着主要的数据管理任务，并管理用户使用环境，进行用户语言的处理，调用其他SAS模块和产品。

也就是说，SAS系统的运行，首先必须启动BASE SAS模块，它除了本身所具有数据管理、程序设计及描述统计计算功能以外，还是SAS系统的中央调度室。

它除可单独存在外，也可与其他产品或模块共同构成一个完整的系统。

各模块的安装及更新都可通过其安装程序非常方便地进行。

本文利用SAS软件进行描述性统计、聚类分析等统计分析方法，将学生按照多指标综合考虑进行聚类。

数据来源：选取2010—2011第一学期统计学选教课成绩单，选取性别系别等变量进行考察。

将中文名称改为英文。

数据类型如下所示：当输入字符型的变量时，需要加上符号$在该变量的后面，用于区分数值型变量，所以用$来作为后缀。

删除缺考错误分数等异常值。

命名为2010stat.xls二、描述性统计分析（一）导入数据首先建立永久磁盘路径，导入数据集statlibname path "D:\sas\";run;（二）描述性统计分析然后进行描述性统计对性别、平时成绩、期末成绩、总评成绩进行计算，代码如下：proc means data=path.stat;var sex s1 s2 s3;run;输出结果如下：从结果可以分析出，总体学生平时成绩平均分为86.28分，总评成绩均分为77.15分。

SAS数据分析实验报告

SAS数据分析实验报告

数理与土木工程学院实验报告课程名称：《统计软件SPSS、SAS及实践》实验结果（包括程序代码、程序结果分析）第一题：②基于数据集transaction，将变量“Revenue”中的缺失数据用其均值代替；data a;set a;array s(*) aa1-aa2;n=n(of s(*));mean=mean(of s(*));sum=sum( of s(*));do i=1to dim(s);if s(i)=.then s(i)=mean;end;run;proc print;run;③基于②，将取值全部缺失的变量删除。

data a;set a;array aa aa1-aa2;do over aa;if col=.then delete;end;run;proc transpose data=a out=transaction(drop=_name_);var aa1-aa2;run;proc print;run;第二题：a) 建立一个数据集合读入数据，变量为length，width和 height；data b;input length width height;cards;32 18 1216 15 2448 12 3215 30 4520 30 36;run;proc print data=b;run;b) 使用 set 语句,利用a)的数据集建立一个新数据集，它包括a）的所有数据，并建立三个新变量：每个c) 使用b）建立的数据集建立一个新数据集，只包括其中的volume 和 cost 变量。

data d;set c(keep=volume cost);run;proc print data=d;run;第三题：a)对车的标志（brand）的频数画竖直条形图。

libname mydata 'D:\data';proc print data=edcar;run;data e;set edcar; run;proc gchart;vbar brand;run;b)c)data g;set f;proc means data=g ;run;第四题：试分析：该地区单身人士的收入与住房面积之间是否相关？如果线性相关，确定一元线性回归方程，并做显著性检验。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验报告实验项目名称SAS的描述统计功能所属课程名称统计分析及SAS实现实验类型验证性实验实验日期2016-10-20班级数学与应用数学学号姓名成绩⑴利用INSIGHT模块画出直方图：图2.1 INSIGHT模块绘制频数直方图⑵利用“分析家”绘制频数直方图：图2.2“分析家”绘制频数直方图⑶编程绘制频数直方图：proc gchart data=lmf.p21;vbar grade;run;图2.3 编程绘制频数直方图②求出上述数据的平均值、中位数、四分之一分位点及四分之三分位点：⑴利用INSIGHT模块求平均值、中位数、四分之一分位点及四分之三分位点：图2.4 利用INSIGHT模块求统计量表2.1 利用INSIGHT模块求矩统计量：矩统计量（moment）表2.2 利用INSIGHT模块求分位数：分位数（quantiles）由表2.1、表2.2得出，均值（mean）为77.7167，中位数（med）为81.0000，四分之一分位点（Q1）为72.0000，四分之三分位点（Q3）为86.0000。

⑵利用“分析家”求平均值、中位数、四分之一分位点及四分之三分位点：Ⅰ. 利用Summary Statistics菜单计算描述性统计量：图2.5 Summary Statistics菜单计算描述性统计量Ⅱ. 利用Distributions菜单计算描述性统计量：表2.3 利用“分析家”模块求矩统计量：矩统计量（moment）表2.4 “分析家”求基本统计测度：基本统计测度（Basic Statistical Measure）表2.5 “分析家”求分位数：分位数（quantiles）由表2.3、表2.4、表2.5得出，均值（mean）为77.71667，中位数（med）为81.00000，四分之一分位点（Q1）为72.0，四分之三分位点（Q3）为86.0。

⑶利用编程求平均值、中位数、四分之一分位点及四分之三分位点：proc means data=lmf.p21 mean median Q1Q3;var grade;run;表2.6 编程求数据的平均值、中位数、四分之一分位点及四分之三分位点：由表2.6得出，均值（mean）为77.7166667，中位数（med）为81.0000000，四分之一分位点（Q1）为72.0000000，四分之三分位点（Q3）为86.0000000。

【练习2-2】掷一枚均匀子42次，记录朝上一面的点数，画出记录的频数和频率直方图，并说明记录的分布规律。

3 24 15 15 3 4 3 5 64 25 3 1 34 1 45 1 63 3 1 24 26 3 4 6 6 16 2 4 5 2 6【解答】①利用编程计算频数：proc freq data=lmf.p22;table dice;run;表2.7 编程计算频数频数（freq）由表得出出现点数1的次数为7；出现点数2的次数为6；出现点数3的次数为8；出现点数4的次数为8；出现点数5的次数为6；出现点数6的次数为7。

②利用编程绘制频率直方图：proc gchart data=lmf.p22;vbar dice;run;图2.4 编程绘制频数直方图表2.7、图2.4可以说明，骰子的数字分布是均匀的，每点掷出的概率计划一样，而在这42次中，3、4两点概率值最高且一样，2、5两点出现概率最低且一样，1、6两点出现概率适中且一样。

【练习2-5】某高校对本校财经类学科硕士毕业生的收入状况进行调查，抽查了30位毕业生，得到他们的年收入数据如下（单位：千元）：30.7 30.7 31.1 30.5 32.229.9 30.2 30.3 32.3 31.829.7 29.1 30.6 31.2 32.730.3 28.9 30.3 30.9 33.328.8 30.0 30.1 32.2 32.129.3 30.4 30.6 32.9 30.3①求年收入的均值、中位数和四分位数；②求年收入的极差和标准差；③绘制年收入的盒形图，并概括年收入的分布情况。

【解答】①利用编程求年收入的均值、中位数和四分位数：proc means data=lmf.p23 mean median Q1Q3;var income;run;表2.8求描述年收入位置的统计量：由表2.8得出，均值（mean）为30.7800000，中位数（median）为30.5500000，下四分位数（Q1）为30.1000000，上四分位数（Q3）为31.8000000。

②利用编程求年收入的极差和标准差：proc means data=lmf.p23 range std;var income;run;表2.9求描述年收入离散程度的统计量：③⑴利用INSIGHT绘制年收入的盒形图：图2.5 INSIGHT绘制年收入盒形图⑵概括年收入的分布情况：由图2.5得出，50%的硕士研究生的年收入在30.6千元以上，25%的硕士研究生的年收入小于30.1千元，75%的硕士研究生的年收入小于31.6千元。

【练习2-6】某城市自来水水费收缴员某次对某一居民楼内各用户两个月的用水量查表记录如下（单位：m3）：47 23 22 13 20 11 19 9 20 9 20 9 129 10 12 7 8 10 10 15 10 4 13 13 6 62 6 23 14 9 8 6 5 12 15 20 20 14 10 47 10 12 17 9 5 17 68 30 9 35 20 25 20 25 20 14 8 10 24 11 16 16 20 9 试对该居民楼的用水情况做出分析。

【解答】①利用“分析家”通过distributions菜单计算用水量的描述性统计量：图2.6 “分析家”求解统计量得出结果如表2.10、2.11、2.12：表2.10 用水量的矩统计量（moments）：表2.11 用水量的基本统计测度（Basic Statistics Measures）：表2.12 用水量的百分位数（quantiles）：由表 2.10、2.11、2.12得出⑴用水量的位置分布的统计量：均值（mean）为16.64615m3，中位数（median）为13.00000m3，众数（mode）为20.00000m3，上四分位数（Q3）为20m3，下四分位数（Q1）为9m3；⑵用水量的分散程度的统计量：极值（range）为64.00000m3，标准差（std dev)为12.21223m3，方差(var) 为149.13846m3。

②利用編程做出频数直方图：proc gchart data=lmf.p24;vbar WatConspt;run;图2.7 用水量的频率直方图③利用INSIGHT作出用水量的盒形图：图2.8 用水量的盒形图由①、②、③得出该居民楼两个月内的用水量主要集中在20m3，75%的居民用水量小于20m3，50%的居民用水量小于13m3，25%的居民用水量小于9m3，平均用水量约为16m3，极差为64m3，说明该楼居民用水量的差异大。

【练习2-7】某高校学生逃课的情况进行抽样调查的结果如下：e e e2 G2004 male 2 G2005 female2 G2005female3 G2004female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female2 G2005female3 G2005female2 G2004 male 2 G2005 female3 G2004 male 3 G2005female（其中各变量表示含义：1:从不逃课；2:偶尔逃课；3:经常逃课；G2004:2004级；G2005:2005级；male：男；female：女）①利用INSIGHT模块做出直方图从整体上对逃课情况进行分析：图2.9 整体上逃课情况由图2.9得出，从不逃课的有8人，偶尔逃课的有66人，经常逃课的有26人，说明该校学生大多偶尔逃课，但经常逃课的也较多，从不逃课的很少，该校的学习氛围不够浓。

②利用INSIGHT绘制直方图对两个年级逃课状况进行比较分析:图2.10 两个年级逃课情况由图2.10可以看出，2005级从不逃课的学生多于2004级，多6人；2005级偶尔逃课的学生多于2004级，多4人；2005级经常逃课的学生少于2004级，少10人。

总体来看2004级学生逃课情况较严重，学习氛围不够。

③利用统计图形对男女生逃课进行比较分析：⑴利用INSIGHT作出直方图对男女生逃课进行比较：图2.11 INSIGHT绘制男女逃课分布情况⑵利用“分析家”作出直方图对男女生逃课进行比较：图2.12 “分析家”绘制男女逃课分布情况由图2.11、图2.12得出，不同年级男、女从不逃课人数差不多，男生多一点；不同年级男生偶尔逃课人数少于女生；不同年级男生经常逃课人数少于女生。

说明女生在学校里较守纪，逃课情况和男生相比较好。

【小结】通过本章学习，掌握了SAS中利用INSIGHT、“分析家”、编程三个模块对数据进行描述统计，学会熟练地使用三个模块绘制直方图、盒形图等统计图形，并且能够通过图形以及基本统计量对数据进行分析、归纳得出实际结论。

指导教师评语及成绩：评语：成绩：指导教师签名：批阅日期：。