神经网络实验2

2023年秋江苏开放大学神经网络与深度学习形考二作业试题列表单选题题型：单选题客观题分值5分难度：简单得分：51以下卷积运算的输出结果为A11 12<br>10 1115 16<br>&nbsp;6&nbsp;15C10 11<br>11 12D11 12<br>10 11学生答案：B老师点评：题型：单选题客观题分值5分难度：中等得分：52以下关于神经⽹络的训练过程，描述错误的是？A【mini-batch】从训练数据中随机选出⼀部分数据，这部分数据称为mini-batch，我们的⽬标是减少mini-batch损失函数的值。

【随机梯度下降】stochastic gradient descent：“随机”代表在梯度下降中随机初始⼀个学习率，并不断尝试多个值，寻求最好的结果C【计算梯度】为了减⼩mini-batch的损失函数，需要求出各个权重参数的梯度D【更新参数】梯度反⽅向表示损失函数的值减⼩最多的⽅向，将权重参数沿梯度反⽅向进⾏微⼩更新学生答案：B老师点评：题型：单选题客观题分值5分难度：一般得分：53多义现象可以被定义为在⽂本对象中⼀个单词或短语的多种含义共存。

下列哪⼀种⽅法可能是解决此问题的最好选择？A随机森林B以上所有⽅法卷积神经⽹络D强化学习学生答案：C老师点评：题型：单选题客观题分值5分难度：中等得分：54在⼀个神经⽹络⾥，知道每⼀个神经元的权重和偏差是最重要的⼀步。

如果以某种⽅法知道了神经元准确的权重和偏差，你就可以近似任何函数。

实现这个最佳的办法是什么？A以上都不正确B搜索所有权重和偏差的组合，直到得到最优值C随机赋值，祈祷它们是正确的赋予⼀个初始值，检查与最优值的差值，然后迭代更新权重学生答案：D题型：单选题客观题分值5分难度：一般得分：55以下场景中适合采⽤⼀对多结构RNN的是？A基于帧粒度的视频分类B⽣成图⽚说明C情感分析D机器翻译学生答案：B题型：单选题客观题分值5分难度：一般得分：56在典型CNN⽹络AlexNet中，原始图⽚是⼤⼩为227*227的三通道数据，经过96个⼤⼩为11*11的卷积核卷积后得到96个⼤⼩为55*55的特征图，若padding = 0 ，则卷积核的步⻓为多少？4B1C2D3学生答案：A老师点评：题型：单选题客观题分值5分难度：一般得分：57】在神经⽹络的学习中，权重的初始值特别重要，设定什么样的权重初始值，经常关系到神经⽹络的学习能否成功。

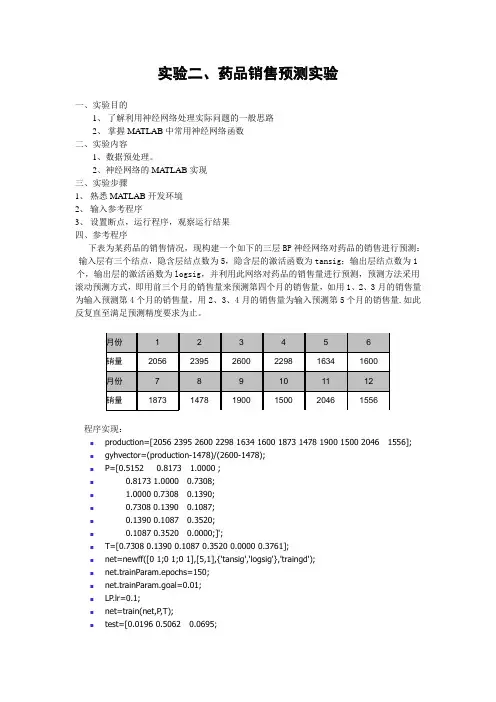
实验二、药品销售预测实验一、实验目的1、了解利用神经网络处理实际问题的一般思路2、掌握MATLAB中常用神经网络函数二、实验内容1、数据预处理。

2、神经网络的MA TLAB实现三、实验步骤1、熟悉MATLAB开发环境2、输入参考程序3、设置断点，运行程序，观察运行结果四、参考程序下表为某药品的销售情况，现构建一个如下的三层BP神经网络对药品的销售进行预测：输入层有三个结点，隐含层结点数为5，隐含层的激活函数为tansig；输出层结点数为1个，输出层的激活函数为logsig，并利用此网络对药品的销售量进行预测，预测方法采用滚动预测方式，即用前三个月的销售量来预测第四个月的销售量，如用1、2、3月的销售量为输入预测第4个月的销售量，用2、3、4月的销售量为输入预测第5个月的销售量.如此反复直至满足预测精度要求为止。

程序实现：⏹production=[2056 2395 2600 2298 1634 1600 1873 1478 1900 1500 2046 1556];⏹gyhvector=(production-1478)/(2600-1478);⏹P=[0.5152 0.8173 1.0000 ;⏹0.8173 1.0000 0.7308;⏹ 1.0000 0.7308 0.1390;⏹0.7308 0.1390 0.1087;⏹0.1390 0.1087 0.3520;⏹0.1087 0.3520 0.0000;]';⏹T=[0.7308 0.1390 0.1087 0.3520 0.0000 0.3761];⏹net=newff([0 1;0 1;0 1],[5,1],{'tansig','logsig'},'traingd');⏹net.trainParam.epochs=150;⏹net.trainParam.goal=0.01;⏹LP.lr=0.1;⏹net=train(net,P,T);⏹test=[0.0196 0.5062 0.0695;⏹0.3761 0.0196 0.5062;⏹0 0.3761 0.0196;⏹0.5152 0.8173 1.0000 ;⏹0.8173 1.0000 0.7308;⏹ 1.0000 0.7308 0.1390;⏹0.7308 0.1390 0.1087;⏹0.1390 0.1087 0.3520;⏹0.1087 0.3520 0.0000;⏹0.3520 0 0.3761;⏹0 0.3761 0.0196;⏹0.3761 0.0196 0.5062;]';⏹y=sim(net,test);⏹x=[1:12];⏹figure;⏹plot(x,gyhvector,'rs',x,y,'bo');⏹set(gca,'xtick',x);五、思考题1. 当goal=0.01和goal=0.0001的时候，给出结果图。

神经⽹络学习笔记2-多层感知机，激活函数1多层感知机
定义：多层感知机是在单层神经⽹络上引⼊⼀个或多个隐藏层，即输⼊层，隐藏层，输出层
2多层感知机的激活函数：
如果没有激活函数，多层感知机会退化成单层
多层感知机的公式： 隐藏层 H=XW h+b h
输出层 O=HW0+b0=(XW h+b h)W0+b0=XW h W0+b0W0+b0
其中XW h W0相当于W，b0W0+b0相当于b，即WX+b的形式，与单层的同为⼀次函数，因此重新成为了单层
3激活函数的作⽤
（1）让多层感知机成为了真正的多层感知机，否则等于⼀层的感知机
（2）引⼊⾮线性，使⽹络逼近了任意的⾮线性函数,弥补了之前单层的缺陷
4激活函数的特质
(1) 连续可导（允许少数点不可导），便于数值优化的⽅法学习⽹络参数
(2）激活函数尽可能简单，提⾼计算效率
(3）激活函数的导函数的导函数的值域要在合适的区间，否则影响训练的稳定和效率
5 常见的激活函数
1 sigmod型
常见于早期的神经⽹络，RNN和⼆分类项⽬，值域处于0到1，可以⽤来输出⼆分类的概率
弊端:处于饱和区的函数⽆法再更新梯度，向前传播困难
2 tahn（双曲正切）
3 ReLu（修正线性单元）
最常⽤的神经⽹络激活函数，不存在饱和区，虽然再z=0上不可导，但不违背激活函数的特质（允许在少数点上不可导），⼴泛运⽤于卷积⽹络等。

人工神经网络实验报告
本实验旨在探索人工神经网络在模式识别和分类任务中的应用效果。

实验设置包括构建神经网络模型、数据预处理、训练网络以及评估网
络性能等步骤。

首先，我们选择了一个经典的手写数字识别任务作为实验对象。

该
数据集包含了大量手写数字的灰度图片，我们的目标是通过构建人工
神经网络模型来实现对这些数字的自动识别。

数据预处理阶段包括了对输入特征的标准化处理、数据集的划分以
及对标签的独热编码等操作。

通过对原始数据进行预处理，可以更好
地训练神经网络模型，提高模型的泛化能力。

接着，我们构建了一个多层感知机神经网络模型，包括输入层、隐
藏层和输出层。

通过选择合适的激活函数、损失函数以及优化算法，
我们逐步训练网络，并不断调整模型参数，使得模型在训练集上达到
较高的准确率。

在模型训练完成后，我们对网络性能进行了评估。

通过在测试集上
进行预测，计算模型的准确率、精确率、召回率以及F1-score等指标，来全面评估人工神经网络在手写数字识别任务上的表现。

实验结果表明，我们构建的人工神经网络模型在手写数字识别任务
中表现出色，准确率高达95%以上，具有较高的识别准确性和泛化能力。

这进一步验证了人工神经网络在模式识别任务中的强大潜力，展
示了其在实际应用中的广阔前景。

总之，本次实验通过人工神经网络的构建和训练，成功实现了对手写数字的自动识别，为人工智能技术在图像识别领域的应用提供了有力支持。

希望通过本实验的研究，可以进一步推动人工神经网络技术的发展，为实现人工智能的智能化应用做出更大的贡献。

deeplearning tutorial (2) 原理简介+代码详解【原创实用版】目录一、Deep Learning 简介二、Deep Learning 原理1.神经网络2.梯度下降3.反向传播三、Deep Learning 模型1.卷积神经网络（CNN）2.循环神经网络（RNN）3.生成对抗网络（GAN）四、Deep Learning 应用实例五、Deep Learning 代码详解1.TensorFlow 安装与使用2.神经网络构建与训练3.卷积神经网络（CNN）实例4.循环神经网络（RNN）实例5.生成对抗网络（GAN）实例正文一、Deep Learning 简介Deep Learning 是一种机器学习方法，其主要目标是让计算机模仿人脑的工作方式，通过多层次的抽象表示来理解和处理复杂的数据。

Deep Learning 在图像识别、语音识别、自然语言处理等领域取得了显著的成果，成为当前人工智能领域的研究热点。

二、Deep Learning 原理1.神经网络神经网络是 Deep Learning 的基本构成单元，它由多个神经元组成，每个神经元接收一组输入信号，根据权重和偏置计算输出信号，并将输出信号传递给其他神经元。

神经网络通过不断调整权重和偏置，使得模型能够逐渐逼近目标函数。

2.梯度下降梯度下降是一种优化算法，用于求解神经网络的权重和偏置。

梯度下降算法通过计算目标函数关于权重和偏置的梯度，不断更新权重和偏置，使得模型的预测误差逐渐减小。

3.反向传播反向传播是神经网络中计算梯度的一种方法。

在训练过程中，神经网络根据实际输出和预期输出的误差，按照梯度下降算法计算梯度，然后沿着梯度反向更新权重和偏置，使得模型的预测误差逐渐减小。

三、Deep Learning 模型1.卷积神经网络（CNN）卷积神经网络是一种特殊的神经网络，广泛应用于图像识别领域。

CNN 通过卷积层、池化层和全连接层等操作，对图像进行特征提取和分类，取得了在图像识别领域的突破性成果。

MATLAB神经⽹络（2）BP神经⽹络的⾮线性系统建模——⾮线性函数拟合2.1 案例背景在⼯程应⽤中经常会遇到⼀些复杂的⾮线性系统，这些系统状态⽅程复杂，难以⽤数学⽅法准确建模。

在这种情况下，可以建⽴BP神经⽹络表达这些⾮线性系统。

该⽅法把未知系统看成是⼀个⿊箱，⾸先⽤系统输⼊输出数据训练BP神经⽹络，使⽹络能够表达该未知函数，然后⽤训练好的BP神经⽹络预测系统输出。

本章拟合的⾮线性函数为y=x12+x22该函数的图形如下图所⽰。

t=-5:0.1:5;[x1,x2] =meshgrid(t);y=x1.^2+x2.^2;surfc(x1,x2,y);shading interpxlabel('x1');ylabel('x2');zlabel('y');title('⾮线性函数');2.2 模型建⽴神经⽹络结构：2-5-1从⾮线性函数中随机得到2000组输⼊输出数据，从中随机选择1900 组作为训练数据，⽤于⽹络训练，100组作为测试数据，⽤于测试⽹络的拟合性能。

2.3 MATLAB实现2.3.1 BP神经⽹络⼯具箱函数newffBP神经⽹络参数设置函数。

net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)P：输⼊数据矩阵；T：输出数据矩阵；S：隐含层节点数；TF：结点传递函数。

包括硬限幅传递函数hardlim、对称硬限幅传递函数hardlims、线性传递函数purelin、正切型传递函数tansig、对数型传递函数logsig；x=-5:0.1:5;subplot(2,6,[2,3]);y=hardlim(x);plot(x,y,'LineWidth',1.5);title('hardlim');subplot(2,6,[4,5]);y=hardlims(x);plot(x,y,'LineWidth',1.5);title('hardlims');subplot(2,6,[7,8]);y=purelin(x);plot(x,y,'LineWidth',1.5);title('purelin');subplot(2,6,[9,10]);y=tansig(x);plot(x,y,'LineWidth',1.5);title('tansig');subplot(2,6,[11,12]);y=logsig(x);plot(x,y,'LineWidth',1.5);title('logsig');BTF：训练函数。

卷积神经⽹络学习——第⼆部分：卷积神经⽹络训练的基本流程卷积神经⽹络学习——第⼆部分：卷积神经⽹络训练的基本流程import torchimport torchvisionimport torch.nn as nnimport torch.optim as optimimport torch.nn.functional as Ffrom torch.autograd import Variablefrom torchvision import datasets, transforms# 步骤⼀：数据载⼊# pose()将各种预处理操作组合到⼀起# 2.transforms.ToTensor()将图⽚转换成 PyTorch 中处理的对象 Tensor.在转化的过程中 PyTorch ⾃动将图⽚标准化了，也就是说Tensor的范⽤是(0,1)之间# 3.transforms.Normalize()要传⼊两个参数:均值、⽅差，做的处理就是减均值，再除以⽅差。

将图⽚转化到了(-1,1)之间# 4.注意因为图⽚是灰度图，所以只有⼀个通道，如果是彩⾊图⽚，有三个通道，transforms.Normalize([a,b,c],[d,e,f])来表⽰每个通道对应的均值和⽅差。

data_tf = pose([transforms.ToTensor(),transforms.Normalize([0.5],[0.5])])# PyTorch 的内置函数 torchvision.datasets.MNIST 导⼊数据集# 这⾥存储的还是MNIST数据集的格式，但是不⼀样的是这个数据集当中的元素是以tensor格式存储的train_dataset = datasets.MNIST(root = '/Users/air/Desktop/【2020秋】数据科学基础/第三次作业',train = True,transform = data_tf,download = True)test_dataset = datasets.MNIST(root = '/Users/air/Desktop/【2020秋】数据科学基础/第三次作业',train = False,transform = data_tf)# 定义超参数BATCH_SIZE = 128 # 训练的包的⼤⼩，通过将训练包分为2的倍数以加快训练过程的⽅式LR = 1e-2 # 学习率，学习率太⼩会减慢训练效果，学习率太⾼会导致准确率降低EPOCHS = 5 # 定义循环次数，避免因为次数太多导致时间过长# torch.utils.data.DataLoader 建⽴⼀个数据迭代器，传⼊数据集和 batch size, 通过 shuffle=True 来表⽰每次迭代数据的时候是否将数据打乱。

一、介绍bert-vits2模型bert-vits2是一种基于Transformer架构的预训练模型，它通过自监督学习和大规模语料库的训练，可以提取句子和文档中的语义信息。

该模型在自然语言处理领域有着广泛的应用，包括文本分类、情感分析、机器翻译等任务。

本文将重点介绍bert-vits2的训练参数，以便进一步理解其内部结构和工作原理。

二、bert-vits2的训练参数概述1. 模型架构：bert-vits2采用Transformer架构，包括多层的编码器和解码器。

编码器用于将输入的文本数据转换成隐含表示，解码器则用于生成输出的文本数据。

每个编码器和解码器由多个Transformer 模块组成，每个Transformer模块包括多头自注意力机制和前馈神经网络。

整个模型的参数包括编码器和解码器的权重矩阵、偏置项等。

2. 学习率：学习率是训练过程中一个重要的超参数，它决定了模型参数在每次迭代中的更新步长。

在bert-vits2的训练中，学习率通常设置为一个较小的值，以便保证模型在训练过程中能够收敛到一个较好的局部最优解。

3. 批大小：批大小是指每次训练时所使用的样本数量。

在bert-vits2的训练中，通常会选择一个适当的批大小，以便在限制计算资源的情况下提高训练效率。

4. 正则化参数：为了防止模型过拟合训练数据，bert-vits2中通常会使用正则化技术，如L2正则化等。

正则化参数可以控制正则项在总损失函数中的权重，从而平衡模型的拟合和泛化能力。

5. 优化器：优化器是用于更新模型参数的算法，bert-vits2常用的优化器包括Adam、SGD等。

优化器的选择和参数设置会直接影响模型的训练速度和性能。

三、bert-vits2的训练参数调优1. 学习率调度：在bert-vits2的训练中，通常会使用学习率调度技术，即在训练过程中逐渐减小学习率。

这样可以在训练初期较大的学习率有助于快速收敛，而在接近最优解时较小的学习率有助于稳定模型。

2-1 分析为什么平方损失函数不适用于分类问题？损失函数是一个非负实数，用来量化模型预测和真实标签之间的差异。

我们一般会用损失函数来进行参数的优化，当构建了不连续离散导数为0的函数时，这对模型不能很好地评估。

直观上，对特定的分类问题，平方差的损失有上限(所有标签都错，损失值是一个有效值)，但交叉熵则可以用整个非负域来反映优化程度的程度。

从本质上看，平方差的意义和交叉熵的意义不一样。

概率理解上，平方损失函数意味着模型的输出是以预测值为均值的高斯分布，损失函数是在这个预测分布下真实值的似然度，softmax 损失意味着真实标签的似然度。

在二分类问题中y = { + 1 , − 1 }在C 分类问题中y = { 1 , 2 , 3 ， ⋅ ⋅ ⋅ ， C }。

可以看出分类问题输出的结果为离散的值。

分类问题中的标签，是没有连续的概念的。

每个标签之间的距离也是没有实际意义的，所以预测值和标签两个向量之间的平方差这个值不能反应分类这个问题的优化程度。

比如分类 1,2,3, 真实分类是1, 而被分类到2和3错误程度应该是一样的,但是明显当我们预测到2的时候是损失函数的值为1/2而预测到3的时候损失函数为2，这里再相同的结果下却给出了不同的值，这对我们优化参数产生了误导。

至于分类问题我们一般采取交叉熵损失函数（Cross-Entropy Loss Function ）来进行评估。

2-2 在线性回归中，如果我们给每个样本()()(,)n n x y 赋予一个权重()n r ，经验风险函数为()()()211()()2N n n T n n R w r y w x ==−∑，计算其最优参数*w ，并分析权重()n r 的作用.答：其实就是求一下最优参数*w ,即导数为0，具体如下：首先，取权重的对角矩阵:()(),,,n P diag r x y w =均以向量(矩阵）表示，则原式为：21()||||2T R P Y X Ω=−Ω ,进行求导：()0T R XP Y X ∂=−−Ω=∂Ω，解得：*1()T XPX XPY −Ω=，相比于没有P 时的Ω：1()T withoutP XX XY −Ω=，可以简单理解为()n r 的存在为每个样本增加了权重，权重大的对最优值ω的影响也更大。

《计算智能与智能系统》课程实验实验题目：神经网络数值实验实验一、利用感知器进行分类输入代码：%画输入向量的图像P = [-0.5 -0.5 +0.3 -0.1 -4; -0.5 +0.5 -0.5 +1.0 5];T = [1 1 0 0 1];plotpv(P,T); % plotpv函数利用感知器的输入向量和目标向量来画输入向量的图像%建立神经网络net = newp([-40 1;-1 50],1);hold on%添加神经元的初始化值到分类图linehandle = plotpc(net.IW{1},net.b{1}); % plotpc函数用来画分类线%训练神经网络E = 1; % E为误差net.adaptParam.passes = 3; % 决定在训练过程中重复次数while (sse(E)) % sse函数是用来判定误差E的函数[net,Y,E] = adapt(net,P,T); % 利用输入样本调节神经网netlinehandle = plotpc(net.IW{1},net.b{1},linehandle);% 画出调整以后的分类线drawnow; % 延迟一段时间end%模拟simp = [0.7; 1.2];a = sim(net,p);% 利用模拟函数sim计算出新输入p的神经网络的输出plotpv(p,a);circle = findobj(gca,'type', 'line');set(circle,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;axis([-2 2 -2 2]);输出：实验二、BP神经网络（1）输入代码：%画出非线性函数图像k = 1;p = [-1:.05:1];t = sin(k*pi*p);plot(p,t,'-')title('要逼近的非线性函数');xlabel('时间');ylabel('非线性函数');%未训练网络输出n = 10;net = newff(minmax(p), [n,1], {'tansig''purelin'}, 'trainlm'); % 对于该初始网络，可以应用sim()函数观察网络输出y1 = sim(net,p);% 同时绘制网络输出曲线，并与原函数相比较figure;plot(p,t,'-',p,y1,'--')title('未训练网络的输出结果');xlabel('时间');ylabel('仿真输出－－原函数－');%进行网络训练net.trainParam.epochs = 50;net.trainParam.goal = 0.01;net = train(net,p,t);%进行网络测试y2 = sim(net,p);figure;plot(p,t,'-',p,y1,'--',p,y2,'-.')title('训练后网络的输出结果');xlabel('时间');ylabel('仿真输出');输出：结果分析：从上图可知，没有经过训练的网络，其输出结果模拟效果比较差，经过训练的BP神经网络的模拟效果较好。

人工神经网络原理及仿真实例课程设计1. 概述人工神经网络（Artificial Neural Network，简称ANN）是一种模仿人脑神经元行为的计算模型，可用于模拟人脑信息处理，实现智能化决策。

ANN可以通过对神经元之间的信号传递和处理来学习输入数据的特征，从而进行分类、预测或其他任务。

本课程设计旨在介绍ANN的原理和实际应用，通过对仿真实例的讲解，让学习者能够理解ANN的工作机制，并能独立实现简单的ANN网络，用于解决实际问题。

2. 课程目标通过学习本课程，学习者将能够：1.理解ANN的基本原理和概念。

2.熟悉常用的神经网络模型和训练算法。

3.了解ANN在分类、预测等领域的应用。

4.掌握编写简单ANN模型的能力。

5.能够运用所学知识设计并实现一个ANN应用程序。

3. 课程内容3.1 ANN基本原理及模型介绍1.神经元的结构和作用。

2.神经元之间的连接和信号传递。

3.ANN的结构和类型。

4.ANN的学习过程和训练算法。

3.2 ANN实际应用1.ANN在分类问题中的应用。

2.ANN在预测问题中的应用。

3.ANN在模式识别中的应用。

4.ANN在控制问题中的应用。

3.3 ANN仿真实例讲解1.实例1：手写数字识别。

2.实例2：股票价格预测。

3.实例3：人脸识别。

3.4 课程实践学习者将根据所学内容，设计并实现一个ANN应用程序，可以选择一个自己感兴趣的应用领域，如数据分类、预测或控制等问题，将所学知识应用到实际中。

4. 评估方式学习者将需要提交实现的ANN应用程序，并进行演示和论文撰写。

评估方式如下：1.代码实现质量（30%）：包括代码风格、可读性、可维护性等。

2.功能实现情况（30%）：包括是否实现了所选应用的基本功能要求。

3.演示效果（20%）：包括演示过程中的稳定性和结果准确性。

4.论文质量（20%）：包括对所学知识的理解和运用、论文结构和语言表达等。

5. 参考资料1.Michael A. Nielsen.。

神经调节生物课教案：学习神经网络的构成和功能2学习神经网络的构成和功能神经网络是模拟人类大脑的计算模型，具有处理各种信息的能力，可以用于图像识别、语音识别、自然语言处理等多个领域。

在这门课程中，我们将学习神经网络的构成和基本原理，了解神经网络的基本功能和应用，同时通过实践，掌握神经网络的基本设计和训练方法。

一、神经元和神经网络神经元是神经网络的基本组成部分，它具有接受和传递信息的功能。

神经元由细胞体、树突和轴突组成。

树突是接收信息的结构，轴突是传递信息的结构。

神经元的工作原理是：当树突收到足够的刺激时，就会产生电信号，这个电信号会经过轴突传递给其他神经元。

神经网络是由神经元相互连接构成的。

神经元之间的连接形成了神经网络的拓扑结构。

神经网络的拓扑结构包括前馈神经网络、反馈神经网络和自组织神经网络等多种结构。

神经网络的拓扑结构和神经元的连接方式决定了神经网络的功能和性能。

二、神经网络的基本功能1.分类和识别：神经网络可以将输入的数据进行分类和识别，例如图像识别、语音识别、文字识别等等。

2.预测和回归：神经网络可以根据历史数据预测未来的趋势和结果，例如股价预测、房价预测、气温预测等等。

3.控制和优化：神经网络可以根据输入的信号进行控制和优化，例如工业控制、自动驾驶、控制等等。

三、神经网络的基本设计和训练方法1.神经网络的结构设计：神经网络的结构由输入层、隐藏层和输出层组成。

输入层用来接收输入的数据，输出层用来输出最终的结果，隐藏层用来处理输入数据，提取特征等。

2.神经网络的参数调整：神经网络的参数调整包括激活函数的选择、权重和偏置的初始化、损失函数的选择等等。

3.神经网络的训练方法：神经网络的训练方法包括前向传播、反向传播和梯度下降等。

前向传播是指输入数据经过神经网络得到输出结果的过程，反向传播是指通过误差反向传播调整神经网络参数的过程，梯度下降是指通过求解损失函数的梯度来调整神经网络参数的过程。

四、实践操作1.神经网络的模型训练：将手写数字数据集导入到神经网络中，通过模型训练和调整，使得神经网络能够准确地识别手写数字。