当前位置：文档之家 › 奇函数与偶函数的傅里叶级数解读

奇函数与偶函数的傅里叶级数解读

  • 格式：ppt
  • 大小：252.00 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

正弦级数和余弦级数(3)

正弦级数和余弦级数(3)
解：求正弦级数，应对 f (x) 作奇式延拓，此时
an 0(n 0,1,2,) ，
bn
2
0
f
(x)sin nxdx 2
(x1)sin nxdx
0
2[
xcosnx n
sin nx n2
cos nx ] n
0
2 (1cosncosn) n
2 2,n 1,3,5,, n 2, n 2,4,6,.
[0,] 上，便得 f (x) 的余弦级数展开式，其中
a
n
2
F (x)cosnxdx 2
0
0
f (x)cosnxdx(n 0,1,2,3,) ，
bn 0(n 1,2,3,) .
6
注例：2具．体将计函算数anf (和x)bn x时1，（只0 用x 到 f）(x分)c别os展nx开和成f正(x弦)s级in n数x 在和[0,余]弦上级的数积。分，故不必写出延拓函数F (x) 。
傅里叶级数。
解：∵u(t) 是周期为 2 的偶函数，
∴bn 0(n 1,2,) 。
而 an
2
u(t
)c
osntdt
2
0
E s in
t
cosntdt
0
2
E
0 [sin(n
1 2
)t
sin(n
1 2
)t]dt
E
[
cos(n
1 2
)t
c
os(n
1 )t 2
]
E
[
1
1
]
n 1
n1 0 n1 n1
6.4.3 正弦级数和余弦级数
一、奇函数和偶函数的傅里叶级数
定理 设 f (x) 是周期为 2 的函数，在一个周期上可积，则

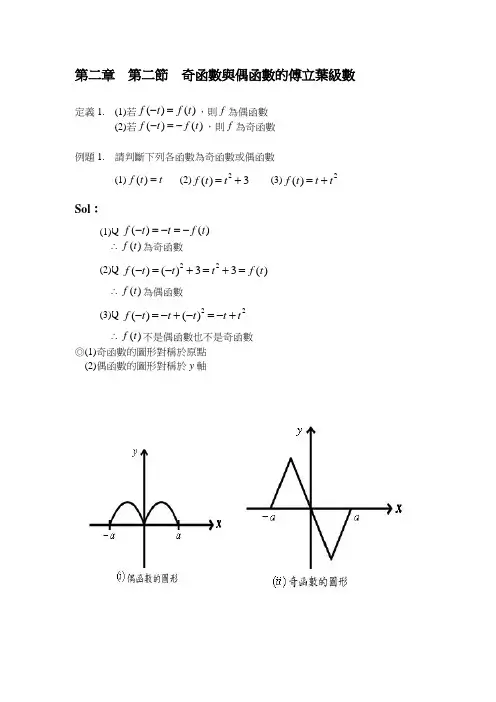
奇函数与偶函数的傅立叶级数解读

奇函数与偶函数的傅立叶级数解读

第二章 第二節 奇函數與偶函數的傅立葉級數定義1. (1)若()()f t f t -=，則f 為偶函數(2)若()()f t f t -=-，則f 為奇函數例題1. 請判斷下列各函數為奇函數或偶函數(1)()f t t = (2)2()3f t t =+ (3)2()f t t t =+Sol ：(1)()()f t t f t -=-=-∴()f t 為奇函數 (2)22()()33()f t t t f t -=-+=+=∴()f t 為偶函數 (3)22()()f t t t t t -=-+-=-+∴()f t 不是偶函數也不是奇函數◎(1)奇函數的圖形對稱於原點(2)偶函數的圖形對稱於y 軸定理1. (1)若f 為偶函數，則()2()lllf t dt f t dt -=⎰⎰(2)若f 為奇函數，則()0llf t d t -=⎰定義2. (奇函數的傅立葉級數)若週期函數f 為奇函數，則f 的傅立葉級數(又稱為傅立葉正弦級數)為1()s i n nn n t f t b l π∞==∑ 其中 02()s i n l n n tb f t dt l lπ=⎰定義3. (偶函數的傅立葉級數)若週期函數f 為偶函數，則f 的傅立葉級數(又稱為傅立葉餘弦級數)為011()c o s 2n n n tf t a a l π∞==+∑其中 002()la f t dt l =⎰02()c o s l n n ta f t dt l lπ=⎰例題2. 將函數3,50()3,05t f t t --<<⎧=⎨<<⎩展開成傅立葉級數Sol ：()f t 為奇函數00,0n a a ⇒==02()s i n l n n t b f t dt l l π=⎰55002653s i n (c o s )5555n t n tdt n πππ-==⎰ 6(c o s 1)n n ππ-=-12,1,3,5,0,2,4,6,n n n π⎧=⎪=⎨⎪=⎩∴()f t 的傅立葉(正弦)級數為 121315(s i n s i n s i n )53555t t t ππππ+++例題3. 將函數()f t t = (t ππ-≤≤) 展開成傅立葉級數Sol ：()f t 為偶函數0n b ⇒=200222()2t a f t dt tdt ππππππ===⨯⎰⎰21(0)πππ=-=n a =2π()c o s f t n t dt π⎰2c o s t n td t ππ=⎰(利用分部積分法)00211s i n s i n t n t n t d t n n πππ⎡⎤=-⎢⎥⎣⎦⎰ 02211(s i n 0)c o s n t nnππππ⎡⎤=-+⎢⎥⎣⎦2210(cos 1)n n ππ⎡⎤=+-⎢⎥⎣⎦20,2,4,6,4,1,3,5,n n n π=⎧⎪=⎨-=⎪⎩∴()f t 的傅立葉(餘弦)級數為 224cos3cos5(cos )235t tt t ππ=-+++◎底下的兩個例題是將原來並非奇、偶函數的函數經過平移後，變成奇、偶函數，再求解的例子例題4. 試求週期為2π之週期函數()f t 的傅立葉級數,0(),0t f t t πππ-<<⎧=⎨<<⎩Sol ：上面第一個圖形為函數()f t 的圖形，其既不是偶函數也不是奇函數，但如果將f 平移，即令1()()2f t f t π=-得1f 的圖形如上面第二個圖形⇒1f 為一奇函數1()f t ∴的傅立葉級數為11()sin n n f t b nt ∞==∑1022()sin ()sin 2n b f t n dt n dt ππππππππ==-⎰⎰02s i n 2n d t ππππ=⎰011cos (cos 1)nt n n nππ--==- 0,2,4,6,2,1,3,5,n n n=⎧⎪=⎨=⎪⎩∴11()s i n n n f t b nt ∞==∑=sin3sin52(sin )35t tt +++故1()()2f t f t π=+=2π+sin3sin52(sin )35t tt +++。

余弦级数

余弦级数

二、函数展开成正弦级数或余弦级数
奇延拓与偶延拓： 设函数f(x)定义在区间[0，π]上并且满足收敛定理的条件，我 们在开区间(−π，0)内补充函数f(x)的定义，得到定义在(−π，π]上 的函数F(x)，使它在(−π，π)上成为奇函数(偶函数)．按这种方式 拓广函数定义域的过程称为奇延拓(偶延拓)．限制在(0，π]上， 有F(x) = f(x)．
π
0
π
0
2 π + 2 π ⋅ n , n = 1, 3, 5, ⋅ ⋅ ⋅ , = − 2 , n = 2, 4, 6, ⋅ ⋅ ⋅ . n 函数的正弦级数展开式为 2 π 1 π x+1 = [(π+2)sin x− sin 2π+ (π+2)sin 3− sin 4π+ · · · ] π 3 2 4 (0<x<π)． 在端点x=0及x=π处，级数的和显然为零，它不代表原来函数f(x) 的值．
2
π
π
0
π
0
=
2
π
[−
x sin nx cos nx sin nx π + − ]0 2 n n n
0, n = 2, 4, 6, ⋅ ⋅ ⋅ , 2 = 2 (cos nπ − 1) = 4 nπ − n 2π , n = 1, 3, 5, ⋅ ⋅ ⋅ .
函数的余弦级数展开式为 π 4 1 1 x+1= +1 − (cos x+ 2 cos 3 x + 2 cos 5 x + · · · ) (0≤ x ≤π)． π 2 3 5
例2 将周期函数
1 u(t) =E | sin t | 2
展开成傅里叶级数，其中E是正的常数． 解 所给函数满足收敛定理的条件，它在整个数轴上连续， 因此u(t)的傅里叶级数处处收敛于u(t)． 因为u(t)是周期为2π的偶函数，所以bn =0(n=1, 2, · · ·)，而 4E 4E 2 π (n=0, 1, 2, · · ·)． =− an = ∫ f(t)cos ntdt 2 (4n − 1)π π 0 u(t)的傅里叶级数展开式为 4E 1 1 1 1 u(t) = t− cos 2t− cos 3t− ( − cos π 2 3 15 35 1 cos nt− · · ·) (−∞<t<+∞)． − 2 4n − 1

傅里叶级数

傅里叶级数

傅里叶级数（Fourier Series ）引言正弦函数是一种常见而简单的周期函数，例如描述简谐振动的函数 就是一个以ωπ2为周期的函数。

其中y 表示动点的位置，t 表示时间，A 为振幅，ω为角频率，ϕ为初相。

但在实际问题中，除了正弦函数外，还会遇到非正弦的周期函数，它们反映了较复杂的周期运动，我们也想将这些周期函数展开成由简单的周期函数例如三角函数组成的级数。

具体地说，将周期为)2(ωπ=T 的周期函数用一系列以T 为周期的正弦函数)sin(n n t n A ϕω+组成的级数来表示，记为其中),3,2,1(,,0 =n A A n n ϕ都是常数。

将周期函数按上述方式展开，它的物理意义就是把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加。

在电工学上，这种展开称为谐波分析。

其中常数项0A 称为)(t f 的直流分量；)sin(11ϕω+t A 称为一次谐波（又叫做基波）；而)2sin(22ϕω+t A ， )3sin(33ϕω+t A 依次称为二次谐波，三次谐波，等等。

为了下面讨论方便起见，我们将正弦函数)sin(n n t n A ϕω+按三角公式变形，得 t n A t n A t n A n n n n n n ωϕωϕϕωsin cos cos sin )sin(+=+， 令x t A b A a A a n n n n n n ====ωϕϕ,cos ,sin ,200，则上式等号右端的级数就可以改写成这个式子就称为周期函数的傅里叶级数。

1.函数能展开成傅里叶级数的条件（1） 函数)(x f 须为周期函数；（2） 在一个周期内连续或只有有限个第一类间断点；（如果0x 是函数)(x f 的间断点，但左极限)0(0-x f 及右极限)0(0+x f 都存在，那么0x 称为函数)(x f 的第一类间断点）（3） 在一个周期内至多只有有限个极值点。

若满足以上条件则)(x f 能展开成傅里叶级数，且其傅里叶级数是收敛的，当x 是)(x f 的连续点时，级数收敛于)(x f ，当x 是)(x f 的间断点时，级数收敛于)]0()0([21++-x f x f 。

奇函数与偶函数的傅里叶级数-精品文档

奇函数与偶函数的傅里叶级数-精品文档

2 2 a f ( x ) d x ( x ) d x , 0 0 0
b 0( n 1 , 2 , 3 , ) . n
又因为 f(x) 处处连续 ， 故所求的傅里叶级数收敛
于 f(x)， 即
4 1 1 f ( x ) (cos x 2cos 3 x 2cos 5 x ) 2 3 5 ( x ) .

0
0
( 因在 [0 , ] 上， (x) = f(x) ). 周期偶延拓的结果为余弦级数，其傅里叶系 数公式为
(12 .6.8) b 0 ( n 1 , 2 , ) n 2 2 a ( x ) cos nx d x f ( x ) cos nx d x n 0 0
而奇函数在对称区间上的积分为零 ， 所以 1 a f ( x )cos nx d x 0 ( n 0 , 1 , 2 , ) . n 又因 f(x)sinnx 在区间 () 内是偶函数 ，
故有
2 b f ( x ) sin nx d x( n 1 , 2 , 3 , ) . n 0
2 a ( x )cos nx d x n f 0
2 ( x )cos nx d x 0 2 x 2 [ si nx ] n si nx n d x ( n 0 ) 0 0 n n
4 1 ,3 ,5 , , 2 2 , n n 2 [ 1 ( 1 )] n n 2 , 4 , 6 , . 0 , n
( n 1,2, )

上 展开 成 余弦 级 数
x x 数 ( x ) 在区 [ 0 , 间 例 5 试将函 f 4 2

高数：正弦级数和余弦级数

高数：正弦级数和余弦级数
∞
练习题答案
( 1) n+1 2 nπ + 2 sin ] sin nx . 一, f ( x ) = ∑ [ n nπ 2 n =1 ( x ≠ ( 2n + 1) π, n = 0, ±1, ±2,)
∞
4 2 π2 2 二, f ( x ) = ∑ [( 1) n ( 3 ) 3 ] sin nx n n n π (0 ≤ x < π) ;
( ∞ < t < +∞)
二,函数展开成正弦级数或余弦级数
非周期函数的周期性开拓
设f ( x )定义在[0, π]上, 延拓成以2π为周期的 函数 F ( x ).
f ( x ) 0 ≤ x ≤ π 且F ( x + 2π ) = F ( x ), , 令 F ( x) = g( x ) π < x < 0
同理可证(2) 同理可证 定理证毕. 定理证毕
∞ n =1
定义 如果 f ( x ) 为奇函数,傅氏级数 ∑ bn sin nx 为奇函数,
称为正弦级数. 称为正弦级数. 正弦级数
a0 ∞ 为偶函数, 如果 f ( x ) 为偶函数, 傅氏级数 + ∑ a n cos nx 2 n =1
称为余弦级数. 称为余弦级数. 余弦级数
证明
(1) 设f ( x )是奇函数 ,
1 π a n = ∫ π f ( x ) cos nxdx = 0 π 奇函数
( n = 0,1,2,3,)
1 π 2 π bn = ∫ π f ( x ) sin nxdx = ∫0 f ( x ) sin nxdx π π 偶函数 ( n = 1,2,3,)
b.在[0, π ]上, 展成周期为2π的傅氏级数唯一;

傅里叶级数和函数

傅里叶级数和函数

傅里叶级数和函数傅里叶级数和函数是数学中重要的概念，广泛应用于物理、工程、计算机科学等领域。

本文将介绍傅里叶级数和函数的概念、性质、应用，并给出相关实例，以帮助读者更加深入理解。

一、傅里叶级数的概念傅里叶级数指的是将一个周期函数表示为一系列正弦余弦函数的线性组合。

具体而言，设f(x)为定义在区间[-L,L]上的周期函数，则其傅里叶级数为：f(x) = a0/2 + ∑[an*cos(nπx/L) + bn*sin(nπx/L)]其中，a0,a1,a2,...,an,b1,b2,...,bn为一系列常数，又称为傅里叶系数，多项式∑成为称为傅里叶级数。

二、傅里叶函数的概念傅里叶函数指的是由傅里叶级数展开得到的一系列正弦余弦函数。

具体而言，傅里叶函数包括正弦函数、余弦函数、复指数函数等。

三、傅里叶级数和函数的性质傅里叶级数和函数具有以下性质：1. 傅里叶级数是周期为2L的函数。

2. 傅里叶级数及其导数在周期内可积。

3. 傅里叶级数对应的傅里叶函数构成一组完备正交基。

4. 对于周期函数f(x)，其傅里叶级数和函数的系数可以使用奇偶性、对称性、平移性等方式求得。

四、傅里叶级数和函数的应用傅里叶级数和函数在物理、工程、计算机科学等领域有广泛应用，例如：1. 信号分析和处理：傅里叶级数可以将不同频率的信号进行分解，而傅里叶函数可用于频域滤波和信号重构。

2. 图像处理和压缩：傅里叶变换可将图片分解为不同频率的正弦余弦函数，从而实现图片压缩和去噪等操作。

3. 物理学中的波动和振动：声波、电磁波、机械波等可以被表示为傅里叶级数和函数的组合。

五、实例以信号处理为例，假设有一个周期为T的方波信号，其傅里叶级数为：f(x) = 4/π * ∑[1/(2n-1)*sin(2π(2n-1)x/T)]则该信号的傅里叶级数系数为an = 4/(π(2n-1))，bn = 0。

其对应的傅里叶函数为：f(x) = 4/π * [sin(2πx/T) + 1/3*sin(6πx/T) +1/5*sin(10πx/T) + ...]通过傅里叶级数可以得到该方波信号的频域表示，即不同频率正弦函数在信号中的占比，从而可以用于滤波、降噪等信号处理操作。

01-偶函数与奇函数的傅里叶级数

01-偶函数与奇函数的傅里叶级数

于是偶函数 f 的傅里叶级数只含余弦函数的项, 即
f ( x) a0 2
n1
an
cos
nπx l
,
(7)
其中 an 如 (6) 式所示. (7) 式右边的级数称为余弦级数.
同理, 若 f 是以 2l 为周期的奇函数, 或是定义在 [l, l] 上的奇函数, 类似可得
数学分析 第十五章 傅里叶级数
f
(x)
a0 2
n1
an
cos nx,
(10)
其中
an
2 π
π
f ( x)cos nxdx,
0
n 0,1,2,.
(11)
当 f 为奇函数时, 则它展成的正弦级数为
f ( x) bn sin nx,
(12)
其中
n1
b 2 π f ( x)sin nx dx, n 0,1,2,.
n π0
§2 以2l为周期的函数的展开式 以2l为周期的函数的傅里叶级数 偶函数与奇函数的傅里叶级数
第六讲 偶函数与奇函数 的傅里叶级数
数学分析 第十五章 傅里叶级数
高等教育出版社
§2 以2l为周期的函数的展开式 以2l为周期的函数的傅里叶级数 偶函数与奇函数的傅里叶级数
偶函数与奇函数的傅里叶级数
设 f 是以 2l 为周期的偶函数, 或是定义在[l, l] 上 的偶函数, 则在[l, l] 上, f ( x)cos nx 是偶函数, f ( x)sin nx是奇函数. 因此, f 的傅里叶系数(4)是
高等教育出版社
§2 以2l为周期的函数的展开式 以2l为周期的函数的傅里叶级数 偶函数与奇函数的傅里叶级数
an
1 l
bn
2 l

傅里叶级数基础知识

傅里叶级数基础知识

傅里叶级数基础知识傅里叶级数是数学中的一个重要概念，它在信号处理、图像处理、物理学等领域有着广泛的应用。

本文将介绍傅里叶级数的基础知识，包括傅里叶级数的定义、性质以及应用。

一、傅里叶级数的定义傅里叶级数是一种将周期函数表示为正弦函数和余弦函数的无穷级数的方法。

对于一个周期为T的函数f(t)，它可以表示为以下形式的级数：f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中，a0、an、bn是系数，ω是角频率，n是正整数。

二、傅里叶级数的性质1. 周期函数的傅里叶级数是收敛的，即级数的和可以无限接近于原函数。

2. 傅里叶级数是唯一的，即给定一个周期函数，它的傅里叶级数是唯一确定的。

3. 傅里叶级数具有线性性质，即两个周期函数的线性组合的傅里叶级数等于它们各自的傅里叶级数的线性组合。

4. 傅里叶级数的系数可以通过积分计算得到，具体的计算公式为：an = (2/T) * ∫[0,T] f(t)*cos(nωt) dtbn = (2/T) * ∫[0,T] f(t)*sin(nωt) dt三、傅里叶级数的应用1. 信号处理：傅里叶级数可以将一个信号分解为不同频率的正弦波的叠加，从而实现信号的频域分析和滤波处理。

2. 图像处理：傅里叶级数可以将一个图像分解为不同频率的正弦波的叠加，从而实现图像的频域滤波和压缩等处理。

3. 物理学：傅里叶级数在物理学中有着广泛的应用，例如在波动现象、振动现象、电磁场等方面的研究中都可以使用傅里叶级数进行分析和计算。

四、总结傅里叶级数是一种将周期函数表示为正弦函数和余弦函数的无穷级数的方法。

它具有收敛性、唯一性和线性性质等基本性质，可以通过积分计算得到系数。

傅里叶级数在信号处理、图像处理、物理学等领域有着广泛的应用。

通过傅里叶级数的分析和计算，我们可以更好地理解和处理周期函数的特性，从而在实际应用中发挥作用。

以上就是傅里叶级数的基础知识的介绍。

希望本文能够帮助读者对傅里叶级数有一个初步的了解，并对其在实际应用中的重要性有所认识。

5-1傅里叶级数

5-1傅里叶级数

第五章 傅里叶变换
教学内容： 傅里叶变换公式、性质以及计算方法和应用。 要求： 理解傅里叶积分与傅里叶变换以及复数形式的傅 里叶变换。掌握非周期函数的傅里叶变换。理解 δ 函数的含义、性质以及在物理中的应用。
傅里叶生平
1768年生于法国 1807年提出“任何周期信 号都可用正弦函数的级数 表示” 1822年发表“热的分析理 论”，首次提出“任何非 周期信号都可用正弦函数 的积分表示”
2 l n n 2
将[]2展开，逐项积分，得
n n l l 1 2 2 2 2 2 [ f ( x)] dx 2la0 lak lbk 2a0 f ( x)dx l 2l l k 1 k 1
2 a k
k 1
n
l
l
n l kx kx f ( x) cos dx 2 bk f ( x) sin dx 0 l l l k 1
§5.1 傅里叶级数
一、傅里叶级数 对周期为2l的函数f(x)=f(x+2l)，可取三角函数族
2x kx 1 ， cos ， cos ， ... ， cos ， ... l l l x 2x kx sin ， sin ， ... ， sin ， ... l l l
x
( 1)
作为基本函数族，将f(x)展开成级数
f ( 0) f ( 0) 0 2 2 2
在连续点 x (2k 1) 处收敛于f(x)。
傅里叶系数计算：
1 a0 2 1 2
f ( x)dx


ak
2 0
f ( x) cos kxdx

1

1 x xdx 2 2

whx奇函数和偶函数的傅里叶级数

whx奇函数和偶函数的傅里叶级数
b.在[0, π ]上, 展成周期为2π的傅氏级数唯一;
c .在[− π, π]上连续且只有有限个极 值点时, 级数处处收敛于f ( x ).
思考题
设f ( x )是在[a, b]上定义的函数 , 应如何选择
A, B, 才能使 F ( t ) = f ( At + B )成为[ − π, π]上
定义的函数 .
(0 ≤ x ≤ π )
π 4 1 1 1 x + 1 = + 1 − (cos x + 2 cos 3 x + 2 cos 5 x + 2 cos 7 x ) π 2 3 5 7
y = x +1
三、小结
1、基本内容: 奇函数和偶函数的傅氏系数;正弦级数与余 弦级数;非周期函数的周期性延拓; 2、需澄清的几个问题.(误认为以下三情况正确) a.只有周期函数才能展成傅氏级数;
u( t )为偶函数 , ∴ bn = 0,
( n = 1,2,)
− 2π
−π
u( t )
E
0
π
2π
t
a0 =
2
π
∫0
π
2 π 4E u( t )dt = ∫0 E sin tdt = , π π
2 π 2 π a n = ∫0 u( t ) cos ntdt = ∫0 E sin t cos ntdt π π E π = ∫ [sin( n + 1)t − sin( n − 1)t ]dt
同理可证(2) 定理证毕.
∞ n =1
定义 如果 f ( x ) 为奇函数,傅氏级数 ∑ bn sin nx
称为正弦级数.
a0 ∞ 如果 f ( x ) 为偶函数, 傅氏级数 + ∑ a n cos nx 2 n =1

奇、偶函数的傅里叶级数

奇、偶函数的傅里叶级数

an cos nx n1
称为余弦级数.
奇、偶函数的傅里叶级 数
例 1 将函数 f ( x) x在（- , ] 展开为傅里叶级数.
解：函数f (x) x在( , ]是奇函数，
an =0
n 0,1, 2
bn
1
f ( x)sin nxdx
2
0
x sin nxdx
(1)n1
2 n
x
当x
n1
bn
sin nx
2(sin
x
sin 2x 2
时，傅里叶级数收敛于
sin 3x
3
)
x
f ( 0) f ( 0) 0
2
2
奇、偶函数的傅里叶级数
例2、将函数f ( x) x2在[ , ]展成傅里叶级数.
解：函数f ( x) x2在[ , ]是偶函数，
2
a0
x2dx
奇、偶函数的傅里叶级数
n1
( 2
1
8 )sin x 2
2
sin 2x ( 2
3
8 33
)
sin
3
x
当x 时，傅里叶级数收敛于
0 x
f ( 0) f ( 0) 2 2 0
2
2
奇、偶函数的傅里叶级数
按偶式展开，延拓的偶函数
x2, 0 x
f
(
x)
x
2
,
x 0
即f ( x) x2 , x [ , ]
)
x
奇、偶函数的傅里叶级数
将函数在[0, ]展成傅里叶级数：
（1）按奇式展开：将函数在[- , ]延拓为奇函数
an =0
n 0,1, 2

常用傅里叶级数公式总结

常用傅里叶级数公式总结

常用傅里叶级数公式总结傅里叶级数是一种非常重要的数学工具，可以将周期函数分解为一系列正弦和余弦函数的和，从而方便进行分析和计算。

在信号处理、图像处理、物理学等领域都有广泛的应用。

本文将以常用傅里叶级数公式为线索，介绍傅里叶级数的基本概念和性质。

1. 傅里叶级数的基本形式任何周期为T的周期函数f(t)，都可以表示为正弦函数和余弦函数的线性组合，即傅里叶级数。

其基本形式为：f(t) = a0 + Σ(an*cos(2πnft) + bn*sin(2πnft))其中，a0为直流分量，an和bn分别为函数f(t)的傅里叶系数，f为基本频率，n为正整数。

2. 傅里叶级数的计算公式傅里叶系数an和bn的计算公式为：an = (2/T) * ∫[0,T] f(t)*cos(2πnft) dtbn = (2/T) * ∫[0,T] f(t)*sin(2πnft) dt这两个公式描述了函数f(t)在频率为nf时的正弦和余弦分量的大小，通过计算这些系数，可以得到傅里叶级数的展开式。

3. 傅里叶级数的性质傅里叶级数具有许多重要的性质，其中包括线性性、偶函数和奇函数的傅里叶级数、周期延拓性等。

这些性质使得傅里叶级数在实际应用中具有广泛的适用性。

4. 傅里叶级数的收敛性对于一个周期为T的周期函数f(t)，其傅里叶级数展开并不一定收敛于原函数f(t)。

在一定条件下，傅里叶级数可以收敛于原函数，这就是傅里叶级数的收敛性问题。

5. 傅里叶级数的频谱分析傅里叶级数可以将一个周期函数表示为不同频率的正弦和余弦函数的叠加，从而可以对信号进行频谱分析。

通过分析不同频率成分的幅值和相位，可以了解信号的频谱特性，对信号进行处理和识别。

6. 傅里叶级数的离散化在数字信号处理中，通常需要对离散信号进行傅里叶变换。

离散傅里叶变换（DFT）和快速傅里叶变换（FFT）是常用的算法，可以高效地计算离散信号的频谱。

7. 傅里叶级数的应用傅里叶级数在信号处理、通信、图像处理、物理学等领域都有广泛的应用。

傅里叶级数的理解

傅里叶级数的理解

傅里叶级数的理解
一、傅里叶级数的定义
傅里叶级数是一种将周期函数表示为无穷级数的方法，它是由法国数学家约瑟夫·傅里叶在19世纪初提出的。

傅里叶级数是将一个周期函数表示为无穷个正弦函数和余弦函数的线性组合，其中每个正弦函数和余弦函数都具有一定的幅度和相位。

二、傅里叶级数的展开
傅里叶级数的展开是将一个周期函数表示为无穷个正弦函数和余弦函数的线性组合的过程。

三、傅里叶级数的三角形式
傅里叶级数的另一种表示形式是三角形式，它将每个正弦和余弦函数合并为一个三角函数形式。

这种形式更加简洁，并且可以更容易地看出函数的对称性和周期性。

四、傅里叶系数的计算
傅里叶系数的计算是傅里叶级数展开的关键步骤，它可以通过对函数的积分来得出。

五、傅里叶级数的收敛性
傅里叶级数是一个无穷级数，因此需要满足一定的条件才能收敛到原函数。

基本函数的傅里叶级数展开公式

基本函数的傅里叶级数展开公式

基本函数的傅里叶级数展开公式傅里叶级数展开公式是一种将周期函数表示为一组正弦和余弦函数的线性组合的方法。

对于基本函数而言，其傅里叶级数展开公式可以表示为：1. 正弦函数对于周期为2π的正弦函数f(x) = sin(x)，其傅里叶级数展开公式为：f(x) = a0/2 + Σ( n=1 to ∞ ) [an sin(nx)]其中a0/2是函数f(x)的平均值，an是函数f(x)的傅里叶系数，它们的计算公式为：a0/2 = (1/π) ∫( -π to π ) f(x) dxan = (1/π) ∫( -π to π ) f(x) sin(nx) dx2. 余弦函数对于周期为2π的余弦函数f(x) = cos(x)，其傅里叶级数展开公式为：f(x) = a0/2 + Σ( n=1 to ∞ ) [bn cos(nx)]其中a0/2是函数f(x)的平均值，bn是函数f(x)的傅里叶系数，它们的计算公式为：a0/2 = (1/π) ∫( -π to π ) f(x) dxbn = (1/π) ∫( -π to π ) f(x) cos(nx) dx3. 偶函数对于周期为2π的偶函数f(x)，其傅里叶级数展开公式只包含余弦函数项，即：f(x) = a0/2 + Σ( n=1 to ∞ ) [an cos(nx)]其中a0/2是函数f(x)的平均值，an是函数f(x)的傅里叶系数，它们的计算公式为：a0/2 = (1/π) ∫( -π to π ) f(x) dxan = (2/π) ∫( 0 to π ) f(x) cos(nx) dx4. 奇函数对于周期为2π的奇函数f(x)，其傅里叶级数展开公式只包含正弦函数项，即：f(x) = Σ( n=1 to ∞ ) [an sin(nx)]其中an是函数f(x)的傅里叶系数，它们的计算公式为：an = (2/π) ∫( 0 to π ) f(x) sin(nx) dx以上就是基本函数的傅里叶级数展开公式的详细解释。

傅里叶级数

傅里叶级数

得信号的傅立叶展开式为： 得信号的傅立叶展开式为：
f (t ) = 1 4 1 1 sin(Ωt ) + sin(3Ωt ) + sin(5Ωt ) + ⋯ + sin( nΩt ) + ⋯, n = 1,3,5,⋯ π 3 5 n
它只含一、 奇次谐波分量。 它只含一、三、五、…奇次谐波分量。
n
因为傅里叶系数 将
an b 和
n
Fn =
1 1 1 An e jϕn = ( An cos ϕ n + jAn sin ϕ n ) = (an + jbn ) 2 2 2
系数公式带入上式得
1 Fn = T
∫
T 2
−T 2
1 f (t ) cos(nΩt )dt − j T
∫
T 2
−T 2
f (t ) sin(nΩt )dt
0, 2 = [1 − cos(nπ )] = 4 nπ nπ ,
n = 2,4,6,⋯ n = 1,3,5,⋯
将系数代入下面的式子： 将系数代入下面的式子：
∞ a0 ∞ f (t ) = + ∑ an cos(nΩt ) + ∑ bn sin( nΩt ) 2 n =1 n =1
某函数是否为奇（或偶）函数不仅与周期函数 某函数是否为奇（或偶）函数不仅与周期函数 的波形有关 而且与时间坐标原点的选择 有关， 时间坐标原点的选择有关 的波形有关，而且与时间坐标原点的选择有关 如下图是三角波的偶函数。 。如下图是三角波的偶函数。 f (t )
T 1 − 2 T 2
0
f (t )
坐标原点左移
∑Aeϕe
n
n

偶函数的傅里叶级数展开式中

偶函数的傅里叶级数展开式中

偶函数的傅里叶级数展开式中
在傅里叶级数展开中，偶函数可以表示为余弦函数的级数。

具
体而言，假设f(x)是一个周期为2π的偶函数，其傅里叶级数展开
式可以表示为：
f(x) = a0/2 + Σ(ancos(nx))。

其中，a0/2是常数项，an是展开系数，n为正整数，cos(nx)
是余弦函数。

展开系数an可以通过计算函数f(x)与余弦函数cos(nx)的内积
来得到。

根据傅里叶级数的正交性质，当n不等于0时，内积为0，即：
an = (2/π) ∫[0,π] (f(x)cos(nx)) dx.
这个积分表示在一个周期内函数f(x)与余弦函数cos(nx)的乘
积在整个周期上的平均值。

对于偶函数来说，由于其关于y轴对称，所以展开系数an中的
正弦函数项为0，只剩余弦函数项。

需要注意的是，傅里叶级数展开式是在一个周期内对函数进行展开，所以展开系数an只描述了函数在一个周期内的特征。

总结起来，偶函数的傅里叶级数展开式中只包含余弦函数项，展开系数an可以通过计算函数与余弦函数的内积得到。

这种展开式可以将偶函数表示为一系列余弦函数的线性组合，从而更好地理解和分析偶函数的性质。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3
.
由于 f ( x)在 (0, 上连续,且延拓的函数在 x = 0，
处连续， 因此
x2
2
1
1
x cos x cos 2x cos 3x
4
6
4
9
(0≤ x ≤ ) .
例6
试将函数
f (x)

x x
,
,
0≤ x ≤
x

2
≤
22
即为 f(x) 在 [0 , ] 上的傅里叶级数， (x) 称为f(x)
的周期延拓函数.
在理论上或实际工作中，下面的周期延拓是 最为常用: 将 f(x) 先延拓到 ( , 0) ，使延拓后 的函数成为奇函数 ，然后再延拓为以 2 为周期 的函数 . 这种延拓称为周期奇延拓;
y
2

bn sinnx .
n1
此时傅氏系数
an 0 (n 0 , 1 , 2, ) .
bn

2

f ( x)sinnxdx
0
(n 1 , 2 , 3 , ) .
这 是 因 为an

1
f ( x)cos nxdx 中 cos nx是 偶

函 数 . 于是在区间 ( ) 内 f(x)cosnx 为奇函数 ，
2

(n 1 , 2, )

( x)cos nxdx

2
0

(12.6.8)

f ( x)cos nxdx
0
(n 1,2, )
例 5 试将函数 f ( x) x2 x 在区间[0, 42
上展开成余弦级数
解 按式 (12.6.8) 计算傅里叶级数，
2 x2
而奇函数在对称区间上的积分为零 ， 所以
1
an
f ( x)cos nxdx 0

(n 0 , 1 , 2, ) .
又因 f(x)sinnx 在区间 () 内是偶函数 ，
故有
2
bn
f ( x)sinnxdx
0
(n 1 , 2 , 3 , ) .
同理可以推出，当函数 f(x) 是偶函数时， 其

2[
n
x
sinnx]0

2 n

sinnx dx
0
(n 0)
4

2 n2
[1

(1)n
]


n2
0
, ,
n 1 , 3 , 5 , , n 2 , 4 , 6 , .
2
2
a0
0
f ( x) dx
( x) dx ,展开Fra bibliotek为余弦级数， 即
a0
2


an
n1
cos nx.
此时傅里叶系数为
an
2
0
f ( x)cos nxdx(n 0 , 1 , 2, ) .
bn 0 (n 1 , 2, 3 , ) .
(12.6.6)
例 4 设周期函数 f (x) 在其一个周期上的表 达式
x , ≤ x 0 ,
0
2
(n 0 , 1 , 2, ) .

( x)sinnxdx

2

0
0
f ( x)sinnxdx
( 因在 [0 , ] 上， (x) = f(x) ).
(12.6.7) (n 1,2, )
周期偶延拓的结果为余弦级数，其傅里叶系
数公式为
bn
an


0
设函数 f(x) 定义在 [0 , ] 上，我们设想有一
个函数 (x)，它是定义在 ( ) 上 且以 2 为 周期的函数，而在 [0 , ] 上， (x) = f(x). 如果 (x) 满足收敛定理的条件，那么 (x) 在 ( )
上就可展开为傅里叶级数， 取其 [0 , ] 上一段，
展开成正弦级数 .
解 按公式(12.6.7)
2
bn
f ( x)sinnxdx
0
2

2
2 f ( x)sinnxdx
0


f ( x)sinnxdx
2
2
2
x sinnxdx

2
0



2
(x

) si nnxdx 2
2

x sinnxdx
8.4 正弦级数与余弦级数
8.4.1、奇函数与偶函数的傅里叶级数 8.4.3 函数 f(x) 在 [0 , ] 上展开为正
弦级数与余弦级数
8.4.1、奇函数与偶函数的傅里叶级数
展开式中只含有正弦函数的傅里叶级数，称为 正弦函数，只含有余弦函数包括常数项的称为余弦 级数.
假设以 2 为周期的周期函数 f(x) 在 [ , ]内 是奇函数，那么傅里叶级数一定是正弦级数. 即
f (x)
x ,
0≤ x .
试将其展开成傅里叶级数 .
解 函数 f (x) 的图形如图所示 ，
f(x)

O

x
由图形的对称性可知 f(x) 是偶函数，因此我们应 根据(12.6.6) 式计算傅里叶系数.
an

2

f ( x)cos nxdx
0
2
( x)cos nxdx 0
an
(
0
4
x)cos nxdx

2 [( n
x2 4


x ) s in nx ]0

2 n2
[(
x 2

)cos
nx
]0

1 n3 [sinnx
]0

1 n2
(n 1 , 2, 3 , ) .
2 x2
2
a0
(
0
4
x)dx
0
bn 0 (n 1 , 2, 3 , ) .
又因为 f(x) 处处连续 ，故所求的傅里叶级数收敛 于 f(x)， 即
f
(x)

2

4
(cos
x

1 32
cos 3x

1 52
cos 5x

)
( x ) .
8.4.3 函数 f(x) 在 [0 , ] 上展开 为正弦级数与余弦级数
2 3
O
x
周期奇延拓
将 f(x) 先延拓到( , 0)，使延拓后的函数为偶函数，
然后再延拓为以 2 为周期的函数，这种延拓称为
周期偶延拓. y
2 O 2 3 x
周期偶延拓
显然，周期奇延拓的结果为正弦级数，其傅
里叶系数按公式 (12.6.5) 计算. 即
an bn
0

sinnxdx
2
2 ( x cosnx 1
n
0n
cosnx dx)
0
1

cosnx
n

2

1
((1)n1
cos