轴向拉(压)杆强度校核(例题)

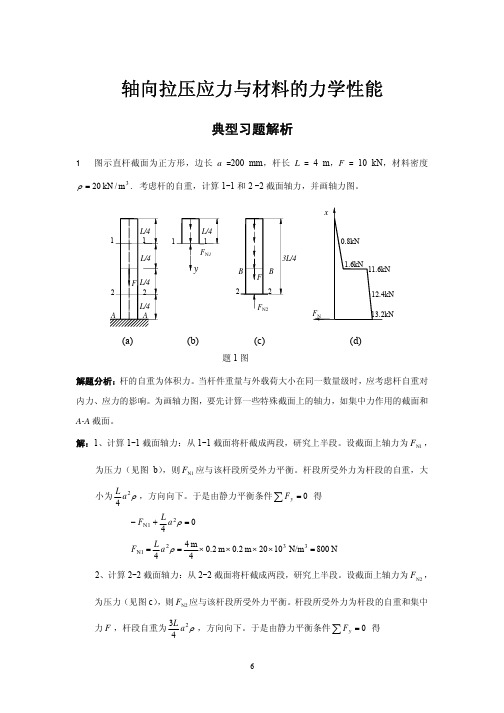
第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EC横截面上的应力。

解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。

由平衡条件可知：②以C节点为研究对象，其受力图如图所示。

由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。

荷载，材料的密度，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。

解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

1.2 轴类零件的分类根据承受载荷的不同分为：1）转轴:定义：既能承受弯矩又承受扭矩的轴2）心轴:定义：只承受弯矩而不承受扭矩的轴3）传送轴:定义：只承受扭矩而不承受弯矩的轴4）根据轴的外形，可以将直轴分为光轴和阶梯轴;5）根据轴内部状况，又可以将直轴分为实心轴和空。

1.3轴类零件的设计要求1.3。

1、轴的设计概要⑴轴的工作能力设计。

主要进行轴的强度设计、刚度设计,对于转速较高的轴还要进行振动稳定性的计算。

⑵轴的结构设计.根据轴的功能，轴必须保证轴上零件的安装固定和保证轴系在机器中的支撑要求，同时应具有良好的工艺性。

一般的设计步骤为：选择材料，初估轴径，结构设计，强度校核，必要时要进行刚度校核和稳定性计算。

1.3。

2、轴的材料轴是主要的支承件,常采用机械性能较好的材料。

常用材料包括：碳素钢：该类材料对应力集中的敏感性较小,价格较低，是轴类零件最常用的材料。

常用牌号有：30、35、40、45、50。

采用优质碳素钢时应进行热处理以改善其性能。

受力较小或不重要的轴，也可以选用Q235、Q255等普通碳钢。

45钢价格相对比较便宜,经过调质(或正火)后，可得到较好的切削性能，而且能获得较高的强度和韧性等综合机械性能，淬火后表面硬度可达45-52HRC，是轴类零件的常用材料。

合金钢具有更好的机械性能和热处理性能，可以适用于要求重载、高温、结构尺寸小、重量轻等使用场合的轴，但对应力集中较敏感，价格也较高。

设计中尤其要注意从结构上减小应力集中，并提高其表面质量。

40Cr等合金结构钢适用于中等精度而转速较高的轴类零件,这类钢经调质和淬火后，具有较好的综合机械性能。

轴承钢GCr15和弹簧钢65Mn,经调质和表面高频淬火后,表面硬度可达50—58HRC，并具有较高的耐疲劳性能和较好的耐磨性能，可制造较高精度的轴。

精密机床的主轴（例如磨床砂轮轴、坐标镗床主轴）可选用38CrMoAIA氮化钢。

这种钢经调质和表面氮化后,由于此钢氮化层硬度高，耐磨性好,而且能保持较软的芯部，因此耐冲击韧性好，还具备一定的耐热性和耐蚀性。

机械零件的承载能力计算一、零件的强度和刚度条件（一）拉（压）杆的强度计算在进行强度计算中，为确保轴向拉伸（压缩）杆件有足够的强度，把许用应力作为杆件实际工作应力的最高限度，即要求工作应力不超过材料的许用应力。

于是，强度条件为：≤（3-19）应用强度条件进行强度计算时会遇到以下三类问题。

一是校核强度。

已知构件横截面面积，材料的许用应力以及所受载荷，校核（3-31）式是否满足，从而检验构件是否安全。

二是设计截面。

已知载荷及许用应力?，根据强度条件设计截面尺寸。

三是确定许可载荷。

已知截面面积和许用应力，根据强度条件确定许可载荷。

例3-6? 某冷镦机的曲柄滑块机构如图3-49（a）所示。

连杆接近水平位置时，镦压力=3.78MN( l MN=106N)。

连杆横截面为矩形，高与宽之比（图3-49（b）所示），材料为45号钢，许用应力=90MPa，试设计截面尺寸和。

解? 由于镦压时连杆AB近于水平，连杆所受压力近似等于镦压力，轴力=3.78MN。

根据强度条件可得：A≥(mm2)以上运算中将力的单位换算为，应力的单位为MPa或N/mm2，故得到的面积单位就是（mm2）注意到连杆截面为矩形，且，故(mm2)=173.2(mm)，=1.4=242(mm)所求得的尺寸应圆整为整数，取=175mm，h=245mm。

1.某张紧器（图3-50）工作时可能出现的最大张力=30kN ( lkN=103N)，套筒和拉杆的材料均为钢，=160MPa，试校核其强度。

解? 此张紧器的套筒与拉杆均受拉伸，轴力=30kN。

由于截面面积有变化。

必须找出最小截面。

对拉杆，20螺纹内径=19.29mm，=292mm2，对套筒，内径=30mm，外径=40mm，故=550mm2 。

最大拉应力为：故强度足够。

例3-7? 某悬臂起重机如图3-51（a）所示。

撑杆为空心钢管，外径105mm，内径95mm。

钢索1和2互相平行，且钢索1可作为相当于直径=25mm的圆杆计算。

第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a ） 解：（1）求指定截面上的轴力 F N =-11F F F N -=+-=-222 （2）作轴力图轴力图如图所示。

（b ） 解：（1）求指定截面上的轴力 F N 211=-02222=+-=-F F N （2）作轴力图F F F F N =+-=-2233 轴力图如图所示。

（c ） 解：（1）求指定截面上的轴力 F N 211=-F F F N =+-=-222 （2）作轴力图F F F F N 32233=+-=- 轴力图如图所示。

（d ） 解：（1）求指定截面上的轴力 F N =-11F F a aFF F qa F N 22222-=+⋅--=+--=- （2）作轴力图中间段的轴力方程为： x aFF x N ⋅-=)( ]0,(a x ∈ 轴力图如图所示。

[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积2400mm A =，试求各横截面上的应力。

解：（1）求指定截面上的轴力kN N 2011-=-)(10201022kN N -=-=- )(1020102033kN N =-+=- （2）作轴力图轴力图如图所示。

（3）计算各截面上的应力 MPa mm N A N 504001020231111-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σ MPa mm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积21200mm A =，22300mm A =，23400mm A =，并求各横截面上的应力。

解：（1）求指定截面上的轴力kN N 2011-=-)(10201022kN N -=-=- )(1020102033kN N =-+=- （2）作轴力图轴力图如图所示。