直线与方程(2012年高三数学一轮复习精品次资料)
- 格式:doc
- 大小:717.00 KB
- 文档页数:21



2012届高考数学第一轮基础知识点复习:直线方程与直线系§7.1直线方程与直线系班级姓名学号例1:已知点A(2,3),B(-3,-2),若直线l过点P(1,1),且与线段AB相交,求直线l的斜率k的取值范围。
例2:一条直线经过P(3,2),并且分别满足下列条件,求直线方程。
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍(2)夹在两坐标间的线段被P分成1:2(3)与x轴,y轴正半轴交于A、B两点,且△AOB的面积最小例3:一直线被两直线L1:4x+y+6=0,L2:3x-5y-6=0截得线段中点恰好是坐标原点,求这条直线的方程。
例4:在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在直线方程为y=0,若点B的坐标为(1,2),求点A和点C 的坐标。
【备用题】求证:不论a取何值,直线(a+1)x-(2a+5)y-6=0必过一定点。
【基础训练】1、直线的倾斜角是:()A、arctan()B、arctan()C、π-arctanD、π-arctan2、若直线ax+by+c=0通过第一,二,三象限,则:A、ab>0,bc>0B、ab>0,bc0D、ab3、光线由点P(2,3)射到直线x+y=-1上,反射后过点Q(1,1),则反射光线方程为:()A、-x+y=0B、4x-5y+31=0C、4x-5y+1=0D、4x-5y+16=04、直线xcosθ+y+2=0的倾斜角的取值范围是:A、B、C、D、需视θ的取值而定5、直线过点(-2,-1),且在两坐标轴上的截距相等,则直线方程为。
6、直线L1,L2的方程分别为y=mx和y=n x(m,n≠0),L1的倾斜角是L2倾斜角的2倍,L1的斜率是L2的斜率的4倍,则mn=。
【拓展练习】1、下列命题中正确的是:()A、经过点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示B、经过定点A(0,b)的直线都可以用方程y=kx+b表示C、经过任意两个不同点P1(x1,y1),P2(x2,y2)的直线都可用方程(x2-x¬1)(y-y1)=(y2-y1)(x-x1)表示D、不经过原点的直线都可以用方程表示2、设点P(a,b),Q(c,d)是直线y=mx+k上两点,则|PQ|等于()A、B、C、D、3、直线x+y=2,x-y=2,x+ay=3围成一个三角形,则:A、a≠±1B、a≠1且a≠2C、a≠-1且a≠2D、a≠±1且a≠24、经过两直线11x+3y-7=0和12x+y-19=0的交点,且与A(3,-2),B(-1,6)等距离的直线的方程是。


2012年高三数学一轮复习精品资料:第八章平面解析几何【知识特点】1、本章内容主要包括直线与方程、圆与方程、圆锥曲线,是解析几何最基本,也是很重要的内容,是高中数学的重点内容,也是高考重点考查的内容之一;2、本章内容集中体现了用坐标法研究曲线的思想与方法,概念、公式多,内容多,具有较强的综合性;3、研究圆锥曲线的方法很类似,因此可利用类比的方法复习椭圆、双曲线、抛物线的定义与几何性质,掌握解决解析几何问题的最基本的方法。
【重点关注】1、关于直线的方程,直线的斜率、倾斜角,几种距离公式,两直线的位置关系,圆锥曲线的定义与性质等知识的试题,都属于基本题目,多以选择题、填空题形式出现,一般涉及两个以上的知识点,这些将是今后高考考查的热点;2、关于直线与圆的位置关系,圆与圆的位置关系的题目出现次数较多,既有选择题、填空题,也有解答题。
既考查基础知识的应用能力,又考查综合运用知识分析问题、解决问题的能力;3、直线与圆锥曲线联系在一起的综合题多以高档题出现,要求学生分析问题的能力,计算能力较高;4、注重数学思想方法的应用解析法、数形结合思想、函数与方程的思想、转化与化归的思想、分类讨论思想及待定系数法在各种题型中均有体现,应引起重视。
【地位和作用】解析几何是17世纪数学发展的重大成果之一,其本质是用代数方法研究图形的几何性质,体现了数形结合的重要数学思想。
在本模块中,学生将在平面直角坐标系中建立直线和圆的代数方程,运用代数方法研究它们的几何性质及其相互位置关系,并了解空间直角坐标系。
体会数形结合的思想,初步形成用代数方法解决几何问题的能力。
在平面解析几何初步的教学中,教师应帮助学生经历如下的过程:首先将几何问题代数化,用代数的语言描述几何要素及其关系,进而将几何问题转化为代数问题;处理代数问题;分析代数结果的几何含义,最终解决几何问题。
这种思想应贯穿平面解析几何教学的始终,帮助学生不断地体会“数形结合”的思想方法。

高三数学第一轮知识点:直线与方程第1篇:高三数学第一轮知识点:直线与方程导语:直线与方程就是直线的方程,在几何问题的研究中,我们常常直接依据几何图形中点,直线,平面间的关系研究几何图形的*质。
以下是小编整理高三数学第一轮知识点的资料,欢迎阅读参考。
(1)直线的倾斜角定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是0180(2)直线的斜率①定义:倾斜角不是90的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用k表示。
即。
斜率反映直线与轴的倾斜程度。
当时,。
当时,;当时,不存在。
②过两点的直线的斜率公式:注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90(2)k与p1、p2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
(3)直线方程①点斜式:直线斜率k,且过点注意:当直线的斜率为0时,k=0,直线的方程是y=y1。
当直线的斜率为90时,直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
②斜截式:,直线斜率为k,直线在y轴上的截距为b③两点式:()直线两点,④截矩式:其中直线与轴交于点,与轴交于点,即与轴、轴未完,继续阅读 >第2篇:高三数学一轮直线与方程的知识点一、直线与方程(1)直线的倾斜角定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是0180(2)直线的斜率①定义:倾斜角不是90的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用k表示。
即。
斜率反映直线与轴的倾斜程度。
当时,。
当时,;当时,不存在。
②过两点的直线的斜率公式:注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90(2)k与p1、p2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。

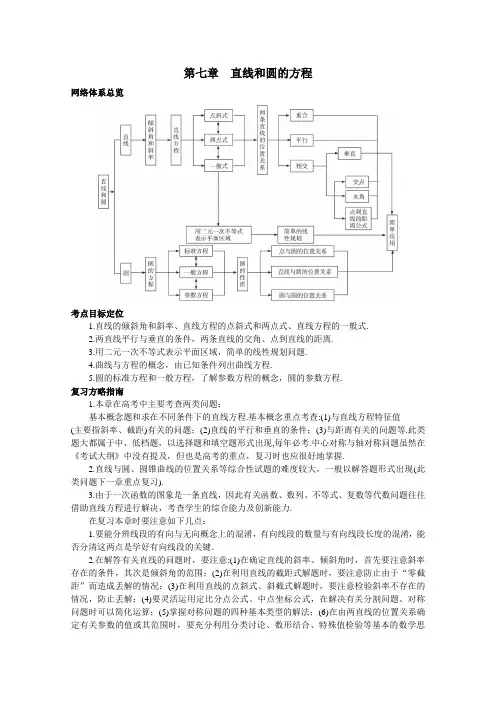
第七章直线和圆的方程网络体系总览考点目标定位1.直线的倾斜角和斜率、直线方程的点斜式和两点式、直线方程的一般式.2.两直线平行与垂直的条件,两条直线的交角、点到直线的距离.3.用二元一次不等式表示平面区域,简单的线性规划问题.4.曲线与方程的概念,由已知条件列出曲线方程.5.圆的标准方程和一般方程,了解参数方程的概念,圆的参数方程.复习方略指南1.本章在高考中主要考查两类问题:基本概念题和求在不同条件下的直线方程.基本概念重点考查:(1)与直线方程特征值(主要指斜率、截距)有关的问题;(2)直线的平行和垂直的条件;(3)与距离有关的问题等.此类题大都属于中、低档题,以选择题和填空题形式出现,每年必考.中心对称与轴对称问题虽然在《考试大纲》中没有提及,但也是高考的重点,复习时也应很好地掌握.2.直线与圆、圆锥曲线的位置关系等综合性试题的难度较大,一般以解答题形式出现(此类问题下一章重点复习).3.由于一次函数的图象是一条直线,因此有关函数、数列、不等式、复数等代数问题往往借助直线方程进行解决,考查学生的综合能力及创新能力.在复习本章时要注意如下几点:1.要能分辨线段的有向与无向概念上的混淆,有向线段的数量与有向线段长度的混淆,能否分清这两点是学好有向线段的关键.2.在解答有关直线的问题时,要注意:(1)在确定直线的斜率、倾斜角时,首先要注意斜率存在的条件,其次是倾斜角的范围;(2)在利用直线的截距式解题时,要注意防止由于“零截距”而造成丢解的情况;(3)在利用直线的点斜式、斜截式解题时,要注意检验斜率不存在的情况,防止丢解;(4)要灵活运用定比分点公式、中点坐标公式,在解决有关分割问题、对称问题时可以简化运算;(5)掌握对称问题的四种基本类型的解法;(6)在由两直线的位置关系确定有关参数的值或其范围时,要充分利用分类讨论、数形结合、特殊值检验等基本的数学思想方法.7.1 直线的方程巩固·夯实基础一、自主梳理1.直线的倾斜角和斜率(1)直线与x 轴相交时直线向上的方向与x 轴的正方向形成的角叫直线l 的倾斜角,记为α,直线与x 轴平行或重合时倾斜角为0°;倾斜角的范围为[0°,180°].(2)斜率:当倾斜角α≠90°时,tan α表示直线的斜率,常用k 表示即k=tan α.当α=90°时斜率不存在,当直线l 过P 1(x 1,y 1)、B(x 2,y 2)且x 1≠x 2时k=2121x x y y --. 2.直线的方向向量直线的方向向量的坐标为(m,n),当k 存在时坐标可记为(1,k).3.直线方程的三种形式(1)点斜式:y-y 1=k(x-x 1).特例:y=kx+b 表示在y 轴上截距为b 且斜率为k 的直线,该直线方程叫直线方程的斜截式.(2)两点式:121y y y y --=121x x x x --.特例:a x +by =1,其中a 、b 表示直线在x 、y 轴上的截距,该方程叫直线方程的截距式.(3)一般式:Ax+By+C=0.二、点击双基1.直线经过原点和点(-1,-1),则它的倾斜角是( )A.45°B.135°C.45°或135°D.0°解析:tan α=k=0101----=1,∴α=45°.选A. 答案:A2.已知m ≠0,则过点(1,-1)的直线ax+3my+2a=0的斜率为( ) A.31 B.-31C.3D.-3 解析:由题意知a+3m ·(-1)+2a=0,即m=a. ∴k=-m a 3=-31.故选B. 答案:B3.直线xcos α+3y+2=0的倾斜角范围是 …( )A.[6π,2π]∪(2π,65π) B.[0,6π]∪[65π,π] C.[0,65π] D.[6π,65π] 解析:设直线的倾斜角为θ,则tan θ=-31cos α.又-1≤cos α≤1,∴-33≤tan θ≤33.∴θ∈[0,]∪[65π,π). 答案:B4.过点P(2,-3),倾斜角比直线y=2x-1的倾斜角大45°的直线方程为__________________. 解析:设直线y=2x-1的倾斜角为θ,∴tan θ=2.∴k=tan(θ+45°)=︒-︒+45tan tan 145tan tan θθ=2112-+=-3. ∴所求直线方程为y+3=-3(x-2),即3x+y-3=0.答案:3x+y-3=05.下列四个命题:①经过定点P 0(x 0,y 0)的直线都可以用方程y-y 0=k(x-x 0)表示;②经过任意两个不同的点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(x 2-x 1)(x-x 1)=(y 2-y 1)(y-y 1)表示;③不经过原点的直线都可以用方程a x +by =1表示;④经过定点A(0,b)的直线都可以用方程y=kx+b 表示.其中真命题的序号为_________________________________________________________.解析:对命题①④,方程不能表示倾斜角是90°的直线;对命题③,当直线平行于一条坐标轴时,则直线在该坐标轴上截距不存在,故不能用截距式表示直线.只有②正确.答案:②诱思·实例点拨【例1】 已知△ABC 的三个顶点是A(3,-4)、B(0,3)、C(-6,0),求它的三条边所在的直线方程. 剖析:一条直线的方程可写成点斜式、斜截式、两点式、截距式和一般式等多种形式.使用时,应根据题目所给的条件恰当选择某种形式,使得解法简便.由顶点B 与C 的坐标可知点B 在y 轴上,点C 在x 轴上,于是BC 边所在的直线方程用截距式表示,AB 所在的直线方程用斜截式的形式表示,AC 所在的直线方程利用两点式或点斜式表示均可,最后为统一形式,均化为直线方程的一般式.解:如右图,因△ABC 的顶点B 与C 的坐标分别为(0,3)和(-6,0),故B 点在y 轴上,C 点在x 轴上,即直线BC 在x 轴上的截距为-6,在y 轴上的截距为3,利用截距式,直线BC 的方程为6-x +3y =1,化为一般式为x-2y+6=0.由于B 点的坐标为(0,3),故直线AB 在y 轴上的截距为3,利用斜截式,得直线AB 的方程为y=kx+3.又由顶点A(3,-4)在其上,所以-4=3k+3.故k=-37. 于是直线AB 的方程为y=-37x+3,化为一般式为7x+3y-9=0. 由A(3,-4)、C(-6,0),得直线AC 的斜率k AC =)6(304----=-94. 利用点斜式得直线AC 的方程为y-0=-94(x+6), 化为一般式为4x+9y+24=0.也可用两点式,得直线AC 的方程为40---y =)6(3)6(----x ,再化简即可. 讲评:本题考查了求直线方程的基本方法,正确选用直线方程的几种形式可使计算简化,过程简捷.【例2】 一条直线经过点P(3,2),并且分别满足下列条件,求直线方程:(1)倾斜角是直线x-4y+3=0的倾斜角的2倍;(2)与x 、y 轴的正半轴交于A 、B 两点,且△AOB 的面积最小(O 为坐标原点).剖析:(2)将面积看作截距a 、b 的函数,求函数的最小值即可.解:(1)设所求直线倾斜角为θ,已知直线的倾斜角为α,则θ=2α,且tan α=41,tan θ=tan2α=158,从而方程为8x-15y+6=0. (2)设直线方程为a x +b y =1,a >0,b >0,代入P(3,2),得a 3+b 2=1≥2ab 6,得ab ≥24,从而S △AOB =12ab ≥12,此时a 3=b2, ∴k=-a b =-32. ∴方程为2x+3y-12=0.讲评:此题(2)也可以转化成关于a 或b 的一元函数后再求其最小值.【例3】 过点A(3,-1)作直线l 交x 轴于B 点,交直线l 1:y=2x 于C 点,且BC =2,求直线l 的方程.剖析:∵直线l 过定点A(3,-1),可设直线l 的方程为点斜式,再用另外条件求斜率k 即可. 解法一:当k 不存在时,B(3,0)、C(3,6),|BC|=6,|AB|=1,不合题意.设直线l:y+1=k(x-3),显然k ≠0且k ≠2,∴B(3+k1,0). 由⎩⎨⎧-=+=),3(1,2x k y x y 得C(231-+k k ,262-+k k ).又=2,∴(231-+k k -3-k 1,262-+k k )=2(k1,1). ∴262-+k k =2,得k=-23. ∴l 的方程为3x+2y-7=0.解法二:设C(x 1,2x 1),∴直线l 的方程为y+1=31211-+x x (x-3).∴B(12711+x x ,0). 又BC =2AB ,∴AC =3AB ,即(x 1-3,2x 1+1)=3(12711+x x -3,1). ∴2x 1+1=3.∴x 1=1.故直线l 的方程为y+1=313-(x-3),即3x+2y-7=0. 讲评:(1)知点利用点斜式求直线时,要验证斜率k 不存在的情况.(2)向量在解析几何中常出现,常把向量用坐标来体现.如解法二. 链接·拓展已知两直线a 1x+b 1y+1=0和a 2x+b 2y+1=0的交点为P (2,3),求过两点Q 1(a 1,b 1)、Q 2(a 2,b 2)(a 1≠a 2)的直线方程.剖析:利用点斜式或直线与方程的概念进行解答.解:∵P(2,3)在已知直线上,∴⎩⎨⎧=++=++.0132,01322211b a b a ∴2(a 1-a 2)+3(b 1-b 2)=0, 即2121a a b b --=-32. ∴所求直线方程为y-b 1=-32(x-a 1). ∴2x+3y-(2a 1+3b 1)=0,即2x+3y+1=0.。

§ 直线方程与直线系班级 姓名 学号例1:已知点A (2,3),B (-3,-2),若直线过点)0,0(1<<=+b a b y a x a b -b a -a b b a 3]65,2()2,6[ππππ ),65[]6,0[πππ ]65,0[π和=nm, n ≠0,L 1的倾斜角是L 2倾斜角的2倍,L 1的斜率是L 2的斜率的4倍,则mn= 。
【拓展练习】1、下列命题中正确的是: ( )A 、经过点1=+by a x 上两点,则|PQ|等于 ( ) A 、21||m c a +- B 、21||m c a ++ C 、21||m d b +- D 、21||m d b ++3、直线=2, -=2, a=3围成一个三角形,则:A 、a ≠±1B 、a ≠1且a ≠2C 、a ≠-1且a ≠2D 、a ≠±1且a ≠24、经过两直线113-7=0和12-19=0的交点,且与A (3,-2),B (-1,6)等距离的直线的方程是 。
5、一直线过点A (-3,4),且在两轴上的截距之和为12,则此直线方程是 。
6、平面上有相异两点Aco θ,in 2θ和B (0,1),求经过A 、B 两点直线的斜率及倾斜角的范围。
7、已知直线L :=a2和A (1,4),B (3,1)两点,当直线L 与线段AB 相交时,求实数a 的取值范围。
8、已知P (2,1),过P 作一直线,使它夹在已知直线2-3=0,25-10=0间的线段被点P 平分,求直线方程。
9、求证:不论a, b为何实数,直线2ababa-b=0均通过一定点,并求此定点坐标。
10、已知点F(6,4)和直线L1:=4,求过P的直线L,使它和L1以及轴在第一象限内围成的三角形的面积最小。

高考数学一轮总复习第 53 讲 直线的方程同步测控理第 53 讲直线的方程1. (2011 ·龙岩质检 ) 已知 l 1: y =x ,若直线 l 2⊥ l 1,则直线 l 2 的倾斜角为 () π π A. 4 B . k π+ 4 ( k ∈ Z)3π 3π C. 4D . k π+ 4 ( k ∈Z)2.( 改编题 ) 已知过点 P ( - 4, m +1) 和 Q ( m - 1, 6) 的直线斜率等于1,那么 m 的值为()A . 1B . 4C .1或 3D .1或43. 过两点 ( - 1, 1) 和 (0 , 3) 的直线在 x 轴上的截距为 ()33A .-2 B. 2C .3D .-34. 将直线 y =3x 绕原点逆时针旋转 90°,再向右平移 1 个单位长度,获得的直线方程为______________.5.(2011 ·郑州模拟 ) 已知直线 l 1 的方向向量为 a = (1 ,3) ,直线 l 2 的方向向量为 b =( - 1, k ) .若直线 l 2 经过点 (0 ,5) 且 l 1⊥ l 2,则直线 l 2 的方程为 __________.6.(2012 ·贵阳模拟 ) 直线 l 经过点 A (1 ,2) ,在 x 轴上的截距的取值范围是 ( - 3,3) ,则其斜率的取值范围是 __________________ .7. 等腰△ ABC 的极点为 A ( - 1,2) ,又直线 AC 的斜率为 3,点 B 的坐标为 ( -3,2) ,求直线 AC 、 BC 及∠ A 的均分线所在的直线方程.118.(2011 ·常州模拟 ) 若 ab <0,则过点 P (0 ,- b ) 与 Q ( a , 0) 的直线 PQ 的倾斜角的取值范围是 ( )A . (0 , π )B . ( π,π )2 2π πC . ( -π,- 2 )D . ( - 2 , 0)9. 设点 M ( - 3,4) 和 N (3 ,2) ,直线 l 经过点 P (2 ,-1) ,若直线 l 与线段 MN 有交点,则直线 l 的斜率 k 的取值范围是 ____________________ .10.(2011 ·莆田月考 ) 已知两点A( - 1, 2) ,B( m, 3) .(1)求直线 AB的方程;3(2) 已知实数m∈[-3-1,3- 1] ,求直线AB的倾斜角α的取值范围.第 53讲1. C 2.A 3.A1 114. y =- 3x + 3 5. x + 3y -15= 0 6. k > 2或 k <- 1 7.分析:由点斜式得直线 AC 的方程为 y =3x + 2+ 3.由于∥ 轴,又△是以A 为极点的等腰三角形且直线的倾斜角为π,AB xABCAC 3π 2π因此直线 BC 的倾斜角 α 为 6 或 3 .①当 α= π时,直线 BC 的方程为 y =3x +2+ 3.6 3又∠ A 的角均分线的倾斜角为2π ,3因此∠ A 的角均分线所在直线的方程为y =- 3 +2- 3.x2π②当 α=3 时,直线 BC 的方程为 y =- 3x + 2-3 3.又∠ A 的角均分线的倾斜角为π ,63 3因此∠ A 的角均分线所在直线的方程为y = 3 x + 2+ 3 .1- b - 0 a8. B 分析: k PQ =1 = b <0,0- a又倾斜角的取值范围为 [0 ,π ) ,π故直线 PQ 的倾斜角的取值范围为 ( 2 ,π ) .9. ( -∞,- 1] ∪[3 ,+∞)分析:由于 M ( - 3, 4) ,N (3 , 2) ,P (2 ,- 1) ,4+ 1 2+1 因此 k =- 3- 2=- 1, k =3-2=3.PM PN画出表示图,如上图,则可知k ≤- 1 或 k ≥ 3. 10.分析: (1) 当 m =- 1 时,直线 AB 的方程为 x =- 1;1当 m ≠- 1 时,直线 AB 的方程为 y -2= m + 1( x + 1) .π(2) ①当 m =- 1 时, α= 2 ;②当 ≠- 1 时, +1∈[ -3 ,0) ∪(0, 3] , mm313因此 k = m + 1∈( -∞,-3] ∪[3 ,+∞ ) ,π ππ2π因此 α∈[6 , 2)∪(2 ,3 ] .π2π综合①②知,直线AB的倾斜角α∈[6,3].。
2012年高三数学一轮复习精品资料:第八章平面解析几何【知识特点】1、本章内容主要包括直线与方程、圆与方程、圆锥曲线,是解析几何最基本,也是很重要的内容,是高中数学的重点内容,也是高考重点考查的内容之一;2、本章内容集中体现了用坐标法研究曲线的思想与方法,概念、公式多,内容多,具有较强的综合性;3、研究圆锥曲线的方法很类似,因此可利用类比的方法复习椭圆、双曲线、抛物线的定义与几何性质,掌握解决解析几何问题的最基本的方法。
【重点关注】1、关于直线的方程,直线的斜率、倾斜角,几种距离公式,两直线的位置关系,圆锥曲线的定义与性质等知识的试题,都属于基本题目,多以选择题、填空题形式出现,一般涉及两个以上的知识点,这些将是今后高考考查的热点;2、关于直线与圆的位置关系,圆与圆的位置关系的题目出现次数较多,既有选择题、填空题,也有解答题。
既考查基础知识的应用能力,又考查综合运用知识分析问题、解决问题的能力;3、直线与圆锥曲线联系在一起的综合题多以高档题出现,要求学生分析问题的能力,计算能力较高;4、注重数学思想方法的应用解析法、数形结合思想、函数与方程的思想、转化与化归的思想、分类讨论思想及待定系数法在各种题型中均有体现,应引起重视。
【地位和作用】解析几何是17世纪数学发展的重大成果之一,其本质是用代数方法研究图形的几何性质,体现了数形结合的重要数学思想。
在本模块中,学生将在平面直角坐标系中建立直线和圆的代数方程,运用代数方法研究它们的几何性质及其相互位置关系,并了解空间直角坐标系。
体会数形结合的思想,初步形成用代数方法解决几何问题的能力。
在平面解析几何初步的教学中,教师应帮助学生经历如下的过程:首先将几何问题代数化,用代数的语言描述几何要素及其关系,进而将几何问题转化为代数问题;处理代数问题;分析代数结果的几何含义,最终解决几何问题。
这种思想应贯穿平面解析几何教学的始终,帮助学生不断地体会“数形结合”的思想方法。
从新课改近两年来的高考信息统计可以看出,命题呈现出以下特点:1、各种题型均有所体现,分值大约在19-24分之间,比重较高,以低档题、中档题为主;2、主要考查直线及圆的方程,圆锥曲线的定义、性质及综合应用,符合考纲要求,这些知识属于本章的重点内容,是高考的必考内容,有时还注重在知识交汇点处命题;3、预计本章在今后的高考中仍将以直线及圆的方程,圆锥曲线的定义、性质及直线与圆锥曲线的位置关系为主命题,且难度有所降低;更加注重与其他知识交汇,充分体现以能力立意的命题方向。
第一节直线与方程【高考目标定位】一、直线的倾斜角与斜率(一)考纲点击1、理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式;2、能根据两条直线的斜率判定这两条直线平行或垂直。
(二)热点提示1、直线的倾斜角和斜率、两直线的位置关系是高考热点;2、主要以选择、填空题的形式出现,属于中低档题目。
二、直线的方程(一)考纲点击1、掌握确定直线位置的几何要素;2、掌握直线方程的几种形式(点斜式、两点及一般式),了解斜截式与一次函数的关系。
(二)热点提示1、直线的方程是必考内容,是基础知识之一;2、在高考中多与其他曲线结合考查,三种题型可出现,属于中低档题。
三、直线的交点坐标与距离公式(一)考纲点击1、能用解方程组的方法求两条相交直线的交点坐标;2、掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
(二)热点提示1、本节重点体现一种思想——转化与化归的思想,这种思想是高考的热点之一;2、本部分在高考中主要以选择、填空为主,属于中低档题目。
【考纲知识梳理】一、直线的倾斜角与斜率 1、直线的倾斜角与斜率 (1)直线的倾斜角①关于倾斜角的概念要抓住三点: ⅰ.与x 轴相交; ⅱ.x 轴正向; ⅲ.直线向上方向.②直线与x 轴平行或重合时,规定它的倾斜角为00. ③倾斜角α的范围000180α≤<. (2)直线的斜率①直线的斜率就是直线倾斜角的正切值,而倾斜角为090的直线斜率不存在。
②经过两点的直线的斜率公式是③每条直线都有倾斜角,但并不是每条直线都有斜率。
2、两条直线平行与垂直的判定 (1)两条直线平行对于两条不重合的直线12,l l ,其斜率分别为12,k k ,则有1212//l l k k ⇔=。
特别地,当直线12,l l 的斜率都不存在时,12l l 与的关系为平行。
(2)两条直线垂直如果两条直线12,l l 斜率存在,设为12,k k ,则12121l l k k ⊥⇔=-注:两条直线12,l l 垂直的充要条件是斜率之积为-1,这句话不正确;由两直线的斜率之积为-1,可以得出两直线垂直,反过来,两直线垂直,斜率之积不一定为-1。
如果12,l l 中有一条直线的斜率不存在,另一条直线的斜率为0时,12l l 与互相垂直。
二、直线的方程 1、直线方程的几种形式为直线上一定点,k 为斜率是直线上两定点注:过两点的直线是否一定可用两点式方程表示?(不一定。
(1)若,直线垂直于x 轴,方程为;(2)若,直线垂直于y 轴,方程为;(3)若,直线方程可用两点式表示)2、线段的中点坐标公式 若点的坐标分别为,且线段的中点M 的坐标为(x,y ),则此公式为线段的中点坐标公式。
三、直线的交点坐标与距离公式 1.两条直线的交点 设两条直线的方程是,两条直线的交点坐标就是方程组的解,若方程组有唯一解,则这两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立。
2.几种距离 (1)两点间的距离 平面上的两点间的距离公式特别地,原点O (0,0)与任一点P (x,y )的距离(2)点到直线的距离点到直线的距离;(3)两条平行线间的距离两条平行线间的距离注:(1)求点到直线的距离时,直线方程要化为一般式;(2)求两条平行线间的距离时,必须将两直线方程化为系数相同的一般形式后,才能套用公式计算。
【热点难点精析】一、直线的倾斜角与斜率 (一)直线的倾斜角 ※相关链接※2.已知斜率k 的范围,求倾斜角α的范围时,若k 为正数,则α的范围为(0,)2π的子集,且k=tan α为增函数;若k 为负数,则α的范围为(,)2ππ的子集,且k=tan α为增函数。
若k 的范围有正有负,则可所范围按大于等于0或小于0分为两部分,针对每一部分再根据斜率的增减性求倾斜角范围。
※例题解析※〖例〗已知直线的斜率k=-cosα (α∈R ).求直线的倾斜角β的取值范围。
思路解析:cos α的范围→斜率k 的范围→tan β的范围→倾斜角β的取值范围。
解答:1cos 1,1cos 1.11,1tan 1,30,443[0,],.44k ααβππββπππβπ-≤≤∴-≤-≤-≤≤∴-≤≤∴≤≤≤≤⎡⎫∴⎪⎢⎣⎭即或倾斜角的范围为(二)直线的斜率及应用 ※相关链接※ 1、斜率公式:2121y y k x x -=-与两点顺序无关,即两点的横纵坐标在公式中前后次序相同;2、求斜率的一般方法:(1)已知直线上两点,根据斜率公式 212121()y y k x x x x -=≠-求斜率;(2)已知直线的倾斜角α或α的某种三角函数根据tan k α=来求斜率; 3、利用斜率证明三点共线的方法:已知112233(,),(,),(,),A x y B x y C x y 若123AB AC x x x k k ===或,则有A 、B 、C 三点共线。
注:斜率变化分成两段,090是分界线,遇到斜率要谨记,存在与否需讨论。
※例题解析※〖例〗设,,a b c 是互不相等的三个实数,如果333(,)(,)(,)A a a B b b C c c 、、在同一直线上,求证:0a b c ++=思路解析:若三点共线,则由任两点所确定的直线斜率相等或都不存在。
解答:(三)两条直线的平行与垂直〖例〗已知点M (2,2),N (5,-2),点P 在x 轴上,分别求满足下列条件的P 点坐标。
(1)∠MOP=∠OPN (O 是坐标原点); (2)∠MPN 是直角。
思路解析:∠MOP=∠OPN ⇒OM//PN ,∠MPN 是直角⇒MP ⊥NP ,故而可利用两直线平行和垂直的条件求得。
解答:0(,0),(1),//.200(2)21,(5),205521,7,(7,0).5(2)90,, 1.2222(2),(5),1,252516,(1,0)(6,0).OM NP OM NP MP NP MP NP P x MOP OPN OM NP k k k k x x x x P x MPN MP NP k k k x k x x x x x x x P ∠=∠∴∴=---====≠---∴=∴=-∠=∴⊥∴=-=≠=≠∴⨯=-----== 设又即又解得或即或注:(1)充分掌握两直线平行的条件及垂直的条件是解决本题的关键,对于斜率都存在且不重合的两条直线1l 和2l ,。
若有一条直线的斜率不存在,那么另一条直线的斜率是多少一定要特别注意。
(2)注意转化与化归思想的应用。
(3)利用斜率的几何意义可以证明不等式,利用两斜率之间的关系可以判断两直线的平行或垂直,数形结合的思想方法可帮助我们很直观地分析问题,抓住问题的实质。
二、直线的方程 (一)直线方程的求法 ※相关链接※1、求直线方程应先选择适当的直线方程形式并注意各种形式的适用条件。
基本方法包括利用条件直接求直线的基本量和利用待定系数法求直线的基本量。
用待定系数法求直线方程的步骤: (1)设所求直线方程的某种形式; (2)由条件建立所求参数的方程(组); (3)解这个方程(组)求参数; (4)把所求的参数值代入所设直线方程。
2、求直线方程时,首先分析具备什么样的条件;然后恰当地选用直线方程的形式准确写出直线方程。
要注意若不能断定直线具有斜率时,应对斜率存在与不存在加以讨论。
在用截距式时,应先判断截距是否为0。
若不确定,则需分类讨论。
※例题解析※〖例〗求过点P (2,-1),在x 轴和y 轴上的截距分别为a 、b,且满足a=3b 的直线方程。
思路解析:对截距是否为0分类讨论→设出直线方程→代入已知条件求解→得直线方程。
解答:当a=3,b ≠0时,设所求直线方程为1x y a b +=,即 1.(2,1),3x yP b b+=-又直线过点 2111,.310.3330(0).1(2,1),12,.21.21310.2b x y b b a b y kx k P k k y x x y y x -+==-++====≠--==-=-++==-解得所求直线方程为当时,则所求直线过原点,可设方程为又直线过点则所求直线方程为综上所述,所求直线方程为或(二)用一般式方程判定直线的位置关系 ※相关链接※两条直线位置关系的判定已知直线1111:0l A x B y C ++=,2222:0l A x B y C ++=,则(1)12122112211221111222222//00(0)(0).l l A B A B AC A C B C B C A B CA B C A B C ⇔-=-≠-≠=≠且或或记为:、、不为(2)121212//0.l l A A B B ⇔+= (3)(4)※例题解析※〖例〗已知直线1:260l ax y ++=和直线22:(1)10l x a y a +-+-=,(1)试判断1l 与2l 是否平行;(2)1l ⊥2l 时,求a 的值。